Vensim函数及其应用

vensim延迟函数摘要：1.了解vensim延迟函数的基本概念2.vensim延迟函数的使用方法及注意事项3.实际应用场景分享正文：venSim是一款强大的系统动力学仿真软件，通过构建动态模型来描述和预测现实世界中的复杂现象。

在venSim中，延迟函数是一种重要的功能模块，它可以实现模型中某些变量在特定时间点的输出。

本文将简要介绍venSim延迟函数的基本概念、使用方法及注意事项，并通过实际应用场景进行说明。

一、了解vensim延迟函数的基本概念在venSim中，延迟函数是一种特殊的函数，它允许用户在特定的时间点计算和输出模型变量的值。

延迟函数的输入参数为一个或多个变量，输出结果为这些变量的特定时间点的值。

通过使用延迟函数，用户可以更好地控制模型中变量的动态行为，从而实现对模型的精细化管理。

二、vensim延迟函数的使用方法及注意事项1.使用方法：在venSim中，延迟函数的语法格式如下：```LAG(变量名，时间步长)```其中，变量名表示要进行延迟的变量，时间步长表示延迟的时间间隔。

例如，若变量名为“X”，则延迟函数可以表示为：```LAG(X，10)```这表示输出变量X在当前时间点之前的10个时间步长的值。

2.注意事项：- 延迟函数的时间步长必须为正数，且小于等于模型的时间步长。

- 延迟函数可以应用于任何类型的变量，包括连续变量和离散变量。

- 延迟函数的输出结果为单位时间内变量的平均值，而非精确值。

若需要精确值，请使用其他函数进行计算。

三、实际应用场景分享1.场景一：某供应链管理系统模型中，需要计算每个时间点库存量的平均值。

可以使用延迟函数实现如下：```LAG(库存量，1)```这表示输出每个时间点的库存量在当前时间点之前的平均值。

2.场景二：某经济growth 模型中，需要计算过去5个时间点的经济增长率。

可以使用延迟函数实现如下：```LAG(经济增长率，5)```这表示输出每个时间点的经济增长率在当前时间点之前的5个时间点的平均值。

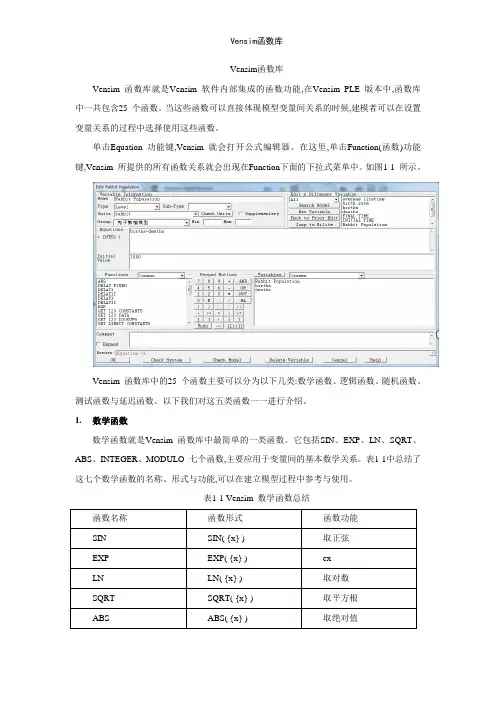
Vensim函数库Vensim 函数库就是Vensim 软件内部集成的函数功能,在Vensim_PLE 版本中,函数库中一共包含25 个函数。

当这些函数可以直接体现模型变量间关系的时候,建模者可以在设置变量关系的过程中选择使用这些函数。

单击Equation 功能键,Vensim 就会打开公式编辑器。

在这里,单击Function(函数)功能键,Vensim 所提供的所有函数关系就会出现在Function下面的下拉式菜单中。

如图1-1 所示。

Vensim 函数库中的25 个函数主要可以分为以下几类:数学函数、逻辑函数、随机函数、测试函数与延迟函数。

以下我们对这五类函数一一进行介绍。

1.数学函数数学函数就是Vensim 函数库中最简单的一类函数。

它包括SIN、EXP、LN、SQRT、ABS、INTEGER、MODULO 七个函数,主要应用于变量间的基本数学关系。

表1-1中总结了这七个数学函数的名称、形式与功能,可以在建立模型过程中参考与使用。

表1-1 Vensim 数学函数总结函数名称函数形式函数功能SIN SIN( {x} ) 取正弦EXP EXP( {x} ) exLN LN( {x} ) 取对数SQRT SQRT( {x} ) 取平方根ABS ABS( {x} ) 取绝对值2.逻辑函数Vensim 函数库中另一类重要的函数就是逻辑函数。

在建立模型过程中,有时候变量间的关系需要经过一些比数学计算更复杂的处理,比如判断若干变量中的最大或者最小的值,然后将结果赋予另一个变量。

Vensim_PLE 版本中的逻辑函数包括最大、最小值判断函数与条件函数。

这三个函数在很多模型中的变量关系判断中使用频率都很高。

下面就对这三个函数进行一一介绍。

1)MAX基本形式:MAX ({x1},{x2})函数功能:MAX 后面括号中的x1, x2, ……就是函数的变量。

在运行过程中,MAX 函数对这些变量进行比较,返回其中最大值作为函数值。

vensim中integer函数的运用vensim是一种系统动力学建模工具，被广泛应用于各种领域的系统建模和分析。

在vensim中，integer函数是一种常用的函数，用于将数值转换为整数。

本文将以integer函数的运用为主题，介绍integer函数的使用方法和实例，以及它在系统建模中的重要性和应用价值。

第一部分：integer函数的基本概念和语法integer函数是vensim中的一个函数，用于将数值转换为整数。

它的基本语法如下所示：integer(x)其中，x代表要转换为整数的数值。

integer函数的作用是将小数或者其他形式的数值转换为整数。

在系统动力学建模过程中，常常需要对数值进行取整操作，以便更好地模拟和分析系统的行为。

integer函数提供了一种方便快捷的方法来实现这一目的。

第二部分：integer函数的使用方法和示例integer函数的使用方法非常简单，在vensim的模型中只需在需要取整的地方使用integer函数即可。

下面以几个示例来说明integer函数的具体用法。

例1：假设我们有一个变量x，它的值为3.8。

我们希望将x取整到最接近的整数值。

可以使用以下方法来实现：integer(x)这样就能够将x的值取整到4。

例2：假设我们有一个变量y，它的值为7.2。

我们希望将y取整到最接近的整数值。

可以使用以下方法来实现：integer(y)这样就能够将y的值取整到7。

例3：假设我们有一个变量z，它的值为-2.6。

我们希望将z取整到最接近的整数值。

可以使用以下方法来实现：integer(z)这样就能够将z的值取整到-3。

通过这些示例，我们可以看到integer函数的使用方法非常简单，只需要在需要取整的地方调用这个函数即可。

第三部分：integer函数在系统建模中的重要性和应用价值integer函数在系统建模中有着重要的应用价值。

在实际的系统建模中，往往需要对不同的变量进行取整操作，以更好地模拟和分析系统的行为。

vensim表函数withlookupVensim是一款流行的系统动力学建模软件，它提供了许多强大的功能，其中之一就是表函数withlookup。

这个函数可以帮助用户在模型中使用查找表，从而更加准确地模拟实际情况。

在系统动力学建模中，我们通常需要使用一些函数来描述变量之间的关系。

例如，我们可能需要使用线性函数、指数函数或对数函数来描述某些变量的变化。

然而，在某些情况下，这些函数可能无法准确地描述变量之间的关系。

例如，当我们需要描述一个变量在不同条件下的变化时，使用传统的函数可能会变得非常困难。

这时，我们可以使用查找表来描述变量之间的关系。

查找表是一种将输入值映射到输出值的表格，它可以帮助我们更加准确地描述变量之间的关系。

在Vensim中，我们可以使用表函数withlookup来实现这一功能。

使用withlookup函数，我们可以将输入值映射到输出值。

例如，我们可以使用withlookup函数来描述某个变量在不同温度下的变化。

我们可以将温度作为输入值，将变量的值作为输出值，然后在表格中输入不同的温度和对应的变量值。

当我们需要模拟这个变量在不同温度下的变化时，只需要使用withlookup函数即可。

除了可以使用withlookup函数来描述变量之间的关系外，我们还可以使用它来进行插值。

插值是一种将输入值映射到输出值的方法，它可以帮助我们更加准确地描述变量之间的关系。

在Vensim中，我们可以使用withlookup函数来进行线性插值或样条插值。

Vensim的表函数withlookup是一种非常强大的工具，它可以帮助我们更加准确地描述变量之间的关系。

无论是在描述变量在不同条件下的变化，还是在进行插值时，withlookup函数都可以帮助我们实现这一目标。

因此，如果你正在使用Vensim进行系统动力学建模，不妨尝试一下withlookup函数，相信它会给你带来意想不到的效果。

vensim延迟函数-回复【vensim延迟函数】是系统动力学建模软件Vensim中的一个重要函数，它用于模拟系统中事件之间的时间延迟。

在系统动力学建模中，时间延迟是指一个事件发生后，影响到系统其他部分的时间间隔。

一. 简介系统动力学建模是一种分析和解决复杂问题的方法，主要用于研究系统中各个元素之间的相互作用和变化规律。

而Vensim作为一种系统动力学建模软件，提供了丰富的函数和工具来支持模型的构建和仿真。

二. vensim延迟函数的定义和语法vensim延迟函数的目的是模拟系统中的时间延迟，并将延迟引入系统模型中。

它的基本语法如下：Delay(Input, Time Delay)其中，"Input"表示输入的变量或表达式，"Time Delay"表示时间延迟的长度。

三. vensim延迟函数的应用场景延迟函数在系统动力学建模中的应用非常广泛，特别是在涉及到时间上的变化和相互关系的模型中。

下面以一个简单的需求和供应模型为例来说明vensim延迟函数的具体应用：假设有一个市场需求模型和供应模型，其中市场需求与市场供应之间存在时间延迟。

我们希望利用vensim延迟函数来模拟这个延迟效应，进而分析市场的均衡状态和价格变化。

四. 构建供应模型和需求模型首先，我们需要构建一个动态的市场需求模型和供应模型。

市场需求模型可以表示为：Market_Demand = D_0 + a * Price - b * Delay(Supply_Quantity, Delay_Time)其中，D_0为常数，表示无价格时市场的需求量；a和b为常数，表示价格对需求量的影响；"Price"表示商品的价格；"Supply_Quantity"表示供应量；"Delay_Time"表示供应与需求之间的时间延迟。

类似地，我们可以构建市场供应模型：Market_Supply = S_0 + c * Delay(Demand_Quantity, Delay_Time) - d * Price其中，S_0为常数，表示无价格时市场的供应量；c和d为常数，表示需求量对供应量的影响；"Demand_Quantity"表示需求量。

vensim中表函数的运用-回复【vensim中表函数的运用】【引言】vensim是一种系统动力学建模和模拟软件，广泛应用于各个领域的研究和决策支持中。

表函数是vensim中的一项核心功能，它允许用户根据自己的需要定义并使用表格来替代复杂的计算公式，使模型的构建更加灵活和可控。

本文将深入探讨vensim中表函数的运用，从表的定义、数据输入、函数运算、输出结果以及常见问题等方面进行一步一步的回答。

【正文】一、表的定义在vensim中，表函数的定义是通过创建一个表格对象来实现的。

用户可以在模型视图中打开表格编辑器，通过输入数据来定义一个新的表。

表格编辑器可以根据用户的需要调整大小，并能够添加任意数量的行和列。

通过在每个单元格中输入数据，用户可以定义表中的具体数值。

二、数据输入数据的输入是表函数的关键步骤。

用户可以通过两种方式输入数据，即手动输入和导入外部文件。

手动输入是最常见的方式，用户可以直接在表格编辑器中逐个单元格地输入数据。

对于大规模的数据，可以选择导入外部文件，如Excel文件，来一次性地加载数据。

无论是手动输入还是导入外部文件，用户都可以根据自己的需求调整数据的格式和范围。

三、函数运算表函数的运算是通过在模型中使用所定义的表格对象来实现的。

在建模的过程中，用户可以在方程中使用表格作为模型输入的参数，以及作为模型输出的结果。

用户可以根据需要对表格中的数据进行求和、平均、插值等各种运算操作。

vensim提供了一系列的表函数，如LOOKUP、INTEG、TABDOT，用户可以根据具体的情况选择合适的函数来实现功能。

四、输出结果表函数的输出结果可以通过模型运行来获得。

用户可以将定义好的表格对象与其他模块进行连接，以实现模型中不同变量之间的相互作用。

通过运行模型，vensim会自动根据表格中的数据进行计算，并将计算结果反馈给用户。

用户可以通过查看模型运行结果和输出图表来了解表函数的运行情况。

五、常见问题在使用表函数过程中，用户可能会遇到一些常见的问题。

vensim中integer函数的运用-回复vensim中的integer函数是用于将实数转换为整数的函数。

在模拟建模中，我们经常遇到需要使用整数的情况，例如人口数量、数量统计等。

integer函数可以将实数四舍五入为最接近的整数，并将结果返回。

在vensim中，integer函数的语法为：INTEGER(x)其中，x为需要转换为整数的实数。

integer函数会将x四舍五入为最接近的整数，并返回整数结果。

下面，我们将详细介绍integer函数的使用方法和实际应用场景。

首先，我们来看一个使用integer函数的简单示例。

假设我们需要模拟一个城市的人口增长情况，初始人口为1000人，每年增长率为2.5。

在vensim中，我们可以使用integer函数来计算每年的人口数量：1. 创建一个变量Population来表示人口数量，使用initial函数设置初始人口为1000。

2. 创建一个变量GrowthRate来表示人口增长率，使用constant函数设置增长率为0.025（即2.5）。

3. 创建一个变量Year来表示模拟的年份，使用time函数生成从初始年份开始的连续年份序列。

4. 创建一个变量YearlyGrowth来表示每年新增的人口数量，使用Population * GrowthRate计算。

5. 创建一个变量TotalPopulation来表示累计人口数量，使用integral函数计算每年新增人口数量的累计值。

6. 创建一个变量IntegerPopulation来表示每年的整数人口数量，使用integer函数将Population的值四舍五入为整数。

通过以上步骤，我们实现了对人口数量的模拟和计算。

在实际应用中，integer函数常常用于人口数量统计、物品数量计算等场景中。

例如，假设我们需要模拟一个超市的销售情况，每天的销售数量可能是实数（例如1.5、2.8等），但是我们需要将其转换为整数进行统计和分析。

第8章 Vensim PLE 软件包中系统动力学函数系统动力学所以能处理复杂的系统问题，除提出流位流率系简化流率基本入树建模法去描述系统外，还有一个重要原因是其专用软件都设计了一系列通用的系统动力学函数。

第一节数学、逻辑、测试函数§ 8.1.1 数学函数Vensim PLE备有五种普通数学函数供用户使用.1．SIN（X）定义1：SIN（X）为三角正弦函数,X须以弧度表示，其值小于8。

35×105当自变量是角度时，应通过乘以2π/360 转化为弧度。

2．EXP（X）定义2：EXP（X) = e X ，e是自然对数的底，e=2.7182…，X的值必须小于36。

人们常用指数函数去描述系统，有了上面函数将会带来很大方便。

3。

LN（X），变量X大于零.即以e为底的对数函数，它与EXP(X）互为反函数，这样可以用EXP（X）和LN（X）来计算非以e为底的幂函数和对数函数。

4. SQRT（X）=√X—,X必须是非负量。

5。

ABS（X) = │X│,对X取绝对值。

§ 8.1。

2 逻辑函数逻辑函数的作用类似于其它计算机语言中的条件语句,Vensim PLE的逻辑函数有三种。

1.最大函数MAX（P，Q)MAX表示从两个量中选取较大者,P和Q是被比较的两个量,结果也是在这两个量中选取。

P 若P≥Q定义1：若MAX（P,Q)=Q 若P≤Q其中P,Q是变量或常量，则MAX（P，Q）为最大函数。

可用MAX函数从多个量中选取较大者.如从P，Q，D三个量中选择较大者可用:MAX（D，MAX(P,Q）)。

最小函数 Q 若P≥Q定义2:若MIN(P，Q）=P若P≤Q 则MIN（P,Q）为最小函数。

MIN同MAX一样，可以从MIN（P，Q)基本功能中派生出各种用法。

3。

选择函数IF THEN ELSE(C，T，F）定义3：若IF THEN ELSE(C,T,F）T C条件为真时= （C为逻辑表达式）F 否则则IF THEN ELSE（C，T,F）为选择函数。

vensim中time函数用法
在Vensim中，time函数用于获取系统模拟的当前时间。

time()函数没有参数，返回一个浮点数，表示从模拟开始到当前时间经过的模型时间步长。

下面是使用time函数的一个示例：
1. 创建一个模型变量`Time`，类型为`Auxiliary`，并设置其初始值为`time()`。

2. 在模型的其他部分中可以使用`Time`变量来表示当前的模拟时间。

例如，可以通过以下方式在模型中使用`Time`变量：
```
Stock: Population = INTEG ( Births - Deaths )
Births = Birth_Rate * Population
Deaths = Death_Rate * Population
Birth_Rate = IF THEN ELSE ( Time < 10 , 0.02 , 0.01 )
Death_Rate = IF THEN ELSE ( Time < 20 , 0.01 , 0.02 )
```
在这个例子中，`Time`变量被用作控制`Birth_Rate`和
`Death_Rate`变量的函数。

根据当前的模拟时间，当时间小于10时，`Birth_Rate`为0.02，当时间大于等于10时，为0.01；当时间小于20时，`Death_Rate`为0.01，当时间大于等于20
时，为0.02。

这样可以在模拟过程中根据时间变量的变化来改变模型的行为。

V ensim中的主要函数A FUNCTION OF(#,A,B,C,,,) 。

Shows "generic" relationships -automatically generated by Sketch tool.ABS(A)求a的绝对值。

Returns the absolute value of A.ACTIVE INITIAL(A,N)。

Defines an Auxiliary with distinct active and initial values.DELAY1(I,T)一阶物质延迟（现实中几乎没有这种情况高版本中已没有此函数）。

First order exponential delay of I for time T conserving I.DELAY1I(I,T,N)一阶信息延迟。

Same as DELAY1 but starting at N.DELAY3(I,T)三阶物质延迟。

A third order exponential delay of I for time T conserving I. DELAY3I(I,T,N)三阶信息延迟。

Same as DELAY3 but starting at N.EXP(X)e的指数函数。

Returns e(2.718...) to the X power.IF THEN ELSE(cond,X,Y)选择判断。

Returns X if condition is non-zero(cond >=0), otherwise Y.INITIAL(A)返回A的初始值。

Returns the value of A at initialization time and holds it constant.INTEG(R,N) 。

Performs numerical integration of R starting at N (defi nes a Level).LN(X)x的自然对数。