北理工数值分析大作业
- 格式:doc
- 大小:660.00 KB
- 文档页数:26

数值分析大作业一一、算法设计方案1、求λ1和λ501的值:思路:采用幂法求出按模最大特征值λmax,该值必为λ1或λ501,若λmax小于0,则λmax=λ1;否则λmax=λ501。
再经过原点平移,使用幂法迭代出矩阵A-λmax I的特征值,此时求出的按模最大特征值即为λ1和λ501的另一个值。
2、求λs的值:采用反幂法求出按模最小的特征值λmin即为λs,其中的方程组采用LU分解法进行求解。
3、求与μk最接近的特征值:对矩阵A采用带原点平移的反幂法求解最小特征值,其中平移量为:μk。
4、A的条件数cond(A)=| λmax/λmin|;5、A的行列式的值:先将A进行LU分解,再求U矩阵对角元素的乘积即为A 行列式的值。
二、源程序#include<iostream>#include<iomanip>#include<math.h>#define N 501#define E 1.0e-12 //定义精度常量#define r 2#define s 2using namespace std;double a[N];double cc[5][N];void init();double mifa();double fmifa();int max(int aa,int bb);int min(int aa,int bb);int max_3(int aa,int bb,int cc);void LU();void main(){double a1,a2,d1,d501=0,ds,det=1,miu[39],lamta,cond;int i,k;init();/*************求λ1和λ501********************/a1=mifa();if(a1<0)d1=a1; //若小于0则表示λ1的值elsed501=a1; //若大于0则表示λ501的值for(i=0;i<N;i++)a[i]=a[i]-a1;a2=mifa()+a1;if(a2<0)d1=a2; //若小于0则表示λ1的值elsed501=a2; //若大于0则表示λ501的值cout<<"λ1="<<setiosflags(ios::scientific)<<setprecision(12)<<d1<<"\t";cout<<"λ501="<<setiosflags(ios::scientific)<<setprecision(12)<<d501<<endl;/**************求λs*****************/init();ds=fmifa();cout<<"λs="<<setiosflags(ios::scientific)<<setprecision(12)<<ds<<endl;/**************求与μk最接近的特征值λik**************/cout<<"与μk最接近的特征值λik:"<<endl;for(k=0;k<39;k++){miu[k]=d1+(k+1)*(d501-d1)/40;init();for(i=0;i<N;i++)a[i]=a[i]-miu[k];lamta=fmifa()+miu[k];cout<<"λi"<<k+1<<"\t\t"<<setiosflags(ios::scientific)<<setprecision(12)<<lamta<<en dl;}/**************求A的条件数**************/cout<<"矩阵A的条件式";cond=abs(max(abs(d1),abs(d501))/ds);cout<<"cond="<<setiosflags(ios::scientific)<<setprecision(12)<<cond<<endl;/**************求A的行列式**************/cout<<"矩阵A的行列式";init();LU();for(i=0;i<N;i++){det*=cc[2][i];}cout<<"det="<<setiosflags(ios::scientific)<<setprecision(12)<<det<<endl;system("pause");}/**************初始化函数,给a[N]赋值*************/void init(){int i;for(i=1;i<=501;i++)a[i-1]=(1.64-0.024*i)*sin((double)(0.2*i))-0.64*exp((double)(0.1/i)); }/**************幂法求最大绝对特征值**************/double mifa(){int i,k=0;double u[N],y[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++) //控制最大迭代次数为2000{/***求y(k-1)***/double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;}/****求新的uk****/u[0]=a[0]*y[0]+b*y[1]+c*y[2];u[1]=b*y[0]+a[1]*y[1]+b*y[2]+c*y[3]; //前两列和最后两列单独拿出来求中D间的循环求for(i=2;i<N-2;i++){u[i]=c*y[i-2]+b*y[i-1]+a[i]*y[i]+b*y[i+1]+c*y[i+2];}u[N-2]=c*y[N-4]+b*y[N-3]+a[N-2]*y[N-2]+b*y[N-1];u[N-1]=c*y[N-3]+b*y[N-2]+a[N-1]*y[N-1];/***求beta***/double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}//cout<<"Beta"<<k<<"="<<Beta<<"\t"; 输出每次迭代的beta /***求误差***/error=abs(Beta-Beta_)/abs(Beta);if(error<=E) //若迭代误差在精度水平内则可以停止迭代{return Beta;} //控制显示位数Beta_=Beta; //第个eta的值都要保存下来,为了与后个值进行误差计算 }if(k==2000){cout<<"error"<<endl;return 0;} //若在最大迭代次数范围内都不能满足精度要求说明不收敛}/**************反幂法求最小绝对特¬征值**************/double fmifa(){int i,k,t;double u[N],y[N]={0},yy[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++){double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;yy[i]=y[i]; //用重新赋值,避免求解方程组的时候改变y的值}/****LU分解法解方程组Au=y,求新的***/LU();for(i=2;i<=N;i++){double temp_b=0;for(t=max(1,i-r);t<=i-1;t++)temp_b+=cc[i-t+s][t-1]*yy[t-1];yy[i-1]=yy[i-1]-temp_b;}u[N-1]=yy[N-1]/cc[s][N-1];for(i=N-1;i>=1;i--){double temp_u=0;for(t=i+1;t<=min(i+s,N);t++)temp_u+=cc[i-t+s][t-1]*u[t-1];u[i-1]=(yy[i-1]-temp_u)/cc[s][i-1];}double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}error=abs(Beta-Beta_)/abs(Beta);if(error<=E){return (1/Beta);}Beta_=Beta;}if(k==2000){cout<<"error"<<endl;return 0;} }/**************求两数最大值的子程序**************/int max(int aa,int bb){return(aa>bb?aa:bb);}/**************求两数最小值的子程序**************/int min(int aa,int bb){return(aa<bb?aa:bb);}/**************求三数最大值的子程序**************/int max_3(int aa,int bb,int cc){ int tt;if(aa>bb)tt=aa;else tt=bb;if(tt<cc) tt=cc;return(tt);}/**************LU分解**************/void LU(){int i,j,k,t;double b=0.16,c=-0.064;/**赋值压缩后矩阵cc[5][501]**/for(i=2;i<N;i++)cc[0][i]=c;for(i=1;i<N;i++)cc[1][i]=b;for(i=0;i<N;i++)cc[2][i]=a[i];for(i=0;i<N-1;i++)cc[3][i]=b;for(i=0;i<N-2;i++)cc[4][i]=c;for(k=1;k<=N;k++){for(j=k;j<=min(k+s,N);j++){double temp=0;for(t=max_3(1,k-r,j-s);t<=k-1;t++)temp+=cc[k-t+s][t-1]*cc[t-j+s][j-1];cc[k-j+s][j-1]=cc[k-j+s][j-1]-temp;}//if(k<500){for(i=k+1;i<=min(k+r,N);i++){double temp2=0;for(t=max_3(1,i-r,k-s);t<=k-1;t++)temp2+=cc[i-t+s][t-1]*cc[t-k+s][k-1];cc[i-k+s][k-1]=(cc[i-k+s][k-1]-temp2)/cc[s][k-1];}}}}三、程序结果。

北航数值分析全部三次大作业第一次大作业是关于解线性方程组的数值方法。
我们被要求实现各种常用的线性方程组求解算法,例如高斯消元法、LU分解法和迭代法等。
我首先学习了这些算法的原理和实现方法,并借助Python编程语言编写了这些算法的代码。
在实验中,我们使用了不同规模和条件的线性方程组进行测试,并比较了不同算法的性能和精度。
通过这个作业,我深入了解了线性方程组求解的原理和方法,提高了我的编程和数值计算能力。
第二次大作业是关于数值积分的方法。
数值积分是数值分析中的重要内容,它可以用于计算曲线的长度、函数的面积以及求解微分方程等问题。
在这个作业中,我们需要实现不同的数值积分算法,例如矩形法、梯形法和辛普森法等。
我学习了这些算法的原理和实现方法,并使用Python编写了它们的代码。
在实验中,我们计算了不同函数的积分值,并对比了不同算法的精度和效率。
通过这个作业,我深入了解了数值积分的原理和方法,提高了我的编程和数学建模能力。
第三次大作业是关于常微分方程的数值解法。
常微分方程是数值分析中的核心内容之一,它可以用于描述众多物理、化学和生物现象。
在这个作业中,我们需要实现不同的常微分方程求解算法,例如欧拉法、龙格-库塔法和Adams法等。
我学习了这些算法的原理和实现方法,并使用Python编写了它们的代码。
在实验中,我们解决了一些具体的常微分方程问题,并比较了不同算法的精度和效率。
通过这个作业,我深入了解了常微分方程的原理和方法,提高了我的编程和问题求解能力。
总的来说,北航数值分析课程的三次大作业非常有挑战性,但也非常有意义。
通过这些作业,我在数值计算和编程方面得到了很大的提升,也更加深入地了解了数值分析的理论和方法。
虽然这些作业需要大量的时间和精力,但我相信这些努力将会对我未来的学习和工作产生积极的影响。

北航数值分析报告大作业第三题(fortran)“数值分析“计算实习大作业第三题——SY1415215孔维鹏一、计算说明1、将x i=0.08i,y j=0.5+0.05j分别代入方程组(A.3)得到关于t,u,v,w的的方程组,调用离散牛顿迭代子函数求出与x i,y j对应的t i,u j。
2、调用分片二次代数插值子函数在点(t i,u j)处插值得到z(x i,y j)=f(x i,y j),得到数表(x i,y j,f(x i,y j))。
3、对于k=1,2,3,4?,分别调用最小二乘拟合子函数计算系数矩阵c rs 及误差σ,直到满足精度,即求得最小的k值及系数矩阵c rs。
4、将x i?=0.1i,y j?=0.5+0.2j分别代入方程组(A.3)得到关于t?,u?,v?,w?的的方程组,调用离散牛顿迭代子函数求出与x i?,y j?对应的t i?,u j?,调用分片二次代数插值子函数在点(t i?,u j?)处插值得到z?(x i?,y j?)=f(x i?,y j?);调用步骤3中求得的系数矩阵c rs求得p(x i?,y j?),打印数表(x i?,y j?,f(x i?,y j?),p(x i?,y j?))。
二、源程序(FORTRAN)PROGRAM SY1415215DIMENSIONX(11),Y(21),T(6),U(6),Z(6,6),UX(11,21),TY(11,21),FXY(11,21), C(6,6) DIMENSIONX1(8),Y1(5),FXY1(8,5),PXY1(8,5),UX1(8,5),TY1(8,5)REAL(8) X,Y,T,U,Z,FXY,UX,TY,C,E,X1,Y1,FXY1,PXY1,UX1,TY1OPEN (1,FILE='第三题计算结果.TXT')DO I=1,11X(I)=0.08*(I-1)ENDDODO I=1,21Y(I)=0.5+0.05*(I-1)ENDDO!*****求解非线性方程组,得到z=f(t,u)的函数*******DO I=1,11DO J=1,21CALL DISNEWTON_NONLINEAR(X(I),Y(J),UX(I,J),TY(I,J)) ENDDO ENDDO!*************分片二次插值得到z=f(x,y)***********DO I=1,11DO J=1,21CALL INTERPOLATION(UX(I,J),TY(I,J),FXY(I,J))ENDDO ENDDOWRITE (1,"('数表(x,y,f(x,y)):')")WRITE (1,"(3X,'X',7X,'Y',10X,'F(X,Y)')")DO I=1,11DO J=1,21WRITE(1,'(1X,F5.2,2X,F5.3,2X,E20.13)') X(I),Y(J),FXY(I,J) ENDDOWRITE (1,"('')")ENDDO!***********最小二乘拟合得到P(x,y)**************N=11M=21WRITE (1,'(" ","K和σ分别为:")')DO K=1,20CALL LSFITTING(X,Y,FXY,C,N,M,K,K,E) WRITE (1,'(I3,2X,E20.13)') K-1,EIF(ETA).OR.(A(L,K)==TA)) THENTA=A(L,K)TL=LDO J=K,NT(K,J)=A(K,J)A(K,J)=A(TL,J)A(TL,J)=T(K,J)ENDDOTB(K)=B(K)B(K)=B(TL)B(TL)=TB(K)ENDIF ENDDODO I=K+1,NM(I,K)=A(I,K)/A(K,K)A(I,K)=0DO J=K+1,NA(I,J)=A(I,J)-M(I,K)*A(K,J) ENDDOB(I)=B(I)-M(I,K)*B(K)ENDDOENDDO!回代过程X(N)=B(N)/A(N,N)DO K=N-1,1,-1S=0.0DO J=K+1,NS=S+A(K,J)*X(J)ENDDOX(K)=(B(K)-S)/A(K,K)ENDDORETURNEND!***********求向量的无穷数************ SUBROUTINE NORM(X,N,A) DIMENSION X(N)REAL(8) X,AA=ABS(X(1))DO I=2,NIF(ABS(X(I))>ABS(X(I-1))) THENA=ABS(X(I)) ENDIFENDDORETURNEND!**************分片二次代数插值************** SUBROUTINE INTERPOLATION(U,V,W) PARAMETER (N=6,M=6)DIMENSION X(N),Y(M),Z(M,N),LK(3),LR(3)REAL(8) X,Y,Z,H,TREAL(8) U,V,W,LK,LR !U,V分别为插值点处的坐标,W为插值结果INTEGER R!**********************数据赋值********************** DATA Y/0.0,0.2,0.4,0.6,0.8,1.0/DATA X/0.0,0.4,0.8,1.2,1.6,2.0/DATA Z/-0.5,-0.42,-0.18,0.22,0.78,1.5,&&-0.34,-0.5,-0.5,-0.34,-0.02,0.46,&&0.14,-0.26,-0.5,-0.58,-0.5,-0.26,&&0.94,0.3,-0.18,-0.5,-0.66,-0.66,&&2.06,1.18,0.46,-0.1,-0.5,-0.74,&&3.5,2.38,1.42,0.62,-0.02,-0.5/H=0.4T=0.2!******************计算K,R************************* IF(UX(N-1)-H/2) THENK=N-1ELSEDO I=3,N-2IF((U>X(I)-H/2).AND.(UY(M-1)-T/2) THENR=M-1 ELSEDO J=3,M-2IF((V>Y(J)-T/2).AND.(VN) P=N IF(P>20) P=20IF(Q>M) Q=MIF(Q>20) Q=20XX=0YY=0D1=NAPX(1)=0.0DO I=1,NAPX(1)=APX(1)+X(I)ENDDOAPX(1)=APX(1)/D1DO J=1,MV(1,J)=0.0DO I=1,NV(1,J)=V(1,J)+Z(I,J)ENDDOV(1,J)=V(1,J)/D1ENDDOIF(P>1) THEND2=0.0APX(2)=0.0DO I=1,NG=X(I)-APX(1)D2=D2+G*GAPX(2)=APX(2)+(X(I)-XX)*G*G ENDDO APX(2)=APX(2)/D2BX(2)=D2/D1DO J=1,MV(2,J)=0.0DO I=1,NG=X(I)-APX(1)V(2,J)=V(2,J)+Z(I,J)*G ENDDOV(2,J)=V(2,J)/D2ENDDOD1=D2ENDIFDO K=3,PD2=0.0APX(K)=0.0DO J=1,MV(K,J)=0.0ENDDODO I=1,NG1=1.0G2=X(I)-APX(1)DO J=3,KG=(X(I)-APX(J-1))*G2-BX(J-1)*G1 G1=G2 G2=GENDDOD2=D2+G*GAPX(K)=APX(K)+X(I)*G*GDO J=1,M V(K,J)=V(K,J)+Z(I,J)*G ENDDOENDDODO J=1,MV(K,J)=V(K,J)/D2ENDDOAPX(K)=APX(K)/D2BX(K)=D2/D1D1=D2ENDDOD1=MAPY(1)=0.0DO I=1,MAPY(1)=APY(1)+Y(I)ENDDOAPY(1)=APY(1)/D1DO J=1,PU(J,1)=0.0DO I=1,MU(J,1)=U(J,1)+V(J,I) ENDDO U(J,1)=U(J,1)/D1ENDDOIF(Q>1)THEND2=0.0APY(2)=0.0DO I=1,MG=Y(I)-APY(1)D2=D2+G*G APY(2)=APY(2)+(Y(I))*G*G ENDDO APY(2)=APY(2)/D2BY(2)=D2/D1DO J=1,PU(J,2)=0.0DO I=1,MG=Y(I)-APY(1)U(J,2)=U(J,2)+V(J,I)*GENDDOU(J,2)=U(J,2)/D2ENDDOD1=D2ENDIFDO K=3,QD2=0.0APY(K)=0.0DO J=1,PU(J,K)=0.0ENDDODO I=1,MG1=1.0G2=Y(I)-APY(1)DO J=3,KG=(Y(I)-APY(J-1))*G2-BY(J-1)*G1 G1=G2 G2=GENDDOD2=D2+G*GAPY(K)=APY(K)+Y(I)*G*G DO J=1,PU(J,K)=U(J,K)+V(J,I)*G ENDDOENDDODO J=1,PU(J,K)=U(J,K)/D2ENDDOAPY(K)=APY(K)/D2BY(K)=D2/D1D1=D2ENDDOV(1,1)=1.0V(2,1)=-APY(1)V(2,2)=1.0DO I=1,PDO J=1,QA(I,J)=0.0ENDDOENDDODO I=3,QV(I,I)=V(I-1,I-1)V(I,I-1)=-APY(I-1)*V(I-1,I-1)+V(I-1,I-2)IF(I>=4) THENDO K=I-2,2,-1V(I,K)=-APY(I-1)*V(I-1,K)+V(I-1,K-1)-BY(I-1)*V(I-2,K) ENDDO ENDIFV(I,1)=-APY(I-1)*V(I-1,1)-BY(I-1)*V(I-2,1)ENDDO DO I=1,PIF(I==1) THENT(1)=1.0T1(1)=1.0ELSEIF(I==2) THENT(1)=-APX(1)T(2)=1.0T2(1)=T(1)T2(2)=T(2)ELSET(I)=T2(I-1)T(I-1)=-APX(I-1)*T2(I-1)+T2(I-2) IF(I>=4) THENDO K=I-2,2,-1T(K)=-APX(I-1)*T2(K)+T2(K-1)-BX(I-1)*T1(K) ENDDOENDIFT(1)=-APX(I-1)*T2(1)-BX(I-1)*T1(1)T2(I)=T(I)DO K=I-1,1,-1T1(K)=T2(K)T2(K)=T(K)ENDDOENDIFDO J=1,QDO K=I,1,-1DO L=J,1,-1A(K,L)=A(K,L)+U(I,J)*T(K)*V(J,L) ENDDOENDDOENDDOENDDODT1=0.0DO I=1,NX1=X(I)DO J=1,MY1=Y(J)X2=1.0DD=0.0DO K=1,PG=A(K,Q)DO KK=Q-1,1,-1G=G*Y1+A(K,KK)ENDDOG=G*X2DD=DD+GX2=X2*X1ENDDODT=DD-Z(I,J)DT1=DT1+DT*DTENDDOENDDORETURNEND三、计算结果数表(x,y,f(x,y)): X Y UX TY F(X,Y) 0.00 0.500 1.345 0.243 0.17E+000.00 0.550 1.322 0.269 0.66E+000.00 0.600 1.299 0.295 0.35E+000.00 0.650 1.277 0.322 0.94E+000.00 0.700 1.255 0.350 0.30E-020.00 0.750 1.235 0.377 -0.87E-010.00 0.800 1.215 0.406 -0.58E+000.00 0.850 1.196 0.434 -0.72E+000.00 0.900 1.177 0.463 -0.54E+000.00 0.950 1.159 0.492 -0.86E+000.00 1.050 1.125 0.550 -0.74E+00 0.00 1.100 1.109 0.580 -0.06E+00 0.00 1.150 1.093 0.609 -0.00E+00 0.00 1.200 1.0790.639 -0.18E+00 0.00 1.250 1.064 0.669 -0.52E+00 0.00 1.3001.050 0.699 -0.19E+00 0.00 1.350 1.037 0.729 -0.48E+00 0.001.400 1.024 0.759 -0.68E+00 0.00 1.450 1.011 0.790 -0.52E+00 0.00 1.500 1.000 0.820 -0.29E+000.08 0.500 1.415 0.228 0.67E+00 0.08 0.550 1.391 0.253 0.08E+00 0.08 0.600 1.368 0.279 0.02E+00 0.08 0.650 1.346 0.306 0.47E+00 0.08 0.700 1.325 0.333 0.57E+00 0.08 0.750 1.304 0.360 0.48E-01 0.08 0.800 1.284 0.388 -0.73E-01 0.08 0.850 1.265 0.416 -0.16E+00 0.08 0.900 1.246 0.444 -0.29E+00 0.08 0.950 1.229 0.473 -0.36E+00 0.08 1.000 1.211 0.502 -0.08E+00 0.08 1.050 1.194 0.531 -0.29E+00 0.08 1.100 1.178 0.560 -0.78E+00 0.08 1.150 1.163 0.589 -0.93E+00 0.08 1.200 1.148 0.619 -0.44E+00 0.08 1.250 1.133 0.649 -0.92E+00 0.08 1.300 1.119 0.679 -0.71E+000.08 1.400 1.093 0.739 -0.37E+00 0.08 1.450 1.080 0.769-0.83E+00 0.08 1.500 1.068 0.799 -0.92E+000.16 0.500 1.483 0.214 0.31E+00 0.16 0.550 1.460 0.239 0.64E+00 0.16 0.600 1.437 0.264 0.91E+00 0.16 0.650 1.414 0.290 0.06E+00 0.16 0.700 1.393 0.316 0.70E+00 0.16 0.750 1.372 0.343 0.59E+00 0.16 0.800 1.352 0.370 0.12E+00 0.16 0.850 1.333 0.398 0.77E-02 0.16 0.900 1.315 0.426 -0.83E-01 0.16 0.950 1.297 0.454-0.58E+00 0.16 1.000 1.279 0.483 -0.20E+00 0.16 1.050 1.2620.512 -0.11E+00 0.16 1.100 1.246 0.541 -0.74E+00 0.16 1.1501.231 0.570 -0.09E+00 0.16 1.200 1.216 0.600 -0.59E+00 0.16 1.250 1.201 0.629 -0.66E+00 0.16 1.300 1.187 0.659 -0.71E+00 0.16 1.350 1.174 0.689 -0.32E+00 0.16 1.400 1.161 0.718-0.56E+00 0.16 1.450 1.148 0.748 -0.31E+00 0.16 1.500 1.136 0.778 -0.75E+000.24 0.500 1.551 0.201 0.66E+01 0.24 0.550 1.527 0.2250.03E+000.24 0.650 1.482 0.275 0.64E+00 0.24 0.700 1.460 0.3010.47E+00 0.24 0.750 1.439 0.327 0.34E+00 0.24 0.800 1.419 0.354 0.24E+00 0.24 0.850 1.400 0.381 0.69E+00 0.24 0.900 1.381 0.409 0.04E-01 0.24 0.950 1.363 0.437 -0.42E-01 0.24 1.000 1.346 0.465 -0.06E+00 0.24 1.050 1.329 0.494 -0.59E+00 0.24 1.100 1.313 0.523 -0.83E+00 0.24 1.150 1.297 0.552 -0.15E+00 0.24 1.200 1.282 0.581 -0.19E+00 0.24 1.250 1.267 0.610 -0.84E+00 0.24 1.300 1.253 0.640 -0.66E+00 0.24 1.350 1.240 0.669 -0.30E+00 0.24 1.400 1.227 0.699 -0.86E+00 0.24 1.450 1.214 0.729 -0.84E+00 0.24 1.500 1.202 0.759 -0.77E+000.32 0.500 1.617 0.188 0.28E+01 0.32 0.550 1.593 0.212 0.49E+01 0.32 0.600 1.570 0.236 0.68E+00 0.32 0.650 1.547 0.261 0.75E+00 0.32 0.700 1.526 0.286 0.60E+00 0.32 0.750 1.505 0.312 0.77E+00 0.32 0.800 1.485 0.339 0.05E+00 0.32 0.850 1.466 0.365 0.99E+00 0.32 0.900 1.447 0.393 0.27E+00 0.32 1.000 1.411 0.448 -0.01E-02 0.32 1.050 1.395 0.477-0.41E-01 0.32 1.100 1.378 0.505 -0.18E+00 0.32 1.150 1.3630.534 -0.25E+00 0.32 1.200 1.347 0.563 -0.29E+00 0.32 1.2501.333 0.592 -0.90E+00 0.32 1.300 1.319 0.621 -0.00E+00 0.32 1.350 1.305 0.650 -0.40E+00 0.32 1.400 1.292 0.680 -0.54E+00 0.32 1.450 1.279 0.710 -0.79E+00 0.32 1.500 1.267 0.739-0.91E+000.40 0.500 1.681 0.177 0.91E+01 0.40 0.550 1.658 0.1990.00E+01 0.40 0.600 1.634 0.223 0.83E+01 0.40 0.650 1.612 0.247 0.02E+01 0.40 0.700 1.591 0.272 0.94E+00 0.40 0.750 1.570 0.298 0.49E+00 0.40 0.800 1.550 0.324 0.94E+00 0.40 0.850 1.530 0.350 0.40E+00 0.40 0.900 1.512 0.377 0.33E+00 0.40 0.950 1.493 0.405 0.99E+00 0.40 1.000 1.476 0.432 0.68E+00 0.40 1.050 1.459 0.460 0.08E-01 0.40 1.100 1.443 0.488 -0.84E-01 0.40 1.150 1.427 0.517-0.98E+00 0.40 1.200 1.412 0.545 -0.27E+00 0.40 1.250 1.397 0.574 -0.06E+000.40 1.350 1.369 0.632 -0.66E+00 0.40 1.400 1.356 0.662-0.37E+00 0.40 1.450 1.343 0.691 -0.43E+00 0.40 1.500 1.331 0.721 -0.12E+000.48 0.500 1.745 0.166 0.69E+01 0.48 0.550 1.721 0.188 0.02E+01 0.48 0.600 1.698 0.211 0.74E+01 0.48 0.650 1.676 0.235 0.40E+01 0.48 0.700 1.654 0.259 0.23E+01 0.48 0.750 1.634 0.284 0.56E+00 0.48 0.800 1.613 0.310 0.28E+00 0.48 0.850 1.594 0.336 0.49E+00 0.48 0.900 1.575 0.363 0.31E+00 0.48 0.950 1.557 0.390 0.66E+00 0.48 1.000 1.539 0.417 0.30E+00 0.48 1.050 1.522 0.444 0.34E+00 0.48 1.100 1.506 0.472 0.07E-01 0.48 1.150 1.490 0.500 -0.62E-01 0.48 1.200 1.475 0.529 -0.45E+00 0.48 1.250 1.460 0.557 -0.86E+00 0.48 1.300 1.446 0.586 -0.39E+00 0.48 1.350 1.432 0.615 -0.22E+00 0.48 1.400 1.419 0.644 -0.67E+00 0.48 1.450 1.406 0.674-0.55E+00 0.48 1.500 1.394 0.703 -0.14E+000.56 0.500 1.808 0.156 0.48E+010.56 0.600 1.761 0.200 0.10E+01 0.56 0.650 1.739 0.2230.68E+01 0.56 0.700 1.717 0.247 0.94E+01 0.56 0.750 1.696 0.272 0.33E+01 0.56 0.800 1.676 0.297 0.11E+00 0.56 0.850 1.657 0.323 0.63E+00 0.56 0.900 1.638 0.349 0.97E+00 0.56 0.950 1.620 0.375 0.52E+00 0.56 1.000 1.602 0.402 0.56E+00 0.56 1.050 1.585 0.429 0.47E+00 0.56 1.100 1.568 0.457 0.20E+00 0.56 1.150 1.552 0.485 0.13E+00 0.56 1.200 1.537 0.513 0.09E-01 0.56 1.250 1.522 0.541 -0.47E-01 0.56 1.300 1.508 0.570 -0.99E+00 0.56 1.350 1.4940.599 -0.82E+00 0.56 1.400 1.481 0.627 -0.26E+00 0.56 1.4501.468 0.657 -0.71E+00 0.56 1.500 1.455 0.686 -0.98E+000.64 0.500 1.870 0.147 0.74E+01 0.64 0.550 1.846 0.1680.10E+01 0.64 0.600 1.823 0.190 0.54E+01 0.64 0.650 1.801 0.213 0.42E+01 0.64 0.700 1.779 0.236 0.56E+01 0.64 0.750 1.758 0.260 0.03E+01 0.64 0.800 1.738 0.285 0.42E+01 0.64 0.850 1.718 0.310 0.41E+010.64 0.950 1.681 0.362 0.36E+00 0.64 1.000 1.664 0.388 0.18E+00 0.64 1.050 1.646 0.415 0.28E+00 0.64 1.100 1.630 0.443 0.07E+00 0.64 1.150 1.614 0.470 0.66E+00 0.64 1.200 1.598 0.498 0.09E+00 0.64 1.250 1.584 0.526 0.50E-01 0.64 1.300 1.569 0.554 -0.88E-01 0.64 1.350 1.555 0.583 -0.76E+00 0.64 1.400 1.542 0.611 -0.66E+00 0.64 1.450 1.529 0.640 -0.33E+00 0.64 1.500 1.516 0.669 -0.56E+00 0.72 0.500 1.931 0.139 0.94E+01 0.72 0.550 1.907 0.159 0.84E+01 0.72 0.600 1.884 0.181 0.36E+01 0.72 0.650 1.862 0.203 0.40E+01 0.72 0.700 1.840 0.226 0.47E+01 0.72 0.750 1.819 0.249 0.56E+01 0.72 0.800 1.799 0.273 0.19E+01 0.72 0.850 1.779 0.298 0.37E+01 0.72 0.900 1.760 0.323 0.86E+01 0.72 0.950 1.742 0.349 0.76E+00 0.72 1.000 1.724 0.375 0.24E+00 0.72 1.050 1.707 0.402 0.55E+00 0.72 1.100 1.691 0.429 0.97E+00 0.72 1.150 1.675 0.456 0.27E+00 0.72 1.200 1.659 0.484 0.31E+000.72 1.300 1.630 0.539 0.49E+00 0.72 1.350 1.616 0.5680.72E-02 0.72 1.400 1.602 0.596 -0.69E-01 0.72 1.450 1.589 0.625 -0.67E+00 0.72 1.500 1.576 0.653 -0.20E+000.80 0.500 1.992 0.131 0.31E+01 0.80 0.550 1.968 0.1510.44E+01 0.80 0.600 1.945 0.172 0.41E+01 0.80 0.650 1.922 0.193 0.45E+01 0.80 0.700 1.900 0.216 0.00E+01 0.80 0.750 1.879 0.239 0.10E+01 0.80 0.800 1.859 0.263 0.16E+01 0.80 0.850 1.840 0.287 0.52E+01 0.80 0.900 1.821 0.312 0.02E+01 0.80 0.950 1.802 0.337 0.38E+01 0.80 1.000 1.784 0.363 0.89E+01 0.80 1.050 1.767 0.389 0.28E+00 0.80 1.100 1.751 0.416 0.09E+00 0.80 1.150 1.734 0.4430.23E+00 0.80 1.200 1.719 0.470 0.93E+00 0.80 1.250 1.704 0.498 0.15E+00 0.80 1.300 1.689 0.525 0.86E+00 0.80 1.350 1.675 0.553 0.64E+00 0.80 1.400 1.662 0.582 0.74E-01 0.80 1.450 1.649 0.610 -0.37E-01 0.80 1.500 1.636 0.638 -0.81E+00K和σ分别为:0 0.93E+031 0.61E+012 0.92E-023 0.53E-034 0.16E-055 0.77E-07系数矩阵Crs(按行)为:0.00E+01 -0.83E+01 0.56E+00 0.97E+00 -0.03E+00 0.70E-010.91E+01 -0.99E+00 -0.96E+01 0.17E+01 -0.66E+00 0.10E-01 0.77E+00 0.42E+01 -0.10E+00 -0.81E+00 0.81E+00 -0.62E-01-0.25E+00 -0.21E+00 0.97E+00 -0.18E+00 0.49E+00 -0.63E-010.34E+00 -0.56E+00 0.69E-01 0.51E+00 -0.77E-01 0.27E-01-0.94E-01 0.94E+00 -0.58E+00 0.69E-01 -0.50E-01 0.53E-02 数表(x,y,f(x,y),p(x,y)):X Y F(X,Y) P(X,Y)0.100 0.700 0.58E+00 0.05E+000.100 1.100 -0.66E+00 -0.26E+00 0.100 1.300 -0.68E+00-0.31E+00 0.100 1.500 -0.52E+00 -0.49E+000.200 0.700 0.54E+00 0.19E+00 0.200 0.900 -0.63E-01 -0.65E-01 0.200 1.100 -0.90E+00 -0.90E+00 0.200 1.300 -0.84E+00 -0.90E+00 0.200 1.500 -0.03E+00 -0.04E+000.300 0.700 0.82E+00 0.09E+00 0.300 0.900 0.48E+00 0.11E+00 0.300 1.100 -0.63E+00 -0.88E+00 0.300 1.300 -0.72E+00 -0.96E+00 0.300 1.500 -0.34E+00 -0.84E+000.400 0.700 0.79E+00 0.89E+00 0.400 0.900 0.56E+00 0.63E+00 0.400 1.100 -0.83E-01 -0.04E-01 0.400 1.300 -0.72E+00 -0.71E+00 0.400 1.500 -0.85E+00 -0.07E+000.500 0.700 0.56E+01 0.92E+01 0.500 0.900 0.51E+00 0.23E+00 0.500 1.100 0.59E+00 0.27E+00 0.500 1.300 -0.53E+00 -0.11E+00 0.500 1.500 -0.67E+00 -0.33E+000.600 0.900 0.14E+00 0.75E+00 0.600 1.100 0.19E+00 0.32E+00 0.600 1.300 -0.70E-01 -0.82E-01 0.600 1.500 -0.08E+00 -0.75E+00 0.700 0.700 0.89E+01 0.29E+01 0.700 0.900 0.91E+01 0.11E+010.700 1.100 0.60E+00 0.97E+00 0.700 1.300 0.22E-01 0.06E-01 0.7001.500 -0.53E+00 -0.80E+00 0.800 0.700 0.09E+01 0.06E+01 0.800 0.900 0.32E+01 0.50E+01 0.800 1.100 0.03E+00 0.79E+00 0.800 1.300 0.25E+00 0.50E+00 0.800 1.500 -0.14E+00 -0.28E+00。

第一章作业:1.举日常生活的例子说明数据采集的应用? 工业部门:可以通过对信号的测量(数据获取)、处理控制及管理,实现对生产过程的测、控自动化与一体。
? 天气预报:气象信息的采集、分析? 网络舆情:微信、博社交媒体等息的采集分析2.举日常生活的例子说明什么是信号上下课的铃声,交通灯信号,汽车的鸣镝声,闹钟,眼神、表情,肢体动作,体育比赛时的信令枪等。
3.用自己的语言说明信号与信息的区别与联系信号是信息系统的实际工作对象,信号是多种多样的,通常表现为随时间变化的某些物理量。
信号是信息的载体。
信号是信息的物理表现形式,或者说传递函数。
信号是含有能量的物质,具可观测性。
信息既不是物质,也不是能量。
信息是号的内容。
4.什么是系统?系统是由若干相互依赖、作用的事物组合而成具有特定功能的整体。
一个系统,对于给定的输入(激励),将会有既的输出(响应)。
系统是一个相对的概念,可以分为多小的组成。
5.什么是数据采集,其主要目标是什么?就是将要获取的信息通过传感器转换为信号,并经信号调理、采样、量化、编码和传输等步骤,最后送到计算机系统中进行处理、分析、存储和显示。
两个目标:精度、速度。
6.请画出典型的数据获取系统框图7.数据处理的主要任务具体有哪些?? 对采集信号作标度变换? 消除数据中的干扰信号? 分析计算数据的内在特征8.数据采集系统的主要性能指标有哪些?? 系统分辨率? 系统精度:?是指当系统工作在额定采集速率下,整个数据所能达到的转换精度。
? 采集速率:系统每个通道、每秒可采集的有效数据量。
? 动态范围:是指某个确定的物理量变化范围。
? 非线性失真:是由电路系统的非线性而引起的波形失真。
第二章1下图所示信号中,acd是连续信号,b是离散信号,d是周期信号,abc是非周期信号,a是能量信号,bcd是功率信号,abc是物理可实现信号。
(c) (d)?信号的自变量连续,称为连续信号。
?信号的自变量离散,称为离散信号。

《数值分析B》课计算实习第一题设计文档与源程序姓名:杨彦杰学号:SY10171341 算法的设计方案(1)运行平台操作系统:Windows XP;开发平台:VC6.0++;工程类型:文档视图类;工程名:Numanalysis;(2)开发描述首先新建类CMetrix,该类完成矩阵之间的相关运算,包括相乘、加减等,以主程序方便调用;题目的解算过程在视图类CNumanalysisView中实现,解算结果在视图界面中显示;(3)运行流程(4)运行界面2、全部源代码(1)类CMetrixMetrix.h文件:class CMetrix{public:double** MetrixMultiplyConst(double**A,int nRow,int nCol,double nConst);//矩阵乘常数double** MetrixMultiplyMetrix(double**A,double**mA,int nRow,int nCol);//矩阵相乘double** MetrixSubtractMetrix(double **A, double **subA, int nRow,int nCol);//矩阵减矩阵double VectorMultiplyVector(double*V,double*mulV,int nV);//向量点积double** VectorMultiplyVectortoMetrix(double*V,double*VT,int nV);//向量相乘为矩阵double* VectorSubtractVector(double*V,double*subV,int nV);//向量相减double* VectorMultiplyConst(double *V, int nV, double nConst);//向量乘常数double LengthofVector(double *V,int nV);//求向量的长度double* MetrixMultiplyVector(double**A,int nRow,int nCol,double*V,int nV);//矩阵与向量相乘double** AtoAT(double **A,int Row,int Col);//矩阵转置运算void FreeMem();CMetrix(int nRow,int nCol);uCMetrix();virtual ~CMetrix();double* vector; //过渡向量double** B; //过渡矩阵};Metrix.cpp文件:CMetrix::CMetrix(int nRow, int nCol){B = new double*[nRow];for (int i = 0;i < nCol;i++){B[i] = new double[nCol];}vector = new double[nRow];}CMetrix::~CMetrix(){delete vector;B = NULL;delete B;}double** CMetrix::AtoAT(double **A, int nRow, int nCol){for (int row = 0;row < nRow;row++){for (int col = 0;col < nCol;col++){B[col][row] = A[row][col];}}return B;}double* CMetrix::MetrixMultiplyVector(double **A, int nRow, int nCol, double *V, int nV) {if (nCol != nV){AfxMessageBox("矩阵列数和向量维数不等,不能相乘!");return 0;}double sum = 0.0;for (int row = 0;row < nRow;row++){for (int col = 0;col < nCol;col++){sum += A[row][col]*V[col];}vector[row] = sum;sum = 0.0;}return vector;}double CMetrix::LengthofVector(double *V, int nV){double length = 0.0;for (int col = 0;col < nV;col++){length += V[col]*V[col];}return length;}double* CMetrix::VectorMultiplyConst(double *V, int nV, double nConst){for (int col = 0;col < nV;col++){vector[col] = V[col]*nConst;}return vector;}double* CMetrix::VectorSubtractVector(double *V, double *subV, int nV){for (int col = 0;col < nV;col++){vector[col] = V[col]-subV[col];}return vector;}double** CMetrix::VectorMultiplyVectortoMetrix(double*V, double *VT, int nV){for (int row = 0;row < nV;row++){for (int col = 0;col < nV;col++){B[row][col] = V[row]*VT[col];}}return B;}double CMetrix::VectorMultiplyVector(double *V, double *mulV, int nV){double length = 0.0;for (int col = 0;col < nV;col++){length += V[col]*mulV[col];}return length;}double** CMetrix::MetrixSubtractMetrix(double **A, double **subA, int nRow, int nCol) {for (int row = 0;row < nRow;row++){for (int col = 0;col < nCol;col++){B[row][col] = A[row][col]-subA[row][col];}}return B;}double** CMetrix::MetrixMultiplyMetrix(double **A, double **mA, int nRow, int nCol) {double sum = 0.0;for (int row = 0;row < nRow;row++){for (int col = 0;col < nCol;col++){for(int n = 0;n < nCol;n++){sum += A[row][n]*mA[n][col];}B[row][col] = sum;sum = 0.0;}}return B;}double** CMetrix::MetrixMultiplyConst(double **A, int nRow, int nCol, double nConst) {for (int row = 0;row < nRow;row++){for (int col = 0;col < nCol;col++){B[row][col] = A[row][col]*nConst;}}return B;}(2)类CNumanalysisViewNumanalysisview.hclass CNumanalysisView : public CEditView{…………public:double Sign(double x);void DisplayVector(double*V,int nV); // 显示向量数据void DisplayMetrix(double **A,int Row,int Col); //显示矩阵void DisplayText(CString str); //显示文本protected://{{AFX_MSG(CNumanalysisView)afx_msg void OnQRanalyze(); //运行主函数…………};Numanalysisview.cppvoid CNumanalysisView::OnQRanalyze(){//开辟空间int nRow = 10;int nCol = 10;CString str;CMetrix Metrix(nRow,nCol);double tempa = 0.0;double *V = new double[nCol]; //分配10*10矩阵空间double *ur = new double[nCol];double *pr = new double[nCol];double *qr = new double[nCol];double *wr = new double[nCol];double *tempV = new double[nCol];double **Ar = new double*[nRow];double **C = new double*[nRow];double **Cr = new double*[nRow];double **tempA = new double*[nRow];double **A = new double*[nRow];double **R = new double*[nRow];for (int col = 0;col < nRow;col++){A[col] = new double[nCol];Ar[col] = new double[nCol];C[col] = new double[nCol];Cr[col] = new double[nCol];tempA[col] = new double[nCol];R[col] = new double[nCol];}//矩阵A求解for (int i = 0;i < nRow;i++){for (int j = 0;j < nCol;j++){if(i == j)A[i][j] = 1.5*cos((i+1.0)+1.2*(j+1.0));elseA[i][j] = sin(0.5*(i+1.0)+0.2*(j+1.0));}}//--------------------拟上三角化-------------------------// double dr = 0.0,cr = 0.0,hr = 0.0,tr = 0.0;for (int r = 0;r < nCol - 2;r++){dr = 0.0;for (i = r+1;i < nCol;i++) //dr{dr += A[i][r]*A[i][r];}dr = sqrt(dr);for (i = r+2;i < nCol;i++) //判断air是否全为零tempa += fabs(A[i][r]);if (tempa <= IPSLEN)continue;if (A[r+1][r] == 0.0) //crcr = dr;elsecr = -1*Sign(A[r+1][r])*dr;hr = cr*cr - cr*A[r+1][r]; //hrstr.Format("dr = %.6e, cr = %.6e, hr = %.6e",dr,cr,hr);for (int row = 0;row < nRow;row++) //ur{if (row < r+1)ur[row] = 0.0;else if (row == r+1)ur[row] = A[row][r]-cr;elseur[row] = A[row][r];}tempA = Metrix.AtoAT(A,nRow,nCol);for (row = 0;row < nRow;row++){for (col = 0;col < nCol;col++)Ar[row][col] = tempA[row][col];}tempV = Metrix.MetrixMultiplyVector(Ar,nRow,nCol,ur,nCol); //pr memcpy(pr,tempV,nCol*8);tempV = Metrix.VectorMultiplyConst(pr,nCol,1.0/hr);memcpy(pr,tempV,nCol*8);tempV = Metrix.MetrixMultiplyVector(A,nRow,nCol,ur,nCol); //qr memcpy(qr,tempV,nCol*8);tempV = Metrix.VectorMultiplyConst(qr,nCol,1.0/hr);memcpy(qr,tempV,nCol*8);tr = Metrix.VectorMultiplyVector(pr,ur,nCol)/hr; //trtempV = Metrix.VectorMultiplyConst(ur,nCol,tr); //wr memcpy(wr,tempV,nCol*8);tempV = Metrix.VectorSubtractVector(qr,wr,nCol);memcpy(wr,tempV,nCol*8);tempA = Metrix.VectorMultiplyVectortoMetrix(wr,ur,nCol); //Arfor (row = 0;row < nRow;row++){for (col = 0;col < nCol;col++)Ar[row][col] = tempA[row][col];}tempA = Metrix.MetrixSubtractMetrix(A,Ar,nRow,nCol);for (row = 0;row < nRow;row++){for (col = 0;col < nCol;col++)A[row][col] = tempA[row][col];}tempA = Metrix.VectorMultiplyVectortoMetrix(ur,pr,nCol);for (row = 0;row < nRow;row++){for (col = 0;col < nCol;col++)Ar[row][col] = tempA[row][col];}tempA = Metrix.MetrixSubtractMetrix(A,Ar,nRow,nCol);for (row = 0;row < nRow;row++){for (col = 0;col < nCol;col++){A[row][col] = tempA[row][col];if (fabs(A[row][col]) < IPSLEN){A[row][col] = 0.0;}}}}DisplayText("矩阵A拟上三角化后所得的矩阵为:");DisplayMetrix(A,nRow,nCol);for (int row = 0;row < nRow;row++) //用于计算特征向量{for (col = 0;col < nCol;col++)R[row][col] = A[row][col];}// -------------------------------------------------////--------------------带双步位移的QR分解-------------------------// int m = nCol;struct EigenVal //定义特征值结构,实数和虚数{double Realnum;double Imagnum;};EigenVal *eigenvalue = new EigenVal[m];EigenVal tmpEigen1,tmpEigen2;double b = 0.0,c = 0.0,delta = 0.0,s = 0.0,t = 0.0;double *vr = new double[m];for (int k = 1;k < 100; k++){//m代表矩阵阶数,判断式中直接用,运算中需要-1while (m > 1 && fabs(A[m-1][m-2]) <= IPSLEN)//第三步和第四步{eigenvalue[m-1].Realnum = A[m-1][m-1];eigenvalue[m-1].Imagnum = 0.0;m = m - 1;}if (m == 1){eigenvalue[m-1].Realnum = A[m-1][m-1];eigenvalue[m-1].Imagnum = 0.0;DisplayText("已求出A的全部特征值:");break;}b = -(A[m-2][m-2]+A[m-1][m-1]); //第五步求一元二次方程式的根s1,s2c = A[m-2][m-2]*A[m-1][m-1]-A[m-2][m-1]*A[m-1][m-2];delta =b*b - 4*c;if (delta >= 0.0){tmpEigen1.Realnum = (-b-sqrt(delta))/2;tmpEigen1.Imagnum = 0.0;tmpEigen2.Realnum = (-b+sqrt(delta))/2;tmpEigen2.Imagnum = 0.0;}else{tmpEigen1.Realnum = -b/2;tmpEigen1.Imagnum = -sqrt(fabs(delta))/2 ;tmpEigen2.Realnum = -b/2;tmpEigen2.Imagnum = sqrt(fabs(delta))/2;}if (m == 2) //第六步 m=2时结束运算{eigenvalue[m-1] = tmpEigen1;eigenvalue[m-2] = tmpEigen2;DisplayText("已求出A的全部特征值:");break;}else //第七步 m > 1{if (fabs(A[m-2][m-3]) <= IPSLEN){eigenvalue[m-1] = tmpEigen1;eigenvalue[m-2] = tmpEigen2;m = m - 2;continue;}}for (int row = 0;row < m;row++) //Mk求之前需要把A付给C{for (int col = 0;col < m;col++)C[row][col] = A[row][col];}double **I = new double*[m]; //第九步求Mk和Mk的QR分解for (int i = 0;i < m;i++) //求单位矩阵I,分配m*m矩阵空间{I[i] = new double[m];}for (i = 0;i < m;i++){for (int j = 0;j < m;j++){if(i == j)I[i][j] = 1;else I[i][j] = 0;}}s = A[m-2][m-2]+A[m-1][m-1];t = A[m-2][m-2]*A[m-1][m-1] - A[m-2][m-1]*A[m-2][m-1];tempA = Metrix.MetrixMultiplyMetrix(A,A,m,m);//A*Afor (row = 0;row < m;row++){for (col = 0;col < m;col++)Ar[row][col] = tempA[row][col];}tempA = Metrix.MetrixMultiplyConst(A,m,m,s);//s*Afor (row = 0;row < m;row++){for (col = 0;col < m;col++)A[row][col] = tempA[row][col];}tempA = Metrix.MetrixSubtractMetrix(Ar,A,m,m);//A*A-s*Afor (row = 0;row < m;row++){for (col = 0;col < m;col++)A[row][col] = tempA[row][col]; }tempA = Metrix.MetrixMultiplyConst(I,m,m,-1*t);//-t*Ifor (row = 0;row < m;row++){for (col = 0;col < m;col++)Ar[row][col] = tempA[row][col]; }tempA = Metrix.MetrixSubtractMetrix(A,Ar,m,m);//A*A - s*A + r*I for (row = 0;row < m;row++){for (col = 0;col < m;col++){A[row][col] = tempA[row][col];if (fabs(A[row][col]) < IPSLEN){A[row][col] = 0.0;}}}delete I;//Mk的QR分解for (int r = 0;r < m - 1;r++){dr = 0.0;for (i = r;i < m;i++) //dr{dr += A[i][r]*A[i][r];}dr = sqrt(dr);for (i = r+1;i < m;i++) //判断air是否全为零tempa += fabs(A[i][r]);if (tempa <= IPSLEN)continue;if (A[r][r] == 0.0) //crcr = dr;elsecr = -1*Sign(A[r][r])*dr;hr = cr*cr - cr*A[r][r]; //hrfor (int row = 0;row < m;row++) //ur{if (row < r)ur[row] = 0.0;else if (row == r)ur[row] = A[row][r]-cr;elseur[row] = A[row][r];}tempA = Metrix.AtoAT(A,m,m); //Btfor (row = 0;row < m;row++){for (col = 0;col < m;col++)Ar[row][col] = tempA[row][col];}tempV = Metrix.MetrixMultiplyVector(Ar,m,m,ur,m); //Bt*ur memcpy(vr,tempV,m*8);tempV = Metrix.VectorMultiplyConst(vr,m,1.0/hr); //vr = Bt*ur/hr memcpy(vr,tempV,m*8);tempA = Metrix.VectorMultiplyVectortoMetrix(ur,vr,m);//Ur*vrfor (row = 0;row < m;row++){for (col = 0;col < m;col++)Ar[row][col] = tempA[row][col];}tempA = Metrix.MetrixSubtractMetrix(A,Ar,m,m); //Br-ur*vrfor (row = 0;row < m;row++){for (col = 0;col < m;col++){A[row][col] = tempA[row][col];if (fabs(A[row][col]) < IPSLEN){A[row][col] = 0.0;}}}tempA = Metrix.AtoAT(C,m,m); //Ctfor (row = 0;row < m;row++){for (col = 0;col < m;col++)Cr[row][col] = tempA[row][col]; }tempV = Metrix.MetrixMultiplyVector(Cr,m,m,ur,m); //pr memcpy(pr,tempV,m*8);tempV = Metrix.VectorMultiplyConst(pr,m,1.0/hr);memcpy(pr,tempV,m*8);tempV = Metrix.MetrixMultiplyVector(C,m,m,ur,m); //qr memcpy(qr,tempV,m*8);tempV = Metrix.VectorMultiplyConst(qr,m,1.0/hr);memcpy(qr,tempV,m*8);tr = Metrix.VectorMultiplyVector(pr,ur,m)/hr; //trtempV = Metrix.VectorMultiplyConst(ur,m,tr); //wr memcpy(wr,tempV,m*8);tempV = Metrix.VectorSubtractVector(qr,wr,m);memcpy(wr,tempV,m*8);tempA = Metrix.VectorMultiplyVectortoMetrix(wr,ur,m);//Cr+1for (row = 0;row < m;row++){for (col = 0;col < m;col++)Cr[row][col] = tempA[row][col]; }tempA = Metrix.MetrixSubtractMetrix(C,Cr,m,m);for (row = 0;row < m;row++){for (col = 0;col < m;col++)C[row][col] = tempA[row][col]; }tempA = Metrix.VectorMultiplyVectortoMetrix(ur,pr,m);for (row = 0;row < m;row++){for (col = 0;col < m;col++)Cr[row][col] = tempA[row][col]; }tempA = Metrix.MetrixSubtractMetrix(C,Cr,m,m);for (row = 0;row < m;row++){for (col = 0;col < m;col++){C[row][col] = tempA[row][col];if (fabs(C[row][col]) < IPSLEN){C[row][col] = 0.0;}}}}str.Format("矩阵A%d QR分解结束后所得到的矩阵为:",m);//计算结果输出DisplayText(str);DisplayMetrix(A,m,m);for (row = 0;row < m;row++) //Mk的QR分解后需要把C付给A{for (col = 0;col < m;col++)A[row][col] = C[row][col];}str.Format("迭代完成后的矩阵A%d = ",k);DisplayText(str);DisplayMetrix(A,m,m);}DisplayText("矩阵A的全体特征值如下: ");for (i = 0;i<nCol;i++){str.Format("%.6e + j%.6e",eigenvalue[i].Realnum,eigenvalue[i].Imagnum);DisplayText(str);}// -------------------------------------------------//求实特征值的特征向量,在拟上三角矩阵基础上直接求解即可////(A-egiI)X = 0.0;m = nRow;for (row = 0;row < nRow;row++) //用于计算特征向量{for (col = 0;col < nCol;col++)A[row][col] = R[row][col];}double **I = new double*[m]; //求单位矩阵I,分配m*m矩阵空间double sum = 0.0;for (i = 0;i < m;i++){I[i] = new double[m];}for (i = 0;i < m;i++){for (int j = 0;j < m;j++){if(i == j)I[i][j] = 1;else I[i][j] = 0;}}for (i = 0;i < nRow;i++){if (eigenvalue[i].Imagnum != 0.0){str.Format("特征值%.6e+j%.6e为虚数,不需要求特征向量。


《数据结构与算法设计》实验报告——实验二学院:自动化学院班级:____学号:__姓名:_____一、实验目的1、熟悉VC 环境,学习使用C 语言实现栈的存储结构。
2、通过编程、上机调试,进一步理解栈的基本概念。
3、锻炼动手编程,独立思考的能力。
二、实验内容实现简单计算器的功能,请按照四则运算加、减、乘、除、幂(^)和括号的优先关系和惯例,编写计算器程序。
要求支持运算符:+、-、*、/、%、()和=:① 从键盘输入一个完整的表达式,以回车作为表达式输入结束的标志;② 输入表达式中的数值均为大于等于零的整数,如果中间计算过程中出现小数也只取整进行计算。
例如,输入:4+2*5= 输出:14 输入:(4+2)*(2-10)= 输出:-48 三、程序设计 1、概要设计为实现上述程序功能,应使用两个栈,分别寄存操作数与运算符。
为此,需要栈的抽象数据结构。
(1)、栈的抽象数据类型定义为: ADT Stack{数据对象:D={|,1,2,,,0}i i a a ElemSet i n n ∈=≥数据关系:R1=11{,|,,2,,}i i i i a a a a D i n --<>∈=约定n a端为栈顶,1a端为栈底。
基本操作:InitStack(&S)操作结果:创建一个空栈S。
GetTop(S,&e)初始条件:栈S已存在且非空。
操作结果:用e返回S的栈顶元素。
Push(&S,e)初始条件:栈S已存在。
操作结果:插入元素e为新的栈顶元素。
Pop(&S,&e)初始条件:栈S已存在且非空。
操作结果:删除S的栈顶元素,并用e返回其值。
In(m,a[])操作结果:若m是运算符,返回TRUE。
Precede(m, n)初始条件:m,n为运算符。
操作结果:若m优先级大于n,返回>,反之亦然。
Operation(a, theta,b)初始条件:a,b为整数,theta为运算符。

数值分析大作业数值分析大作业姓名:黄晨晨学号:S1*******学院:储运与建筑工程学院学院班级:储建研17-2实验3.1 Gauss消去法的数值稳定性实验实验目的:理解高斯消元过程中出现小主元即很小时引起方程组解数值不定性实验内容:求解方程组Ax=b,其中(1)A1=0.3×10?1559.14315.291?6.130?1211.29521211,b1=59.1746.7812;(2)A2=10?7013 2.099999999999625?15?10102,b2=85.90000000000151;实验要求:(1)计算矩阵的条件数,判断系数矩阵是良态的还是病态的(2)用Gauss列主元消去法求得L和U及解向量x1,x2∈R4(3)用不选主元的高斯消去法求得L和U及解向量x1,x2∈R4(4)观察小主元并分析对计算结果的影响(1)计算矩阵的条件数,判断系数矩阵是良态的还是病态的代码:format longeformat compactA1=[0.3*10^-15,59.14,3,1;5.291,-6.130,-1,2;11.2,9,5,2;1,2,1,1] b1=[59.17;46.78;1;2]n=4C1=cond(A1,1) %C1为A1矩阵1范数下的条件数C2=cond(A1,2) %C2为A1矩阵2范数下的条件数C3=cond(A1,inf) %C3为1矩阵谱范数下的条件数结果:C1 =1.362944708720448e+02C2 =6.842955771253409e+01C3 =8.431146*********e+01显然A1矩阵为病态矩阵将矩阵A2,b2输入上述代码中求得A2矩阵的条件数为:C1 =1.928316831682894e+01C2 =8.993938090170119e+00C3 =1.835643564356072e+01显然A2矩阵也为病态矩阵(2)用Gauss列主元消去法求得L和U及解向量x1,x2∈R4代码:for k=1:n-1a=max(abs(A1(k:n,k)))if a==0returnendfor i=k:nif abs(A1(i,k))==ay=A1(i,:)A1(i,:)=A1(k,:)A1(k,:)=yx=b1(i,:)b1(i,:)=b1(k,:)b1(k,:)=xbreakendendif A1(k,k)~=0A1(k+1:n,k)=A1(k+1:n,k)/A1(k,k)A1(k+1:n,k+1:n)=A1(k+1:n,k+1:n)-A1(k+1:n,k)*A1(k,k+1:n) elsebreakendendL=tril(A1,0);for i=1:nL(i,i)=1;endLU=triu(A1,0)y1=L\b1x1=U\y1得到如下结果:x1 =3.845714853511634e+001.609517394778522e+00-1.547605454206655e+011.041130489899787e+01将A2=[10,-7,0,1;-3,2.0999********,6,2;5,-1,5,-1;0,1,0,2]b2=[8;5.900000000001;5;1]代入上述代码求得结果如下:X2 =4.440892098500626e-16-9.999999999999993e-019.999999999999997e-011.000000000000000e+00(3)用不选主元的高斯消去法求得L和U及解向量x1,x2∈R4代码:format longeformat compactA1=[0.3*10^-15,59.14,3,1;5.291,-6.130,-1,2;11.2,9,5,2;1,2,1,1] b1=[59.17;46.78;1;2][L,U]=lu(A1)y1=L\b1x1=U\y1求得如下结果:x1=3.845714853511634e+001.609517394778522e+00-1.547605454206655e+011.041130489899787e+01将A2=[10,-7,0,1;-3,2.0999********,6,2;5,-1,5,-1;0,1,0,2] b2=[8;5.900000000001;5;1]代入上述代码,求得结果如下:x 2 =4.440892098500626e-16 -9.999999999999993e-01 9.999999999999997e-01 9.999999999999999e-01(2)(3)求得结果相同,可验证结果正确。

《数据结构与算法设计》实验报告——实验二学院:自动化学院班级:06111001学号:**********姓名:宝竞宇一、实验目的掌握栈的建立,输入,删除,出栈等基本操作。
应用栈解决实际问题。
二、实验内容实现简单计算器的功能,请按照四则运算加、减、乘、除、幂(^)和括号的优先关系和惯例,编写计算器程序。
要求支持运算符:+、-、*、/、%、()和=:①从键盘输入一个完整的表达式,以回车作为表达式输入结束的标志;②输入表达式中的数值均为大于等于零的整数,如果中间计算过程中出现小数也只取整进行计算。
例如,输入:4+2*5= 输出:14输入:(4+2)*(2-10)= 输出:-48三、程序设计1、概要设计抽象数据类型定义:两个栈结构,分别用来储存数据和计算符号宏定义:函数“成功”,“失败的返回值”在主程序程序中先依次输入各表达式,存入相应各栈,然后,调用“判断函数”来判断计算符的优先次序,然后再利用计算函数来计算,表达式值。
其中还有,取栈顶元素函数,存入栈函数。
2、详细设计数据类型实现:struct t{ char dat[200];int top;}prt;入栈函数:存入数组,栈顶指针上移void pushd(long int a){ prd.dat[prd.top++]=a;}出栈:取出对应值,栈顶指针下移long int popd( ){ return prd.dat[--prd.top];}比较优先级:建立数组,比较返回大于小于号。
计算函数:以字符型输入,运算符号,用switch来分支计算判断,返回计算数值long int operation ( long int x, long int y, char a){ s witch(a){ case '+': return x+y;case '-': return x-y;case '*': return x*y;case '/': if ( y )return x/y;else{ printf("Divide 0.\n");return 0;}case '%': return (long int) fmod(x,y);case '^': if (y>=0 ) return (long int) pow(x,y);else return (0);default: printf("Error No. 3\n");return 0;}}主程序:在主程序内,以字符串的形式输入表达式,然后分别调用函数存入各相应栈,然后用数组判断,比较运算符的优先顺序。

课程设计课程名高等数值计算称:设计题数值计算B课程设计目:学号:姓名:完成时2014年10月20日间:题目一:非线性方程求根用Newton 法计算下列方程(1) 310x x --=,初值分别为01x =,00.45x =,00.65x =;(2) 32943892940x x x +-+=其三个根分别为1,3,98-。
当选择初值02x =时给出结果并分析现象,当6510ε-=⨯,迭代停止。
一、摘要非线性方程的解析解通常很难给出,因此非线性方程的数值解就尤为重要。
本实验通过使用常用的求解方法二分法和Newton 法及改进的Newton 法处理几个题目,分析并总结不同方法处理问题的优缺点。
观察迭代次数,收敛速度及初值选取对迭代的影响。
二、数学原理构造迭代函数的一条很重要的途径是,用近似方程来代替原方程去求根。
因此,如果能将非线性方程用线性方程来代替的话,求近似根问题就很容易解决,而且十分方便。
Newton 法就是把非线性方程线性化的一种方法。
在求解非线性方程()0f x =时,它的困难在于()f x 是非线性函数,为克服这一困难,考虑它的线性展开。
设当前点为k x ,在k x 处的Taylor 展开式为()()()()k k k f x f x f x x x '≈+-令()0f x =,可以得到上式的近似方程()()()0k k k f x f x x x '+-=设()0k f x '≠,解其方程得到1()(0,1,)()k k k k f x x x k f x +=-='…这就是牛顿迭代公式。
用牛顿迭代公式求方程()0f x =根的方法称为牛顿迭代法。
牛顿迭代法的几何意义为,不断用切线来近似曲线得到方程的根,我们知道方程()0f x=的实根*x是函数()y f x=的图形与横坐标的交点,1kx+是函数()f x在点(,())k kx f x处的切线与x轴的交点,此时就是用切线的零点代替曲线的零点,因此,牛顿迭代法又称为切线法。
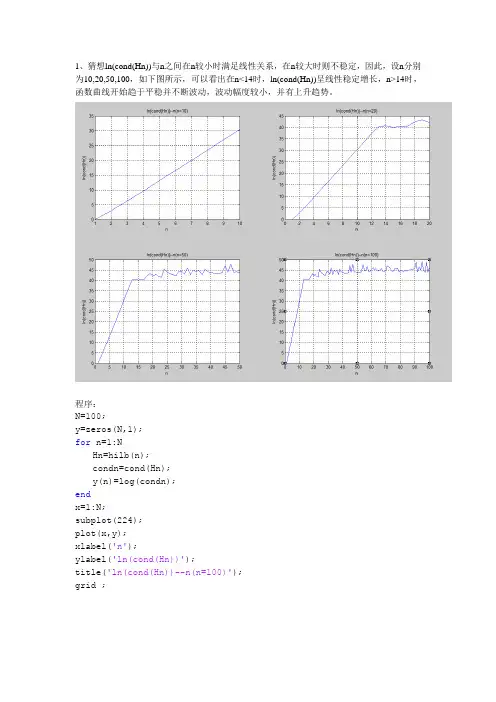
1、猜想ln(cond(Hn))与n之间在n较小时满足线性关系,在n较大时则不稳定,因此,设n分别为10,20,50,100,如下图所示,可以看出在n<14时,ln(cond(Hn))呈线性稳定增长,n>14时,函数曲线开始趋于平稳并不断波动,波动幅度较小,并有上升趋势。
程序:N=100;y=zeros(N,1);for n=1:NHn=hilb(n);condn=cond(Hn);y(n)=log(condn);endx=1:N;subplot(224);plot(x,y);xlabel('n');ylabel('ln(cond(Hn))');title('ln(cond(Hn))--n(n=100)');grid ;2、可以看出,log(cond(Hnpre)/cond(Hn))在y=0上下波动。
对比整个曲线图,可以发现,经过预处理,条件数有所下降,但下降值不大。
程序:x=1:100;y=zeros(100,1);y1=zeros(100,1);y2=zeros(100,1);for n=1:100Hn=hilb(n);inv_D=zeros(n);for i=1:ninv_D(i,i)=1/sqrt(Hn(i,i));endHnpre=inv_D*Hn*inv_D;y(n)=log(cond(Hnpre)/cond(Hn));y1(n)=log(cond(Hnpre));y2(n)=log(cond(Hn));end%plot(x,y1);plot(x,y,'r',x,y1,'g',x,y2,'k');legend('y','y1','y2');xlabel('n');ylabel('log(cond(Hnpre)/cond(Hn))');title('log(cond(Hnpre)/cond(Hn))--n(n=100)');grid on;3、设b所有值为1,n x1 x2 x34 -4.0000E+00 -4.0000E+00 -4.0000E+00 6.0000E+01 6.0000E+01 6.0000E+01 -1.8000E+02 -1.8000E+02 -1.8000E+02 1.4000E+02 1.4000E+02 1.4000E+0255.0000E+00 5.0000E+00 5.0000E+00 -1.2000E+02 -1.2000E+02 -1.2000E+026.3000E+02 6.3000E+02 6.3000E+02 -1.1200E+03 -1.1200E+03 -1.1200E+03 6.3000E+02 6.3000E+02 6.3000E+026 -6.0000E+00 -6.0000E+00 -6.0000E+00 2.1000E+02 2.1000E+02 2.1000E+02 -1.6800E+03 -1.6800E+03 -1.6800E+03 5.0400E+03 5.0400E+03 5.0400E+03 -6.3000E+03 -6.3000E+03 -6.3000E+03 2.7720E+03 2.7720E+03 2.7720E+0377.0000E+00 7.0000E+00 7.0000E+00 -3.3600E+02 -3.3600E+02 -3.3600E+02 3.7800E+03 3.7800E+03 3.7800E+03-1.6800E+04 -1.6800E+04 -1.6800E+04 3.4650E+04 3.4650E+04 3.4650E+04 -3.3264E+04 -3.3264E+04 -3.3264E+04 1.2012E+04 1.2012E+04 1.2012E+048 -8.0000E+00 -8.0000E+00 -8.0000E+00 5.0400E+02 5.0400E+02 5.0400E+02 -7.5600E+03 -7.5600E+03 -7.5600E+03 4.6200E+04 4.6200E+04 4.6200E+04 -1.3860E+05 -1.3860E+05 -1.3860E+05 2.1622E+05 2.1622E+05 2.1622E+05 -1.6817E+05 -1.6817E+05 -1.6817E+05 5.1480E+04 5.1480E+04 5.1480E+0499.0000E+00 9.0000E+00 9.0001E+00 -7.2000E+02 -7.2000E+02 -7.2000E+02 1.3860E+04 1.3860E+04 1.3860E+04 -1.1088E+05 -1.1088E+05 -1.1088E+05 4.5045E+05 4.5045E+05 4.5045E+05 -1.0090E+06 -1.0090E+06 -1.0090E+06 1.2613E+06 1.2613E+06 1.2613E+06 -8.2368E+05 -8.2368E+05 -8.2368E+05 2.1879E+05 2.1879E+05 2.1879E+0510 -9.9980E+00 -9.9987E+00 -1.0001E+01 9.8983E+02 9.8989E+02 9.9005E+02 -2.3756E+04 -2.3758E+04 -2.3761E+04 2.4021E+05 2.4022E+05 2.4025E+05 -1.2611E+06 -1.2612E+06 -1.2613E+06 3.7833E+06 3.7835E+06 3.7839E+06 -6.7260E+06 -6.7263E+06 -6.7269E+06 7.0006E+06 7.0008E+06 7.0015E+06 -3.9378E+06 -3.9380E+06 -3.9383E+06 9.2370E+05 9.2373E+05 9.2380E+05111.0927E+01 1.0988E+01 1.0992E+01 -1.3124E+03 -1.3188E+03 -1.3192E+03 3.8410E+04 3.8580E+04 3.8587E+04 -4.7823E+05 -4.8015E+05 -4.8022E+05 3.1396E+06 3.1513E+06 3.1515E+06 -1.2060E+07 -1.2102E+07 -1.2102E+072.8484E+07 2.8575E+07 2.8576E+07 -4.1864E+07 -4.1989E+07 -4.1990E+073.7293E+07 3.7398E+07 3.7398E+07 -1.8420E+07 -1.8469E+07 -1.8469E+07 3.8689E+06 3.8786E+06 3.8785E+0612 -9.6349E+00 -1.2768E+01 -1.1739E+01 1.4311E+03 1.8176E+03 1.6833E+03-5.1063E+04 -6.3363E+04 -5.9039E+047.7783E+05 9.4708E+05 8.8711E+05-6.3022E+06 -7.5528E+06 -7.1069E+063.0320E+07 3.5851E+07 3.3868E+07-9.1788E+07 -1.0728E+08 -1.0171E+081.7935E+082.0753E+08 1.9736E+08-2.2572E+08 -2.5889E+08 -2.4688E+081.7662E+082.0099E+08 1.9214E+08-7.8125E+07 -8.8290E+07 -8.4591E+071.4921E+07 1.6757E+07 1.6087E+07可以看出,当n<9时,三种方法计算出的结果几乎一致,当n>9时,三种方法计算出的结果相差越来越大。
本资料由理硕教育整理,理硕教育是全国唯一专注于北理工考研辅导的学校,相对于其它机构理硕教育有得天独厚的优势。
丰富的理工内部资料资源与人力资源确保每个学员都受益匪浅,确保理硕教育的学员初试通过率89%以上,复试通过率接近100%,理硕教育现开设初试专业课VIP一对一,初试专业课网络小班,假期集训营,复试VIP一对一辅导,复试网络小班,考前专业课网络小班,满足学员不同的需求。
因为专一所以专业,理硕教育助您圆北理之梦。
详情请查阅理硕教育官网第 4 章广义线性表——多维数组和广义表课后习题讲解1. 填空⑴数组通常只有两种运算:()和(),这决定了数组通常采用()结构来实现存储。
【解答】存取,修改,顺序存储【分析】数组是一个具有固定格式和数量的数据集合,在数组上一般不能做插入、删除元素的操作。
除了初始化和销毁之外,在数组中通常只有存取和修改两种操作。
⑵二维数组A中行下标从10到20,列下标从5到10,按行优先存储,每个元素占4个存储单元,A[10][5]的存储地址是1000,则元素A[15][10]的存储地址是()。
【解答】1140【分析】数组A中每行共有6个元素,元素A[15][10]的前面共存储了(15-10)×6+5个元素,每个元素占4个存储单元,所以,其存储地址是1000+140=1140。
⑶设有一个10阶的对称矩阵A采用压缩存储,A[0][0]为第一个元素,其存储地址为d,每个元素占1个存储单元,则元素A[8][5]的存储地址为()。
【解答】d+41【分析】元素A[8][5]的前面共存储了(1+2+…+8)+5=41个元素。
⑷稀疏矩阵一般压缩存储方法有两种,分别是()和()。
【解答】三元组顺序表,十字链表⑸广义表((a), (((b),c)),(d))的长度是(),深度是(),表头是(),表尾是()。
【解答】3,4,(a),((((b),c)),(d))⑹已知广义表LS=(a,(b,c,d),e),用Head和Tail函数取出LS中原子b的运算是()。
课程设计2013年07月20日设计题目 《数值分析》课程设计学生姓名 ****学 号 ####专业班级指导教师1.1水手、猴子和椰子问题算法分析:设椰子起初的数目为0p ,第一至第五次猴子在夜里藏椰子后,椰子的数目分别为0p ,1p ,2p ,3p ,4p ,再设最后每个人分得x 个椰子,由题意得:15541(1),0,1,2,3,4.(1)=5155k k p p k x p p x +=-==-+所以利用逆向递推方法求解:n=input('n='); for x=1:n p=5*x+1; for k=1:5 p=5*p/4+1; endif p==fix(p) break end enddisp([x,p])执行代码后得: n= 1023 15621 (输入n=1000000) 即最后每个人分得1023个椰子,椰子总数为156211.2当0,1,2,,100n = 时,选择稳定的算法计算积分10d 10nxn xe I x e --=+⎰ 由1100(1)1110010101,1010110(1)10x x n x nxnxn n n x e I I dx e e e I I dx e dx e e n---+---+-++==+++===-+⎰⎰⎰ 得0111(1)1011[(1)],100,99,...,1.10n n n I I I e I n n -+⎧=-⎪⎪⎨⎪=--=⎪⎩由上式可知求n I 时,1n I +的误差的影响被缩小了。
n=100时100I 的近似值为0。
matlab 代码为fprintf('稳定算法:\n')y0=0;n=100;plot(n,y0,'r*');hold onfprintf('y[100]=%10.6f',y0);while(1)y1=1/10*[(1-exp(-n))/n-y0];fprintf('y[%10.0f]=%10.6f',n-1,y1);plot(n-1,y1,'r*') if(n<=1) break;endy0=y1;n=n-1;if mod(n,3)==0,fprintf('\n'),end,end(具体值已省略)编程实现得下图。
文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 1文档来源为:从网络收集整理.word版本可编辑. 利用组中值计算均值是假定各组数据在各组中是均匀分布的,计算结果是准确的。( ) 判断题 10.0 错误 未判断 ×
平均差与方差的主要区别是对离差的处理方式不同。( ) 判断题 10.0 正确 未判断 ×
在实际调查中,调查对象中的每一个单位必然是调查单位。( ) 判断题 10.0 错误 未判断 ×
如果数据呈正态分布,则均值大小不受数据中极端值的影响。( ) 判断题 10.0 正确 未判断 ×
时期数的特点是可以连续累计。( ) 判断题 10.0 正确 未判断 ×
抽样调查是利用全体中的一部分进行推断,就不可避免地会有推断误差。() 判断题 10.0 正确 未判断 ×
次数分配表是直观表示统计数据整理结果的唯一形式。() 判断题 10.0 错误 未判断 ×
甲地职工工资的标准差为30元,乙地职工工资的标准差为25元,所以甲地职工工资的差异适度一定大于乙地。() 判断题 10.0 错误 未判断 ×
调查对象与调查单位具有一定的对应关系。如果调查对象是全部商业企业,则调查单位是( )。 单选题 10.0 1 ×
确定连续变量的组限时,相邻组的组限是( )。 单选题 10.0 2 ×
本次作业总分值:100.0 得分:0.0 正确的题数:0 题目总数:10 正确率:0.0%
某连续变量组距数列,某末组为开口组,下限为500 ,又知其邻组的组中值为480 ,则末组组中值为520 。( ) 判断题 8.0 正确 未判断 ×
两组数据的均值相等,标准差大的,离散程度也大。( ) 判断题 8.0 正确 未判断 ×
统计报表是我国定期取得统计数据的一种重要方式。() 判断题 8.0 正确 未判断 ×
抽样调查是利用全体中的一部分进行推断,就不可避免地会有推断误差。() 判断题 8.0 正确 未判断 ×
数值分析大作业数值分析大作业学号:*********专业:机械工程学生姓名:***2014年10月摘要:在自然科学与工程技术中,很多问题的解决常常归结为求解线性方程组Ax=b 。
随着计算机的发展,利用计算机这个强有力的计算工具去求解线性方程组是一个非常实用的问题。
在求解大型线性方程组时,直接法在多次消元,回代的过程中,四则运算的误差累计与传播无法控制,致使计算结果的精度就无法保证,特别是求解大型稀松矩阵时,还要对系数矩阵进行分解。
而迭代法相对于直接法而言,具有保持迭代矩阵不变的特点,计算程序一般也比较简单,且对于许多问题收敛速度比较快。
比较常用的迭代法有雅克比迭代法、高斯一塞德尔迭代法和逐次超松弛迭代法等,本次研究目的是通过求解一个线性方程组来比较它们的迭代效果,验证一些已有的结论。
1.数学原理1.1雅可比迭代法将线性方程组的系数矩n n ij R a A ?∈=)(分解为A=D+L+U ,其中D 是由A 的主对角元素构成的对角矩阵,L 是由A 的严格下三角部分构成的严格下三角矩阵, U 是由A 的严格上三角部分构成的严格上三角矩阵,即,2211=nn a a a D.0000,0000,1223113121,21323121==--n n n n n n n n a a a a a a U a a a a a a L若系数矩阵A 的对角元素),,2,1(0n i a ii =≠,则矩阵D 非奇异,取M=D ,N=-(L+U),则J J g x G b D x U L D x +=++-=--11)(,因而,构造的迭代法为:.),(,11)()1(b D g U L D G g x G x J J J k J k --+=+-=+=1.2高斯-赛得尔迭代法将线性方程组的系数矩n n ij R a A ?∈=)(分解为A=D+L+U 。
若系数矩阵A 的对角元素不等于0,则矩阵D 非奇异,取M=L+D ,N=-U ,则()()G G g x G b D L Ux D L x +=+++-=--11因而,构造的迭代法为:()().,,11)()1(b D L g U D L G g x G x G G G k G k --++=+-=+=1.3逐次超松弛迭代法线性方程组的系数矩n n ij R a A ?∈=)(分解为A=D+L+U 。
北京理工大学数据结构作业(全)北理工数据结构作业第二章作业1、在什么情况下用顺序表比链表好?(题集2.3)需要对线性表进行随机存取时,顺序表比链表好。
2、已知L是带表头结点的非空单链表,且P结点既不是首元结点,也不是尾元结点,试从下列提供的答案中选择合适的语句序列。
(题集2.7)a.删除P结点的直接后继结点的语句序列是11 3 14。
b.删除P结点的直接前驱结点的语句序列是10 12 8 3 14。
c.删除P结点的语句序列是10 12 7 3 14。
d.删除首元结点的语句序列是12 11 3 14。
e.删除尾元结点的语句序列是12 11 3 14。
(1)p = p->next;(2)p->next = p;(3)p->next = p->next->next;(4)p = p->next->next;(5)while ( p!=NULL ) p=p->next;(6)while ( q->next!=NULL ) { p=q; q=q->next; }(7)while ( p->next!=q ) p=p->next;(8)while ( p->next->next!=q ) p=p->next;(9)while ( p->next->next!=NULL ) p=p->next;(10)q=p;(11)q=p->next;(12)p=l;(13)l=l->next;(14)free(q);3、算法设计。
设顺序表va中的数据元素递增有序,请设计一算法,将x插入到顺序表的适当位置,以保持该表的有序性。
(题集2.11)typedef struct{ElemType *elem;int length;int listsize;}Sqlist;Status ListInsert_Sq(Sqlist &va , ElemType x){if(va.length==va.listsize) return ERROR;for(i=va.length-1;i>=0&&xva.elem[i+1]=x;va.length++;return OK;}4、算法设计。
数值分析上机作业 第 1 章 1.1计算积分,n=9。(要求计算结果具有6位有效数字) 程序: n=1:19; I=zeros(1,19); I(19)=1/2*((exp(-1)/20)+(1/20)); I(18)=1/2*((exp(-1)/19)+(1/19));
for i=2:10 I(19-i)=1/(20-i)*(1-I(20-i)); end format long disp(I(1:19))
结果截图及分析:在MATLAB中运行以上代码,得到结果如下图所示:当计算
到数列的第10项时,所得的结果即为n=9时的准确积分值。取6位有效数字可得. 1.2分别将区间[-10.10]分为100,200,400等份,利用mesh或surf命令画出二元函数
z= 的三维图形。
程序: >> x = -10:0.1:10; y = -10:0.1:10; [X,Y] = meshgrid(x,y); Z = exp(-abs(X))+cos(X+Y)+1./(X.^2+Y.^2+1); subplot(2,2,1); mesh(X,Y,Z); title('步长0.1')
>> x = -10:0.2:10; y = -10:0.2:10; [X,Y] = meshgrid(x,y); Z = exp(-abs(X))+cos(X+Y)+1./(X.^2+Y.^2+1); subplot(2,2,1); mesh(X,Y,Z); title('步长 0.2')
>>x = -10:0.05:10; y = -10:0.05:10; [X,Y] = meshgrid(x,y); Z = exp(-abs(X))+cos(X+Y)+1./(X.^2+Y.^2+1); subplot(2,2,1); mesh(X,Y,Z); title('步长0.05') 结果截图及分析:由图可知,步长越小时,绘得的图形越精确。 第 2 章 试用MATLAB编程实现追赶法求三对角方程组的算法,并考虑梯形电路电阻问题:电路中的电流128{,,,}iiiL满足下列线性方程组:
1212323434545656767878
22/252025202520252025202520250iiVRiiiiiiiiiiiiiiiiiiii
设220,27VVR,求各段电路的电流量。
处理思路:观察该方程的系数矩阵可知,它是一个三对角矩阵,故可运用追赶法对其进行求解。
程序: for i=1:8 a(i)=-2;b(i)=5;c(i)=-2;d(i)=0; end a(1)=0;b(1)=2;c(8)=0;d(1)=220/27; for i=2:8 a(i)=a(i)/b(i-1); b(i)=b(i)-c(i-1)*a(i); d(i)=d(i)-a(i)*d(i-1); end d(8)=d(8)/b(8); for i=7:-1:1 d(i)=( d(i)-c(i)*d(i+1) )/b(i); end for i=1:8 x(i)=d(i); end x 结果截图及分析:在MATLAB中运行以上代码,得到结果如下图所示:图中8
个值依次为128{,,,}iiiL
的数值。 第 3 章 试分别用(1)Jacobi迭代法;(2)Gauss-Seidel解线性方程组 12345
10123412191232721735143231211743511512xxxxx
迭代初始向量取(0)(0,0,0,0,0)Tx.
3.1 Jacobi迭代法 程序: >> A=[10 1 2 3 4; 1 9 -1 2 -3; 2 -1 7 3 -5; 3 2 3 12 -1; 4 -3 -5 -1 15]; b=[12;-27;14;-17;12]; x0=[0;0;0;0;0]; D=diag(diag(A)); I=eye(5); L=-tril(A,-1); B=I-D\A; g=D\b; y=B*x0+g; n=1; while norm(y-x0)>=1.0e-6 x0=y; y=B*x0+g; n=n+1; end fprintf('%8.6f\n',y); n 结果截图及分析: 得到此结果时迭代次数为67次,达到精度要求。
3.2 Gauss-Seidel迭代法: 程序: >> A=[10 1 2 3 4; 1 9 -1 2 -3; 2 -1 7 3 -5; 3 2 3 12 -1; 4 -3 -5 -1 15]; b=[12;-27;14;-17;12]; x0=[0;0;0;0;0];
D=diag(diag(A)); U=-triu(A,1); L=-tril(A,-1); M=(D-L)\U; g=(D-L)\b; y=M*x0+g; n=1; while norm(y-x0)>=1.0e-6 x0=y; y=M*x0+g; n=n+1; end fprintf('%8.6f\n',y);
结果截图及分析:
Gauss-Seidel迭代法只需要迭代38次即可满足精度要求。 第 4 章 设A=162621666612,取先用幂法迭代3次,得到A的按模最大特征值的近似值,取为其整数部分,再用反幂法计算A的按模最大特征值的更精确的近似值,要求误差小于.
程序: A=[12 6 -6; 6 16 2; -6 2 16]; x0=[1;1;1]; y=x0;b=max(abs(x0));k=1; while ( k<4 ) x=A*y;b=max(abs(x));y=x./b; k=k+1; fprintf('eig1 equals %6.4f\n',b); end >> bb0=fix(b); I=eye(3,3); x0=[1;1;1]; y=x0;l=0;bb=max(abs(x0));k=1; while ( abs(bb-l)>=1.0e-10 ) l=bb; x=(A-bb0*I)\y;bb=max(abs(x));y=x./bb; eig=l+b; >> fprintf('eig2(%d) equals %12.10f\n',k, eig); k=k+1; end
实验截图及分析: 由图可知,由幂法3次迭代后得到的特征值为19.4,而由反幂法得到的特征值为20.3999999999.误差小于 第 5 章 试编写MATLAB函数实现Newton插值,要求能输出插值多项式。对函数f(x)=在区间[-5,5]上实现10次多项式插值。要求: (1)输出插值多项式。 (2)在区间[-5,5]均匀插入99个节点,计算这些节点上函数f(x)的近似值,并在同一图上画出原函数和插值多项式的图形。 (3)观察龙格现象,计算插值函数在各节点处的误差,并画出误差图。
5.1输出插值多项式 程序: x=-5:1:5; y=1./(1+4*(x.^2)); newpoly(x,y)
function [c,d]=newpoly(x,y) n=length(x); d=zeros(n,n); d(:,1)=y'; for j=2:n for k=j:n d(k,j)=(d(k,j-1)-d(k-1,j-1))/(x(k)-x(k-j+1)); end end c=d(n,n); for k=(n-1):-1:1 c=conv(c,poly(x(k))); m=length(c); c(m)=c(m)+d(k,k); end end
结果及分析: ans = Columns 1 through 2 -0.3049 Columns 3 through 4 0.8483 0.0000 Columns 5 through 6 -0.6720 0.0000 Columns 7 through 8 0.2312 0.0000 Columns 9 through 10 -1.1025 0.0001 Column 11 1.0000 10次插值多项式由高到低系数为Columns 1至Column 11