
二次函数与圆的综合
2
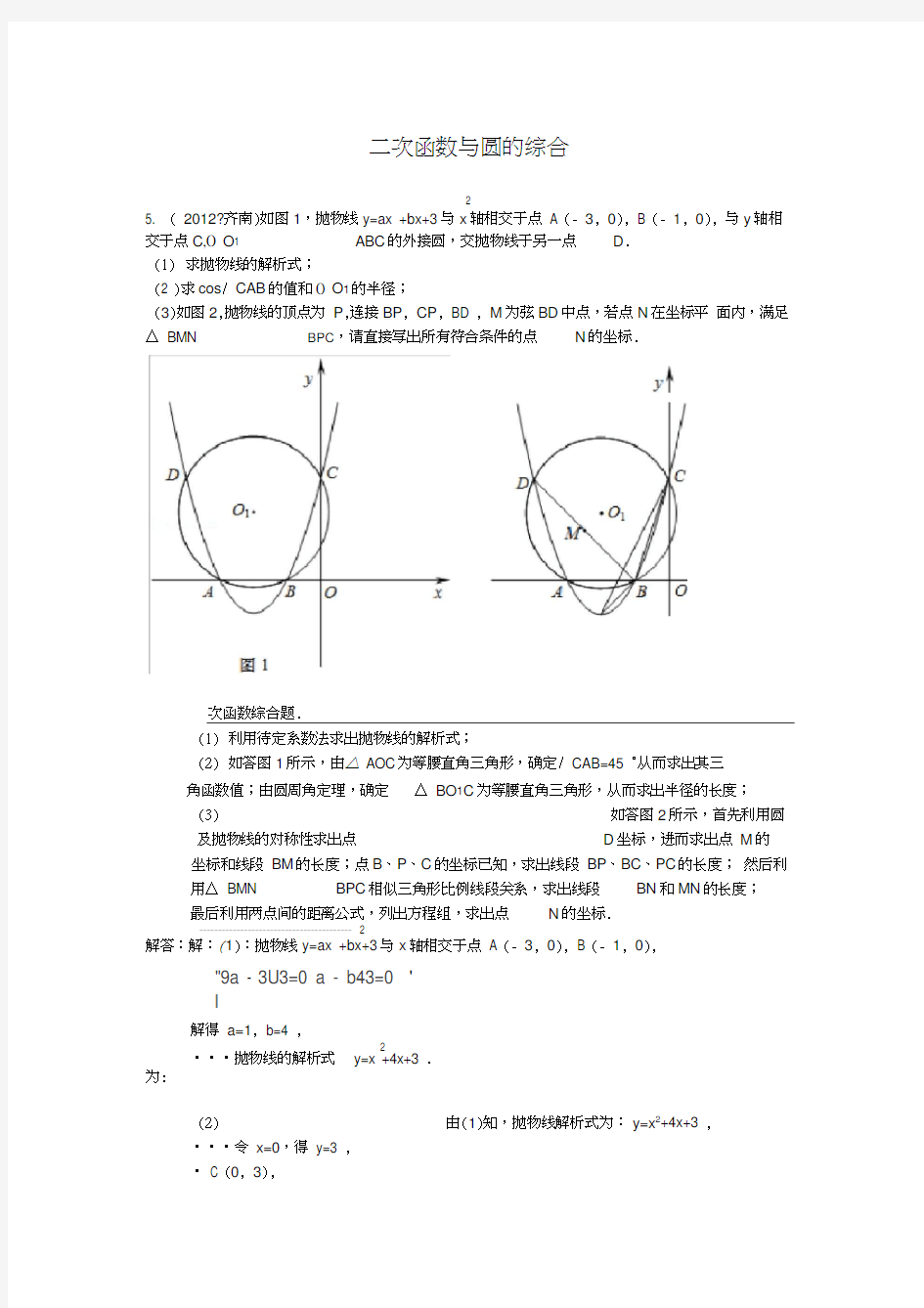
5. ( 2012?齐南)如图1,抛物线y=ax +bx+3与x 轴相交于点 A (- 3, 0), B (- 1, 0), 与y 轴相交于点C ,O O 1 ABC 的外接圆,交抛物线于另一点 D . (1) 求抛物线的解析式;
(2 )求cos / CAB 的值和O O 1的半径;
(3)如图2,抛物线的顶点为 P ,连接BP , CP , BD , M 为弦BD 中点,若点N 在坐标平 面内,满足△ BMN
BPC ,请直接写出所有符合条件的点
N 的坐标.
次函数综合题
.
(1) 利用待定系数法求出抛物线的解析式;
(2) 如答图1所示,由△ AOC 为等腰直角三角形,确定/ CAB=45 °从而求出其三 角函数值;由圆周角定理,确定 △ BO 1C 为等腰直角三角形,从而求出半径的长度;
(3)
如答图2所示,首先利用圆及抛物线的对称性求出点 D 坐标,进而求出点 M 的
坐标和线段 BM 的长度;点B 、P 、C 的坐标已知,求出线段 BP 、BC 、PC 的长度; 然后利
用△ BMN
BPC 相似三角形比例线段关系,求出线段
BN 和MN 的长度;
最后利用两点间的距离公式,列出方程组,求出点
N 的坐标.
----------------------------------------- 2
解答:解:(1):抛物线y=ax +bx+3与x 轴相交于点 A (- 3, 0), B (- 1, 0),
"9a - 3U3=0 a - b43=0 '
I
解得 a=1, b=4 , ???抛物线的解析式
为:
(2)
由(1)知,抛物线解析式为: y=x 2+4x+3 ,
???令 x=0,得 y=3 , ? C (0, 3),
2
y=x +4x+3 .
? OC=OA=3,则△ AOC为等腰直角三角形,???/ CAB=45 °
??? cos/ CAB= —
2
在Rt△ BOC中,由勾股定理得:BC=叶 + 32=V15-
如答图1所示,连接O i B、O l C,
由圆周角定理得:/ BO i C=2/ BAC=90 °
?△ BO1C为等腰直角三角形,
? -O O i的半径O〔B=
2 2
(3)抛物线y=x +4x+3= (x+2) - 1,?顶点P坐标为(-2,- 1),对称轴为x= - 2.
又??? A (- 3, 0) , B (- 1 , 0),可知点A、B关于对称轴x= 如答图2所示,由圆及抛物线的对称性可知:点D、点C (0, ?- D (- 4, 3).
又???点M为BD中点,B (- 1 , 0), 2对称.
3)关于对称轴对称,
? BM=
在厶BPC 中,B (- 1 , 0) , P (- 2, - 1) , C ( 0 , 3), 由两点间的距离公式得:BP= . ■: , BC= |II , PC= / 7.
?/△ BMN BPC ,
BN IN
?,即
"BP_BC_PC, 7TWI5TV?
设N (x, y),由两点间的距离公式可得:
(览+1) \y
2
24 (y-f5心后2
解之得,
7 =-3 1 2
?点N的坐标为(二, 1
9,或(#
? M (
r 2 o 2
MN= 匚
解得:BN=
I
圉1
点评:本题综合考查了二次函数的图象与性质、待定系数法、圆的性质、相似三角形、勾股定理、两点间的距离公式等重要知识点,涉及的考点较多,试题难度较大?难点在于第(3)问,需要认真分析题意,确定符合条件的点N有两个,并画出草图;然后寻
找线段之间的数量关系,最终正确求得点N的坐标.
2
6. (2011?遵义)已知抛物线y=ax +bx+3 (a老)经过A (3, 0), B (4, 1)两点,且与y 轴交于点C.
(1 )求抛物线y=ax +bx+3 (a和)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点卩,使厶PAB是以AB为直
角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三
点的圆交直线AB于点F,当△ OEF的面积取得最小值时,求点E的坐标.
考点:
二次函数综合题.
分析: (1) 根据A ( 3, 0), B (4, 1)两点利用待定系数法求二次函数解析式;
(2) 从当△ PAB 是以AB 为直角边的直角三角形,且/ PAB=90。与当△ PAB 是以AB 为直角边的直角三角形,且/
PBA=90 °分别求出符合要求的答案;
(3) 根据当0E // AB 时,△ FEO 面积最小,得出 OM=ME ,求出即可.
解答:
解:(1)v 抛物线 y=ax +bx+3 (a 和)经过 A (3, 0) , B (4, 1)两点, (16时4b 十3二1’ 解得律, y= I 2 - -^x+3 ;
2 2
???点C 的坐标为:(0, 3); (2)假设存在,分两种情况:
①当厶PAB 是以AB 为直角边的直角三角形,且/ PAB=90 °
如图1,过点B 作BM 丄x 轴于点M , ??? A ( 3, 0), B ( 4, 1), ? AM=BM=1 , ???/ BAM=45 ° , ???/ DAO=45 ° ? AO=DO , TA 点坐标为(3, 0), ? D 点的坐标为:(0 , 3),
?直线AD 解析式为:y=kx+b ,将A , D 分别代入得: ? 0=3k+b , b=3, ? k = - 1 , ? y = - x+3,
? y =七2-禺+3= - x+3 ,
2 2
2
? x - 3x=0 ,
解得:x=0或3,
??? y=3 , y=0 (不合题意舍去),
P点坐标为(0, 3),
???点P、C、D重合,
②当厶PAB是以AB为直角边的直角三角形,且/ PBA=90 °如图2,过点B作BF丄y轴于点F,
由(1)得,FB=4,/ FBA=45 °
???/ DBF=45 °
? DF=4 ,
? D点坐标为:(0, 5), B点坐标为:(4, 1),
?直线BD解析式为:y=kx+b,将B, D分别代入得:
? 1=4k+b, b=5,
? k= - 1,
? y= - x+5,
? y=丄2- 虽+3= - x+5,
2 2
2
? x - 3x- 4=0 ,
解得:X仁-1 , x2=4 (舍),
? y=6,
? P点坐标为(-1, 6),
?点P 的坐标为:(-1, 6), (0 , 3);
(3)如图3:作EM丄AO于M,
???直线AB的解析式为:y=x - 3 ,
? tan/ OAC=1 ,
?/ OAC=45 °
?/ OAC= / OAF=45 °
? AC丄AF,
OE最小时S A FEO最小,
??? OE丄AC时OE最小,
?/ AC 丄AF
? OE // AF
?/ EOM=45 ° ,
? MO=EM ,
?/ E在直线CA上,
? E点坐标为(x, - x+3),
? x= - x+3 ,
解得:x=三,
■- E点坐标
为
点评:此题主要考查了二次函数的综合应用以及待定系数法求函数解析式,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
7. ( 2011?襄阳)如图,在平面直角坐标系xoy中,AB在x轴上,AB=10,以AB为直径的O0'与y 轴正半轴交于点C,连接BC , AC .CD是O 0的切线,AD丄CD于点D, tan/ CAD= 丄抛物线
y=ax2+bx+c过A, B, C三点.
(1 )求证:/ CAD= / CAB ;
(2)①求抛物线的解析式;
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形?若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
4
考点: 分析: 二次函数综合题. I
(1) 连接0C ,由CD 是O O 的切线,可得 0C 丄
CD ,则可证得 0C // AD ,又由
O 'A=0 C ,则可证得/ CAD= / CAB ;
(2) ① 首先证得△ CAO BCO ,根据相似三角形的对应边成比例,可得 2 OC =OA ?OB ,又由 tan / CAO=tan / CAD= ,则可求得CO , AO , BO 的长,然后 利用待定系数法即可求得二次函数的解析式; ② 首先证得△ FO C s^ FAD ,由相似三角形的对应边成比例,即可得到 F 的坐标, 求得直线DC 的解析式,然后将抛物线的顶点坐标代入检验即可求得答案; (3)根据题意分别从 PA // BC 与PB // AC 去分析求解即可求得答案, 小心不要漏解. 解答: (1) 证明:连接O C , ??? CD 是O O 的切线, ??? O C 丄 CD , ?/ AD 丄 CD , ? O 'C // AD ,
???/ O CA= / CAD ,
?/ O A=O C , ???/ CAB= / O CA ,
???/ CAD= / CAB ;
(2) 解:①T AB 是O O 的直径,
???/ ACB=90 °
?/ OC 丄 AB ,
???/ CAB= / OCB ,
? △ CAO BCO ,
?八
…OA"QC ,
2
即 OC =OA ?OB ,
■/ tan / CAO=tan / CAD= —,
2 ? AO=2CO , 又??? AB=10 ,
2
?- OC =2CO (10 - 2CO ), ?/ CO > 0,
??过A 、C 两点的直线解析式为
y=
2X +4 ,
2
? C0=4 , A0=8 , BO=2 ,
?A (- 8, 0), B (2, 0), C (0, 4),
??抛物线y=ax +bx+c 过点A , B , C 三点, ■- c=4,
?抛物线的解析式为:y=-丄x 2
-邑
4
②设直线DC 交x 轴于点F , ? △ AOC ◎△ ADC , ? AD=AO=8 , ?/ O'C // AD , ? △ FOC FAD ,
° AF =_AD
?? 8 ( BF+5 ) =5 ( BF+10 ),
1:
f4a+2M4=0 (6牝-二0 F 1
—— i
b =
3 ■ 2
解得: x+4 ;
2
10
,F 丄,0);
设直线DC 的解析式为
?? BF= y=kx+m ,
解得:
k=
~i
rr 匚4
??直线DC 的解析式为 y= - 3+4 ,
4
由y=
:得顶点E 的坐标为(-
3,
25
4
), 将 E (- 3,
代入直线DC 的解析式y=-上x+4中,
4
25 右边 =-_X (- 3) +4=上产左边
, 4
4
???抛物线顶点 E 在直线CD
上;
(3)存在,P i (- 10,- 6) , P 2 (10,- 36).
①?/ A (- 8, 0) , C (0 , 4), -寺2
-
丄(x+3) 2+ -
4
4
??直线p B 的解析式为r -
1,
( 4 2
二 P i (- 10,- 6).
②求P 2的方法应为过点 A 作与BC 平行的直线, 可求出BC 解析式,进而求出与之平行的直线的解析式, 与求 P i 同法,可求出 x i =- 8, y i =0 (舍去);X 2=10, y 2= - 36.
此题考查了待定系数法求函数的解析式, 相似三角形的判定与性质, 点与函数的关系, 直角梯形等知识?此题综合性很强,难度较大,解题的关键是注意数形结合与方程思 想的应用.
& ( 2011?潍坊)如图,y 关于x 的二次函数y= - . (x+m ) (x -3m )图象的顶点为 M ,
3m
图象交x 轴于A 、B 两点,交y 轴正半轴于 D 点.以AB 为直径作圆,圆心为 C .定点E 的坐标为(-3, 0),连接ED . (m >0)
(1) 写出A 、B 、D 三点的坐标;
(2) 当m 为何值时M 点在直线ED 上?判定此时直线与圆的位置关系; (3)
当m 变化时,用 m 表示△ AED 的面积S ,并在给出的直角坐标系中画出 S 关于m 的
函数图象的示意
解得产-10
,
,y=0 图.
l/
A
「 °
------------------ m
设过点B 且与直线AC 平行的直线解析式为:
y= _x+b ,把 B (2, 0)代入得 b= - 1,
2
(舍
去),
二次函数综合题. :压轴题;分类讨论.
:(1)根据x 轴,y 轴上点的坐标特征代入即可求出 A 、B 、D 三点的坐标;
(2) 待定系数法先求出直线 ED 的解析式,再根据切线的判定得出直线与圆的位置 关
系;
(3) 分当0v m v 3时,当m >3时两种情况讨论求得关于 m 的函数. :解:(
1) 令 y =0,则-J (x+m )(x -3m ) =0,解得 X1 = - m ,x2=3m ; 令 x=0,贝U y= -
' ( 0+m ) (0 - 3m ) = ;;m .
故 A (- m , 0), B (3m , 0), D (0, _ ;m ).
-3k+b=0 b=73in
解得,k=遞m b= .
3
■/ m > 0,
? m=1 .所以,当 m=1时,M 点在直线DE 上. 连接CD , C 为AB 中点,C 点坐标为
?/ 0D= _「;,OC=1 , ? CD=2 , D 点在圆上
2 2 2
又??? 0E=3 , DE 2=0D 2+0E 2=12 ,
2 2
EC =16, CD =4,
2 2 2
? CD +DE =EC . ? / EDC=90 ° ?直线ED 与O C 相切.
当m >3
时,°AE D ^AE
. ?0D = /m (m -3).
即 s=—m 2_
2
S 关于m 的函数图象的示意图如右:
(3)当 O v m v 3 时,V AED = ±AE .
S=—
(2)设直线ED 的解析式为y=kx+b ,将
(-3, 0), D (0,
「;m )代入得:
?直线ED 的解析式为y=丄上m 「 3
x+
-;m.
将y= - __' (x+m ) (x - 3m )化为顶点式:
3m
2
+ ':
:
3
???顶点M 的坐标为(m , 警).代入 y= Jmx+ .彷 得:
m 2=m
?OD=
::
m ( 3 - m )
2
9. (2011?邵阳)如图所示,在平面直角坐标系 Oxy 中,已知点A (-』,0),点C (0, 3),
4
点B 是x 轴上一点(位于点 A 的右侧),以AB 为直径的圆恰好经过点 C . (1) 求/ ACB 的度数;
(2) 已知抛物线y=ax +bx+3经过A 、B 两点,求抛物线的解析式;
(3) 线段BC 上是否存在点D ,使△ BOD 为等腰三角形?若存在,则求出所有符合条件的 点D 的坐标;若不存在,请说明理由.
考点:二次函数综合题. 专题:综合题.
分析:(1)根据直径所对的圆周角是直角可以得到/
ACB 的度数
.
(2) 利用三角形相似求出点 B 的坐标,然后把 A , B 两点的坐标代入抛物线求出抛 物线的
解析式. (3)
分别以OB 为底边和腰求出等腰三角形中点
D 的坐标.
解答:解:(1)v 以AB 为直径的圆恰好经过 点C ,
???/ ACB=90 ° (2):公 AOCCOB , 2
?- OC =AO ?OB ,
??? A (―』,0),点 C ( 0, 3),
4
二羸°C=3 ,
4
2
又:CO =AO?OB ,
七彳罰,
??? OB=4 ,
??? B (4, 0)把 A 、B 、C 三点坐标代入得
(3)① OD=DB ,如图:
D 在OB 的中垂线上,过 D 作DH 丄OB ,垂足是 H ,贝U H 是OB 中点.
DH =£OC ,OH=*OB
,
?- D (2,号),
②BD=BO ,如图:
过D 作DG 丄OB ,垂足是G , ?
0 G =CD =
DG OB CB OC ,
■/ OB=4 , CB=5 ,
? CD=BC - BD=BC - OB=5 - 4=1 ,
DGL N 3 DG=
?? OG=亠, 目,
一
二 —
点评:本题考查的是二次函数的综合题,(1)根据圆周角的性质求出角的度数. (2)用待定系数法求出抛物线的解析式. (3)根据等腰三角形的性质确定点D的坐标.
个人懂你,就是时时关心你;就是刻刻在乎你;就是凡事想着你。懂你的人,会想着你的冷暖,想着你的忧乐,想着你是否安好。
懂你,是心灵的一种呵护,是生命的一种温度,是彼此间的一种温馨。
因为有人懂你,你流在眼角的泪水有人擦;因为有人懂你,你欢笑时有人陪你笑;因为有人懂你,你寂寞时有人陪;因为有人懂你,你有难时有人帮;因为有人懂你,你痛苦时有人安慰。
懂你的人是你的知己,甚至比知己更知己。知己也只能是无话不说,心心相印,情同手足,休戚与共。
而懂你的人则更进一层,如若懂得,你的一个眼神,便能会意;你的一个暗示,便能心领;你任何一个神情,便会心有灵犀。
懂你的人,会对你心领神会,了如指掌,会对你的了解犹如了解自己。
懂,是世界上最温情的语言。浅浅的微笑,却包含着深深的喜欢;淡淡的祝福,却包含着浓浓的情意;短短的问候,却包含着长长的思念。
有时只说了只言片语,却胜似万语千言;有时只是一个眼神,一个动作,却能让你心间温暖如春。
懂你的人,最懂你的苦衷,最懂你的心累,最懂你的真诚,最懂你的内心世界。因为懂得,所以心相同;因为懂得,所以才心疼;因为懂得,所以才感动!
懂你,是一种深深的理解;懂你,是一种默默的喜欢;懂你,是一种暖暖的陪伴。
有一个懂你的人,真的就是一种幸福。你不会十全十美,他也不会十全十美,但两个都不完美的人却能撞出心灵的火花,却能达到无与伦比的默契,却能达成无法形容的融合,该是怎样的互懂?!
最懂你的人,也许会一直默默的陪伴在你的身边;也许会在天涯海角;但他总会在心里默默的守护你,总会在心里默默祈祷你幸福安康!
人与人之间最美是懂得,同事之间,只有互懂,才能互相理解;朋友之间,只有互懂,才能互相担待;夫妻之间,只有互懂,才能融洽度日;知己之间,只有互懂,才能长久长远;人与人之间,只有互懂,才能结识、结缘!
互懂,说起来容易做起来难!父母与子女之间,如果能互懂,就没有不孝和刁难;夫妻之间,如果能互懂,就没有争吵和硝烟;朋友同事之间,如果能互懂,就没有是非和埋怨;
官场之间,如果能互懂,就没有争斗和谗言;人与人之间,如果能互懂,就没有愧疚和不安。其实,懂,应该是相互的。
水尾中学中考专项训练(压轴题)答案 1.(四川模拟)如图,Rt △ABC 内接于⊙O ,∠ACB =90°,AC =23,BC =1.以AC 为一边,在AC 的右侧作等边△ACD ,连接BD ,交⊙O 于点E ,连接AE ,求BD 和AE 的长. 解:过D 作DF ⊥BC ,交BC 的延长线于F ∵△ACD 是等边三角形 ∴AD =CD =AC =23,∠ACD =60° ∵∠ACB =90°,∴∠ACF =90° ∴∠DCF =30°,∴DF = 1 2 CD =3,CF =3DF =3 ∴BF =BC +CF =1+3=4 ∴BD = BF 2 +DF 2 = 16+3 =19 ∵AC =23,BC =1,∴AB = AC 2 +BC 2 = 13 ∵BE +DE =BD ,∴AB 2 -AE 2 + AD 2 -AE 2 =BD 即 13-AE 2 + 12-AE 2 =19 ∴13-AE 2 =19- 12-AE 2 两边平方得:13-AE 2=19+12-AE 2-2 19(12-AE 2 ) 整理得:19(12-AE 2 ) =9,解得AE = 7 19 57 2.(四川模拟)已知Rt △ABC 中,∠ACB =90°,∠B =60°,D 为△ABC 外接圆⊙O 上 AC ︵ 的中点. (1)如图1,P 为 ABC ︵ 的中点,求证:PA +PC =3PD ; (2)如图2,P 为 ABC ︵ 上任意一点,(1)中的结论还成立吗?请说明理由. (1)证明:连接AD ∵D 为AC ︵ 的中点,P 为 ABC ︵ 的中点 ∴PD 为⊙O 的直径,∴∠PAD =90° D D P 图1 图2
圆与二次函数综合题 1、已知:二次函数y=x2-kx+k+4的图象与y轴交于点c,且与x轴的正半轴交于A、B两点(点A 在点B左侧)。若A、B两点的横坐标为整数。 (1)确定这个二次函数的解析式并求它的顶点坐标;(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合。设四边形PBCD的面积为S,求S与t的函数关系式; (3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程)。 2、(1)已知:关于x、y的方程组有两个实数解,求m的取值范围; (2)在(1)的条件下,若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点,与y轴交于点C,且△ABC的面积等于12,确定此抛物线及直线y=(m+1)x-2的解析式; (3)你能将(2)中所得的抛物线平移,使其顶点在(2)中所得的直线上吗?请写出一种平移方法。 3、已知:二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数。 (1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式。 4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像,确定当x取什么值时,y1>0,y1=0,y1<0; (2)根据(1)的结论,确定函数y2= (|y1|-y1)关于x的解析式; (3)若一次函数y=kx+b(k 0)的图像与函数y2的图像交于三个不同的点,试确定实数k与b应满足的条件。 5、已知:如图,直线y= x+ 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点。 (1)求以OA、OB两线段长为根的一元二次方程; (2)C是⊙M上一点,连结BC交OA于点D,若∠COD=∠CBO, 写出经过O、C、A三点的二次函数的解析式; (3)若延长BC到E,使DE=2,连结EA,试判断直线EA与 ⊙M的位置关系,并说明理由。(河南省) 6、如图,已知点A(tan ,0)B(tan ,0)在x轴正半轴上,点A在点B的左 边,、是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角。 (1)若二次函数y=-x2- 5/2kx+(2+2k-k2)的图像经过A、B两点,求它的解析式; (2)点C在(1)中求出的二次函数的图像上吗?请说明理由。(陕西省)
二次函数与圆 1、如图,AB 是⊙O 的直径,弦BC=2cm ,∠ABC=60o. (1)求⊙O 的直径; (2)若D 是AB 延长线上一点,连结CD ,当BD 长为多少时,CD 与⊙O 相切; (3)若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动,同时动点F 以1cm/s 的 速度从B 点出发沿BC 方向运动,设运动时间为)20)((< 2、如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3). (1)求此抛物线的解析式 (2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明; (3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积. 3、如图,抛物线2 23y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作 PF DE ∥交抛物线于点F ,设点P 的横坐标为m ; ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设BCF △的面积为S ,求S 与m 的函数关系式. 图6 x y F E H N M P D C B A O 二次函数和圆 【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x = (1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次 函数图象的解析式; (2) 若二次函数图象的顶点为 D ,问当k 为何值时,四边形ADBP 为菱形. 【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线3 2 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积. 【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B. (1)求直线CB的解析式; (2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x 轴的交点恰为点E、F,求该抛物线的解析式; (3)试判断点C是否在抛物线上? (4)在抛物线上是否存在三个点,由它构成的三角形与 △AOC相似?直接写出两组这样的点. 【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E. (1)求m的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin(α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、 二次函数与圆综合提高(压轴题) 1、如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点, 且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图 形L. (1)求△ABC的面积; (2)设AD=x,图形L的面积为y,求y关于x的函数解析式; (3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.解 解:(1)如图3,作AH⊥BC于H, 答: ∴∠AHB=90°. ∵△ABC是等边三角形, ∴AB=BC=AC=3. ∵∠AHB=90°, ∴BH=BC= 在Rt△ABC中,由勾股定理,得 AH=. ∴S△ABC==; (2)如图1,当0<x≤1.5时,y=S△ADE. 作AG⊥DE于G, ∴∠AGD=90°,∠DAG=30°, ∴DG=x,AG=x, ∴y==x2, ∵a=>0,开口向上,在对称轴的右侧y随x的增大而增大, ∴x=1.5时,y 最大=, 如图2,当1.5<x<3时,作MG⊥DE于G, ∵AD=x, ∴BD=DM=3﹣x, ∴DG=(3﹣x),MF=MN=2x﹣3, ∴MG=(3﹣x), ∴y=, =﹣; (3),如图4,∵y=﹣; ∴y=﹣(x2﹣4x)﹣, y=﹣(x﹣2)2+, ∵a=﹣<0,开口向下, ∴x=2时,y最大=, ∵>, ∴y最大时,x=2, ∴DE=2,BD=DM=1.作FO⊥DE于O,连接MO,ME.∴DO=OE=1, ∴DM=DO. ∵∠MDO=60°, ∴△MDO是等边三角形, ∴∠DMO=∠DOM=60°,MO=DO=1. ∴MO=OE,∠MOE=120°, ∴∠OME=30°, ∴∠DME=90°, ∴DE是直径, S⊙O=π×12=π. 2、(2013?压轴题)如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4), 点B的坐标为(4, 0),点C的坐标为 (﹣4,0),点P在 射线AB上运动,连 结CP与y轴交于点 D,连结BD.过P, D,B三点作⊙Q与 y轴的另一个交点 为E,延长DQ交⊙Q于点F,连结EF,BF. (1)求直线AB的函数解析式; (2)当点P在线段AB(不包括A,B两点)上时. ①求证:∠BDE=∠ADP; ②设DE=x,DF=y.请求出y关于x的函数解析式; (3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由. 解:(1)设直线AB的函数解析式为y=kx+4, 代入(4,0)得:4k+4=0, 解得:k=﹣1, 则直线AB的函数解析式为y=﹣x+4; (2)①由已知得: OB=OC,∠BOD=∠COD=90°, 又∵OD=OD, ∴△BOD≌△COD, 【例1】.如图,点()40M ,,以点M 为圆心、2为半径的圆与x 轴交于点A B ,.已知抛物 21 6 y x bx c =++过点A 和B ,与y 轴交于点C . ⑴ 求点C 的坐标,并画出抛物线的大致图象. ⑵ 点()8Q m ,在抛物线21 6 y x bx c =++上,点P 为此抛物线对称轴上一个动点,求 PQ PB + 最小值. ⑶ CE 是过点C 的M ⊙的切线,点E 是切点,求OE 所在直线的解析式. 【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式 2y x =-+并且线段CM 的长为(1)求抛物线的解析式。 (2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的长。 (3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。 【例2】如图,在平面直角坐标系中,以点(04)C ,为圆心,半径为4的圆交y 轴正半轴于点A , AB 是C ⊙的切线. 动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动,点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动,且动点P 、 Q 从点A 和点O 同时出发,设运动时间为t (秒). ⑴当1t =时,得到1P 、1Q 两点,求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ; ⑵当t 为何值时,直线PQ 与C ⊙相切?并写出此时点P 和点Q 的坐标; ⑶在⑵的条件下,抛物线对称轴l 上存在一点N ,使NP NQ +最小,求出点N 的坐标并说明理由. 提示:(1)先求出t=1时,AP 和OQ 的长,即可求得P 1,Q 1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l 的解析式. (2)当直线PQ 与圆C 相切时,连接CP ,CQ 则有Rt △CMP ∽Rt △QMC (M 为PG 与圆的切点),因此可设当t=a 秒时,PQ 与圆相切,然后用a 表示出AP ,OQ 的长即PM ,QM 的长(切线长定理).由此可求出a 的值. (3)本题的关键是确定N 的位置,先找出与P 点关于直线l 对称的点P ′的坐标,连接P ′Q ,那么P ′Q 与直线l 的交点即为所求的N 点,可先求出直线P ′Q 的解析式,进而可求出N 点的坐标. 【巩固】已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与 二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线 l 过()01-,点. ⑴ 求一次函数与二次函数的解析式; ⑵ 判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明; ⑶ 把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x 二次函数与圆的综合 Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】 二次函数与圆的综合 5.(2012?济南)如图1,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D. (1)求抛物线的解析式; (2)求cos∠CAB的值和⊙O1的半径; (3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 考 点: 二次函数综合题. 分析:(1)利用待定系数法求出抛物线的解析式; (2)如答图1所示,由△AOC为等腰直角三角形,确定∠CAB=45°,从而求出其三角函数值;由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度;(3)如答图2所示,首先利用圆及抛物线的对称性求出点D坐标,进而求出点M的坐标和线段BM的长度;点B、P、C的坐标已知,求出线段BP、BC、PC的长度;然后利用△BMN∽△BPC相似三角形比例线段关系,求出线段BN和MN的长度;最后利用两点间的距离公式,列出方程组,求出点N的坐标. 解答:解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0), ∴, 解得a=1,b=4, ∴抛物线的解析式为:y=x2+4x+3. (2)由(1)知,抛物线解析式为:y=x2+4x+3, ∵令x=0,得y=3, ∴C(0,3), ∴OC=OA=3,则△AOC为等腰直角三角形, ∴∠CAB=45°, ∴cos∠CAB=. 在Rt△BOC中,由勾股定理得:BC==. 如答图1所示,连接O1B、O1C, 由圆周角定理得:∠BO1C=2∠BAC=90°, ∴△BO1C为等腰直角三角形, ∴⊙O1的半径O1B=BC=. (3)抛物线y=x2+4x+3=(x+2)2﹣1, ∴顶点P坐标为(﹣2,﹣1),对称轴为x=﹣2. 又∵A(﹣3,0),B(﹣1,0),可知点A、B关于对称轴x=﹣2对称. 如答图2所示,由圆及抛物线的对称性可知:点D、点C(0,3)关于对称轴对称,∴D(﹣4,3). 又∵点M为BD中点,B(﹣1,0), ∴M(,), ∴BM==; 在△BPC中,B(﹣1,0),P(﹣2,﹣1),C(0,3), 由两点间的距离公式得:BP=,BC=,PC=. 二次函数和圆 【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x = (1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二 次函数图象的解析式; (2) 若二次函数图象的顶点为D , 问当k 为何值时,四边形ADBP 为菱形. 【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积. 【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B. (1)求直线CB的解析式; (2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x 轴的交点恰为点E、F,求该抛物线的解析式; (3)试判断点C是否在抛物线上? (4)在抛物线上是否存在三个点,由它构成的三角形与 △AOC相似?直接写出两组这样的点. 【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E. (1)求m的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin(α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已 圆与二次函数综合题 1.已知圆P 的圆心在反比例函数k y x =(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次 函数图象的解析式; (2) 若二次函数图象的顶点为 D ,问当k 为何值时,四边形ADBP 为菱形. 2.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32 y x =-+ 与坐标轴交于D 、E 。设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标; (2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标; (3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的 面积. (3) (2) 3.如图,已知抛物线y = ax 2 + bx -3与x 轴交于A 、B 两点,与y 轴交于C 点,经过A 、B 、 C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴 交于D ,抛物线的顶点为E . (1)求m 的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin (α-β)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由. 4.如图,点P在y轴上,半径为3的⊙P分别交x轴于A、B两点,AB=4,交y轴负半轴于点C,连接AP并延长交⊙P于点D,过D作⊙P的切线分别交x轴、y轴于点F、G; (1)求直线FG的解析式; (2)连接CD交AB于点E,求PCD ∠ tan的值; (3)设M是劣弧BC上的一个动点,连接DM交x轴于点N,问:是否存在这样的一个常数k,始终满足AN·AB+DN·DM=K,如果存在,请求出K的值,如果不存在,请说明理由; (图1) (图2) 5.已知:如图, 抛物线2 33 y x x =--x轴分别交于A B ,两点,与y轴交于C点,M经过原点O及点A C ,,点D是劣弧OA上一动点(D点与A O ,不重合).(1)求抛物线的顶点E的坐标;(2)求M的面积; (3)连CD交AO于点F,延长CD至G,使2 FG=,试探究当点D运动到何处时,直线GA与M相切,并请说明理由. 6.(0) A m,(0) m<,以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连结BE与AD相交于点F. (1)求证:BF DO =; (2)设直线l是BDO △的边BO的垂直平分线,且与BE相交于点G.若G是BDO △的 2020中考数学二次函数与圆综合 例题1.在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(3,0)-,若将经过A 、C 两点的直线y kx+b =沿y 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线2x =-. (1)求直线AC 及抛物线的函数表达式; (2)如果P 是线段AC 上的一点,设三角形ABP 、三角形BPC 的面积分别为ABP S △、BPC S △,且2:3ABP BPC S S =△△:,求点P 的坐标; (3)设Q 的半径为1,圆心Q 在抛物线上运动,则在运动的过程中是否存在Q 与坐标轴相切的情况?若存在,求出圆心Q 的坐标;若不存在,请说明理由.并探究:若设Q 的半径为r ,圆心Q 在抛物线上运动,则当r 取何值时,Q 与两坐标轴同时相切? 例题2.在平面直角坐标系中,抛物线经过(0,0)O 、(4,0)A 、3,B ? ?? 三点.(1)求此抛物线的解析式; (2)以OA 的中点M 为圆心,OM 的长为半径作M ,在(1)中的抛物线上是否存在这样的点P ,过点P 作M 的切线l ,且l 与x 轴的夹角为30??若存在,请求出此时点P 的坐标;若不存在,请说明理由.(注意:本题中的结果保留根号) 例题3.如图,抛物线2134 y x x =-++与x 轴交于点A 、B ,与y 轴交于点C ,顶点为点D ,对称轴l 与直线BC 交于点E ,与x 轴交于点F . (1)求直线BC 的解析式. (2)设点P 为该抛物线上的一个动点,以点P 为圆心、r 为半径作P ⊙. ①当点P 运动到点D 时,若P ⊙与直线BC 相交,求r 的取值范围; ②若5 r =,是否存在点P 使P ⊙与直线BC 相切?若存在,请求出点P 的坐标;若不存在,请说明理由. 例题4.已知,如图4-1,抛物线2y ax bx c =++经过点1(,0)A x ,2(,0)B x ,(0,2)C -,其顶点为D .以AB 为直径的M 交y 轴于点E 、F ,过点E 作M 的切线交x 轴于点N .30ONE ∠=?,12||8x x -=. (1)求抛物线的解析式及顶点D 的坐标; (2)如图4-2,点Q 为 EBF 上的动点(Q 不与E 、F 重合),连结AQ 交y 轴于点H ,问:AH AQ ?是否为定值?若是,请求出这个定值;若不是,请说明理由. 图4-1图4-2 二次函数与圆的综合 Last revision date: 13 December 2020. 二次函数与圆的综合 5.(2012?济南)如图1,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D. (1)求抛物线的解析式; (2)求cos∠CAB的值和⊙O1的半径; (3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 考 点: 二次函数综合题. 分析:(1)利用待定系数法求出抛物线的解析式; (2)如答图1所示,由△AOC为等腰直角三角形,确定∠CAB=45°,从而求出其三角函数值;由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度;(3)如答图2所示,首先利用圆及抛物线的对称性求出点D坐标,进而求出点M的坐标和线段BM的长度;点B、P、C的坐标已知,求出线段BP、BC、PC的长度;然后利用△BMN∽△BPC相似三角形比例线段关系,求出线段BN和MN的长度;最后利用两点间的距离公式,列出方程组,求出点N的坐标. 解答:解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0), ∴, 解得a=1,b=4, ∴抛物线的解析式为:y=x2+4x+3. (2)由(1)知,抛物线解析式为:y=x2+4x+3, ∵令x=0,得y=3, ∴C(0,3), ∴OC=OA=3,则△AOC为等腰直角三角形, ∴∠CAB=45°, ∴cos∠CAB=. 在Rt△BOC中,由勾股定理得:BC==. 如答图1所示,连接O1B、O1C, 由圆周角定理得:∠BO1C=2∠BAC=90°, ∴△BO1C为等腰直角三角形, ∴⊙O1的半径O1B=BC=. (3)抛物线y=x2+4x+3=(x+2)2﹣1, ∴顶点P坐标为(﹣2,﹣1),对称轴为x=﹣2. 又∵A(﹣3,0),B(﹣1,0),可知点A、B关于对称轴x=﹣2对称. 如答图2所示,由圆及抛物线的对称性可知:点D、点C(0,3)关于对称轴对称,∴D(﹣4,3). 又∵点M为BD中点,B(﹣1,0), ∴M(,), ∴BM==; 在△BPC中,B(﹣1,0),P(﹣2,﹣1),C(0,3), 由两点间的距离公式得:BP=,BC=,PC=. 一、二次函数与圆综合 【例1】 已知:抛物线2:(1)(2)M y x m x m =+-+-与x 轴相交于12(0)(0)A x B x ,,,两点, 且12x x <. (Ⅰ)若120x x <,且m 为正整数,求抛物线M 的解析式; (Ⅱ)若1211x x <>,,求m 的取值范围; (Ⅲ)试判断是否存在m ,使经过点A 和点B 的圆与y 轴相切于点(02)C , ,若存在,求出2:(1)(2)M y x m x m =+-+-的值;若不存在,试说明理由; (Ⅳ)若直线:l y kx b =+过点(07)F ,,与(Ⅰ)中的抛物线M 相交于P Q ,两点,且使 1 2 PF FQ =,求直线l 的解析式. 【例2】 已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式 2y x =-+并且线段CM 的长为(1)求抛物线的解析式。 (2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的 长。 (3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。 【例3】 已知:在平面直角坐标系xOy 中,一次函数4y kx k =-的图象与x 轴交于点A ,抛物线 2 y ax bx c =++经过O ,A 两点. ⑴试用含a 的代数式表示b ; ⑵设抛物线的顶点为D ,以D 为圆心,DA 为半径的圆被x 轴分为劣弧和优弧两部分.若将劣弧 沿x 轴翻折,翻折后的劣弧落在⊙D 内,它所在的圆恰与OD 相切,求⊙D 半径的长及抛物线的 解析式; ⑶设点B 是满足(2)中条件的优弧上的一个动点,抛物线在x 轴上方的部分上是否存在这样的点 P ,使得4 3 POA OBA =∠∠?若存在,求出点P 的坐标;若不存在,说明理由. B 例题精讲 二次函数与圆综合 专题63 构造圆与隐形圆在二次函数中的综合问题 1、如图,在直角坐标系中,直线y=﹣1 3x ﹣1与x 轴,y 轴的交点分别为A 、B ,以x=﹣1为对称轴的抛物线 y=x 2+bx+c 与x 轴分别交于点A 、C ,直线x=﹣1与x 轴交于点D . (1)求抛物线的解析式; (2)在线段AB 上是否存在一点P ,使以A ,D ,P 为顶点的三角形与△AOB 相似?若存在,求出点P 的坐标;如果不存在,请说明理由; (3)若点Q 在第三象限内,且tan△AQD=2,线段CQ 是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由. 【答案】(1)y=x 2+2x ﹣3;(2)存在;点P 坐标为(﹣1,?23 )或(-65 ,-3 5 ); (3)存在,CQ 最小值为 √37?√5 2 . 【解析】(1)△直线y=﹣1 3x ﹣1与x 轴交于A 点, △点A 坐标为(﹣3,0), 又△直线x=﹣1为对称轴, △点C 坐标为(1,0), △抛物线解析式为:y=(x+3)(x ﹣1)=x 2+2x ﹣3; (2)存在; 由已知,点D 坐标为(﹣1,0),点B 坐标为(0,﹣1), 设点P 的坐标为(a ,﹣13 a ﹣1), △当△AOB△△ADP 时, AD AO = DP OB ,即23 = 1 3 a+11 , 解得:a=﹣1; 点P 坐标为(﹣1,?2 3); △当△AOB△△APD 时, 过点P 作PE△x 轴于点E , 则△APE△△PED , △PE 2=AE?ED , △(﹣1 3a ﹣1)2=(a+3)(﹣a ﹣1), 解得a 1=﹣3(舍去),a 2=﹣6 5, △点P 坐标为(﹣6 5 ,﹣3 5 ); (3)存在,CQ 最小值为 √37?√5 2 ; 如图,取点F (﹣1,﹣1),过点ADF 作圆,则点E (﹣2,﹣1 2)为圆心, 1.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E. (1)求m的值及抛物线的解析式;∴抛物线的解析式为y=x2-2x-3 (2)设∠DBC = ,∠CBE = ,求sin(-)的值; (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE 相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说 明理由. 2.如图所示,已知在直角梯形OABC 中,AB OC BC x ∥,⊥轴于点(11)(31)C A B ,,、,.动 点P 从O 点出发,沿x 轴正方向以每秒1个单位长度的速度移动.过P 点作PQ 垂直于直.线.OA ,垂足为Q .设P 点移动的时间为t 秒(04t <<),OPQ △与直角梯形OABC 重叠部分的面积为S . (1)求经过O A B 、、三点的抛物线解析式; (2)求S 与t 的函数关系式; (3)将OPQ △绕着点P 顺时针旋转90°,是否存在t ,使得OPQ △的顶点O 或Q 在抛物线上?若存在,直接写出t 的值;若不存在,请说明理由. ∴所求抛物线解析式为214 33 y x x =-+ 3.如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3). (1)求抛物线的解析式及顶点B的坐标; (2)求证:CB是△ABE外接圆的切线; (3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由; (4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围. 点B(1,4).综上,得:P1(0,0),P2(9,0),P3(0,﹣). ∴y=-x2+2x+3. 二次函数与圆的综合集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY- 二次函数与圆的综合5.(2012济南)如图1,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B (﹣1,0),与y轴相交于点C,⊙O 1 为△ABC的外接圆,交抛物线于另一点D.(1)求抛物线的解析式; (2)求cos∠CAB的值和⊙O 1 的半径; (3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 考 点: 二次函数综合题. 分析:(1)利用待定系数法求出抛物线的解析式; (2)如答图1所示,由△AOC为等腰直角三角形,确定∠CAB=45°,从而求出其三角函数值;由圆周角定理,确定△BO 1 C为等腰直角三角形,从而求出半径的长度; (3)如答图2所示,首先利用圆及抛物线的对称性求出点D坐标,进而求出点M的坐标和线段BM的长度;点B、P、C的坐标已知,求出线段BP、BC、PC的长度;然后利用△BMN∽△BPC相似三角形比例线段关系,求出线段BN和MN的长度;最后利用两点间的距离公式,列出方程组,求出点N 的坐标. 解答:解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0), ∴, 解得a=1,b=4, ∴抛物线的解析式为:y=x2+4x+3. (2)由(1)知,抛物线解析式为:y=x2+4x+3, ∵令x=0,得y=3, ∴C(0,3), ∴OC=OA=3,则△AOC为等腰直角三角形, ∴∠CAB=45°, ∴cos∠CAB=. 在Rt△BOC中,由勾股定理得:BC==. 如答图1所示,连接O 1 B、O 1 C, 由圆周角定理得:∠BO 1 C=2∠BAC=90°, 2019 初三数学中考专题复习 二次函数和圆 专题综合检测 1.下列关系式中,属于二次函数的是(x 为自变量)( ) =18x 2 =-x 2 -1 =1x 2 =a 4x 4 2.抛物线y =2x 2 ,y =-2x 2 ,y =12 x 2 的共同性质是( ) A.开口向上 B.对称轴是y 轴 C.都有最高点 随x 的增大而增大 3.若二次函数y =(x -m)2-1,当x≤1时,y 随x 的增大而减小,则m 的取值范围是( ) =1 >1 ≥1 ≤1 4.如图,AB 是⊙O 的直径.若∠BAC =35°,那么∠ADC =( ) ° ° ° ° 5.在同圆中,下列四个命题:①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中真命题有( ) 个 个 个 个 6.如图,CD 是⊙O 的直径,弦AB ⊥CD 于E ,连接BC 、BD.下列结论错误的是( ) =BE B. =DE D. .∠DBC =90° 7.如图,AD 、AE 、CB 均为⊙O 的切线,D 、E 、F 分别是切点,AD =8,则△ABC 的周长为( ) D.不能确定 8.如果二次函数y =ax 2+bx +c 的图象如图所示,那么一次函数y =bx +c 和反比例函数y =b x 在同一坐标系中的图象大致是( ) 9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O ,三角尺的直角顶点C 落在直尺的10cm 处,铁片与直尺的唯一公共点A 落在直尺的14cm 处,铁片与三角尺的唯一公共点为B.下列说法错误的是( ) A.圆形铁片的半径是4cm B.四边形AOBC 为正方形 C.弧AB 的长度为4πcm D.扇形OAB 的面积是4πcm 2 10.已知二次函数y =ax 2+bx +c(a≠0)的图象如图所示,并且关于x 的一元二次方程ax 2+bx +c -m =0有两个不相等的实数根,下列结论:①b 2-4ac <0;②abc >0;③a -b +c <0;④m >-2,其中正确的个数有( ) 11.如图,扇形OAB 的圆心角为120°,半径为3,则该扇形的弧长为 (结果保留π). 中考专题: 圆与函数综合题 1、如图,平面直角坐标系中,以点C (22为半径的圆与轴交于A 、B 两点. (1)求A 、B 两点的坐标; (2)若二次函数2y x bx c =++的图象经过点A 、B ,试确定此二次函数的解析式. 2、如图,半径为2的⊙C 与x 轴的正半轴交于点A ,与y 轴的正半轴交于点B ,点C 的坐标为(1, 0).若抛物线2 3 y x bx c =++过A 、B 两点. (1)求抛物线的解析式; (2)在抛物线上是否存在点P ,使得∠PBO=∠POB ?若存在,求出点P 的坐标;若不存在说明理由; (3)若点M 是抛物线(在第一象限内的部分)上一点,△MAB 的面积为S ,求S 的最大(小)值. 3、如图,抛物线2y ax bx c =++的对称轴为轴,且经过(0,01 16 )两点,点P 在抛物线上运动,以P 为圆心的⊙P 经过定点A (0,2), (1)求a,b,c 的值; (2)求证:点P 在运动过程中,⊙P 始终与轴相交; (3)设⊙P 与轴相交于M ()1x ,0,N ()()21 2x ,0x x 两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标。 4、如图,二次函数y =x 2 +bx -3b +3的图象与x 轴交于A 、B 两点(点A 在点B 的左边),交y 轴于 点C ,且经过点(b -2,2b 2 -5b -1). (1)求这条抛物线的解析式; (2)⊙M 过A 、B 、C 三点,交y 轴于另一点D ,求点M 的坐标; (3)连接AM 、DM ,将∠AMD 绕点M 顺时针旋转,两边MA 、MD 与x 轴、y 轴分别交于点E 、F ,若△DMF 为等腰三角形,求点E 的坐标. D A C PCBOCx y 如图,点P 在y 轴上,⊙P 轴于A B ,两点,连结BP 并延长交⊙P 于C ,过点C 的直线2y x b =+交x 轴于D ,且⊙P 的半径为5,4AB =. (1)求点B P C ,,的坐标; (2)求证:CD 是⊙P 的切线; (3)若二次函数2(1)6y x a x =-+++的图象经过点B ,求这个二次函数的解析式, 并写出使二次函数值小于一次函数2y x b =+值的x 的取值范围. 如图,已知抛物线y = ax 2 + bx -3与x 轴交于A 、B 两点,与y 轴交于C 点,经过A 、B 、C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴交于D ,抛物线的顶点为E . (1)求m 的值及抛物线的解析式; (2)设∠DBC = α,∠CBE = β,求sin (α-β)的值; (3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCE 相似?若存在, 请指出点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由. 如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线 216 y x bx c =++ 过点A 和B ,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象. (2)点Q (8,m )在抛物线216y x bx c = ++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值. (3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式. 如图,已知)212 5,31(),0,1(B A 为直角坐标系内两点,点C 在x 轴上,且OA OC 2=,以A 点为圆心,OA 为半径作⊙A 。直线CD 切⊙O 于D 点,连结OD 。 (1)求点D 的坐标; (2)求经过O 、B 、D 三点的抛物线的解析式; (3)判断在(2)中所得的抛物线上是否存在一点P ,使DCP ?∽OCD ??若存在,求出P 点的坐标;若不存在,请说明理由。 圆与二次函数综合题 1. 抛物线交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3). (1)求二次函数的关系式; (2)在抛物线对称轴上是否存在一点P,使P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由; (3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径. 3. 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B 两点(A点在B点左侧),与y轴交于点C. (1)求抛物线的解析式及A、B、C三点的坐标 (2)若直线y=kx+b经过C、M两点,且与x轴交于点D,证明四边形CDAN是平行四边形. (3)点P在抛物线的对称轴x=1上运动,请探索,在x轴上方是否存在这样的点P,使以P为圆心的圆经过A、B两点,且与直线CD相切,若存在,请求出点P的坐标,若不存在,请说明理由. 4.已知:如图,抛物线的图象与x轴分别交于A(-3,0),B(1,0)两点,与y轴交于点 (1)求抛物线的顶点E的坐标; (2)求⊙M的面积; (3)连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由. 5.在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,)三点(1)求此抛物线的解析式 (2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l ,且l与x轴的夹角为30°,若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号) 6. 已知二次函数的图象如图. (1)求它的对称轴与x轴交点D的坐标; (2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式; (3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由. 二次函数与圆综合动 点问题 1.在直角坐标平面内,O 为原点,点A 的坐标为(1,0),点C 的坐标为(0,4),直线CM ∥x 轴(如图所示).点B 与点A 关于原点对称,直线y =x +b (b 为常数)经过点B ,且与直线CM 相交于点D ,联结OD . (1)求b 的值和点D 的坐标; (2)设点P 在x 轴的正半轴上,若△POD 是等腰三角形,求点P 的坐标; 2.如图,射线OA ⊥射线OB ,半径r =2cm 的动圆M 与OB 相切于点Q (圆M 与OA ?没有公共点),P 是OA 上的动点,且PM =3cm ,设OP =x cm ,OQ =y cm . (1)求x 、y 所满足的关系式,并写出x 的取值范围. (2)当△MOP 为等腰三角形时,求相应的x 的值. C M O x y 1 3 4 1 A 1 B D y =x +b 2 O P A Q M B 3.如图,在平面直角坐标系中,抛物线经过A (-1,0),B (4,0),C (0,-4),⊙M 是△ABC 的外接圆,M 为圆心. (1)求抛物线的解析式; (2)求阴影部分的面积; (3)在x 轴的正半轴上有一点P ,作PQ ⊥x 轴交BC 于Q ,设PQ =k ,△CPQ 的面积为S ,求S 关于k 的函数关系式,并求出S 的最大值. y O x A B P M Q C 4.如图,在平面直角坐标系中,半圆M 的圆心M 在x 轴上,半圆M 交x 轴于A (-1,0)、B (4,0)两点,交y 轴于点C ,弦AC 的垂直平分线交y 轴于点D ,连接AD 并延长交半圆M 于点E . (1)求经过A 、B 、C 三点的抛物线的解析式; (2)求证:AC =CE ; (3)若P 为x 轴负半轴上的一点,且OP = 2 1 AE ,是否存在过点P 的直线,使该直线与(1)中所得的抛物线的两个交点到y 轴的距离相等?若存在,求出这条直线的解析式;若不存在.请说明理由. M O A C B x E D y二次函数与圆结合的压轴题Word版
二次函数与圆综合训练(含解析)
二次函数和圆综合(压轴题+例题+巩固+答案解析)
二次函数与圆的综合完整版
初中中招二次函数和圆的综合体包含答案
圆与二次函数综合练习
2020中考数学 二次函数与圆综合
二次函数与圆的综合
7二次函数与圆综合
专题63 构造圆与隐形圆在二次函数中的综合问题(解析版)
二次函数与圆结合的综合题
二次函数与圆的综合
初三数学中考专题复习二次函数和圆专题综合检测
中考专题:圆与二次函数结合题
中考中二次函数与圆综合题
二次函数与圆综合题
二次函数与圆综合动点问题