第二章 插值法
- 格式:doc
- 大小:801.00 KB
- 文档页数:19





第二章 插值法⏹ 多项式插值的存在性 ⏹ Lagrange 插值 ⏹ Newton 插值 ⏹ Hermit 插值 ⏹ 分段低次插值 ⏹ 三次样条插值在生产实践和科学研究所遇到的大量函数中,相当一部分是通过测量或实验得到的。
虽然其函数关系)(x f y =在某个区间[]b a ,是客观存在的,但是却不知道具体的解析表达式,只能通过观察、测量或实验得到函数在区间a ,b]上一些离散点上的函数值、导数值等,因此,希望对这样的函数用一个比较简单的函数表达式来近似地给出整体上的描述。
还有些函数,虽然有明确的解析表达式,但却过于复杂而不便于进行理论分析和数值计算,同样希望构造一个既能反映函数的特性又便于计算的简单函数,近似代替原来的函数。
插值法就是寻求近似函数的方法之一.在用插值法寻求近似函数的过程中,根据所讨论问题的特点,对简单函数的类型可有不同的选取,如多项式、有理式、三角函数等,其中多项式结构简单,并有良好的性质,便于数值计算和理论分析,因此被广泛采用。
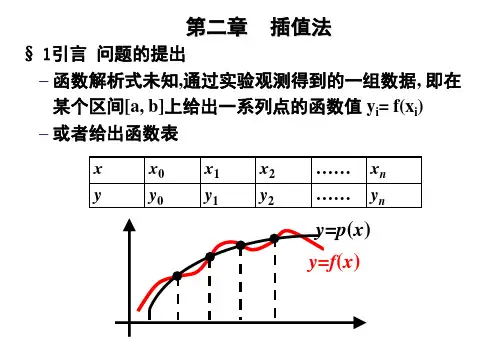
本章主要介绍多项式插值、分段多项式插值和样条插值. 2.1 插值多项式的存在唯一性 2.1.1 插值问题设函数)(x f y =在区间],[b a 上有定义,且已知函数在区间],[b a 上n+1个互异点n x x x ,,,10 处的函数值)(i i x f y = i=0,1,…,n ,若存在一个简单函数)(x p y =,使其经过)(x f y =上的这n+1个已知点),(,),,(),,(1100n n y x y x y x (图5-1),即n i y x p i i ,,1,0 ,)( == (2.1.1)那么,函数)(x p 称为插值函数,点n x x x ,,,10 称为插值节点,],[b a 称为插值区间,求)(x p 的方法称为插值法,)(x f 称为被插函数。
若)(x p 是次数不超过n 的多项式,记为)(x p n ,即n n n x a x a a x p +++= 10)(则称)(x p n 为n 次插值多项式,相应的插值法称为多项式插值;若)(x p 为分段多项式,称为分段插值,多项式插值和分段插值称为代数插值。





1 第二章 插值方法/* Interpolation */ 2.1 引言 函数逼近 问题的引出:现实应用中常用函数yfx表示某种内在规律的数量关系,但是情况往往是: 1)yfx在某个区间[a,b]存在,有时候是连续的,但是只能通过实验或观
测得到一系列点ix的函数值iy(得到函数表),而无法得到fx的表达式 2)函数表达式已知,但计算复杂(如sinyx,lgyx等)使用不方便,通常也使用函数表。如:三角函数表,对数表,平方根表,立方根表等。 问题:有时需要求不在函数表上的函数值怎么办? 解决方法:根据所给的yfx的函数表,构造一个简单的函数Px近似替代fx(存在误差!),称为函数逼近。 称Px为逼近函数,fx为被逼近函数。Px通常选择一类比较简单的函数,如代数多项式或分段代数多项式。 函数逼近的方法有很多,例如Taylor级数,Fourier级数,有限元方法、边界
元方法,小波分析等,大学科叫逼近论。 本课程讨论连续函数的逼近,主要介绍插值法。 插值 (interpolation) 已知,,yfxxab的函数表 x 01nxxx
y 01nyyy 2
求:Px使 iiyPx 0,1,2,,in
—— 插值问题
称Px为fx的插值函数;fx为被插值函数;01nxxx
为插值结点;
,ab为插值区间;求插值函数Px
的方法称为插值法。
当Px为多项式时,相应的插值法为多项式插值;Px为分段的多项式,称为分段插值;Px为三角多项式,称为三角插值。 插值法的几何示意图,P14图2.1 多项式插值是数值分析的基本工具,常用来计算被插函数的近似函数值,零、极点,导数、积分(第四章 数值积分和数值微分),解微分方程(第五章)、积分方程等。
2.2 拉格朗日插值 2.2.1 插值多项式的存在唯一性 问题:用不同的多项式插值方法得到的插值多项式的形式有可能不同,它们是否等价?(可以转化为相同的标准式?) 答案是肯定的! 两点确定一条直线( 一次多项式 ) 三点确定一个抛物线( 二次多项式 ) 是否n+1点确定一个n次多项式? 给定n+1个互异的插值点01nxxx
,求符合插值条件iiyPx的次数不
超过n的插值多项式 2012n
nPxaaxaxax
——(标准式) 3
Px
存在且唯一!证明见P14,定理2.1。
可以通过求解方程组得到系数012,,naaaa,从而得到Px的表达式,但是这样做不但计算复杂,且难以得到Px的简单表达式。 当n=20时,在108次/秒的计算机上计算需要几十万年! 2.2.2 线性插值与抛物插值 线性插值 当n=1时: 已知 xk, xk+1;yk, y k+1, 求线性插值多项式 101()Lxaax 使得:1()kkLxy
且111()kkLxy. 可见,1()Lx是过(,)kkxy和11(,)kkxy的一条直线。
111()kkkkkkyyLxyxxxx
点斜式
11111()kkkkkkkkxxxxLxyyxxxx
两点式
令11kkkkxxlxxx,11kkkkxxlxxx则:111()kkkkLxlxylxy 称klx及1klx为一次插值基函数,或线性插值基函数。 注意:基函数 10ijijijlxij 抛物线插值 当n=2时: 已知xk-1,xk, xk+1;yk-1, yk, y k+1, 求二次插值多项式 2()Lx 使得:211()kkLxy,
2()kkLxy,211()kkLxy。 可见,2()Lx是过11(,)kkxy,(,)kkxy和11(,)kkxy的抛物线。 4
利用基函数法构造 10ijijijlxij
i , j = k-1, k, k+1
因此构造 11111kkkkkkkxxxxlxxxxx
1111kkkkkkkxxxxlxxxxx
11111kkkkkkkxxxxlxxxxx
此时: 21111()kkkkkkLxlxylxylxy
称1klx,klx及1klx为二次插值基函数,或抛物插值基函数。
2.2.3 拉格朗日插值多项式 从n=1和n=2的情形,可推广到n>1的情形: 只要构造n次插值的基函数满足:
10ijijijlxij
,0,1,2,,ijn 注意:n+1个节点
然后令n次插值多项式 1()nniiiLxlxy 显然有()niiLxy成立。 每个0ilx有n个根,分别为0111,,,,,iinxxxxx,因此第i个基函数
ilx
可以写成: 01110niiiinijjijlxCxxxxxxxxxxCxx
又: 1iilx,故:01nijiijjCxx 5
因此: 01110111iiniiiiiiiinxxxxxxxxxxlxxxxxxxxxxx
这n+1个n次多项式01,,nlxlxlx为节点01,,,nxxx上的n次插值基函数。
n次插值多项式 0()nniiiLxlxy称为拉格朗日插值多项式。 记:101nnxxxxxxx 则:10111niiinxxxxxxxxxxx
于是:101()nnniiinxLxyxxx 问题:如图2.1(P14),插值多项式在插值点上的误差为0,但是在其他位置上的估计误差是未知的。 如何估计出在其他点上的误差限? 1)如果fx是n次多项式,则fx和()nLx等价,误差为0; 2)如果fx不是n次多项式,如何处理? 为了解决第2)种情况,我们引入差值余项的概念,估计出插值多项式估计误差的上界!
2.2.4 插值余项( Remainder ) 在[a,b]上用()nLx近似fx,其截断误差()nnRxfxLx,称为插值多项式的余项或插值余项。
定理2.2:关于插值余项的估计(P18) 证明:插值多项式在n+1个插值点上的误差为0,因此 6
0nRx至少有n+1个根,可以写成
10nniniRxKxxxKxx
——要求nRx需求Kx
任意固定,0,1,,ixxin(估计x点的误差),构造变量为t的函数 0nniitRtKxtx
—— 此时,Kx为与t无关的常量!
0t有n+2个根,分别为01,,,,nxxxx,故t在[a,b]上有n+2个零点;
由罗尔定理,t在t的两个零点之间至少有一个零点,故t在[a,b]上有n+1个零点;(注意:t是对t求导) 同理,t在[a,b]上有n个零点,1nt在[a,b]上有1个零点。 中间步骤:(注意,对t求导!)
1110nnnnniitRtKxtx
11110nnnnnniitftLtKxtx
nLt为n次多项式,故而
1nnLt
为0。因此,
111!nntftnKx
因此记做:111!0nnfnKx
于是:1,,1!nfKxabn且依赖于x。 故:1111!nnnnfRxKxxxn 余项表达式只有在fx的高阶导数存在时才能应用,又因为,ab的具体位置通常不可能给出,因此常计算()nLx逼近fx的截断误差限: 111!nnnMRxxn
, 其中
11maxnnaxbMfx
。