
《振动力学》习题集(含答案)
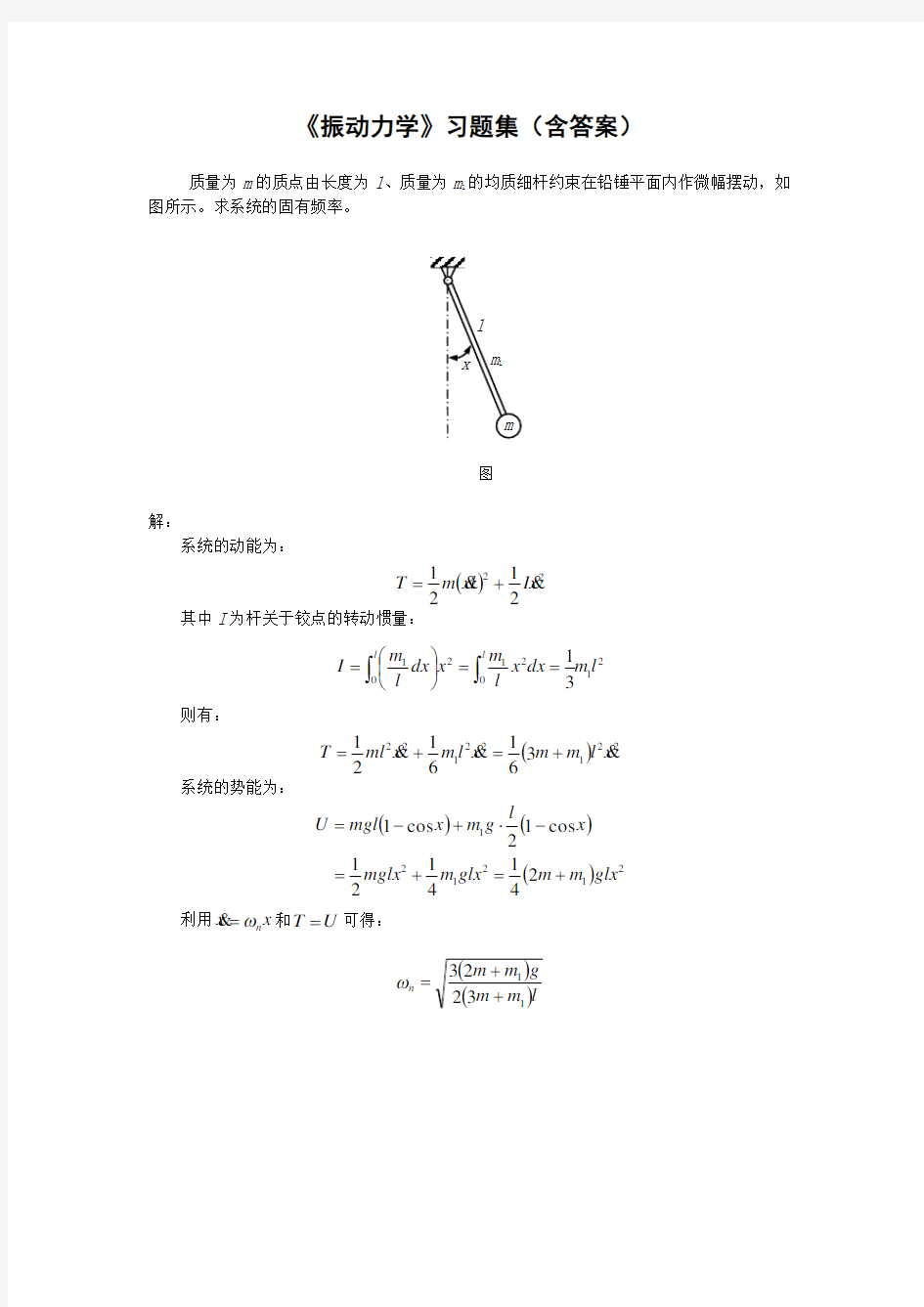
质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。求系统的固有频率。
图
解:
系统的动能为:
()22
2
121x I l x m T &&+=
其中I 为杆关于铰点的转动惯量:
2102120131l m dx x l m x dx l m I l l ??==??
?
??=
则有:
()2
212212236
16121x l m m x l m x ml T &&&+=+=
系统的势能为:
()()()2
1212124
1
4121 cos 12
cos 1glx m m glx m mglx x l
g m x mgl U +=+=-?
+-=
利用x x
n ω=&和U T =可得: ()()l
m m g
m m n 113223++=
ω
质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。求系统的固有频率。
图
解:
如图,令θ为柱体的转角,则系统的动能和势能分别为:
2222224321212
1θθθ&&&mR mR mR I T B =??
? ??+==
()[]()22
22
12θθa R k a R k U +=+?=
利用θωθ
n =&和U T =可得: ()m
k
R a R mR a R k n 34342
2
+=+=ω
转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。求系
统的固有频率。
图
解:
系统的动能为:
22
1θ&J T =
2k 和3k 相当于串联,则有:
332232 , θθθθθk k =+=
以上两式联立可得:
θθθθ3
22
33232 , k k k k k k +=+=
系统的势能为:
()232323212
332222*********θθθθ??
????+++=++=k k k k k k k k k k U
利用θωθ
n =&和U T =可得: ()()
3232132k k J k k k k k n +++=
ω
在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。求固有频率。
图
答案图
解:
对m 进行受力分析可得:
33x k mg =,即3
3k mg
x =
如图可得:
()()2
2221111 ,k b a mga k F x k b a mgb k F x +==+==
()()mg k k b a k b k a b a x x a x x x x 212
2
21212110++=+-+='+= ()mg k mg k k k b a k b k a x x x 0
3212
2212301
1=??
????+++=+=
则等效弹簧刚度为:
()()2
12322
312
3
212
k k b a k k b k k a k k k b a k e ++++= 则固有频率为:
()()(
)[
]
2
22132212
321b k a k k b a k k m b a k k k m k e n ++++==ω
质量1m 在倾角为α的光滑斜面上从高h 处滑下无反弹碰撞质量2m ,如图所示。确定
mg b
a a F +=
2
x x 2
系统由此产生的自由振动。
图
答案图
解:
对1m 由能量守恒可得(其中1v 的方向为沿斜面向下):
21112
1
v m gh m =
,即gh v 21=
对整个系统由动量守恒可得:
()02111v m m v m +=,即gh m m m v 22
110+=
令2m 引起的静变形为2x ,则有:
22sin kx g m =α,即k
g m x α
sin 22=
令1m +2m 引起的静变形为12x ,同理有:
()k g m m x αsin 2112+=
得:
k
g m x x x α
sin 12120=
-=
则系统的自由振动可表示为:
t x t x x n n
n ωωωsin cos 0
0&+
=
其中系统的固有频率为:
2
1m m k
n +=
ω
注意到0v 与x 方向相反,得系统的自由振动为:
t v t x x n n
n ωωωsin cos 0
0-
=
质量为m 、长为l 的均质杆和弹簧k 及阻尼器c 构成振动系统,如图所示。以杆偏角
θ
为广义坐标,建立系统的动力学方程,给出存在自由振动的条件。若在弹簧原长处立即释手,问杆的最大振幅是多少?发生在何时?最大角速度是多少?发生在何时?是否在过静平衡位置时?
图
答案图
解:
利用动量矩定理得:
l l c a a k I ?-?-=θθθ&&&, 23
1ml I =
033222
=++θθθka cl ml &&&, 2
23ml ka n =ω
n ml cl ξω232
2=, 3
2 1123mk
l a c m c n
a a k l mg ?=?
02θ, 2
02ka mgl
=
θ
面积为S 、质量为m 的薄板连接于弹簧下端,在粘性流体中振动,如图所示。作用于
薄板的阻尼力为Sv F d 2μ=,2S 为薄板总面积,v 为速度。若测得薄板无阻尼自由振动的周期为0T ,在粘性流体中自由振动的周期为d T 。求系数μ。
l c
图
解:
平面在液体中上下振动时:
02=++kx x S x m &&&μ
2T m k n πω=
=
, d
n d T πξωω212=
-=
n n m S m S ωμξξωμ=?= 22, k
S 222
μξ=
k
S k 2
22
1μξ-=-
2020220
222T T T ST m
k S k T T d d
d -=?-=πμμππ
图所示系统中,已知m ,c ,1k ,2k ,0F 和ω。求系统动力学方程和稳态响应。
图
答案图(a) 答案图(b)
解:
等价于分别为1x 和2x 的响应之和。先考虑1x ,此时右端固结,系统等价为图(a ),受力为图(b ),故:
()()x c x k x c c x k k x m &&&&112121+=++++ t A c A k kx x c x m 1111111cos sin ωωω+=++&&&
(1)
21c c c +=,21k k k +=,m
k k n 2
1+=
ω (1)的解可参照释义(),为:
()()
()()
()
()()
2
2
2111
112
2
2111121cos 21sin s s t k
A c s s t k
A k t Y ξθωωξθω+--+
+--=
(2)
其中:
n s ωω1=
,21112s
s tg -=-ξθ ()
()()2
12
12212212
2112
121k k c c k k k k c s ++++=
???
?
??++=+ωωξ
()()
()()
()2
1212
212
2
1
212
211212
21212
2
2 121k k c c m k k
k k c c k k m s s +++-+=
?
?
????+++???? ??+-=+-ωωωωξ
故(2)为:
()()()
()
()()()()
21121
2
2
1
2
21
21
21
2121
1
2
1
2
212
2121111111111sin cos sin θθωω
ω
ωωωθωωθω+-++-++=++-+-+-=
t c c m k k
c k A c c m k k t A c t A
k t x
x k 2x
&2 (11x k - )
11x x c &&-
1
2
()()m k k c c tg k k m k k c tg s s tg 2
1
211
2112
121
211121
1112ωωωωξθ-++=+-+=-=--- 1
1
11
2k c tg ωθ-=
考虑到()t x 2的影响,则叠加后的()t x 为:
()()()()???? ?
?+-++-++-++=--=∑
i i i i i i i i i i i i i k c tg m k k c c tg t c c m k k c k A t x ωωωωωωω1221211
2
1
222122212
22sin
一弹簧质量系统沿光滑斜面作自由振动,如图T 2-1所示。已知,?=30α,m = 1 kg ,k = 49 N/cm ,开始运动时弹簧无伸长,速度为零,求系统的运动规律。
图 T 2-1
答案图 T 2-1
解:
0sin kx mg =α,1.049
21
8.91sin 0=?
?==
k
mg x α
cm
701
10492
=?==-m k n ωrad/s
t t x x n 70cos 1.0cos 0-==ωcm
如图T 2-2所示,重物1W 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2W 从
高度为h 处自由下落到1W 上而无弹跳。求2W 下降的最大距离和两物体碰撞后的运动规律。
图 T 2-2
答案图 T 2-2
解:
2
22221v g
W h W =
,gh v 22=
动量守恒:
122
122v g
W W v g W +=,gh W W W v 221212+=
平衡位置:
11kx W =,k
W x 1
1=
1221kx W W =+,k
W W x 2
112+=
故:
k
W x x x 2
1120=
-= ()2
121W W kg
g W W k n +=+=
ω
故:
t
v t x t
x t x x n n
n n n
n ωωωωωωsin cos sin cos 12
00
0+
-=+-=&
在图所示系统中,已知m ,1k ,2k ,0F 和ω
,初始时物块静止且两弹簧均为原长。
W 2
W 1
求物块运动规律。
图
答案图
解:
取坐标轴1x 和2x ,对连接点A 列平衡方程:
()0sin 012211=+-+-t F x x k x k ω
即:
()t F x k x k k ωsin 022121+=+
(1)
对m 列运动微分方程:
()1222x x k x m --=&&
即:
12222x k x k x m =+&&
(2)
由(1),(2)消去1x 得:
t k k k
F x k k k k x m ωsin 2
120221212+=++
&&
(3)
故:
()
212
12k k m k k n +=
ω
由(3)得:
()()()???
? ??--+=
t t k k m k F t x n n n ωωωωωωsin sin 2221202
在图所示系统中,已知m ,c ,k ,0F 和ω,且t =0时,0x x =,0v x
=&,求系统响应。验证系统响应为对初值的响应和零初值下对激励力响应的叠加。
x k
)1x x k - 2x m &&
(2k
2
图
解:
()()()θωωωξω-++=-t A t D t C e t x d d t cos sin cos 0
()()
2
2
20
211
s s k
F A ξ+-?=
,2
1
12s
s
tg
-=-ξθ ()θθcos cos 000A x C A C x x -=?+==
()()()()
θωωωωωωωωξωξωξω--+-++-=--t A t D t C e
t D t C e t x d d d d t
d d t sin cos sin sin cos 000&
()d
d
d A C
v D A D C v x
ωθ
ωωξωθωωξωsin sin 00000-
+=?++-==&
求出C ,D 后,代入上面第一个方程即可得。
由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上,如图所示。当齿轮转动角速度为ω时,偏心质量惯性力在垂直方向大小为
t me ωωsin 2。已知偏心重W = N ,偏心距e = 15.0 cm ,支承弹簧总刚度系数k = N /cm ,
测得垂直方向共振振幅cm X m 07.1=,远离共振时垂直振幅趋近常值cm X 32.00=。求支承阻尼器的阻尼比及在m in 300r =ω运行时机器的垂直振幅。
t ω
图
解:
()()()
()θωξ-+-?
=t s s s M
me t x sin 212
2
22
,2
1
12s s
tg -=-ξθ
s =1时共振,振幅为:
cm M me X 07.1211=?=
ξ
(1)
远离共振点时,振幅为:
cm M
me
X 32.02==
(2)
由(2)2
X me M =
?
由(1)15.0221211
2121==?=?=
?X X X X me me X M me ξ m in 300r =ω,M
k
=
0ω,10ωω=s
故:
()()
m s s s M
me
X 32
2
22
108.321-?=+-?
=ξ
求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是1k 及3k ,悬臂梁的质量忽略
不计。
图 T 2-7
答案图 T 2-7
解:
1k 和2k 为串联,等效刚度为:2
12
112k k k k k +=
。(因为总变形为求和)
12k 和3k 为并联(因为12k 的变形等于3k 的变形),则:
2
13
2312132121312123k k k k k k k k k k k k k k k k +++=++=
+=
123k 和4k 为串联(因为总变形为求和),故:
4
24132312143243142141234123k k k k k k k k k k k k k k k k k k k k k k k k e ++++++=+=
故:
m
k e
n =
ω
如图T 2-9所示,一质量m 连接在一刚性杆上,杆的质量忽略不计,求下列情况系统作垂直振动的固有频率:
(1)振动过程中杆被约束保持水平位置;
(2)杆可以在铅锤平面内微幅转动;
(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
图 T 2-9
答案图 T 2-9
解: (1)保持水平位置:m
k k n 2
1+=ω
(2)微幅转动:
()()()()()()()()()mg
k k l l k l k l mg k k l l k l l k l l l k l mg k k l l k l k l l l l k l l mg l mg
k l l l k l l l l l l k l l mg l l l l x x k F x x x 2
12212
2
21212
12
2122112121222121221121112121212221121112122
11
12111 ++=+-++=+-?+++=??????+-++++=
+-+='+=
故:
()2
2
21212
12
21k l k l k k l l k e
++=
m
k e
n =
ω
求图T 2-10所示系统的固有频率,刚性杆的质量忽略不计。
mg l l
F 2
11
2+=
x x 2
图 T 2-10
答案图 T 2-10
解:
m 的位置:A A x k mg
x x x +=
+=2
2 a F mgl 1=,a mgl
F =
1,1
1ak mgl x =∴
l a x x A =1,1
22
1k a mgl x l a x A ==∴ mg
k k a k l k a mg k a l k k a mgl k mg x x x A 2
122
212122212222 1+=????
??+=+=+=∴
2
2
122
12k l k a k k a k e +=∴,m k e n =ω
图T 2-11所示是一个倒置的摆。摆球质量为m ,刚杆质量可忽略,每个弹簧的刚度为
2
k 。 (1)求倒摆作微幅振动时的固有频率;
(2)摆球质量m 为0.9 kg 时,测得频率()n f 为 Hz ,m 为1.8 kg 时,测得频率为 Hz ,
问摆球质量为多少千克时恰使系统处于不稳定平衡状态?
x 1
x A
图 T 2-1
答案图 T 2-11(1)
答案图 T 2-11(2)
解:(1)
2222
121θ
θ&&ml I T ==
()()
()
2
22222
2
1
2121 cos 121212θθθθθmgl ka mgl ka mgl a k U -=-=--??
? ???=
利用max max U T =,max
max θωθn =& ???
? ??-=-=-=12
2
222mgl ka l g l
g
ml ka ml mgl ka n ω ----------------------------------------------------------------------------------------------------------------------
(2)
若取下面为平衡位置,求解如下:
2222
121θθ&&ml I T ==
()()
mgl
mgl ka mgl mgl ka mgl ka mgl a k U +-=-+=?
?? ??-+=+??? ???=222222222
2
1
2121 2sin 2121cos 21212θθθθθθθ ()0=+U T dt
d ,()02222=-+θθθθ&&&&mgl ka ml ()
022=-+θθmgl ka ml &&
2
2ml
mgl
ka n -=ω
图T 2-17所示的系统中,四个弹簧均未受力,k 1= k 2= k 3= k 4= k ,试问:
θ
零平衡位置
(1)若将支承缓慢撤去,质量块将下落多少距离? (2)若将支承突然撤去,质量块又将下落多少距离?
图 T 2-17
解:
k
k k k k k k k k k k k k k k k 2
1
32
24123412312342312311233223=+=
=+==+=
(1)01234x k mg =,k
mg
x 20=
(2)()t x t x n ωcos 0=,k
mg
x x 420max ==
如图T 2-19所示,质量为m 2的均质圆盘在水平面上可作无滑动的滚动,鼓轮绕轴的转动惯量为I ,忽略绳子的弹性、质量及各轴承间的摩擦力,求此系统的固有频率。
图 T 2-19
解:
系统动能为:
2
2
22212
2
2222
2212
1 2321 2121212121x m x m R I m r x r m x m R x I x m T e &&&&&&=???
? ??++=???
???????? ????? ??++???? ??+=
系统动能为:
22
2221122
21
1222
1 21 2121x k x R R k k x R R k x k V e =
???? ??+=???
?
??+=
根据:
max max V T =,max max x x n ω=&
2
2212
221122
2
3m R I m R R k k n +++=
ω
如图T 2-20所示,刚性曲臂绕支点的转动惯量为I 0,求系统的固有频率。
图 T 2-20
解:
系统动能为:
()()
()2222102221202
1 2
12121θθθθ&&&&l m a m I l
m a m I T ++=++=
系统动能为:
()()()()2
2322212322212
1
2
12121θθθθb k l k a k b k l k a k V ++=++=
根据:
max max V T =,max
max θωθn =& 2
22102
322212l m a m I b k l k a k n
++++=
ω
一长度为l 、质量为m 的均匀刚性杆铰接于O 点并以弹簧和粘性阻尼器支承,如图T 2-24所示。写出运动微分方程,并求临界阻尼系数和无阻尼固有频率的表达式。
图 T 2-24
答案图 T 2-24
解:
利用动量矩方程,有:
l l c a a k J ?-?-=θθθ&&&,23
1ml J = 033222=++θθθka cl ml &&&
2
2
3ml
ka n =ω n ml
cl ξω232
2
=,1=ξ 3
2332322
2mk
l a ml ka m m c n ===ω
2008年振动力学期末考试试题 第一题(20分) 1、在图示振动系统中,已知:重物C 的质量m 1,匀质杆AB 的质量m 2,长为L ,匀质轮O 的质量m 3,弹簧的刚度系数k 。当AB 杆处于水平时为系统的静平衡位置。试采用能量法求系统微振时的固有频率。 解: 系统可以简化成单自由度振动系统,以重物C 的位移y 作为系统的广义坐标,在静平衡位置时 y =0,此时系统的势能为零。 AB 转角:L y /=? 系统动能: m 1动能:2 1121y m T = m 2动能:2222222 22 222)3 1(21))(31(21)31(2121y m L y L m L m J T ====? ω m 3动能:2322 323 33)2 1(21))(21(212 1y m R y R m J T === ω 系统势能: 2 21)21(21)21( y k y g m gy m V + +-= 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有: E y k gy m gy m y m m m V T =+ +-++= +2 212 321) 2 1(2 12 1)2 13 1(2 1 上式求导,得系统的微分方程为: E y m m m k y '=+ + +) 2 131(4321 固有频率和周期为: ) 2 131(43210m m m k + + = ω 2、质量为m 1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮A 连在质量为m 2的物块B 上;轮心C 与刚度系数为k 的水平弹簧相连;不计滑轮A ,绳及弹簧的质量,系统自弹簧原长位置静止释放。试采用能量法求系统的固有频率。 解:系统可以简化成单自由度振动系统,以重物B 的位移x 作为系统的广义坐标,在静平衡位置时 x =0,此时系统的势能为零。 物体B 动能:2 212 1x m T = 轮子与地面接触点为速度瞬心,则轮心速度为x v c 2 1= ,角速度为x R 21=ω,转过的角度为x R 21= θ。轮子动能: )83(21)41)(21(21)4 1( 2 12 1212 122 21212 2 12x m x R R m x m J v m T c =+= + = ω 系统势能: x
泥沙颗粒分析及沉降速度实验 一、试验目的 1、了解在实验室进行泥沙颗粒分析及沉速实验的一般方法; 2、掌握筛分法和移液管法的适用性及操作过程; 3、掌握泥沙颗粒级配曲线的绘制方法及沙样特征值的确定方法; 4、泥沙沉降现象可结合移液管法的操作过程进行观察。 二、试验方法及适用范围 1、筛分法:适用于泥沙粒径大于0.075mm的颗粒。 2、移液管法:适用于粒径小于0.075mm的颗粒。 3、若沙样中粗细颗粒兼有,则要联合使用筛分法及移液管法。 三、实验方法原理 1、对d>0.1mm的泥沙,应用筛分法测量泥沙颗粒级配。筛分法原理是利用孔径不同、逐级叠置的筛子,通过振动分选,再分别称出各级筛上的沙重,计算绘出沙样的级配曲线; 2、对d<0.1mm的泥沙,应用移液管法测量泥沙颗粒级配。移液管法原理为根据泥沙在沉降筒中沉降快慢的不同,来测定不同粒级的泥沙的数量,通过计算分析绘出沙样的级配曲线。 四、筛分法实验 1、仪器设备:振筛机、烘箱、天平、盛沙杯、沉降筒、温度计、干燥器等。试验筛:粗筛:圆孔孔径为60mm,40mm,20mm,10mm,5mm,2mm;细筛:孔径为2.0,1.0,0.5,0.25,0.1,0.075mm。 天平:称量1000g与称量200g;台秤:称量5kg。 振筛机:符合GB9909-88的技术条件。 其它:盛沙杯、沉降筒、温度计、干燥器等。 五、筛分法实验方法 1、将252.37g沙样放在精密天秤上称重,放入容量瓶的水中称其体积107ml,测出湿密度2.359g/ml。 2、将252.37g沙样放入干燥器中烘干,将烘干后的沙样作为试样放在天平/台
秤上称重为238.4g。(称量准确至0.1g,当沙样质量多于500g时,准确至1g). 2、将试样倒入依次叠好的最上层筛中,进行筛析。细筛宜放在振筛机上震摇,震摇时间一般为10-15min。 3、由最大孔径筛开始,顺序将各筛取下,在白纸上用手轻叩摇晃,如仍有土粒漏下,应继续轻叩摇晃,至无土粒漏下为止。漏下的土粒应全部放入下级筛内。并将留在各筛上的试样分别称量,准确至0.1g。称量并计算出小于各级筛的泥沙总重量。 4、各细筛上及底盘内土质量总和与筛前所取试样的质量之差0.92%不大于1%。
《振动力学》习题集(含答案) 1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。求系统的固有频率。 图E1.1 解: 系统的动能为: ()2 22 121x I l x m T += 其中I 为杆关于铰点的转动惯量: 2102120131l m dx x l m x dx l m I l l ??==?? ? ??= 则有: ()2212212236 16121x l m m x l m x ml T +=+= 系统的势能为: ()()()2 1212124 1 4121 cos 12cos 1glx m m glx m mglx x l g m x mgl U +=+=-? +-= 利用x x n ω= 和U T =可得: ()()l m m g m m n 113223++= ω
1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。求系统的固有频率。 图E1.2 解: 如图,令θ为柱体的转角,则系统的动能和势能分别为: 22222243212121θθθ mR mR mR I T B =??? ??+== ()[]()22 22 12θθa R k a R k U +=+?= 利用θωθn = 和U T =可得: ()m k R a R mR a R k n 34342 2 +=+=ω
1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。 求系统的固有频率。 图E1.3 解: 系统的动能为: 2 2 1θ J T = 2k 和3k 相当于串联,则有: 332232 , θθθθθk k =+= 以上两式联立可得: θθθθ3 22 33232 , k k k k k k +=+= 系统的势能为: ()2 32323212332222121212121θθθθ?? ????+++=++= k k k k k k k k k k U 利用θωθn = 和U T =可得: ()() 3232132k k J k k k k k n +++= ω
振动力学 1前言部分 振动力学在其发展过程中逐渐由基础科学转化为基础科学与技术科学的结合.工程问题的需要使振动力学的发展成为必需,而测试和计算技术的进步又为振动力学的发展和应用提供了可能性.除与技术问题的结合以外,学科的交叉不断为振动力学的发展注入新的活力.在数百年发展过程中,振动力学已形成为以物理概念为基础,以数学理论、计算方法和测试技术为工具,以解决工程中振动问题为主要目标的力学分支。 人类对振动现象的认识有悠久的历史。战国时期的古人已定量地总结出弦线发音与长度的关系。在振动力学研究兴起之前,有两个典型的振动问题引起注意,即弦线振动和单摆振动。对单摆摆动的研究起源于Galileo,他在1581年发现摆的等时性。1727年JohnBernoulli研究无重量弹性弦上等距分布等质量质点时,建立无阻尼自由振动系统模型并解出解析解。1728年Euler考察了摆在有阻尼介质中的运动建立并求解了相应的二阶常微分方程。1739年他研究了无阻尼简谐受迫振动,从理论上解释了共振现象。1834年Duhamel将任意外激励视为一系列冲量激励的叠加,从而建立了分析强迫振动的普遍公式.1849年Stokes发现了初位移激励与初速度激励两者响应的联系,并且由此对外激励得到与Duhamel相同的结果. 非线性振动的研究使得人们对振动机制有了新的认识.除自由振动、受迫振动和参数振动以外,还有一类广泛存在的振动,即自激振动.1925年Cartan父子研究了无线电技术中出现的一类二阶非线性微分方程的周期解.1926年vanderPol建立一类描述三极电子管振荡的方称为vanderPol方程,他用图解法证明孤立闭轨线的存在,又用慢变系数法得到闭轨线的近似方程.1928年Lienard证明以 Cartan 方程和vanderPol方程为特例的一类方程存在闭轨线,1929年Андронов阐明了vanderPol的自激振动对应于Poincaré研究过的极限环。 2主题部分
一、 1.在单自由度振动系统中,结构振动响应的频率与外加荷载的频率无关(×) 2.在含有阻尼的单自由度振动系统中,结构振动的固有频率与阻尼无关(×) 3.对于图示简支梁,不计梁的质量,分别将物体M 从在距梁中点正上方高H1和H2处 自由释放,H1=2H2,则振动的频率是一样的(√) 二、 1.如图所示,除支撑不同外,其余均相同。(B ) A.图a 振动周期大 B.图b 振动周期大 C.振动周期一样 D.不能判断 2.一物体从高度为h 的地方落下,系统振动频率是(C ) A.h 越大,频率越大 B.h 越大,频率越小 C.与h 无关 D.不能断定 3.对于一个有阻尼的单自由度强迫振动系统来讲,振动响应频率(C ) A.仅由外荷载频率确定 B.仅由系统固有频率确定 C.在系统振动响应一段时间后,仅与外荷载频率有关 D.在系统振动响应一段时间后,仅与系统固有频率有关 4.对于多自由度系统来讲,假设无重频现象,则两个不同的振型φi 和φj 的关系为(C ) A.j T i φφ?一定为零 B.j T i φφ?一定不为零 C.j T i M φφ一定为零 D.j T i K φφ可能不是零 5.对于一个三自由度系统,设某阶段振型为[]T 1,2,1=φ,骑广义质量为4,则其正则振型为(A )
A.[]T 5,0,1,5.0=φ B.[]T 25.0,5.0,25.0=φ C. []T 1,2,1=φ D.[]T 2,4,2=φ 三、一个单自由度振动系统,自由振动试验测得经过6周后振幅降为原来的1/10,试求阻尼比和在简谐荷载作用下发生共振时的放大系数(15) 解:ξπδm y y m i i y 2ln '==+ m=6 ∴10ln ln 6 =+i i y y ∴0611.06210ln =?=πξ 197.821==ξ μ 四、试写出图示结构的运动方程和位移动力系数(EI 为常数, t F t F θsin )(=) 解:a 12=F a 2 11=F 2____ M 1____M EI a 38311=δ EI a 65312=δ )(16 5)(1112t F t F Fe ==δδ )(16 5t F ky y m =+?? 3 383)2(3a EI a EI k == 383ma EI m k ==ω 211βμ-= EI ma 322θω?β== 32833a m EI EI θμ-= 五、如图所示结构,层间高度均为L ,m1=m2=m ,求系统的固有圆
《振动力学》习题集(含答案) 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。求系统的固有频率。 图 解: 系统的动能为: ()22 2 121x I l x m T &&+= 其中I 为杆关于铰点的转动惯量: 2102120131l m dx x l m x dx l m I l l ??==?? ? ??= 则有: ()2 212212236 16121x l m m x l m x ml T &&&+=+= 系统的势能为: ()()()2 1212124 1 4121 cos 12 cos 1glx m m glx m mglx x l g m x mgl U +=+=-? +-= 利用x x n ω=&和U T =可得: ()()l m m g m m n 113223++= ω
质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。求系统的固有频率。 图 解: 如图,令θ为柱体的转角,则系统的动能和势能分别为: 2222224321212 1θθθ&&&mR mR mR I T B =?? ? ??+== ()[]()22 22 12θθa R k a R k U +=+?= 利用θωθ n =&和U T =可得: ()m k R a R mR a R k n 34342 2 +=+=ω
转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。求系统 的固有频率。 图 解: 系统的动能为: 22 1θ& J T = 2k 和3k 相当于串联,则有: 332232 , θθθθθk k =+= 以上两式联立可得: θθθθ3 22 33232 , k k k k k k +=+= 系统的势能为: ()232323212 332222*********θθθθ?? ????+++=++=k k k k k k k k k k U 利用θωθ n =&和U T =可得: ()() 3232132k k J k k k k k n +++= ω
有限元方法在振动力学上的应用分析 Xxxxx xxxxxxxxx
有限元方法在振动力学上的应用分析 摘要:有限元法是一种可用于精确地(但近似)解决许多复杂的振动问题的数值方法。对于基本的一维元素进行有限元分析,能得到质量矩阵与刚度矩阵和所需的力矢量,对于二维三维,元素矩阵会转换成相关的更高维的空间。使用一致的和集中质量矩阵的有限元方程并结合边界条件能为复杂系统提供解释。最后,使用MA TLAB程序得到在轴向载荷下的指定节点位移,固有振动频率和特征值分析。[1] 关键词:有限元振动力学固有频率特征值 目录 1发展背景 (3) 1.1有限元的发展背景 (3) 1.2有限元法应用于工程计算的发展背景 (3) 2基础理论推导 (4) 2.1有限元理论 (4) 2.2理论推导 (4) 3参数影响 (8) 3.1边界条件的影响 (8) 3.2网格划分对有限元模态分析的影响 (8) 3.3单元类型的影响 (8) 4实例分析 (9) 4.1杆件分析 (9) 4.2梁的自然频率 (10) 5结论 (11)
1,发展背景 1.1有限元的发展背景 有限元法是R.Courant于1943年首先提出的。自从提出有限元概念以来,有限元理论及其应用得到了迅速发展。过去不能解决或能解决但求解精度不高的问题,都得到了新的解决方案。传统的FEM假设:分析域是无限的;材料是同质的,甚至在大部分的分析中认为材料是各向同性的;对边界条件简化处理。但实际问题往往是分析域有限、材料各向异性或边界条件难以确定等。为解决这类问题,美国学者提出用GFEM (Gener-alized Finite Element Method)解决分析域内含有大量孔洞特征的问题。[2] 比利时学者提出用HSM (the Hybrid metis Singular element of Membrane plate)解决实际开裂问题。 在FEM应用领域不断扩展、求解精度不断提高的同时,FEM也从分析比较向优化设计方向发展。印度Mahanty博士用ANSYS对拖拉机前桥进行优化设计,结果不但降低了约40%的前桥自重,还避免了在制造过程中的大量焊接工艺,降低了生产成本。[3] 目前在进行大型复杂工程结构中的物理场分析时,为了估计并控制误差,常用基于后验误差估计的自适应有限元法。基于后处理法计算误差,与传统算法不同,将网格自适应过程分成均匀化和变密度化2个迭代过程。在均匀化迭代过程中,采用均匀网格尺寸对整体区域进行网格划分,以便得到一个合适的起始均匀网格;[4]在变密度化迭代过程中只进行网格的细化操作,并充分利用上一次迭代的结果,在单元所在的曲边三角形区域内部进行局部网格细化,保证了全局网格尺寸分布的合理性,使得不同尺寸的网格能光滑衔接,从而提高网格质量。整个方案简单易行,稳定可靠,数次迭代即可快速收敛,生成的网格布局合理,质量高。 1.2 有限元法应用于工程计算的发展背景 FEM作为求解数学物理问题的一种数值方法,已经历了50余年的发展。20世纪50年代,它作为处理固体力学问题的方法出现。1943年,Courant第一次提出单元概念。1945~1955年,Argyris等人在结构矩阵分析方面取得了很大进展。1956年,Turner、Clough等人把刚架位移法的思路推广应用于弹性力学平面问题。1960年,Clough首先把解决弹性力学平面问题的方法称为“有限元法”,并描绘为“有限元法 = Rayleigh Ritz法 + 分片函数”。几乎与此同时,我国数学家冯康也独立提出了类似方法。FEM理论研究的重大进展,引起了数学界的高度重视。自20世纪60年代以来,人们加强了对FEM数学基础的研究。如大型线性方程组和特征值问题的数值方法、离散误差分析、解的收敛性和稳定性等。FEM理论研究成果为其应用奠定了基础,计算机技术的发展为其提供了条件。20世纪70年代以来,相继出现了一些通用的有限元分析(FEA: Finite Element Analysis)系统,如SAP、ASKA、NASTRAN等,这些FEA系统可进行航空航天领域的结构强度、刚度分析,从而推动了FEM在工程中的实际应用。20世纪80年代以来,随着工程工作站的出现和广泛应用,原来运行于大中型机上的FEA系统得以在其上运行,同时也出现了一批通用的FEA系统,如ANSYS-PC、NISA,SUPERSAP 等。20世纪90年代以来,随着微机性能的显著提高,大批FEA系统纷纷向微机移植,出现了基于Windows的微机版FEA系统。经过半个多世纪的发展,FEM已从弹性力学平面问题扩展到空间问题、板壳问题;从静力问题扩展到动力问题、稳定问题和波动问题;从线性问题扩展到非线性问题;从固体力学领域扩展到流体力学、传热学、电磁学等其他连续介质领域;从单一物理场计算扩展到多物理场的耦合计算。它经历了从低级到高级、从简单到复杂的发展过程,目前已成为工程计算最有效的办法之一。[5]
1.转动惯量为J 的圆盘由三段抗扭刚度分别为1k 、2k 和3k 的轴约束,如图所示。求系统的固有频率。 解: 系统的动能为 2 2 1?=θJ T 2k 和3k 相当于串联,则 32θθθ += 3322θθk k = 联立以上两式得 θθ3 23 2k k k += θθ3223k k k += 系统的势能为 ( )[]2 2 33222213 23 23212 1212121θ θθθk k k k k k k k k k U +++= ++= 利用θωθn =? 和U T =可得 () () 3232132n k k J k k k k k +++= ω 2.面积为S ,质量为m 的薄板连接于弹簧下端,在粘性流体中振动,如图所示。作用于薄板的阻尼力为νμS F d 2=,S 2为薄板总面积,ν为速度。若测得薄板无阻尼自由振动的周期为0T ,在粘性流体中自由振动的周期为d T 。求系数μ。
解: 平面在液体中上下振动时: 02=++? ? ?kx x S x m μ d n d n T T m k πξ ωωπω2-1,220==== k S m S m S n n 222,22μξωμξξωμ==?= k S k 2 22 --1μξ= 2020220 -2-22T T T ST m k S k T T T T d d d πμμ=?= 3.如图所示均匀刚性杆质量为1m ,求系统的频率方程。 解:
先求刚度矩阵。 令0x 1,==θ得: 22212111a k b k a a k b b k k +=?+?= b k 221-k = 令1,0==x θ得: a k k 212-= 222-k k = 则刚度矩阵为:?? ? ? ??+=2222221--k a k a k a k b k K 再求质量矩阵。 令0,1==? ?? ?x θ ,得: 0,3 1 212111==m a m m
… 2008年振动力学期末考试试题 第一题(20分) 1、在图示振动系统中,已知:重物C 的质量m 1,匀质杆AB 的质量m 2,长为L ,匀质轮O 的质量m 3,弹簧的刚度系数k 。当AB 杆处于水平时为系统的静平衡位置。试采用能量法求系统微振时的固有频率。 解: 系统可以简化成单自由度振动系统,以重物C 的位移y 作为系统的广义坐标,在静平衡位置时 y =0,此时系统的势能为零。 AB 转角: 系统动能: % m 1动能: m 2动能: m 3动能: 系统势能: 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有: 上式求导,得系统的微分方程为: E y m m m k y '=+++) 2 1 31(4321 固有频率和周期为: ~ ) 2 131(43210m m m k ++= ω 2、质量为m 1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮A 连在质量为m 2的物块B 上;轮心C 与刚度系数为k 的水平弹簧相连;不计滑轮A ,绳及弹簧的质量,系统自弹簧原长位置静止释放。试采用能量法求系统的固有频率。 解:系统可以简化成单自由度振动系统,以重物B 的位移x 作为系统的广义坐标,在静平衡位置时 x =0,此时系统的势能为零。 物体B 动能:2212 1 x m T = 轮子与地面接触点为速度瞬心,则轮心速度为x v c 21=,角速度为x R 21=ω,转过的角度为x R 21 = θ。轮子动能: )83 (21)41)(21(21)41(212121212221212212x m x R R m x m J v m T c =+=+=ω \ x
2005级 《振动力学》 课程试题(A 卷) 二、基本概念与简单计算题:(共 50 分) 1.(5分)某粘滞阻尼振动系统,8个振动周期后振幅由10mm 减为1mm ,求 阻尼比。 解:对数衰减率01 ln n X n X δ ??= ???110ln 81??= ???1 ln 108 = ………………..(3分) 而2 21πξδ ξ = -,则阻尼比2 2 4δ ξ π δ = +=0.046……………………(2分) 2. (10分)求图示系统微幅振动的微分方程和固有频率。已知l 、k 、m 、c 、F 。 不计水平杆的质量。 解:方程 493ml cl kl F θ θθ=--+ …………….(6分) 固有频率 3 n k m ω= …………………… …………….(4分) 或 2 2 2194d n mk c m ωωξ =-=-……………………….(4分) 3. (10分)求单自由度无阻尼标准m -k 振动系统在图示干扰力作用下的零初值 响应。 解:干扰力0000 10()0 t F t t F t t t t ??? -≤≤? ? =??? ? >?….(2分) 000 01 ()(1cos )sin 0n n n n F x t t t t t t t t ωωωω??= --+≤≤ ??? ………..(4分) 题二.2图 m c k F l l l 题二、3图 F (t ) F 0 t 0 t
0000 01 ()cos [sin ()sin ]n n n n n F x t t t t t t t t t ωωωωω??=- + --> ??? ……………………..(4分) 4. (15分)图示系统,均质杆 长为l 质量为m ,上端由铰链悬挂,下端用弹性系数为k 1和k 2的弹簧与光滑水平面上的质量m 1和m 2相连处于自然平衡状态。(1)建立系统的微振动微分方程。(2)写出频率方程(可以不求出固有频率) 解:(1)1 12 2213 m x m l x m θ????? ??? ? ???????????? ? 1112 1122222001()02 00k k l x k l k k l m gl k l x k l k θ-?? ?????????? ??+-++ -=????????????????-? ? .(10分) (2)频率方程…… ………(5分) 5. (10分)左端固定,右端自由的均匀杆,长度为l ,轴向拉压刚度为EA ,单 位长度杆的质量为m ,轴向位移用u 表示,轴向力用P 表示。求杆纵向振动(一维波动方程)的固有频率与固有振型。 解:一维波动方程: 2 2(,)u x t x ??2 2 2 1(,)u x t a t ?= ?,0 《振动力学》2015春节学期作业 一、无阻尼自由振动 1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的 ?时(即机构处于平衡位置时),两弹簧无转动惯量为J,两弹簧的弹簧系数均为k,且当=0 伸缩,试求该机构的摆动频率。 (答案:ω) 2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。求该系统的固有频率。(忽略刚性杆件和弹簧的质量) (答案:ω) 3、如图所示,悬臂梁长为L ,截面抗弯刚度为EI ,梁的自由端有质量为m 的质量块,弹簧刚度为k ,求系统的固有频率。 (答案:ω= ) 4、如图所示,半径为R 的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有角频率。 (答案:ω= ) 5、如图所示,抗弯刚度为623010(N m )EI =?? 的梁AB ,借弹簧支撑于A,B 两点处,弹簧系数均为300(/)k N m = 。忽略梁的质量,试求位于B 点左边3m 处,重量为1000()W N = 的物块自由振动的周期。 (答案:T=0.533s ) 6、一个重W 的水箱,借助四根端点嵌固的竖置管柱支撑着。每根柱子的长为L,抗弯刚度为EI 。试求该水箱顺水平方向自由振动的周期。(管柱的质量忽略不计) (答案:2T = ) 7、《结构动力学基础》,第2章课后习题,第1题、第2题、第8题 二、有阻尼自由振动 1、如图所示,库伦曾用下述方法测定液体的粘性系数' c :在弹簧上悬挂一薄板A ,先测出薄板在空气中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。设液体对薄板的阻力等于2A 'c v ,其中2A 为薄板的表面面积,v 为薄板的速度。如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。空气对薄板的阻力不计。 (答案:' c = ) 2、物体质量为2kg ,挂在弹簧下端。弹簧常数k=48.02N/cm,求临界阻尼系数。 (答案:196Ns/m ) 3、挂在弹簧下端的物体,质量为1.96kg ,弹簧常数k=0.49N/cm,阻尼系数c=0.196Ns/cm 。设在t=0时刻将物体从平衡位置向下拉5cm ,然后无初速度地释放,求此后的运动。 振动力学实验报告 学院:___________________ 班级:___________________ 学号:___________________ 姓名:___________________ 山东科技大学 单自由度系统振动实验报告 实验者姓名:________ 院系:_______系_______专业_______班_______组实验日期:________年________月________日 自由振动法测量单自由度系统的参数 一、实验目的 二、实验对象和装置 三、实验步骤 四、实验数据记录和整理 1、无阻尼单自由度自由振动系统实验测量: 计算单自由度振动的振动频率、周期、固有频率、衰减系数、相对阻尼系数周期、频率和阻尼系数: 2、有阻尼单自由度自由振动系统实验测量: 计算单自由度振动的振动频率、周期、固有频率、阻尼系数、相对阻尼系数: 五、简答 1、上述无阻尼自由振动实验中,为什么振动曲线呈现衰减状态? 2、简述阻尼对于自由振动周期、频率的影响。 用冲击激励法测量系统的频率响应函数 实验者姓名:________ 院系:_______系_______专业_______班_______组实验日期:________年________月________日 一、实验目的 二、实验对象和装置 三.实验步骤 四、实验数据记录和整理 1、无阻尼单自由度自由振动系统实验测量: 2、有阻尼单自由度自由振动系统实验测量: 五、简答 1、力锤施加力的大小是否影响单自由度系统的振动频率和阻尼,为什么? 2、实验过程中,力锤敲击质量块时应注意什么? SINOCERA? YE6251振动力学实验系统 实 验 指 导 书 (参考) 江苏联能电子技术有限公司 一、软件安装 运行光盘中YE6251控制软件目录中的setup.exe即可完成控制软件的安装。 用USB接口线连接计算机的USB口与调理器的USB口,打开调理器电源,这时计算机会提示找到新设备,并需要安装驱动程序,这时请指定驱动程序的安装路径为上面安装程序的目录下的 AQU采集器驱动\Win98(或Win2k或WinXP) 二、软件操作 1、登录输入 2、试验项目选择 选择当前的试验项目,包括系统名称、试验项目名称。下面以“简支梁系统”,用“冲击激励法测量模态参数”以例说明具体使用过程。 选择试验项目后,系统会自动显示本实验的实验向导,这样实验时可按照上面的实验向导的 步骤进行实验。 3、通道参数设置 当选择一个试验项目时,系统已经给出一个大致合理的通道设置,当然用户也可进行部分修改。通道参数包括测点号设置,通道是否测量设置,工程单位设置,以及满量程设置(也即通道增益选择),本试验实际是用第5通道测力锤信号,用第6通道测量加速度信号. “测点号”是描述测点位置的信息。 一般试验与通道号相对应,如通道号1,对应的测点号为1,通道号2对应的测点为2。 对于模态试验时,一般将实验对象划分为若干个测点,如简支梁划分为10等份(两端固定),共需测量9个测点,分别为测点1到测点9(自左向右),测量的方法一般为:如选择测点3位置作为原点,将加速度传感器置于第3点,用力锤依次敲击测点1到测点9,对应的力锤信号命名为f1到f9,对应的加速度信号命名为1到9,这样f1(激励)与1(响应)对应,f9(激励)与9(响应)对应,共测量了9组传递函数. “测量选择”表示左边的对应的通道是否测量。双击可以在测量与不测量之间切换。 “满量程”表示当前通道所通道测量的满度值。 对于位移通道有2档增益,1倍、10倍,对应的位移满量程为5000um、500um。 对于力通道有3档增益,1倍、 10倍、100倍,对于的力的满量程为5000N 、500N、50N。 对于加速度通道4档增益,1倍、 10倍、100倍、1000倍,对于的力的满量程为5000m/s2 、500m/s2、 50m/s2、 5m/s2 注意:当信号调理单元将力通道的增益设置为10倍时,请记住一定要在通道参数栏将该通道的满度值设置为500N(第2档),力通道的增益设置为100倍时,请记住一定要在通道参数栏将该通道的满度值设置为50N(第3档). 4、系统参数设置 振动力学期末考试试题和答案 振动力学(试题) 2008 一、填空(每空2分) 1、设周期振动信号的周期为,则其傅里叶级数的展开的基频为,T ,,, 2、单自由度粘性阻尼系统的阻尼因子与阻尼系数的关系为,,, , 作用下系统响应的稳态振3、单自由度粘性阻尼系统在简谐力ptsin,0 动的幅值为,,, 4、粘性阻尼一周期内所消耗的能量与频率成,,,比。 5、无阻尼多自由度系统的主振型正交关系为,,,,,, 6、写出多自由度系统再频率域的输入与输出之间的关系,,,,, 7、写出瑞利商的表达式,,,,,, r8、多自由度系统中共存在个主固有频率,其相应的主振型,,, 正交。 9、无阻尼多自由度系统,利用里兹法计算出的主振型关于M、K是 否正交,,,,(答是或否) 10、写出如图T-1所示梁的左端边界条件,,,,,,,,,, y L x K 图T-1 二、(20分)系统如图T-2所示,杆AB为刚性、均质,长度为,总L 质量为,弹簧刚度为,阻尼系数为。求系统的固有频率及阻mck 尼因子。 图T-2 三、系统如图T-3所示。求系统的固有频率与主振型。 k k k k k m m m X X X 123 图T-3 四、 五、(20分)简支梁如图T-5所示,弹性模量为E,质量密度为,, 横截面积为A,截面惯性矩为J。求梁在中央受集中弯矩M下的响应。(假设梁的初始状态为零) 图T-5 答案 一、填空(每空2分) 1、周期振动信号的周期为,则其傅里叶级数的展开的基频为 T2/,T 2、单自由度粘性阻尼系统的阻尼因子与阻尼系数的关系为, c ,, 2mk 作用下系统响应的稳态振3、单自由度粘性阻尼系统在简谐力ptsin,0 p10动的幅值为 ,,B222k,,,,,(1)(2) 4、粘性阻尼一周期内所消耗的能量与频率成,正,比。 5、无阻尼多自由度系统的主振型正交关系为加权(M,K)正交: 0()ij,0()ij,,,TTTT ,,,,M,K,,,ijijMij(),Kij(),pipi,, 6、写出多自由度系统在频率域的输入与输出之间的关系 21,其中 xHP()()(),,,,HKMiC()(),,,,,, TXKX7、写出瑞利商的表达式 ()RX,TXMX r8、多自由度系统中共存在个重固有频率,其相应的主振型,,加 权(M,K)正交。 MK9、无阻尼多自由度系统,利用里兹法计算出的主振型关于、是 《土动力学实验》课程教学大纲 课程编号:031157 学分:0 周数:0.75周 大纲执笔人:黄茂松大纲审核人:李镜培 说明:《土动力学实验》是033027《土动力学》及031349《土动力学与基础抗震》课程的实验部分,该课程有课号、有学时、无学分。 一、实验性质与目的 《土动力学实验》是土木工程专业的实践环节课程。 其主要教学目的为:使学生了解土的动力特性,掌握地震区场地评价方法,了解砂土液化的基本概念及评价方法和处理措施,掌握基础振动分析方法并能够进行动力基础的设计,掌握地基基础的抗震强度验算方法以及抗震措施,掌握一些基本的实验方法如:地基土动力参数的测试、基础动力测试、桩基础动力检测等。 二、课程面向专业 土木工程专业 三、实验基本要求 1.通过实验掌握振动理论以及波动理论中的有关知识; 2.通过实验掌握波速测试的方法; 3.通过实验掌握激振法测试地基土动力特性参数的操作与数据处理。 四、实验教学基本内容 1.振动模型实验:对一质量-弹簧-阻尼体系激振,采集振动信号,采用质量-弹簧-阻尼体系振动理论分析振动数据。 2.波动模型实验:对一杆件的杆端进行激振,采集振动信号,采用应力波在一维杆件中的传播方程对数据进行处理。 3.波速测试现场实验:采用跨孔法测试地基土的剪切波波速。 4.激振法现场实验:采用竖向强迫激振法测试地基土的抗压刚度系数。 五、实验内容和主要仪器设备与器材配置 六、实验预习和实验报告的要求、考核方式 学生应当在实验以前掌握与实验有关的各方面的知识,如理论方面、操作方面、数据处理方面、工程应用方面。实验结束后编写实验报告,实验报告中要包括上面提到的四方面的内容。考核方式包括以下几个方面:1、实验操作;2、数据处理;3、报告编写。 七、学时分配 八、教材、实验指导书与主要参考书 教材: 《土动力学》,自编教材。 主要参考书: 《土与基础振动》,F.E Richart,Jr.U .S .A。 《土动力学》,Dao U.S.A浙江大学翻译。 实验指导书名称: 《土动力学基础》 上海交通大学2008年振动力学期末考试试题 第一题(20分) 1、在图示振动系统中,已知:重物C的质量m1,匀质杆AB的质量m2,长为L,匀质轮O的质量m3,弹簧的刚度系数k。当AB杆处于水平时为系统的静平衡位置。试采用能量法求系统微振时的固有频率。 解: 系统可以简化成单自由度振动系统,以重物C的位移y作为系统的广义坐标,在静平衡位置时y=0,此时系统的势能为零。 AB转角: 系统动能: m1动能: m2动能: m3动能: 系统势能: 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而 有: 上式求导,得系统的微分方程为: 固有频率和周期为: 2、质量为m1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过 定滑轮A连在质量为m2的物块B上;轮心C与刚度系数为k的水平弹簧相连;不计滑轮A,绳及弹簧的质量,系统自弹簧原长位置静止释放。试采用能量法求 系统的固有频率。 解:系统可以简化成单自由度振动系统,以重物B的位移x作为系统的广义坐标,在静平衡位置时x=0,此时系统的势能为零。 物体B动能: 轮子与地面接触点为速度瞬心,则轮心速度为,角速度为,转过的角度为。轮子动能: 系统势能: 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,有:上式求导得系统的运动微分方程: 固有频率为: 第二题(20分) 1、在图示振动系统中,重物质量为m,外壳质量为2m,每个弹簧的刚度系数均为k。设外壳只能沿铅垂方向运动。采用影响系数方法:(1)以x1和x2为广义坐标,建立系统的微分方程;(2)求系统的固有频率。 解: 系统为二自由度系统。 当x1=1,x2=0时,有:k11=2k,k21=-2k 当x2=1,x2=1时,有:k22=4k,k12=-2k 因此系统刚度矩阵为: 系统质量矩阵为: 系统动力学方程为: 频率方程为: 解出系统2个固有频率: , 请打双面 习题与综合训练第一章 2-1一单层房屋结构可简化为题2-1图所示的模型,房顶质量为m,视为一刚性杆;柱子 高h,视为无质量的弹性杆, 其抗弯刚度为EJ。求该房屋 作水平方向振动时的固有 频率。 解:由于两根杆都是弹性的,可以看作是两根相同的弹簧的并联。 等效弹簧系数为k 则 其中为两根杆的静形变量,由材料力学易知 = 则= 设静平衡位置水平向右为正方向,则有 所以固有频率 2-2一均质等直杆,长为 l,重量为W,用两根长h的相同的铅垂线悬挂成水平位置,如题2-2图所示。试写出此杆绕通过重心的铅垂轴作微摆动的振动微分方程,并求出振动固有周期。 解:给杆一个微转角θ θ=hα 2F=mg 由动量矩定理: 其中 2-3求题2-3图中系统的固有频率,悬臂梁端点的刚度分别是和,悬臂梁的质量忽略不计。 解:悬臂梁可看成刚度分 别为k1和k3的弹簧,因此,k1 与k2串联,设总刚度为k1ˊ。 k 1 ˊ与k3并联,设总刚度为k2 ˊ。k2ˊ与k4串联,设总刚度 为k。即为 ,, mg kδ =δ δ 3 24 mgh EJ = k3 24EJ h " m x kx =- 3 n 24 mh EJ p= 2 a a h a mg a mg Fa M ml I M I 8 2 2 cos sin 12 1 2 2 - = - ≈ ? - = == = α θ α θ&& 1 2 cos sin≈ ≈ θ α α h l ga p h a mg ml n2 2 2 2 2 3 4 12 1 = = ? +θ θ&& g h a l ga h l p T n 3 π2 3 π2 π2 2 2 = = = 1 k3k 2 1 2 1 1k k k k k + = ' 2 1 2 1 3 2k k k k k k + + = ' 4 2 4 1 2 1 3 2 3 1 4 2 1 4 3 2 4 2 1 k k k k k k k k k k k k k k k k k k k k + + + + + + = θ F sinα 2 θ α F h mg θ F 2008年振动力学期末考试试题 大学期末考试https://www.doczj.com/doc/f54918307.html, 第一题(20分) 1、在图示振动系统中,已知:重物C的质量m1, 匀质杆AB的质量m2,长为L,匀质轮O的质量 m3,弹簧的刚度系数k。当AB杆处于水平时为 系统的静平衡位置。试采用能量法求系统微振 时的固有频率。 解: 系统可以简化成单自由度振动系统,以重物C的位移y作为系统的广义坐标,在静平衡位置时y=0,此时系统的势能为零。 AB转角: 系统动能: m1动能: m2动能: m3动能: 系统势能: 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有: 上式求导,得系统的微分方程为: 固有频率和周期为: 2、质量为m1的匀质圆盘置于粗糙水平面上,轮缘 上绕有不可伸长的细绳并通过定滑轮A连在质量 为m2的物块B上;轮心C与刚度系数为k的水平 弹簧相连;不计滑轮A,绳及弹簧的质量,系统自 弹簧原长位置静止释放。试采用能量法求系统的固 有频率。 解:系统可以简化成单自由度振动系统,以重物B的位移x作为系统的广义坐标,在静平衡位置时x=0,此时系统的势能为零。 物体B动能: 轮子与地面接触点为速度瞬心,则轮心速度为,角速度为,转过的角度为。轮子动能: 系统势能: 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,有: 上式求导得系统的运动微分方程: 固有频率为: 第二题(20分) 1、在图示振动系统中,重物质量为m,外壳质量为2m, 每个弹簧的刚度系数均为k。设外壳只能沿铅垂方向运 动。采用影响系数方法:(1)以x1和x2为广义坐标, 建立系统的微分方程;(2)求系统的固有频率。 解: 系统为二自由度系统。 当x1=1,x2=0时,有:k11=2k,k21=-2k 当x2=1,x2=1时,有:k22=4k,k12=-2k 因此系统刚度矩阵为: 系统质量矩阵为: DHSY- 1型磁悬浮动力学实验仪 实验一动力学基础实验 随着科技的发展,磁悬浮技术的应用成为技术进步的热点,例如磁悬浮列车。永磁悬浮技术作为一种低耗能的磁悬浮技术,也受到了广泛关注。本实验使用的永磁悬浮技术,是在磁悬导轨与滑块两组带状磁场的相互作斥力之下,使磁悬滑块浮起来,从而减少了运动的阻力,来进行多种力学实验。通过实验,学生可以接触到磁悬浮的物理思想和技术,拓宽知识面,加深牛顿定律等动力学方面的感性知识。 本实验仪可构成不同倾斜角的斜面,通过滑块的运动可研究匀变速运动直线规律,加速度测量的误差消除,物体所受外力与加速度的关系等。 【一】实验目的 1.学习导轨的水平调整,熟悉磁悬导轨和智能速度加速度测试仪的调整和使用; 2.学习矢量分解; 3.学习作图法处理实验数据,掌握匀变速直线运动规律; 4.测量重力加速度g,并学习消减系统误差的方法; 5.探索牛顿第二定律,加深物体运动时所受外力与加速度的关系; 6.探索动摩擦力与速度的关系。 【二】实验原理 1.瞬时速度的测量 一个作直线运动的物体,在△ t时间内,物体经过的位移为△ s,则该物体在△ t时间内的平均速度为 △s v 二 为了精确地描述物体在某点的实际速度,应该把时间△t取得越小越好, △t越小,所求得的平均速度越接近实际速度。当△t T0时,平均速度趋近于一个极 限,即即 =li m^f =li m o v⑴ v 这就是物体在该点的瞬时速度。 但在实验时,直接用上式来测量某点的瞬时速度是极其困难的,因此,一般在一定误 差范围内,且适当修正时间间隔(见图5、6),可以用历时极短的△ t内的平均速度近似 地代替瞬时速度。(整理)《振动力学》课程作业.
振动实验报告
振动力学试验
振动力学期末考试试题和答案
《土动力学实验》
上海交通大学2008年振动力学期末考试试题
振动力学参考答案
2008年期末振动力学考试试题
磁悬浮动力学实验