动态规划讲义
- 格式:pdf
- 大小:312.53 KB
- 文档页数:31

天津大学建筑工程学院目录第一章运筹学及其研究方法 (1)第二章线性规划 (4)2.1 线性规划问题 (4)2.2 两变量线性规划问题的图解法 (8)2.3 特例 (13)2.4 一个食谱问题 (17)第三章单纯形法 (21)3.1 将线性规划化转成标准形式 (21)3.2 单纯形法的预备知识 (23)3.3 单纯形法 (27)3.4 使用单纯形法解最小化问题 (34)3.5 多个最优解 (36)3.6 无界线性规划 (38)3.7 LINDO程序包 (39)3.8 退化和单纯形法的收敛 (43)3.9 大M法 (45)3.10 两阶段单纯形法 (50)3.11 无符号变量 (55)3.12 使用Excel的“规划求解”解线性规划 (57)第4章灵敏度分析和对偶 (65)4.1 图说敏感度分析 (65)4.2一些重要的公式 (68)4.3 敏感度分析 (74)4.4 求一个线性规划的对偶 (85)4.5 对偶问题的经济学解释 (90)4.6 对偶法则和结果 (92)4.7 影子价格 (99)4.8 对偶和敏感度分析 (105)4.9 互补松弛 (107)4.10 对偶单纯形法 (110)第5章整数规划 (118)5.1 整数规划简介 (118)5.2 建立整数规划问题 (120)5.3 解纯整数规划问题的分支定界法 (123)5.4 使用分支定界法解混合整数规划 (131)5.5 使用分支定界法解0-1整数规划 (132)5.6 割平面法 (133)第6章确定型动态规划 (138)6.1 两个智力测验 (138)6.2 网络问题 (138)第一章运筹学及其研究方法在第二次世界大战期间,英国军事将领邀请了一批科学家和工程师帮助分析一些军事问题:雷达布置,护航、轰炸和反潜作战的组织,矿山开采等。
在军事活动中,数学与科学方法的应用称为“操作研究”(operation research),我国则意译为“运筹学”。

第1章线性规划Chapter 1 Linear Programming本章内容提要线性规划是运筹学的重要内容。
本章介绍线性规划数学模型、线性规划的基本概念以及求解线性规划数学模型的基本算法——单纯形法。
学习本章要求掌握以下内容:⏹线性规划模型的结构⏹线性规划的标准形式,非标准形式转化为标准形式⏹线性规划的图解以及相应的概念。
包括:约束直线,可行半空间,可行解,可行域,凸集,极点,目标函数等值线,最优解⏹线性规划的基本概念。
包括:基,基础解,基础可行解,基变量,非基变量,进基变量,离基变量,基变换⏹单纯形法原理。
包括:基变量和目标函数用非基变量表出,检验数,选择进基变量的原则,确定离基变量的方法,主元,旋转运算⏹单纯形表。
包括初始单纯形表的构成,单纯形表运算方法⏹初始基础可行解,两阶段法⏹退化的基础可行解§1.1 运筹学和线性规划1.1.1 运筹学运筹学(Operations Research)是二十世纪三十年代二次大战期间由于战争的需要发展起来的一门学科。
当时,英国组织了一批自然科学和工程科学的学者,和军队指挥员一起,研究大规模战争提出的一些问题。
如轰炸战术的评价和改进、反潜艇作战研究等,研究结果在战争实践中取得了明显得效果。
这些研究当时在英国称为Operational Research,直译为作战研究。
战争结束以后,这些研究方法不断发展完善,并逐步形成学科理论体系,其中一些主要的理论和方法包括:线性规划,网络流,整数规划,动态规划,非线性规划,排队论,决策分析,对策论,计算机模拟等。
这些理论和方法在经济管理领域也得到了广泛应用,Operations Research也转义成为“作业研究”。
我国将Operations Research译成“运筹学”,非常贴切地将Operations Research这一英文术语所包含的作战研究和作业研究两方面的涵义都体现了出来。
现在,运筹学已经成为管理科学重要的基础理论和应用方法,是管理科学专业基本的必修课程之一。

数学0701(一级学科:数学)数学是一门在非常广泛意义下研究自然现象和社会现象中的数量关系和空间形式的科学。
它的根本特点是从自然现象的量的侧面抽象出一般性的规律,预见事物的发展并指导人们能动地认识和改造世界。
数学是各门科学的基础,在自然科学、社会科学、工程技术等方面起着思想库的作用;又是经济建设和技术进步的重要工具。
数学科学是一个范围广阔、分支众多、应用广泛的科学体系。
本学科目前在基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论五个二级学科招收硕士研究生。
基础数学是数学的核心和灵魂.它的思想、方法和结论是整个数学科学的基础。
基础数学包括数理逻辑、数论、代数、几何、拓扑、函数论、泛函分析、微分方程等众多分支学科。
计算数学是研究如何用计算机解决各种数学问题的科学,主要研究与各类科学计算和工程计算相关的计算方法,对各种算法进行理论和数值分析,设计和研究用数值模拟方法来代替某些耗资巨大甚至难以实现的实验,研制专用或通用科学工程应用软件和数值软件等。
它的核心是提出和研究求解各种数学问题的高效而稳定的算法。
概率论与数理统计是研究随机现象内在规律性的科学。
概率论旨在从理论上研究随机现象的数量规律,是数理统计的基础。
数理统计是研究如何有效地收集、分析和使用随机性数据的学科,为概率论的实际应用提供了广阔的天地。
应用数学是联系数学与现实世界的重要桥梁,主要研究自然科学、工程技术、信息、经济、金融、管理、社会和人文科学中的数学问题,包括建立相应的数学模型,利用数学方法解决实际问题,研究具有实际背景和应用前景的数学理论等。
运筹学与控制论以数学和计算机为主要工具,从系统和信息处理的观点出发,研究解决社会、经济、金融、军事、生产管理、计划决策等各种系统的建模、分析、规划、设计、控制及优化问题,是一个包括众多分支的学科。
运筹学结合数学、计算机科学、管理科学,通过对建模方法和最优化方法的研究,为各类系统的规划设计、管理运行和优化决策提供理论依据。
第一章绪论一运筹学的发展历史1学科起源:二战期间英美等国军事部门集中多学科人员,研究提高武器系统效能,如反空袭雷达控制系统,使雷达和高炮相配合。
诺将物理学家布莱克特(Blackett)领导研究小组“Operational Research”,多学科构成(布莱克特马戏团)。
战争结束后专家转移到企业和院校——学科形成。
2我国古代的运筹思想:齐王赛马——齐王“上中下”,田忌“下上中”丁渭修皇宫——北宋真宗宰相丁渭(澶chan州之盟的主和派),主持皇宫失火后的修复。
宫前大街取土、引汴河运料、完工后回填废土。
3我国近代以来:50年代开始钱学森、许志国等引进运筹学理论,华罗庚教授回国后从事优选法和统筹法研究推广(烧茶壶的故事)4翻译:来自汉高祖“夫运筹帷幄之中,决胜千里之外,吾不如子房;填国家,抚百姓,给饷馈,不绝粮道,吾不如萧何;连百万之众,战必胜,攻必取,吾不如韩信。
”台湾地区直译为“运作研究”。
二运筹学的特点运筹学存在多种定义,如“依照给定目标和条件,从众多方案中选择最优方案的最优化技术”,学科特点:最优化、定量化1 多种专家的协作2 科学的方法:从实际情况出发,通过假设的模型打到一个符合实际的结论3 目的在于解决实际问题。
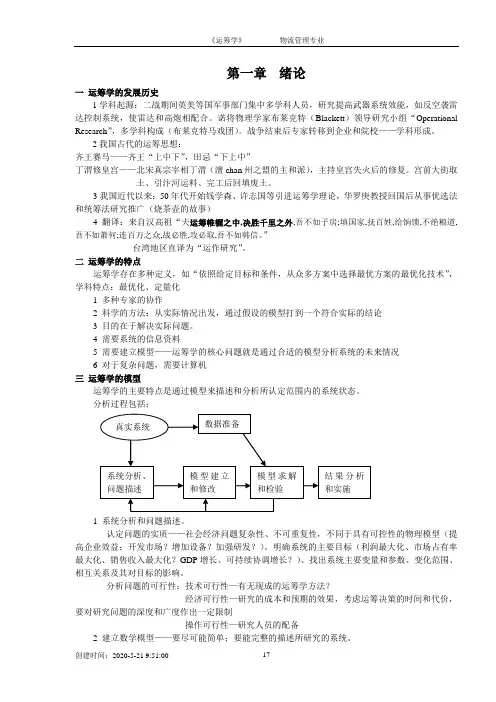
4 需要系统的信息资料5 需要建立模型——运筹学的核心问题就是通过合适的模型分析系统的未来情况6 对于复杂问题,需要计算机三运筹学的模型运筹学的主要特点是通过模型来描述和分析所认定范围内的系统状态。
分析过程包括:1 系统分析和问题描述。
认定问题的实质——社会经济问题复杂性、不可重复性,不同于具有可控性的物理模型(提高企业效益:开发市场?增加设备?加强研发?)。
明确系统的主要目标(利润最大化、市场占有率最大化、销售收入最大化?GDP增长、可持续协调增长?)、找出系统主要变量和参数、变化范围、相互关系及其对目标的影响。
分析问题的可行性:技术可行性—有无现成的运筹学方法?经济可行性—研究的成本和预期的效果,考虑运筹决策的时间和代价,要对研究问题的深度和广度作出一定限制操作可行性—研究人员的配备2 建立数学模型——要尽可能简单;要能完整的描述所研究的系统。

ASA共有十一门必修课:1.微积分和线性代数(100);2.概率论与数理统计(110);3.应用统计方法(120);4.复利数学(140);5.精算数学(150);6.风险理论(151);7.生存模型(160);8.经济保障计划概论(200);9.精算实务概论(210);10.资产管理和公司财务概论(220);11.资产和负债管理原理(230)。
以上十一门课共255学分,其余45学分要在另外24门选修课(略)中任选三~四门获得。
考生在获得ASA资格证书后方可参加FSA课程考试,通常把FSA考试分为若干方向,如:团体和健康保险、个人寿险和年金、财务、投资等,每个方向下设若干门课程,取得FSA 资格必须通过某一专门方向的所有课程,再选考其它若干门课程,使学分达到150分,连同ASA共450学分即可成为FSA。
考试在每年五月、十一月进行,考生每次报考门数自定,考完为止。
有关考试信息推荐您去{环球网校-精算师}频道查询准精算师部分的考试内容包括:科目名称科目代码科目名称科目代码中国精算师资格考试数学基础Ⅰ 01 生命表基础 06中国精算师资格考试数学基础Ⅱ 02 寿险精算实务 07中国精算师资格考试复利数学 03 非寿险精算数学与实务 08中国精算师资格考试寿险精算数学 04 综合经济基础 09中国精算师资格考试风险理论 05精算师部分的考试内容包括:科目代码课程名称备注中国精算师资格考试011 保险公司财务管理必考中国精算师资格考试012 保险法及相关法规必考中国精算师资格考试013 个人寿险与年金精算实务必考中国精算师资格考试014 社会保障选考中国精算师资格考试015 资产负债管理选考中国精算师资格考试016 高级非寿险精算实务选考中国精算师资格考试017 团体寿险选考中国精算师资格考试018 意外伤害和健康保险选考中国精算师资格考试019 高级投资学选考中国精算师资格考试020 养老金计划选考中国精算师资格考试021 精算职业后续教育(PD)必修,精算师部分要求完成3门必考课程,2门选考课程及精算职业后续教育后,并具有三年以上的精算工作经验,方可具备资格。

接下来,讨论DSGE的学习。
在教材上,DSGE模型的学习是三板斧。
第一个是DSGE的思想和技巧:Cooley,1995,Frontiers of Business Cycle Research。
推荐这本书,而不是其他,是有原因的。
在RBC中,竞争性均衡模型的构建语言是递归竞争性均衡,换言之,就是Sargent等所说的用“大K、小k技巧”来表述理性预期思想。
而在其他教材中,更多的是直接定义竞争性均衡:消费者最优、厂商最优、两者最优的结构构成所有市场的供给与需求、市场出清要求供求相等(价格随之决定)——如果竞争性均衡搞不明白,可以看看Williamson的宏观经济学这本教材,再加Varian的中微做补充。
这本书里面的重要知识是:RBC模型、社会计划者问题、竞争性均衡角度构建的非最优经济环境、校准。
不需要看的是模型的求解,因为选取的一些求解方法有些老旧了,现在不怎么常用。
第二个是动态规划:Stokey,Lucas with Prescott,1989,名字就不写了,大家都知道。
主要目的是三个:其一是用来做参考书,以便什么时候需要证明解的存在和唯一性时拿出来翻阅;其二是了解动态规划的术语;第三个是拿来提高数学(尤其是代数)功底。
第三个是动态规划的一系列应用:Ljungqvist and Sargent,2000,名字就不写了,大家都知道。
这本书不好啃,而且啃了未必有所裨益,因为里面的专题实在太多了,而且,一些详细介绍的研究方法存在严重的过时,而一些重要的研究方法又只有只言片语。
举例来说,线性二次型动态规划,现在用得很少,书上很多地方都是用它来求解;再者,Blanchard and Kahn 求解、King-Plosser-Rebelo求解(或Uhlig的tookit)、状态空间、极大似然、GMM 等等重要方法,都是只言片语。
以上三本书实际上有个良好的替代品:Dirk Kreuger的Macroeconomic Theory。

算法导论读书笔记【篇一:《算法概论》读书笔记及读后感】《算法概论》读书笔记12计转1 12130907 李酉辰第0章本章较为简短,没有深入系统地涉及某些内容。
主要以fibonacci 数列的例子,让我体会了递归和递推思想的差别。
针对fibonacci数列例子直接递归解法中涉及的重复计算,优化出递推方式,展示了思考问题中自顶向下与自底向上的不同思考角度可能产生较大的算法效率差别,同时隐约体现记忆化搜索的思想。
另外本章较为详细介绍了大o复杂度度量标准。
第1章本章以rsa算法为例,细致深入讨论了rsa算法涉及的相关数论知识,诸如取模运算、模下的四则运算与逆元概念、取模幂运算、素性检测。
在素性检测部分有经典的欧几里德算法、扩展欧几里德算法,同时引入随机化算法概念,以极高的概率保证素性检测有效性。
通过本章的学习,我对过去不曾深入考虑或者说真正考虑的基础性运算有了更深的理解。
之前对乘除运算复杂度总是在以单元操作的概念下以o(1)带过,以后会更加细致地考虑乘除等基本运算的复杂度。
另外,本章以rsa为案例,系统地展示了针对某一问题,如何从基础性知识入手,一步一步学习案例所需基础知识,并将其整合从而解决案例。
素性检测与素因子分解,两个看似相去不远的问题,其复杂性天差地别的现实,从一般角度让人们想到的是类似问题的解决难度可能差别很大仅此而已,而rsa算法展示了如何深入的多想一步,利用这种情况设计出优雅的解决方案。
这思想很值得我借鉴与利用。
第2章本章介绍分治算法思想,提及分治,相信每一个学习算法的人都不会陌生,经典的《算法导论》中就已合并排序为例在开篇不久就引入分治概念。
本书介绍分治的角度与众不同,不似《导论》中总是介绍比较显而易见的可以分治的案例。
本书列举了矩阵相乘、快速傅立叶变换等数学领域分治的应用案例,在这些案例之中,分治的应用很多情况下隐藏的较为深,并非显而易见,加大了分析难度。
但是更能让我感受到分治应用之广泛,可能在学习本章之前,许多类型的题目我不会想到去向分治的角度思考,因为不易看出,但是本章给我的备忘录上加了一条:永远不要忽视分治,针对陌生题目,不要轻易就否决掉往分治角度思考的路线。


大学先修先修课程1、计算概论(信息学学科)本课程的内容主要分为两个部分:(1)C++语言,约占课时量的5%;(2)C++语言设计解题算法,约占课时量的95%;在C++语言部分,主要为C++语言基础知识,C++语言设计解题算法部分主要是用C++语言编程求解信息学竞赛的相关问题。
需要编写具有一定技术难度的程序。
学习过程类似于迭代过程:周期一:感性认识计算机程序;周期二:认识程序的组成部分;周期三:了解各种算法;周期四:使用C++中的STL;该课程测试平台由北京大学计算机学院提供。
因课程内容较难,考试为请全国统考,所以建议有信息学竞赛经验的同学参加。
授课大纲计算机基础知识程序设计基础指针、结构体与链表图论和动态规划算法在竞赛中的应用线段树等高级数据结构的使用竞赛试题选讲参考资料基本资料主要参考本课程所提供的讲义,以及来自/的相关练习题。
“练习题”是程序设计训练的重点!本课程所有的练习题都是在线练习(在线提交程序代码,在线反馈代码执行结果),届时,会要求各位同学登录/选择相应的练习题完成作业。
最终的全国统考也是通过/网站完成。
2、《普通地质学》课程介绍课程安排:每周一次课,每次一小时。
2014年5月开始授课,2015年寒假后参加北大先修课的统一考试。
课程目标:普通地质学涉及物理学、化学、自然地理学等多学科内容。
课程面向大学专业选择对地理及相关专业有兴趣的同学。
课程开设通过讨论、活动等形式介绍地球科学的研究方向;激发学生学习地球科学的兴趣;提供学生学习的空间和资源。
课程内容:普通地质学是地球科学的一个分支,主要研究地质学的概况和一些基本知识。
普通地质学的研究对象是地球,其范围包括了从地核到外层大气的整个地球,但主要是固体地球的部分。
该门课程的研究内容主要包括三个方面一、地球的物质组成和构造主要研究组成固体地球的元素、矿物、岩石以及地球的结构构造。
其研究内容主要是地球的静态特征。
二、地球的形成和演化这部分是普通地质学研究的主体,主要研究包括地球及类地行星的起源、地球各圈层的形成及相互关系,地球的内力和外力作用对固体地球演化的影响。


奇门遁甲高级讲义叶飘然编著(内部讲义禁止外传翻印必究)奇门运筹与择日运筹学的概念与含义运筹学作为一门现代科学,是在第二次世界大战期间首先在英美两国发展起来的,有的学者把运筹学描述为就组织系统的各种经营作出决策的科学手段。
P.M.Morse与G.E.Kimball在他们的奠基作中给运筹学下的定义是:“运筹学是在实行管理的领域,运用数学方法,对需要进行管理的问题统筹规划,作出决策的一门应用科学。
”运筹学的另一位创始人定义运筹学是:“管理系统的人为了获得关于系统运行的最优解而必须使用的一种科学方法。
”它使用许多数学工具(包括概率统计、数理分析、线性代数等)和逻辑判断方法,来研究系统中人、财、物的组织管理、筹划调度等问题,以期发挥最大效益。
<现代运筹学的起源可以追溯到几十年前,在某些组织的管理中最先试用科学手段的时候。
可是,现在普遍认为,运筹学的活动是从二次世界大战初期的军事任务开始的。
当时迫切需要把各项稀少的资源以有效的方式分配给各种不同的军事经营及在每一经营内的各项活动,所以美国及随后美国的军事管理当局都号召大批科学家运用科学手段来处理战略与战术问题,实际上这便是要求他们对种种(军事)经营进行研究,这些科学家小组正是最早的运筹小组。
<第二次世界大战期间,“OR”成功地解决了许多重要作战问题,显示了科学的巨大物质威力,为“OR”后来的发展铺平了道路。
当战后的工业恢复繁荣时,由于组织内与日俱增的复杂性和专门化所产生的问题,使人们认识到这些问题基本上与战争中所曾面临的问题类似,只是具有不同的现实环境而已,运筹学就这样潜入工商企业和其它部门,在50年代以后得到了广泛的应用。
对于系统配置、聚散、竞争的运用机理深入的研究和应用,形成了比较完备的一套理论,如规划论、排队论、存贮论、决策论等等,由于其理论上的成熟,电子计算机的问世,又大大促进了运筹学的发展,世界上不少国家已成立了致力于该领域及相关活动的专门学会,美国于1952年成立了运筹学会,并出版期刊《运筹学》,世界其它国家也先后创办了运筹学会与期刊,1957年成立了国际运筹学协会。
第一讲 运筹学引论1.1 运筹起源提到运筹学,咱们中国人自然会想到那句“运筹帷幄之中,决胜千里之外”,古代军事安排及谋略可以叫做运筹,但这个意义并不是指现在我们要学习的这门课,当然运筹学最早的运用也是在军事中,二战时期,被称为“运用研究”(Operational Research),我国在1956年曾用过运用学的名词,到1957年正式定名为运筹学。
二战后英、美军队中相继成立了更为正式的运筹研究组织,最早投入运筹学领域工作的是诺贝尔奖金获得者美国物理学家勃拉凯特(Blackett),他领导的运筹学小组被戏称为勃拉凯特马戏团,其实是一个由各方面专家组成的交叉学科小组。
最早建立运筹学会的国家是英国(1948年),接着是美国(1952年)、法国(1956年)、日本和印度(1957年)等。
欧洲运筹学协会(EURO)成立于1975年,亚太运筹学协会(APORS)成立于1985年。
我国的运筹学会成立在1980年。
在1959年英、美、法三国的运筹学会发起成立了国际运筹学联合会(IFORS),以后各国的运筹学会纷纷加入,我国于1982年加入该会。
1.2 运筹学的应用运筹学的应用范围非常广泛,从军事方面到现在各行各业几乎都能用到。
如生产型企业的生产问题,包括生产计划、原料采购、库存销售等,还有物流运输当中的物资调运、车辆排班,交通网络路径规划,最优决策,服务型的排队等候过程以及决策博弈分析,在此不一一列举。
本来运筹学作为数学的一个分支,但是越来越尤其独特性,在实际中应用非常多,所以不管是什么专业学点运筹学都是非常有好处的,尤其现在运筹学作为很多经管学科的必修课,交通运输物流等专业亦是如此,而且在全国硕士研究生入学考试中很多学校作为初始科目,比如北京交通大学、西南交通大学,同济大学也在近年初试科目中加入了运筹学作为可选科目,前面列举为交通专业,经管类就更不用说了,也有不少学校作为复试科目,另外还有运筹学与控制论系统科学这些完全以运筹学为基础的专业。
01数学基础I考试时间:3小时考试形式:客观判断题考试内容和要求:考生应掌握微积分、线性代数和运筹学的基本概念和主要内容。
A.微积分(分数比例约为60%)1.函数、极限、连续2.一元函数微积分3.多元函数微积分4.级数5.常微分方程B.线性代数(分数比例约为30%)1.行列式2.矩阵3.线性方程组4.向量空间5.特征值和特征向量6.二次型C.运筹学(分数比例约为10%)1.线性规划2.整数规划3.动态规划参考书目:1.《高等数学讲义》(第二篇数学分析)樊映川编著高等教育出版社(本书可网上购买)或其他包含内容A 的高等数学教材2.《线性代数》胡显佑四川人民出版社(本书可网上购买)或其他包含内容B的线性代数教材3.《运筹学》(修订版) 1990年《运筹学》教材编写组清华大学出版社(本书可网上购买)或其他包含内容C的运筹学教材02数学基础II考试时间:3小时考试形式:客观判断题考试内容和要求:A.概率论(分数比例约为50%)1.概率的计算、条件概率、全概公式和贝叶斯公式2.随机变量的数字特征,特征函数;3.联合分布律、边际分布函数及边际概率密度的计算4.大数定律及其应用5.条件期望和条件方差6.混合型随机变量的分布函数、期望和方差等B.数理统计(分数比例约为35%)1.统计量及其分布2.参数估计3.假设检验4.方差分析5.列联分析C.应用统计(分数比例约为15%)1.回归分析2.时间序列分析(移动平滑,指数平滑法及ARIMA模型)参考书目:1、《概率论与数理统计》茆诗松,周纪芗编著,中国统计出版社 1999年12月第2版。
2、《统计预测——方法与应用》,易丹辉编著,中国统计出版社,2001年4月第一版。
除以上参考书外,也可参看其他同等水平的参考书。
03复利数学考试时间:2小时考试形式:客观判断题考试内容和要求:1.利息的基本概念(分数比例:8%-15%)2.年金(分数比例:20%-25%)3.收益率(分数比例:15%-25%)4.债务偿还(分数比例:15%-25%)5.债券与其他证券(分数比例:20-25%)6.利息理论的应用与金融分析(分数比例:6%-15%)7.利率风险的估量:久期、凸性及其在债券价值分析中的应用(分数比例:3%-5%)参考书目:《利息理论》(中国精算师资格考试用书)主编刘占国,中国财政经济出版社,2006年11月第1版第1~5章、第6章第6.1节05风险理论考试时间: 2小时考试形式: 客观判断题考试内容和要求:考生应深入理解与掌握基本的保险风险模型:短期个体风险模型、短期聚合风险模型、长期聚合风险模型,以及这些模型的相关性质;掌握效用函数与期望效用原理,以及期望效用原理在保险定价中的应用;掌握随机模拟的基本方法。
全国青少年信息学奥林匹克联赛算法讲义算法讲义 (1)算法基础篇 (2)算法具有五个特征: (2)信息学奥赛中的基本算法(枚举法) (4)采用枚举算法解题的基本思路: (4)枚举算法应用 (4)信息学奥赛中的基本算法(回溯法) (8)回溯基本思想 (8)信息学奥赛中的基本算法(递归算法) (10)递归算法的定义: (10)递归算法应用 (11)算法在信息学奥赛中的应用 (递推法) (14)递推法应用 (14)算法在信息学奥赛中的应用 (分治法) (18)分治法应用 (18)信息学奥赛中的基本算法(贪心法) (21)贪心法应用 (21)算法在信息学奥赛中的应用(搜索法一) (24)搜索算法应用 (25)算法在信息学奥赛中的应用(搜索法二) (28)广度优先算法应用 (29)算法在信息学奥赛中的应用(动态规划法) (32)动态规划算法应用 (33)算法基础篇学习过程序设计的人对算法这个词并不陌生,从广义上讲,算法是指为解决一个问题而采用的方法和步骤;从程序计设的角度上讲,算法是指利用程序设计语言的各种语句,为解决特定的问题而构成的各种逻辑组合。
我们在编写程序的过程就是在实施某种算法,因此程序设计的实质就是用计算机语言构造解决问题的算法。
算法是程序设计的灵魂,一个好的程序必须有一个好的算法,一个没有有效算法的程序就像一个没有灵魂的躯体。
算法具有五个特征:1、有穷性:一个算法应包括有限的运算步骤,执行了有穷的操作后将终止运算,不能是个死循环;2、确切性:算法的每一步骤必须有确切的定义,读者理解时不会产生二义性。
并且,在任何条件下,算法只有唯一的一条执行路径,对于相同的输入只能得出相同的输出。
如在算法中不允许有“计算8/0”或“将7或8与x相加”之类的运算,因为前者的计算结果是什么不清楚,而后者对于两种可能的运算应做哪一种也不知道。
3、输入:一个算法有0个或多个输入,以描述运算对象的初始情况,所谓0个输入是指算法本身定义了初始条件。
运筹学讲义绪论(2学时)参考教材:(1)运筹学基础教程(魏权龄)(2)管理运筹学(韩伯棠)(3)管理运筹学通论(韩大卫)(4)运筹学(胡运权)先修课程:一元微积分、线性代数、概率统计学时:48+(8)主讲教师:狄军锋一、运筹学发展1、运筹学的产生✧最早与1938年出现于英国,简称OR(operational Research)✧夫运筹帷幄之中,决胜于千里之外,吾不如子房。
---史记✧古代运筹学思想:田忌赛马+丁谓挖沟+沈括运军粮✧二战中的运筹学:反潜艇策略、深水炸弹的起爆深度、诺曼底登陆✧运筹学在我国的发展:①50年代中期,钱学森、许国志等教授将运筹学由西方引入我国。
②管梅谷(1962年,山东师范大学):“中国邮递员问题”③华罗庚:优选法(1970)和统筹法(1965)2、运筹学的定义:管理运筹学是一门应用科学,它广泛应用现有的科学技术和数学方法,解决管理中提出的专门问题,为决策者选择最优或较优的决策提供定量依据。
运筹学是一门新兴的交叉学科,来源于军事、管理和经济。
本课程主要介绍用于解决管理领域问题的运筹学,因此称为管理运筹学,也有人称为管理科学。
二、运筹学解决问题的思路提出问题→建模→求解→结果分析与调整→实施二、运筹学的学科内容:线性规划(LP);*整数规划(IP);*非线性规划(NP);*多目标规划(MP);动态规划(DP);对策论(GT);决策分析(DA);存贮论(IC);排队论(QT);图论(Graph Theory)三、章节安排1、绪论(2学时)2、线性规划(14学时)3、动态规划(6学时)4、存储论(6学时)5、对策论(10学时)6、决策论(6学时)7、统筹方法(2学时)8、总复习(2学时)四、应用举例1、猴子运香蕉2、海盗分宝石3、猜生日第二*主要内容1、线性规划的一般形式、压缩形式、矩阵形式、向量形式2、线性规划问题的图解法(3)3、线性规划问题的标准形式4、单纯形方法(4)5、线性规划问题应用举例(3)6、运输问题的解法(4)§1 线性规划问题的基本模型一、 引例【引例1】某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知生产单位产品需的设备台时,A 、B 两种原材料的消耗以及每种产品可获利润如下表所示。
动态规划(一)动态规划的基本思想一、动态规划含义:在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都要做出决策,从而使整个过程达到最好的活动效果。
因此,各个阶段决策确定后,组成一个决策序列,因而也就确定了整个过程的一条活动路线。
这种把一个问题看作是一个前后关联具有链状结构的多阶段过程,就称为多阶段决策过程,这种问题称为多阶段决策问题。
在多阶段决策问题中,各个阶段采取的决策,一般来说是和时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,我们称这种解决多阶段决策最优化的过程为动态规划。
动态规划算法通常用于求解具有某种最优性质的问题。
在这类问题中,可能会有许多可行解。
每一个解都对应于一个值,我们希望找到具有最优值的解。
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。
如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。
我们可以用一个表来记录所有已解的子问题的答案。
不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
这就是动态规划法的基本思路。
具体的动态规划算法多种多样,但它们具有相同的填表格式。
二、设计动态规划法的步骤:1、找出最优解的性质,并刻画其结构特征;2、递归地定义最优值(写出动态规划方程);3、以自底向上的方式计算出最优值;4、根据计算最优值时得到的信息,构造一个最优解。
步骤1-3是动态规划算法的基本步骤。
在只需要求出最优值的情形,步骤4可以省略,步骤3中记录的信息也较少;若需要求出问题的一个最优解,则必须执行步骤4,步骤3中记录的信息必须足够多以便构造最优解。
三、动态规划问题的特征:动态规划的显著特征是:无后效性,有边界条件,且一般划分为很明显的阶段。
动态规划算法的有效性依赖于问题本身所具有的两个重要性质:最优子结构性质和子问题重叠性质。
动态规划一般还存在一条或多条状态转移方程。
1、最优子结构:当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
2、重叠子问题:在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。
动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,在以后尽可能多地利用这些子问题的解。
(二)动态规划算法的基本步骤设计一个标准的动态规划算法,通常可按以下几个步骤进行:1、划分阶段:按照问题的时间或空间特征,把问题分为若干个阶段。
注意这若干个阶段一定要是有序的或者是可排序的(即无后向性),否则问题就无法用动态规划求解。
2、选择状态:将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。
当然,状态的选择要满足无后效性。
3、确定决策并写出状态转移方程:之所以把这两步放在一起,是因为决策和状态转移有着天然的联系,状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。
所以,如果我们确定了决策,状态转移方程也就写出来了。
但事实上,我们常常是反过来做,根据相邻两段的各状态之间的关系来确定决策。
4、写出规划方程(包括边界条件):动态规划的基本方程是规划方程的通用形式化表达式。
一般说来,只要阶段、状态、决策和状态转移确定了,这一步还是比较简单的。
动态规划的主要难点在于理论上的设计,一旦设计完成,实现部分就会非常简单。
根据动态规划的基本方程可以直接递归计算最优值,但是一般将其改为递推计算,实现的大体上的框架如下:标准动态规划的基本框架1.对fn+1(xn+1)初始化; {边界条件}2.for k:=n downto 1 do3. for 每一个xk∈Xk do4. for 每一个uk∈Uk(xk) dobegin5. fk(xk):=一个极值; {∞或-∞}6. xk+1:=Tk(xk,uk); {状态转移方程}7. t:=φ(fk+1(xk+1),vk(xk,uk)); {基本方程(9)式}8. if t比fk(xk)更优 then fk(xk):=t; {计算fk(xk)的最优值}end;9.t:=一个极值; {∞或-∞}10.for 每一个x1∈X1 do11. if f1(x1)比t更优 then t:=f1(x1); {按照10式求出最优指标}12.输出t;但是,实际应用当中经常不显式地按照上面步骤设计动态规划,而是按以下几个步骤进行:1.分析最优解的性质,并刻划其结构特征。
2.递归地定义最优值。
3.以自底向上的方式或自顶向下的记忆化方法(备忘录法)计算出最优值。
4.根据计算最优值时得到的信息,构造一个最优解。
步骤(1)--(3)是动态规划算法的基本步骤。
在只需要求出最优值的情形,步骤(4)可以省略,若需要求出问题的一个最优解,则必须执行步骤(4)。
此时,在步骤(3)中计算最优值时,通常需记录更多的信息,以便在步骤(4)中,根据所记录的信息,快速地构造出一个最优解。
(三)动态规划概述1.基本思想:将问题分解为若干小问题,解子问题,然后从子问题得到原问题的解。
2.特点:将问题分解为子问题,这些子问题往往不相互独立。
(如果可以用分治法求解,分解的子问题太多,因此,用分治法时间代价太高,消耗指数时间)3.且某些子问题可能被重复多次计算,因此将计算过的子问题的结果保存。
一般,放入表中。
4.应用:往往求解具有某种最优性质的问题,此类问题往往具有多个解,我们要找到具有最优值的那个解。
5.步骤:找出最优解的性质,刻画其特征;递归地定义最优值;以自底向上的方式计算出最优值;根据计算最优值时得到的信息,构造一个最优解。
(四)动态规划问题中的术语阶段:把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同。
描述阶段的变量称为阶段变量。
在多数情况下,阶段变量是离散的,用k表示。
此外,也有阶段变量是连续的情形。
如果过程可以在任何时刻作出决策,且在任意两个不同的时刻之间允许有无穷多个决策时,阶段变量就是连续的。
在前面的例子中,第一个阶段就是点A,而第二个阶段就是点A到点B,第三个阶段是点B到点C,而第四个阶段是点C到点D。
状态:状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。
在上面的例子中状态就是某阶段的出发位置,它既是该阶段某路的起点,同时又是前一阶段某支路的终点。
在前面的例子中,第一个阶段有一个状态即A,而第二个阶段有两个状态B1和B2,第三个阶段是三个状态C1,C2和C3,而第四个阶段又是一个状态D。
过程的状态通常可以用一个或一组数来描述,称为状态变量。
一般,状态是离散的,但有时为了方便也将状态取成连续的。
当然,在现实生活中,由于变量形式的限制,所有的状态都是离散的,但从分析的观点,有时将状态作为连续的处理将会有很大的好处。
此外,状态可以有多个分量(多维情形),因而用向量来代表;而且在每个阶段的状态维数可以不同。
当过程按所有可能不同的方式发展时,过程各段的状态变量将在某一确定的范围内取值。
状态变量取值的集合称为状态集合。
无后效性:我们要求状态具有下面的性质:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,所有各阶段都确定时,整个过程也就确定了。
换句话说,过程的每一次实现可以用一个状态序列表示,在前面的例子中每阶段的状态是该线路的始点,确定了这些点的序列,整个线路也就完全确定。
从某一阶段以后的线路开始,当这段的始点给定时,不受以前线路(所通过的点)的影响。
状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展,这个性质称为无后效性。
决策:一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。
在最优控制中,也称为控制。
在许多间题中,决策可以自然而然地表示为一个数或一组数。
不同的决策对应着不同的数值。
描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史。
决策变量的范围称为允许决策集合。
策略:由每个阶段的决策组成的序列称为策略。
对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合。
允许策略集合中达到最优效果的策略称为最优策略。
给定k阶段状态变量x(k)的值后,如果这一阶段的决策变量一经确定,第k+1阶段的状态变量x(k+1)也就完全确定,即x(k+1)的值随x(k)和第k阶段的决策u(k)的值变化而变化,那么可以把这一关系看成(x(k),u(k))与x(k+1)确定的对应关系,用x(k+1)=Tk(x(k),u(k))表示。
这是从k阶段到k+1阶段的状态转移规律,称为状态转移方程。
最优性原理:作为整个过程的最优策略,它满足:相对前面决策所形成的状态而言,余下的子策略必然构成“最优子策略”。
最优性原理:实际上是要求问题的最优策略的子策略也是最优。
让我们通过对前面的例子再分析来具体说明这一点:从A到D,我们知道,最短路径是AàB1àC2àD,这些点的选择构成了这个例子的最优策略,根据最优性原理,这个策略的每个子策略应是最优:AàB1àC2是A到C2的最短路径,B1àC2àD也是B1到D的最短路径……──事实正是如此,因此我们认为这个例子满足最优性原理的要求。
(五)标号法标号法是一种最佳算法,多用于求图的最短路问题。
一、标号法的概念:所谓标号,是指与图的每一个顶点相对应的一个数字。
标号法可以说是动态规划,它采用顺推的方法,对图的每一边检测一次,没有重复的回溯搜索,因此标号法是一种最佳算法。
二、标号法的算法流程:现有一图G,求从起点Vs到终点Ve的最短距离。
设:Sum(j)───顶点Vj的标号,代表的是Vs到Vj的最短距离。
Vj 已标味着Vs到Vj的最短路以及这条路径的长度已求出。
M(i,j)───Vi到Vj的非负长度。
H(j)───顶点Vj的前趋结点。
标号法的算法流程如下:sum(s)←0↓Vs进入队列L↓-----→移出队列L的队首Vk←-----| ↓ || Vk是不是Ve------------------|---→计算结束打印路径| N∣ Y || ↓ || 由Vk扩展出结点Vj || (Vk与Vj之间相连) || Sj←Sum(k)+M(k,j) || ↓ || Sj小于Sum(j) || | || Y | N || | --------------------| || ↓| Sum(j)←Sj| H(j)← Vk| Vj加入队列L并对队列L按Sum值由小到大排序| ↓---------------注意:1.只有两个顶点间的距离为非负时,才可用标号法。