整理后的习题答案(大物)

习 题 一1—1 一质点在平面xOy 内运动，运动方程为x =2t ，2219t y -= (SI)。

(1)求质点的运动轨道；(2)求t =1s 和t =2s 时刻质点的位置矢量；(3)求t =1s 和t =2s 时刻质点的瞬时速度和瞬时加速度；(4)在什么时刻，质点的位置矢量和速度矢量垂直?这时x 、y 分量各为多少?(5)在什么时刻，质点离原点最近?最近距离为多大?[解] 质点的运动方程:t x 2=，2219t y -= (1)消去参数t ，得轨道方程为: 22119x y -= (2)把t=1s 代入运动方程，得j i j i r 172)219(22+=-+=t t 把t =2s 代入运动方程，可得j i j i r 114)2219(222+=⨯-+⨯= (3)由速度、加速度定义式，有4/,0/4/,2/-====-====dt dv a dt dv a t dt dy v dt dx v y y x x y x所以，t 时刻质点的速度和加速度为 j i j i t v v v y x 42-=+= j j i a 4-=+=y x a a所以，t=1s 时，j i v 42-=，j a 4-= t=2s 时，j i v 82-=，j a 4-= (4)当质点的位置矢量和速度矢量垂直时，有 0=⋅v r即 0]42[])219(2[2=-⋅-+j i j i t t t 整理，得 093=-t t解得 3,3;0321-===t t t (舍去) m 19,0,s 011===y x t 时 m 1,m 6,s 322===y x t 时 (5)任一时刻t 质点离原点的距离 222)219()2()(t t t r -+= 令d r/d t =0 可得 t =3所以，t =3s 时，质点离原点最近 r1—2 一粒子按规律59323+--=t t t x 沿x 轴运动，试分别求出该粒子沿x 轴正向运动；沿x 轴负向运动；加速运动，减速运动的时间间隔。

第4章 机械振动4.1基本要求1．掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2．掌握描述简谐振动的解析法、旋转矢量法和图线表示法，并会用于简谐振动规律的讨论和分析3．掌握简谐振动的基本特征，能建立一维简谐振动的微分方程，能根据给定的初始条件写出一维简谐振动的运动方程，并理解其物理意义4．理解同方向、同频率简谐振动的合成规律，了解拍和相互垂直简谐振动合成的特点4.2基本概念1．简谐振动 离开平衡位置的位移按余弦函数（或正弦函数）规律随时间变化的运动称为简谐振动。

简谐振动的运动方程 cos()x A t ωϕ=+2．振幅A 作简谐振动的物体的最大位置坐标的绝对值。

3．周期T 作简谐振动的物体完成一次全振动所需的时间。

4．频率ν 单位时间内完成的振动次数，周期与频率互为倒数，即1T ν=5．圆频率ω 作简谐振动的物体在2π秒内完成振动的次数，它与频率的关系为22Tπωπν==6．相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位，它决定着作简谐振动的物体状态；t=0时的相位称为初相位ϕ7．简谐振动的能量 作简谐振动的系统具有动能和势能。

弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+==8．阻尼振动 振动系统因受阻尼力作用，振幅不断减小。

9．受迫振动 系统在周期性外力作用下的振动。

周期性外力称为驱动力。

10．共振 驱动力的角频率为某一值时，受迫振动的振幅达到极大值的现象。

4.3基本规律1．一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时，其动能和势能都随时间做周期性变化，位移最大时，势能达到最大值，动能为零；物体通过平衡位置时，势能为零，动能达到最大值，但其总机械能却保持不变，且机械能与振幅的平方成正比。

第2章 动量守恒定律与能量守恒定律一 基本要求1 理解冲量、动量等概念。

掌握动量定理及动量守恒定律，能运用它们解简单系统在平面内运动的力学问题。

2 理解功的概念，能计算变力做功的问题 。

3 理解保守力做功的特点和势能的概念，会计算重力、弹性力和万有引力做的功及对应的势能 。

4 理解动能定理、功能原理和机械能守恒定律，掌握运用守恒定律解问题 的思想和方法 。

二 基本概念 １ 质点的动量、冲量质点的动量定义：m =p υ，p 为矢量，也是状态量。

质点的冲量定义 ：21t t dt =⎰I F ，它也是矢量，是过程量。

2 冲力 在解决冲击、碰撞问题时，将两个物体在碰撞瞬间的相互作用力称为冲力，冲力作用时间短，量值变化也很大，所以很难确定每一时刻的冲力，常用平均冲力的冲量来代替变力的冲量 。

3内力和外力 对于质点系，其内部各个质点之间的相互作用力称为内力，质点系以外的其他物体对其中的任一质点的作用力称为外力。

4功 功率（1）功 力对质点所作的功为力在质点位移方向的分量与位移大小的乘积。

cos BBAAW dW d F dr θ==⋅=⎰⎰⎰F r(2) 功率 功随时间的变化率,反映的是做功的快慢。

dW P dt =cos d d P F dt dtυθ⋅==⋅=⋅=F r r F F υ5动能 质量为m 的物体，当它具有速度υ时，定义212m υ为质点在速度为υ时的动能，用k E 表示。

6保守力和非保守力 如果力F 对物体做的功只与物体初、末位置有关而与物体所经过的路径无关，我们把具有这种特点的力称为保守力，否则称为非保力。

保守力做功0ld ⋅=⎰F l ，非保守力作功 0ld ⋅≠⎰F l 。

重力、弹性力、万有引力均为保守力，而摩擦力、汽车的牵引力等都是非保守力。

7势能 系统某点的势能等于在保守力作用下将物体从该点沿任意路径移动到零势能点保守力做的功，用p E 表示。

8机械能，系统的动能和势能统称为机械能，用E 表示。

习题六6—1 一轻弹簧在60N得拉力下伸长30cm。

现把质量为4kg物体悬挂在该弹簧得下端,并使之静止,再把物体向下拉10cm,然后释放并开始计时。

求:(1)物体得振动方程;(2)物体在平衡位置上方5cm时弹簧对物体得拉力;(3)物体从第一次越过平衡位置时刻起,到它运动到上方5cm处所需要得最短时间。

[解] (1)取平衡位置为坐标原点,竖直向下为正方向,建立坐标系设振动方程为x=cos(7、07t+φ)t=0时, x=0、1 0、1=0、1cosφφ=0故振动方程为x=0、1cos(7、07t)(m)(2)设此时弹簧对物体作用力为F,则:F＝k(Δx)=k(x0 +x)=mg/k=40/200=0、2(m)其中x因而有F= 200(0、2-0、05)=30(N)(3)设第一次越过平衡位置时刻为t1,则:0=0、1cos(7、07t1 ) t1 =0、5π/7、07第一次运动到上方5cm处时刻为t2,则-0、05=0、1cos(7、07t2) t2=2π/(3×7、07)故所需最短时间为:Δt=t2 -t1 =0、074s6—2 一质点在x轴上作谐振动,选取该质点向右运动通过点A时作为计时起点(t＝0),经过2s后质点第一次经过点B,再经2s后,质点第二经过点B,若已知该质点在A、B两点具有相同得速率,且AB=10cm,求:(1)质点得振动方程:(1)质点在A点处得速率。

[解] 由旋转矢量图与可知s(1) 以得中点为坐标原点,x轴指向右方。

t=0时,t=2s时,由以上二式得因为在A点质点得速度大于零,所以所以,运动方程为:(2)速度为:当t=2s时6—3 一质量为M得物体在光滑水平面上作谐振动,振幅为12cm,在距平衡位置6cm处,速度为24,求:(1)周期T; (2)速度为12时得位移。

[解] (1) 设振动方程为以、、代入,得:利用则解得(2) 以代入,得:解得: 所以故6—4 一谐振动得振动曲线如图所示,求振动方程。

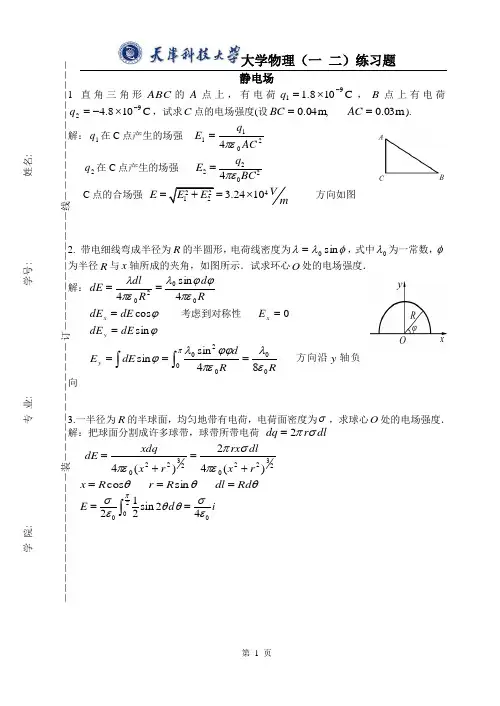
zlwmdxq 由题意设kv f = ，其受力方向在竖直方向上，则有dt dv m ma kv F mg f F mg ==--=-- 变形可得 dt dv kvF m g m =-- 两边同时积分 ⎰⎰=--t vdt dv kvF m g m 00 整理可得)1(t m ke k F mg v ---= 设沉降距离为y ，则dt dy v =)]1([)1(0-+-=--==--⎰⎰t m k t t m k e km t k F mg dt e k F mg vdt y 1moldsyz 由题意有 0''0022T T n R T V p =∴=⋅00000000002169.1)2ln 1()2ln 25(27V p V p V p V p V p Q Q W =-=+-=-= %9)2ln 1(7227)2ln 1(00001=-=-==V p V p Q A η sgxtdddh 由题意'q 所受的电场力的大小 20'2220'8323])3([44aqq a a qq F πεπε=⋅+⨯= 方向由O 指向'q其电势能 a qq a a qq E P 0'2220'2])3([44πεπε=+⨯=zkzcwLd 由题意建立如图所示坐标系，在杆上距离原点O 为x 处取一线元dx ，Ldx q dq =，则其在P 处的电势为 ()()dx x d L L q x d L dq dU P -+=-+=0044εεππ 则 ()dd L L q dx x d L L q U LP +=-+=⎰ln 44000εεππ 此过程中静电力做功d d L L qq d d L L q q U U q W P P +-=+-=-=∞∞ln 4)ln 40()(00000εεππ 则外力做功dd L L qq W W P +==∞ln 4-00επ外 lgwxctzy 由题意做一以轴线为中心，半径为r 高为L 的圆柱面为高斯面，则其电通量为E L r S d E SE ⋅π=⋅=Φ⎰2 根据高斯定理，当1R r <时，02=⋅πI E rL ，则0=I E当21R r R <<时，02ελL E rL II =⋅π，则rE II 02ελπ=，方向垂直于高斯面向外 当2R r >时，02=⋅πIII E rL ，则0=III EcNjcSj （a ）由题意知 a I a IB B P πμπμ2965πc o s 6πc o s 343300=⎪⎭⎫ ⎝⎛-⨯⨯== 方向垂直纸面向里 （b ）由题意知 aI B P πμ40=（即竖直载流导线在P 点的磁感强度） 方向垂直纸面向外 P127 Sfkyyap （a ）由题意知 )451(24522000+=⋅+=πμμπμR I R I R I B O 方向垂直纸面向里 （b ）由题意知 )11(40Rr I B O -=μ 方向垂直纸面向外 Cdyd 根据安培定律，在2L 上取一距离为的线元l d ，则B l d I F d ⨯=2，其大小dl l I I Bdl I dF π22102μ== 则1L 作用在2L 上的力)N (1031.82ln π2π272102102-+⨯====⎰⎰I I l dl I I dF F l d d μμ 方向垂直2L 向上 Zyccz 由题意知上下两矩形边所受磁力之和为零，则线圈所有磁力即i lb b a a II i l b a II i l a I I F F F)(π2)π(2π210101021+-=++-=+=μμμ方向为2F 的方向线圈的磁力矩 0=⨯=B P M mMdyyzzjx （1）由题意知m 1062-⨯=A ，s 2=T ，如图根据旋转矢量可知，3π=ϕ，由此可得 )m )(3ππcos(06.00+=t y （2）设简谐波的波函数为)m ](3π)π(cos[06.0+-=u x t y 由题意知 m/s 2=u ，故其波函数为)m ](3π)2π(cos[06.0+-=xt y （3）有波长、周期和波速的关系，m)(422=⨯==uT λ。

大物试题答案第一部分：选择题1. 答案：B2. 答案：C3. 答案：A4. 答案：D5. 答案：C6. 答案：B7. 答案：A8. 答案：B9. 答案：C10. 答案：D第二部分：填空题11. 答案：速度12. 答案：0.0613. 答案：等于14. 答案：反比15. 答案：2.516. 答案：平行17. 答案：电势差18. 答案：真实倒立缩小19. 答案：2:120. 答案：3000N第三部分：简答题21. 答案：物理量22. 答案：牛顿第一定律23. 答案：滑动摩擦力24. 答案：简谐振动25. 答案：变压器26. 答案：透镜公式27. 答案：2.5×10^4 J28. 答案：焦距29. 答案：凸透镜30. 答案：光的全反射第四部分：计算题31. 答案：45 m/s32. 答案：15 Hz33. 答案：10 N34. 答案：0.2 C35. 答案：10 Ω36. 答案：600 J37. 答案：约为 102.04 kHz38. 答案：5.4 Ω39. 答案：5.0×10^6 ohm·m40. 答案：12.5 V第五部分：解答题41. 答案：由于答案内容较长，建议直接参阅附件中的答案解析。

42. 答案：由于答案内容较长，建议直接参阅附件中的答案解析。

43. 答案：由于答案内容较长，建议直接参阅附件中的答案解析。

44. 答案：由于答案内容较长，建议直接参阅附件中的答案解析。

45. 答案：由于答案内容较长，建议直接参阅附件中的答案解析。

附件：大物试题答案解析题目解析：1. 题目一解析根据题目要求，我们需要选择一个正确的答案。

选项B是正确答案。

2. 题目二解析题目要求选择一个正确答案，选项C是正确答案。

3. 题目三解析根据题目要求，选项A是正确答案。

4. 题目四解析根据题目要求，选项D是正确答案。

5. 题目五解析题目要求选择一个正确答案，选项C是正确答案。

......（以下省略）总结：本次大物试题共包括选择题、填空题、简答题、计算题和解答题等多个题型，共计40道题目。

大学物理习题册计算题及答案三 计算题1. 一质量m = 0.25 kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点。

弹簧的劲度系数k = 25N ·m -1。

(1） 求振动的周期T 和角频率.(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v 0及初相. （3) 写出振动的数值表达式。

解：（1) 1s 10/-==m k ω 63.0/2=π=ωT s（2） A = 15 cm ，在 t = 0时，x 0 = 7。

5 cm,v 0 〈 0 由 2020)/(ωv +=x A得 3.1220-=--=x A ωv m/s π=-=-31)/(tg 001x ωφv 或 4/3∵ x 0 > 0 , ∴ π=31φ（3) )3110cos(10152π+⨯=-t x (SI ）振动方程为)310cos(1015)cos(2πϕω+⨯=+=-t t A x （SI ）﹡2. 在一平板上放一质量为m =2 kg 的物体，平板在竖直方向作简谐振动，其振动周期为T = 21s ，振幅A = 4 cm ，求 （1） 物体对平板的压力的表达式.(2) 平板以多大的振幅振动时，物体才能离开平板。

解：选平板位于正最大位移处时开始计时，平板的振动方程为 t A x π4cos = （SI)t A x ππ4cos 162-=（SI ） （1） 对物体有 x m N mg=- ① t A mg x m mg N ππ4cos 162+=-= （SI) ② 物对板的压力为 t A mg N F ππ4cos 162--=-= (SI ）t ππ4cos 28.16.192--= ③(2) 物体脱离平板时必须N = 0，由②式得 04cos 162=+t A mg ππ (SI ）A qt 2164cos π-=π 若能脱离必须 14cos ≤t π （SI ）即 221021.6)16/(-⨯=≥πg A m三 计算题﹡1。