MATLAB实验 电力系统暂态稳定分析资料报告

电力系统仿真实习报告一、前言随着现代电力系统的发展和规模的扩大，对电力系统的稳定性和可靠性要求越来越高。

电力系统仿真作为一种有效的研究方法，可以在不影响实际运行的情况下，对电力系统进行全面的分析和评估。

本次实习主要通过使用MATLAB软件进行电力系统仿真，以验证电力系统的稳定性和其他特性。

二、电力系统建模1. 构建电力系统的拓扑图，包括发电机、变压器、线路、开关等基本单元。

2. 根据拓扑图，建立适当的电气参数，如电机转矩曲线、线路参数等。

3. 使用MATLAB Simulink下Power System Blockset建立系统的暂态模型和稳态模型。

4. 设置适当的仿真时长和采样频率满足分析需求。

三、电力系统稳态分析1. 设置不同的负荷点分布和拓扑，对比电力系统在各状态下的稳定性。

2. 通过输出压降、电流、转速以及电压相位差等，分析电力系统在各状态下的表现。

3. 对不同拓扑下的电力系统失效特征和限制进行分析。

四、电力系统暂态分析1. 模拟多种故障情况，如短路故障、电源故障、线路断路等。

2. 分析电力系统在故障过程中的响应和恢复情况。

3. 研究故障对电力系统稳定性和可靠性的影响。

五、仿真结果与分析1. 稳态仿真结果表明，电力系统在不同负荷和拓扑下的稳定性较好，各电气参数符合预期。

2. 暂态仿真结果表明，电力系统在故障发生后能够迅速响应并恢复稳定，但部分情况下仍存在一定的电压和频率波动。

3. 故障分析结果显示，短路故障对电力系统的影响最为显著，需采取相应的保护措施。

六、总结与展望通过本次电力系统仿真实习，我对电力系统的稳定性和可靠性有了更深入的了解。

仿真结果表明，电力系统在正常运行和故障情况下均具有一定的稳定性和恢复能力，但仍有改进空间。

未来研究可以进一步探讨电力系统的优化设计和故障预防策略，以提高电力系统的运行效率和可靠性。

七、谢辞感谢我的指导老师，在实习过程中给予我耐心的指导和帮助。

同时，感谢实验室的同学们，在仿真过程中给予我支持和鼓励。

在MATLAB中进行电力系统稳定性分析电力系统稳定性是电力系统运行过程中的一个重要问题。

稳定性分析是指通过对电力系统的各个参数进行计算和仿真，评估系统在不同工作状态下的稳定性能力。

MATLAB作为一款强大的数学软件，提供了许多功能和工具，可以用于进行电力系统稳定性分析。

一、电力系统稳定性简介电力系统稳定性是指电力系统在受到故障扰动后，恢复到合理且可靠的工作状态的能力。

稳定性包括功率稳定性、电压稳定性和频率稳定性。

功率稳定性是指电力系统在故障发生后，能够保持节点功率的平衡；电压稳定性是指电力系统在故障发生后，能够保持各个节点电压的合理范围；频率稳定性是指电力系统在故障发生后，能够保持系统频率的稳定。

二、电力系统稳定性分析方法1. 线性稳定性分析线性稳定性分析方法是指在电力系统小扰动范围内，将系统的非线性特性线性化，分析系统的稳定性。

其中，最常用的方法是潮流灵敏度分析和特征值分析。

潮流灵敏度分析可以通过求解雅可比矩阵进而得到节点电压变化情况，分析功率稳定性和电压稳定性。

MATLAB提供了m文件函数可以方便地进行潮流灵敏度分析。

特征值分析是通过求解电力系统的状态方程和特征方程，得到系统的特征值，进而判断系统的稳定性。

MATLAB提供了特征值求解工具，方便进行特征值分析。

2. 非线性稳定性分析非线性稳定性分析方法主要应用于大扰动条件下的系统稳定性分析，其中最常用的方法是切割法。

切割法是将电力系统分割为多个子系统，分别进行稳定性分析，然后将子系统的稳定性结果进行整合，评估系统的整体稳定性。

MATLAB提供了强大的仿真工具SIMULINK，可以方便地进行系统的划分和仿真。

三、MATLAB在电力系统稳定性分析中的应用1. 系统模型建立在进行电力系统稳定性分析之前，需要建立系统的数学模型。

MATLAB提供了SimPowerSystems工具箱，可以方便地建立电力系统模型，并进行可靠的仿真。

2. 稳定性分析MATLAB提供了多种算法和函数，用于进行电力系统稳定性分析。

基于MATLAB的电力系统稳态仿真分析电力系统稳态仿真分析是指通过建立电力系统的数学模型，在不同工况下进行仿真计算，以评估电力系统的稳定性、可靠性以及电力质量等方面的性能。

MATLAB作为一种强大的数学计算软件，可以在电力系统稳态仿真分析中发挥重要作用。

本文将从电力系统仿真建模、传输线模型、潮流计算、稳定性分析和可靠性评估等方面介绍基于MATLAB的电力系统稳态仿真分析。

首先，在进行电力系统稳态仿真分析之前，需要将电力系统进行建模。

电力系统建模包括发电机模型、负荷模型、变压器模型、传输线模型等。

在MATLAB中，可以使用Simulink工具箱进行建模，通过搭建电力系统的拓扑结构，并将各个设备的数学模型与之关联，可以构建出完整的电力系统模型。

在传输线模型方面，可以使用MATLAB中的传输线模型进行仿真分析。

传输线模型一般分为线性模型和非线性模型两种。

线性模型通常采用传输线方程进行建模，可以描述传输线上电流和电压之间的关系。

非线性模型一般考虑了传输线上的电阻、电感和电容等元件的非线性特性，可以更加精确地模拟传输线的性能。

在潮流计算方面，可以使用MATLAB中的Power System Toolbox进行潮流计算。

潮流计算的目的是计算电力系统中各个节点的电压幅值和相角，通过迭代计算电力系统中各个设备的各项参数，直到系统达到稳态。

MATLAB中的Power System Toolbox提供了多种潮流计算算法，可以根据实际需求选择合适的算法进行计算。

稳定性分析是电力系统稳态仿真分析的重要内容之一、稳态分析包括小扰动稳定性分析和大扰动稳定性分析两个方面。

小扰动稳定性分析主要研究电力系统中的幅值和相角扰动对系统稳定性的影响。

大扰动稳定性分析主要研究系统发生大幅度扰动（如故障）后，系统是否能够迅速恢复并保持稳态。

MATLAB中的Power System Toolbox提供了多种稳定性分析方法，如特征根法、现行化法和直接数值法等，可以进行稳定性评估。

第6章 MATLAB在电力系统稳定性分析中的应用实例
6.2.1 电力系统静态稳定性简介
作用在发电机上的机械转矩和电磁转矩如图6-16所示，转 矩平衡点有a、b两个。
第6章 MATLAB在电力系统稳定性分析中的应用实例
6.2.2 简单电力系统的静态稳定性计算 1．网络参数及运行参数计算 2．稳定运行参数计算 6.2.3 简单电力系统的静态稳定性仿真 1．Simulink模型构建及参数设置 按图6-6所示的单机无穷大系统，搭建研究其静态
A
A
B
B
C
C
L1
A
A
B
B
C
C
L2
ห้องสมุดไป่ตู้
A
a
B
b
C
c
T -2
A B C 110kV Source
Load 5MW
d_theta1_2 d_theta1_2 (deg)
w1 w (pu)
stop
M a ch i n e Signals
STOP
Stop Simulation if loss of synchronism
第6章 MATLAB在电力系统稳定性分析中的应用实例
6.1.1 电力系统暂态稳定性简介
如图6-1（a）所示为一正常运行时的简单电力系统及其等值电路，发 电机经过变压器和双回线路向无限大系统送电。
第6章 MATLAB在电力系统稳定性分析中的应用实例
发电机在正常运行、故障以及故障切除后三种状态下的功角特性曲线 如图6-2所示.
第6章 MATLAB在电力系统稳定性分析中的应用实例
6.1 简单电力系统的暂态稳定性仿真分析
电力系统遭受大干扰后，由于发电机转子上机械转矩 与电磁转矩不平衡，使同步电机转子间相对位置发生 变化，即发电机电势间相对角度发生变化，从而引起 系统中电流、电压和电磁功率的变化。电力系统暂态 稳定就是研究电力系统在某一运行方式，遭受大干扰 后，并联运行的同步发电机间是否仍能保持同步运行、 负荷是否仍能正常运行的问题。在各种大干扰中以短 路故障最为严重，所以通常都以此来检验系统的暂态 稳定。本节将以单机无穷大系统为例介绍利用 MATLAB仿真分析简单电力系统暂态稳定性的方法。

四川师范大学本科毕业设计基于MATLAB的控制系统稳定性分析学生姓名宋宇院系名称工学院专业名称电气工程及其自动化班级 2010 级 1 班学号**********指导教师杨楠完成时间2014年 5月 12日基于MATLAB的控制系统稳定性分析电气工程及其自动化本科生宋宇指导老师杨楠摘要系统是指具有某些特定功能，相互联系、相互作用的元素的集合。

一般来说，稳定性是系统的重要性能，也是系统能够正常运行的首要条件。

如果系统是不稳定，它可以使电机不工作，汽车失去控制等等。

因此，只有稳定的系统，才有价值分析与研究系统的自动控制的其它问题。

为了加深对稳定性方面的研究，本设计运用了MATLAB软件采用时域、频域与根轨迹的方法对系统稳定性的判定和分析。

关键词：系统稳定性 MATLAB MATLAB稳定性分析ABSTRACT System is to point to have certain function, connect with each other, a collection of interacting elements. Generally speaking, the stability is an important performance of system, also is the first condition of system can run normally. If the system is not stable, it could lead to motor cannot work normally, the car run out of control, and so on. Only the stability of the system, therefore, have a value analysis and the research system of the automatic control of other problems. In order to deepen the study of stability, this design USES the MATLAB software using the time domain, frequency domain and the root locus method determination and analysis of the system stability.Keywords: system stability MATLAB MATLAB stability analysis目录摘要 (I)ABSTRACT .......................................................... I I 目录1.绪论 (1)1.1自动控制理论发展概述 (1)1.1.1经典控制理论的发展及其基本内容 (1)1.1.2现代控制理论的发展及其基本内容 (1)1.1.3智能控制理论的发展及其主要内容 (2)1.2本文的章节安排 (2)2控制系统的理论基础 (3)2.1控制系统的基本形式 (3)2.1.1闭环控制系统 (3)2.1.2开环控制系统 (4)2.1.3小结 (4)2.2控制系统的分类 (4)2.3控制系统的稳定性 (5)3 MATLAB基础介绍 (6)3.1MALTAB概述 (6)3.2MATLAB的特点 (6)4稳定性分析的方法介绍 (7)4.1时域分析法 (7)4.1.1时域分析法的概念 (7)4.1.2控制系统的性能指标 (7)4.1.3典型的输入信号 (7)4.1.4系统时域分析函数-Step函数 (8)4.1.5控制系统的时域分析-impulse函数 (10)5根轨迹分析法 (12)5.1根轨迹分析法的概念 (12)5.1.1一般控制系统 (12)5.2绘制控制系统的根轨迹图的一般规则 (12)5.3pzmap函数 (13)5.4rlocus函数 (14)6频域法分析 (16)6.2奈氏图（Nyquist） (16)6.3波德图（Bode） (18)7总结 (22)参考文献 (23)致谢 (24)基于MATLAB的控制系统稳定性分析1.绪论这章讲述了自动控制理论与控制技术概述，主要介绍了几种自动控制理论的发展概况以及基本的内容。

Matlab技术在电力系统暂态分析中的应用解析引言：电力系统是现代社会不可或缺的基础设施之一。

在电力系统运行过程中，超过额定负荷或者突发故障可能会引发暂态问题，例如电压暂降、电流暂增等。

为了更好地理解和解决这些问题，Matlab技术被广泛应用于电力系统暂态分析中。

本文将通过解析Matlab在电力系统暂态分析中的应用，介绍其核心概念和关键技术，并探讨其在实际应用中的优势与挑战。

一、Matlab在电力系统暂态分析中的基本原理和功能1.1 Matlab在电力系统暂态分析中的基本原理电力系统暂态分析是研究电力系统在短时间内突发故障或变化情况下的动态行为和响应机制。

Matlab作为一款高级数学软件，可以进行矩阵运算、数值分析和绘图等功能，使其在电力系统暂态分析中有着广泛的应用。

1.2 Matlab在电力系统暂态分析中的功能Matlab中的信号处理工具箱、控制系统工具箱以及优化工具箱等功能模块，为电力系统暂态分析提供了强大的实验和研究工具。

此外，Matlab还具备多种模拟方法和算法，可以通过数值仿真和实验模拟等手段进行电力系统暂态过程的分析与预测。

二、Matlab技术在电力系统暂态分析中的应用案例2.1 电力系统暂态过程的数值仿真Matlab提供了多种数值模拟方法，可以通过基于ODE的数值解法对电力系统暂态过程进行仿真。

通过建立电力系统的方程组以及与之相关的控制方程，可以模拟和计算暂态事件的响应行为。

2.2 电力系统暂态过程的参数优化在电力系统暂态分析中，参数的准确性对研究结果的可靠性至关重要。

Matlab 中的优化工具箱提供了多种优化算法和函数，可以对电力系统的参数进行优化和调整，以提高分析的准确性和稳定性。

2.3 电力系统暂态过程的故障分析Matlab中的信号处理工具箱可以用于电力系统暂态过程中的故障检测和分析。

通过对电力系统数据的采集和处理，可以确定电力系统中的故障类型和位置，并进一步对故障进行诊断和改善。

Science and Technology &Innovation ┃科技与创新2021年第17期·63·文章编号：2095－6835（2021）17－0063－02基于MATLAB/Simulink 的电力系统暂态稳定性分析与仿真姜玉鹏（国网江苏省电力有限公司邳州市供电分公司，江苏徐州221300）摘要：首先简要介绍了电力系统稳定性的概念、分类、特点以及提高系统稳定性的措施。

之后采用MATLAB 中的Simulink 仿真工具对简单电力系统的暂态稳定性进行了建模和仿真分析，并且对提高稳定性的几种措施分别进行了仿真验证。

关键词：电力系统；暂态稳定性；Simulink ；仿真中图分类号：TM712；TM743文献标志码：A DOI ：10.15913/ki.kjycx.2021.17.0231引言电力系统的稳定性指当系统受到扰动后，不发生自发振荡或非周期性失步，而能自动恢复到初始稳定运行状态或过渡到新的稳定运行状态的能力。

电力系统的稳定性分析，对于促进电力系统的安全、可靠运行有重大意义。

Simulink 是MATLAB 提供的系统建模仿真工具。

Simulink 的electrical 工具箱提供了各种电力元器件专业模块，包括稳定性仿真分析所用的电力系统稳定器（PSS ）、同步发电机、无穷大电源模块等。

2电力系统稳定性2.1电力系统稳定性分类电力系统稳定性分为静态稳定性和暂态稳定性。

静态稳定性是指系统在稳定运行状态下，受到小的扰动后，能恢复到原来的运行状态的能力；暂态稳定性是指系统在稳定运行状态下，受到较大扰动后，能够过渡到新的稳定运行状态的能力。

2.2提高暂态系统稳定性的措施提高暂态稳定，首先考虑的是减少扰动后系统的加速面积，减小大扰动后发电机机械功率和电磁功率的功率差额。

工程中通常采用自动励磁调节器、快速自动重合闸、加装电力系统稳定器（PSS ）等。

但单一措施只能对某一范围内的扰动有效果，当扰动超出一定范围后，单纯靠一种调节措施效果较差，因而工程实际中通常是对各种稳定性措施的综合应用。

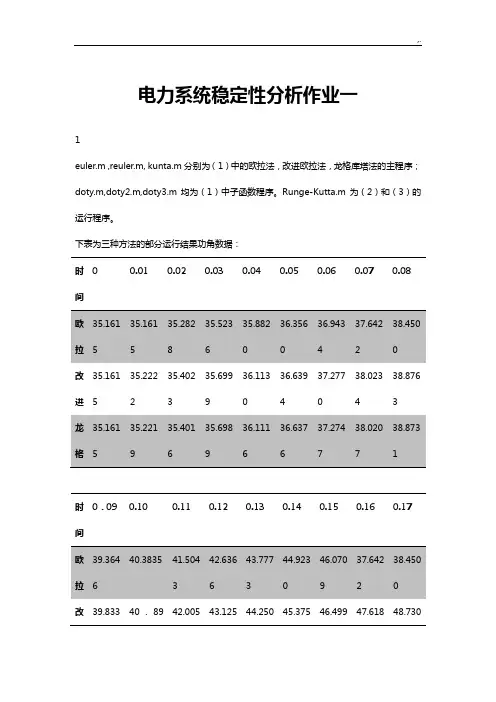
电力系统稳定性分析作业一1euler.m ,reuler.m, kunta.m分别为（1）中的欧拉法，改进欧拉法，龙格库塔法的主程序；doty.m,doty2.m,doty3.m均为（1）中子函数程序。

Runge-Kutta.m为（2）和（3）的运行程序。

下表为三种方法的部分运行结果功角数据：时间00.010.020.030.040.050.060.070.08改进35.161535.222235.402335.699936.11336.639437.27738.023438.8763时间0．090.100.110.120.130.140.150.160.17改39.83340．8942.00543.12544.25045.37546.49947.61848.730进 2 18 1 6 1 7 5 7 5（1）欧拉法在matlaB中输入命令[t,x,y,z]=euler('doty','doty2','doty3',0,5,0.1,0.01)可得t-w曲线，t-δ曲线分别如下图所示。

具体功角，角速度数据分别见文件1.mat 和2.mat（2）欧拉改进法在matlab命令窗口输入[t,x,y,z]=reuler('doty','doty2','doty3',0,5,0.1,0.01)t-w曲线，t-δ曲线分别如下图所示。

具体功角，角速度数据分别见文件3.mat 和4.mat（3）龙格库塔法在matlab命令窗口输入[t,x,y,z]=kunta('doty','doty2','doty3',0,5,0.1,0.01)t-w曲线，t-δ曲线分别如下图所示。

具体功角，角速度数据分别见文件5.mat 和6.mat2运行Runge-Kutta,将参数阻尼D设置为0.05，不断更改参数切除时间t的值，当t=0.2728和t=0.2730时，运行程序分别得到如下两图：则当阻尼D=0.05 时，临界切除时间CCT=0.2729类似可以求得：阻尼D=0.2时，临界切除时间为CCT=0.5729由以上数据我们可以看出：阻尼增大时，临界切除时间也增大了。

实验报告
( 2006-- 2007年度第二学期)
名称：电力系统暂态分析课内实验题目：电力系统稳定性演示实验院系：电气与电子工程学院
班级：
学号：
学生姓名：
指导教师：
实验时数：2学时
成绩：
日期：2007年4月40日
电力系统暂态分析课内实验—电力系统稳定性演示
1 一、实验的目的与要求
通过该环节的学习，可以帮助学生进一步认识电力系统稳定的各种物理现象并增强对电力系统相关课程理论的理解。

二、实验正文
（１）大致了解WDT-III 型电力系统综合自动化实验台的功能
（2）了解如何绘制功角特性曲线
（3）观察电力系统失稳的现象
（4）观察不同类型的短路故障对电力系统稳定的影响
三、实验总结或结论
了解WDT-III 型电力系统综合自动化实验台
掌握电力系统机电暂态分析的原理
四、思考题
（1）WDT-III 型电力系统综合自动化实验台的功能有哪些？
（2）什么是功角特性曲线？其稳定运行点在哪儿？
（3）提高电力系统稳定性的措施有哪些？哪些措施通过本次实验仿真？
（４）实验中失去稳定的现象有哪些？
（５）不同类型的短路故障对电力系统稳定的影响有什么不同？
五、参考文献
1． 《电力系统暂态分析》，李光琦，中国电力出版社，1995年，第二版；
2． 《电力系统自动化》，李先彬，中国电力出版社，1986年，第二版；。

第6章 电力系统稳态与暂态仿真
4) “LTI视窗”(Use LTI Viewer)按键 打开窗口，使用“控制系统工具箱”(Control System Toolbox)的LTI视窗。 5) “阻抗依频特性测量”(Impedance vs. Frequency Measurement)按键 打开窗口，如果模型文件中含阻抗测量模块，该窗口中 将显示阻抗依频特性图。 6) “FFT分析”(FFT Analysis)按键 打开FFT分析窗口。 7) “报表生成”(Generate Report)按键 打开窗口，产生稳态计算的报表。
(1) 显示测量电压、测量电流和所有状态变量的稳态值； (2) 改变仿真初始状态； (3) 进行潮流计算并对包含三相电机的电路进行初始化 设置； (4) 显示阻抗的依频特性图；
第6章 电力系统稳态与暂态仿真
(5) 显示FFT分析结果； (6) 生成状态—空间模型并打开“线性时不变系 统”(LTI)时域和频域的视窗界面； (7) 生成报表，该报表中包含测量模块、电源、非线性 模块和电路状态变量的稳态值，并以后缀名.rep保存； (8) 设计饱和变压器模块的磁滞特性。 6.1.1 主窗口功能简介 MATLAB提供的Powergui模块在SimPowerSystems库中， 图标如图6-1所示。
第6章 电力系统稳态与暂态仿真
第6章 电力系统稳态与暂态仿真
6.1 Powergui模块 6.2 电力系统稳态仿真 6.3 电力系统电磁暂态仿真 6.4 电力系统机电暂态仿真 习题
第6章 电力系统稳态与暂态仿真
6.1 Powergui模块
Powergui模块为电力系统稳态与暂态仿真提供了有用的 图形用户分析界面。通过Powergui模块，可以对系统进行可 变步长连续系统仿真、定步长离散系统仿真和相量法仿真， 并实现以下功能：

电⼒系统静态稳定暂态稳定实验报告电⼒系统静态、暂态稳定实验报告⼀、实验⽬的1．了解和掌握对称稳定情况下，输电系统的各种运⾏状态与运⾏参数的数值变化范围；2．通过实验加深对电⼒系统暂态稳定内容的理解3．通过实际操作，从实验中观察到系统失步现象和掌握正确处理的措施⼆、原理与说明实验⽤⼀次系统接线图如图1所⽰：图1. ⼀次系统接线图实验中采⽤直流电动机来模拟原动机，原动机输出功率的⼤⼩，可通过给定直流电动机的电枢电压来调节。

实验系统⽤标准⼩型三相同步发电机来模拟电⼒系统的同步发电机，虽然其参数不能与⼤型发电机相似，但也可以看成是⼀种具有特殊参数的电⼒系统的发电机。

发电机的励磁系统可以⽤外加直流电源通过⼿动来调节，也可以切换到台上的微机励磁调节器来实现⾃动调节。

实验台的输电线路是⽤多个接成链型的电抗线圈来模拟，其电抗值满⾜相似条件。

“⽆穷⼤”母线就直接⽤实验室的交流电源，因为它是由实际电⼒系统供电的，因此，它基本上符合“⽆穷⼤”母线的条件。

为了进⾏测量，实验台设置了测量系统，以测量各种电量（电流、电压、功率、频率）。

为了测量发电机转⼦与系统的相对位置⾓（功率⾓），在发电机轴上装设了闪光测⾓装置。

此外，台上还设置了模拟短路故障等控制设备。

电⼒系统静态稳定问题是指电⼒系统受到⼩⼲扰后，各发电机能否不失同步恢复到原来稳定状态的能⼒。

在实验中测量单回路和双回路运⾏时，发电机不同出⼒情况下各节点的电压值，并测出静态稳定极限数值记录在表格中。

电⼒系统暂态稳定问题是指电⼒系统受到较⼤的扰动之后，各发电机能否过渡到新的稳定状态，继续保持同步运⾏的问题。

在各种扰动中以短路故障的扰动最为严重。

正常运⾏时发电机功率特性为：P1＝（Eo×Uo）×sinδ1/X1；短路运⾏时发电机功率特性为：P2＝（Eo×Uo）×sinδ2/X2；故障切除发电机功率特性为：P3＝（Eo×Uo）×sinδ3/X3；对这三个公式进⾏⽐较，我们可以知道决定功率特性发⽣变化与阻抗和功⾓特性有关。

1.正常运行 2.故障阶段 3.故障及时切除 4.故障切除过晚
6.1.1 电力系统的暂态稳定性简介
图6-1 简单电力系统及其等值电路 a)正常运行方式及其等值电路 b)故障情况及其等值电路 c)故障切除后及其等值电路
图6-2 简单系统正常运行、故障 及故障切除后的功率特性
图6-3 振荡过程
图6-4 故障切除过晚的情形
图6-7 序网及短路时的等值电路图 a)负序网络 b)零序网络 c)短路时的等值电路
图6-8 系统故障期间的δ-t曲线
图6-9 故障切除后系统的δ-t曲线
A B C AA BB C A B C
<Stator v oltage v q (pu)> <Stator v oltage v d (pu)> <Rotor speed dev iation dw (pu)> <Output activ e power Peo (pu)> <Rotor speed wm (pu)>
Load 5MW
d_theta1_2 d_theta1_2 (deg)
w1 w (pu)
stop
M a ch i n e Signals
STOP
Stop Simulation if loss of synchronism
M a ch i n e Sco p e
图6-18
图6-19 发电机励磁系统模块结构
6.2 简单电力系统的静态稳定性仿真分 析
6.2.1 电力系统静态稳定性简介 6.2.2 简单电力系统的静态稳定性计算
图6-16 静态稳定的概念
图6-17 小干扰后功角的变化 a) 在a点运行 b) 在b点运行
6.2.2 简单电力系统的静态稳定性计算

Matlab在电力系统稳定控制与优化中的应用技巧电力系统是现代工业社会运行的重要基础设施，其稳定运行对于保障电能供应至关重要。

而在电力系统的稳定控制与优化中，Matlab作为一种强大的计算工具，发挥着重要的作用。

本文将探讨Matlab在电力系统稳定控制与优化中的应用技巧。

一、电力系统稳定性分析电力系统稳定性是指电力系统在面对各种扰动和故障时，能够在一定时间内恢复到稳定状态的能力。

稳定性分析是探究电力系统的稳定性特性和运行状态的重要手段。

Matlab提供了丰富的工具箱，如Power System Toolbox，可以用于进行电力系统稳定性分析。

1.1 利用Matlab进行电力系统稳定性分析中的动态仿真动态仿真是分析电力系统暂态过程的重要手段，它可以通过模拟电力系统中各元件的动态响应来研究电力系统的运行特性。

在Matlab中，我们可以利用Simulink进行电力系统的动态仿真。

Simulink提供了丰富的电力系统模型库，包括发电机、变压器、输电线路等元件，可以通过搭建仿真模型来进行电力系统的稳定性分析。

1.2 利用Matlab进行电力系统稳定性分析中的稳定极限计算稳定极限是指电力系统在最大扰动下仍能保持稳定的极限情况。

在电力系统规划和设计中，稳定极限的计算是重要的任务之一。

而Matlab提供了一系列的计算函数，如Matpower工具箱，可以用于计算电力系统的稳定极限。

二、电力系统优化电力系统优化是指在满足一定约束条件下，通过对电力系统各元件的调整，使得电力系统达到最佳的运行状态。

而Matlab作为一个强大的数值计算工具，提供了各种优化算法和工具箱，可以用于电力系统的优化问题。

2.1 利用Matlab进行电力系统潮流计算潮流计算是电力系统优化的基础，它可以用于计算电力系统各节点的电压和功率。

在Matlab中，我们可以利用Power System Toolbox提供的工具函数进行电力系统的潮流计算。

通过调用这些函数，我们可以建立电力系统的潮流计算模型，计算各节点的电压和功率。

实验二电力系统暂态稳定分析实验目的本次实验旨在通过分析电力系统暂态稳定性，理解电力系统中的稳定性问题，并掌握电力系统的建模和计算方法。

实验原理电力系统暂态稳定性主要是指电力系统在发生大幅度干扰后，是否能够恢复到稳定状态。

因此，暂态稳定性分析主要是对电力系统对外干扰的响应进行预测和评估。

电力系统暂态稳定性分析一般采用时间域仿真方法和频率域方法，其中，时间域仿真法主要是通过对电力系统的微分方程进行数值求解，得到电力系统的动态响应；而频率域方法则是将电力系统的微分方程用拉普拉斯变换转化成复数域的代数方程，通过对这些代数方程进行解析求解，得到电力系统的频率响应。

实验步骤1. 电力系统建模电力系统建模是电力系统暂态稳定性分析的基础，具体步骤如下：•确定电力系统的拓扑结构；•确定电力系统的各个元件（发电机、变压器、线路等）的参数和运行状态；•根据电力系统的拓扑结构和元件参数，列出微分方程或代数方程，得到电力系统的数学模型。

2. 干扰信号的设计在进行暂态稳定分析之前，需要确定干扰信号，在此实验中，我们选择加入一个突然的三相短路干扰信号。

3. 稳定性分析3.1 时间域仿真法•利用Matlab或其他仿真软件，实现电力系统的微分方程求解，得到电力系统随时间的响应；•分析电力系统的响应，判断其是否能够恢复到稳定状态。

3.2 频率域方法•将电力系统的微分方程用拉普拉斯变换转化成复数域的代数方程；•对代数方程进行解析求解，得到电力系统的频率响应；•分析电力系统的频率响应，判断其是否具有稳态解。

4. 结果分析根据时间域仿真法和频率域方法得到的结果，对电力系统的稳定性进行评估和分析。

实验通过本次实验，我们深入了解了电力系统暂态稳定性的原理和计算方法，通过对电力系统的建模和仿真分析，可以有效提高电力系统的稳定性和可靠性。

参考资料•《电力系统分析教程》•《电力系统稳定分析与控制》•《电力系统稳定性分析》。

Use MATLAB software programming, saving memory to a large extent, reduce the amount of computation. By this calculation we understand that a number of engineering calculation and solve engineering problems
MATLAB is an interactive, object-oriented programming language, widely used in industry and academia, mainly for matrix calculation. Using iteration, the amendment through the establishment of matrix iterative equation to turn, gradually moving towards a true value to calculate the voltage electricity grid, power distribution.
二、设计资料及参数
（一）设计原始资料
1、待设计电气设备பைடு நூலகம்统图
2、电力系统网络各元件参数
3、电力系统电气元件的使用规
4、电力工程电气设计手册
（二）设计参考资料
1、《电力系统稳态分析》，珩，中国电力，2007，第三版
2、《电力系统分析》，韩祯祥，大学，2005，第三版
3、《电力系统分析课程实际设计与综合实验》，祝书萍，中国电力，2007，第一版
潮流计算是电力系统分析中的一种最基本的计算，即根据给定电力系统的网络结构和参数，在满足电力系统运行状态参数的边界条件情况下，确定电力系统稳态运行状态的最基本的方法。它的任务是在给定的接线方式和运行条件下，确定系统的运行状态，如各母线上的电压（幅值和相角）、网络中的功率分布及功率损耗等，是电力系统的稳态计算。潮流计算是对电力系统正常运行状况的分析和计算，即电力系统中的电压、电流、功率的计算，即潮流计算；潮流计算方法很多：高斯—塞德尔法、牛顿—拉夫逊法、P-Q分解法、直流潮流法，以及由高斯—塞德尔法、牛顿—拉夫逊法演变的各种潮流计算方法。

实验二电力系统暂态稳定分析一、实验目的1. 通过实验加深对电力系统暂态稳定内容的理解，使理论教学与实践结合,提高学生的感性认识；2. 学生通过实际操作,从试验中观察到系统失步现象和掌握正确处理的措施.二、实验原理电力系统的暂态稳定问题是指电力系统受到较大的扰动之后，各发电机能否继续保持同步运行的问题,在各种扰动中,以短路故障的扰动最为严重。

在故障发生时及故障切除通过强励磁增加发电机的电势，可用于提高系统的稳定性。

由于电力系统发生瞬间单相接地故障较多，发生瞬间单相故障时采用自动重合闸，使系统进入正常工作状态.这两种方法都有利于提高系统的稳定性.暂态稳定是指电力系统在某个运行情况下突然受到大的干扰后，能否经过暂态过程达到新的稳态运行状态或则恢复到原来的状态。

这里所谓的大干扰是相对小干扰来说的，一般指短路故障，突然断开线路或则发电机等。

如果收到干扰后系统能够回到稳态运行，就说系统在这种运行情况下是暂态稳定。

反之，各发电机组转子间一直有相对运动，相对角不断变化,系统的功率、电流、电压都不断振荡，导致系统不能继续运行下去,则称系统在这种运行情况下不能保持暂态稳定。

一个系统的暂态稳定情况和系统原来的运行方式及干扰方式有关，同一个系统在某个运行方式下和某种干扰下系统是暂态稳定，而在另一个运行方式和另外一种干扰下它也可能是不稳定的。

干扰最严重的是三相短路故障，单相接地故障比较多.系统的暂态时间有些可以在1S内都失去同步，有些可以维持几分钟。

模拟电力系统暂态稳定性实验接线图一般采用发电机-变压器-双回线路—无穷大系统。

以下我们来分析一下发电机在正常运行—短路故障-故障切除三种状态下功率特性曲线。

如下图：原动机输出的机械功率用PT表示,发电机向系统送的电磁功率用P0表示。

正常运行的时候PT= P0.假设不计故障之后几秒钟调速器的作用，机械功率始终保持P0，图中a表示发电机正常运行点在曲线PⅠ上，发生短路后功率特性降为PⅡ，由于转子的惯性,转子角度不会立刻变化，运行点有a变至b点，电磁功率显著减小，而原动机PT不变,三相短路时PⅡ曲线越低，此时将加速，其相对速度和相对角度（同步）增加，有b点向c点移动，如果故障一直存在，则始终存在过剩功率，发电机一直加速，直到系统失去同步.实际上，此时继电保护动作,故障切除，功率特性曲线变为PⅢ，发电机的运行点有c点变为e点,此时发电机的输出功率大于机械功率,转子速度减小,但是此时的速度还是大于同步转速的，功角还是在继续增大，到达f时，速度相等，制动结束，但是在f点是不能稳定运行的,此时机械功率和电磁功率不相等,转子减速，功角减小,有f点向e、k点转换，在到达k点以前一直减速，转换子速度低于同步转速，在k点虽然2个功率相等但是速度不平衡，继续减速，一旦低于k点，开始加速，如果没有阻尼，则在PⅢ曲线上来回振荡，实际上存在阻尼的,振荡几次稳定运行的k点.如果故障切除的时间比较晚，在到达h时转子速度还是大于同步转速，越过h点后,继续加速，系统回不到原来点，系统失去同步。

毕业设计《基于matlab故障点的暂态稳定的影响的仿真分析》摘要：目录：摘要第一章：电力系统认识第二章：Matlab介绍第三章：故障点介绍第四章：暂态稳定介绍？第五章：仿真实验第六章：整理数据并分析第七章：总结毕业设计第一章：电力系统认识1.1电力系统的出现使电能得到广泛应用，推动了社会生产各个领域的变化，开创了电力时代，出现了近代史上的第二次技术革命。

20世纪以来，电力系统的大发展使动力资源得到更充分的开发，工业布局也更为合理，使电能的应用不仅深刻地影响着社会物质生产的各个侧面，也越来越广地渗透到人类日常生活的各个层面。

电力系统的发展程度和技术水准已成为各国经济发展水平的标志之一。

发展简况最早的电力系统是简单的住户式供电系统，由小容量发电机单独向灯塔、轮船、车间等照明供电。

白炽灯的发明，使电能的应用进入千家万户，从而出现了中心电站式供电系统，如1882年T.A.爱迪生在纽约主持建造了珍珠街电站。

它装有6台直流发电机,总容量为900马力（约670千瓦）,用110伏电压供给电灯照明（开始时，近1300盏灯）。

19世纪90年代初，三相交流输电研究成功，随之，三相感应电动机及交流功率表也先后研制成功，推动了电力系统的发展。

1895年在美国尼亚加拉建成了复合电力系统，这是早期交流电力系统的代表。

它装有单机容量为5000马力的交流水力发电机，用二相制交流2.2千伏向地区负荷供电,又用三相制交流11千伏输电线路与巴伐洛电站相连，还使用了变压器和交直流变换器将交流电变为100～230伏直流电，供应照明、化工、动力等负荷。

尼亚加拉电力系统的成功，结束了长达10年的关于直流输电（以爱迪生为代表）与交流输电（以G.威斯汀豪斯为代表）方案之争。

交流电力系统可以提高输电电压，增加装机容量，延长输电距离，节省导线材料，具有无可争辩的优越性。

交流输电地位的确定，成为电力系统大发展的新起点。

进入20世纪后，人们普遍认识到扩大电力系统规模可以在能源开发、工业布局、负荷调整、安全与经济运行等方面带来显著的社会经济效益。