
.
习题62
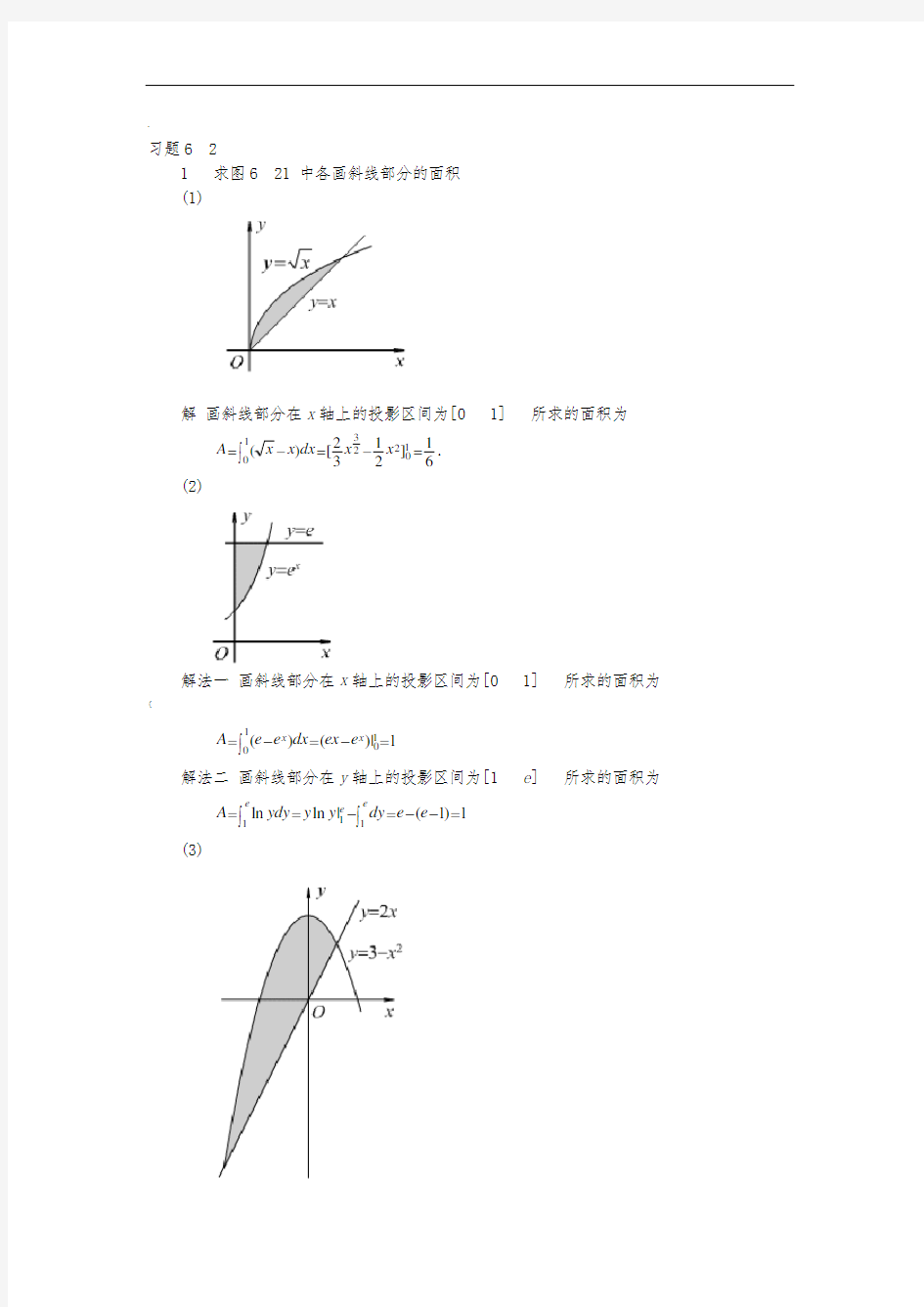
1 求图621 中各画斜线部分的面积 (1)
解 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为
6
1
]2132[)(1022310=-=-=?x x dx x x A . (2)
解法一 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为 (
1
|)()(101
0=-=-=?x x e ex dx e e A
解法二 画斜线部分在y 轴上的投影区间为[1 e ] 所求的面积为
1)1(|ln ln 1
11=--=-==??e e dy y y ydy A e
e e
(3)
解 画斜线部分在x 轴上的投影区间为[3 1] 所求的面积为
3
32
]2)3[(1
32=
--=?-dx x x A
(4)
》
解 画斜线部分在x 轴上的投影区间为[
1 3] 所求的面积为
3
32
|)313()32(3132312=-+=-+=--?x x x dx x x A
2. 求由下列各曲线所围成的图形的面积
(1) 22
1
x y =与x 2y
28(两部分都要计算)
解
3
8
8282)218(220220*********--=--=--=????dx x dx x dx x dx x x A
34
238cos 16402+=-=?ππ
tdt
3
4
6)22(122-
=-=ππS A
—
(2)x
y 1
=与直线y
x 及x 2
解
所求的面积为 ?-=-=2
12ln 2
3)1(dx x x A
(3) y e x
y e
x
与直线x 1
解
所求的面积为
?-+=-=-102
1
)(e
e dx e e A x x
\
(4)y =ln x , y 轴与直线y =ln a , y =ln b (b >a >0). 解
所求的面积为
a b e dy e A b
a y b
a y -===?ln ln ln ln 3 求抛物线y x 24x 3及其在点(0 3)和(3 0)处的切线所围成的图形的面积
解
y 2 x 4
~
过点(0, 3)处的切线的斜率为4 切线方程为y 4(x 3) 过点(3, 0)处的切线的斜率为2 切线方程为y 2x 6 两切线的交点为)
3 ,2
3( 所求的面积为
49
]34(62[)]34(34[23
023
2
32=-+--+-+-+---=??dx x x x x x x A
4 求抛物线y 2
=2px 及其在点),2
(p p 处的法线所围成的图形的面积
解
2y y 2p
在点),2
(p p
处
1)
,2(==
'p p y p y 法线的斜率k 1
$
法线的方程为)
2
(p
x p y --=- 即y p x -=
2
3
求得法线与抛物线的两个交点为),2(p p 和)
3,2
9
(p p -
法线与抛物线所围成的图形的面积为 2
332323
16)612123()223(
p y p y y p dy p y y p A p p p
p =--=--=--?
5 求由下列各曲线所围成的图形的面积
(1)2a cos
解
所求的面积为 》
??==-202222
2cos 4)cos 2(21πππθθθθd a d a A a 2
(2)x a cos 3
t , y a sin 3t ;
解
所求的面积为 ?
?
?===204
220
2330sin cos 34)cos ()sin (44π
πtdt t a t a d t a ydx A a
2
20620428
3]sin sin [12a tdt tdt a ππ
π
=-=??
。
(3)=2a (2+cos ) ! 解
所求的面积为
2
20
2220
218)cos cos 44(2)]cos 2(2[2
1a d a d a A πθθθθθππ
=++=+=??
6 求由摆线x a (t sin t ) y a (1cos t )的一拱(0t 2)与横轴所围成
的图形的面积
解
所求的面积为 ???-=--==a
a a dt t a dt t a t a ydx A 20222020
)cos 1()cos 1()cos 1(π
π22023)2
cos 1cos 21(a dt t t a a
=++-=?
%
7 求对数螺线ae ()及射线所围成的图形面积
解
所求的面积为 )(4
21)(21222222ππππθππθθθ----===
??e e a d e a d ae A
8 求下列各曲线所围成图形的公共部分的面积
(1)3cos 及1cos 解
( 曲线
3cos 与
1cos
交点的极坐标为)3
,23(πA )3
,23(π-B 由对称性
所求的面积为
πθθθθπππ4
5])cos 3
(21)cos 1(21[2232302=++=??d d A
(2)θρsin 2=及θρ2cos 2=
解
曲线θρsin 2=与θρ2cos 2=的交点M 的极坐标为M )
6
,22(π 所求的面积为
2
316]2cos 21)sin 2(21[246602-+=+=??πθθθθπππd d A
·
9 求位于曲线y =e x 下方该曲线过原点的切线的左方以及x
轴上方之间的图形的面积
解 设直线y kx 与曲线y e x 相切于A (x 0 y 0)点 则有
???
??=='==k e x y e y kx y x x 0
)(0
000
求得x 01 y 0e k e
所求面积为
,
2
1ln 21)ln 1(00020e dy y y y y y e dy y y e e e e
e
=
?+-=-??
10 求由抛物线y 24ax 与过焦点的弦所围成的图形的面积的最小值
解 设弦的倾角为
由图可以看出
抛物
线与过焦点的弦所围成的图形的面积为 1
0A A A +=
显然当2
πα=时
A 10 当2
πα<时
A 10
因此 抛物线与过焦点的弦所围成的图形的面积的最小值为 2
03
03
83822a x a dx ax A a a
===?
11 把抛物线y 24ax 及直线x x 0(x 00)所围成的图形绕x 轴旋转 计算所得旋转体的体积
,
解 所得旋转体的体积为
2
020
2
22400
x a x a axdx dx y V x
x x ππππ====??
12 由y x 3 x 2 y 0所围成的图形
分
别绕x 轴及y 轴旋转 计算所得两个旋转体的体积
解 绕x 轴旋转所得旋转体的体积为
ππππ7
128712072
06
2
02
=
===??x dx x dx y V x
绕y 轴旋转所得旋转体的体积为 &
??-=-??=8
3
2
80
22
3282dy
y dy x V y ππππ
πππ5
6453328035=-=y
13 把星形线3/23/23/2a y x =+所围成的图形 绕x 轴旋转 计算所得
旋转体的体积
解 由对称性 所求旋转体的体积为 dx x a dx y V a
a
??-==0
3
323
20
2)(22ππ
3
023
43
23
23
4
2
105
32)33(2a dx x x a x a a a
ππ=-+-=?
14 用积分方法证明图中球缺的体积为)
3(2H R H V -=π
证明 ??---==R
H
R R H R dy y R dy y x V )()(222
ππ
【
)
3
()31(232H R H y y R R
H R -=-=-ππ
15 求下列已知曲线所围成的图形 按指定的轴旋转所产生
的旋转体的体积 (1)2
x y = 2
y x = 绕y 轴
解 ππππ10
3)5121()(1
0521
02
21
0=-=-=??y y dy y ydy V
(2)a
x
a y ch = x 0 x a y 0 绕x 轴
解 ???===102302
2
02
ch
ch )(udu a au x dx a
x a dx x y V a
a
πππ令 ?
10
22310
223)2
1221(4)2(4
u u u
u e u e a du e e a ---+=++=?ππ
)2sh 2(4
3
+=
a π
(3)16
)5(22=-+y x 绕x 轴
解 ??------+=44
2244
2
2)165()165(dx x dx x V ππ 2
4
021601640π?=-=dx x
(4)摆线x a (t sin t ) y a (1cos t )的一拱 y 0 绕直线y 2a 解 ??--=π
πππa a dx y a dx a V 202202)2()2( ?----=π
ππ20223)sin ()]cos 1(2[8t t da t a a a
)
232023237sin )cos 1(8ππππ
a tdt t a a =+-=?
16 求圆盘222a y x ≤+绕x b (b >a >0)
旋转所成旋转体的体积
解 ??------+=a a
a
a dy y a
b dy y a b V 2222
22
)()(ππ 2
20
2228ππb a dy y a b a
=-=?
17 设有一截锥体 其高为h 上、下底
均为椭圆 椭圆的轴长分别为2a 、2b 和2A 、2B 求这截锥体的体积
解 建立坐标系如图 过y 轴上y 点作垂直于y 轴的平面
则
平面与截锥体的截面为椭圆 易得其长短半轴
分别为
y
h
a A A -- y
h
b B B --
截面的面积为π
)()(y h
b B B y h a A A --?--
|
于是截锥体的体积为
]
)(2[6
1)()(0bA aB AB ab h dy y h b B B y h a A A V h
+++=--?--=?ππ
18 计算底面是半径为R 的圆 而垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积
解 设过点x 且垂直于x 轴的截面面积为
A (x ) 由已知条件知 它是边长为x R -2的
等边三角形的面积 其值为 )(3)(22x R x A -=
所以 3
223
34)(3R dx x R V R
R
=-=?
-
19 证明 由平面图形0a x b 0y f (x )绕y 轴旋转所成的旋转体的体积为 ?=b
a
dx
x xf V )(2π
[
证明 如图
在x 处取一宽为dx 的小曲边
梯形 小曲边梯形绕y 轴旋转所得的旋转体的体积近似为
2x f (x )dx 这就是体积元素 即
dV 2x f (x )dx
于是平面图形绕y 轴旋转所成的旋转体的体积为 ??==b
a
b
a
dx
x xf dx x xf V )(2)(2ππ
20 利用题19和结论 计算曲线y sin x (0x )和x 轴
所围成的图形绕y 轴旋转所得旋转体的体积
解 200
2)sin cos (2cos 2sin 2πππππ
π
π
=+-=-==??x x x x xd xdx x V 21 计算曲线y ln x 上相应于83≤≤x 的一段弧的长度
解 ??
?
+=+='+=83283
2
83
2
1)1(1)(1dx
x
x dx x dx x y s
,
令t x =+21 即1
2-=t x 则
23ln 2111111
1322323
22223
2
2+=-+=-=-?-=????
dt t dt dt t t dt t t
t t s
22 计算曲线)3(3x x y -=上相应于
1x
3的一段弧的长度
解 x
x x y 31-= x
x y 2
121-='
x
x y 4121412+-=' )
1(2112x
x y +='+
所求弧长为
34
32)232(21)1(213131-=+=+=?x x x dx x
x s
23 计算半立方抛物线32)1(32-=x y 被抛物线32x y =截得的一段
弧的长度
/
解 由??
???=-=3)1(32232x y x y 得两曲线的交点的坐标为)
36 ,2(
)
3
6 ,2(-
所求弧长为?'+=2
1
212dx
y s
因为 2
)
1(22-='x y y y
x y 2
)1(-=
' )1(23)1(32)1()1(34
2
42
-=--=-=
'x x x y x y
所以 ]1)25[(98)13(13232)1(23122321
2
1
-=--=-+=??
x d x dx x s
24 计算抛物线y 22px 从顶点到这曲线上的一点M (x y )的弧长
解 ??
?+=+='+=y y
y dy y p p dy p y dy y x s 0
220
20
2
1)(1)(1
;
y y p y p y p y p 0
22222])ln(22[1++++=
p
y p y p
y p p y 2
222ln 22++++=
25 计算星形线t a x 3cos = t a y 3sin =的
全长
解 用参数方程的弧长公式
dt t y t x s ?'+'=20
22)()(4π
??+-?=20
2222]cos sin 3[)]sin (cos 3[4π
dt t t a t t a
a
tdt t 6cos sin 1220
==?π
26 将绕在圆(半径为a )上的细线放开拉直 使细线与圆周始终相切 细线端点画出的轨迹叫做圆的渐伸线 它的方程为 "
)
sin (cos t t t a x +=
)
cos (sin t t t a y -=
计算这曲线上相应于t 从0变到的一段弧的
长度
解 由参数方程弧长公式 ?
?
+='+'=π
π
220
2
2
)sin ()cos ()]([)]([dt t at t at dt t y t x s
2
02
ππ
a tdt a ==?
27 在摆线x a (t sin t ) y a (1cos t )上求分摆线第
一拱成1 3的点的坐标
解 设t 从0变化到t 0时摆线第一拱上对应的弧长为s (t 0) 则 ??+-='+'=0
00
2202
2
0]sin [)]cos 1([)]([)]([)(t t dt t a t a dt t y t x t s
-
)
2
cos 1(42sin 2000
t
a dt t a t -==?
当t 02时 得第一拱弧长s (2)8a 为求分摆线第一拱为1 3的点为A (x y ) 令
a
t a 2)2
cos 1(40
=-
解得3
20π
=t 因而分点的坐标为
横坐标a
a x )2332()32sin 32(-=-=πππ
纵坐标a
a y 2
3)32cos 1(=-=π
故所求分点的坐标为)
2
3 ,)2332((a a -π
28 求对数螺线θρa e =相应于自
0到的一段弧长
%
解 用极坐标的弧长公式
θθθρθρ?
θθ?
d a
e e d s a a ??+='+=0
220
2
2
)()()()(
)1(112
2-+=+=?
θ?
θ
θa a e a
a d e a
29 求曲线
1相应于自43=θ至3
4=θ的一段弧长
解 按极坐标公式可得所求的弧长 ?
?
-+='+=344
3222344
32
2
)1()1()()(θθ
θθθρθρd d s
23
ln 1251134
4322+=+=?θθθd
30 求心形线
a (1cos
的全长
¥
解 用极坐标的弧长公式
θθθθθρθρπ
π
d a a d s ??
-++='+=0
2220
2
2
)sin ()cos 1(2)()(2
a
d a 82
cos 40==?π
θθ
习题63
1 由实验知道
弹簧在拉伸过程中
需要的力F (单位
N )
与伸长量s (单位 cm)成正比 即F ks (k 为比例常数) 如果
把弹簧由原长拉伸6cm 计算所作的功
解 将弹簧一端固定于A 另一端在自由长度时的点O 为坐标原点 建立坐标系 功元素为dW ksds 所求功为 182
16
026
0===?s k ksds W k(牛厘米)
2 直径为20cm 、高80cm 的圆柱体内充满压强为10N/cm 2的蒸汽 设温度保持不变
要使蒸汽体积缩小一半 问需要作多少功 》
解 由玻马定律知
π
π80000)8010(102=??==k PV
设蒸气在圆柱体内变化时底面积不变 高度减小x 厘米时压强
为P (x )牛/厘米2 则
ππ80000)]80)(10[()(2=-?x x P π
-=80800
)(x P
功元素为dx x P dW )()10(2?=π
所求功为 2ln 8008018000080800)10(40040
2
ππππ
π=-=-??=??
dx dx W (J)
3 (1)证明 把质量为m 的物体从地球表面升高到h 处所作的
功是 -
h
R mgRh W +=
其中g 是地面上的重力加速度 R 是地球的半径
(2)一颗人造地球卫星的质量为173kg 在高于地面630km 处进入轨道
问把这颗卫星从地面送到630的高空处
克服地球引力
要作多少功已知g 98m/s 2 地球半径R 6370km
证明 (1)取地球中心为坐标原点 把质量为m 的物体升高的功元素为
dy y kMm dW 2=
所求的功为 )
(2h R R mMh k dy y kMm W h R R
+?==?
+
(2)5
3
33
2411
1075.910
)6306370(106370106301098.51731067.6?=?+???????=-W (kJ) ~
4 一物体按规律3ct x =作直线运动 媒质的阻力与速度的平方成正比 计算物体由x 0移至x a 时 克服媒质阻力所作的功
解 因为3ct x = 所以
2
3)(cx
t x v ='= 阻力4
22
9t
kc kv f -=-= 而32)(c
x t = 所以
3432342
9)(9)(x kc c
x kc x f -=-=
功元素dW
f (x )dx 所求之功为
37
320
3
43203
43
20
7
2799)]([a kc dx x kc
dx x kc dx x f W a a
a
===-=?
??
5 用铁锤将一铁钉击入木板 设木板对铁钉的阻力与铁钉击
入木板的深度成正比
在击第一次时
将铁钉击入木板1cm 如
果铁锤每次打击铁钉所做的功相等 问锤击第二次时
铁钉又击
入多少
解 设锤击第二次时铁钉又击入h cm 因木板对铁钉的阻力f 与铁钉击入木板的深度x (cm)成正比
即f kx
功元素dW f
dx kxdx
|
击第一次作功为
k
kxdx W 211
01==?
击第二次作功为
)2(2
12112h h k kxdx W h
+==?+
因为2
1W W = 所以有
)2(21212h h k k +=
解得12-=h (cm)
6 设一锥形贮水池 深15m 口径20m 盛满水 今以唧
筒将水吸尽 问要作多少功
\
解 在水深x 处 水平截面半径为x
r 3210-= 功元素为
dx
x x dx r x dW 22)3210(-=?=ππ
所求功为
?-=15
02)3
210(dx x x W π
?+-=15
032)9
440100(dx x x x π 1875(吨米)(kJ) 7 有一闸门 它的形状和尺寸如图 水面超过门顶2m 求
闸门上所受的水压力
解 建立x 轴
方向向下
原点在水面
,
水压力元素为
xdx dx x dP 221=??=
闸门上所受的水压力为
21252
25
2
===?x xdx P (吨)=205 8(kN)
8 洒水车上的水箱是一个横放的椭圆柱体 尺寸如图所示 当水箱装满水时 计算水箱的一个端面所受的压力
解 建立坐标系如图 则椭圆的方程为
¥
11)43()43(22
22=+-y x
压力元素为
dx x x dx x y x dP 22)4
3()43(38)(21--?=??=
所求压力为 ??
-??+=--?=222
30
22cos 4
3cos 43)sin 1(4338)43()43(38π
πtdx t t dx x x P
ππ
169
cos 49202==?tdx (吨)(kN)
(提示 积分中所作的变换为t x sin 4
343=-)
9 有一等腰梯形闸门 它的两条底边各长10m 和6m 高为20m 较长的底边与水面相齐 计算闸门的一侧所受的水压力
!
解 建立坐标系如图 直线AB 的方程为
x
y 1015-=
压力元素为
dx
x x dx x y x dP )5110()(21-?=??=
所求压力为
1467)5
110(20
0=-?=?dx x x P (吨)14388(千牛)
10 一底为8cm 、高为6cm 的等腰三角形片 铅直地沉没在水中 顶在上 底在下且与水面平行 而顶离水面3cm 试求它每