下载文档原格式
最短路径问题数学模型
最短路径问题是指在一个给定的图中，求出两个顶点之间的最短路径的问题。
在实际生活中，这类问题很常见，比如我们要从一个城市到另一个城市，就需要找到最短的路线。
这个问题可以用数学模型来描述。
首先，我们可以把这个问题抽象成一个图论问题，其中图的顶点表示城市，边表示两个城市之间的道路。
每条边都有一个权值表示道路的长度。
假设我们要求从顶点s到顶点t的最短路径，我们可以用一个数组d来记录s到各个顶点的最短距离，初始化为无穷大。
然后，我们可以使用一种叫做Dijkstra算法的算法来求解这个问题。
具体的过程是：
1. 初始化d[s]=0，d[v]=无穷大（v≠s）。
2. 从未标记的节点中选择标号最小的节点v，对v进行标记。
3. 更新所有v的出边相邻节点的距离，具体为：若d[v]+v到该节点的距离< d[该节点]，则更新d[该节点]为d[v]+v到该节点的距离。
4. 重复步骤2和3，直到所有节点都被标记。
5. d[t]即为s到t的最短距离。
这个算法的时间复杂度为O(n^2)，其中n是节点数。
当然，还有更快的算法，比如Floyd算法，但是它的时间复杂度更高，达到了O(n^3)。
总之，最短路径问题是一个经典的数学问题，可以用图论和算法
来描述和求解。
熟练掌握这个问题对于计算机科学专业的学生来说非常重要。
数据结构第19讲_关键路径与最短路径_C 在数据结构的学习过程中，我们经常会遇到需要寻找最短路径的问题。
最短路径问题是指在图中寻找连接两个顶点之间最短路线的问题。
在实际生活中，最短路径问题广泛应用于交通、通信等领域。
在本篇文章中，我们将介绍关键路径和最短路径的概念，以及它们在实际问题中的应用。
首先，让我们来介绍关键路径。
关键路径是指在项目管理中，连接起始点和终止点的最长路径，也是项目完成所需要的最短时间。
关键路径可以通过计算活动的最早开始时间（EST）和最晚开始时间（LST）来确定。
活动的EST是指在没有任何限制条件下，活动可以最早开始的时间；而LST则是指在不影响项目完成时间的前提下，活动可以最晚开始的时间。
关键路径的长度等于项目的最早完成时间和最晚完成时间相等的活动的持续时间之和。
通过确定关键路径，我们可以优化项目进度，提高项目的整体效率。
接下来，让我们来介绍最短路径。
最短路径是指在图中寻找连接两个顶点之间最短路线的问题。
最短路径可以通过使用一些经典的算法来解决，例如迪杰斯特拉算法和弗洛伊德算法。
迪杰斯特拉算法是一种贪心算法，通过计算出从起点到其他顶点的最短路径，然后逐步扩展路径长度来逐步求解最短路径问题。
弗洛伊德算法是一种动态规划算法，通过构建一个关于各个顶点之间最短路径长度的矩阵来求解最短路径问题。
最短路径问题在实际生活中具有广泛应用，例如在地图导航中，我们需要找到从起点到目的地的最短路线；在网络通信中，我们需要找到网络中两个节点之间传输数据的最短路径。
在本篇文章中，我们介绍了关键路径和最短路径的概念，以及它们在实际问题中的应用。
关键路径用于确定项目完成所需的最短时间，而最短路径用于寻找连接两个顶点之间最短路线的问题。
这些概念都是数据结构中的重要内容，对于我们理解和解决实际问题具有重要意义。
最短路径问题_⽐赛题⽬2011年CUDA校园编程竞赛指定题⽬?最短路径问题最短路径问题(Shortest Path Problem)是经典图论问题之⼀，具有重⼤研究价值和⼯程意义。
从学术⾓度来说，图灵奖得主EdsgerDijkstra针对该问题的⼀系列⼯作是现代算法研究的起点之⼀，以他的名字命名的Dijkstra最短路径算法成为计算机科学家武器库中的基本装备。
从⼯程意义上讲，最短路径问题是对⼤量⼯程问题的直观抽象。
最典型的例⼦当然是导航，我们在⾕歌地图上寻找驾车路径时，显然就是要找到⼀条物理距离最短或者⾏驶时间最短的路线。
此外，机器⼈路径规划、集成电路布线、计算机⽹络路由等应⽤都需要寻找最短路径。
因此，今年我们选择该问题作为CUDA校园编程竞赛指定题⽬。
最短路径问题是在图(graph)的概念上定义的。
这⾥的“图”服从图论中的定义，但是不需要学习图论也可以理解其概念。
⼀个图由节点(vertex或者node)集合和边(edge或者arc)集合组成，图1是⼀个例⼦。
其中，标有数字的圆圈是节点，分别具有编号0到5，即节点0到节点5⼀共六个。
两个节点之间可以由⼀条边连接，由相应节点标志，例如图1中连接节点0和1的边可以记作(0,1)。
边可以有⽅向或⽆⽅向，本次竞赛中只考虑有⽅向的边，因此图1中的边都有箭头。
这时可以⼀条边(i,j)是由节点i指向节点j，当然反过来也⾏，相应的图被称为有向图。
每条边上⼀般可以有⼀个权重，表⽰某种属性，图1⾥⾯每条边旁边的数字就是相应权重。
对本次竞赛⽽⾔，可以把权重理解为相应节点之间的真实物理距离，因此权重是⼤于0的实数。
图1. 图及其节点和边在⼀个图⾥⾯，从某⼀节点i开始，经由⼀系列边可以到达某个节点k，则i→k称为⼀条路径(path)，该路径的长度是所有经过的边上的权重之和。
如果从某⼀节点出发，能够找到⾄少⼀条去往其它任何节点的路径，则该图是连通的，本次竞赛只考虑连通图。
连通图中的任意两个节点i和j之间⼀般来说存在多条路径，最短路径问题就是找到其中最短的⼀条。
最短路径问题的动态规划算法动态规划是一种解决复杂问题的有效算法。
最短路径问题是指在给定的图中找到从起点到终点路径中距离最短的路径。
本文将介绍动态规划算法在解决最短路径问题中的应用。
1. 最短路径问题简介最短路径问题是图论中的经典问题之一，旨在找到从图中一点到另一点的最短路径。
通常使用距离或权重来衡量路径的长度。
最短路径问题有多种算法可以解决，其中动态规划算法是一种常用且高效的方法。
2. 动态规划算法原理动态规划算法的核心思想是将原问题分解为更小的子问题，并存储已解决子问题的结果，以供后续使用。
通过逐步解决子问题，最终得到原问题的解。
在最短路径问题中，动态规划算法将路径分解为多个子路径，并计算每个子路径的最短距离。
3. 动态规划算法步骤（1）定义状态：将问题转化为一个状态集合，每个状态表示一个子问题。
（2）确定状态转移方程：通过递推或计算得到子问题之间的关系，得到状态转移方程。
（3）确定初始状态：设置与最小子问题相关的初始状态。
（4）递推求解：根据状态转移方程，逐步计算中间状态，直到得到最终解。
（5）回溯路径：根据存储的中间状态，找到最短路径。
4. 动态规划算法示例以经典的Dijkstra算法为例，演示动态规划算法在解决最短路径问题中的应用。
假设有带权重的有向图G，其中节点数为n，边数为m。
算法步骤如下：（1）定义状态：对于图G中的每个节点v，定义状态d[v]代表从起点到节点v的最短距离。
（2）确定状态转移方程：d[v] = min(d[u]+w[u,v])，其中u为节点v 的直接前驱节点，w[u,v]为边(u,v)的权重。
（3）确定初始状态：设置起点s的最短距离d[s]为0，其他节点的最短距离d[v]为无穷大。
（4）递推求解：根据状态转移方程逐步计算中间状态d[v]，更新最短距离。
（5）回溯路径：根据存储的前驱节点，从终点t开始回溯，得到最短路径。
5. 动态规划算法的优缺点优点：（1）求解速度快，适用于大规模问题。
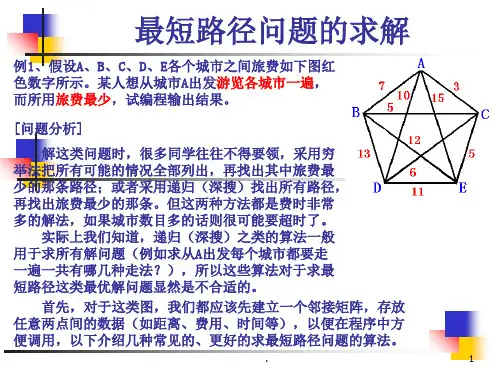
实验八最短路径实验一、实验目的通过最短路径求解的实验，帮助学生熟练掌握图的顶点和边的概念，以及其存储实现；掌握图的基本运算和利用图解决实际问题的基本方法。
二、实验内容以严蔚敏《数据结构（C语言版）》教科书图7.33交通图为例，求解最短路径。
具体内容包括：1、用文本文件组织图的顶点和图的边。
2、图的存储表示：从文件中输入图的顶点和图的边，并转换为图的存储结构表示。
3、求解交通图的最短路径，并用文件保存图的最短途径数据。
4、求解从一个城市出发到其它所有城市的最短路径。
5、求解从一个城市到另一个城市的最短路径。
三、实验仪器微型计算机实验用编程语言：Turbo C 2.0，Borland C 3.0等以上版本四、实验原理图是顶点的集合和边的集合。
边定义了顶点之间的关系。
1、图的存储表示（1）图的顶点的表示在交通图中，图的一个顶点表示一个城市的名字。
城市的名字用一个字符串表示。
因此，图的顶点集用一个二维字符数组表示，也可以说以字符串为单位的一维数组表示。
用C语言定义为：char city[CityNum][NameLenght];图的顶点在图中的位置用顶点名（城市名）在一维顶点向两种的序号表示。
顶点在图的位置（序号）与顶点的输入顺序有关。
对于同一个图，顶点的输入顺序不同，顶点在图中的位置不同，但不影响计算结果。
（2）图的边的表示在交通图中，边表示城市之间的交通线路，在本例中假设交通线路为铁路。
边上的权值表示铁路的长度（公里数）。
考虑铁路都是双向行使，交通图用无向图来表示。
为了方便求的任给两个城市是否有铁路相连，以及铁路的长度，用邻接矩阵表示交通图中各城市之间的邻接关系。
用C语言定义为：int arc[CityNum][CityNum]（3）图的总体存储表示图的总体存储表示定义如下：#define CityNum 30 //最大城市结点数#define NameLenght 12 //城市名字长度#define Infinity 10000 //若城市间没有路径距离设定为Infinitytypedef char Vextype[NameLenght];typedef int Arctype;typedef struct{ Vextype vexs[CityNum]; // 顶点数组Arctype arcs[CityNum][CityNum]; //边矩阵，权值w ijint vexnum,arcnum; //顶点数,边数} Mgraph2、最短路径的表示最短路径值用矩阵表示，其定义如下：int dist[CityNum][CityNum]其中，dist[i][j]表示第i个城市到第j个城市的最短路径值路径顶点序列用路径矩阵表示，定义如下：int Path[CityNum][CityNum]其中，Path[i][j]表示第i个城市到第j个城市的路径上，第j个城市的前一个城市（序号）。
HUNAN UNIVERSITY 课程实习报告
题 目： 最短路径问题 学生姓名 刘乐 学生学号 20080820208 专业班级 通信工程2班 指导老师 朱宁波 完 成 日 期 2010年5月17日 一、 需 求 分 析： 1. 本程序来自于实际问题中选择带权值交通路线，使得费用最低从某一场所到另一场所。 2. 本程序要求： （1）从文件中读取有限网中顶点的数量和顶点间票价的矩阵。 （2）以用户指定的起点和终点，输出从起点到终点的花费。 3在dos系统下输入起点和终点。并输出最短路径。 4测试数据：
二、 概要设计 为实现上述功能需要用到图的存储结构。 利用邻接矩阵构造图，并求出某一顶点到另一顶点的最短路径并打印输出。 算法基本思想 根据题目要求用弗洛伊德算法可以实现两点最短路径问题。弗洛伊德算法仍然使用图的邻接矩阵arcs[n+1][n+1]来存储带权有向图。算法的基本思想是:设置一个n x n的矩阵A(k)，其中除对角线的元素都等于0外，其它元素a(k)[i][j]表示顶点i到顶点j的路径长度，K表示运算步骤。开始时，以任意两个顶点之间的有向边的权值作为路径长度，没有有向边时，路径长度为∞，当K=0时, A (0)[i][j]=arcs[i][j]，以后逐步尝试在原路径中加入其它顶点作为中间顶点，如果增加中间顶点后，得到的路径比原来的路径长度减少了，则以此新路径代替原路径，修改矩阵元素。
程序设计流程 程序由三个模块组成： （1） 输入模块：起点终点和各点间的权值这都从文件中读取。 （2） 求最短路径模块：通过弗洛伊德算法求出起点终点最短路径。 （3） 输出模块：完成弗洛伊德算法后，把最短路径给出，并给出具体路径。 三、 详细设计 1. 因为设计中顶点数和权值都是从文件中读取，因此初始化一个最大顶点数和最大权值。 #define mvnum 100 //最大顶点数 #define maxint 10000 2 本程序用图来实现故要定义图的存储结构 typedef struct{ char vexs[mvnum]; int arcs[mvnum][mvnum]; }MGraph;//定义图的存储结构 弗洛伊德算法求最短路径： void Floyd(MGraph *G,int n) { int i,j,k,v,w;
for(i=1;i<=n;i++)//设置路径长度和路径初值 for(j=1;j<=n;j++) { if(G->arcs[i][j]!=maxint) P[i][j]=j;//j是i的后继 else P[i][j]=0; D[i][j]=G->arcs[i][j]; } for(k=1;k<=n;k++) {//做K次迭代，每次均试图将顶点扩充到当前求得的i到j的最短路径上 for(i=1;i<=n;i++) for(j=1;j<=n;j++) { if(D[i][k]+D[k][j]{ D[i][j]=D[i][k]+D[k][j];//修改路径长度 P[i][j]=P[i][k];
} } } printf("输入起点：v:"); scanf("%d",&v); printf("输入终点：w:"); scanf("%d",&w); k=P[v][w];//K为起点V的后继顶点 if(k==0) { printf("顶点%d到%d无路径！\n",v,w); printf("\n"); } else { if(v!=w) { printf("从顶点%d到%d的最短路径是：%d",v,w,v); while(k!=w) { printf("→%d",k);//输出后继顶点 k=P[k][w];//继续找下一个后继顶点 } printf("→%d",w);//输出终点W printf("路径长度：%d\n",D[v][w]); printf("\n"); } else printf("您已经在这个地方了！\n"); printf("\n"); } }//Floyd 主程序： void main() { FILE *fp; MGraph *G; int n,e,v; int xz=1; G=(MGraph *)malloc(sizeof(MGraph)); printf("输入图中顶点个数和边数n,e: "); fp=fopen("chengxu.txt","r"); fscanf(fp,"%d,%d\n",&n,&e); 从文件中读取n，e printf("%d,%d\n",n,e); int i,j,k,w; for(i=1;i<=n;i++)//输入顶点信息 G->vexs[i]=(char)i; for(i=1;i<=n;i++) for(j=1;j<=n;j++) G->arcs[i][j]=maxint;//初始化邻接矩阵 printf("请输入与各边相关的顶点及边的权值：\n"); for(k=1;k<=e;k++) //读入e条边，建立邻接矩阵 { fscanf(fp,"%d,%d,%d",&i,&j,&w); G->arcs[i][j]=w; } for(i=1;i<=n;i++) { for(j=1;j<=n;j++) printf("%d\t",G->arcs[i][j]); printf("\n"); } printf("有向图的存储结构建立完毕！\n"); printf("\n"); fclose(fp); while(xz!=0) { printf("******求点之间的最短路径******\n"); printf("================================\n");
printf("求任意的两个点之间的最短路径\n"); printf("================================\n"); printf(" 请选择：2 ，选择0退出 ："); scanf("%d",&xz); if(xz==2) Floyd(G,n);
printf("结束求最短路径，再见！\n"); printf("\n"); } } 四、算法具体步骤： 弗洛伊德算法流程图： 算法的时空分析：算法时间复杂度同迪杰斯特拉算法时间复杂度相同也为 o（n^3） 输入输出格式： 五、 实验心得： 本次实验主要是在宿舍完成的，因此去了就是让助教老师看了一下就通过了，因为书上学到这个弗洛伊德算法比迪杰斯特拉算法简单易理解些，我就主要用这种方法实现了，这次实验不仅熟悉了文件的读取内容，而且对新学的内容有了更深的理解，我想数据结构这门课就是需要时刻与对应程序问题结合才能真正的融会贯通，我在网上搜集了一些数据结构各章节有关的程序，正在看，相信会有更多提高。 六、 实验源程序： #include #include #define mvnum 100 //最大顶点数 #define maxint 10000 enum boolean{FALSE,TURE}; int D1[mvnum]; int D2[mvnum],P2[mvnum]; int D[mvnum][mvnum],P[mvnum][mvnum];
typedef struct{ char vexs[mvnum]; int arcs[mvnum][mvnum]; }MGraph;//定义图的存储结构 void Floyd(MGraph *G,int n) { int i,j,k,v,w;
for(i=1;i<=n;i++)//设置路径长度和路径初值 for(j=1;j<=n;j++) { if(G->arcs[i][j]!=maxint) P[i][j]=j;//j是i的后继 else P[i][j]=0; D[i][j]=G->arcs[i][j]; } for(k=1;k<=n;k++) {//做K次迭代，每次均试图将顶点扩充到当前求得的i到j的最短路径上 for(i=1;i<=n;i++) for(j=1;j<=n;j++) { if(D[i][k]+D[k][j]{ D[i][j]=D[i][k]+D[k][j];//修改路径长度 P[i][j]=P[i][k];
} } } printf("输入起点：v:"); scanf("%d",&v); printf("输入终点：w:"); scanf("%d",&w); k=P[v][w];//K为起点V的后继顶点 if(k==0) { printf("顶点%d到%d无路径！\n",v,w); printf("\n"); } else { if(v!=w) { printf("从顶点%d到%d的最短路径是：%d",v,w,v);
