
半变异函数和协方差函数将邻近事物比远处事物更相似这一假设加以量化。半变异函数和协方差都将统计相关性的强度作为距离函数来测量。
对半变异函数和协方差函数建模的过程将半变异函数或协方差曲线与经验数据拟合。目标是达到最佳拟合,并将对现象的认知纳入模型。之后模型便可用于预测。
在拟合模型时,浏览数据中的方向自相关。基台、变程和块金是模型的重要特征。如果数据中有测量误差,请使用测量值误差模型。跟踪这一链接来了解如何将模型与经验半变异函数拟合。
半变异函数
半变异函数定义为
γ(si,sj) = ? var(Z(si) - Z(sj)),
其中 var 是方差。
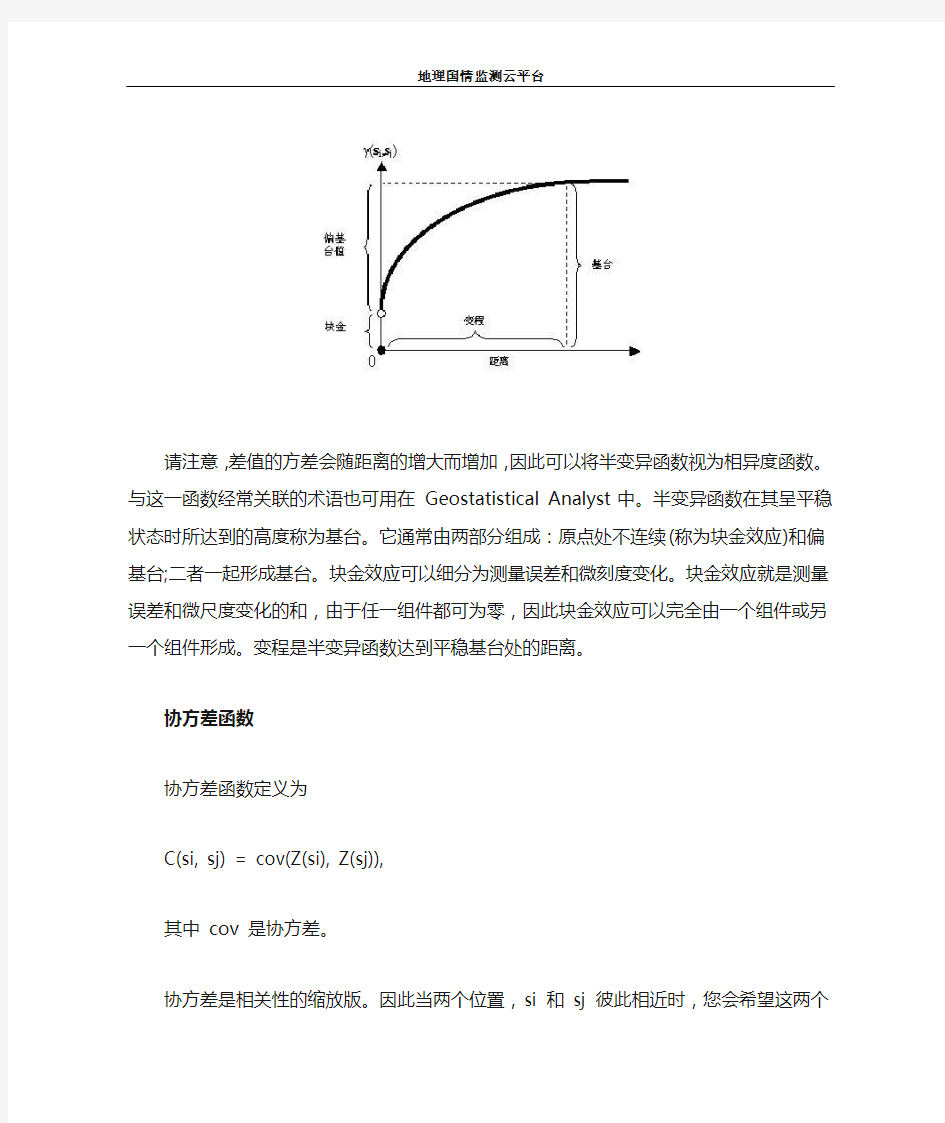
如果两个位置 si 和 sj,在 d(si, sj) 的距离测量上彼此相近,那么您会希望这两个位置相似,以便缩小两个位置的差值 Z(si) - Z(sj) 的大小。当 si 和 sj 距离逐渐增大时,它们变得越来越不相似,它们的值 Z(si) - Z(sj) 的差异也会增大。在下图中可以看到这一情况,其中显示了典型半变异函数的解析图。
请注意,差值的方差会随距离的增大而增加,因此可以将半变异函数视为相异度函数。与这一函数经常关联的术语也可用在 Geostatistical Analyst 中。半变异函数在其呈平稳状态时所达到的高度称为基台。它通常由两部分组成:原点处不连续(称为块金效应)和偏基台;二者一起形成基台。块金效应可以细分为测量误差和微刻度变化。块金效应就是测量误差和微尺度变化的和,由于任一组件都可为零,因此块金效应可以完全由一个组件或另一个组件形成。变程是半变异函数达到平稳基台处的距离。
协方差函数
协方差函数定义为
C(si, sj) = cov(Z(si), Z(sj)),
其中 cov 是协方差。
协方差是相关性的缩放版。因此当两个位置,si 和 sj 彼此相近时,您会希望这两个位置相似,而他们的协方差(相关性)会变大。当 si 和 sj 距离逐渐增大时,它们变得越来越不相似,并且它们的协方差会变为零。在下图中可以看到这一情况,下图显示典型协方差函数的解析图。
请注意,协方差函数随距离的增大而减小,因此可将其视为一种相似度函数。
半变异函数和协方差函数之间的关系
在半变异函数和协方差函数之间存在以下关系:
γ(si, sj) = sill - C(si, sj),
从图中可看出该关系。由于这一相等关系,您可以在 Geostatistical Analyst 中使用两种函数中的任一种来执行预测。(Geostatistical Analyst 中所有半变异函数都拥有基台。)
半变异函数和协方差不是任意函数皆可。为使预测具有非负的克里金标准误差,只有部分函数可以用作半变异函数和协方差。Geostatistical Analyst 提供了多种可接受的选项,您可以为数据尝试不同的选项。您也可以通过同时添加多个模型的方式获得模型 - 此构造提供有效的模型,可以在 Geostatistical Analyst 中添加其中的最多四个模型。有一些当半变异函数存在时,协方差函数却不存在的实例。例如,有一个线性半变异函数,但它没有基台,并且没有相对应的协方差函数。Geostatistical Analyst 中仅使
用带有基台的模型。在选择“最佳”半变异函数模型时,没有必须遵守的规则。您可以查看经验半变异函数或协方差函数并选择看起来适合的模型。你也可以使用验证和交叉验证作为指南。
1.1.1函数的平均变化率课时作业 A 级 基础巩固 一、单选题 1.函数()2y f x x ==在区间[] 00x x x +?,上的平均变化率为1k ,在区间[]00x x x -?,上的平均变化率为2k ,则1k 与2k 的大小关系为( ) A .12k k > B .12k k < C .12k k = D .不能确定 2.设函数2()1f x x =-,当自变量x 由1变到1.1时,函数的平均变化率是( ) A .2.1 B .0.21 C .1.21 D .0.121 3.一质点的运动方程是253s t =-,则在时间[1,1]t +?内相应的平均速度为( ) A .36t ?+ B .36t -?+ C .36t ?- D .36t -?- 4.函数2()sin f x x x =-在[0,π]上的平均变化率为( ) A .1 B .2 C .π D .2π 5.函数1y x = 在1x =到3x =之间的平均变化率为( ) A .23 B .23- C .1 3- D .13 6.某物体沿水平方向运动,其前进距离s (米)与时间t (秒)的关系为()252s t t t =+, 则该物体在运行前2秒的平均速度为( )(米/秒) A .18 B .13 C .9 D .132 7.函数2y x x =+在1x =到1x x =+?之间的平均变化率为( ) A .2x ?+ B .3x ?+ C .()22x x ?+? D .()23x x ?+? 8.函数()2f x x =在区间[]1,2-上的平均变化率为( ) A .-1 B .1 C .2 D .3 B 级 综合提升 9.函数2()1f x x =-在区间[]1,m 上的平均变化率为3,则实数m 的值为( ) A .3 B .2 C .1 D .4 10.某公司的盈利y (元)和时间x (天)的函数关系是()y f x =,假设
学案1.1 .1 函数的平均变化率 编者:刘志英2009.2.18 【课标点击】 (一)学习目标 (1)掌握平均变化率的概念;能通过计算平均变化率了解曲线的陡峭程度,能理解平均变化率的实际意义; (2)能熟练计算函数在某区间上平均变化率. (二)教学重点,难点 (1)掌握平均变化率的概念并能熟练地计算. 【课前准备】 (一)问题导引 问题一: 如图,某市2004年4月20号最高气温为33.4C,而此前的两天,4月19号和4月18号最高气温分别为24.4C和18.6C,短短两天时间气温“陡增”14.8C,人们无不感叹:“天气热得太快了”. 问题二:(1)将该市2004年3月18号最高气温为3.5C与4月18号最高气温18.6C进行比较,两者的温差为15.1C,甚至超过了14.8C,人们却不发出上述感叹,为什么?
(2)从图象上观察,,B C 之间的曲线较,A B 之间的曲线谁更“陡峭”? 问题答案: 用比值33.418.6()3432C B C B y y x x ----来近似地量化,B C 之间的曲线的陡峭程度,并称该比值为气温在区间[32,34]上的平均变化率. 即气温在区间[1,32]上的平均变化率为 18.6 3.515.10.532131 -=≈-. 即气温在区间[32,34]上的平均变化率为33.418.614.87.434322-==-. 虽然,B C 与,A B 之间温差几乎相同,但平均变化率却相差很大. 【学习探究】 (一)自学课本第3、4页 知识点梳理: 1, 自变量的改变量 2, 函数值的该变量 3, 函数的平均变化率 (二)思考与讨论 函数()f x 在区间12[,]x x 上的平均变化率表示为:2121 ()()f x f x x x --. 可以吗? 在图形上的表现为:平均变化率是曲线陡峭程度的“数量化”,或者说,曲线陡峭程度是平均变化率的“视觉化”。 (三).典例示范 例1.某婴儿从出生到第12个月的体重变化如图,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率. 解:从出生到第3个月,婴儿体重的平均变化 率为:6.5 3.51(/)30 kg -=-月. 从第6个月到第12个月,婴儿体重的平均变化 率为:118.60.4(/)126 kg -=-月. 例2. 如图水经过缸吸管从容器甲中流向容器乙,t s 后容器甲中水的体积0.1()5t V t e -=
§2 方差、协方差与相关系数 方差 例1 比较甲乙两人的射击技术,已知两人每次击中环数分布为: ξ:7 8901 0601...?? ??? η:67891001 02040201.....?? ???. 问哪一个技术较好 首先看两人平均击中环数,此时8E E ξη==,从均值来看无法分辩孰优孰劣. 但从直观上看,甲基本上稳定在8环左右,而乙却一会儿击中10环,一会儿击中6环,较不稳定.因此从直观上可以讲甲的射击技术较好. 上例说明:对一随机变量,除考虑它的平均取值外,还要考虑它取值的离散程度. 称ξ-E ξ为随机变量ξ对于均值E ξ的离差(deviation),它是一随机变量. 为了给出一个描述离散程度的数值,考虑用()E E ξξ-,但由于 ()E E ξξ-=E E ξξ-=0对一切随机变量均成立,即ξ的离差正负相消,因此 用()E E ξξ-是不恰当的. 我们改用()2 E E ξξ-描述取值ξ的离散程度,这 就是方差. 定义 1 若()2 E E ξξ-存在,为有限值,就称它是随机变量ξ的方差(variance),记作Var ξ, Var ξ=()2E E ξξ- (1) 但Var ξ的量纲与ξξ的标准差(standard deviation). 方差是随机变量函数()2 E ξξ-的数学期望,由§1的(5)式,即可写出方差的计算公式
Var ξ=2()d ()x E F x ξ ξ+∞ -∞-?=22()(),,()()d .i i i x E P x x E p x x ξξξξ+∞ -∞?-=???-?∑?离散型,连续型 (2) 进一步,注意到 ()2 E E ξξ-= ()222E E E ξξξξ??-+??=()22E E ξξ- 即有 Var ξ=()2 2 E E ξξ-. (3) 许多情况,用(3)式计算方差较方便些. 例1(续) 计算例1中的方差Var ξ与Var η. 解 利用(3)式 2 E ξ= ∑=i i i x P x ) (2 ξ=72×+82×+92×=, Var ξ= ()2 2E E ξξ-=82=. 同理, Var η= ()2 2 E E ηη-= = > Var ξ, 所以η取值较ξ分散. 这说明甲的射击技术较好. 例2 试计算泊松分布P(λ)的方差. 解 2 2 01 ! (1)!k k k k E k e k e k k λ λ λλξ∞ ∞ --====-∑∑ 1 1(1) (1)! (1)!k k k k k e e k k λ λ λλ∞ ∞ --===-+--∑∑ 2 ! ! j j j j j e e j j λ λ λλλ λ∞ ∞ --===+∑∑ 2 λλ=+ 所以Var ξ=22 λλλλ+-=. 例3 设ξ服从[ a, b ]上的均匀分布U [a, b],求Var ξ.
§1.1 导 数 1.1.1 函数的平均变化率 【学习要求】 1.理解并掌握平均变化率的概念. 2.会求函数在指定区间上的平均变化率. 3.能利用平均变化率解决或说明生活中的一些实际问题. 【学法指导】 从山坡的平缓与陡峭程度理解函数的平均变化率,也可以从图象上数形结合看平均变化率的几何意义. 填一填:知识要点、记下疑难点 1.函数的平均变化率:已知函数y =f (x ),x 0,x 1是其定义域内不同的两点,记Δx = x 1-x 0 ,Δy =y 1-y 0=f (x 1)-f (x 0)=f (x 0+Δx )-f (x 0) ,则当Δx ≠0时,商 f x 0+Δx -f x 0Δx =_Δy Δx ___叫做函数y =f (x )在x 0到x 0+Δx 之间的 平均变化率 . 2.函数y =f (x )的平均变化率的几何意义:Δy Δx =_____f (x 2)-f (x 1)x 2-x 1_____ 表示函数y =f (x )图象上过两点(x 1,f (x 1)),(x 2,f (x 2))的割线的 斜率 . 研一研:问题探究、课堂更高效 [问题情境] 在爬山过程中,我们都有这样的感觉:当山坡平缓时,步履轻盈;当山坡陡峭时,气喘吁吁.怎样用数学反映山坡的平缓与陡峭程度呢?下面我们用函数变化的观点来研究这个问题. 探究点一 函数的平均变化率 问题1 如何用数学反映曲线的“陡峭”程度? 答 如图,表示A 、B 之间的曲线和B 、C 之间的曲线的陡峭程度,可以近似地用直 线的斜率来量化. 如用比值y C -y B x C -x B 近似量化B 、C 这一段曲线的陡峭程度,并称该比值是曲线在[x B ,x C ]上的平均变化率. 问题2 什么是平均变化率,平均变化率有何作用? 答 如果问题中的函数关系用y =f (x )表示,那么问题中的变化率可用式子f (x 2)-f (x 1)x 2-x 1 表示,我们把这个式子称为函数y =f (x )从x 1到x 2的平均变化率,平均变化率可以描述一个函数在某个范围内变化的快慢. 例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率. 解 从出生到第3个月,婴儿体重平均变化率为 6.5-3.53-0 =1(千克/月). 从第6个月到第12个月,婴儿体重平均变化率为 11-8.612-6 =2.46=0.4(千克/月). 问题3 平均变化率有什么几何意义? 答 设A (x 1,f (x 1)),B (x 2,f (x 2))是曲线 y =f (x )上任意不同的两点,函数y =f (x ) 的平均变化率Δy Δx =f (x 2)-f (x 1)x 2-x 1 =f (x 1+Δx )-f (x 1)Δx 为割线AB 的斜率. x 1,x 2是定义域内不同的两点,因此Δx ≠0,但Δx 可正也可负;Δy =f (x 2)-f (x 1)是相应Δx =x 2-x 1的改变量,Δy 的值可正可负,也可为零.因此,平均变化率可正可负,也可为零. 跟踪训练1 如图是函数y =f (x )的图象,则: (1)函数f (x )在区间[-1,1]上的平均变化率为________; (2)函数f (x )在区间[0,2]上的平均变化率为________.
自相关函数在不同的领域,定义不完全等效。在某些领域,自相关函数等 同于自协方差(autocovariance)。 统计学 R(k) = \frac{E[(X_i - \mu)(X_{i+k} - \mu)]}{\sigma^2} 信号处理 R_f(\tau) = f(\tau) * f^*(-\tau)= \int_{-\infty}^{\infty} f(t+\tau)f^*(t)\, dt = \int_{-\infty}^{\infty} f(t)f^*(t-\tau)\, dt,其中“*”是卷积算符,(\cdot)^*为取共轭。 同一时间函数在瞬时t和t+a的两个值相乘积的平均值作为延迟时间t 的函数,它是信号与延迟后信号之间相似性的度量。延迟时间为零时,则 成为信号的均方值,此时它的值最大。 编辑本段 自相关函数的性质 以下以一维自相关函数为例说明其性质,多维的情况可方便地从一维 情况推广得到。 对称性:从定义显然可以看出R(i) = R(?i)。连续型自相关函数为偶 函数 当f为实函数时,有: R_f(-\tau) = R_f(\tau)\, 当f是复函数时,该自相关函数是厄米函数,满足: R_f(-\tau) = R_f^*(\tau)\, 其中星号表示共轭。 连续型实自相关函数的峰值在原点取得,即对于任何延时τ,均有 |R_f(\tau)| \leq R_f(0)。该结论可直接有柯西-施瓦兹不等式得到。离 散型自相关函数亦有此结论。 周期函数的自相关函数是具有与原函数相同周期的函数。 两个相互无关的函数(即对于所有τ,两函数的互相关均为0)之和 的自相关函数等于各自自相关函数之和。 由于自相关函数是一种特殊的互相关函数,所以它具有后者的所有性质。 连续时间白噪声信号的自相关函数是一个δ函数,在除τ = 0 之外 的所有点均为0。 维纳-辛钦定理(Wiener–Khinchin theorem)表明,自相关函数和功 率谱密度函数是一对傅里叶变换对: R(\tau) = \int_{-\infty}^\infty S(f) e^{j 2 \pi f \tau} \, df
第三章 协方差传播律 一、 公式汇编 广义传播律 T YY XX T ZZ XX T YZ XX D FD F D KD K D FD K ?=?=??=?220022 002200()()()T YY XX T ZZ XX YZ XX Q F Q F Q K Q K Q F Q K σσσσσσ?=??=??=?T YY XX T ZZ XX YZ XX Q FQ F Q KQ K Q FQ K ? =??=??=? 独立观测值权倒数 2 2211221111Z n n f f f P L P L P L P ?????????=+++ ? ? ?????????? 方差与协因数阵 202020XX XX YY YY XY XY D Q D Q D Q σσσ===22022 020i ii j jj ji ij Q Q Q σσσσσσ=== 2 210 XX XX XX D Q P σσ-== 权2 02i i p σσ= 二、 解题指南 1.观测值及其方差阵 写成向量、矩阵形式 ,XX X D 2 按要求写出函数式,对函数式求全微分,写成矩阵形式 函数式 ),,2,1(),,,,(21n i X X X f Z n i i == 全微分 写成矩阵形式: dZ KdX =
3应用协方差传播律求方差或协方差阵。 T ZZ XX D KD K = 三、 例题讲解 在三角形ABC 中观测三个内角 ,将闭合差平均分配后得到各角值及其方差阵为: 1 23?4010'30"??5005'20"?8944'10"L L L L ????????==?????????????? ??633363336LL D --????=--????--?? 解:1.观测量 及其方差 123????L L L L ????=??????? ? ??633363336LL D --????=--????--?? 2.写出函数式 1 2 3 3 ??sin sin ??sin sin a b L L S S S S L L == 线性化 013 2 3 ??ln ln ln sin ln sin ??ln ln ln sin ln sin a b S S L L S S L L =+-=+- 11332 2 3 3 ????cot cot ????cot cot a a a b b b dS S L dL S L dL dS S L dL S L dL =-=- 写成矩阵形式 11 332 33???cot 0cot ???0cot cot ?a a a b b b dL dS S L S L dS dL dS S L S L dL ??????-??==?????? -??????? ????? 1 313 2 33??cot cot ?0???cot cot ?0a a a b b b S L S L dL dS dS dL dS S L S L dL ρρρ ρ????-? ????? ? ?==????? ???????-???? ??? ?133?1146041??09625?dL dL KdL dL ρ????-??==????-???????? 3.应用协方差传播律求方差或协方差阵 263311460114604136309620962533645Dss ρ--???? -??????=--??????-??????----???? 1 2 3 ???,,L L L 已知边长S0=1500.000m,求Sa 、Sb 的长度及他们的协方差阵 Dss
>> temp1=[1 2 3]; >> temp2=[3 4 1]; >> xtemp=temp1.*temp2 %matlab所谓的向量点击,结果还是向量!!!!!!! xtemp = 3 8 3 >> te=temp1*temp2' %这是数学上两个向量点击,然后在matlab里面的计算方法,结果就是一个值了,含义是两个向量的相似度!!不过没有归一化(没有 按照方差归一) te = 14 >> 2.相关和协方差的关系:如函数: function rou=calcuateSimilary(Beye,data_new) %Beye,data_new前者是去噪前的18*751的数据,后者去去噪后的18导的 %%下面是用概率论里面的相关系数来做的,分别计算比如18导各自的相关系数,结果是18*1的向量 [m,n]=size(Beye); rou=zeros(m,1); for i=1:m temp=cov(Beye(i,:),data_new(i,:));%没有办法,cov函数不像数学公式,matlab的cov函数得到的一定是一个协方差矩阵 %所以对两个向量而言,取反斜对角的任何一个(对称的)就是他们两个的方差。然后按照下面的其实是一个归一化公式 %就是得到了两个向量的相关系数,也其实是衡量的两个变量的相似程度(而且是归一化以后的,否者不好衡量),注意 %注意和信号处理里面的相关函数区分,相关函数在0点的值就是两个变量没有归一化的协方差也就是上面的那个temmp值(如果去了均值,内积就是协方差 %见信号处理里面的什么交流功率和直流功率和相关函数的关系那个图),而相关函数在其它点的值是为了衡量信号如果错位后的相似程度。如果错位后两个 %信号居然达到最大的值,那表示这两个信号时间上延迟后才最像或者说有可能是同一个信号的延迟再现,所以用在衡量寻找信号的潜在周期嘛。 rou(i)=temp(1,2)/(sqrt(cov(Beye(i,:)))*sqrt(cov(data_new(i,:)))); end
引用MATLAB... -matlab 协方差 [n,d]=numden(ex):变为有理分式形式,提取最小分母因子d,相应份子公因子n XLimMode…:轴范围模式 直方图平衡:hellostep 不克不及包容交互式操作、动画、步伐调试等,包含上述号令的步伐也不克不及运行,只能在MATLAB中运行后再复制到notebook中; Error:引发、显示指定的错误 Laplace变换:laplace C和C 同享库 Dbclear:清除断点 Welch方法:对分段的数据施用非长方形,减低由于叠合引起段间的计数相关性,也有助于克服长方形窗的旁瓣效应 双线性变换法:求出s=f(z),然后带到模拟滤波器的函数表达式H(s),得到数字滤波器的H(z)供给的函数为[bz,az]=bilinear(b,a,Fs).
XTick…:确定轴刻度位置 椭圆滤波器:ellipap(n,rp,rs) 鼠标键盘对应原则 约束最小二乘法设计,施用户在设计FIR滤波器的时无须定义幅值响应中的过渡带H=fircls(n,f,a,up,lo)up和lo长度和a相称时分别描写各频带最大限度和下限的向量a 的长度和f不必相称 M文件中包含了所有GUI组建的callbacks(回调函数),自己填写相关里容即可其中的函数有: 随机数天生:所有函数基于rand,randn,且以rnd末端 Any(a)或 prec默认uint8,fid文件句柄
Evaluate loop:循环运行输入细胞 count1可选N,inf,[M,N];prec取值精度,默以为uchar Isinteger 判断整容类型 Axes:坐标轴比例设置 描写随机序列的模子有:自回归(AR)模子、移动均等(MA)模子、自回归移动均等(ARMA)三种 MCC是调用MATLAB编译器的号令 17.4 MATLAB引擎 XTickMode…:刻度位置模式 harmmean调和均值 Libpointer:创建一个指向外部库指针 3.3 字符与字符串 12.1 函数的表示
§1.1.1函数的平均变化率 【学习目标】 1.通过实例,领悟由平均变化率到瞬时变化率刻画现实的过程. 2.了解导数概念的实际背景,知道瞬时变化率就是导数. 【自主学习】 1.平均变化率的概念是什么? 2.Δx,Δy的值一定是正值吗?平均变化率一定为正值吗? 3.函数在某点处附近的平均变化率是什么? 4.观察函数f (x )的图象,平均变化率y x ?=?1212)()(x x x f x f --表示什么? 5.求函数在某点处附近的平均变化率的步骤什么? 6.“Δx →0”的意义是什么?函数f (x )在x 0处的附近的平均变化率与 Δx 有关吗? 【自主检测】 1.函数y =f (x )的自变量x 由x 0改变到x 0+Δx 时,函数值的改变量Δy 为( ) A .f (x 0+Δx ) B .f (x 0)+Δx C .f (x 0)·Δx D .f (x 0+Δx )-f (x 0) 2.已知函数f (x )=x x +-2的图象上的一点)2,1(--A 及临近一点)2,1(y x B ?+-?+-,则=??x y . 3.过曲线y =f (x )=x 3上两点P (1,1)和Q (1+Δx ,1+Δy )作曲线的割线,求出当 Δx =0.1时割线的斜率 . 【典型例题】 例1 已知函数f (x )=2x 2+3x -5. (1)求当x 1=4,且Δx =1时,函数增量Δy 和平均变化率Δy Δx ; (2)求当x 1=4,且Δx =0.1时,函数增量Δy 和平均变化率 Δy Δx ; (3)若设x 2=x 1+Δx .分析(1)(2)题中的平均变化率的几何意义. 例2.求函数f (x )=3x x -+图象从点(1,2)A 到点(1,2)B x y +?+?的平均变化率. 例3.求1y x =在区间00[,]x x x ?+的平均变化率. 【课堂检测】 1.质点运动规律为32 +=t s ,则在时间)3,3(t ?+中相应的平均速度为 A.3 B.6 C.9 D.12 ( )
§ 导 数 函数的平均变化率 【学习要求】 1.理解并掌握平均变化率的概念. 2.会求函数在指定区间上的平均变化率. 3.能利用平均变化率解决或说明生活中的一些实际问题. 【学法指导】 从山坡的平缓与陡峭程度理解函数的平均变化率,也可以从图象上数形结合看平均变化率的几何意义. 填一填:知识要点、记下疑难点 1.函数的平均变化率:已知函数y =f (x ),x 0,x 1是其定义域内不同的两点,记Δx = x 1-x 0 ,Δy =y 1-y 0=f (x 1)-f (x 0)=f (x 0+Δx )-f (x 0) ,则当Δx ≠0时,商 f x 0+Δx -f x 0Δx =_Δy Δx ___叫做函数y =f (x )在x 0到x 0+Δx 之间的 平均变化率 . 2.函数y =f (x )的平均变化率的几何意义:Δy Δx =_____f (x 2)-f (x 1)x 2-x 1_____ 表示函数y =f (x )图象上过两点(x 1,f (x 1)),(x 2,f (x 2))的割线的 斜率 . 研一研:问题探究、课堂更高效 [问题情境] 在爬山过程中,我们都有这样的感觉:当山坡平缓时,步履轻盈;当山坡陡峭时,气喘吁吁.怎样用数学反映山坡的平缓与陡峭程度呢?下面我们用函数变化的观点来研究这个问题. 探究点一 函数的平均变化率 问题1 如何用数学反映曲线的“陡峭”程度? 答 如图,表示A 、B 之间的曲线和B 、C 之间的曲线的陡峭程度,可以近似地用直 线的斜率来量化. 如用比值y C -y B x C -x B 近似量化B 、C 这一段曲线的陡峭程度,并称该比值是曲线在[x B ,x C ]上的平均变化率. 问题2 什么是平均变化率,平均变化率有何作用? 答 如果问题中的函数关系用y =f (x )表示,那么问题中的变化率可用式子f (x 2)-f (x 1)x 2-x 1 表示,我们把这个式子称为函数y =f (x )从x 1到x 2的平均变化率,平均变化率可以描述一个函数在某个范围内变化的快慢. 例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率. 解 从出生到第3个月,婴儿体重平均变化率为 错误!=1(千克/月). 从第6个月到第12个月,婴儿体重平均变化率为 11-12-6 =错误!=(千克/月). 问题3 平均变化率有什么几何意义? 答 设A (x 1,f (x 1)),B (x 2,f (x 2))是曲线 y =f (x )上任意不同的两点,函数y =f (x ) 的平均变化率Δy Δx =f (x 2)-f (x 1)x 2-x 1 =f (x 1+Δx )-f (x 1)Δx 为割线AB 的斜率. x 1,x 2是定义域内不同的两点,因此Δx ≠0,但Δx 可正也可负;Δy =f (x 2)-f (x 1)是相应Δx =x 2-x 1的改变量,Δy 的值可正可负,也可为零.因此,平均变化率可正可负,也可为零. 跟踪训练1 如图是函数y =f (x )的图象,则: (1)函数f (x )在区间[-1,1]上的平均变化率为________; (2)函数f (x )在区间[0,2]上的平均变化率为________.
从自协方差函数()()4.3,664.2,4084.7,,210-=γγγ出发, 建立MA(2)模型如下: 0102030405060708090100 -8 -6-4-202468 10 02468 101214161820 Lag S a m p l e A u t o c o r r e l a t i o n Sample Autocorrelation Function (ACF)
⒈ 利用公式 ??? ? ??∏-???? ??=???? ??C A b b 212211 γγσ 20T C C σγ=-∏ 其中1 lim T k k k k -→∞ ∏=ΩΓΩ,0100A ??= ???,10C ?? = ???,1212k k k k γγγγ+??? Ω= ???L L 计算出0000.42 =σ 和)8500.0,3600.0(),(21-=b b 。 ⒉所要求的模型为21*85.0*36.0--+-=t t t t X εεε t Z ∈,其中{}t ε是)4,0(WN 。 附:Matlab 程序 A=[0 1;0 0;]; C=[1;0]; gamma=[-2.664;3.4]; k=50; Omega=zeros(2,k); Omega(1,1)=-2.664; Omega(2,1)=3.4; Omega(1,2)=3.4; Gamma=zeros(k,k); for i=1:k Gamma(i,i)=7.4084; end for i=2:k Gamma(i,i-1)=-2.664; Gamma(i-1,i)=-2.664; end for i=3:k Gamma(i,i-2)=3.4;
§2 方差、协方差与相关系数 2.1方差 例1 比较甲乙两人的射击技术,已知两人每次击中环数分布为: ξ:78901 0601...?? ??? η:67 891001 02040201.....?? ???. 问哪一个技术较好? 首先看两人平均击中环数,此时8E E ξη==,从均值来看无法分辩孰优孰劣. 但从直观上看,甲基本上稳定在8环左右,而乙却一会儿击中10环,一会儿击中6环,较不稳定.因此从直观上可以讲甲的射击技术较好. 上例说明:对一随机变量,除考虑它的平均取值外,还要考虑它取值的离散程度. 称ξ-E ξ为随机变量ξ对于均值E ξ的离差(deviation),它是一随机变量. 为了给出一个描述离散程度的数值,考虑用()E E ξξ-,但由于()E E ξξ-=E E ξξ-=0对一切随机变量均 成立,即ξ的离差正负相消,因此用()E E ξξ-是不恰当的. 我们改用( )2 E E ξξ-描述取 值ξ的离散程度,这就是方差. 定义1 若()2 E E ξξ-存在, 为有限值,就称它是随机变量ξ的方差(variance),记作Var ξ, Var ξ=( )2 E E ξξ- (1) 但Var ξ的量纲与ξ 不同,为了统一量纲,有时用ξ的标准差(standard deviation). 方差是随机变量函数( )2 E ξξ-的数学期望,由§1的(5)式,即可写出方差的计算公式 Var ξ=2()d ()x E F x ξ ξ+∞ -∞-?=22()(),, ()()d .i i i x E P x x E p x x ξξξξ+∞ -∞?-=???-?∑?离散型,连续型 (2) 进一步,注意到 ()2 E E ξξ-=()222E E E ξξξξ??-+??=()22E E ξξ- 即有 Var ξ= ()2 2 E E ξξ-. (3) 许多情况,用(3)式计算方差较方便些. 例1(续) 计算例1中的方差Var ξ与Var η.
协方差的意义和计算公式 学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合,依次给出这些概念的公式描述,这些高中学过数学的孩子都应该知道吧,一带而过。 很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。 为什么需要协方差? 上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义: 来度量各个维度偏离其均值的程度,标准差可以这么来定义:
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。 从协方差的定义上我们也可以看出一些显而易见的性质,如: 协方差多了就是协方差矩阵 上一节提到的猥琐和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算n! / ((n-2)!*2) 个协方差,那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义: 这个定义还是很容易理解的,我们可以举一个简单的三维的例子,假设数据集有三个维度,则协方差矩阵为 可见,协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。 Matlab协方差实战 上面涉及的内容都比较容易,协方差矩阵似乎也很简单,但实战起来就很容易让人迷茫了。必须要明确一点,协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。这个我将结合下面的例子说明,以下的演示将使用Matlab,为了说明计算原理,不直接调用Matlab的cov函数(蓝色部分为Matlab代码)。 首先,随机产生一个10*3维的整数矩阵作为样本集,10为样本的个数,3为样本的维数。mysample = fix(rand(10,3)*50)
1.1.1 函数的平均变化率 明目标、知重点 1.理解并掌握平均变化率的概念.2.会求函数在指定区间上的平均变化率.3.能利用平均变化率解决或说明生活中的一些实际问题. 1.函数的平均变化率 已知函数y =f (x ),x 0,x 1是其定义域内不同的两点,记Δx =x 1-x 0,Δy =y 1-y 0=f (x 1)-f (x 0)=f (x 0+Δx )-f (x 0),则当Δx ≠0时,商 f x 0+Δx -f x 0Δx =Δy Δx 叫做函数y =f (x )在x 0到x 0+Δx (或[x 0+Δx ,x 0])之间的平均变化率. 2.函数y =f (x )的平均变化率的几何意义 Δy Δx =f x 2-f x 1 x 2-x 1 表示函数y =f (x )图象上过两点(x 1,f (x 1)),(x 2,f (x 2))的割线的斜 率. [情境导学] 某市2013年5月30日最高气温是33.4℃,而此前的两天5月29日和5月28日最高气温分别是24.4℃和18.6℃,短短两天时间,气温“陡增”14.8℃,闷热中的人们无不感叹:“天气热得太快了!”但是,如果我们将该市2013年4月28日最高气温3.5℃和5月28日最高气温18.6℃进行比较,可以发现二者温差为15.1℃,甚至超过了14.8℃,而人们却不会发出上述感慨,这是什么原因呢?显然原因是前者变化得“太快”,而后者变化得“缓慢”,那么在数学中怎样来刻画变量变化得快与慢呢? 探究点一 函数的平均变化率 思考1 如何用数学反映曲线的“陡峭”程度? 答 如图,表示A 、B 之间的曲线和B 、C 之间的曲线的陡峭程度,可以近似地用直线的斜率来量化.
互相关函数在工程中具有重要的应用价值: 1、在混有周期成分的信号中提取特定的频率成分,例如: 用相关分析法分析复杂信号的频谱 相关分析法分析复杂信号的频谱的工作原理如图3.24所示。 图3.24 利用相关分析法分析信号频谱的工作原理框图 2、线性定位和相关测试,例如: 用相关分析法确定深埋地下的输油管裂损位置 如图3.25所示。漏损处K 可视为向两侧传播声音的声源,在两侧管道上分别放置传感器1和2。因为放置传感器的两点相距漏损处距离不等,则漏油的声响传至两传感器的时间 就会有差异,在互相关函数图上处有最大值,这个就是时差。设为两传感器的安装中心线至漏损处的距离,为音响在管道中的传播速度,则 用来确定漏损处的位置,即线性定位问题,其定位误差为几十厘米,该方法也可用于弯曲的管道。 图3.25 利用相关分析进行线性定位实例 用相关法测试热轧钢带运动速度 图3.26所示是利用互相关分析法在线测量热轧钢带运动速度的实例。在沿钢板运动的方向上相距L处的下方,安装两个凸透镜和两个光电池。当热轧钢带以速度移动时,热轧钢带表面反射光经透镜分别聚焦在相距L的两个光电池上。反射光强弱的波动,通过光电池转换成电信号。再把这两个电信号进行互相关分析,通过可调延时器测得互相关函数出现 最大值所对应的时间,由于钢带上任一截面P经过A点和B点时产生的信号x(t)和y(t)是完全相关的,可以在x(t)与y(t)的互相关曲线上产生最大值,则热轧钢带的运动速度为
。 图3.26 利用相关分析法进行相关测速 利用互相关函数进行设备的不解体故障诊断 若要检查一小汽车司机座位的振动是由发动机引起的,还是由后桥引起的,可在发动机、司机座位、后桥上布置加速度传感器,如图3.27所示,然后将输出信号放大并进行相关分析。可以看到,发动机与司机座位的相关性较差,而后桥与司机座位的互相关较大,因此,可以认为司机座位的振动主要由汽车后桥的振动引起的。 图3.27 车辆振动传递途径的识别
3.1.1函数的平均变化率 一【学习目标】: 1.通过实例了解函数平均变化率的意义 2.掌握求函数)(x f 在0x 到x x +0之间的平均变化率 二、【学习重难点】: 1. 函数平均变化率意义的理解; 2. 求函数)(x f 在0x 到x x +0之间的平均变化率 三、【自主学习】: 1、在教材中,我们利用山坡的陡峭程度来理解函数的平均变化率,即将登山者的水平位置用来表示,竖直位置用来表示,构造出)(x f y =的函数关系。 (1)如果山坡是一条直线,那么)(x f y =的陡峭程度用直线的来表示,为什么? (2)如果山坡是曲线,那么)(x f y =的陡峭程度如何表示? 2、函数的平均变化率 一般地,已知函数)(x f y =,,记作 ,,则当 商的平均变化率。 注意(1)0)(x x f 在处是否有意义; (2)y x ??、的含义、求法及围; (3)平均变化率的大小、符号是由谁决定 四、【课探究】 问题1 掌握求函数)(x f y =的平均变化率的过程与方法,并注意上述三点。 1、求函数2 x y =在下列区间上的平均变化率。
(1)],[00x x x x ?+∈;(2)]4,1[∈x 变式:求()2 21y f x x ==+在0x 到0x x +?之间的平均变化率, 并求当01 1,2 x x =?= 时平均变化率的值。 2、求函数x y 1 = 在],[00x x x x ?+∈的平均变化率(0000≠?+≠x x x ,且), 思考:若]4,1[∈x ,]4,1[-∈x 是否能求出函数的平均变化
3、求函数x y = 在)0(00>=x x x 附近的平均变化率。 五、【当堂检测】 1、在平均变化率的定义中,自变量的增量x ?满足( ) A x ?>0 B x ?< 0 C ≠?x 0 D x ?= 0 2、质点运动规律s= 2 t +3,则当x=2,x ?=0.1时,y ?的值为 ( ) A 0.40 B 0.41 C 0.43 D 0.44 3、在x=1附近,取x ?=0.3,在四个函数○ 1y=x ○2y=2x ○3 y= 3 x ○4 y=x 1 中,平均变化率最大的是 ( ) A ○1 B ○2 C ○3 D ○4 4、已知函数y= x 2、当自变量x 由2变到23 ,函数值的增量y ?为 。 5、已知曲线y=2 x - 1 两点A ( 2, 3)、B (2+x ?,3+y ?),当x ?=1时,割线AB 的斜率是;当x ?=0.1时,割线AB 的斜率是。
协方差的意义和计算公式 统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合,依次给出这些概念的公式描述,这些都比较简单,大家自己看看吧 均值: 标准差: 方差: 很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。 为什么需要协方差? 上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义: 来度量各个维度偏离其均值的程度,标准差可以这么来定义:
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。 从协方差的定义上我们也可以看出一些显而易见的性质,如: 协方差多了就是协方差矩阵 上一节提到的猥琐和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算 个协方差,那自然而然的我们会想到使用矩阵来组织这些数据。给 出协方差矩阵的定义: 这个定义还是很容易理解的,我们可以举一个简单的三维的例子,假设数据集有 三个维度,则协方差矩阵为 可见,协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。Matlab协方差实战 上面涉及的内容都比较容易,协方差矩阵似乎也很简单,但实战起来就很容易让人迷茫了。必须要明确一点,协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。这个我将结合下面的例子说明,以下的演示将使用Matlab,为了说明计算原理,不直接调用Matlab的cov函数(蓝色部分为Matlab代码)。 首先,随机产生一个10*3维的整数矩阵作为样本集,10为样本的个数,3为样本的维数。 1 M ySample = fix(rand(10,3)*50)
第三章 协方差传播律 一、 公式汇编 广义传播律 T YY XX T ZZ XX T YZ XX D FD F D KD K D FD K ?=?=??=?220022 002200()()()T YY XX T ZZ XX YZ XX Q F Q F Q K Q K Q F Q K σσσσσσ?=??=??=?T YY XX T ZZ XX YZ XX Q FQ F Q KQ K Q FQ K ? =??=??=? 独立观测值权倒数 2 22 1122 1111 Z n n f f f P L P L P L P ?????????=+++ ? ? ?????????? 方差与协因数阵 202020XX XX YY YY XY XY D Q D Q D Q σσσ===22022 020i ii j jj ji ij Q Q Q σσσσσσ=== 221 00XX XX XX D Q P σσ-== 权 202i i p σσ= 二、 解题指南 1.观测值及其方差阵 写成向量、矩阵形式 ,XX X D 2 按要求写出函数式,对函数式求全微分,写成矩阵形式 函数式
),,2,1(),,,,(21n i X X X f Z n i i == 全微分 写成矩阵形式: dZ KdX = 3应用协方差传播律求方差或协方差阵。 T ZZ XX D KD K = 三、 例题讲解 在三角形ABC 中观测三个内角 ,将闭合差平均分配后得到各角值及其方差阵为: 1 23?4010'30"??5005'20"?8944'10"L L L L ????????==????????? ????? ??633363336LL D --????=--????--?? 解:1.观测量 及其方差 123????L L L L ????=??????? ? ??633363336LL D --????=--????--?? 2.写出函数式 12 03 3 ??sin sin ??sin sin a b L L S S S S L L == 线性化 013 2 3 ??ln ln ln sin ln sin ??ln ln ln sin ln sin a b S S L L S S L L =+-=+- 1133 2 2 3 3 ????cot cot ????cot cot a a a b b b dS S L dL S L dL dS S L dL S L dL =-=- 1 2 3 ???,,L L L 已知边长S0=1500.000m,求Sa 、Sb 的长度及他们的协方差阵 Dss