FPGA查找表法sin函数的实现

stm323950查表法例程STM32系列是一款高性能、低功耗的32位微控制器（MCU）系列，深受广大电子爱好者和专业工程师的喜爱。

在STM32系列的开发过程中，查表法（Lookup Table）是一种常用的技术，用于高效地实现一些特定的应用，如数学运算、数据转换等。

本文将介绍STM32中如何使用查表法，以及查表法的原理和实现方法。

首先，我们来了解一下查表法的原理。

查表法是一种通过查找预先存储的数据表来实现运算的方法。

一般来说，这个表是一个以问题的输入作为索引，输出作为值的二维数组。

当需要进行运算时，只需要从表中查找对应的值，而不需要进行复杂的计算过程。

这样可以大大提高程序的运行效率和节省宝贵的处理器资源。

在STM32的编程中，查表法可以应用于很多场景。

下面以两个常见的例子来说明。

第一个例子是三角函数计算。

三角函数的计算通常是比较耗费计算资源的任务，特别是在嵌入式系统中。

通过使用查表法，可以将三角函数的计算转化为查表操作，从而大大降低计算的复杂度和时间。

以求正弦函数为例，我们可以根据正弦函数的特点，生成一个固定步长的正弦函数表，表中每一项对应一个输入值。

然后，当需要求某个输入值的正弦函数值时，只需要查找对应的表项即可，而不需要进行实时的数学计算。

这样可以大幅提高计算速度，同时节省处理器的计算资源。

第二个例子是数据转换。

在嵌入式系统中，数据转换也是一个常见的任务。

例如，将模拟信号转换为数字信号，或者将一个数据域的表示方式转换为另一种表示方式等。

通过使用查表法，可以将这些复杂的转换过程转化为查表操作，提高程序的运行效率和可维护性。

在STM32的开发中，使用查表法非常简单。

首先，需要定义一个查表数组，数组的大小根据实际需要而定，通常是一个固定步长的数组。

然后，根据问题的输入值，可以通过索引来获取对应的输出值。

对于非常大的查表，可以使用哈希函数等一些技术来提高查表的速度和效率。

总结起来，STM32系列的查表法是一种高效的编程技术，可以用于实现一些复杂的运算和数据转换。

正交信号发生器的FPGA设计与仿真作者：雷能芳来源：《价值工程》2011年第24期摘要：正交信号发生器的FPGA 实现通常都是基于查找表的方法，为了达到高精度要求，需要耗费大量的ROM 资源去建立庞大的查找表。

文中提出了一种基于流水线CORDIC 算法的实现方案，可有效地节省FPGA 的硬件资源。

并根据DSP 开发工具DSP Builder的优点，采用VHDL文本与Simulink 模型图相结合的方法进行了FPGA设计，仿真结果验证了设计的正确性及可行性。

Abstract: The common approach to implement orthogonal signal generator on FPGA is based on look-up tables, which require a huge volume of ROM to achieve high resolution. This paper proposes a pipelined architecture for implementation of orthogonal signal generator on FPGA, which, based on CORDIC algorithm, can save considerable hardware resources and improve the speed performance as well. According to advantages of DSP Builder, the system is designed by utilizing VHDL and Simulink module. The correctness and feasibility of this design is verified by simulation result.关键词：CORDIC算法；FPGA；DSP Builder；正交信号Key words: CORDIC algorithm；FPGA；DSP Builder；orthogonal signal中图分类号：TP391.9文献标识码：A 文章编号：1006-4311（2011）２4-0140-020引言正交信号发生器是电子技术领域中最基本的电子仪器，广泛应用于通信系统、电子对抗、电子测量、科研教学等领域。

FPGA DDS IP 核实现DDS （Direct Digital Synthesizer ），即直接数字频率合成器，本文主要介绍如何调用Xilinx 的DDS IP 核生成某一频率的Sin 和Cos 信号，以及LFM 信号。

1.相关参数的介绍及求解（1）DDS 输出频率输出频率out f 是系统时钟频率clk f 、相位累加器中相位数据位宽)(n B θ和相位增量θ∆的函数。

)(2n B clk out f f θθ∆=因此，要得到输出频率out f ，要求相位增量θ∆为clk Bout f f n )(2θθ=∆如果要采用时分复用的多个通道，则降低每个通道的有效时钟效率。

对于C 个通道，要求相位增量为clk Bout f Cf n )(2θθ=∆（2）频率分辨率频率分辨率f ∆是系统时钟频率clk f 和相位累加器数据位宽)(n B θ的函数。

)(2n B clk f f θ=∆对于时分复用的多通道，频率分辨率随通道数的增加而提高，对于C 个通道：Cf f n B clk )(2θ=∆（3）相位增量相位增量值是无符号的，当相位增量值与相位位宽匹配时，也可以将其看作有符号数。

假设相位增量和相位数据位宽均为N ，如果看成无符号数，范围由0到N 2表示的是(] 3600，的角度范围；如果看成有符号数，则范围变成)1(2--N 到)1(2-N ，相位表示的是[) 180180，-的角度范围。

根据正弦信号的周期性和对称性，两种表示范围内的信号采样是一致的。

相位增量定义了综合其的输出频率。

相位增量是系统时钟频率clk f 、输出频率out f 和相位数据位宽)(n B θ的函数。

clk B out f f n )(2θθ=∆2.线性调频信号线性调频信号的时间函数表达式可表示为2,2[)],2(exp[)(20T T t Kt t f j t s -∈+=ππ其瞬时频率为]2,2[,)(21)(0T T t Kt f t dt d t f -∈+==ϕπ其中，TB K =，B 为信号调频宽度，T 为信号脉宽。

fpga 对数运算
FPGA（现场可编程门阵列）是一种可编程逻辑设备，可用于实现各种数字电路功能。

对于对数运算，在FPGA中可以使用不同的方法进行实现，具体取决于需求和设计约束。

一种常见的方法是通过查找表（Look-Up Table, LUT）实现对数运算。

LUT是FPGA中最基本的元素，可以存储和查找预先计算好的函数值。

通过在LUT中存储预先计算好的对数函数值，并通过输入信号的取值索引相应的输出值，可以实现对数运算。

另一种方法是使用近似算法进行对数运算。

在FPGA中可以使用多项式逼近、级数展开等方法来近似计算对数函数。

这种方法可以提供较高的计算精度，但同时也会引入一定的计算误差。

需要注意的是，在设计FPGA的对数运算模块时，需要考虑计算延迟、资源占用和精度等因素。

根据具体要求和限制，可以选择合适的实现方法来实现对数运算。

excel中sin 函数Sin函数是数学中常见的一种三角函数，它在Excel中也有着广泛的应用。

Sin函数的全称是正弦函数，它表示一个角的正弦值。

在Excel中，我们可以使用Sin函数来计算角度的正弦值。

在Excel中，Sin函数的使用方法非常简单。

我们只需要在一个单元格中输入“=SIN(角度)”即可，其中“角度”是我们要计算正弦值的角度。

例如，如果要计算30度的正弦值，我们可以在一个单元格中输入“=SIN(30)”，然后按下回车键即可得到结果。

Sin函数的返回值是一个介于-1和1之间的数值。

正弦函数的图像是一条波浪线，它在0度、180度、360度等角度处的值为0，在90度、270度等角度处的值为1或-1。

通过使用Sin函数，我们可以计算任意角度的正弦值，从而进行各种数学运算和数据分析。

除了计算正弦值，Sin函数在Excel中还有其他一些常见的用途。

例如，我们可以使用Sin函数来生成波形图或周期性数据。

通过调整Sin函数中的角度参数，我们可以改变波形的形状和周期。

这在一些科学实验、信号处理和音频分析等领域非常有用。

在Excel中，Sin函数还可以与其他函数进行组合使用，实现更复杂的计算。

例如，我们可以将Sin函数的返回值作为其他函数的参数，从而实现更加灵活的计算。

这种组合使用可以帮助我们解决一些复杂的数学问题，提高工作效率和准确性。

在使用Sin函数时，我们需要注意一些常见的问题。

首先，角度参数需要使用弧度制而不是角度制。

如果我们要计算角度为30度的正弦值，需要将30度转换为弧度，然后再作为参数传入Sin函数中。

其次，Sin函数在计算时可能会出现一些舍入误差，这是由于计算机浮点数的精度限制所导致的。

因此，在进行精确计算时，我们需要注意误差的影响。

Sin函数是Excel中非常有用的一个函数，它可以帮助我们计算角度的正弦值，并在各种数学运算和数据分析中发挥重要作用。

通过合理利用Sin函数，我们可以更好地处理数学问题，提高工作效率和准确性。

正弦波的产⽣ 最近的⼀个项⽬，和正弦波息息相关。

因此，我总结了⼀下⽹上关于产⽣正弦波的⼏种⽅法。

若有幸被⼤家看到，欢迎⼤家补充。

（1）递推法 假设数字⾓频率w，这我们要取的正弦波的点⼀次为sin(w*0),sin(w*1),sin(w*2)...sin(w*(n-1)),sin(wn)... sin(wn) =sin(w(n-1)+w) =sin(w(n-1))*cos(w)+cos(w(n-1))*sin(w) =sin(w(n-1))*cos(w)+[sin(nw)-sin(wn-2w)]/2 sin(wn)=2*cos(w)*sin(w(n-1))-sin(w(n-2)); 给出任意相邻两个sin(wn)的值，既可以计算下⼀个正弦波的幅度值。

通过改变不同的初始值（相位），我们可以得到正弦或余弦波。

此⽅法中，cos(w)为常数，可以通过（固定系数乘法）加法实现。

所需资源⾮常少，稳定性⾼，误差⼩，但注意w的精度。

易于⽤软件实现。

（2）系统函数法 在滤波器章节中，有⼏种特殊的滤波器，其中⼀种就是正弦波发⽣器。

已知正弦波的的系统函数为： H(z)=sin(w)*z-1/(1-2*cos(w)*z-1+z-2);余弦波系统函数类似； 由此可以画出正弦波发⽣器（滤波器）的结构图。

易于FPGA和CPU实现。

其中Z表延迟单元，sin(w)和cos(w)都为常数。

结构简单，只⽤加法器或固定系数的乘法器实现，稍稍改动可同时产⽣正余弦波。

（3）cordic⽅法 强⼤的cordic，可以轻松计算包括开⽅，取模，正余弦等多种运算的神级算法。

推荐使⽤，精度最⾼。

逻辑较上⾯两种多。

cordic配置:旋转模式，x为幅度，y为0,，z为相位。

（4）查表法 将正弦波的幅度预先存⼊rom中，通过相位累加器产⽣rom读地址。

实现中要消耗⼀定量的存储器资源。

优点是精度⾼，实现简单，可以实现很多种类型的周期信号。

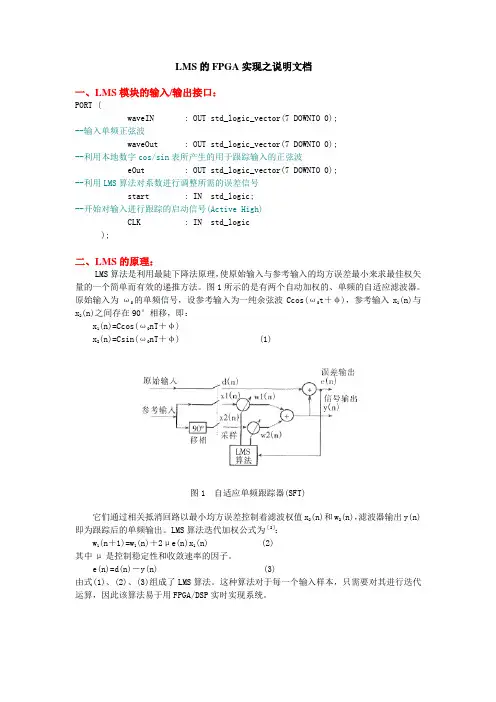
LMS的FPGA实现之说明文档一、LMS模块的输入/输出接口：PORT (waveIN : OUT std_logic_vector(7 DOWNTO 0);--输入单频正弦波waveOut : OUT std_logic_vector(7 DOWNTO 0);--利用本地数字cos/sin表所产生的用于跟踪输入的正弦波eOut : OUT std_logic_vector(7 DOWNTO 0);--利用LMS算法对系数进行调整所需的误差信号start : IN std_logic;--开始对输入进行跟踪的启动信号(Active High)CLK : IN std_logic);二、LMS的原理：LMS算法是利用最陡下降法原理，使原始输入与参考输入的均方误差最小来求最佳权矢量的一个简单而有效的递推方法。

图1所示的是有两个自动加权的、单频的自适应滤波器。

原始输入为ω0的单频信号，设参考输入为一纯余弦波Ccos(ω0t＋φ)，参考输入x1(n)与x2(n)之间存在90°相移，即：x1(n)=Ccos(ω0nT＋φ)x2(n)=Csin(ω0nT＋φ)(1)图1 自适应单频跟踪器(SFT)它们通过相关抵消回路以最小均方误差控制着滤波权值x2(n)和w2(n)，滤波器输出y(n)即为跟踪后的单频输出。

LMS算法迭代加权公式为［2］：w1(n＋1)=w1(n)＋2μe(n)x1(n) (2)其中μ是控制稳定性和收敛速率的因子。

e(n)=d(n)－y(n) (3)由式(1)、(2)、(3)组成了LMS算法。

这种算法对于每一个输入样本，只需要对其进行迭代运算，因此该算法易于用FPGA/DSP实时实现系统。

三、LMS的FPGA实现：结构设计总的算法流程：err = waveIN – waveOut; (注：设计中waveIN由costest模块产生)wCos = wCos + μ*err; wSin = wSin + μ*err;Qcos = wCos*CosOut; Qsin = wSin*SinOut;waveOut = Qcos + Qsin;模块(一) GenerateTHETA在Start信号为‘1’后，每个时钟周期上升沿将THETA(costest IP Core 的输入)与sTHETA(cosfunc IP Core 的输入)加1，这样costest/cosfunc就可以在下一个周期输出对应的sin或是cos值(此两个IP Core的详细资料可以参见工程目录下的sincos.pdf)。

基于FPGA 的简易信号发生器设计与实现作者：吕兆承李营全桂英沈晓波陈帅来源：《江苏科技信息》 2018年第21期摘要：基于FPGA技术，文章认为采用Verilog语言在Altera公司的Cyclone IV系列器件上实现了一个简易信号发生器。

该系统可产生正弦波、方波、三角波和锯齿波4种波形信号，可实现频率调整。

通过SignalTap II对系统输出波形进行实时测试，验证设计的正确性。

该信号发生器具有简单、可靠、精度高、可移植性好等特点。

关键词：信号发生器；Verilog HDL；FPGA中图分类号：TN741 文献标识码：A0 引言信号发生器作为简易的信号源，用于产生测试信号，在教学、科研、工业等领域中有着广泛的应用。

传统的信号发生器是使用模拟电路或者专用芯片搭建而成，存在连线复杂，稳定性较差，且不易扩展和调试等缺陷［1］。

以现场可编程逻辑门阵列（FieldProgrammable Gate Array，FPGA）技术为核心的信号发生器的设计实现，提高了系统可靠性，实现了系统信息实时快速测量，使得信号发生器电路更加简单和精确［2-3］。

1 波形产生原理基于FPGA的信号发生器采用直接数字合成技术（Direct Digital Synthesis，DDS）实现波形的数字化处理，它按一定的相位间隔，将产生的波形幅度的二进制数据存储于高速存储器（ROM），用参考频率源作为时钟，从ROM中取出波形数据，在通过D/A转换和滤波电路便可得到模拟波形［4-5］。

该方法的主要优点是输出相位连续、相对带宽较大、频率分辨率很高、可编程，准确度和稳定度都比较高。

如图1所示，简易信号发生器设计核心部分由计数器构成的地址信号发生器和存储波形数据器ROM组成。

波形存储器ROM存储着发生器的波形数据，包括正弦波、三角波、方波和锯齿波波形数据。

在时钟脉冲作用下，将计数器输出作为波形存储器的寻址地址，读取ROM中存放的波形数据并送往外围器件，从而得到连续的波形。

sin函数计算算法数学中有很多经典的函数，而其中一种非常重要且广泛使用的函数就是sin函数。

sin函数在几何学、物理学、工程学以及计算机科学等领域都扮演着重要的角色。

本文将详细介绍sin函数的计算算法，以及它的应用和意义。

首先，让我们来了解sin函数的定义。

sin函数是一个周期性函数，其定义域为实数集，值域为[-1, 1]。

它与单位圆上的角度的正弦值相对应。

sin函数的图像呈现出周期性的波动，形状像是一条连续的波浪线。

计算sin函数的算法有多种，其中最常见的是泰勒级数展开法。

根据数学原理，我们可以将任意函数表示为幂级数的形式。

sin函数可以通过泰勒级数展开为以下形式：sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...其中，x为自变量，阶乘（n!）表示n的阶乘，也就是n! = n * (n-1) * (n-2) * ... * 2 * 1。

通过展开sin函数的泰勒级数，我们可以使用有限个项的求和来近似计算sin函数的值。

这在计算机中非常有用，因为计算机可以通过有限的计算资源来迅速计算得到sin函数的近似值。

然而，使用泰勒级数展开计算sin函数的效率不高。

为了提高计算速度，我们可以使用其他近似算法，如查表法。

查表法将sin函数的值预先计算存储在一个查找表中，然后根据输入的角度查找对应的sin值。

这种方法会显著提高计算速度，但需要牺牲一定的存储空间。

除了计算sin函数的值，它在实际应用中也起到了非常重要的作用。

在几何学中，我们可以使用sin函数来计算三角形的各种属性，如边长、角度和面积。

在物理学中，sin函数可以用来描述周期性运动，如振动和波动。

在工程学和计算机科学中，sin函数常被用来处理信号和图像，如图像压缩、音频处理和信号滤波。

通过计算sin函数的值，我们可以研究和分析周期性现象，从而揭示自然界和人类行为背后的规律和模式。

同时，sin函数的计算算法也推动了计算机科学和工程学的发展，为我们解决各种实际问题提供了重要的数学工具。

sin函数的使用方法sin函数是数学中常见的一种三角函数，它在计算机科学、物理、工程等领域都有广泛的应用。

在本文中，我们将介绍sin函数的使用方法，并探讨它在实际问题中的应用。

我们来了解一下sin函数的定义。

sin函数是以角度作为自变量，输出一个值在-1到1之间的函数。

它的图像是一个周期性变化的曲线，具有一些特点，比如对称性、周期性等。

在使用sin函数时，我们需要注意一些重要的细节。

首先，角度的单位通常是弧度，而非度数。

弧度是一个无单位的量，表示角度的大小。

我们可以通过将角度乘以π/180来将其转换为弧度。

例如，30度等于π/6弧度。

sin函数的计算可以通过数学库或计算器来完成。

在大多数编程语言中，都提供了sin函数的库函数。

我们可以通过调用这些函数来计算sin值。

例如，在Python中，我们可以使用math库中的sin函数来计算sin值。

sin函数的应用非常广泛。

它在几何学中用于计算三角形的各种属性，如角度、边长和面积等。

在物理学中，sin函数常用于描述周期性现象，比如振动和波动等。

在工程领域，sin函数常用于电路分析和信号处理等方面。

除了基本的sin函数，我们还可以使用一些相关的函数来扩展其功能。

例如，cos函数表示角度的余弦值，tan函数表示角度的正切值。

这些函数在实际问题中也有重要的应用。

在实际问题中，我们经常需要使用sin函数来解决一些复杂的计算问题。

例如，我们可以使用sin函数来模拟天体运动、计算物体的运动轨迹等。

另外，sin函数还可以用于信号处理中的滤波、音频合成和图形处理等方面。

总结一下，sin函数是一种常见的三角函数，用于描述角度和周期性现象。

在使用sin函数时，我们需要注意角度单位和函数的计算方法。

sin函数在数学、物理和工程等领域有着广泛的应用。

通过掌握sin函数的使用方法，我们可以解决一些实际问题，并深入理解数学和科学的本质。

基于FPGA的Cordic算法实现的设计与验证CORDIC(Coordinate RotationDigita1Computer)算法即坐标旋转数字计算方法，是J?KVO1/r1于1959年首次提出，主要用Q⅝函数、双曲线、指数、对数的计算。

该算法通过基本的加和移位运算代替乘法运算，使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数。

本文是基于FPGA实现Cordic算法的设计与验证，使用Veri1og HD1设计，初步可实现正弦、余弦、反正切函数的实现。

将复杂的运算转化成FPGA擅长的加减法和乘法，而乘法运算可以用移位运算代替。

CordiC算法有两种模式，旋转模式和向量模式。

可以在圆坐标系、线性坐标系、双曲线坐标系使用。

本文线初步实现在圆坐标系下的两种模式的算法实现。

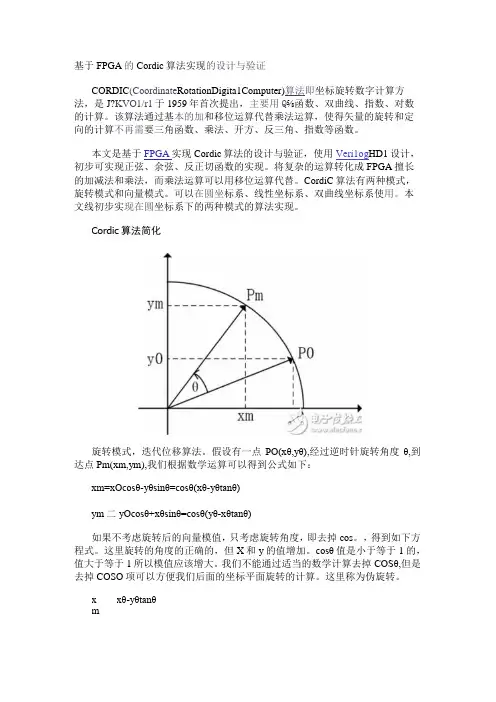
Cordic算法简化旋转模式，迭代位移算法。

假设有一点PO(xθ,yθ),经过逆时针旋转角度θ,到达点Pm(xm,ym),我们根据数学运算可以得到公式如下：xm=xOcosθ-yθsinθ=cosθ(xθ-yθtanθ)ym二yOcosθ+xθsinθ=cosθ(yθ-xθtanθ)如果不考虑旋转后的向量模值，只考虑旋转角度，即去掉cos。

，得到如下方程式。

这里旋转的角度的正确的，但X和y的值增加。

cosθ值是小于等于1的，值大于等于1所以模值应该增大。

我们不能通过适当的数学计算去掉COSθ,但是去掉COSO项可以方便我们后面的坐标平面旋转的计算。

这里称为伪旋转。

xθ-yθtanθxmym-yθ-xθtanθCordic的方法核心就是伪旋转，将旋转角θ细化成若干个大小固定的角度θi,规定满足tanBi=2^-i,通过一系列的迭代旋转，每次旋转θi,i为迭代次数，规定ΣBi的范围即旋转角度θ的范围为［-99.7,99.7］。

如果θ的大于这个范围则可通过三角运算操作转化到该范围的角度。

我们通过事先将所有每次旋转的角度计算出来，由于每次旋转的角度是固定的，所以经过i次旋转的EOi可能会超过O,所以就必须设置一个方向值di,如果旋转角度之和己经小于θ,则di为1下次旋转继续为顺时针旋转，如果旋转角度之和大于。

基于FPGA的函数信号发生器设计函数信号发生器是一种能够产生不同类型信号的测试设备，通常在电子电路实验中使用。

基于FPGA的函数信号发生器设计利用可编程逻辑器件FPGA，可以实现更高的灵活性和可定制性，同时减少了硬件开发成本。

本文将详细介绍基于FPGA的函数信号发生器的设计原理、主要模块和实现方法。

一、设计原理二、主要模块1.时钟生成器模块：时钟信号是产生各种信号波形的基础，因此需要设计一个时钟生成器模块来产生稳定的时钟信号。

可以使用FPGA内部的锁相环（PLL）或计数器来实现。

2.波形选择模块：为了产生不同类型的信号波形，需要设计一个波形选择模块。

通过该模块，用户可以选择所需的信号波形，如正弦波、方波、三角波等。

3. 波形生成模块：根据用户的选择，使用FPGA内部的逻辑门电路来实现不同类型的信号波形的生成。

可以利用查找表（Look-Up Table，简称LUT）来存储不同波形的采样点数据，并通过控制逻辑将这些数据输出为相应的信号波形。

4.频率控制模块：通过频率控制模块，可以对信号波形的频率进行控制。

可以根据用户的输入，通过改变时钟信号的频率或改变波形采样点的间隔来实现频率的调节。

5.幅值控制模块：通过幅值控制模块，可以对信号波形的幅值进行控制。

可以通过改变逻辑门的阈值电压或者改变DAC（数字模拟转换器）的输出电平来实现幅值的调节。

三、实现方法2.硬件设计：根据设计需求，选择合适的FPGA芯片、外部时钟源、AD/DA转换器等外部器件。

根据电路原理图，进行相应的电路布局和连线。

在确认电路无误后，进行焊接和组装工作。

在软件和硬件设计完成后，可以通过控制板上的按钮、旋钮等输入设备来调节信号波形的频率、幅值等参数，从而实现不同类型的信号波形的生成。

总结：基于FPGA的函数信号发生器设计利用FPGA的可编程特性，可以实现信号波形的灵活生成和控制。

通过设计合适的模块，可以产生多种类型的信号波形，并对其频率、幅值等参数进行调节。

fpga 对数计算FPGA对数计算概述：FPGA（现场可编程门阵列）是一种灵活可编程的硬件设备，它可以用来实现各种复杂的计算任务。

对数计算作为一种常见的数学运算，也可以通过FPGA来实现。

本文将介绍FPGA对数计算的原理、实现方法以及相关应用。

一、对数计算的原理对数是数学中的一种运算，常用来解决指数方程等问题。

对数的运算可以通过数学公式来实现，但在硬件设备中，可以通过一系列逻辑电路来模拟对数运算的过程。

FPGA作为一种可编程的硬件设备，可以通过配置逻辑门和寄存器等元件来实现对数计算。

二、FPGA对数计算的实现方法1. 分段线性插值法分段线性插值法是一种常用的对数计算方法。

它将对数运算分为若干个小段，并在每个小段内进行线性插值计算。

在FPGA中，可以通过配置查找表（LUT）来实现线性插值计算，从而实现对数的近似计算。

2. 泰勒级数展开法泰勒级数展开法是一种数值逼近方法，可以用来计算复杂函数的近似值。

对数函数也可以通过泰勒级数展开来进行近似计算。

在FPGA中，可以通过配置加法器和乘法器等元件来实现泰勒级数展开法，从而实现对数的近似计算。

三、FPGA对数计算的应用1. 信号处理在通信系统中，对数运算常用于信号的压缩、调制等处理过程中。

通过FPGA实现对数运算，可以提高信号处理的速度和精度，提升通信系统的性能。

2. 图像处理在图像处理中，对数运算常用于图像的增强、滤波等处理过程中。

通过FPGA实现对数运算，可以加速图像处理的速度，提高图像的质量和清晰度。

3. 科学计算在科学计算领域，对数运算常用于解决复杂的数值计算问题。

通过FPGA实现对数运算，可以提高计算的速度和精度，加快科学计算的过程。

四、总结本文介绍了FPGA对数计算的原理、实现方法以及相关应用。

FPGA作为一种灵活可编程的硬件设备，可以通过配置逻辑电路来实现对数运算，从而提高计算的速度和精度。

FPGA对数计算在信号处理、图像处理和科学计算等领域具有广泛的应用前景。

excel如何使用sin函数在Excel中使用sin函数非常简单，只需要按照以下步骤操作即可：1. 打开Excel并创建一个新的工作表。

2.在一些单元格中输入数值，表示角度（以弧度为单位）。

3.在另一个单元格中键入以下公式：=SIN(角度单元格的地址)。

例如，如果你在A1单元格中输入角度值，那么你可以在B1单元格中输入=SIN(A1)。

4. 按下回车键，Excel会计算并显示sin函数的结果。

下面是一些关于sin函数在Excel中常用的应用示例：1.计算角度的正弦值假设你想要计算30度的正弦值。

你可以在A1单元格中输入30，然后在B1单元格中输入=SIN(A1)，Excel会返回0.5，这是30度的正弦值。

2.绘制正弦曲线你可以使用sin函数在Excel中绘制正弦曲线。

首先，在A列中输入一系列连续的角度值，例如从0到360（或更大）的递增值。

然后，在B列中应用sin函数，使用=A1*PI(/180计算角度值的弧度表示，然后在C列中输入=SIN(B1)计算正弦值。

接下来，选择B列和C列中的所有数据，然后点击插入选项卡中的"散点图"按钮，选择合适的散点图类型即可绘制出正弦曲线。

3.创建动态正弦波你可以使用Excel的其他功能，如数据验证和滚动条控件，创建一个动态的正弦波。

首先，在一些单元格中设置一个角度值，然后在另一个单元格中使用sin函数计算其正弦值。

接下来，添加一个数据验证规则，使角度值只能在一定范围内变化。

最后，插入一个滚动条控件，将其链接到角度值的单元格，这样你可以通过滚动条控制正弦波的运动。

4.批量计算角度的正弦值假设你有一列角度值需要计算其正弦值。

你可以在一个单元格中输入sin函数，然后将其拖动到需要计算正弦值的单元格范围内，Excel会自动适应不同的角度值，并计算其正弦值。

这样你就可以一次性计算多个角度的正弦值。

综上所述，Excel中的sin函数非常强大，你可以使用它进行各种数学计算和数据分析。

基于FPGA的CORDIC算法的分析和实现作者：刘伟亮来源：《电脑知识与技术》2013年第04期摘要：该文分析了CORDIC算法为作为硬件实现基本的运算的方法，实现了开方、正弦、余弦、乘法、除法、正切、反正切，和一些双曲函数的实现。

提供了一种基于流线设计的CORDIC算法的实现，在每层流水线上都可实现6种计算，共用一个加法器。

减少了硬件内部资源的使用。

通过是实现的结果可以看到计算结果在水线级数STAGE+3 个CLK信号后实现了连续的实时计算结果。

关键词：CORDIC；流水线设计；共用；基本运算中图分类号：TP301 文献标识码：A 文章编号：1009-3044（2013）04-0841-03The Analysis and Implementation of CORDIC Algorithm Based on FPGALIU Wei-liang（Chongqing University of Posts and Telecommunications， Chongqing 400065， China）Abstract： This paper analyzed the CORDIC algorithm for hardware implementation of basic operation method， realized the root， sine， cosine， multiplication， division， tangent， inverse tangent， and some hyperbolic function. Provide a method based on pipeline design CORDIC algorithm， each line can be realized 6 kinds of calculation， sharing one adder. Reducing the hardware resource use. Is to achieve the results you can see through calculation results in line series STAGE+3 CLK signal after achieving a continuous real-time calculation results.Key words： CORDIC； pipeline design； share； basic operations1 概述随着现代数字电路中工作频率的不断提高，计算结果要求随时按工作要求实时计算，然而在实际工作中软件语言实现的算法实时性不高，在硬件中计算数据只有加法和位移的操作。