排队模型(matlab代码)

3 6 1 5 6 7 22 3 4 6 11 45 5 2 0 4 11 9 1 2 8 26 3 10 5 12 47 4 2 3
(1) (2) (3) (4) (5) (1) (2) (3) (4) (5) (1) (2) (3) (4) (5) i τi si ti wi i τi si ti wi i τi si ti wi 13 49 1 3 5 23 86 6 2 2 33 117 4 4 7
现实生活中的排队系统序Leabharlann 到达的顾客 号要求服务内容
服务机构
1 不能运转的机器 修理
修理技工
2 修理技工
领取修配零件 发放修配零件的管理员
3 病人
诊断或做手术 医生(或包括手术台)
4 电话呼唤
通话
交换台
5 文件搞
打字
打字员
6 提货单
提取存货
仓库管理员
7 驶入港口的货船 装(卸)货
装(卸)货码头(泊位)
二、排队系统的特征及其组成
1、排队系统的特征即拥挤现象的共性 1）、有请求服务的人或物 2）、有为顾客服务的人或物 3）、具有随机性 4）、服务的数量超过服务机构的容量
2、排队系统的三大基本组成部分
1）、输入过程(顾客到达的方式) a、顾客的总体（顾客源）的组成可能是有限的，也
可能是无限的； b、顾客相继到达的时间间隔可以是确定的，也可以
平均服务率： 41/127=0.32(人/分钟)
六、典型排队系统模型的结构及应用
M/M/C等待制排队模型研究要点： a、系统意义 b、状态转移速度图与状态转移速度矩阵 c、状态概率方程 d、系统的基本数量指标
Passion分布
设N(t)表示在时间[0, t)内到达顾客数； 令Pn(t1, t2)表示在时间区间[t1, t2)（t2 > t1）内有n（0） 个顾客到达的概率，即 Pn(t1, t2)=P{ N(t2) –N(t1)=n } （t2>t1，n0） Passion分布的三条件：

0.325 hour
0.033 hour
0.889 hour
0.048 hour
文档仅供参考，如有不当之处，请联系改正。
案例求解 3
即
W1
=W
= Wq
+
1 m
=
Lq l
+
1 m
=
P0(l m)s r s!(1- r)2 l
+
1 m
其中
r= l sm
åé s-1 (l / m)n (l / m)s 1 ù
➢ 非强占性优先权(Nonpreemptive Priorities)——虽然一种高优先级
旳顾客到达，也不能强制让一种正在接受服务旳低优先级顾客返回排队。
➢ 强占性优先权(Preemptive Priorities)——若有高优先级旳顾客到达，
服务员即中断对低优先级顾客旳服务，并立即开始为高优先级顾客服务。
N
l = å li
i=1
r= l m
k
å 【注:】这里假设了 li < sm，
i=1
从而使其能到达稳定状态。
文档仅供参考，如有不当之处，请联系改正。
计算公式 2
抢占性优先权(基于M/M/1)
1/ m
Wk = Bk-1Bk
for k=0,1,2,…,N
文档仅供参考，如有不当之处，请联系改正。
案例求解 3
文档仅供参考，如有不当之处，请联系改正。
案ቤተ መጻሕፍቲ ባይዱ求解 3
W1-1/μ W2-1/μ W3-1/μ
Preemptive Priorities
s=1
s=2
0.024 hour
0.154 hour

M/M/C排队模型及其应用摘要：将随机服务系统中M/M/C排队模型应用到理发服务行业中。

通过对某理发店进行调查，以10min为一个调查单位调查顾客到达数，统计了72个调查单位的数据，又随机调查了113名顾客服务时间，得到了单位时间内到达的顾客数n和为每位顾客服务的时间t，然后利用 2拟合检验，得到单位时间的顾客到达舒服从泊松分布，服务时间服从负指数分布，从而建立起M/M/C等待制排队模型，通过计算和分析M/M/C排队模型的主要指标，得到理发店宜招聘的最佳理发师数目。

排队论主要对由于受随机因素的影响而出现排队系统进行研究，它广泛应用于通信、交通与运输、生产与服务、公共服务事业以及管理运筹等一切服务系统。

在具体应用方面，把排队理论直接应用到实际生活方面也有不少的文献。

另外，排队论和其他学科知识结合起来也有不少应用。

我们可以从现实生活中去的数据资料，基于排队系统基本知识和M/M/C排队模型基本理论和统计学有关知识，通过分析研究，得出一些结论，为实际问题的解决提供参考资料，从而拓宽了该模型的应用领域，并对其他模型的系统应用也有一定的启示作用。

1 M/M/C排队模型定义若顾客的到达间隔服从参数为λ的负指数分布，到达的人数服从泊松分布，每位顾客的服务时间服从参数为μ的负指数分布，且顾客的到达时间与服务时间独立，系统有C个服务台，称这样的排队模型为M/M/C排队模型。

M/M/C排队模型也可以对应分为标准的M/M/C模型、系统容量有限的M/M/C模型和顾客源有限的M/M/C模型3种。

假定顾客到达服从参数为λ的泊松分布，每个顾客所需的服务时间服从参数为μ的指数分布，顾客到达后若有空闲的服务台就按到达的先后顺序接受服务，若所有的服务台均被占用时，顾客则排成一队等候。

令N（t）=i表示时刻t系统中恰有i位顾客，系统的状态集合为{0,1,2,…}。

可证{ N（t），t>0}为生灭过程，而且有：.....2C 1,C n C ...,21n n {....,21n nn，μ，，μ，，，++=====μλλ由此可见，服务台增加了，服务效率提高了。

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。

它是数学运筹学的分支学科。

也是研究服务系统中排队现象随机规律的学科。

广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。

排队论研究的内容有3个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。

其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。

一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中虚线所包括的部分。

排队系统又称服务系统。

服务系统由服务机构和服务对象（顾客）构成。

服务对象到来的时刻和对他服务的时间（即占用服务系统的时间）都是随机的。

描述一个排队系统一般需要分析其三个组成部分：输入过程、排队规则和服务机构。

输入过程输入过程考察的是顾客到达服务系统的规律。

它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述，一般分为确定型和随机型两种。

例如，在生产线上加工的零件按规定的间隔时间依次到达加工地点，定期运行的班车、班机等都属于确定型输入。

随机型的输入是指在时间t内顾客到达数n（t）服从一定的随机分布。

如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布，即式中λ为单位时间顾客期望到达数，称为平均到达率；1/λ为平均间隔时间。

在排队论中，讨论的输入过程主要是随机型的。

排队规则排队规则分为等待制、损失制和混合制三种。

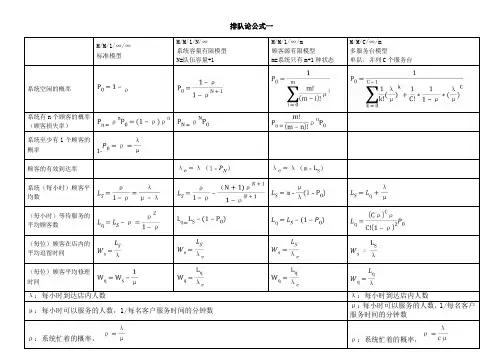
M/M/1/∞/∞标准模型M/M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队，并列C个服务台
系统空闲的概率ρ
系统有n个顾客的概率
（顾客损失率）
系统至少有1个顾客的
概率1-
顾客的有效到达率
系统（每小时）顾客平
均数
（每小时）等待服务的
平均顾客数
=
（每位）顾客在店内的
平均逗留时间
（每位）顾客平均修理
时间
λ：每小时到达店内人数λ：每小时到达店内人数
μ：每小时可以服务的人数，1/每名客户服务时间的分钟数μ：每小时可以服务的人数，1/每名客户服务时间的分钟数
ρ：系统忙着的概率，ρ：系统忙着的概率，
M/G/1/∞/∞M/D/1/N/∞M//1/∞/m 系统（每小时）顾客平均数
（每小时）等待服务的平均
顾客数
（每位）顾客在店内的平均
逗留时间
（每位）顾客平均修理时间
λ：每小时到达店内人数
μ：每小时可以服务的人数，1/每名客户服务时间的分钟数E(v):服务时间v的期望
D(v):方差
ρ：系统忙着的概率，λ：每小时到达店内人数
μ：每小时可以服务的人数，1/每名客户服务时间的分钟数
:服务时间v的期望
D(v):方差
ρ：系统忙着的概率，。

cmLiu@shufe
Operations Research
9.2 几个常用的概率分布
9.2.1 经验分布 9.2.2 泊松分布 9.2.3 负指数分布 9.2.4 爱尔朗分布
cmLiu@shufe
Operations Research
9.2.1 经验分布
主要指标
平均间隔时间 = 总时间 到达顾客总数
Operations Research
9.1.3 排队论研究的基本问题
（3）系统优化问题的研究 研究排队系统的目的就是通过对该系统概率规律的研究， 实现系统的优化。系统的优化包括最优设计和最优运营问 题。前者属于静态问题，它是在输入和服务参数给定的情 况下，确定系统的设计参数，以使服务设施达到最大效益 或者服务机构实现最为经济。后者属于动态问题，它是指 对于一个给定的系统，在系统运行的参数可以随着时间或 状态变化的情况下，考虑如何运营使某个目标函数达到最 优。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
一般的排队过程可以这样描述：顾客由顾客源出发，到达 服务机构（服务台、服务员）前，按排队规则排队等待接 受服务，服务机构按服务规则给顾客服务，顾客接受完服 务后就离开。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
尽管排队系统是多种多样的，但所有的排队系统都是由输入过程、排 队规则、服务机构及服务规则三个基本部分组成的。 （1）输入过程 描述顾客来源以及顾客到达排队系统的规律。 一般从以下几个方面对输入过程进行描述：顾客源中顾客的数量是 有限还是无限；顾客到达的方式是单个到达还是成批到达；顾客的到 达是否相互独立（以前到达的顾客对以后达到的顾客没有影响，则称 顾客的达到是相互独立的，否则就是有关联的）；顾客相继到达的间 隔时间分布是确定型的还是随机型的（如果是随机分布，需要知道单 位时间内的顾客到达数或者顾客相继到达时间间隔的概率分布）；输 入的过程是平稳的还是非平稳的（若相继到达的间隔时间分布参数 （如期望值、方差等）都是与时间无关的，则称输入过程是平稳的， 否则称为非平稳）。 本章主要讨论顾客的到达是相互独立的、输入过程是平稳的情形。

现代物业・新建设 2012年第11卷第10期高校食堂排队模型的研究李欣 肖芳园 杨牡丹（湖南工程学院管理学院，湖南 湘潭 411104）摘 要：在国内大多数高校中，学生食堂是学生就餐的主要场所，显而易见，食堂排队问题是一个无法回避的现实问题。

虽然增加窗口数量可以减少学生排队就餐的时间，但同时也增加了食堂的运营成本。

因此，如何在两者之间进行权衡，确定最佳的窗口数量，对学生和食堂来说都至关重要。

针对高校食堂排队问题进行研究，讨论建立简单的排队模型的基本思路。

关键词：高校食堂；排队；模型中图分类号：G647 文献标识码：A 文章编号：1671-8089（2012）10-0037-03一、食堂就餐排队模型探究的必要性（一）从生活细节着手，构建和谐校园食堂是学生就餐的场所，根据调查，在校学生选择在食堂就餐的比例高达80%以上，因此，如何确定最佳的窗口数量，让学生在最短时间内打到饭菜的同时又兼顾食堂的利益，是摆在眼前的一个非常现实的问题。

学生食堂的存在和发展状况不仅关系到在校学生的生活问题，而且在某种程度上也关系到学生们的身体健康和学习状况。

本研究通过构建一个简单的食堂排队模型，来解决学生就餐时排队等候时间过长的问题，从学生生活细节着手，为在校学生创造一个文明、和谐的就餐环境，有益于构建和谐校园。

（二）降低食堂管理成本，实现资源优化配置食堂既是学校的硬件设施之一，又是学校管理的重要组成部分。

通过对食堂排队模型的探究，得出食堂需要开设的窗口数量，有助于学校加强对食堂的管理，为进一步加强和改善食堂监管工作提供了依据。

此外，通过排队模型得出最佳窗口数量，避免窗口开设过少致使学生排队等候时间过长以及开设窗口过多导致人力的浪费。

因此，排队模型的建立与实现可以有效地降低食堂的管理成本，帮助实现资源的优化配置。

（三）响应国家政策，建设资源节约型社会国家主席胡锦涛在党的第十六届五中全会上强调要加快建设资源节约型社会，指出这是从我国国情出发的一项重大决策。

龙源期刊网
带优先权与不耐烦顾客排队模型的模拟仿真作者：秦海林刘建民
来源：《现代电子技术》2012年第20期
摘要：考虑一个有两类顾客到达的单服务台的排队系统。

两类顾客的到达过程均为泊松过程，第一类顾客较第二类顾客具有强占优先权，且第二类顾客由于第一类顾客的到达而变得不耐烦，其“耐性时间”服从负指数分布。

两类顾客的服务时间服从相同参数的负指数分布，服务规则是强占优先服务，在高负荷条件下用Matlab编程对此排队系统进行模拟仿真，为处理此类排队问题提供了一个新方法。

关键词：泊松过程；强占优先权；高负荷条件；系统模拟仿真
中图分类号：TN911-34； O226文献标识码：A。

排队模型之港口系统本文通过排队论和蒙特卡洛方法解决了生产系统的效率问题，通过对工具到达时间和服务时间的计算机拟合，将基本模型确定在//1M M排队模型，通过对此基本模型的分析和改进，在概率论相关理论的基础之上使用计算机模拟仿真（蒙特卡洛法）对生产系统的整个运行过程进行模拟，得出最后的结论。

好。

关键词：问题提出：一个带有船只卸货设备的小港口，任何时间仅能为一艘船只卸货。

船只进港是为了卸货，响铃两艘船到达的时间间隔在15分钟到145分钟变化。

一艘船只卸货的时间有所卸货物的类型决定，在15分钟到90分钟之间变化。

那么，每艘船只在港口的平均时间和最长时间是多少？若一艘船只的等待时间是从到达到开始卸货的时间，每艘船只的平均等待时间和最长等待时间是多少？卸货设备空闲时间的百分比是多少？船只排队最长的长度是多少？问题分析：排队论：排队论(Queuing Theory) ，是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，又称随机服务系统理论，为运筹学的一个分支。

本题研究的是生产系统的效率问题，可以将磨损的工具认为顾客，将打磨机当做服务系统。

【1】M M：较为经典的一种排队论模式，按照前面的Kendall记号定义，//1前面的M代表顾客(工具)到达时间服从泊松分布，后面的M则表示服务时间服从负指数分布，1为仅有一个打磨机。

蒙特卡洛方法：蒙特卡洛法蒙特卡洛(Monte Carlo)方法，或称计算机随机模拟方法，是一种基于“随机数”的计算方法。

这一方法源于美国在第一次世界大战进研制原子弹的“曼哈顿计划”。

该计划的主持人之一、数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法，为它蒙上了一层神秘色彩。

（2）排队论研究的基本问题1.排队系统的统计推断:即判断一个给定的排队系统符合于哪种模型，以便根据排队理论进行研究。

2.系统性态问题:即研究各种排队系统的概率规律性，主要研究队长分布、等待时间分布和忙期分布等统计指标,包括了瞬态和稳态两种情形。

体检排队问题摘要本文讨论的是如何安排顾客的体检顺序，以提高设备利用率、降低顾客等待时间的问题。

本文的创新之处在于利用计算机编程模拟排队模型,结合调查得到的资料，直接利用编程模拟产生了每个人的体检顺序及其相应的时间,使得解答更加周密、全面,而且模拟时只需要输入原始数据即可得到相应的结果,操作简便易行，故而具备较强的实用性。

本文依据顾客的到达人数的随机性,建立了以体检时间最小为目标函数的微分模型，即排队模型，又巧妙地将对原目标函数的求解转化为求每个项目当前排队人数问题,从而运用微分、利用MA ＴLAB 软件编程对个人的体检顺序做出定性的分析,并代入数据予以检验。

问题一，根据建立的模型，利用MATLA Ｂ软件插值拟合体检人员到达率与时间的关系)(t ϕ,再根据到达率,计算出t ∆时间内的到达人数)(t P ∆。

最后,计算出当前每个项目的等待时间()i j i A t S ⨯,通过比较得出等待时间较少的体检顺序。

问题二,利用问题一的模型，本文设计出一组较为合理的数据来验证上述结论。

问题三，我们将团体体检分为将团体视为一个整体，将团体的各队员全部分开情况予以讨论。

经过模型计算,得到团队体检顺序的较优值,其结果见正文。

关键词：插值拟合、M ＡT ＬAB 、体检项目、贪心算法一、问题重述某城市的体检中心每天有许多人前去体检，全部体检项目包括：抽血、内科、外科、B超、五官科、胸透、身高、体重、…等等。

每个人的体检项目可能各不相同，假设每个体检项目的服务时间是确定的，并且只有１个医生值班，每次只能为１个客户服务。

为提高设备利用率、降低客人的等待时间,中心请你帮助完成如下任务：1.请你为某个新来的客人安排他的体检顺序，使其完成需要的全部检查的时间尽量少(在各个体检项目处都可能有人排队等待）;2.设计1组数据来验证上述结论。

3.接待团体客人时,如何安排每个人的体检顺序,使得体检中心能尽快完成任务,设计1组数据来验证该结论。

对那些 j j'的，须在计算时，在 t 上附加 ' 、后再计算费
用即可。
第20页/共38页
为了防止那些还未准备好的飞机，在就绪之前就对其发出起飞 的命令，置一架飞机在它预定起飞时间以前的某窗口起飞的损 失为无穷大，并假如考虑1，2，3中的费用，得到计算费用的 通式：
cij =
K (TA )t (eat 1)ap K (TA ) r (eat 1)ap b
费用: 1.燃料附加费 2.乘客误机费
3.乘客不满意的损失
下面分别建立几个费用的计算公式
第10页/共38页
1.燃料附加费
由于晚点，飞机必须以尽可能快的速度飞行，故燃料随晚点 的时间长短而变化，然而既使晚点，只要为达到最大时限，就 可以以低于最大安全速度飞行。并在起飞后就可近似地保持常 速，因此燃料消耗在时间内应恒定，由于不知道燃料消耗如何 随飞行速度变化，选用了近似的线性函数，即单位时间增加油 耗的费用函数为：
t ：飞机晚点时间，或从 t0 计起，飞机真正起飞时间；
t d : 为一架飞机预定起飞的时间（ d 为 departure）;
TA ：为一架飞机预定到达的时间（A 为 Arrive）;
：为等长的时间间隔时间段的长度，也称为起飞窗口； j ：为第 j 个窗口的标号；
k ：用来决定某飞机单位时间增加燃料费用的常系数，它一般与飞
TA
d vmax
d (TA Td )vav
第15页/共38页
2.乘客误机费
设为乘客耽误了转机而必须补偿的费用，这里取为常数
（假设5）。如果对各人的补偿费确实不同，则取为各人费
用的数学期望----平均值，且重新安排旅程只发生在飞机晚点
时间超过了时限时才发生，故费用如下计算

LINGO函数有了前几节的基础知识，再加上本节的内容，你就能够借助于LINGO建立并求解复杂的优化模型了。

LINGO有9种类型的函数：1．1．基本运算符：包括算术运算符、逻辑运算符和关系运算符2．2．数学函数：三角函数和常规的数学函数3．3．金融函数：LINGO提供的两种金融函数4．4．概率函数：LINGO提供了大量概率相关的函数5．5．变量界定函数：这类函数用来定义变量的取值范围6．6．集操作函数：这类函数为对集的操作提供帮助7．7．集循环函数：遍历集的元素，执行一定的操作的函数8．8．数据输入输出函数：这类函数允许模型和外部数据源相联系，进行数据的输入输出9．9．辅助函数：各种杂类函数4.1基本运算符这些运算符是非常基本的，甚至可以不认为它们是一类函数。

事实上，在LINGO中它们是非常重要的。

4.1.1算术运算符算术运算符是针对数值进行操作的。

LINGO提供了5种二元运算符：＾乘方﹡乘／除﹢加﹣减LINGO唯一的一元算术运算符是取反函数“﹣”。

这些运算符的优先级由高到底为：高﹣（取反）＾﹡／低﹢﹣运算符的运算次序为从左到右按优先级高低来执行。

运算的次序可以用圆括号“（）”来改变。

例4.1算术运算符示例。

2﹣5／3，(2﹢4)／5等等。

4.1.2逻辑运算符在LINGO中，逻辑运算符主要用于集循环函数的条件表达式中，来控制在函数中哪些集成员被包含，哪些被排斥。

在创建稀疏集时用在成员资格过滤器中。

LINGO具有９种逻辑运算符：#not#否定该操作数的逻辑值，＃not＃是一个一元运算符#eq#若两个运算数相等，则为true；否则为flase#ne# 若两个运算符不相等，则为true；否则为flase#gt# 若左边的运算符严格大于右边的运算符，则为true；否则为flase#ge#若左边的运算符大于或等于右边的运算符，则为true；否则为flase#lt#若左边的运算符严格小于右边的运算符，则为true；否则为flase#le#若左边的运算符小于或等于右边的运算符，则为true；否则为flase#and#仅当两个参数都为true时，结果为true；否则为flase#or# 仅当两个参数都为false时，结果为false；否则为true这些运算符的优先级由高到低为：高#not##eq# #ne# #gt# #ge# #lt# #le#低#and# #or#例4.2逻辑运算符示例2 #gt#3 #and#4 #gt# 2，其结果为假（0）。

排队论（Queueing Theory）
现实生活中的实例：
进餐馆就餐 到图书馆借书 去售票处购票 在车站等车等等
课件
2
一、排队系统的特征及排队论：
顾客为了得到某中服务而到达系统，若不能获得服 务而允许排队等待，则加入等待队伍，待获得服务后离
开系统。
课件
3
排队的形式：
顾客到达 队列 服务完成后离去 服务台

服务台1 顾客到达 队列

队列1
服务台2 服务台s
服务完成后离去

顾客到达
队列2 队列s



服务台1 服务台2

服务完成后离去 服务完成后离去 服务完成后离去


服务台s 课件
4
随机服务系统：
排队系统 输入 来源 顾客 队列 服务机构 服务完离开
课件
5
二、排对系统的描述
系统由三个部分组成：
输入过程 排队和排队规则 服务机制

M/D/1


D/M/1


M/E k/1

课件
30
结束语


排队论是专门研究带有随机因素，产生 拥挤现象的优化理论。也称为随机服务 系统。 排队论应用十分广泛。
课件
31
n 1
1
因此：
pn (1 )
n
n 0,1,
课件
23
②几个主要数量指标 平均队长：
L npn n(1 )
n n 0 n 0



1


平均排队长：
Lq (n 1) pn L (1 p0 ) L

【关键字】问题本科毕业设计论文设计(论文)题目 ______食堂窗口设置问题的研究______指导教师姓名___________ 丁晓东__________________学生姓名 _____________林挺挺________________学生学号 __________0110_____________院系_______理学院_________专业____数学与应用数学_____班级_______应数1103_______食堂窗口设置问题的研究i学生姓名：林挺挺指导教师：丁晓东浙江工业大学理学院摘要本文针对食堂窗口设置问题，首先对统计数据利用matlab编程和spss两种软件进行泊松分布检验。

通过求均值处理并剔除误差较大的数据后可得到所有数据都符合泊松分布。

然后基于排队论理论，结合层次分析法的思想，建立了食堂人流模型，并且借鉴等待制排队模型（M/M/C模型）提出本题的四个窗口合理性分析模型。

此外，由于所给数据的局限性，还考虑了“食堂开设窗口好坏”的评价模型，给出合理评价准则。

并在此基础上分析了各时段的原始人流量数据所对应的最佳应当开放的窗口数，以此来预测之后各时间段的窗口最佳开放数量。

关键词：排队论泊松分布层次分析法Research on the problem of setting up the dining room windowStudent: Lin Tingting Advisor: Dr. Ding XiaodongCollege of of TechnologyAbstractThis thesis is aimed at the problem of setting up the dining room window. Firstly，the statistical data is tested by MATLAB and SPSS two softwares. After the mean processing and deleting the error of the large data, we can find that all the data is in the Poisson distribution. Then based on queuing theory, combinediiwith the idea of analytic hierarchy process (AHP), established the flow model of the canteen, and reference wait queuing model (M / M / C) put forward the four window analyses the rationality of the model. In addition, because of the limitations of the data, the evaluation model of the open window is considered, and the reasonable evaluation criteria is given. Based on this, the best open window number is analyzed, which can predict the best open number of windows for each time period..The key word: Queuing theory Poisson distribution Analytic hierarchy process目录iAbstract ............................................ 错误!未定义书签。

Matlabyalmip⼯具编写⾃动驾驶模型预测控制（MPC）代码⽬录前⾔在⽆⼈驾驶的运动控制中，模型预测控制（MPC）算法得到了⼴泛使⽤，龚建伟的《⽆⼈驾驶车辆模型预测控制》⼀书对MPC算法进⾏了细致的讲解，并提供了代码，⾮常值得参考和学习。

但书中各系数矩阵的推导对于初学者来说极难理解，代码结构也过于复杂，改动代码容易报错。

采⽤yalmip⼯具可以很⼤程度简化代码，利于初学者对应理解MPC公式与代码，代码修改起来也⾮常容易。

⼀、yalmip简介yalmip是由Lofberg开发的⼀种免费的优化求解⼯具。

它是⼀个建模⼯具，甚⾄可以称为⼀种“语⾔”，通过这种“语⾔”来描述模型，然后再调⽤其他求解器（如quadprog、gurobi、fmincon等）来求解模型。

其最⼤特⾊在于集成许多外部的优化求解器，形成⼀种统⼀的建模求解语⾔，提供了Matlab的调⽤API，减少学习者学习成本。

⼆、车辆模型1.车辆运动学模型2.离散化3.线性化这⾥使⽤针对状态轨迹的线性化⽅法（《⽆⼈驾驶车辆模型预测控制》(第⼆版)第五章代码所使⽤的⽅法），与第三、四章的存在参考系统的性线化⽅法略有不同，本质上区别不⼤，具体可以参考《⽆⼈驾驶车辆模型预测控制》(第⼀版)的介绍。

若使⽤较复杂的模型，可借助jacobian函数求解雅可⽐矩阵A,B三、MPC 优化问题定义程序⽬标是对轨迹进⾏跟踪，设计成本函数第⼀项：状态量与参考轨迹误差的平⽅，第⼆项：控制量的平⽅。

约束依次为初始状态约束，车辆运动学模型，控制量约束，控制增量约束。

优化问题如下所⽰：四、Matlab 代码本⽂编写的代码主要为了对标《⽆⼈驾驶车辆模型预测控制》（第⼆版）第四章的代码，主体参照S函数形式编写，便于结合Carsim 使⽤。

以下主要介绍yalmip编写的MPC计算函数：1.函数输⼊1syms x y phi delta v L T 2%x ：横坐标；y ：纵坐标；phi:航向⾓；delta ：前轮偏⾓；3%v ：速度；L ：轴距；T ：离散时间4kesi=[v*cos(phi);v*sin(phi);v*tan(delta)/L]*T+[x;y;phi];%离散化⽅程5X=[x,y,phi];%状态量6u=[v,delta];%控制量7A=jacobian(kesi,X)8B=jacobian(kesi,u)A,B：模型（系统）矩阵；Q,R：权重矩阵；N：控制步长；kesi：当前状态量和控制量；state_k1：下⼀时刻状态量；umin,umax,delta_min,delta_max：控制量和控制增量约束矩阵；Ref： 参考轨迹；MPC_solver：求解器。

传染病传播模型（SIS）Matlab代码function spreadingability=sir(A,beta,mu)for i=1:length(A)for N=1:50%随机次数InitialState=zeros(length(A),1);InitialState(i)=1;time=5;%传播时间I(N,:)=sire(A,InitialState,beta,mu,time);endspreadingability(i,1)=mean(mean(I));%节点i的传播能⼒endendfunction I=sire(A,InitialState,beta,mu,time)%******************************% A邻接矩阵% InitialState初始感染状态% beta感染率% mu恢复率% time传播时间%*****************************Infected=InitialState;recover=[];Infected_temp=zeros(size(Infected));for t=1:1:time %⼀共进⾏时长time的演化%%%若i是易感节点, 则对i以⼀定概率进⾏传染x1=find(Infected==0);a1=rand(size(x1));b1=beta*(A(x1,:)*Infected);%已经被感染的节点以⼀定概率去感染其他节点xx1=setdiff(find(a1<b1),recover);Infected_temp(x1(xx1))=1;%不是recover的节点以⼀定概率被感染xx2=setdiff(find(a1>=b1),recover);Infected_temp(x1(xx2))=0;%对不是recover且没被感染的其他节点保留易感状态%%%若i是染病节点, 则对i以⼀定概率进⾏移除（recover）x2=find(Infected==1); %如果是已经被感染的节点a2=rand(size(x2));xx3=find(a2<mu);%对染病节点以⼀定概率进⾏recoverrecover=[recover;xx3];%更新被recover节点;xx4=find(a2>=mu);Infected_temp(x2(xx4))=1;%余下未被recover的节点仍保留感染能⼒Infected=Infected_temp;I(t)=sum(Infected); %记录每个时间步的染病节点数量endend susceptible-infected-recovered（SIR）传染病模型常⽤来计算节点影响⼒标准测量。

p
k 0

k
1
n 1 1k 1n 1－ m n 1 1 ] [ 1 k 0 k ! n ! p0 k n n 1 n 1 [ ( m n 1)] k 0 k ! n !
1 1
3 多服务窗混合制排队模型M/M/n/m
0 1 2

n-1
n n
n+1 n
n+2 n

2
3
(n-1)
n
服务窗还有空闲
n个服务窗全忙
2 多服务窗等待制排队模型M/M/n
求平稳分布
令1 , ， 1 n
1k nk k p0 p0 k! k! pk k n n 1 p k p 0 0 n! n !n k n


(n 1)!(n 1 )
1n p0
2

n n!(1 )2
1n p0
平均系统内逗留时间
Ws Ls

Ws Wq W服 Wq
1

2 多服务窗等待制排队模型M/M/n
来到系统的顾客必须排队等待的概率
nn k C (n, ) C (n, 1 ) pk p0 k n k n n !
p
k 0
m
k
1
n 1
k C k! k p0 [ Cm 1k m k n 1k ]1 k 0 k n n !n
4 多服务窗闭合式排队模型M/M/n/m/m
目标参量
Lq (k n) pk
k n m m
Ls kpk
k 0