哈工大-计算机图形学-作业-圆弧的算法描述

绘弧的算法绘弧是计算机图形学中的常见操作，用于绘制曲线或弧线形状。

在计算机图形学中，有多种算法可以实现绘制弧线的功能，本文将介绍其中几种常见的算法。

一、中点画圆法中点画圆法是一种常见的绘制圆弧的算法。

该算法通过计算圆弧上每个点的坐标来实现绘制。

具体步骤如下：1. 计算圆弧的起点和终点的坐标，以及圆心的坐标。

2. 计算圆弧的半径。

3. 初始化绘制点的坐标。

4. 根据圆弧的起点和终点坐标，确定绘制的起始角度和终止角度。

5. 循环遍历绘制点，通过计算每个点对应的角度和半径，计算出点的坐标。

6. 绘制圆弧。

二、贝塞尔曲线贝塞尔曲线是一种常用的曲线绘制算法，可以绘制平滑的曲线。

贝塞尔曲线可以通过控制点来定义曲线的形状。

常见的贝塞尔曲线有二次贝塞尔曲线和三次贝塞尔曲线。

1. 二次贝塞尔曲线二次贝塞尔曲线由起点、终点和一个控制点来定义。

通过调整控制点的位置，可以改变曲线的形状。

2. 三次贝塞尔曲线三次贝塞尔曲线由起点、终点和两个控制点来定义。

通过调整控制点的位置，可以改变曲线的形状。

贝塞尔曲线的绘制可以通过递归算法来实现。

具体步骤如下：1. 计算贝塞尔曲线上每个点的坐标。

2. 根据控制点的位置，计算出曲线上每个点的坐标。

3. 绘制贝塞尔曲线。

三、Bresenham算法Bresenham算法是一种直线绘制算法，也可以用于绘制圆弧。

该算法基于直线的斜率和误差修正来计算圆弧上的点。

具体步骤如下：1. 计算圆弧的起点和终点的坐标，以及圆心的坐标。

2. 初始化绘制点的坐标。

3. 计算圆弧的半径。

4. 根据圆弧的起点和终点坐标，确定绘制的起始角度和终止角度。

5. 根据起始角度和终止角度，计算圆弧上每个点的坐标。

6. 绘制圆弧。

以上是几种常见的绘制弧线的算法，每种算法都有其适用的场景和特点。

在实际应用中，可以根据具体需求选择合适的算法进行绘制。

通过合理选择和优化算法，可以高效地绘制出各种形状的弧线。

绘弧的算法在计算机图形学和图像处理中具有重要的应用价值，为实现各种美观的图形效果提供了基础支持。

工件圆弧半径怎么计算公式在机械加工中，圆弧是一种常见的形状，它在很多工件中都会出现。

在进行机械加工时，我们常常需要计算工件圆弧的半径，以便确定加工工艺和工艺参数。

本文将介绍工件圆弧半径的计算公式及其应用。

工件圆弧半径的计算公式可以根据圆弧的几何特征和加工要求来确定。

一般来说，工件圆弧的半径可以通过以下几种方式来计算：1. 根据圆弧的几何特征计算。

当我们已知圆弧的圆心角和弧长时，可以通过以下公式来计算圆弧的半径：R = L / θ。

其中，R表示圆弧的半径，L表示圆弧的弧长，θ表示圆弧的圆心角。

2. 根据加工要求计算。

在实际加工中，有时候我们需要根据工件的设计要求来确定圆弧的半径。

例如，当我们已知工件的外轮廓和内轮廓时，可以通过以下公式来计算圆弧的半径：R = (D1 D2) / 2。

其中，R表示圆弧的半径，D1表示外轮廓的直径，D2表示内轮廓的直径。

3. 根据加工工艺计算。

在某些情况下，我们需要根据加工工艺来确定圆弧的半径。

例如，当我们已知工件的切削速度和进给速度时，可以通过以下公式来计算圆弧的半径：R = Vc / (n f)。

其中，R表示圆弧的半径，Vc表示切削速度，n表示主轴转速，f表示进给速度。

以上是几种常见的工件圆弧半径计算公式，它们可以根据不同的情况来确定工件圆弧的半径。

在实际加工中，我们需要根据具体情况来选择合适的计算公式，并结合加工要求和工艺参数来确定工件圆弧的半径。

工件圆弧半径的计算公式不仅可以帮助我们确定加工工艺和工艺参数，还可以帮助我们进行工件设计和加工工艺优化。

因此，掌握工件圆弧半径的计算方法对于提高加工效率和加工质量具有重要意义。

在实际工程中，我们还需要注意工件圆弧半径的计算精度和计算方法的适用范围。

有时候，我们需要结合实际情况进行修正和调整，以确保计算结果的准确性和可靠性。

总之，工件圆弧半径的计算公式是机械加工中的重要内容，它对于确定加工工艺和工艺参数具有重要意义。

我们需要根据具体情况选择合适的计算方法，并结合实际情况进行修正和调整，以确保计算结果的准确性和可靠性。

哈斯系统编程圆弧
摘要：
1.哈斯系统简介
2.哈斯系统编程圆弧的方法
3.哈斯系统编程圆弧的优点
4.哈斯系统编程圆弧的应用案例
正文：
哈斯系统（Hass System）是一款集设计、编程、控制于一体的数控系统，广泛应用于各类数控机床。

哈斯系统的强大功能，使得用户可以轻松地实现各种复杂的加工工艺，特别是在编程圆弧方面，哈斯系统表现出了极高的灵活性和便捷性。

哈斯系统编程圆弧的方法非常简单。

用户只需在编程界面中输入相应的圆弧指令，系统便会自动计算出圆弧的各个参数，如圆心坐标、半径、起始角度和终止角度等。

此外，哈斯系统还支持G 代码编程，用户可以通过编写G 代码指令，实现对圆弧的精确控制。

哈斯系统编程圆弧具有诸多优点。

首先，哈斯系统可以实现对圆弧的精确控制，提高了加工精度。

其次，系统可以根据加工工艺的需求，自动调整圆弧参数，提高了加工效率。

最后，哈斯系统的编程界面友好直观，降低了操作难度，使得编程人员能够更加专注于工艺设计和优化。

在实际应用中，哈斯系统编程圆弧的案例比比皆是。

例如，在加工汽车零部件时，需要对某些零件进行弧形槽的加工。

利用哈斯系统的圆弧编程功能，可以轻松地实现对弧形槽的精确加工，确保零件的尺寸精度和表面质量。

总之，哈斯系统在编程圆弧方面具有显著的优势，可以有效提高数控机床的加工精度和效率。

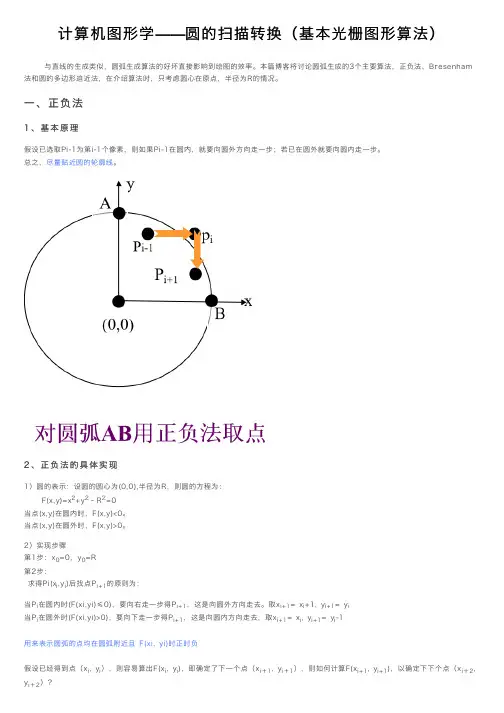
计算机图形学——圆的扫描转换（基本光栅图形算法）与直线的⽣成类似，圆弧⽣成算法的好坏直接影响到绘图的效率。

本篇博客将讨论圆弧⽣成的3个主要算法，正负法、Bresenham 法和圆的多边形迫近法，在介绍算法时，只考虑圆⼼在原点，半径为R的情况。

⼀、正负法1、基本原理假设已选取Pi-1为第i-1个像素，则如果Pi-1在圆内，就要向圆外⽅向⾛⼀步；若已在圆外就要向圆内⾛⼀步。

总之，尽量贴近圆的轮廓线。

2、正负法的具体实现1）圆的表⽰：设圆的圆⼼为(0,0),半径为R，则圆的⽅程为：F(x,y)=x2+y2–R2=0当点(x,y)在圆内时，F(x,y)<0。

当点(x,y)在圆外时，F(x,y)>0。

2）实现步骤第1步：x0=0，y0=R第2步：求得Pi(x i,y i)后找点P i+1的原则为：当P i在圆内时(F(xi,yi)≤0)，要向右⾛⼀步得P i+1，这是向圆外⽅向⾛去。

取x i+1= x i+1, y i+1= y i当P i在圆外时(F(xi,yi)>0)，要向下⾛⼀步得P i+1，这是向圆内⽅向⾛去，取x i+1= x i, y i+1= y i-1⽤来表⽰圆弧的点均在圆弧附近且 F(xi, yi)时正时负假设已经得到点（x i, y i），则容易算出F(x i, y i)，即确定了下⼀个点（x i＋1, y i＋1），则如何计算F(x i+1, y i+1)，以确定下下个点（x i＋2, y i＋2）？分为两种情况：右⾛⼀步后：x i+1=x i+1，y i+1=y i，此时：F(x i+1, y i+1)=x i+12+y i2-R2=x i2+y i2-R2+2x i+1 = F(x i, y i)+2x i+1下⾛⼀步后：x i+1=x i，y i+1=y i-1， 此时：F(x i+1, y i+1)=x i2+（y i-1)2-R2= F(x i, y i)-2y i+1由此可得：确定了F(xi+1, yi+1)之后，即可决定下⼀个点(xi+2, yi+2)，选择道理同上。

halcon 计算圆弧xld的中心Halcon是一款强大的图像处理软件，可以用于计算圆弧的中心。

在本文中，我们将介绍如何使用Halcon计算圆弧的中心，并通过实例详细说明其原理和使用方法。

在使用Halcon计算圆弧中心之前，我们首先需要了解什么是圆弧。

圆弧是由一段弧线所组成的，它是一个圆的一部分。

圆弧有两个关键的参数，即起始角度和终止角度，通过这两个参数我们可以确定一个圆弧。

而圆弧的中心则是圆心和圆弧的起始点和终止点之间的中点。

在Halcon中，我们可以使用xld（eXtended Line Description）数据结构来表示圆弧。

xld是一种高级的数据结构，用于表示线和弧线等几何对象。

xld中包含了圆弧的起始点、终止点、中心点和半径等信息，我们可以通过这些信息来计算圆弧的中心。

下面我们通过一个实例来演示如何使用Halcon计算圆弧的中心。

假设我们有一张图像，其中包含了一个圆弧。

我们首先需要对图像进行预处理，以便找到圆弧的边缘。

在Halcon中，我们可以使用边缘检测算法（如Sobel算子或Canny算子）来检测图像的边缘。

接下来，我们可以使用Halcon提供的圆弧拟合算法来拟合圆弧的形状。

通过圆弧拟合算法，我们可以得到圆弧的起始点、终止点、中心点和半径等信息。

我们可以使用Halcon提供的函数来计算圆弧的中心。

具体而言，我们可以使用get_circle_center函数来计算圆弧的中心坐标。

该函数需要传入圆弧的起始点、终止点和中心点作为参数，并返回圆弧的中心坐标。

在实际使用中，我们可以将以上过程封装成一个函数，以便在需要时调用。

通过调用该函数，我们可以方便地计算圆弧的中心，并将其用于后续的处理和分析。

本文介绍了如何使用Halcon计算圆弧的中心。

通过对图像的预处理、圆弧拟合和中心计算等步骤，我们可以准确地得到圆弧的中心坐标。

Halcon作为一款功能强大的图像处理软件，为我们提供了便捷而高效的计算工具，使得图像处理工作更加简单和准确。

圆弧的公式圆弧是我们在日常生活及学习中经常接触到的几何图形之一。

在许多领域，圆弧的公式是非常重要的。

在本文中，将讨论圆弧的公式及其应用。

首先，让我们看一下圆弧的定义。

一个圆弧是位于圆周上的一段弧线，可以用圆心角度数或圆的弧度衡量。

一个完整的圆弧所包含的圆心角是360度或2π弧度。

当我们知道圆的半径和圆心角度数或弧度时，我们可以使用以下公式计算圆弧的长度：$Length = r\theta$其中r是圆的半径，而$\theta$是圆心角的度数或弧度。

例如，如果一个圆的半径为5 cm，圆心角为60度，则圆弧的长度为：$Length = 5\times\frac{60}{360}\times 2\pi = \frac{5}{3}\pi \text{ cm}$另一个方法是将度数转换为弧度，然后使用以下公式：$Length = r\theta$其中r是圆的半径，而$\theta$是圆心角度数转换为弧度后的值。

例如，如果一个圆的半径为8 cm，圆心角为120度，则圆弧的长度为：$Length = 8\times\frac{120}{360}\times \pi = \frac{4}{3}\pi \text{ cm}$圆弧的长度可以用于计算圆周的长度。

当我们知道圆的半径时，可以使用以下公式计算圆周的长度：$Circumference = 2\pi r$例如，如果一个圆的半径为10 cm，则其周长为：$Circumference =2\pi\times10=20\pi \text{ cm}$圆弧的另一个应用是在建筑设计中。

例如，在设计拱门或穹顶的时候，需要计算圆弧的长度和半径。

圆弧的长度还可以用于计算轮胎的周长、电线的长度等等。

除了圆弧的长度，我们还可以计算圆弧的面积。

当我们知道圆弧的半径和圆心角时，可以使用以下公式计算圆弧的面积：$Area = \frac{1}{2}r^2(\theta-\sin\theta)$其中r是圆的半径，而$\theta$是圆心角的度数或弧度。

实验三圆生成算法的实现班级 学号 姓名 分数一、实验目的和要求：通过圆生成算法的上机调试，掌握：1．VC++图形函数的使用方法；2．圆和椭圆弧的生成原理；3．理解圆生成的基本原理，掌握几种常见的圆生成算法。

二、实验内容：1、以函数形式编写圆的生成算法，然后在VCAD绘图小系统中的绘图----圆子菜单下找到合适的程序修改点，通过调试来验证你编写的画圆算法的正确性。

2、以函数形式编写角度DDA椭圆弧生成算法，然后在VCAD 绘图小系统中的绘图----圆弧子菜单下找到合适的程序修改点，将本实验要求你编写的画圆弧算法插入工程文件中，通过调试来验证你编写的画圆弧算法的正确性。

3、利用中点画图算法，在屏幕上生成任意一段1/8弧。

利用图的对称性，将(1)题生成的圆弧扩展为一个整圆。

三、实验结果分析：1、圆被定义为到给定中心位置(x,y)距离为r的点集2、比较三种算法的结果：像素逼近效果由好到差依次为：B算法、DDA算法、中点算法执行速度由快到慢依次为：中点算法、DDA算法、B算法1.程序代码：void CMyView::DrawCir(int Start, int R, int a, int b){CDC* pDc=GetDC();int x,y;int e=Start-R;x=Start;y=R;pDc->SetPixel(y+a,x+b,RGB(0,0,255));pDc->SetPixel(-y+a,x+b,RGB(0,0,255));pDc->SetPixel(y+a,-x+b,RGB(0,0,255));pDc->SetPixel(-y+a,-x+b,RGB(0,0,255)); pDc->SetPixel(x+a,y+b,RGB(0,0,255));pDc->SetPixel(-x+a,y+b,RGB(0,0,255));pDc->SetPixel(x+a,-y+b,RGB(0,0,255));pDc->SetPixel(-x+a,-y+b,RGB(0,0,255)); if(e<0){e=e+2*x+3;x++;}pDc->SetPixel(x,y,RGB(0,0,255));while(x<y){if(e<0){e=e+2*x+3;x++;}else{e=e+2*(x-y)+5;x++;y--;}pDc->SetPixel(y+a,x+b,RGB(0,0,255)); pDc->SetPixel(-y+a,x+b,RGB(0,0,255)); pDc->SetPixel(y+a,-x+b,RGB(0,0,255)); pDc->SetPixel(-y+a,-x+b,RGB(0,0,255)); pDc->SetPixel(x+a,y+b,RGB(0,0,255)); pDc->SetPixel(-x+a,y+b,RGB(0,0,255)); pDc->SetPixel(x+a,-y+b,RGB(0,0,255)); pDc->SetPixel(-x+a,-y+b,RGB(0,0,255));}}void CMyView::OnDrawCir(){CMyView::DrawCir(0,50,200,300);}2．程序代码：#include<graphics.h>void circlepoints(int x,int y,int color){int m,n,xasp,yasp;float aspectratio;m=200;n=200;getaspectratio(&xasp,&yasp);aspectratio = xasp/yasp;putpixel(x+m,y*aspectratio+n,color);putpixel(y+m,x*aspectratio+n,color);putpixel(-y+m,x*aspectratio+n,color);putpixel(-x+m,y*aspectratio+n,color);putpixel(y+m,-x*aspectratio+n,color);putpixel(x+m,-x*aspectratio+n,color);putpixel(-x+m,-y*aspectratio+n,color);putpixel(-y+m,-x*aspectratio+n,color);}void midpointcircle(int r,int c){int x,y;float d;x=0; y=r; d=5.0/4-r;circlepoints(x,y,c);while(y>x){if(d<=0)d+=2.0*x+3;else{d+=2.0*(x-y)+5;y--;}x++;circlepoints(x,y,c);}}main(){int a,b;int graphdriver = DETECT;int graphmode = 0;initgraph(&graphdriver,&graphmode,””);cleardevice( );a= 200; b= 2;midpointcircle(a,b);getch( );closegraph( );}.1.运行结果：2.运行结果：。