course3_1101

《信息检索与利用》实习报告（理工科版）2014--- 2015学年第 1 学期指导教师柳翔学院材料学院班级高分子1101姓名黄健学号 3110705023报告完成日期 2014.12.20 总成绩说明：（1）本报告60分。

报告完成后应将此说明部分（1）至（5）项全部删除再打印成纸质的。

课程结束后八天内由班长按学号收齐交老师。

报告总长不能超过四张纸。

（2）检索式是运用逻辑运算符将检索词连接起来用于检索文献信息的运算式。

CNKI中国知网专业检索示例：CF>=10 AND TI=仿真*成形*(薄板+板材+板料)-金属ANDYE>=2000 NOT JN%(车辆+汽车)；SCI检索举例：ZP=212013 AND AU=zhang yk not (TI=“laser shock”and (TI=steel or TI= aluminum alloy))。

（3）逻辑运算符有：①布尔逻辑运算符：and、or、not、*、+、-；②位置运算符：near、w、pre、n等；③通配符：*、？、$等；④精确匹配算符：“”、{ }等。

注意：不同的数据库所使用的逻辑运算符各不相同。

（4）同学们在检索过程中若自行拟定了某些限定条件（如检索字段、学科范围、期刊类别等），请在“其他限定条件”中注明。

（5）本报告中的中文题录格式可参照国家标准GB/T 7714《文后参考文献著录规则》。

一、中文期刊论文数据库检索（从CNKI中国期刊全文数据库、重庆维普中文科技期刊数据库中任选一个检索）(10分)CNKI中国期刊全文数据库检索年限：_ 2010其他限定条件：无检出篇数：_ 26题录1篇（格式如：[1]张永康，陈菊芳，许仁军.AM50镁合金激光冲击强化实验研究[J].中国激光，2008，35(7)：1068-1072.）[1]廖瑞金,郑升讯,杨丽君,刘玲,叶开颜. 不同温度下XLPE电缆中电树枝的生长特性[J].高电压技术. 2010(10)：70-71二、中文电子图书数据库检索（从超星数字图书馆、书生之家数字图书馆、方正Apabi数字图书馆三个数据库中任选一个检索）（10分）超星数字图书馆检索年限： 2001-2009其他限定条件：无检出篇数： 10题录1篇(格式如：[2]傅璇琮，谢灼华．中国藏书通史[M]．宁波：宁波出版社，2001.）[2] 刘广建 . 超高分子量聚乙烯[M]．北京：化学工业出版社，2001.三、外文期刊数据库检索（工科同学选取EI数据库，理科同学选取SCI数据库）（10分）EI 检索年限：_ 2009-2014其他限定条件：无检出篇数：_ 15题录1篇(author-date格式如：Punj, Girish N., and Richard Staelin. 1983. A Modelof Consumer Information Search Behavior for New Automobiles. Journal of ConsumerResearch 9, no. 4: 366-380.).Yu, Yuan-Shan; Tang, Dao-Bang; Xu, Yu-Juan; Liu, Zhong-Yi; Wu, Ji-Jun.2014. Theaccuracy of rapid detection of bacterial count by bioluminescence assay withCTAB-extracted ATP. Modern FoodScienceandTechnology, v30,n2, p269-273 四、标准文献数据库检索（10分）数据库名称CSSN检出篇数 926题录1篇（格式如：[1]国家质检总局.GB/T 2821-2003齿轮几何要素代号［DB/OL］.(2003-11-25)[2011-9-15] /pages/nv_search/standard_info_details.jsp.其中DB表示的是数据库，OL表示网上资源，2003-11-25是标准发布日期，2011-09-15是检索日期。

Creative Education Studies 创新教育研究, 2020, 8(6), 1097-1101Published Online December 2020 in Hans. /journal/ceshttps:///10.12677/ces.2020.86179“一流课程建设”背景下大学工科专业《灌溉排水工程学》课程教学改革与实践探索张国辉，杨启良*，武亮，王铭明，张祖莲昆明理工大学，云南昆明收稿日期：2020年11月9日；录用日期：2020年12月17日；发布日期：2020年12月23日摘要课程是人才培养的核心要素，课程质量直接决定人才培养质量，依托昆明理工大学水利水电工程专业“灌溉排水工程学”课程，开展一流课程建设背景下大学工科专业《灌溉排水工程学》课程教学改革与实践探索。

完成了线上线下混合式教学、分组讨论教学、科研与教学实践相结合、实际工程案例分析教学、网络教学资源的有效利用等教学改革措施。

同时构建多样性与过程性考核机制，实现教考分离，过程性与多样性考核方式包括期中考试成绩、课堂笔记成绩、积分条成绩、分组讨论成绩等。

实施结果表明该课程教学与考核改革措施总体成效显著，学生学习主动性与课堂活跃度大幅提高，考核成绩显著提高，学生评价与认可度较好。

关键词一流课程建设，灌溉排水工程学，教学改革，考核创新Teaching Reform and Practice Explorationof “Irrigation and Drainage Engineering”Course under the Background ofFirst-Class CourseGuohui Zhang, Qiliang Yang*, Liang Wu, Mingming Wang, Zulian ZhangKunming University of Science and Technology, Kunming YunnanReceived: Nov. 9th, 2020; accepted: Dec. 17th, 2020; published: Dec. 23rd, 2020*通讯作者。

20 13 –2014学年第一学期武昌理工学院试题课程名称：法律英语考生专业班级：法学1101班考试时间： 90 分钟 A √ B 卷开闭√卷请注意：考生不得在试题纸上答题.( 含填空、选择等客观题) 题号I II III IV V 总分阅卷人题分20 20 20 20 20 100得分I. Literary terms translation: English into Chinese. (20 points, 1 point for each)1. bar examination2. constitutional supremacy3.capital punishment4.substantive law5. Equity law6.party7. barrister 8.case method9. Separation of powers 10.litigant11. Trial court mon law13. Tort law 14.civil procedure15. The Senate 16.corporation law17. Judicial system 18.rules of evidence19. Appellate court 20. First degree of murderII. Literary terms translation: Chinese into English. (20 points, 1 point for each) 1.被上诉人 2.模拟法庭3.新政4.检察官起诉书5.最高法院6.财产法7.强制执行8.刑法9.牛津条例10.行政行为11.巡回法院12.专职律师13.听证会14.法律文书15.三级审判制16.正当程序17.普选18.司法审查19.死刑处罚20.不动产III. True or false statements. (20 points, 1 point for each)1.The United States belongs to the common law system.2.Nebraska has adopted a two-tiered system in its judicial system.3.It is quite easy to define law and American Law.4.The three branches of the United States are: the legislative, executive and judicial system.5.The legislature generally makes laws while the jurisdiction enforces laws.6.Federal law courts are superior to state or district law courts.7.Killing another person in self-defense is justifiable homicide.8. There are three factors necessary to create a contract: an offer, acceptance, and consideration.9. Torts include all negligence cases as well as intentional wrongs which result in harm.10. Equity law originally appears as a remedy to common law.11. Contract and agreement are the same according to American contract law.12. Slander is criminal not tortuous according to Federal law.13. House counsel, generally speaking, serves private business concern.14. In America, law school students usually go to work for government for a certain period of time.15. Law school hierarchy exists in almost all American law schools.16. Battery does not belong to intentional tort.17. A judge is not removed from his post even if he has made some gross misconduct.18. In America, the Constitution is superior to all other state laws.19. Two presidents have been impeached in the United States by far.20. There is no general homicide law in Federal Homicide Law.IV. Short questions. (20 points, 5 points for each)1. What are the two main legal systems in the world and what are their main differences?2.What are the basic requirements for admission to practice law in the United States?3. How are laws classified in Anglo-American countries?4. What activities is a lawyer permitted to engage in besides practicing law?V. Passage translation. (20 points, 10 points for each)1.No two legal systems, then, are exactly alike. Each is specific to its country or its jurisdiction. This does not mean, of course, that every legal system is entirely different from every other legal system. Not at all. When two countries are similar in culture and tradition, their legal systems are likely to be similar as well. No doubt the law of E1Salvador is very much like the Law of Honduras. The laws of Australia and New Zealand are not that far apart.2.About Miranda Warning:You have the right to remain silent and refuse to answer questions.Anything you do say may be used against you in a court of law.You have the right to consult an attorney before speaking to the police and to have an attorney present during questioning now or in the future.If you cannot afford an attorney, one will be appointed for you before any questioning if you wish.If you decide to answer questions now without an attorney present you will still have the right to stop answering at any time until you talk to an attorney.。

sname char(20),
ssex char(2),程”表course
Create table course
(
cno char(4) primary key,
cname char(20),
ccredit smallint
);
建立学生选课表sc
Create table sc
(
tno char(6)primary key,
jbgz int,
zwgz int,
bj int,
Foreign key (tno) referencest(tno)
);
4. 用命定在已存在的学生表student中增加一个sdept（系）的新的属性列；
alter table student add sdept char(20);
实验二：创建数据表，修改表结构
一、实验目的：
掌握建立一个数据库表结构的方法和步骤，了解数据库表的基本组成。
二、实验要求：（必做）
硬件：Intel Pentium120或以上级别的CPU，大于16MB的内存。
软件：Windows 95/98/2000操作系统，关系数据库管理系统SQL SERVER 2000。
5. 用命定将学生表student中sname属性列的数据类型修改为变长字符串varchar(10)。
alter table student alter column snamevarchar(10);
6. 在数据库中建立一个临时表
建立一个临时表
create table linshi
(lin int
2.删除该临时表
drop table linshi cascade;
SQL SERVER 2000对CASCADE与RESTRICT处理策越是相同的。

课程考核标准英文《课程考核标准》In an education system, designing an effective course assessment standard is essential to ensure the quality of education and the fairness of evaluation. Course assessment standards determine the criteria for evaluating a student's performance and understanding of the subject matter. It is a necessary tool for educators to measure the effectiveness of the teaching and learning process.The course assessment standard typically includes a combination of various evaluation methods, such as quizzes, exams, projects, presentations, and class participation. These assessment methods are designed to gauge a student's knowledge, skills, and understanding of the course material. The standard also outlines the weightage of each assessment component, which helps in determining the overall grade for the course.In addition, the assessment standard should be transparent and clearly communicated to the students at the beginning of the course. This allows students to understand the expectations and requirements for their performance in the course. It also helps in promoting a sense of fairness and equity among the students.Moreover, the assessment standard should be designed in a way that aligns with the learning objectives of the course. The assessment methods should be relevant to the course content and be able to measure the desired learning outcomes. This ensures that the assessment is meaningful and contributes to the overall learning process.Furthermore, the assessment standard should be reviewed and updated regularly to keep it relevant and up-to-date with the changing educational needs and trends. This includes incorporating feedback from students and educators to improve the assessment methods and criteria.In conclusion, a well-designed course assessment standard is crucial for the effective evaluation of students' performance and understanding of the course material. It ensures fairness, transparency, and alignment with the learning objectives, ultimately contributing to the quality of education.。

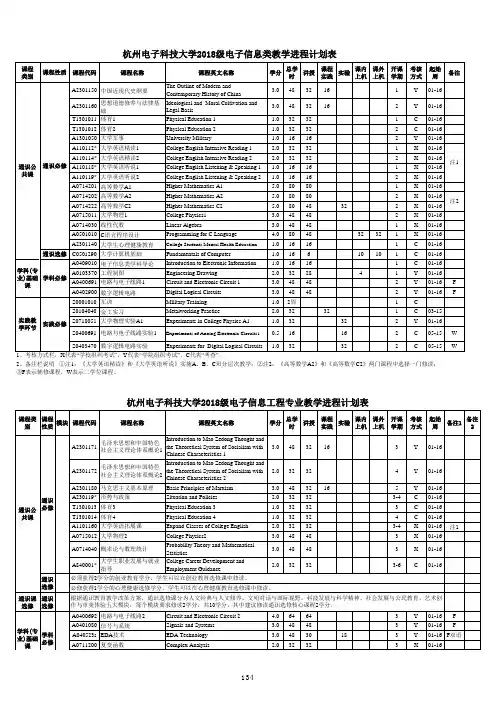
杭州电子科技大学2018级电子信息类教学进程计划表
2、备注栏说明①注1：《大学英语精读》和《大学英语听说》实施A、B、C班分层次教学；②注2：《高等数学A2》和《高等数学C2》两门课程中选择一门修读；
③F表示辅修课程，W表示二学位课程。

杭州电子科技大学2018级电子信息工程专业教学进程计划表
1、考核方式栏，X代表“学校组织考试”，Y代表“学院组织考试”，C代表“考查”。

2、备注栏说明①注1：《大学英语拓展课》为指定选修课程，分为英语技能课、专门用途英语和跨文化交际三类，学生自由选择；②注2：三个模块中任选一个方向修读8学分；
③注3：专业选修课至少修读7学分；④注4：须获得2个课外选修学分；⑤注5：F表示辅修课程，Z表示第二专业课程，W表示第二学位课程，辅修只修读F类课程（要求修读30学分），第二专业修读F+Z课程（要求修读46学分），第二学位修读F+Z+W课程（要求修读61学分）。

• Here is a typical procedure in an audio-lingual course • (1)Student hear a model dialogue • (2) Student repeat each line of dialogue • (3)Certain key words or phrases may be changed • (4)Key structure from the dialogue serves the basis for pattern drills of different kinds • (5) Student practice substitutions in the pattern drills
Audio-lingual Method
外语系 1101班 姜欢
Pare one:
• definition • procedure
Part two:
• background • relative theories • principles
Part three:
• techniques • advantages • disadvantages
• Students were often found to be unable to transfer skills acquired through audio-lingualism to real communication outside the classroom. • The studying procedure is boring and unsatisfying.
• Definition
• The Audio-lingual Method is a method of foreign language teaching which emphasizes the teaching of listening and speaking before reading and writing. • It use dialogues as the main form of language presentation and drills as the main training techniques.

6
7
8
2
2
2
Unit 4 Verbal Communication
CAI & Blackboard 意识和能力，达到有效交流的目的。
communication; to
66
Chapter 4 Common Response
understand the cultural
1．通过学习，学生能够了解语言及非语
Formulas of English and Chinese
assumption
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，通力根1保过据护管生高线产中敷工资设艺料技高试术中卷0资不配料仅置试可技卷以术要解是求决指，吊机对顶组电层在气配进设置行备不继进规电行范保空高护载中高与资中带料资负试料荷卷试下问卷高题总中2体2资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况1卷中下安，与全要过，加度并强工且看作尽护下可1都关能可于地以管缩正路小常高故工中障作资高；料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高，核中或对资者定料对值试某，卷些审弯异核扁常与度高校固中对定资图盒料纸位试，置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置，线高尤弯中其曲资要半料避径试免标卷错高调误等试高，方中要案资求，料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高，技料课中并3术试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术，、以术来管及避架系免等统不多启必项动要方高式案中，；资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资，中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置，作调合并试理且技利进术用行，管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵：导活在。。分对对线于于盒调差处试动，过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调，问试应题技采，术用作是金为指属调发隔试电板人机进员一行，变隔需压开要器处在组理事在；前发同掌生一握内线图部槽纸故内资障，料时强、，电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料，试试线卷卷缆试切敷验除设报从完告而毕与采，相用要关高进技中行术资检资料查料试和，卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

MATERIAL SAFETY DATA SHEETDATE PREPARED: SEP 3, 2009MSDS NO.: 090317P HT 3 SERIES (SEE SECTION 16)SECTION 1 CHEMICAL PRODUCT AND COMPANY IDENTIFICATIONPRODUCT NAME: PHT 3 Series (See Section 16)CHEMICAL NAME:PETROLEUM RESINCHEMICAL FAMILY:PETROLEUM RESIN PRODUCT DESCRIPTION:Pale yellow to amber solidCAS NO.: 68410-16-2_____________________________________________CONTACT ADDRESS:PUYANG HENGTAI PETROCHEMICAL INDUSTRY CO.,LTD WEST SECTION OF PUSHANG ROAD,PUYANG,HENAN,CHINAP.O. Box 457000CONTECT PERSON: WEI HAN_____________________________________________________________________SECTION 2 COMPOSITION/INFORMATION ON INGREDIENTSThe composition of this mixture may be proprietary information. In theevent of a medical emergency, compositional information will be providedto a physician or nurse. _____________________________________________________________________SECTION 3 HAZARDS IDENTIFICATIONPOTENTIAL HEALTH EFFECTSEYE CONTACT:Irritating, and will injure eye tissue if not removed promptly. SKIN CONTACT:Frequent or prolonged contact may irritate. Low order of toxicity. Exposure to hot material may cause thermal burns and adhesion of the solidified product to the skin.INHALATION:Negligible hazard at ambient temperature (-28 to 58 Deg C; 0 to 130 DegC)Vapors and/or aerosols which may be formed at elevated temperatures may be irritating to eyes and respiratory tract.INGESTION:Low order of toxicity._____________________________________________________________________SECTION 4 FIRST AID MEASURESEYE CONTACT:Immediately flush eyes with large amounts of water for at least 15 minutes. Get prompt medical attention.SKIN CONTACT:Flush with large amounts of water; use soap if available. For hot product, immediately immerse in or flush the affected area with large amounts of cold water to dissipate heat. Cover with clean cotton sheeting or gauze and get prompt medical attention. No attempt shouldbe made to remove material from skin or to remove contaminated clothing,as the damaged flesh can be easily torn.INHALATION:In case of adverse exposure to vapors and/or aerosols formed at elevated temperatures, immediately remove the affected victim from exposure. Administer artificial respiration if breathing is stopped. Keep at rest. Call for prompt medical attention.INGESTION:First aid is normally not required.SECTION 5 FIRE-FIGHTING MEASURESFLASH POINT: 290 Deg C. METHOD: ASTM D92 NOTE: MinimumFLAMMABLE LIMITS: NOTE: Not ApplicableAUTOIGNITION TEMP: NOTE: Not ApplicableGENERAL HAZARDSolid material, may burn at or above the flashpoint, and airborne dust may explode if ignited . Static Discharge, material can accumulate static charges which can cause an incendiary electrical discharge .FIRE FIGHTINGUse water spray to cool fire exposed surfaces and to protect personnel. Isolate "fuel" supply to fire. Extinguish the fire by cooling with water spray.DECOMPOSITION PRODUCTS UNDER FIRE CONDITIONSNo unusualSECTION 6 ACCIDENTAL RELEASE MEASURESLAND SPILLEliminate sources of ignition. Prevent additional discharge ofmaterial,if possible to do so without hazard. For small spills implementcleanup procedures; for large spills implement cleanup procedures and,if in public area, keep public away and advise authorities. Recover spilled material and place in suitable containers for recycle or disposal. Consult an expert on disposal of recovered material and ensure conformity to local disposal regulations.WATER SPILLPrevent additional discharge of material, if possible to do so without hazard. Advise authorities if floating material enters a watercourse or sewer. If possible, try to contain floating material . Skim from surface. Consult an expert on disposal of recovered material and ensureconformity to local disposal regulations. _____________________________________________________________________SECTION 7 STORAGE AND HANDLINGELECTROSTATIC ACCUMULATION HAZARDYes, use proper bonding and/or grounding procedure.STORAGE TEMPERATURE Deg C:Ambient LOADING/UNLOADING TEMPERATURE Deg C:Ambient STORAGE/TRANSPORT PRESSURE mmHg:Atmospheric LOADING/UNLOADING VISCOSITY cSt:Not ApplicableSTORAGE AND HANDLING:Keep container closed. Handle and open containers with care. Store ina cool, well ventilated place away from incompatible materials. Do NOT handle or store near an open flame, heat or other sources of ignition. Protect material from direct sunlight. Material will accumulate static charges which may cause an electrical spark (ignition source). Use proper bonding and/or groundingprocedures._____________________________________________________________________SECTION 8 EXPOSURE CONTROLS/PERSONAL PROTECTIONEXPOSURE CONTROLSLocal exhaust ventilation of process equipment may be needed to control particulate exposures to below the recommended exposure limit. See personal protection recommendations.PERSONAL PROTECTIONFor open systems where contact is likely, wear long sleeves, chemical resistant gloves, and chemical goggles. Where contact may occur, wear safety glasses with side shields. Where contact may occur with hot materials, wear thermal resistant gloves, arm protection and a face shield. Where concentrations in air may exceed the limits given in this Section and engineering, work practice or other means of exposure reduction are not adequate.WORKPLACE EXPOSURE GUIDELINESPuyang Ruisen Petroleum resins Co.,Ltd recommends that the lowerexposure levels be observed as reasonable worker protection. THE RECOMMENDED FOLLOWING THRESHOLD LIMIT VALUES:A TWA of 10 mg/m3 for inhalable particulate (total dust) and a TWA of3 mg/m3 for respirable particulate (total dust) for ParticulatesNot Otherwise Classified (PNOC). Puyang Ruisen Petroleum resins Co.,Ltd RECOMMENDS THE FOLLOWINGOCCUPATIONAL EXPOSURE LIMITS: a TWA of 10 mg/m3 total dust for nuisance dust._____________________________________________________________________SECTION 9 PHYSICAL AND CHEMICAL PROPERTIESSPECIFIC GRAVITY at Deg C:0.67 at 43SOLUBILITY IN WATER, wt. % at Deg C:NegligibleVISCOSITY OF LIQUID, cSt at Deg C:Not ApplicableFREEZING/MELTING POINT, Deg C:Not ApplicableBOILING POINT, Deg C:Not Available_____________________________________________________________________SECTION 10 STABILITY AND REACTIVITYSTABILITY:StableCONDITIONS TO AVOID INSTABILITY:Do not heat above 200 C (392 F).HAZARDOUS POLYMERIZATION:Will not occurCONDITIONS TO AVOID HAZARDOUS POLYMERIZATION:Not ApplicableMATERIALS AND CONDITIONS TO AVOID INCOMPATIBILITY:NoneHAZARDOUS DECOMPOSITION PRODUCTS:No unusual_____________________________________________________________________SECTION 11 TOXICOLOGICAL INFORMATIONPlease refer to Section 3 for available information on potential health effects._____________________________________________________________________SECTION 12 ECOLOGICAL INFORMATIONNo specific ecological data are available for this product. Please referto Section 6 for information regarding accidental releases and Section15 for regulatory reporting information._____________________________________________________________________SECTION 13 DISPOSAL CONSIDERATIONSPlease refer to Sections 5, 6 and 15 for disposal and regulatoryinformation.SECTION 14 TRANSPORT INFORMATIONDEPARTMENT OF TRANSPORTATION (DOT):DOT SHIPPING DESCRIPTION: SEE SECTION 16,_____________________________________________________________________SECTION 15 REGULATORY INFORMATIONThis product is listed as a UVCB (Unknown, Variable Composition or Biological) Chemical at CAS Registry Number 68478-07-9_____________________________________________________________________SECTION 16 OTHER INFORMATIONSolid resin is not DOT regulated. DOT SHIPPING DESCRIPTION: ELEVATED TEMPERATURE MATERIAL This MSDS is applicable to the following products:C-1085, C-1100, C-1101R-5100, R-5101A-1085, A-1090, A-1095, A-1100, A-1101, A-1110, A-1120REFERENCE NUMBER: SUPERSEDES ISSUEDATE:PHT-HT-00600October 10, 2009This information relates to the specific material designated and maynot be valid for such material used in combination with any other materialsor in any process. Such information is to the best of our knowledge andbelief, accurate and reliable as of the date compiled. However, norepresentation, warranty or guarantee is made as to its accuracy,reliability or completeness.It is the users responsibility to satisfy himself as to the suitabilityand completeness of such information for his own particular use. We donot accept liability for any loss or damage that may occur from the useof this information nor do we offer warranty against patent infringement.。

pron.某事；某物 pron.没有什么；没有一件东
西
pron.每人；人人；所有人
当然；自然
八年级上册 Unit 1
953 1 anyone
/'eniwʌn/
pron.任何人
954 2 anywhere
/'eniweə/,/'eni wer/
adv.任何地方
955 3 wonderful
/'wʌndə(r)fl/ adj.精彩的；绝妙的
《美国青少年》
八年级上册 Unit 3
1050 1 outgoing
/'aʊtɡəʊɪŋ/
adj.爱交际的；友好的；外向的
1051 2 both
/bəʊθ/
adj.＆porn.两个；两个都
1052 3 better
/'betə(r)/
adj.&adv（good和well的比较
级）较好的（地）；更好的（地）
adj.有才能的；有才干的 adv.真正；确实 v.在意；担忧；关心
关心；在意
v.笑；发笑n.笑声
adj.严肃的；稳重的
n.镜子 n.小孩；年轻人
八年级上册 Unit 3
1070 21 as long as
只要；既然
1071 22 necessary
/'nesəsəri/ /'nesəseri/
adj.必需的；必要的
n.比赛；竞赛；竞争；
1057 8 fantastic
/fæn'tæstɪk/ adj.极好的；了不起的
1058 9 which
/wɪtʃ/
adj.&pron.哪一个；哪一些

Number ConversionCSE2300WObjectivesThis assignment is to design a circuit that convert a4-bit binary number to several represen-tations in different number systems.You will also learn how to use LogicWorks to build and simulate simple digital circuits.More specifically,you will learn the following things.1.Given logic equations,construct a logic circuit with basic gates in LogicWorks.2.Provide input to your circuit using binary switches and display circuit outputs on binaryprobes,and hex and ASCII displays.3.Exhaustively test a circuit to ensure it works as specified.PrerequisitesThis probably is your initial foray into the digital design process.A knowledge of basic gates is necessary and you should also understand number systems.Since you have not learned how to design a digital circuit yet,the logic equations are given for conversions from binary to decimal. Later in this course,you will be able to write and optimize similar equations yourself.You will need LogicWorks software,a web browser,and a PDF reader.We assume you have all these in the lab.BackgroundDecimal,binary,hexadecimal,and octal are some number systems you will use a lot.The decimal number system(base10)is used for dealing with money,measuring,etc.The computer you are using works in binary(base2).But we do not read binary numbers as well as decimal numbers.Therefore,for programmers,octal(base8)or hexadecimal(base16)is commonly used since these systems are easy to convert to/from binary and also easier to read.For example,considering25510,which of‘FF’and‘11111111’would you like to use?Both of them represent the decimal number255.Thefirst is in hexadecimal and the second is in binary.This lab helps you understand how numbers can be represented in one format and then converted to another.Although your digital circuit may work in binary,very often,you need to display values in other systems.It is important to understand how these conversions are performed with hardware.We have discussed the theory behind the number conversions in lectures.The major thing to remember is the meaning of a base or radix for the number system being used.There aremethods that convert numbers from any base to any other,which are helpful in cases like binary to decimal and vice versa.But,in cases involving only binary,octal,and hexadecimal, the conversions become much easier because of the power relationship between their bases.Consider a binary number100110010001.It can be easily converted into an octal by break-ing the bits into groups of three.1001100100014621To perform the hex version you can break the binary bits into groups of four.100110010001991One of the important aspects of number systems(considering integers only)is the use of preceding zeros.For example,a7-bit binary number,1010011does not convert to hexadecimal by taking thefirst(most significant)bits1010,converting to A16,and then converting the remaining3binary bits to316.The correct way is to add a preceding zero to make the number of binary bits a multiple of4.In the previous example,the bits should be put in groups this way:01010011.Converting each group to a hex digit gives you5316.SpecificationsYou will build a circuit that takes a4-bit binary input and displays it in four different number systems:binary,octal,decimal,and hexadecimal.The circuit also displays the decimal number on ASCII displays.Using LogicWorks,you are to build a circuit with the inputs and outputs arranged as shownConnect the inputs to the hexadecimal displays.The4pins on the hexadecimal display correspond to the4bits which make up the hexadecimal digit.The dot on the display indicates the pin corresponding to the least significant bit(LSB).Connect the inputs to the octal displays.Some values represented by a4-bit binary num-ber need two octal digits,so we use two hexadecimal displays.Although we still use hex displays,you want to make sure only valid octal digits are displayed.It is not difficult to figure how to connect inputs to pins.Think about the conversion process from base2to base8and the values you want to see on the displays.Implement the binary-to-decimal conversion.The conversion from binary to decimal isa little bit more complicated.Suppose A,B,C,and D are the four binary input bits.Two digits in the decimal number can then be generated with the following equations.You may ask which of the four bits is the right most bit,i.e.,LSB.Staring at the equations for a moment,you willfigure it out.•10’s digit–1 s=D·C+D·B–2 s=0–4 s=0–8 s=0•1’s digit–1 s=A–2 s=D ·B+D·C·B–4 s=D ·C+C·B–8 s=D·C ·BConnect the inputs to the ASCII displays.Now you know the value of each decimal digit.You need to generate proper ASCII code for ASCII displays.Notice that the ASCII code(see Additional Reference section)for the numbers0-9all begins with the same4bits.So these four bits can be connected to constant0or1.You can use the “GND”and“5V”components in LogicWorks.TestingSince this circuit is designed to convert a4-bit binary number to a different number system, only16possible combinations exist.You should exhaustively try every possible input.A recommendation for systematically testing is to start from‘0’(00002)and count to‘15’(11112). As you input each binary number,make a table as in Table1.Verify that there are no mistakes(either in the circuit or as you copy the screen results to paper).DeliverablesYou will work individually in this lab.You do not need to implement the circuit physically with chips and wires.Once you have tested and debugged you circuit thoroughly in LogicWorks,Table1:ResultsBinary Hex.Oct.Dec.ASCIID C B A L R L R L R0000000100100011....write a report,following the guidelines described in thefirst lab.Make sure your report has a table summarizing the number and type of chips you used,and a table as shown in the testing section.Your report and LogicWorksfiles must be submitted electronically on HuskyCT.You also need to hand in a hard copy of your report to TA by the due date.Additional ReferenceTable2:ASCII Table0123456789A B C D E F 0NUL SOH STX ETX EOT ENQ ACK BEL BS HT LF VT FF CR SO SI 1DLE DC1DC2DC3DC4NAK SYN ETB AN EM SUB ESC FS GS RS US 2!”#$%&’()*+,-./ 30123456789:;<=>? 4@A B C D E F G H I J K L M N O 5P Q R S T U V W X Y Z[\]ˆ6‘a b c d e f g h i j k l m n o 7p q r s t u v w x y z{—}˜。

▪ Complement of a function ▪ Standard forms
• Product terms, sum terms, SOP, POS • Minterms, Maxterms, SOM, POM • Relationship between SOP and SOM? SOM and POM?
replacing 1’s by 0’s and 0’s by 1’s.
• Use DeMorgan's Theorem to complement a function: 1) Interchange AND and OR operators
2).Complement each constant value and literal
2
F1
D7
X
X
D6
X
3
I1=A
D5
X
X
4
D4
X
5
F2
A2 D3 D2
X
A1 D1
XX
6 I 2= B
A0 D0
X
7
8
F3
9 I 3= C
10
F3
F2
F1
F0
11
F4
12
I4
0123456789
Chapter 3
▪ Programmable implementation technologies
• PLA
Chapter 3
▪ Design procedure: specification, formulation, optimization, technology mapping, verification ▪ Technology parameters: fan-in, fan-out, noise margin, cost, propagation delay, power dissipation

什么是二进制在现实生活和记数器中，如果表示数的“器件”只有两种状态，如电灯的“亮”与“灭”，开关的“开”与“关”。

一种状态表示数码0，另一种状态表示数码1，1加1应该等于2，因为没有数码2，只能向上一个数位进一，就是采用“满二进一”的原则，这和十进制是采用“满十进一”原则完全相同。

1＋1＝10，10＋1＝11，11＋1＝100，100＋1＝101，101＋1＝110，110＋1＝111，111＋1＋＝1000，……，可见二进制的10表示二，100表示四，1000表示八，10000表示十六，……。

二进制同样是“位值制”。

同一个数码1，在不同数位上表示的数值是不同的。

如11111，从右往左数，第一位的1就是一，第二位的1表示二，第三位的1表示四，第四位的1表示八，第五位的1表示十六。

所谓二进制，也就是计算机运算时用的一种算法。

二进制只由一和零组成。

比方说吧，你上一年级时一定听说过“进位筒”&amp;“数位筒”吧！十进制是个位上满十根小棒就捆成一捆，放进十位筒，十位筒满十捆就捆成一大捆，放进百位筒……二进制也是一样的道理，个位筒上满2根就向十位进一，十位上满两根就向百位进一，百位上满两根……二进制是世界上第一台计算机上用的算法，最古老的计算机里有一个个灯泡，当运算的时候，比如要表达“一”，第一个灯泡会亮起来。

要表达“二”，则第一个灯泡熄灭，第二个灯泡就会亮起来。

二进制就是等于2时就要进位。

0=00000000 1=00000001 2=00000010 3=00000011 4=00000100 5=000 001016=00000110 7=00000111 8=00001000 9=00001001 10=00001010 ……即是逢二进一，二进制广泛用于最基础的运算方式，计算机的运行计算基础就是基于二进制来运行。

只是用二进制执行运算，用其他进制表现出来。

其实把二进制三位一组分开就是八进制, 四位一组就是十六进制NAMEbin_dec_hex - How to use binary, decimal, and hexadecimal notation.DESCRIPTIONMost people use the decimal numbering system. This system uses ten symbols to represent numbers. When those ten symbols are used up, they start all over again and increment the position to the left. The digit 0 is only shown if it is the only symbol in the sequence, or if it is not the first one.If this sounds cryptic to you, this is what I've just said in numbers:0 1 2 3 4 5 6 7 8 9 10 11 12 13 and so on.Each time the digit nine is incremented, it is reset to 0 and the position before (to the left) is incremented (from 0 to 1). Then number 9 can be seen as ``00009'' and when we should increment 9, we reset it to zero and increment the digit just before the 9 so the number becomes ``00010''. Leading zeros we don't write except if it is the only digit (number 0). And of course, we write zeros if they occur anywhere inside or at the end of a number:"00010" -> " 0010" -> " 010" -> " 10", but not " 1 ".This was pretty basic, you already knew this. Why did I tell it? Well, computers usually do not represent numbers with 10 different digits. They only use two different symbols, namely ``0'' and ``1''. Apply the same rules to this set of digits and you get the binary numbering system:0 1 10 11100101110111100010011010101111001101 and so on.If you count the number of rows, you'll see that these are again 14 different numbers. The numbers are the same and mean the same as in the first list, we just used a different representation. This means that you have to know the representation used, or as it is called the numbering system or base. Normally, if we do not explicitly specify the numbering system used, we implicitly use the decimal system. If we want to use any other numbering system, we'll have to make that clear. There are a few widely adopted methods to do so. One common form is to write 1010(2) which means that you wrote down a number in its binary representation. It is the number ten. If you would write 1010 without specifying the base, the number is interpreted as one thousand and ten using base 10.In books, another form is common. It uses subscripts (little characters, more or less in between two rows). You can leave out the parentheses in that case and write down the number in normal characters followed by a little two just behind it.As the numbering system used is also called the base, we talk of the number 1100 base 2, the number 12 base 10.Within the binary system, it is common to write leading zeros. The numbers are written down in series of four, eight or sixteen depending on the context.We can use the binary form when talking to computers (...programming...), but the numbers will have large representations. The number 65'535 (often in the decimal system a ' is used to separate blocks of three digits for readability) would be written down as1111111111111111(2) which is 16 times the digit 1. This is difficult and prone to errors. Therefore, we usually would use another base, called hexadecimal. It uses 16 different symbols. First the symbols from the decimal system are used, thereafter we continue with alphabetic characters. We get 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. This system is chosen because the hexadecimal form can be converted into the binary system very easily (and back).There is yet another system in use, called the octal system. This was more common in the old days, but is not used very often anymore. As you might find it in use sometimes, you should get used to it and we'll show it below. It's the same story as with the other representations, but with eight different symbols.Binary (2)Octal (8)Decimal (10)Hexadecimal (16)(2) (8) (10) (16)00000 0 0 000001 1 1 100010 2 2 200011 3 3 300100 4 4 400101 5 5 500110 6 6 600111 7 7 701000 10 8 801001 11 9 901010 12 10 A01011 13 11 B01100 14 12 C01101 15 13 D01110 16 14 E01111 17 15 F10000 20 16 1010001 21 17 1110010 22 18 1210011 23 19 1310100 24 20 1410101 25 21 15Most computers used nowadays are using bytes of eight bits. This means that they store eight bits at a time. You can see why the octal system is not the most practical for that: You'd need three digits to represent the eight bits and this means that you'd have to use one complete digit to represent only two bits(2+3+3=8). This is a waste. For hexadecimal digits, you need only two digits which are used completely:(2) (8) (10) (16)11111111 377 255 FFYou can see why binary and hexadecimal can be converted quickly: For each hexadecimal digit there are exactly four binary digits. Take a binary number: take four digits from the right and make a hexadecimal digit from it (see the table above). Repeat this until there are no more digits. And the other way around: Take a hexadecimal number. For each digit, write down its binary equivalent.Computers (or rather the parsers running on them) would have a hard time converting a number like 1234(16). Therefore hexadecimal numbers are specified with a prefix. This prefix depends on the language you're writing in. Some of the prefixes are ``0x'' for C, ``$'' for Pascal, ``#'' for HTML. It is common to assume that if a number starts with a zero, it is octal. It does not matter what is used as long as you know what it is. I will use ``0x'' for hexadecimal, ``%'' for binary and ``0'' for octal. The following numbers are all the same, just their representation (base) is different: 021 0x11 17 %00010001To do arithmetics and conversions you need to understand one more thing. It is something you already know but perhaps you do not ``see'' it yet:If you write down 1234, (no prefix, so it is decimal) you are talking about the number one thousand, two hundred and thirty four. In sort of a formula:1 * 1000 = 10002 * 100 = 2003 * 10 = 304 * 1 = 4This can also be written as:1 * 10^32 * 10^23 * 10^14 * 10^0where ^ means ``to the power of''.We are using the base 10, and the positions 0,1,2 and 3. The right-most position should NOT be multiplied with 10. The second from the right should be multiplied one time with 10. The third from the right is multiplied with 10 two times. This continues for whatever positions are used.It is the same in all other representations:0x1234 will be1 * 16^32 * 16^23 * 16^14 * 16^001234 would be1 * 8^32 * 8^23 * 8^14 * 8^0This example can not be done for binary as that system only uses two symbols. Another example:%1010 would be1 * 2^30 * 2^21 * 2^10 * 2^0It would have been easier to convert it to its hexadecimal form and just translate %1010 into 0xA. After a while you get used to it. You will not need to do any calculations anymore, but just know that 0xA means 10.To convert a decimal number into a hexadecimal you could use the next method. It will take some time to be able to do the estimates, but it will be easier when you use the system more frequently. We'll look at yet another way afterwards.First you need to know how many positions will be used in the other system. To do so, you need to know the maximum numbers you'll be using. Well, that's not as hard as it looks. In decimal, the maximum number that you can form with two digits is ``99''. The maximum for three: ``999''. The next number would need an extra position. Reverse this idea and you will see that the number can be found by taking 10^3 (10*10*10 is 1000) minus 1 or 10^2 minus one.This can be done for hexadecimal as well:16^4 = 0x10000 = 6553616^3 = 0x1000 = 409616^2 = 0x100 = 25616^1 = 0x10 = 16If a number is smaller than 65'536 it will fit in four positions. If the number is bigger than 4'095, you must use position 4. How many times you can subtract4'096 from the number without going below zero is the first digit you write down. This will always be a number from 1 to 15 (0x1 to 0xF). Do the same for the other positions.Let's try with 41'029. It is smaller than 16^4 but bigger than 16^3-1. This means that we have to use four positions. We can subtract 16^3 from 41'029 ten times without going below zero. The left-most digit will therefore be ``A'', so we have0xA????. The number is reduced to 41'029 - 10*4'096 = 41'029-40'960 = 69. 69 is smaller than 16^3 but not bigger than 16^2-1. The second digit is therefore ``0'' and we now have 0xA0??. 69 is smaller than 16^2 and bigger than 16^1-1. We can subtract 16^1 (which is just plain 16) four times and write down ``4'' to get0xA04?. Subtract 64 from 69 (69 - 4*16) and the last digit is 5 --> 0xA045.The other method builds up the number from the right. Let's try 41'029 again. Divide by 16 and do not use fractions (only whole numbers).41'029 / 16 is 2'564 with a remainder of 5. Write down 5.2'564 / 16 is 160 with a remainder of 4. Write the 4 before the 5. 160 / 16 is 10 with no remainder. Prepend 45 with 0.10 / 16 is below one. End here and prepend 0xA. End up with 0xA045.Which method to use is up to you. Use whatever works for you. I use them both without being able to tell what method I use in each case, it just depends on the number, I think. Fact is, some numbers will occur frequently while programming. If the number is close to one I am familiar with, then I will use the first method (like 32'770 which is into 32'768 + 2 and I just know that it is 0x8000 + 0x2 = 0x8002).For binary the same approach can be used. The base is 2 and not 16, and the number of positions will grow rapidly. Using the second method has the advantage that you can see very easily if you should write down a zero or a one: if you divide by two the remainder will be zero if it is an even number and one if it is an odd number:41029 / 2 = 20514 remainder 120514 / 2 = 10257 remainder 010257 / 2 = 5128 remainder 15128 / 2 = 2564 remainder 02564 / 2 = 1282 remainder 01282 / 2 = 641 remainder 0641 / 2 = 320 remainder 1320 / 2 = 160 remainder 0160 / 2 = 80 remainder 080 / 2 = 40 remainder 040 / 2 = 20 remainder 020 / 2 = 10 remainder 010 / 2 = 5 remainder 05 / 2 = 2 remainder 12 / 2 = 1 remainder 01 /2 below 0 remainder 1Write down the results from right to left: %1010000001000101Group by four:%1010000001000101%101000000100 0101%10100000 0100 0101%1010 0000 0100 0101Convert into hexadecimal: 0xA045Group %1010000001000101 by three and convert into octal:%1010000001000101%1010000001000 101%1010000001 000 101%1010000 001 000 101%1010 000 001 000 101%1 010 000 001 000 101%001 010 000 001 000 1011 2 0 1 0 5 --> 0120105So: %1010000001000101 = 0120105 = 0xA045 = 41029Or: 1010000001000101(2) = 120105(8) = A045(16) = 41029(10)Or: 1010000001000101(2) = 120105(8) = A045(16) = 41029At first while adding numbers, you'll convert them to their decimal form and then back into their original form after doing the addition. If you use the other numbering system often, you will see that you'll be able to do arithmetics directly in the base that is used. In any representation it is the same, add the numbers on the right, write down the right-most digit from the result, remember the other digits and use them in the next round. Continue with the second digit from the right and so on:%1010 + %0111 --> 10 + 7 --> 17 --> %00010001will become%1010%0111 +|||||||+-- add 0 + 1, result is 1, nothing to remember||+--- add 1 + 1, result is %10, write down 0 and remember 1|+---- add 0 + 1 + 1(remembered), result = 0, remember 1+----- add 1 + 0 + 1(remembered), result = 0, remember 1nothing to add, 1 remembered, result = 1--------%10001 is the result, I like to write it as %00010001For low values, try to do the calculations yourself, then check them with a calculator. The more you do the calculations yourself, the more you'll find that you didn't make mistakes. In the end, you'll do calculi in other bases as easily as you do them in decimal.When the numbers get bigger, you'll have to realize that a computer is not called a computer just to have a nice name. There are many different calculators available, use them. For Unix you could use ``bc'' which is short for Binary Calculator. It calculates not only in decimal, but in all bases you'll ever want to use (among them Binary).For people on Windows: Start the calculator (start->programs->accessories->calculator) and if necessary click view->scientific. You now have a scientific calculator and can compute in binary or hexadecimal.AUTHORI hope you enjoyed the examples and their descriptions. If you do, help other people by pointing them to this document when they are asking basic questions. They will not only get their answer, but at the same time learn a whole lot more.。

大学计算机课程教学成效评测样卷(一）单项选择题（20题,每题2分，共40分)1、下列数中最大的数是（）。

A）(453）8B）（12B）16C）(20B)12D)(300）102、关于“冯•诺依曼计算机”的结构，下列说法中，正确的是（）。

A）冯•诺依曼计算机仅需要三大部件即可：运算器、控制器和存储器B)一般情况下，个人计算机是由中央处理单元（CPU）、存储器、输入设备和输出设备构成，没有运算器和控制器，所以它不是冯•诺依曼计算机C)以“运算器”为中心的冯•诺依曼计算机和以“存储器”为中心的冯•诺依曼计算机是有差别的：前者不能实现并行利用各个部件，受限于运算器；后者可以实现并行利用各个部件D）冯•诺依曼计算机提出“运算"和“存储”完全没有必要3、关于“程序”和“进程"，下列说法中，不正确的是（）。

A）不管是“程序”，还是“进程”，都是指可以被执行的程序代码B）“程序”是指外存上的程序文件,而“进程”是指装载入内存中的程序代码C）“进程”除了指可以被执行的程序代码外,还指包括装载、分配内存空间等相关的工作内容D）“进程"除了包括可由CPU执行的程序代码外，还包括有关该进程相关状态的描述信息，这些信息由操作系统使用，对“进程”实施管理4、在结构化查询语言SQL中，选择语句:“select * from 数据表where范围”用于从给定关系数据库表中按where指定的查询条件选择数据。

已知如下关系：学生Student(S＃, Sname)，课程Course（C＃, Cname，T#），选课SC(S＃，C#，Score)。

其中S#为学号，Sname为学生姓名，C＃为课程编号,Cname 为课程名，T＃为教师编号,Score为成绩。

则以下SQL语句的执行结果是()。

SELECTSname FROMStudent，SC, Course WHERE Student.S#=SC.S# ANDCourse。

杭州电子科技大学物流管理专业Logistics Management培养方案Undergraduate Education Program管理学院制定2014年6月学院负责人：于俭专业负责人：余福茂物流管理专业一、培养目标物流管理专业培养具有系统的经济学、管理学基础理论，掌握现代物流与供应链系统分析、设计、运营、管理的基本理论、方法与技术，熟悉企业生产经营活动中的物流运作，能在企业、科研院所及政府部门从事供应链设计与管理、物流系统优化及运营管理等方面工作的复合型应用型人才。

物流管理专业期待毕业生几年之内达到以下目标：1.能设计高效的物流解决方案并有效的运用系统优化技术；2.从事物流运作管理工作并能担任物流战略经理角色；3.具有高尚的职业道德；4.在与物流管理与工程、管理科学与工程、工商管理或相关领域里成功就业或学习研究生课程；5.通过继续教育或其他终身学习渠道增加知识和提升能力；6.为当地的、本国的、全球的企事业单位服务。

二、毕业要求本专业对于学生的毕业要求如下（1）掌握马克思主义的世界观、方法论，树立正确的世界观、人生观、价值观，养成理性分析问题的能力。

（2）具有运用物流管理与工程所需的经济学、管理学、自然科学及人文社会科学知识的能力。

（3）具有运用物流管理与工程基础知识和物流及供应链管理、设计与优化知识解决问题的能力。

（4）具有一定的物流管理与工程实践和社会实践经历，了解物流管理与工程领域前沿技术及发展趋势，了解物流行业法规，能正确认识物流业务运作对社会的影响。

（5）掌握文献检索、资料查询及运用现代信息技术获取相关信息的基本方法。

（6）具有一定的组织管理能力、表达能力和人际交往能力以及团队协作能力。

（7）具有对终身学习的正确认识、学习能力及适应社会发展能力。

（8）掌握一门外语，能够比较熟练地阅读和理解外文本专业资料，初步具有国际化视野。

（9）了解体育运动的基本知识，初步掌握锻炼身体的基本技能，养成科学锻炼身体的习惯，达到大学生体育合格标准。