
5次拉格朗日插值多项式函数%% 求取五次Lagrange多项式L5(x).
clear;clc;
X = [0.4 0.55 0.65 0.80 0.95 1.05];
Y = [0.41075 0.57815 0.69675 0.90000 1.000000 1.25382]; % 求取插值基函数:L0_(x).
syms x
la_0 = 1;
for ii = 2:length(X)
if(ii == 1)
continue
else
L_0 = (x-X(ii))/(X(1)-X(ii));
la_0 = la_0*L_0;
end
end
L0_x = collect(la_0);
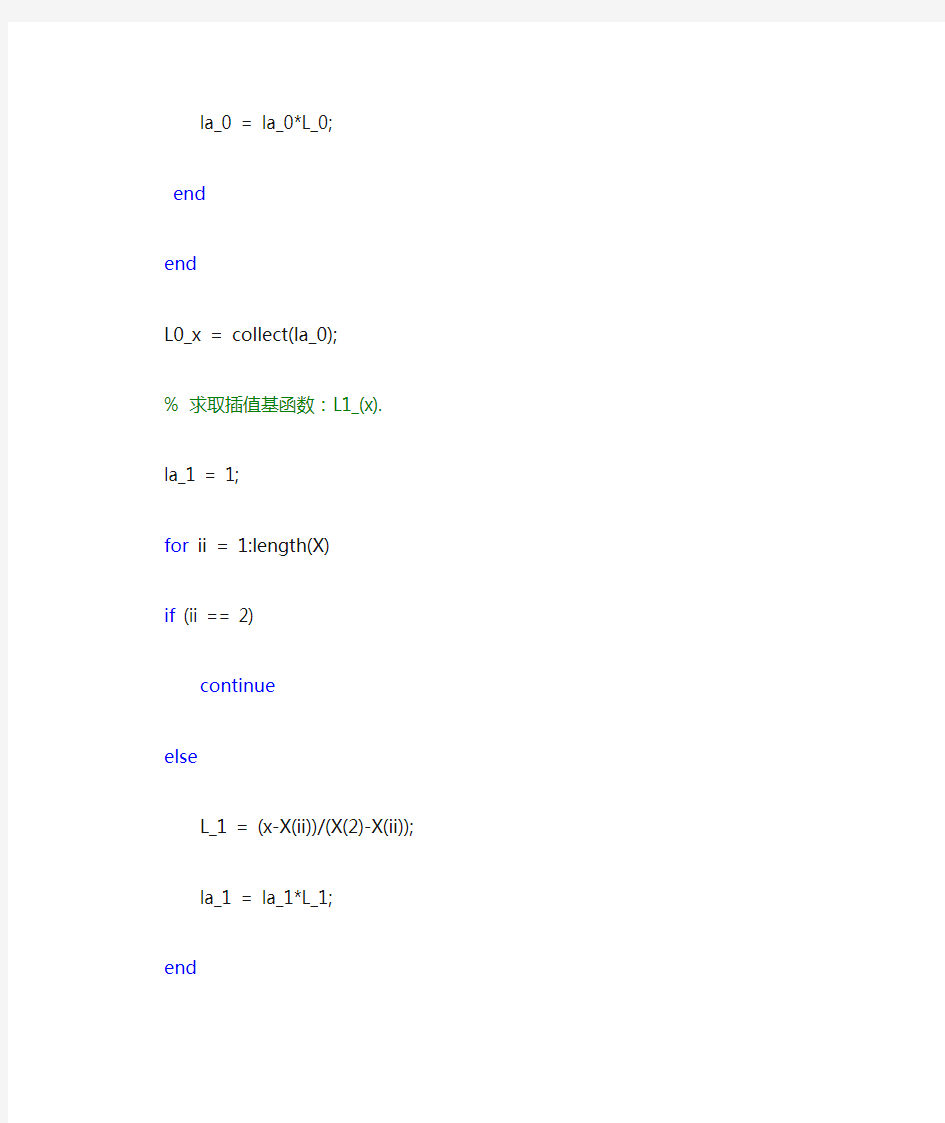
% 求取插值基函数:L1_(x).
la_1 = 1;
for ii = 1:length(X)
if (ii == 2)
continue
else
L_1 = (x-X(ii))/(X(2)-X(ii));
la_1 = la_1*L_1;
end
end
L1_x = collect(la_1);
% 求取插值基函数:L2_(x).
la_2 = 1;
for ii = 1:length(X)
if (ii == 3)
continue
else
L_2 = (x-X(ii))/(X(3)-X(ii));
la_2 = la_2*L_2;
end
end
L2_x = collect(la_2);
% 求取插值基函数:L3_(x).
la_3 = 1;
for ii = 1:length(X)
if (ii == 4)
continue
else
L_3 = (x-X(ii))/(X(4)-X(ii));
la_3 = la_3*L_3;
end
end
L3_x = collect(la_3);
% 求取插值基函数:L4_(x).
la_4 = 1;
for ii = 1:length(X)
if (ii == 5)
continue
else
L_4 = (x-X(ii))/(X(5)-X(ii));
la_4 = la_4*L_4;
end
end
L4_x = collect(la_4);
% 求取插值基函数:L5(x).
la_5 = 1;
for ii = 1:length(X)
if (ii == 6)
continue
else
L_5 = (x-X(ii))/(X(6)-X(ii));
la_5 = la_5*L_5;
end
end
L5_x = collect(la_5);
% 求取五次Lagrange多项式函数.
Lagrange5_x = eval(collect(L0_x*Y(1)+L1_x*Y(2)+L2_x*Y(3)+L3_x*Y(4)+L4_x*Y(5)+L5_x*Y(6 )))
P = sym2poly(Lagrange5_x); % 得到五次Lagrange多项式函数的系数向量.
K1 = polyval(P,0.596); % 进行多项式求值.
fprintf('f(0.596)的值为:f(1.8) = %f\n',K1);
K2 = polyval(P,0.99); % 进行多项式求值.
fprintf('f(0.99)的值为:f(1.8) = %f\n',K1);
% 绘制五次Lagrange多项式函数L5(x).
for jj = 1:length(X)
K = polyval(P,X(jj));
YY(jj)=K;
end
plot(X,YY);
title('\bf\it5次Lagrange插值函数曲线','FontName','黑体','FontSize',12); grid on
xlabel('\itx轴','FontName','黑体','FontSize',12);
ylabel('\ity轴','FontName','黑体','FontSize',12);
插值法和拟合实验报告 一、 实验目的 1.通过进行不同类型的插值,比较各种插值的效果,明确各种插值的优越性; 2.通过比较不同次数的多项式拟合效果,了解多项式拟合的原理; 3.利用matlab 编程,学会matlab 命令; 4.掌握拉格朗日插值法; 5.掌握多项式拟合的特点和方法。 二、 实验题目 1.、插值法实验 将区间[-5,5]10等分,对下列函数分别计算插值节点 k x 的值,进行不同类型 的插值,作出插值函数的图形并与)(x f y =的图形进行比较: ;11)(2x x f += ;a r c t a n )(x x f = .1)(42 x x x f += (1) 做拉格朗日插值; (2) 做分段线性插值; (3) 做三次样条插值. 2、拟合实验 给定数据点如下表所示: 分别对上述数据作三次多项式和五次多项式拟合,并求平方误差,作出离散函数 ),(i i y x 和拟合函数的图形。 三、 实验原理 1.、插值法实验
∏∑∏∏∏∑∑≠==≠=≠=≠=+-==--= =-= ==-=-=----==++==j i j j i i i i i n i i n n j i j j n j i j j i i n j i j j n i i i n i i n n n o i n i i n x x x x x y x l x L x x c n i x x c x x x c x x x x x x x x c y x l x L y x l y x l y x l x L ,00 ,0,0,01100 00 )(l )()() (1 ,1,0, 1)()(l ) ()())(()()()()()()()(, 故, 得 再由,设 2、拟合实验
数值分析实验报告三 插值法(2学时) 一实验目的 1.掌握不等距节点下的牛顿插值公式以及拉格朗日插值公式。二实验内容 1.已知函数表: 用牛顿插值公式求) (y的近似值。 102 2. 已知函数表: 用拉格朗日插值公式计算01 x以及所对应的近似值。 =y .5 4.1= 三实验步骤(算法)与结果 1.不等距节点下的牛顿插值公式 Ⅰ.按差商表计算n阶差商
12111[,,,][,,,] [,,,]i i i n i i i n i i i n i n i f x x x f x x x f x x x x x +++++-+++-= - 其中 Ⅱ.按以下公式,带入x 值 00010120101101()() ()[,] ()()[,,]()()()[,,] n n f x f x x x f x x x x x x x f x x x x x x x x x f x x -=+-+--++--- Ⅲ.得出结果()f x 程序代码: #include"stdio.h" #include"math.h" int main() { int a,i,j; printf("输入x 系数的个数:"); scanf("%d",&a); float d,e=0,c; float x[a]; float y[a-1][a]; printf("输入x 的系数:"); for(i=0;i 拉格朗日插值公式的证明及其应用 摘要: 拉格朗日(Lagrange)插值公式是多项式中的重要公式之一,在理论和实践中都有着广泛的应用.本文阐述了Lagrange 插值的基本理论,譬如:线形插值,抛物插值,Lagrange 多项式等.然后将线形插值,抛物插值,Lagrange 多项式插值分别应用到高中知识中,并且学会用计算机程序来编写.插值法的思想与中国剩余定理一脉相承, 体现了代数中"线性化" (即表示为求和和数乘的形式) 这一基本思路, 大巧若拙.本文的目的是通过介绍拉格朗日插值公式的推导,唯一性,证明过程及其在解题与实际生活问题中的应用来寻找该公式的优点,并且引人思考它在物理,化学等领域的应用.通过实际鉴定过程,利用插值公式计算生活中的成本问题,可以了解它的计算精度高,方法快捷. 关键词: 拉格朗日插值公式 唯一性 证明 解题应用 资产评估 曲线插值问题,直观地说,认为已知的一批数据点()n k k k f x 0,=是准确的,这些数据点所表现的 准确函数关系()x f 是未知的,在这种情况下要作一条近似曲线()x P 且点点通过这些点,插值问题不仅要讨论这种近似曲线()x P 的构造方法,还要讨论点增多时这种近似曲线()x P 是否稳定地收敛于未知函数()x f ,我们先研究一种简单常用的插值——拉格朗日插值. 一.定义,推导及其在解题中的应用 1.线性插值 1.1. 线性插值的定义 假定已知区间[]1,+k k x x 的端点处的函数值()k k x f y =, ()11++=k k x f y ,要求线性插值多项式()x L 1使它满足()k k y x L =1, ()111++=k k y x L . ()x L y 1=的几何意义:通过两点()k k y x ,和()11,++k k y x 的直线, 如图1所示,()x L 1的表达式由几何意义直接给出,即 ()()k k k k k k x x x x y y y x L ---+ =++111 (点斜式), 图1 ()11111++++--+--= k k k k k k k k y x x x x y x x x x x L (两点式). y=L 1x () y=f x () y k+1 y k x k+1 x k o y x #include 课题一:拉格朗日插值法 1.实验目的 1.学习和掌握拉格朗日插值多项式。 2.运用拉格朗日插值多项式进行计算。 2.实验过程 作出插值点(1.00,0.00),(-1.00,-3.00),(2.00,4.00)二、算法步骤 已知:某些点的坐标以及点数。 输入:条件点数以及这些点的坐标。 输出:根据给定的点求出其对应的拉格朗日插值多项式的值。 3.程序流程: (1)输入已知点的个数; (2)分别输入已知点的X坐标; (3)分别输入已知点的Y坐标; 程序如下: #include 插值算法*/ { int i,j; float *a,yy=0.0; /*a作为临时变量,记录拉格朗日插值多项*/ a=(float*)malloc(n*sizeof(float)); for(i=0;i<=n-1;i++) { a[i]=y[i]; for(j=0;j<=n-1;j++) if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]); yy+=a[i]; } free(a); return yy; } int main() { int i; int n; float x[20],y[20],xx,yy; printf("Input n:"); scanf("%d",&n); if(n<=0) { printf("Error! The value of n must in (0,20)."); getch();return 1; } for(i=0;i<=n-1;i++) { printf("x[%d]:",i); scanf("%f",&x[i]); } printf("\n"); for(i=0;i<=n-1;i++) { printf("y[%d]:",i);scanf("%f",&y[i]); } printf("\n"); printf("Input xx:"); scanf("%f",&xx); yy=lagrange(x,y,xx,n); printf("x=%f,y=%f\n",xx,yy); getch(); } 举例如下:已知当x=1,-1,2时f(x)=0,-3,4,求f(1.5)的值。 实验 一 .拉格朗日插值法C 语言的实现 1.实验目的: 进一步熟悉拉格朗日插值法。 掌握编程语言字符处理程序的设计和调试技术。 2.实验要求: 已知:某些点的坐标以及点数。 输入:条件点数以及这些点的坐标 。 输出:根据给定的点求出其对应的拉格朗日插值多项式的值 。 3.程序流程: (1)输入已知点的个数; (2)分别输入已知点的X 坐标; (3)分别输入已知点的Y 坐标; (4)通过调用函数lagrange 函数,来求某点所对应的函数值。 拉格朗日插值多项式如下: 0L ()()0,1,n n j k k j j k x y l x y j n ====∑…… 其中00()()0,1,,()k k x x l x k n x x -= =-k-1k+1n k k-1k k+1k n ……(x-x )(x-x )?…(x-x )…………(x -x )(x -x )?…(x -x ) 程序流程图: ↓ 程序如下: #include 实验二插值法 1、实验目的: 1、掌握直接利用拉格郎日插值多项式计算函数在已知点的函数值;观察拉格郎日插值的龙格现象。 2、了解Hermite插值法、三次样条插值法原理,结合计算公式,确定函数值。 2、实验要求: 1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法; 2)编写上机实验程序,作好上机前的准备工作; 3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果); 4)分析和解释计算结果; 5)按照要求书写实验报告; 3、实验内容: 1) 用拉格郎日插值公式确定函数值;对函数f(x)进行拉格郎日插值,并对f(x)与插值多项式的曲线作比较。 已知函数表:(0.56160,0.82741)、(0.56280,0.82659)、(0.56401,0.82577)、(0.56521,0.82495)用三次拉格朗日插值多项式求x=0.5635时函数近似值。 2) 求满足插值条件的插值多项式及余项 1) 4、题目:插值法 5、原理: 拉格郎日插值原理: n次拉格朗日插值多项式为:L n (x)=y l (x)+y 1 l 1 (x)+y 2 l 2 (x)+…+y n l n (x) n=1时,称为线性插值, L 1(x)=y (x-x 1 )/(x -x 1 )+y 1 (x-x )/(x 1 -x )=y +(y 1 -x )(x-x )/(x 1 -x ) n=2时,称为二次插值或抛物线插值, L 2(x)=y (x-x 1 )(x-x 2 )/(x -x 1 )/(x -x 2 )+y 1 (x-x )(x-x 2 )/(x 1 -x )/(x 1 -x 2 )+y 2 (x -x 0)(x-x 1 )/(x 2 -x )/(x 2 -x 1 ) n=i时, Li= (X-X0)……(X-X i-1)(x-x i+1) ……(x-x n) (X-X0)……(X-X i-1)(x-x i+1) ……(x-x n) 6、设计思想: 拉格朗日插值法是根据n + 1个点x0, x1, ... x n(x0 < x1 < ... x n)的函数值f (x0), f (x1) , ... , f (x n)推出n次多項式p(x),然后n次多項式p (x)求出任意的点x对应的函数值f (x)的算法。 7、对应程序: 1 ) 三次拉格朗日插值多项式求x=0.5635时函数近似值 #include"stdio.h" #define n 5 void main() { int i,j; float x[n],y[n]; float x1; float a=1; float b=1; float lx=0; printf("\n请输入想要求解的X:\n x="); scanf("%f",&x1); printf("请输入所有点的横纵坐标:\n"); for(i=1;i 浅析拉格朗日插值法 目录: 一、 引言 二、 插值及多项式插值的介绍 三、 拉格朗日插值的理论及实验 四、 拉格朗日插值多项式的截断误差及实用估计式 五、 参考文献 一、引言 插值在数学发展史上是个古老问题。插值是和拉格朗日(Lagrange )、牛顿(Newton )、高斯(Gauss )等著名数学家的名字连在一起的。在科学研究和日常生活中,常常会遇到计算函数值等一类问题。插值法有很丰富的历史渊源,它最初来源人们对天体研究——有若干观测点(我们称为节点)计算任意时刻星球的位置(插值点和插值)。现在,人们在诸如机械加工等工程技术和数据处理等科研都有很好的应用,最常见的应用就是气象预报。插值理论和方法能解决在实际中当许多函数表达式未知或形式复杂,如何去构造近似表达式及求得在其他节点处的值的问题。 二、插值及多项式插值 1、插值问题的描述 设已知某函数关系()y f x =在某些离散点上的函数值: 插值问题:根据这些已知数据来构造函数()y f x =的一种简单的近似表达式,以便于计算点,0,1,,i x x i n ≠= 的函数值()f x ,或计算函数的一阶、二阶导数值。 x 0x 0 y y 1 y 1 n y -n y 1 x 1 n x -n x 2、插值的几何意义 插值的几何意义如图1所示: 图1 3、多项式插值 3.1 基本概念 假设()y f x =是定义在区间,a b ????上的未知或复杂函数,但一直该函数在点01n a x x x b ≤<<<≤ 处的函数值01,,n y y y 。找一个简单的函数,例如函数 ()P x ,使之满足条件 (),0,1,2,, i P x y i n == (3.1) 通常把上述01n x x x <<< 称为插值节点,把()P x 称为()f x 的插值多项式,条件(3.1)称为插值条件,并把求()P x 的过程称为插值法。 3.2 插值多项式的存在性和唯一性 如果插值函数是如下m 次的多项式: 1 011()m m m m m P x a x a x a x a --=+++ 那么插值函数的构造就是要确定()m P x 表达式中的m+1个系数 011,,,m m a a a a - 。由于插值条件包含n+1独立式,只要m=n 就可证明插值函数多项式是唯一存在。 实际上,由n+1个插值条件可得 插值法数值上机实验报告 实验题目: 利用下列条件做插值逼近,并与R (x) 的图像比较 考虑函数:R x y=1 1+x2 (1)用等距节点X i=?5+i,i=0,1,...,10.给出它的10次Newton插值多项式的图像; π),i=0,1,...,20.给出它的20次Lagrange插值多项式(2)用节点X i=5cos(2i+1 42 的图像; (3)用等距节点X i=?5+i,i=0,1,...,10.给出它的分段线性插值函数的图像;(4)用等距节点X i=?5+i,i=0,1,...,10.给出它的三次自然样条插值函数的图像; (5)用等距节点X i=?5+i,i=0,1,...,10.给出它的分段三次Hermite插值函数的图像; 实验图像结果: 实验结果分析: 1.为了验证Range现象,我还特意做了10次牛顿插值多项式和20次牛顿插值多项式的对比图像,结果如下图(图对称,只截取一半) 可以看出,Range现象在高次时变得更加明显。这也是由于高次多项式在端点处的最值随次数的变大很明显。可以料定高次多项式在两侧端点处剧烈震荡,在更小的间距内急剧上升然后下降,Range现象非常明显。 2.分析实验(2)的结果,我们会惊讶地发现,由于取21个点逼近,原本预料的Range现象会很明显,但这里却和f(x)拟合的很好。(即下图中Lagrange p(x)的图像)。可是上图中取均匀节点的20次牛顿多项式逼近的效果在端点处却很差。料想是由于节点X i=5cos2i+1 42 π ,i=0,1,...,20 取得很好。由书上第五章的 知识,对于函数y=1 1+x ,y 1 2对应的cherbyshev多项式的根恰好为X i= 5cos2i+1 42 π ,i=0,1,...,20 。由于所学限制,未能深入分析。 (3)比较三次样条插值图像和Hermit插值图像对原函数图像的逼近情形。见下图: 多项式插值法和拉格朗日插值 教案一多项式插值法和拉格朗日插值 基本内容提要 1 多项式插值法的基本概念 2 插值多项式的存在性与唯一性分析 3 拉格朗日插值多 项式的构造及截断误差 4 截断误差的实用估计式 5 逐次线性插值法教学目的和要求 1 熟练掌握多项式插值法的基本概念 2 理解插值多项式的存在性与唯一性 3 掌握拉 格朗日插值法 4 掌握截断误差的估计方法 5 理解逐次线性插值法的基本思想,掌握Aitken逐次线性插值法 6 掌握运用拉格朗 日插值法处理问题的基本过程教学重点 1 拉格朗日插值基函数及拉格朗日插值多项式的构造 2 拉格朗日插值多项式的截断 误差分析 3 逐次线性插值法的基本思想教学难点 1 插值多项式存在唯一性条件的讨论分析 2 插值误差的分析与估计 3 Aitken逐次线性插值法的计算过程课程类型新知识理论课教学方法 结合提问,以讲授法为主教学过程 问题引入 实际问题中许多变量间的依赖关系往往可用数学中的函数概念刻画,但在多数情况下,这些函数的表达式是未知的,或者函数已知,但形式十分复杂。基于未知函数或复杂函数 的某些已知信息,如何构造这些函数的近似表达式?如何计算这些函数在其它点处的函数值?所构造的近似表达式与真实函数的误差是多少?插值理论与方法就是解决这些问题的 有效工具之一。 §2.1 多项式插值 2.1.1 基本概念 假设f(x)是定义在区间[a,b]上的未知或复杂函数,但已知该函数在点a≤x0 P(xi)=yi,i=0,1,2,L,n,即在给定点xi处,P(x)与f(x)是相吻合的。 (2.1) 把P(x)称为f(x)的插值多项式(函通常把上述x0 数), f(x)称为被插函数。[a,b]称为插值区间,条件(2.1)称为插值条件,并把 求P(x)的过程称为插值法。 i. 拉格朗日插值多項 ii. 式與泰勒多項式的誤差分析 iii. 朱亮儒★ 曾政清☆ 陳昭地★ iv. ★國立臺灣師範大學數學系教授 v. ☆臺北市立建國高級中學數學教師 vi. vii. 摘要:本文旨於提供拉格朗日插值多項式與泰勒多項式誤差項估計值的初 等簡易證明,並探討其應用價值。 viii. 關鍵字:拉格朗日插值多項式、泰勒多項式、誤差項 ix. 一 引言 x. 有鑑於教育部99普通高級中學數學課綱在第一冊多項式的運算為迴避解三元一次方程組,首次出現插值多項式及其應用(以不超過三次插值多項式為限)([1][2][3]),99數學課綱包含插值多項式部分如下: xi. 求 xii. 32()2563f x x x x =-++ xiii. (1)(1)(2)(1)(2)(3)a b x c x x d x x x =+-+--+--- xiv. 中的, , , a b c d . xv. ()f x 除以()()x a x b --的餘式為通過()(),(),,()a f a b f b 的插值多項 式。 xvi. 若f 有,a b 兩實根,則f 可寫成()()()()f x q x x a x b =--的型式。 xvii. 透過因式定理證明插值多項式的唯一性。 xviii. 設通過(1,1),(2,3),(3,7)的多項式為 ()(1)(1)(2)f x a b x c x x =+-+--,求,,a b c 及12f ?? ??? . xix. 插值多項式:通過(11,3),(12,5),(13,8)的多項式可表示為 xx. (12)(13)(11)(13)(11)(12)()358(1112)(1113)(1211)(1213)(1311)(1312) x x x x x x f x ------=? +?+?------, xxi. 求(11.5)f 的值。 xxii. 此處暫不處理下面的題型:「設通過(1, 1), (2, 3), (3, 7)的多項式為 2()f x a bx cx =++,求,,a b c 。」此類題型將在數學的IV 的聯立方程組章節中處理。 xxiii. 此處自然而然讓人想到拉格朗日(Lagrange, J. L., 1736-1816)其人奇事,羅 列如下: xxiv. 他出生於義大利西北部的杜林(Turin),從小就極有數學天分,於18歲開始 撰寫數學論文,在數論上曾提出一個著名的定理:「任意正整數都可以表成四個平方數的和」。 xxv. 他是第一位證明均值定理(The Mean Value Theorem)的大數學家。(均值定理 在高三選修甲微分的單元中會學到([4]),它是僅次於微積分基本定理的極重要的存在定理) xxvi. 他在30歲時,應腓特烈二世的邀請到柏林作為其宮廷數學大師長達20年 之久。 实验题目: 用多项式模型进行数据拟合实验 1 实验目的 本实验使用多项式模型对数据进行拟合,目的在于: (1)掌握数据拟合的基本原理,学会使用数学的方法来判定数据拟合的情况; (2)掌握最小二乘法的基本原理及计算方法; (3)熟悉使用matlab 进行算法的实现。 2 实验步骤 2.1 算法原理 所谓拟合是指寻找一条平滑的曲线,最不失真地去表现测量数据。反过来说,对测量 的实验数据,要对其进行公式化处理,用计算方法构造函数来近似表达数据的函数关系。由于函数构造方法的不同,有许多的逼近方法,工程中常用最小平方逼近(最小二乘法理论)来实现曲线的拟合。 最小二乘拟合利用已知的数据得出一条直线或曲线,使之在坐标系上与已知数据之间的距离的平方和最小。模型主要有:1.直线型2.多项式型3.分数函数型4.指数函数型5.对数线性型6.高斯函数型等,根据应用情况,选用不同的拟合模型。其中多项式型拟合模型应用比较广泛。 给定一组测量数据()i i y x ,,其中m i ,,3,2,1,0Λ=,共m+1个数据点,取多项式P (x ),使得 min )]([020 2=-=∑∑==m i i i m i i y x p r ,则称函数P (x )为拟合函数或最小二乘解,此时,令 ∑==n k k k n x a x p 0 )(,使得min ])([02 002=??? ? ??-=-=∑∑∑===m i n k i k i k m i i i n y x a y x p I ,其中 n a a a a ,,,,210Λ为待求的未知数,n 为多项式的最高次幂,由此该问题化为求),,,(210n a a a a I I Λ=的极值问题。 由多元函数求极值的必要条件:0)(200 =-=??∑∑==m i j i n k i k i k i x y x a a I ,其中n j ,,2,1,0Λ= 得到: ∑∑∑===+=n k m i i j i k m i k j i y x a x )(,其中n j ,,2,1,0Λ=,这是一个关于n a a a a ,,,,210Λ的线 性方程组,用矩阵表示如下所示: 浙江大学城市学院实验报告 课程名称 科学计算 实验项目名称 函数的数值逼近-插值 实验成绩 指导老师(签名 ) 日期 一. 实验目的和要求 1. 掌握用Matlab 计算Lagrange 、分段线性、三次样条三种插值的方法,改变节点的数目, 对三种插值结果进行初步分析。 2. 通过实例学习如何用插值方法解决实际问题。 二. 实验内容和原理 1) 编程题2-1要求写出Matlab 源程序(m 文件),并对每一行语句加上适当的注释语句; 2) 分析应用题2-2,2-3,2-4,2-5要求将问题的分析过程、Matlab 源程序、运行结果和结 果的解释、算法的分析等写在实验报告上。 2-1 编程 编写Lagrange 插值函数的Matlab 程序,其中n 个插值节点以数组0x ,0y 输入,m 个待求点的自变量以数组x 输入。输出数组y 为m 个待求点的函数值。 Lagrange 插值:=lagr(0,0,)y x y x Step 1 输入插值节点数组0x ,0y 和待求节点x ; Step 2 数组0x 的长度为n ,x 的长度为m ; Step 3 对1,2, ,i n =,构造第i 个插值基函数 111111(0)(0)(0)(0) ()(00)(00)(00)(00) i i n i i i i i i i n x x x x x x x x l x x x x x x x x x -+-+----= ---- 并计算在m 个待求点上的基函数值。 Step 4 根据公式1 0()n i i i y y l x == ∑分别计算m 个待求点上的函数值。 并对程序的每一行语句加上适当的注释语句。 对拉格朗日插值法与牛顿插值法的学习和比较 摘要:根据对拉格朗日插值法和牛顿插值法的理解,本文主要介绍了拉格朗日插值法和牛顿插值法的相关内容以及它们的区别。 关键词:拉格朗日插值法;牛顿插值法 The leaning and comparison of the Lagrange interpolation and Newton interpolation Abstract: Based on the understanding of the Lagrange interpolation and Newton interpolation ,this paper mainly describes some related knowledge as well as the difference between these two methods. Keywords: Lagrange interpolation ; Newton interpolation 前言 在工程和科学研究中出现的函数是多种多样的。常常会遇到这样的情况:在某个实际问题中,虽然可以断定所考虑的函数)(x f 在区间],[b a 上存在且连续,但却难以找到它的解析表达式,只能通过实验和观测得到在有限个点上的函数值(即一张函数表)。显然,要利用这张函数表来分析函数)(x f 的性态,甚至直接求出其他一些点上的函数值可能是非常困难的。面对这些情况,总希望根据所得函数表(或结构复杂的解析表达式),构造某个简单函数)(x P 作为)(x f 的近似。这样就有了插值法,插值法是解决此类问题目前常用的方法。 如设函数)(x f y =在区间],[b a 上连续,且在1+n 个不同的点b x x x a n ≤≤,,,10 上分别取值n y y y ,,,10 。 插值的目的就是要在一个性质优良、便于计算的函数类Φ中,求一简单函数)(x P ,使 ),,1,0()(n i y x P i i == 而在其他点i x x ≠上,作为)(x f 的近似。 通常,称区间],[b a 为插值区间,称点n x x x ,,,10 为插值节点,称式i i y x P =)(为插值条件,称函数类Φ为插值函数类,称)(x P 为函数)(x f 在节点n x x x ,,,10 处的插值函数。求插值函数)(x P 的方法称为插值法。 插值函数类Φ的取法不同,所求得的插值函数)(x P 逼近)(x f 的效果就不同。它的选择取决于使用上的需要,常用的有代数多项式、三角多项式和有理函数等。当选用代数多项式作为插值函数时,相应的插值问题就称为多项式插值。本文讨论的拉格朗日插值法与牛顿插值法就是这类插值问题。 在多项式插值中,最常见、最基本的问题是:求一次数不超过n 的代数多项式 n n x a x a a x P +++= 10)( 使),,1,0()(n i y x P i i n ==,其中,n a a a ,,,10 为实数。 实验报告:牛顿差值多项式&三次样条 问题:在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数2 1()25f x x 作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及()f x 的图形。 实验目的:通过编程实现牛顿插值方法和三次样条方法,加深对多项式插值的理解。应用所编程序解决实际算例。 实验要求: 1. 认真分析问题,深刻理解相关理论知识并能熟练应用; 2. 编写相关程序并进行实验; 3. 调试程序,得到最终结果; 4. 分析解释实验结果; 5. 按照要求完成实验报告。 实验原理: 详见《数值分析 第5版》第二章相关内容。 实验内容: (1)牛顿插值多项式 1.1 当n=10时: 在Matlab 下编写代码完成计算和画图。结果如下: 代码: clear all clc x1=-1:0.2:1; y1=1./(1+25.*x1.^2); n=length(x1); f=y1(:); for j=2:n for i=n:-1:j f(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1)); end end syms F x p ; F(1)=1;p(1)=y1(1); for i=2:n F(i)=F(i-1)*(x-x1(i-1)); p(i)=f(i)*F(i); end syms P P=sum(p); P10=vpa(expand(P),5); x0=-1:0.001:1; y0=subs(P,x,x0); y2=subs(1/(1+25*x^2),x,x0); plot(x0,y0,x0,y2) grid on xlabel('x') ylabel('y') P10即我们所求的牛顿插值多项式,其结果为:P10(x)=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0 并且这里也能得到该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.1)。 Fig.1 牛顿插值多项式(n=10)函数和原函数图形 从图形中我们可以明显的观察出插值函数在两端点处发生了剧烈的波动,产生了极大的误差,即龙格现象,当n=20时,这一现象将更加明显。 1.2 当n=20时: 对n=10的代码进行修改就可以得到n=20时的代码。将“x1=-1:0.2:1;”改为“x1=-1:0.1:1;”即可。运行程序,我们得到n=20时的牛顿插值多项式,结果为:P20(x)= 260188.0*x^20 - 1.0121e6*x^18 + 2.6193e-12*x^17 + 1.6392e6*x^16 + 2.248e-11*x^15 - 1.4429e6*x^14 - 4.6331e-11*x^13 + 757299.0*x^12 + 1.7687e-11*x^11 - 245255.0*x^10 + 2.1019e-11*x^9 + 49318.0*x^8 + 3.5903e-12*x^7 - 6119.2*x^6 - 1.5935e-12*x^5 + 470.85*x^4 + 1.3597e-14*x^3 - 24.143*x^2 - 1.738e-14*x + 1.0 同样的,这里得到了该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.2)。 《计算方法》实验报告 学院:信息学院 专业:计算机科学与技术 指导教师: 班级学号: 姓名: 计算机科学与工程系 实验一 插值方法 一. 实验目的 (1)熟悉数值插值方法的基本思想,解决某些实际插值问题,加深对数值插值方法 的理解。 (2)熟悉Matlab 编程环境,利用Matlab 实现具体的插值算法,并进行可视化显示。 二. 实验要求 用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法,并用实例在计算机上计算和作图。 三. 实验容 1. 实验题目 (1)已知概率积分dx e y x x ?-=02 2 π 的数据表 构造适合该数据表的一次、二次和三次Lagrange 插值公式,输出公式及其图形,并计算x =0.472时的积分值。 (2)将区间[-5,5]分为10等份,求作2 11 )(x x f += 的分段线性插值函数,输出函数表达式及其图形,并计算x =3.3152时的函数值。 (3)仿照附录C 中“文件1.2 逐步插值”程序(Neville 算法,课本227页)编写相应的Aitken 逐步插值算法的程序,根据下表所给数据分别利用上述两种算法求正弦积分? ∞-=x dt t t x f sin )(在x =0.462的值,并比较它们的结果。 (4)运行C 中“文件1.3 分段三次Hermite 插值”程序(课本228页),要求自行选择实验数据 2. 设计思想 (1)Lagrange 插值: Lagrange 具有累加的嵌套结构,容易编制其计算程序。事实上,在逻辑上表现为二重循环,循 目录: 一、 引言 二、 插值及多项式插值的介绍 三、 拉格朗日插值的理论及实验 四、 拉格朗日插值多项式的截断误差及实用估计式 五、 参考文献 一、引言 插值在数学发展史上是个古老问题。插值是和拉格朗日(Lagrange )、牛顿(Newton )、高斯(Gauss )等著名数学家的名字连在一起的。在科学研究和日常生活中,常常会遇到计算函数值等一类问题。插值法有很丰富的历史渊源,它最初来源人们对天体研究——有若干观测点(我们称为节点)计算任意时刻星球的位置(插值点和插值)。现在,人们在诸如机械加工等工程技术和数据处理等科研都有很好的应用,最常见的应用就是气象预报。插值理论和方法能解决在实际中当许多函数表达式未知或形式复杂,如何去构造近似表达式及求得在其他节点处的值的问题。 二、插值及多项式插值 1、插值问题的描述 设已知某函数关系()y f x =在某些离散点上的函数值: 插值问题:根据这些已知数据来构造函数()y f x =的一种简单的近似表达式,以便于计算点,0,1,,i x x i n ≠=的函数值()f x ,或计算函数的一阶、二阶导数 值。 2、插值的几何意义 x x 0 y y 1 y 1 n y -n y 1 x 1 n x -n x 插值的几何意义如图1所示: 图1 3、多项式插值 基本概念 假设()y f x =是定义在区间,a b ????上的未知或复杂函数,但一直该函数在点01n a x x x b ≤<< <≤处的函数值01,,n y y y 。找一个简单的函数,例如函数 ()P x ,使之满足条件 (),0,1,2, ,,i P x y i n == () 通常把上述01n x x x << < 称为插值节点,把()P x 称为()f x 的插值多项 式,条件()称为插值条件,并把求()P x 的过程称为插值法。 插值多项式的存在性和唯一性 如果插值函数是如下m 次的多项式: 1011()m m m m m P x a x a x a x a --=++ + 那么插值函数的构造就是要确定()m P x 表达式中的m+1个系数 011,, ,m m a a a a -。由于插值条件包含n+1独立式,只要m=n 就可证明插值函数多 项式是唯一存在。 实际上,由n+1个插值条件可得 拉格朗日多项式插值法浅析 摘要 拉格朗日插值多项式是一种最常见的多项式插值法,也是一种最常用的逼近工具。“学以致用 ”是每一门学科都致力追求的境界,数学自然也不例外。下面,探讨拉格朗日插值法的基本原理、如何构造拉格朗日多项式、拉格朗日多项式的误差界,并用 MATLAB 程序来实现这一数学算法的自动化,为复杂的分析研究提供了一条数学算法的捷径。 【关键词】:拉格朗日多项式 算法实现 MATLAB 在科学研究和实际的工程设计中,几乎所有的问题都可以用)(x f y =来表示其某种内在规律的数量关系。但理想化的函数关系在实际工程应用中是很难寻找 的,对于那些没有明显解析式的函数关系表达式则只能通过实验观察的数据,利用多项式对某一函数的进行逼近,使得这个逼近函数能够反映)(x f 的特性,而且利用多项式就可以简便的计算相应的函数值。例如我们不知道气温随日期变化的具体函数关系,但是我们可以测量一些孤立的日期的气温值,并假定此气温随日期变化的函数满足某一多项式。这样,利用已经测的数据,应用待定系数法便可以求得一个多项式函数f (x )。应用此函数就可以计算或者说预测其他日期的气温值。一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越 准确。当然,构造组合多项式方法比较多,如线性方程求解、拉格朗日系数多项式以及构造牛顿多项式的分段差分和系数表等等,这里只对拉格朗日多项式插值法进行深入探讨。 一、拉格朗日多项式插值算法基本原理 函数)(x f y =在区间[a,b]上有定义,在是[ a,b]上取定的 N + 1个互异节点, 且在这些点处的函数值)(0x f , )(1x f ,…,)(n x f 为已知, 即 yi =f (xi ) , (N i ...1,0=),若存在一个和)(x f 近似的函数)(x P N ,满足 )()(i i N x f x P = (N i ...1,0=) (1) 则称 φ(x) 为 f (x) 的一个插值函数, 点i x 为插值节点,(1)称为插值条件, 区间[a,b]称为插值区间, 而误差函数)()(x P x f E N N -=称为插值余项。即是求一个不超过N 次多项式0111...)(a x a x a x a x P N N N N N ++++=-- (N i ...1,0=) 满足 )()(i i N x f x P = (N i ...1,0=) 算法2实验 一 .拉格朗日插值法C 语言的实现 1.实验目的: 进一步熟悉拉格朗日插值法。 掌握编程语言字符处理程序的设计和调试技术。 2.实验要求: 已知:某些点的坐标以及点数。 输入:条件点数以及这些点的坐标 。 输出:根据给定的点求出其对应的拉格朗日插值多项式的值 。 3.程序流程: (1)输入已知点的个数; (2)分别输入已知点的X 坐标; (3)分别输入已知点的Y 坐标; (4)通过调用函数lagrange 函数,来求某点所对应的函数值。 拉格朗日插值多项式如下: L ()()0,1,n n j k k j j k x y l x y j n == ==∑ …… 其中00()()0,1,,()k k x x l x k n x x -==-k-1k+1n k k-1k k+1k n ……(x-x )(x-x ) …(x-x )…………(x -x )(x -x ) …(x -x ) 程序流程图: ↓ 程序如下: #include 拉格朗日插值公式的证明及其应用
拉格朗日多项式插值(C语言)
数值分析拉格朗日插值法上机实验报告
拉格朗日插值法C语言的实现
插值法实验报告
拉格朗日插值法理论及误差分析
插值法数值上机实验报告
多项式插值法和拉格朗日插值
拉格朗日插值多项式与泰勒多项式的误差分析详全文
用多项式模型进行数据拟合实验报告(附代码)
实验报告五 插值
对拉格朗日插值法与牛顿插值法的学习和比较
数值分析实验报告-插值、三次样条(教育教学)
实验一-插值方法实验
拉格朗日插值法理论及误差分析
拉格朗日多项式插值
拉格朗日插值法C语言的实现(实验报告)