概率论与数理统计笔记第三章二元随机变量及其分布概率论与数理统计笔记(计算机专业)
第16讲二元随机变量,离散型随机变量分布律?
二元随机变量
?
?同一个样本空间的两个随机变量构成的向量?
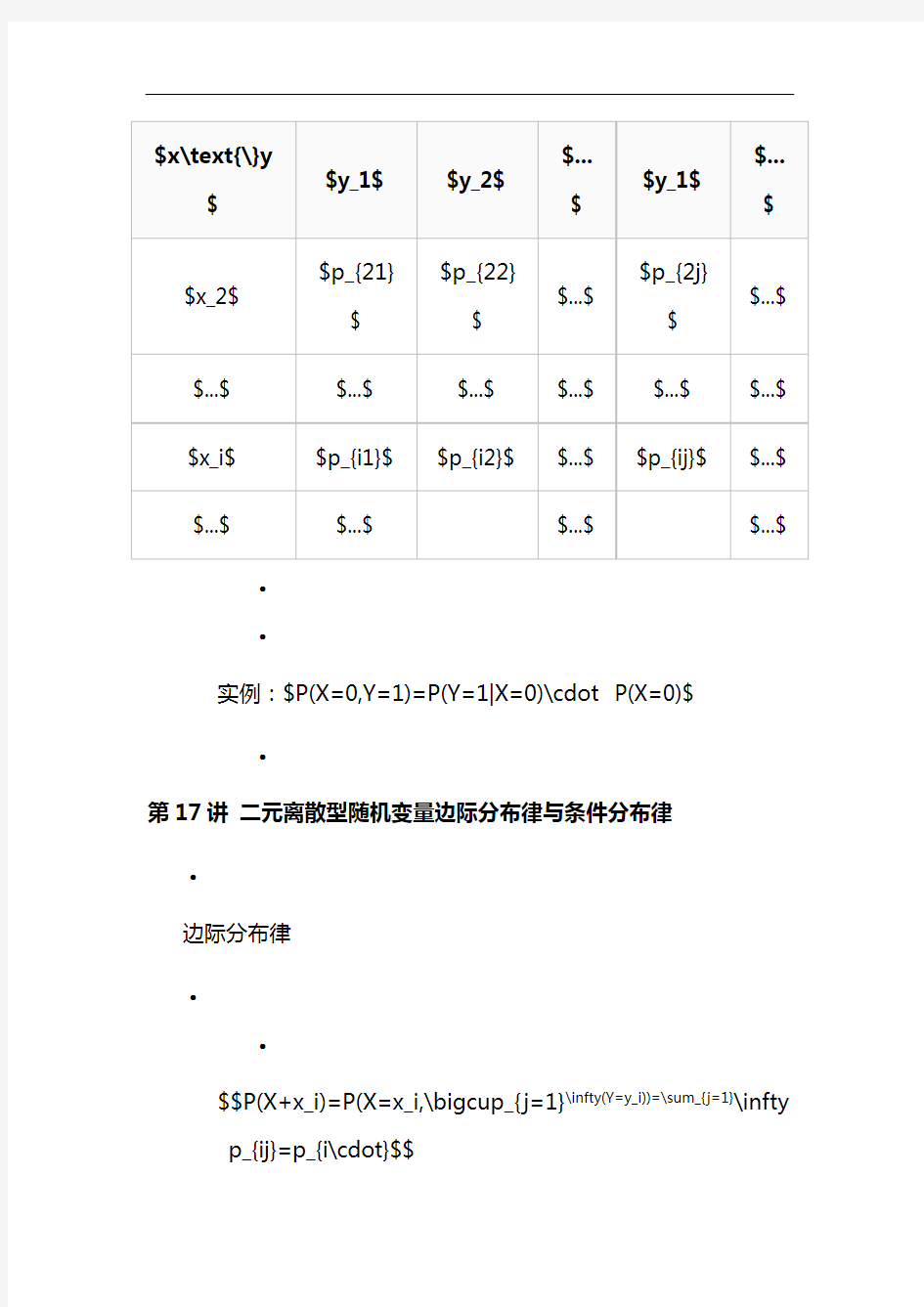
离散型随机变量的分布律
?
?
$$P(X=x_i,Y=y_i)=p_y\ i,j=1,2,...$$
?
?
?
?
实例:$P(X=0,Y=1)=P(Y=1|X=0)\cdot P(X=0)$
?
第17讲二元离散型随机变量边际分布律与条件分布律?
边际分布律
?
?
$$P(X+x_i)=P(X=x_i,\bigcup_{j=1}\infty(Y=y_i))=\sum_{j=1}\infty
p_{ij}=p_{i\cdot}$$
?
?
$$P(Y+y_i)=P_{\cdot y}$$ ?
?
?
?
已知条件分布律一定能求出边际分布律,但已知编辑分布律
不一定能求出条件分布律
?
?
条件分布律
?
?$$P(X=x_i)|Y=y_j)=\frac{p_{ij}}{p_{\cdot j}}\ i=1,2,...
$$
?条件分布律不唯一
第18讲二元随机变量分布函数、边际分布函数及条件分布函数?联合分布函数
?$$F(x,y)=P{(X\leq x)\cap(Y\leq y)}=P(X\leq x,Y\leq y)$$
?边际分布函数
?$$F_x(x)=F(x,+\infty)=\lim_{y\to\infty}F(x,y)$$
?条件分布函数
?若$P(Y=y)>0$
?$$F_{X|Y}(x|y)=P(X\leq x|Y=y)=\frac{P(X\leq x,Y=y)}
{P(Y=y)}$$
?对于连续型随机变量也可以用如上记法,但注意此时的
$y\leq Y\leq \epsilon$
第19讲二元连续型随机变量的联合概率密度
?二元随机变量的联合概率密度
?$$F(x,y)=\int_{-\infty}x\int_{-\infty}yf(u,v)dudv$$
?其中$f(x,y)$ 为$(X,Y)$ 的概率密度
?性质
?$$P((x,y)\in D)=\iint_{D}f(x,y)dxdy$$
?$$\frac{\partial^2F(x,y)}{\partial x\partial y}=f(x,y)
$$
?提示
?此处应具有求二重积分的能力
第20讲二元连续型随机变量的边际概率密度
?二元连续型随机变量的边际概率密度
?$$f_x(x)=\int_{-\infty}^{+\infty}f(x,y)dy$$
?二元连续型随机变量的边际概率函数
?$$F_x(x)=F(x,+\infty)=\int_{-\infty}x[\int_{-\infty}{+\infty}
f(u,y)dy]du$$
第21讲二元连续型随机变量的条件概率密度
?
二元连续型随机变量的条件概率密度
?
?$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$$
?
变式
?
?$$f(x,y)=f_{X|Y}(x|y)\cdot f_Y(y)$$
?
汇总:二元离散型与连续型随机变量分布比较
?
?离散型
?联合分布律
?边际分布律
?条件分布律
?连续型
?联合概率密度
?边际概率密度
?条件概率密度
第22讲二元均匀分布,二元正态分布
?二元均匀分布
?$$f(x,y)=1/A,(x,y)\in D$$
?二元正态分布
?$$\begin{align}&f(x,y)=\frac{1}{2\pi\sigma_1\sigma
_2\sqrt{1-\rho^2}}\times\ &exp{\frac{-1}{2(1-\rho2)}[\frac
{(x-\mu_1)2}{\sigma_12}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\fr
ac{(y-\mu_2)2}{\sigma_2^2}]}\end{align}$$
?$\sigma_1,\sigma_2>0$ ,$-1<\rho<1$
?记为$(X,Y)\sim N(\mu_1,\mu_2,\sigma_12,\sigma_22,\
rho)$
?二元正态分布的边际概率密度
?$$X\sim N(\mu_1,\sigma_2^2)$$
?即边际概率分布服从正态分布
?二元正态分布的条件概率密度
?$$Y|X\sim N(\mu_2+\rho\frac{\sigma_2}{\sigma_1}
(x-\mu_1),(1-\rho2)\sigma_22)$$
?即条件概率分布服从正态分布
第23讲随机变量的独立性
?随机变量的独立性
?$$F(x,y)=F_X(x)F_Y(y)$$
?离散型随机变量的独立性
?$$P(X=x_i,Y=y_j)=P(X=x_i)P(Y=y_j)$$ ?连续型随机变量的独立性
?$$f(x,y)=f_X(x)f_Y(y)$$
?$n$ 元随机变量的分布
?分布函数
?分布律
?概率密度函数
?边际分布
?向量的独立性
?$$F(x_1,x_2,...,x_m,y_1,y_2,...,y_n)=F_1(x_1,x_2,...,x_m) F_2(y_1,y_2,...y_n)$$
?性质
?若两向量独立
1.$X_i$ 与$Y_j$ 相互独立
2.若$g(x_1,x_2,...,x_m)$ 与$h(y_1,y_2,...y_
n)$ 是连续函数,则$g(X_1,X_2,...,X_m)$ 与$h(Y_1,Y
_2,...Y_n)$ 相互独立
?直观理解
?性质1表明,若$X_i$ 与$Y_j$ 相互独立,
则$X_1$ 与$Y_1$ 相互独立,$X_1$ 与$X_2$
相互独立
?性质2表明,若$X_i$ 与$Y_j$ 相互独立,
则$X_1+X_2$ 与$Y_1\times Y_2$ 相互独立
第24讲二元随机变量函数的分布
?二元随机变量函数的分布(如$Z=X ?用分布律,分析各种情况 ?连续型 ?先求$F(x)$,再求导得到 第25讲$Z=X+Y$的分布 ?连续型 ?$$F_z(z)=P(Z\leq z)=\iint_{x+y\leq z}f(x,y)dxdy$$ ?$$f_Z(z)=\int_{-\infty}^{+\infty}f(z-y,y)dy$$ ?卷积公式 ?当$X$ 与$Y$ 相互独立时 ?$$f_Z(z)=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)d y$$ ?拓展:知乎问题:如何通俗易懂地解释卷积? ?关于正态分布的结论 ?若$X$ 与$Y$ 相互独立,$X\sim N(\mu_1,\ sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$,则 ?$$(Z=X+Y)\sim N(\mu_1+\mu_2,\sigma _12+\sigma_22)$$ ?更一般的,若$X_i$ 服从线性分布,则其线性组 合 ?$c_0+c_1 X_1+c_2 X_2+...+c_n X_n\sim N(\mu,\sigma^2)$ ?其中 ?$$\mu=c_0+c_1\mu_1+...+c_n\mu_n,\ \ sigma2=c_12\sigma_12+c_22\sigma_22+...+c_n2\sigma _n^2$$ ?$\Gamma$ 分布Gamma Distribution (非重点,可略过) ?离散型 ?若$X_1,X_2,...,X_n$ 独立且服从$B(1,p)$ 则?$$X_1+X_2+...+X_n\sim B(n,p)$$ ?若$X$ 与$Y$ 相互独立,$X\sim B(n_1,p),Y\sim B (n_2,p)$ 则 ?$$X+Y\sim B(n_1+n_2,p)$$ ?若$X$ 与$Y$ 相互独立,$X\sim \pi(\lambda_1),Y\ sim \pi(\lambda_1+\lambda_2)$ 则 ?$$X+Y\sim \pi(\lambda_1+\lambda_2)$$ 第26讲$max (X,Y)$和$min (X,Y)$的分布 ?若$X$ 与$Y$ 相互独立 ?$$\begin{split}F_{max}(z)&=P(M\leq z)\ &=P(X\le q z,Y\leq z)\ &=P(X\leq z)P(Y\leq z)\end{split}$$ ?$$f_{max}(z)=f_X(z)f_Y(z)$$ ?同理 ?$$f_{min}(z)=1-(1-f_X(z))(1-f_Y(z))$$ ?$n$ 个相互独立的随机变量同理 ?若$X_n$ 相互独立且分布相同 ?$$f_{max}(z)=n[F(z)]^{n-1}f(z)$$ ?$$f_{min}(z)=n[1-F(z)]^{n-1}f(z)$$ ?提示:该小节在第七章第二节“估计量的评价,无偏差性”中有重要应用 概率论总结 目录 一、前五章总结 第一章随机事件和概率 (1) 第二章随机变量及其分布 (5) 第三章多维随机变量及其分布 (10) 第四章随机变量的数字特征 (13) 第五章极限定理 (18) 二、学习概率论这门课的心得体会 (20) 一、前五章总结 第一章随机事件和概率 第一节:1.、将一切具有下面三个特点: (1)可重复性 (2)多结果性 (3)不确定性的试验或观察称为随机试验,简称为试验,常用E表 示。 在一次试验中,可能出现也可能不出现的事情(结果)称为 随机事件,简称为事件。 不可能事件:在试验中不可能出现的事情,记为Ф。 必然事件:在试验中必然出现的事情,记为S或Ω。 2、我们把随机试验的每个基本结果称为样本点,记作e 或ω. 全 体样本点的集合称为样本空间. 样本空间用S或Ω表示. 一个随机事件就是样本空间的一个子集。 基本事件—单点集,复合事件—多点集 一个随机事件发生,当且仅当该事件所包含的一个样本点出现。 事件间的关系及运算,就是集合间的关系和运算。 3、定义:事件的包含与相等 若事件A发生必然导致事件B发生,则称B包含A,记为B?A或A?B。 若A?B且A?B则称事件A与事件B相等,记为A=B。 定义:和事件 “事件A与事件B至少有一个发生”是一事件,称此事件为事件A与事件B的和事件。记为A∪B。用集合表示为: A∪B={e|e∈A,或e∈B}。 定义:积事件 称事件“事件A与事件B都发生”为A与B的积事件,记为A∩B或AB,用集合表示为AB={e|e∈A且e∈B}。 定义:差事件 称“事件A发生而事件B不发生,这一事件为事件A与事件B的差事件,记为A-B,用集合表示为 A-B={e|e∈A,e?B} 。 定义:互不相容事件或互斥事件 如果A,B两事件不能同时发生,即AB=Φ,则称事件A与事件B是互不相容事件或互斥事件。 定义6:逆事件/对立事件 称事件“A不发生”为事件A的逆事件,记为ā。A与ā满足:A∪ā= S,且Aā=Φ。 运算律: 设A,B,C为事件,则有 (1)交换律:A∪B=B∪A,AB=BA (2)结合律:A∪(B∪C)=(A∪B)∪C=A∪B∪C A(BC)=(AB)C=ABC (3)分配律:A∪(B∩C)=(A∪B)∩(A∪C) A(B∪C)=(A∩B)∪(A∩C)= AB∪AC Y= A I B A B 第四章 随机变量的数字特征 1.(1)在下列句子中随机地取一个单词 , X 表示取到的单词所包的字 母个数,写出 X 的分布律并求 E ( X ). “T HE GIR L PU T ON HER BEA U TIF UL RED HA T ”. (2)在上述句子的 30个字母中随机地取一个字母 , Y 表示取 的字母所 在单词所包含的字母数 ,写出 Y 的分布律并求 E (Y ). (3)一人掷骰子 ,如得6点则掷第2次,此时得分为 6 +第次得到的点数 ; 否则得分为 ,且不能再掷 ,求得分 X 的分布律及 E ( X ). .所 8个单 词,其中含2个字母 ,含 解 (1)随机试验 4个字母,含9个字母的各有一个单词 ,另有5个单词含3个字母,所 X 的分布 律为 X 2 3 4 9 1 8 5 8 1 8 1 8 p k 数学期望 1 8 5 8 1 1 15 4 E ( X ) = 2 × + 3 × + 4 × + 9 × . = 8 8 (2)随机试验 字母组成 ,共有30个 ,Y 的可能值也是 2,3,4,9. ,其中 Y = 2的有2个, S 由各个 Y = 3的有 15个, Y = 4的有4个, Y = 9的有9个,所 Y 的分布律为 Y 2 3 4 9 2 30 15 30 4 30 9 30 p k 2 30 + 3 × 15 + 4 × 30 4 30 9 30 73 15 数学期望 E (Y ) = 2 × (3)分布律为 + 9 × . = X 1 2 3 4 5 7 8 9 10 11 1 2 1 6 1 6 1 6 1 6 1 6 1 36 1 36 1 36 1 36 1 36 1 36 p k 习题四 1.设随机变量X 的分布律为 求E (X ),E (X ),E (2X +3). 【解】(1) 11111 ()(1)012;82842 E X =-? +?+?+?= (2) 22 22211115()(1)012;82844 E X =-?+?+?+?= (3) 1 (23)2()32342 E X E X +=+=?+= 2.已知100个产品中有10个次品,求任意取出的5个产品中的次品数的数学期望、方差. 故 ()0.58300.34010.07020.0073E X =? +?+?+?+?+? 0.501,= 5 2 ()[( )]i i i D X x E X P == -∑ 222(00.501)0.583(10.501)0.340(50.501)00.432. =-?+-?++-?= 3.设随机变量且已知E (X )=0.1,E (X )=0.9,求P 1,P 2,P 3. 【解】因1231P P P ++=……①, 又12331()(1)010.1E X P P P P P =-++=-= ……②, 2222 12313()(1)010.9E X P P P P P =-++=+= ……③ 由①②③联立解得1230.4,0.1,0.5.P P P === 4.袋中有N 只球,其中的白球数X 为一随机变量,已知E (X )=n ,问从袋中任取1球为白球的概率是多少? 【解】记A ={从袋中任取1球为白球},则 (){|}{}N k P A P A X k P X k ===∑ 全概率公式 1{}{} 1().N N k k k P X k kP X k N N n E X N N ===== ===∑∑ 5.设随机变量X 的概率密度为 f (x )=?? ? ??≤≤-<≤.,0,21,2, 10,其他x x x x 求E (X ),D (X ). 【解】1 2 2 1 ()()d d (2)d E X xf x x x x x x x +∞ -∞ = =+-? ?? 2 1 3 32011 1.33x x x ?? ??=+-=??????? ? 1 2 2 2 3 20 1 7 ()()d d (2)d 6 E X x f x x x x x x x +∞ -∞ ==+-= ? ?? 故 2 2 1()()[()].6 D X E X E X =-= 6.设随机变量X ,Y ,Z 相互独立,且E (X )=5,E (Y )=11,E (Z )=8,求下列随机变量的数学期望. (1) U =2X +3Y +1; (2) V =YZ -4X . 【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=?+?+= (2) [][4][]4()E V E YZ X E YZ E X =-=- ,()()4()Y Z E Y E Z E X - 因独立 1184568.=?-?= 7.设随机变量X ,Y 相互独立,且E (X )=E (Y )=3,D (X )=12,D (Y )=16,求E (3X -2Y ), D (2X -3Y ). 【解】(1) (32)3()2()3323 3. E X Y E X E Y -=-=?-?= (2) 2 2 (23)2()(3)412916192.D X Y D X DY -=+-=?+?= 8.设随机变量(X ,Y )的概率密度为 第三章 习题参考答案 1.计算习题二第2题中随机变量的期望值。 解:由习题二第2题计算结果 01 12{0}={1}= 3 3 p p p p ξξ====, 得 122 01333 E ξ=?+?= 一般对0-1分布的随机变量ξ有{1}E p p ξξ=== 2.用两种方法计算习题二第30题中周长的期望值,一种是利用矩形长与宽的期望计算,另一种是利用周长期望的分布计算。 解:方法一:先按定义计算长的数学期望 290.3300.5310.229.9E ξ=?+?+?= 和宽的数学期望 190.3200.4210.320E η=?+?+?= 再利用数学期望的性质计算周长的数学期望 (22)229.922099.8E E ζξη=+=?+?= 方法二:利用习题二地30题的计算结果(见下表),按定义计算周长的数学期望 960.09980.271000.351020.231040.0698.8 E ξ=?+?+?+?+?=3.对习题二第31题,(1)计算圆半径的期望值;(2)(2)E R π是否等于2ER π?(3)能否用2 ()ER π来计算远面积的期望值,如果不能 用,又该如何计算?其结果是什么? 解(1)100.1110.4120.3130.211.6ER =?+?+?+?= (2)由数学期望的性质有 (2)223.2E R ER πππ== (3)因为22()()E R E R ππ≠,所以不能用2 ()E R π来计算圆面积 的期望值。利用随机变量函数的期望公式可求得 222222()()(100.1110.4120.3130.2)135.4E R E R ππππ==?+?+?+?= 或者由习题二第31题计算结果,按求圆面积的数学期望 1000.11210.41440.31690.2)135.4E ηπππ=?+?+?+?= 4. 连续随机变量ξ的概率密度为 ,01(,0) ()0,a kx x k a x ??<<>=?? 其它 又知0.75E ξ= ,求k 和a 的值 解 由 1 010()11324 a a k x dx kx dx a k E kx x dx a ?ξ+∞ -∞== =+=?== +??? 解得 2,3 a k == 5.计算服从拉普拉斯分布的随机变量的期望和方差(参看习题二第16题)。 解 因为奇函数在对称区域的积分为零,所以|| 102x E x e dx ξ+∞ --∞==?, 同样由偶函数在对称区域积分的性质可计算 概率论第四章习题解答 1(1)在下列句子中随机地取一个单词,以X 表示取到的单词所饮食的字母个数,写出X 的分布律并求数学期望()E X 。 “THE GIRL PUT ON HER BEAUTIFUL RED HAT ” (2)在上述句子的30个字母中随机地取一个字母,以Y 表示取到的字母所在单词所包含的字母数,写出Y 的分布律并求()E Y (3)一人掷骰子,如得6点则掷第二次,此时得分为6加第二次得到的点数;否则得分为第一次得到的点数,且不能再掷,求得分X 的分布律。 解 (1)在所给的句子中任取一个单词,则其所包含的字母数,即随机变量X 的取值为:2,3,4,9,其分布律为 所以 1 51115()234988884 E X =?+?+?+?=。 (2)因为Y 的取值为2,3,4,9 当2Y =时,包含的字母为“O ”,“N ”,故 121{2}3015 C P Y ===; 当3Y =时,包含的3个字母的单词共有5个,故 135151{3}30302 C P Y ==== 当4Y =时,包含的4个字母的单词只有1个,故 1442{4}303015 C P Y ==== 当9Y =时,包含的9个字母的单词只有1个,故 993{9}303010P Y == == 112314673()234915215103015 E Y =?+?+?+?==。 (3)若第一次得到6点,则可以掷第二次,那么他的得分为:X =7,8,9,10,11,12; 若第一次得到的不是6点,则他的得分为1,2,3,4,5。由此得X 的取值为: 1,2,3,4,5,7,8,9,10,11,12。 X 2 3 4 9 p 18 58 18 18 Y 2 3 4 9 p 115 12 215 310 概率论与数理统计 第二章和第三章 -、选择题 1. 设随机变量,独立同分布,且的分布函数为,则的分布函 数为( A ). (A) (B) (C) (D) 2. 设与为两个分布函数,其相应的概率密度函数与是连续函数, 则必为概率密度的是 ( D ). (A) (B) (C) (D) 3. 设随机变量,记,则( B ). (A) 随着的增加而增加 (B) 随着的增加而增加 (C) 随着的增加而减少 (D) 随着的增加而减少 4. 设随机变量服从正态分布,服从正态分布,且 ,则必有( A ). (A) (B) (C) (D) 二、填空题 1. 设二维随机变量服从正态分布,则. 答案: 2. 设随机变量服从参数为的指数分布,为常数且大于零,则 . 答案: 3. 设随机变量服从参数为的泊松分布,则. X Y X F(x)Z=max{X,Y}2 F (x)F(x)F(y)2 1-[1-F(x)][1-F(x)][1-F(y)]1F ()x 2F ()x 1()f x 2()f x 12()()f x f x 122()()f x F x 212()()f x F x 1212()()()()f x F x F x f x +2 X~N(,) (0)μσσ>2 p=P(X +)μσ≤p μp σp μp σX 211N(,)μσY 222N(,)μσ12P(|X-|<1)>P(|Y-|<1)μμ12<σσ12σσ>12<μμ12μμ>(X,Y)N(1,0;1,1;0)P{XY-Y<0}=12 X 1a P{Y a+1|Y>a}=≤1 1e --X 12 P{X=E(X )}= 概率论与数理统计第 四章答三、案 第三章习题参考答案 1.计算习题二第2题中随机变量的期望值 解:由习题二第2题计算结果 长与宽的期望计算,另一种是利用周长期望的分布计算。 解:方法一:先按定义计算长的数学期望 E 29 0.3 30 0.5 31 0.2 29.9 和宽的数学期望 E 19 0.3 20 0.4 21 0.3 20 再利用数学期望的性质计算周长的数学期望 E E (2 2 ) 2 29.9 2 20 99.8 方法二:利用习题二地30题的计算结果(见下表),按定义计算周长 的数学期望 1 P 0 p{ 0}= , P 1 3 P{ 1}= 2 3 得 1 2 2 E 0」 1 3 3 3 般对0-1分布的随机变量 有 E P P{ 1} 2.用两种方法计算习题二第 30题中周长的期望值, 一种是利用矩形 E 96 0.09 98 0.27 100 0.35 102 0.23 104 0.06 98.8 3.对习题二第31题,(1)计算圆半径的期望值;(2)E (2 R)是否等于2 ER ? (3)能否用(ER)2来计算远面积的期望值,如果不能 用,又该如何计算?其结果是什么? 解(1) E^ = 10x0?1+11X0?4+12X0?3+13X0?2=11?6 (2)由数学期望的性质有 E(27rR) = 27rER = 23?27r (3)因为E5R2)H7rE(Rf,所以不能用TT E(R2}来计算圆面积的期望值。利用随机变量函数的期望公式可求得 E(TT R2)=托E(R2) = ^-(102 X 0.1 +112 X 0.4 +122 X 0.3 +132 X 0.2)= 135.4兀或者由习题二第31题计算结果,按求圆面积的数学期望 £77 = 100^x0.1+121^x0.4 + 144x0.3 + 169x0.2) = 135.4^ 4.连续随机变量J的概率密度为 Ax“,0vxvl(&,a>0) 0,其它 又知^ = 0.75 ,求斤和Q的值 解得a = 2.k =3 5.计算服从拉普拉斯分布的随机变量的期望和方差(参看习题二第 16 题)。 解因为奇函数在对称区域的积分为零,所以砖叮雋严心0, 同样由偶函数在对称区域积分的性质可计算 概率,亦称“或然率”,它是反映随机事件出现的可能性大小。随机事件是指在相同条件下,可能出现也可能不出现的事件。例如,从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察,其中A 事件出现了m次,即其出现的频率为m/n。 频率定义: 随着人们遇到问题的复杂程度的增加,等可能性逐渐暴露出它的弱点,特别是对于同一事件,可以从不同的等可能性角度算出不同的概率,从而产生了种种悖论。另一方面,随着经验的积累,人们逐渐认识到,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一定的稳定性。 公理化定义 柯尔莫哥洛夫于1933年给出了概率的公理化定义,如下: 设E是随机试验,S是它的样本空间。对于E的每一事件A赋于一个实数,记为P(A),称为事件A的概率。这里P(A)是一个集合函数,P(A)要满足下列条件: (1)非负性:对于每一个事件A,有P(A)≥0; (2)规范性:对于必然事件,有P(Ω)=1; (3)可列可加性:设A1,A2……是两两互不相容的事件,即对于i≠j,Ai∩Aj=φ,(i,j=1,2……),则有 P(A1∪A2∪……)=P(A1)+P(A2)+…… 《概率论(经管类)》是2016年科学出版社出版的图书,作者是王文轲,高慧,卫贵武。 内容简介: 本书是一线教师在对近10年的概率论教学经验总结的基础上编写而成的.本书主要内容包括随机事件的概率、一维随机变量及其分布、多维随机变量及其分布,随机变量的数字特征、大数定理及中心极限定理.编写过程遵循由浅入深,由易到难,由具体到抽象的原则,以便学生易于理解和掌握.全书每节都配备了习题,且每章最后配备了总习题,这样便于学生巩固知识,也为自学者提供同步复习的内容,从而达到巩固新知识的目的. 目录: 第一章随机事件的概率 第二章一维随机变量及其分布 第三章多维随机变量及其分布 第四章随机变量的数字特征 第五章大数定律及中心极限定理 参考资料 概率论与数理统计第三、四章答案 第三章 习题参考答案 1.计算习题二第2题中随机变量的期望值。 解:由习题二第2题计算结果 112 {0}={1}= 33 p p p p ξξ====, 得 122 01333 E ξ=?+?= 一般对0-1分布的随机变量ξ有{1}E p p ξξ=== 2.用两种方法计算习题二第30题中周长的期望值,一种是利用矩形长与宽的期望计算,另一种是利用周长期望的分布计算。 解:方法一:先按定义计算长的数学期望 290.3300.5310.229.9E ξ=?+?+?= 和宽的数学期望 190.3200.4210.320E η=?+?+?= 再利用数学期望的性质计算周长的数学期望 (22)229.922099.8E E ζξη=+=?+?= 方法二:利用习题二地30题的计算结果(见下表),按定义计算周长的数学期望 ξ 96 98 100 102 104 p 0.09 0.27 0.35 0.23 0.06 960.09980.271000.351020.231040.0698.8E ξ=?+?+?+?+?=3.对习题二第31题,(1)计算圆半径的期望值;(2)(2)E R π是否等于2ER π?(3)能否用2()ER π来计算远面积的期望值,如果不能 2 2 || 201()2x x D E x e dx x e dx ξξ+∞ +∞---∞ ===? ? 20 | 22x x x e xe dx +∞ -+∞ -=-+=? 6题目略 解 (1)15辆车的里程均值为 1274(9050150)91.33153 ++???+=≈ (2) 记ξ为从188辆汽车中任取一辆记录的里程数,则ξ的分布表如下表所示(a=188) ξ 10 30 50 70 90 110 130 150 170 p 5/a 11/a 16/a 25/a 34/a 46/a 33/a 16/a 2/a 故51124520103017096.1718818818847 E ξ=?+?+???+?=≈ 7题目略 解 记ξ为种子甲的每公顷产量,η为种子乙的每公顷产量,则 45000.1248000.3851000.454000.14944E ξ=?+?+?+?= 45000.2348000.2451000.354000.234959E η=?+?+?+?= 8.一个螺丝钉的重量是随机变量,期望值10g,标准差为1g,100个一盒的同型号螺丝钉重量的期望值和标准差个为多少(假设每个螺丝钉的重量都部首其他螺丝钉重量的影响)? 解 设i ξ为一盒中第i 个螺丝钉的重量(1,2,,100)i =???,则 题设条件为 第四章 数字特征与特征函数 1、解:∑∑∞ =∞=+??? ???????? ??++=+=011 111)1(,k k k k k a a a a a k E ξ,令p a a =+)1(,则10<
概率论知识点总结复习整理
概率论与数理统计_第四版_第四章
概率论与统计(第三版)复旦大学版第四章课后习题答案
概率论与数理统计第三、四章答案
概率论第四章课后习题解答(内容参考)
概率论与数理统计:第二章、第三章和第四章(1)
概率论与数理统计第三、四章答案
概率论第四章
概率论与数理统计第三、四章答案
概率论第四章答案