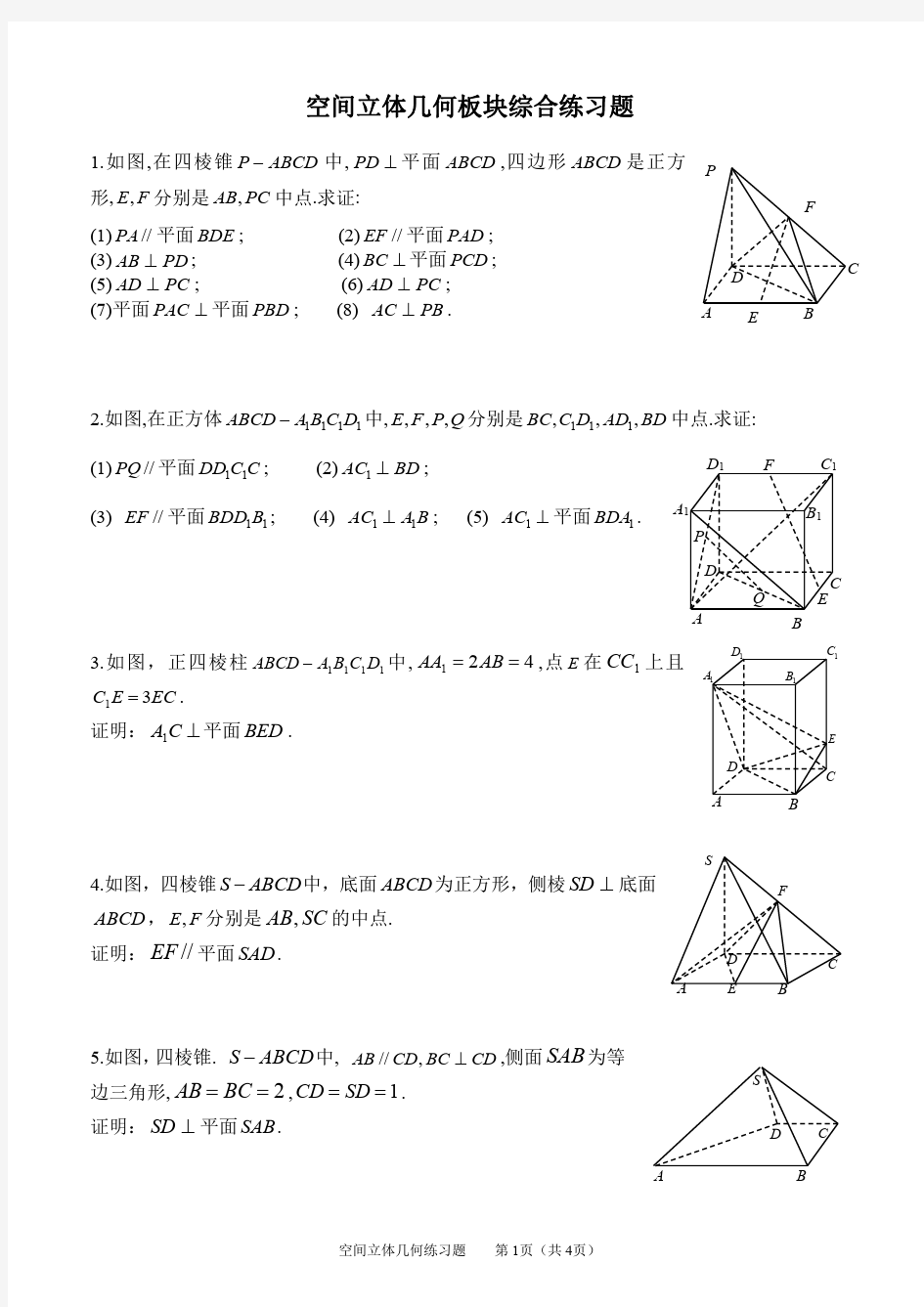

D C 1 A 1 B 1 C 1 D B C A D 立体几何专题----空间角 知识点归纳 1、异面直线所成的角 异面直线所成角的定义: 如图,已知两条异面直线 a , b , 经过空间任一点O作直线 a′∥a , b ′∥b 则把 a ′ 与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角). a b 注1:异面直线所成的角的范围( 0O , 90O ] 注2:如果两条异面直线 a , b 所成的角为直角,我们就称这两条直线互相垂直 , 记为a ⊥ b 注3:在求作异面直线所成的角时,O点常选在其中的一条直线上(如线段的端点,线段的中点等) 2 、直线与平面所成的角 平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角 (1)一条直线垂直于平面,它们所成的角是直角 (2)一条直线和平面平行,或在平面内,它们所成的角是0 ?的角 (3)直线和平面所成角的范围是[0?,90?] 3、二面角: 如右图在二面角的棱l取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则 叫做二面角的平面角. 注:①二面角的平面角的大小与O点位置_____ _。 ②二面角的平面角的范围是_______ 。 ③平面角为______的二面角叫做直二面角。 试题探究: 1、如图:表示正方体 1 1 1 1 D C B A ABCD-, 求异面直线 1 1 CC BA和所成的角。 2、空间四边形ABCD中,2 AD BC ==,,E F分别是, AB CD的中点,3 EF=, 求异面直线, AD BC所成的角。 3、在单位正方体 1111 ABCD A B C D -中,试求直线 1 BD与平面ABCD所成的角. 4、在单位正方体 1111 ABCD A B C D -中,求直线 11 A C与截面 11 ABC D所成的角. 5、将一副三角板如图拼接,∠BAC=∠BCD=90°,AB=AC,∠BDC=60°,且平面ABC⊥平面BCD, (1)求证:平面ABD⊥平面ACD;(2)求二面角A-BD-C的正切值;(3)求异面直线AD与BC所成角的余弦值. a′O b′ a P α O A O A B D C A 1 B 1 C 1 D A F E D B A B D B 1 A 1 C 1 D 1
高中立体几何典型500题及解析(二)(51~100题) 51. 已知空间四边形ABCD 中,AB=BC=CD=DA=DB=AC,M 、N 分别为BC 、AD 的中点。 求:AM 及CN 所成的角的余弦值; 解析:(1)连接DM,过N 作NE∥AM 交DM 于E ,则∠CNE 为AM 及CN 所成的角。 ∵N 为AD 的中点, NE∥AM 省 ∴NE=2 1AM 且E 为MD 的中点。 设正四面体的棱长为1, 则NC=21·23= 4 3且ME=2 1MD= 4 3 在Rt△MEC 中,CE 2=ME 2+CM 2= 163+41=16 7 ∴cos ∠CNE= 324 3 432167)43()43( 2222 22-=??-+=??-+NE CN CE NE CN , 又∵∠CNE ∈(0, 2 π) ∴异面直线AM 及CN 所成角的余弦值为3 2. 注:1、本题的平移点是N ,按定义作出了异面直线中一条的平行线,然后先在△CEN 外计算CE 、CN 、EN 长,再回到△CEN 中求角。 2、作出的角可能是异面直线所成的角,也可能是它的邻补角,在直观图中无法判定,只有通过解三角形后,根据这个角的余弦的正、负值来判定这个角是锐角(也就是异面直线所成的角)或钝角(异面直线所成的角的邻补角)。最后作答时,这个角的余弦值必须为正。
52. .如图所示,在空间四边形ABCD 中,点E 、F 分别是BC 、AD 上的点,已知AB=4,CD=20,EF=7, 3 1 ==EC BE FD AF 。求异面直线AB 及CD 所成的角。 解析:在BD 上取一点G ,使得3 1 =GD BG ,连结EG 、FG 在ΔBCD 中,GD BG EC BE = ,故EG//CD ,并且4 1==BC BE CD EG , 所以,EG=5;类似地,可证FG//AB ,且 4 3 ==AD DF AB FG , 故FG=3,在ΔEFG 中,利用余弦定理可得 cos ∠ FGE= 2 1 5327532222222- =??-+=??-+GF EG EF GF EG ,故∠FGE=120°。 另一方面,由前所得EG//CD ,FG//AB ,所以EG 及FG 所成的锐角等于AB 及CD 所成的角,于是AB 及CD 所成的角等于60°。 53. 在长方体ABCD -A 1B 1C 1D 1中,AA 1=c ,AB=a ,AD=b ,且a >b .求AC 1及BD 所成的角的余弦. A B C D E F G E D 1 C 1 B 1 A 1 A B D C O
第一章 空间几何体 [基础训练A 组] 一、选择题 1.有一个几何体的三视图如下图所示,这个几何体应是一个( ) A.棱台 B.棱锥 C.棱柱 D.都不对 2.棱长都是1的三棱锥的表面积为( ) 3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在 同一球面上,则这个球的表面积是( ) A .25π B .50π C .125π D .都不对 4.正方体的内切球和外接球的半径之比为( ) A B 2 C . 5.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周, 则所形成的几何体的体积是( ) A. 92π B. 72π C. 52π D. 32 π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长 分别是9和15,则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160 二、填空题 1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点, 顶点最少的一个棱台有 ________条侧棱。 2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。 3.正方体1111ABCD A BC D - 中,O 是上底面ABCD 中心,若正方体的棱长为a , 则三棱锥11O AB D -的体积为_____________。 4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形 E BFD 1在该正方体的面上的射影可能是____________。 5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个 长 方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________. 三、解答题 1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用) ,已建的仓库的 主视图 左视图 俯视图
-立体几何中的传统法求空间角 知识点: 一.异面直线所成角:平移法 二.线面角 1.定义法:此法中最难的是找到平面的垂线.1.)求证面垂线,2).图形中是否有 面面垂直的结构,找到交线,作交线的垂线即可。 2.用等体积法求出点到面的距离sinA=d/PA 三.求二面角的方法 1、直接用定义找,暂不做任何辅助线; 2、三垂线法找二面角的平面角. 例一:如图,在正方体错误!未找到引用源。中,错误!未找到 引用源。、错误!未找到引用源。分别是错误!未找到引用 源。、错误!未找到引用源。的中点,则异面直线错误!未 找到引用源。与错误!未找到引用源。所成的角的大小是 ______90______. 考向二线面角 例二、如图,在四棱锥P-ABCD中,底面ABCD是矩 形,AD⊥PD,BC=1, ,PD=CD=2. (I)求异面直线PA与BC所成角的正切值;(II)证明平面PDC⊥平面ABCD; (III)求直线PB与平面ABCD所成角的正弦值。 N A 1
练 习 : 如图 , 在 三棱锥 P ABC -中, PA ⊥底面 ,, 60,A B C P A A B A B C B C A ?? =∠=∠=, 点D ,E 分别在棱,PB PC 上,且//DE BC (Ⅰ)求证:BC ⊥平面PAC ; (Ⅱ)当D 为PB 的中点时,求AD 与平面PAC 所成的角的正弦值; (Ⅰ)∵PA ⊥底面ABC ,∴PA ⊥BC . 又90BCA ? ∠=,∴AC ⊥BC . ∴BC ⊥平面PAC . (Ⅱ)∵D 为PB 的中点,DE//BC ,
∴1 2 DE BC = , 又由(Ⅰ)知,BC ⊥平面PAC , ∴DE ⊥平面PAC ,垂足为点E . ∴∠DAE 是AD 与平面PAC 所成的角, ∵PA ⊥底面ABC ,∴PA ⊥AB ,又PA=A B , ∴△ABP 为等腰直角三角形,∴ AD AB = , ∴在Rt △ABC 中,60ABC ? ∠=,∴1 2 BC AB = . ∴在Rt △ADE 中,sin 24 DE BC DAE AD AD ∠= ==, 考向三: 二面角问题 在图中做出下面例题中二面角 例三:.定义法(2011广东理18) 如图5.在椎体P-ABCD 中,ABCD 是边长为1的棱形, 且∠DAB=60?,PA PD == E,F 分别是BC,PC 的中点. (1) 证明:AD ⊥平面DEF; (2) 求二面角P-AD-B 的余弦值. 法一:(1)证明:取AD 中点G ,连接PG ,BG ,BD 。 因PA=PD ,有PG AD ⊥,在ABD ?中,1,60AB AD DAB ==∠=?,有ABD ?为 等边三角形,因此,BG AD BG PG G ⊥?=,所以AD ⊥平面 PBG ,.AD PB AD GB ?⊥⊥ 又PB//EF ,得AD EF ⊥,而DE//GB 得AD ⊥DE ,又FE DE E ?=,所以AD ⊥ 平面DEF 。
高中空间立体几何典型 例题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
1 如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E=C 1F. 求证:EF ∥平面ABCD. 证明 方法一 分别过E ,F 作EM ⊥AB 于M ,FN ⊥BC 于N ,连接MN. ∵BB 1⊥平面ABCD , ∴BB 1⊥AB ,BB 1⊥BC , ∴EM ∥BB 1,FN ∥BB 1, ∴EM ∥FN. 又∵B 1E=C 1F ,∴EM=FN , 故四边形MNFE 是平行四边形,∴EF ∥MN. 又MN ?平面ABCD ,EF ?平面ABCD , 所以EF ∥平面ABCD. 方法二 过E 作EG ∥AB 交BB 1于G , 连接GF ,则B B G B A B E B 1111=, ∵B 1E=C 1F ,B 1A=C 1B , ∴B B G B B C E C 1111=,∴FG ∥B 1C 1∥BC , 又EG ∩FG =G ,AB ∩BC =B , ∴平面EFG ∥平面ABCD ,而EF ?平面EFG , ∴EF ∥平面ABCD . 2 已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC 的重心.
(1)求证:平面G 1G 2G 3∥平面ABC ; (2)求S △3 21G G G ∶S △ABC . (1)证明 如图所示,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F , 连接DE 、EF 、FD ,则有PG 1∶PD =2∶3, PG 2∶PE =2∶3,∴G 1G 2∥DE . 又G 1G 2不在平面ABC 内, ∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC . 又因为G 1G 2∩G 2G 3=G 2, ∴平面G 1G 2G 3∥平面ABC . (2)解 由(1)知PE PG PD PG 21 =32,∴G 1G 2=32DE . 又DE =21AC ,∴G 1G 2=31 AC . 同理G 2G 3=31AB ,G 1G 3=3 1BC . ∴△G 1G 2G 3∽△CAB ,其相似比为1∶3, ∴S △3 21G G G ∶S △ABC =1∶9. 3如图所示,已知S 是正三角形ABC 所在平面外的一点,且SA =SB =SC ,SG 为△SAB 上的高, D 、 E 、 F 分别是AC 、BC 、SC 的中点,试判断S G 与平面DEF 的位置关系,并给予证明. 解 SG ∥平面DEF ,证明如下: 方法一 连接CG 交DE 于点H , 如图所示.
第十二讲 立体几何之空间角 一、基本知识回顾 空间的角主要包括两条异面直线所成的角、直线与平面所成的角以及二面角。 1) 异面直线所成角 1.022.π??? ? ???????????范围:,平移相交(找平行线替换)求法:向量法??? ??20π, 2) 直线与平面所成角 1.π???????????????? 范围0,2定义2.求法向量法?? ? ? ??2,0π n m n m ??=arcsin θ 若n m ⊥则α//a 或α?a 若n m //则α⊥a 3) 二面角[]1.0.2.π??? ?????? ?? ???? ???? ?????? 范围:定义法(即垂面法)作二面角平面角的方法:三垂线定理及逆定理垂线法 直接法3.求二面角大小的方法射影面积法向量法 θcos S S =' (S 为原斜面面积,S '为射影面积,θ为斜面与射影所成锐二面角的平面 角) 当θ为锐角时,n m n m ??=arccos θ 当θ为锐角时,n m n m ??-=arccos πθ
二、例题讲解 1.在正三棱柱 111 ABC A B C -中,若 1 2, AB BB =求 1 AB与B C 1 所成的角的大小。 解:法一:如图一所示, 设O为C B 1 、B C 1 的交点,D AC 为的中点,则所求角是DOB ∠。 设 1 ,2 BB a AB a == 则,于是在DOB ?中, 1 222 1 1336 ,2, 2222 13 ,, 2 OB BC a BD a a OD AB a BD OB OD ==== ===+ 即90, DOB ∠=?∴? = ∠90 DOB 法二:取 11 A B的中点O为坐标原点,如图建立空间直角坐标系, xyz O-AB 2 1 的长度单位,则由
立体几何专题:空间角 第一节:异面直线所成的角 一、基础知识 1.定义: 直线a 、b 是异面直线,经过空间一交o ,分别a ?//a ,b ?//b ,相交直线a ?b ?所成的锐角(或直 角)叫做 。 2.范围: ?? ? ??∈2,0πθ 3.方法: 平移法、问量法、三线角公式 (1)平移法:在图中选一个恰当的点(通常是线段端点或中点)作a 、b 的平行线,构造一个三角形,并解三角形求角。 (2)向量法: 可适当选取异面直线上的方向向量,利用公式b a = ><=,cos cos θ 求出来 方法1:利用向量计算。选取一组基向量,分别算出 b a ? 代入上式 方法2:利用向量坐标计算,建系,确定直线上某两点坐标进而求出方向向量 ),,(111z y x a = ),,(222z y x b =2 2 22222 1 2 12 12 12121cos z y x z y x z z y y x x ++++++= ∴θ (3)三线角公式 用于求线面角和线线角 斜线和平面内的直线与斜线的射影所成角的余弦之积等于斜线和平面内的直线所成角的余弦 即:θθθcos cos cos 2 1= 二、例题讲练 例1、(2007年全国高考)如图,正四棱柱 1111ABCD A B C D -中, 12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为 例2、在长方体ABCD-A 1B 1C 1D 1中,已知AB=a ,BC=)(b a b >,AA 1= c ,求异面直线D 1B 和AC 所成 的角的余弦值。 方法一:过B 点作 AC 的平行线(补形平移法) A B 1 B 1 A 1D 1 C C D
中小学1对1课外辅导专家 武汉龙文教育学科辅导讲义 授课对象 冯芷茜 授课教师 徐江鸣 授课时间 2013-9-19 授课题目 立体几何中的空间角 课 型 复习课 使用教具 讲义、纸、笔 教学目标 熟悉高考中立体几何题型的一般解法 教学重点和难点 重点:运用空间直角坐标系的方法解决立体几何问题 难点:二面角,线面角的空间想象能力 参考教材 人教版高中教材 高考考纲 历年高考真题 教学流程及授课详案 【知识讲解】 空间角的求法:(所有角的问题最后都要转化为解三角形的问题,尤其是直角三角形) (1)异面直线所成的角:通过直线的平移,把异面直线所成的角转化为平面内相交直线所成的角。异面直线所成角的范围:o o 900≤<α; 注意:若异面直线中一条直线是三角形的一边,则平移时可找三角形的中位线。有的还可以 通过补形,如:将三棱柱补成四棱柱;将正方体再加上三个同样的正方体,补成一个底面是正方形的长方体。 (2)线面所成的角:①线面平行或直线在平面内:线面所成的角为o 0; ②线面垂直:线面所成的角为o 90; ③斜线与平面所成的角:范围o o 900<<α;即也就是斜线与它在平面内的射影所成的角。 (3)二面角:关键是找出二面角的平面角。方法有:①定义法;②三垂线定理法;③垂面法; 注意:还可以用射影法:S S ' cos =θ;其中θ为二面角βα--l 的大小,S 为α内的一个封 闭几何图形的面积;'S 为α内的一个封闭几何图形在β内射影图形的面积。一般用于解选择、填空题。 时 间 分 配 及 备 注
【题海拾贝】 例1在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点. EF平面P AD; (1)求证:// (2)当平面PCD与平面ABCD成多大二面角时, EF平面PCD? 直线 例2已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC = AD = CD = DE = 2a,AB = a, F为CD的中点. (Ⅰ)求证:AF⊥平面CDE; (Ⅱ)求异面直线AC,BE所成角余弦值; (Ⅲ)求面ACD和面BCE所成二面角的大小.
立体几何坐标解法典型例题 1、如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点. (Ⅰ)求证:1AB ⊥平面1A BD ; (Ⅱ)求二面角1A A D B --的大小; (Ⅲ)求点C 到平面1A BD 的距离. 2、如图,在Rt AOB △中, π6 OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到,且二面角B AO C --的直二面角.D 是AB 的中点. (1)求证:平面COD ⊥平面AOB ; (2)求异面直线AO 与CD 所成角的大小. A B C D
3.(2010·上海松江区模拟)设在直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2,∠BAC =90°,E ,F 依次为C 1C ,BC 的中点. (1)求异面直线A 1B 、EF 所成角θ的正弦值; (2)求点B 1到平面AEF 的距离. 4.四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =o ∠, 2AB = ,BC = SA SB == (Ⅰ)证明SA BC ⊥; (Ⅱ)求直线SD 与平面SAB 所成角的大小. D B C A S
5.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB → 的值为( ) A .0 B .1 C .0或1 D .任意实数 5.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值等于( ) A.32 B.1010 C.35 D.25 <二>选择题辨析 [注]: ①两条异面直线在同一平面内射影一定是相交的两条直线.(×) ②直线在平面外,指的位置关系:平行或相交 ③若直线a 、b 异面,a 平行于平面,b 与的关系是相交、平行、在平面内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点. ⑤在平面内射影是直线的图形一定是直线.(×) ⑥在同一平面内的射影长相等,则斜线长相等.(×) ⑦是夹在两平行平面间的线段,若,则的位置关系为相交或平行或异面. [注]: ①直线与平面内一条直线平行,则∥. (×) ②直线与平面内一条直线相交,则与平面相交. (×) ③若直线与平面平行,则内必存在无数条直线与平行. (√) ④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×) ⑤平行于同一直线的两个平面平行.(×) ⑥平行于同一个平面的两直线平行.(×) ⑦直线与平面、所成角相等,则∥.(×) [注]: ①垂直于同一平面....的两个平面平行.(×) ②垂直于同一直线的两个平面平行.(√) ③垂直于同一平面的两条直线平行.(√) αααb a ,b a =b a ,a αa αa αa αa ααa l αβαβ
文科立体几何线面角二面角专题 学校:___________姓名:___________班级:___________考号:___________ 一、解答题 1.如图,在三棱锥中,,,为的中点.(1)证明:平面; (2)若点在棱上,且二面角为,求与平面所成角的正弦值. 2.如图,在三棱锥中,,,为的中点.(1)证明:平面; (2)若点在棱上,且,求点到平面的距离. 3.(2018年浙江卷)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.
(Ⅰ)证明:AB1⊥平面A1B1C1; (Ⅱ)求直线AC1与平面ABB1所成的角的正弦值. 4.如图,在三棱柱中,点P,G分别是,的中点,已知⊥平面 ABC,==3,==2. (I)求异面直线与AB所成角的余弦值; (II)求证:⊥平面; (III)求直线与平面所成角的正弦值. 5.如图,四棱锥,底面是正方形,,,,分别是,的中点.
(1)求证; (2)求二面角的余弦值. 6.如图,三棱柱中,侧棱底面,且各棱长均相等.,,分别为棱,,的中点. (1)证明:平面; (2)证明:平面平面; (3)求直线与直线所成角的正弦值. 7.如图,在四边形ABCD中,AB//CD,∠AB D=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF. (Ⅰ)求证:平面ADE⊥平面BDEF; (Ⅱ)若二面角C BF D的大小为60°,求CF与平面ABCD所成角的正弦值. 8.如图,在四棱锥中,平面,,,
,点是与的交点,点在线段上,且. (1)证明:平面; (2)求直线与平面所成角的正弦值. 9.在多面体中,底面是梯形,四边形是正方形,,,,, (1)求证:平面平面; (2)设为线段上一点,,求二面角的平面角的余弦值. 10.如图,在多面体中,四边形为等腰梯形,,已知,,,四边形为直角梯形,,. (1)证明:平面,平面平面;
空间向量与立体几何 1, 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VADL底面ABC (1)证明AB丄平面VAD (2)求面VAD与面VDB所成的二面角的大小 2, 如图所示,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA丄底面ABCD AB骑, BC=1 , PA=2, E为PD的中点. (1)求直线AC与PB所成角的余弦值; (2)在侧面PAB内找一点N使NE!平面PAC并求出N点到AB和AP的距 离.(易错点,建系后,关于N点的坐标的设法,也是自己的弱项)
3. 如图,在长方体 ABCD-ABCD 中,AD=AA=1, AB=2,点E 在棱 AB 上移动. 证明:DE 丄AD; 当E 为AB 的中点时,求点 A 到面ECD 的距离; 7T AE 等于何值时,二面角 D — EC- D 的大小为-(易错点:在找平面DEC 的法向量的时候,本 来法向量就己经存在了 ,就不必要再去找,但是我认为去找应该没有错吧 ,但法向量找出来了 , 和 那个己经存在的法向量有很大的差别 ,而且,计算结果很得杂,到底问题出在哪里?) 4. 如图,直四棱柱 ABCD — A I B I C I D I 中,底面ABCD 是等腰梯形,AB // CD , AB = 2DC =2, E 为BD i 的中点,F 为AB 的中点,/ DAB = 60° (1)求证:EF //平面 ADD 1A 1; ⑵若BB 1 ~2-,求A 1F 与平面DEF 所成角的正弦值. N : 5 题到 11 题都是运用基底思想解题 5. 空间四边形 ABCD 中, AB=BC=CD AB 丄BC, BC 丄CD , AB 与CD 成60度角,求AD 与BC 所 成角的大小。 (1) (2) (3) A B
专题一:空间角 一、基础梳理 1.两条异面直线所成的角 (1)异面直线所成的角的范围:(0, ]2 π 。 (2)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直。两条异面直线,a b 垂直,记作a b ⊥。 (3)求异面直线所成的角的方法: (1)通过平移,在一条直线上(或空间)找一点,过该点作另一(或两条)直线的平行线; (2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求。 平移技巧有:平行四边形对边平移、三角形中位线平移、补形平移技巧等。 2.直线和平面所成的角(简称“线面角”) (1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角。 一直线垂直于平面,所成的角是直角;一直线平行于平面或在平面内,所成角为0?角。 直线和平面所成角范围:[0, 2 π]。 (2)最小角定理:斜线和平面所成角是这条斜线和平面内 经过斜足的直线所成的一切角中最小的角。 (3)公式:已知平面α的斜线a 与α内一直线b 相交成θ角, 且a 上的射影c 与b 相交成?2角, 则有θ??cos cos cos 21= 。 内的射影所成角,是这条斜线和这个平面内的任一条直 线所成角中最小的角。 3.二面角 (1)二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面。若棱为l ,两个面分别为,αβ的二面角记为l αβ--。 (2)二面角的平面角: 过二面角的棱上的一点O 分别在两个半平面内...... 作棱的两条垂线,OA OB ,则AOB ∠叫做二面角 l αβ--的平面角。 说明:①二面角的平面角范围是[]0,π,因此二面 角有锐二面角、直二面角与钝二面角之分。 ②二面角的平面角为直角时,则称为直二面角, 组成直二面角的两个平面互相垂直。 (3)二面角的求法:(一)直接法:作二面角的平面角的作法:①定义法;②棱的垂面法;③三垂线定理或逆定理法;(注意一些常见模型的二面角的平面角的作法) (二)间接法:面积射影定理的方法。 (4)面积射影定理: 面积射影定理:已知ABC ?的边BC 在平面α内,顶点A α?。设ABC ?的面积为S ,它在平 ?2?1c b a θP αO A B l B' O' A' B O A βα
2011届高考专题复习空间向量与立体几何 一、近年考情分析与2011年广东命题走势 纵观07-10广东试题,我们可以发现,此部分内容涉及试题数及分值为: 立体几何的复习要牢固树立以下的思维脉络:证线面垂直(或平行),转化为证线线垂直(或平行);证面面垂直(或平行),转化为证线面垂直(或平行)或证线线垂直(或平行). 二、广东考题剖析及热点题型讲析 热点1 空间几何体的结构、三视图、直观图 1.(08年广东5)将正三棱柱截去三个角(如图1所示A B C ,,分别是GHI △三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( A ) E F D I A H G B C E F D A B C 侧视 图1 图2 B E A . B E B . B E C . B E D .
2.(10年广东6)如图1,△ABC为正三角形,AA'//BB'//CC',CC'⊥平面ABC且3AA'=3 2 BB' =CC'=AB,则多面体ABC-A'B'C'的正视图(也称主视图)是 ( D ) 3.【2010·陕西文数】若某空间几何体的三视图如图所示,则该几何体的体积是() A.2 B.1 C. D. 【答案】B 本题考查立体图形三视图及体积公式如图,该立体图形为直三棱柱,所以其 体积为. 4.【2010·全国卷2理数】已知正四棱锥中,,那么当该棱锥的体积最大时,它的高为() A.1 B. C.2 D.3 【答案】C
【解析】本试题主要考察椎体的体积,考察告辞函数的最值问题.设底面边长为a ,则高 所以体积 ,设,则 ,当y 取最值时, ,解得a=0或a=4时,体积最大,此时 ,故选C. 5.如下图所示,四边形OABC 是上底为2下底为6,底角为45度的等腰梯形,由斜二侧画法,画出这个梯形的直观图O ’A ’B ’C ’,在直观图中梯形的高为( C ) A 、 32 B 、1 C 、22 D 、12 6.(全国Ⅰ新卷理10)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为 (A) 2a π (B) 2 73 a π (C) 2 113 a π (D) 25a π 【答案】B 解析:如图,P 为三棱柱底面中心,O 为球心,易知 2331,32AP a a OP a =?==,所以球的半径R 满足: 2222 317( )()3212 R a a a =+=,故2 2743 S R a ππ==球 . 热点2 点线面的位置关系 空间点、线、面位置关系是立体几何中的重要关系,在高考中,选择题、填空题几乎年年考,且常以棱柱、棱锥、和正方体为背景,主要考查平面的基本性质、空间直线与直线、直线与
立体几何空间角习题 【基础】空间角是线线成角、线面成角、面面成角的总称。其取值范围分别是:0°< θ ≤90°、0°≤ θ ≤90°、0°< θ ≤180°。 一、选择填空题 1.(1)已知正三棱柱ABC —A 1B 1C 1中,A 1B ⊥CB 1,则 A 1 B 与A C 1所成的角为( ) (A )450 (B )600 (C )900 (D )1200 (2)已知正四棱锥S ABCD -的侧棱长与底面边长都相等,E 是SB 的中点,则AE SD ,所成的角的余弦值为( ) A . 1 3 B C D . 23 (3)Rt ABC ?的斜边在平面α内,顶点A 在α外,BAC ∠在平面α内的射影是BA C '∠,则 BA C '∠的范围是________________。 (4)从平面α外一点P 向平面α引垂线和斜线,A 为垂足,B 为斜足,射线BC α?,这时 PBC ∠为钝角,设,PBC x ABC y ∠=∠=,则( ) A.x y > B.x y = C.x y < D.,x y 的大小关系不确定 (5)相交成60°的两条直线与一个平面α所成的角都是45°,那么这两条直线在平面α内的 射影所成的角是( ) A .30° B .45° C .60° D .90° (6)一条与平面相交的线段,其长度为10cm ,两端点到平面的距离分别是2cm ,3cm ,这条线 段与平面α所成的角是 ;若一条线段与平面不相交,两端点到平面的距离分别是2cm ,3cm ,则线段所在直线与平面α所成的角是 。 (7)PA 、PB 、PC 是从P 点引出的三条射线,每两条夹角都是60°,那么直线PC 与平面PAB 所成角的余弦值是( ) A B A 1 1
空间向量与立体几何典型例题 一、选择题: 1.(2008全国Ⅰ卷理)已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( C ) A . 13 B C D .23 1.解:C .由题意知三棱锥1A ABC -为正四面体,设棱长为a ,则1AB = ,棱柱的高 1 3AO a ===(即点1B 到底面ABC 的距离),故1AB 与底面ABC 所成角的正弦值为113 AO AB =. 另解:设1,,AB AC AA u u u r u u u r u u u r 为空间向量的一组基底,1,,AB AC AA u u u r u u u r u u u r 的两两间的夹角为0 60 长度均为a ,平面ABC 的法向量为111133 OA AA AB AC =--u u u r u u u r u u u r u u u r ,11AB AB AA =+u u u r u u u r u u u r 211112,,33 OA AB a OA AB ?===u u u r u u u r u u u r u u u r 则1AB 与底面ABC 所成角的正弦值为11 1 13OA AB AO AB ?=u u u u r u u u r u u u r u u u r . 二、填空题: 1.(2008全国Ⅰ卷理)等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角 C AB D -- M N ,分别是AC BC ,的中点,则EM AN ,所成角的余弦值等于 6 1 . 1.答案: 1 6 .设2AB =,作CO ABDE ⊥面, OH AB ⊥,则CH AB ⊥,CHO ∠为二面角C AB D -- cos 1CH OH CH CHO ==?∠=,结合等边三角形ABC 与正方形ABDE 可知此四棱锥为正四棱锥,则AN EM ==11(),22AN AC AB EM AC AE =+=-u u u r u u u r u u u r u u u u r u u u r u u u r , 11()()22AN EM AB AC AC AE ?=+?-=u u u r u u u u r u u u r u u u r u u u r 12 故EM AN ,所成角的余弦值1 6 AN EM AN EM ?=u u u r u u u u r u u u r u u u u r 另解:以O 为坐标原点,建立如图所示的直角坐标系, 则点(1,1,0),(1,1,0),(1,1,0),A B E C ----,
专题:空间角 一、基础梳理 1.两条异面直线所成的角 (1)异面直线所成的角的范围:(0, ]2 π 。 (2)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直。两条异面直线,a b 垂直,记作a b ⊥。 (3)求异面直线所成的角的方法: (1)通过平移,在一条直线上(或空间)找一点,过该点作另一(或两条)直线的平行线; (2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求。 平移技巧有:平行四边形对边平移、三角形中位线平移、补形平移技巧等。 1:三棱柱111B A O OAB -,平面11O OBB ⊥平面OAB , 90,601=∠=∠AOB OB O ,且12,OB OO == 3OA =,求异面直线B A 1与1AO 所成角的余弦。 2.直线和平面所成的角(简称“线面角”) (1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角。 一直线垂直于平面,所成的角是直角;一直线平行于平面或在平面内,所成角为0角。 直线和平面所成角范围:0, 2 π 。 (2)最小角定理:斜线和平面所成角是这条斜线和平面内 A B O 1A 1B 1O
经过斜足的直线所成的一切角中最小的角。 (3)公式:已知平面的斜线a 与内一直线b 且a 与相交成 1 角,a 在上的射影c 与b 相交成2 角, 则有θ??cos cos cos 21= 。 由(3)中的公式同样可以得到:平面的斜线和它在平面 内的射影所成角,是这条斜线和这个平面内的任一条直 线所成角中最小的角。 考点二:直线和平面所成的角 例2. 如图,在三棱柱ABC A B C '''-中,四 边形A ABB ''是菱形,四边形BCC B ''是矩形, C B AB ''⊥,02,4,60C B AB ABB '''==∠=, 求AC '与平面BCC B ''所成角的正切。 3:(1)在0 120的二面角P a Q --的两个面P 与Q 内分别有两点A B 、,已知点A 和点B 到棱的距离分别为2,4cm cm ,且线段10AB cm =。求: ①直线AB 和棱a 所成角的正弦值;②直线AB 和平面Q 所成角的正弦值。 A B C A ' B ' C ' ?2 ?1c b a θP α O A B
专题9 立体几何与空间向量 从近几年的高考试题来看,所考的主要内容是: (1)有关线面位置关系的组合判断,试题通常以选择题的形式出现,主要是考查空间线线、线面、面面位置关系的判定与性质; (2)有关线线、线面和面面的平行与垂直的证明,试题以解答题中的第一问为主,常以多面体为载体,突出考查学生的空间想象能力及推理论证能力; (3)线线角、线面角和二面角是高考的热点,选择题、填空题皆有,解答题中第二问必考,一般为中档题,在全卷的位置相对稳定,主要考查空间想象能力、逻辑思维能力和转化与化归的应用能力. 预测2021年将保持稳定,一大二小.其中客观题考查面积体积问题、点线面位置关系(各种角的关系或计算)等;主观题以常见几何体为载体,考查平行或垂直关系的证明、线面角或二面角三角函数值的计算等. 一、单选题 1.(2020·山东高三下学期开学)设,,m n l 为三条不同的直线,,a β为两个不同的平面,则下面结论正确的是( ) A .若,,//m n αβαβ??,则//m n B .若//,//,m n m n αβ⊥,则αβ⊥ C .若,,m n αβαβ⊥⊥⊥,则m n ⊥ D .//,//,,m n l m l n αα⊥⊥,则l α⊥ 【答案】C 【解析】 A 选项中,,m n 可能异面; B 选项中,,αβ也可能平行或相交;D 选项中,只有,m n 相交才可推出l α⊥. C 选项可以理解为两个相互垂直的平面,它们的法向量相互垂直. 故选:C 2.(2020届山东省潍坊市高三模拟二)已知三棱锥D ABC -的所有顶点都在球O 的球面上,2AB BC ==, AC =D ABC -体积的最大值为2,则球O 的表面积为( ) A .8π B .9π C . 25π 3 D . 1219 π 【答案】D 【解析】
高中数学立体几何经典常考题型 题型一:空间点、线、面的位置关系及空间角的计算 空间点、线、面的位置关系通常考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角,求空间角一般都可以建立空间直角坐标系,用空间向量的坐标运算求解. 【例1】如图,在△ABC 中,∠ABC = π4 ,O 为AB 边上一点,且3OB =3OC =2AB ,已知PO ⊥平 面ABC ,2DA =2AO =PO ,且DA ∥PO. (1)求证:平面PBD ⊥平面COD ; (2)求直线PD 与平面BDC 所成角的正弦值. (1)证明 ∵OB =OC ,又∵∠ABC =π 4, ∴∠OCB =π4,∴∠BOC =π 2. ∴CO ⊥AB. 又PO ⊥平面ABC , OC ?平面ABC ,∴PO ⊥OC. 又∵PO ,AB ?平面PAB ,PO ∩AB =O , ∴CO ⊥平面PAB ,即CO ⊥平面PDB. 又CO ?平面COD , ∴平面PDB ⊥平面COD. (2)解 以OC ,OB ,OP 所在射线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示. 设OA =1,则PO =OB =OC =2,DA =1. 则C(2,0,0),B(0,2,0),P(0,0,2),D(0,-1,1), ∴PD →=(0,-1,-1),BC →=(2,-2,0),BD →=(0,-3,1).
设平面BDC 的一个法向量为n =(x ,y ,z ), ∴?????n ·BC →=0,n · BD →=0,∴???2x -2y =0,-3y +z =0, 令y =1,则x =1,z =3,∴n =(1,1,3). 设PD 与平面BDC 所成的角为θ, 则sin θ=????? ? ??PD →·n |PD →||n | =??????1×0+1×(-1)+3×(-1)02+(-1)2+(-1)2×12+12+32=222 11. 即直线PD 与平面BDC 所成角的正弦值为22211. 【类题通法】利用向量求空间角的步骤 第一步:建立空间直角坐标系. 第二步:确定点的坐标. 第三步:求向量(直线的方向向量、平面的法向量)坐标. 第四步:计算向量的夹角(或函数值). 第五步:将向量夹角转化为所求的空间角. 第六步:反思回顾.查看关键点、易错点和答题规范. 【变式训练】 如图所示,在多面体A 1B 1D 1-DCBA 中,四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,E 为B 1D 1的中点,过A 1,D ,E 的平面交CD 1于F . (1)证明:EF ∥B 1C . (2)求二面角E -A 1D -B 1的余弦值. (1)证明 由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D ,又A 1D ?面A 1DE ,B 1C ?面A 1DE ,于是B 1C ∥面A 1DE.又B 1C ?面B 1CD 1,面A 1DE ∩面B 1CD 1=EF ,所以EF ∥B 1C.
届高三文科数学立体几何空间角专题复习 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-
2015届高三文科数学立体几何空间角专题复习 考点1:两异面直线所成的角 例1.如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 是棱CC 1的中点 (Ⅰ)求异面直线A 1M 和C 1D 1所成的角的正切值; (Ⅱ)证明:平面ABM ⊥平面A 1B 1M 1 例2.(2010全国卷1文数)直三棱柱111ABC A B C -中,若 90BAC ∠=?,1AB AC AA ==,则异面直线1BA 与1AC 所成的 角等于( C ) (A) 30° (B) 45° (C) 60° (D) 90° 变式训练: 1.(2009全国卷Ⅱ文)已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 中点,则异面直线BE 与1CD 所形成角的余弦值为( C ) (A ) 1010 (B) 15 (C ) 31010 (D) 35 2.如图,直三棱柱111ABC A B C -,90BCA ?∠=,点1D 、1F 分别是11A B 、11A C 的中点, 1BC CA CC ==,则1BD 与1AF 所成角的余弦值是( ) A . 1030 B .21 C .15 30 D . 10 15 3.(2012年高考(陕西理))如图,在空间直角坐标系中有直三棱 111ABC A B C -,12CA CC CB ==,则直线1BC 与直线1AB 夹角的余弦值为 ( ) A . 55 B . 53 C . 5 5 D .35 第3题图 第4题图 第5题图 4.(2007全国Ⅰ·文)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线 1A B 与1AD 所成角的余弦值为( )