(完整word版)西安高新一中初中东区小升初录取结果

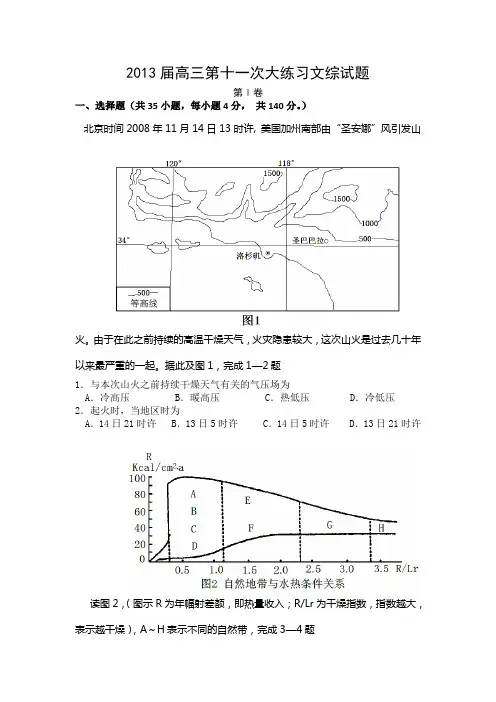
2013届高三第十一次大练习文综试题第Ⅰ卷一、选择题（共35小题，每小题4分，共140分。

）北京时间2008年11月14日13时许, 美国加州南部由“圣安娜”风引发山火。

由于在此之前持续的高温干燥天气，火灾隐患较大，这次山火是过去几十年以来最严重的一起。

据此及图1，完成1—2题1．与本次山火之前持续干燥天气有关的气压场为A．冷高压 B．暖高压 C．热低压 D．冷低压2．起火时，当地区时为A．14日21时许 B．13日5时许 C．14日5时许 D．13日21时许读图2，（图示R为年幅射差额，即热量收入；R/Lr为干燥指数，指数越大，表示越干燥），A～H表示不同的自然带，完成3—4题3．关于图中自然带的描述，正确的是A．A→B→C→D自然带的更替反映了山地垂直自然带变化B．A→B→C→D自然带的更替主要体现了水分条件的差异C．C→F→G→H自然带的更替主要体现了热量条件的差异D．C→F→G→H自然带的更替体现了从沿海向内陆的自然带变化4．图中E自然带是A．热带雨林带 B．热带草原带 C．温带荒漠带 D．温带草原带图3中甲乙两图分别为我国境内两条著名河流的流量变化图，读图并回答5—7题5．下列说法正确的是A．甲河最有可能是黄河 B．乙河可能位于西北地区C．甲乙两河冬季均有结冰现象 D．甲乙两河河水均有冰川融水6．下列现象或地理事物不可能出现在乙河及其流域的是A．洪涝、干旱 B．凌汛、春汛C．泥石流、滑坡 D．中华鲟、白鳍豚7．下列关于甲河及其流域的叙述正确的是A．该河下游生态环境日趋恶化 B．该流域主要的新能源是太阳能和地热能C．该河主要依靠雨水补给 D．该流域农业地域类型属水稻种植业读图4，完成8—9题8．形成人均耕地面积和粮食单产变化的主要因素是A．人口与生态；科技 B．城市化与水土流失；耕作方式C．产业结构调整；生物技术 D．农业政策与人口政策；生产投入9．2002年人均粮食产量突变的可能原因是A．大批农民外出打工，导致劳动力减少 B．农业机械化的推广，提高了生产率C．该年份风调雨顺，农业增产 D．因市场因素，扩大了粮食播种面积中航飞机有限责任公司2009年2月18日在西安高新技术产业开发区正式挂牌成立。

一、初一数学有理数解答题压轴题精选（难）1．阅读下面的材料：点A、B在数轴上分别表示实数a，b，A，B两点之间的距离表示为|AB|当A、B两点中有一点在原点时，设点A在原点，如图①|AB|=|OB|=|b|=|a﹣b|当A、B两点都不在原点时，（ 1 ）如图②，点A，B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|（2 ）如图③，点A、B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a ﹣b|（ 3 ）如图④，点A、B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=|a﹣b|综上所述，数轴上A、B两点之间的距离|AB|=|a﹣b|请用上面的知识解答下面的问题：（1）数轴上表示﹣2和﹣4的两点之间的距离是________，数轴上表示1和﹣3的两点之间的距离是________.（2）数轴上表示x和﹣1的两点A和B之间的距离是________，如果|AB|=2，那么x为________.（3）当|x+1|+|x﹣2|=5时的整数x的值________.（4）当|x+1|+|x﹣2|取最小值时，相应的x的取值范围是________.【答案】（1）2；4（2）x+1；1或-3（3）-2或3（4）-1≤ x≤2【解析】【解答】（1）数轴上表示﹣2和﹣4的两点之间的距离是|﹣2﹣（﹣4）|=2；数轴上表示1和﹣3的两点之间的距离是|1﹣（﹣3）|=4故答案为:2，4（2）数轴上x与-1的两点间的距离为|x-（-1）|=|x+1|，如果|AB|=2，则x+1=±2，解得x=1或-3；故答案为：|x+1|，1或-3（3）解方程|x+1|+|x﹣2|=5，且x为整数.当x+1＞0，x-2＞0，则（x+1）+（x-2）=5，解得x=3当x+1＜0，x-2＜0，则-（x+1）-（x-2）=5，解得x=-2当x+1与x-2异号，则等式不成立.故答案为：3或-2.（ 4 ）根据题意得x+1≥0且x-2≤0，则-1≤x≤2；【分析】（1）直接根据数轴上A、B两点之间的距离|AB|＝|a−b|，代入数值运用绝对值的意义即可求解；（2）直接根据数轴上A、B两点之间的距离|AB|＝|a−b|，列出方程，求解即可；（3）由数轴上A、B两点之间的距离|AB|＝|a−b|可知，|x＋1|＋|x−2|表示点x到−1与2两点距离之和，由于,2与-1之间的距离是3小于5，故表示数x的点，不可能在-1与2之间，然后分数轴上表示x的点在数轴上表示数字1的点的右边及数轴上表示x的点在数轴上表示数字-2的点的左边两种情况考虑即可解决问题；（4）由数轴上A、B两点之间的距离|AB|＝|a−b|可知，|x＋1|＋|x−2|表示点x到−1与2两点距离之和，根据两点之间线段最短即可得出x的取值范围.2．如图1，A、B两点在数轴上对应的数分别为﹣12和4.（1）直接写出A、B两点之间的距离；（2）若在数轴上存在一点P，使得AP＝ PB，求点P表示的数.（3）如图2，现有动点P、Q，若点P从点A出发，以每秒5个单位长度的速度沿数轴向右运动，同时点Q从点B出发，以每秒2个单位长度的速度沿数轴向左运动，当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动，求：当OP＝4OQ时的运动时间t的值.【答案】（1）解：A、B两点之间的距离是：4﹣（﹣12）＝16（2）解：设点P表示的数为x.分两种情况：①当点P在线段AB上时，∵AP＝ PB，∴x+12＝（4﹣x），解得x＝﹣8；②当点P在线段BA的延长线上时，∵AP＝ PB，∴﹣12﹣x＝（4﹣x），解得x＝﹣20.综上所述，点P表示的数为﹣8或﹣20（3）解：分两种情况：①当t≤2时，点Q从点B出发，以每秒2个单位长度的速度沿数轴向左运动，此时Q点表示的数为4﹣2t，P点表示的数为﹣12+5t，∵OP＝4OQ，∴12﹣5t＝4（4﹣2t），解得t＝，符合题意；②当t＞2时，点Q从原点O开始以每秒3个单位长度的速度沿数轴向右运动，此时Q点表示的数为3（t﹣2），P点表示的数为﹣12+5t，∵OP＝4OQ，∴|12﹣5t|＝4×3（t﹣2），∴12﹣5t＝12t﹣24，或5t﹣12＝12t﹣24，解得t＝，符合题意；或t＝，不符合题意舍去.综上所述，当OP＝4OQ时的运动时间t的值为或秒【解析】【分析】（1）根据两点间的距离公式即可求出A、B两点之间的距离；（2）设点P表示的数为x.分两种情况：①点P在线段AB上；②点P在线段BA的延长线上.根据AP＝ PB列出关于x的方程，求解即可；（3）根据点Q的运动方向分两种情况：①当t≤2时，点Q从点B出发，以每秒2个单位长度的速度沿数轴向左运动；②当t＞2时，点Q从原点O开始以每秒3个单位长度的速度沿数轴向右运动，根据OP＝4OQ列出关于t的方程，解方程即可.3．若点A、B、C在数轴上对应的数分别为a、b、c满足|a+5|+|b﹣2|+|c﹣3|＝0.（1）在数轴上是否存在点P，使得PA+PB＝PC？若存在，求出点P对应的数；若不存在，请说明理由；（2）若点A，B，C同时开始在数轴上分别以每秒1个单位长度，每秒3个单位长度，每秒5个单位长度沿着数轴正方向运动经过t秒后，试问AB﹣BC的值是否会随着时间t的变化而变化？请说明理由.【答案】（1）解：∵a，b，c满足|a+5|+|b﹣2|+|c﹣3|=0，∴a=﹣5，b=2，c=3.设点P对应的数为x.当x＜﹣5时，﹣5﹣x+2﹣x=3﹣x，解得：x=﹣6；当﹣5≤x＜2时，x﹣（﹣5）+2﹣x=3﹣x，解得：x=﹣4；当2≤x＜3时，x﹣（﹣5）+x﹣2=3﹣x，解得：x=0（舍去）；当x≥3时，x﹣（﹣5）+x﹣2=x﹣3，解得：x=﹣6（舍去）.综上所述：在数轴上存在点P，使得PA+PB=PC，点P对应的数为﹣6或﹣4.（2）解：AB﹣BC的值不变，理由如下：当运动时间为t秒时，点A对应的数为t﹣5，点B对应的数为3t+2，点C对应的数为5t+3，∴AB﹣BC=3t+2﹣（t﹣5）﹣[5t+3﹣（3t+2）]=6.∴AB﹣BC的值不变.【解析】【分析】由绝对值的非负性可求出a，b，c的值.（1）设点P对应的数为x，分x ＜﹣5，﹣5≤x＜2，2≤x＜3及x≥3四种情况考虑，由PA+PB=PC利用两点间的距离公式，即可得出关于x的一元一次方程，解之即可得出结论；（2）找出当运动时间为t秒时点A，B，C对应的数，进而可求出AB﹣BC=6，此题得解.4．已知数轴上顺次有A、B、C三点分别表示数a、b、c，并且满足(a+12)2+|b+5|=0，b与c互为相反数。

九年级英语期中复习(一)第1卷(共45分)1.单项选择(共10小题，计10分)1.The traffic signs___________ people ___________after drinkingA warn; not to drive B.warn: to drive C.avoid; driving D. avoid; not to drive2.We don't allow ____________in our offices, but we allow people_________ in the smoking rooms.A.to smoke; to smokeB. smoking; to smokeC.smoking; smokingD.to smoke; smoking3. These blouses are ___________cotton, so they feel ________.A.made of: comfortableB. made from; comfortableC. made from, comfortablyD. made of; comfortably4.The boy seemed to be ____________in study than before, his teacher advised his parents__ ___________their son in person.A.less interested; to talk withB. less interested; talk withC. more interested; talk withD. more interested; talking with5.Diana________walk to work, but now she is used to________ because the road is crowded and she wants to keep fit.A.didn't use to, walkB. used to, walkinged to; walkD. didn't use to, walking6.People who learn___________ and well will achieve their dreams________ than others.A. wisely, easierB. wise: more easilyC.wise; easierD. wisely; more easily7.This year, Shenzhou XIV_____________ into the space. It made us__________ proud.A.is sent; isB. was sent; feelC. sends; feelsD. sent; felt38________Jane ___________ her brother is going to the movies this weekend. One of them has to stay at home to look after their sick mother.A.Neither, norB. Not only; but alsoC.Either; orD. Both; and79.-Excuse me, I’m new here. Could you please tell me_______________?-In five minutesA. how soon will the next subway arriveB. how long the next subway arrivesC. how soon the next subway will arriveD. how long the next subway will arrive10.-Could you help me with my English?--_____________.A. Never mind.B. OK, I could.C. With pleasure.D. You are welcome.IL.完形填空(共20小题，计20分)第一节:阅读下面短文，按照句子结构的语法性和上下文连贯的要求从各小题的四个选项中选出一个最佳答案，使短文连贯完整。

2018-2019学年陕西省西安市高新一中 高一第一学期期中考试数学试题数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、单选题1．已知集合 ，集合 ，则 A ． B ． C ． D ．2．集合{}|0 2 A x x =≤≤，{}|1 2 B y y =≤≤，下图中能表示从集合A 到集合B 的映射的是A ．B ．C．D ．3．方程 的解所在区间是A ．B ．C ．D ．4．由于被墨水污染,一道数学题仅能见到如下文字：已知二次函数y=ax2+bx+c 的图象过点(1,0)…求证：这个二次函数的图象关于直线x=2对称。

根据现有信息,题中的二次函数不一定具有的性质是A ．在x 轴上截得的线段的长度是2B ．与y 轴交于点（0,3）C ．顶点是(−2,−2)D ．过点(3,0)5．若偶函数f (x )在(－∞，0)内单调递减，则不等式f (－1)＜f (lg x )的解集是A ．0,10（）BCD6．若 ，则 的大小关系为 A ． B ．C ．D ．7．函数的零点个数为 A ．0 B ．1 C ．2 D ．38．已知定义在R 上的奇函数f(x)满足 ，当 时, ,则 A ．B ．C ．D ．9．已知函数当 时， ，则 的取值范围是 A ．B ．C ．（ ，） D ．10．定义在 上的奇函数 ，当 时，，则关于 的函数 的所有零点之和为A ．B ．C ．D ．二、填空题11．设 ，若，则 _____．12．若集合 ，且 ，则实数a 的可能取值组成的集合是___________.13．已知 是定义域为 的奇函数，满足 ，若 ，则 ________14．若函数 且 在区间（0，）内恒有 ，则 的单调递增区间为_________.此卷只装订不密封班级姓名准考证号考场号座位号15．已知集合.（1）分别求，；（2）已知集合若，求实数a的取值范围.16．计算：（1）．（2）．17．已知函数是定义在R上的奇函数.（1）判断并证明在上的单调性.（2）若对任意实数t,不等式恒成立，求实数k的取值范围18．已知函数.（1）当时，求函数的最小值；（2）在（1）的条件下，师傅是否存在实数m>n>3,使得的定义域为，值域为？若存在，求出m,n的值；若不存在，请说明理由.19．已知函数.（1）当时，若，且对任意的，都存在，使得成立，求实数a的取值范围；（2）当时，求x的取值范围.20．设.则的最小值为______.21．设二次函数满足条件：（1）当时，且；（2）当时，；（3）在R上的最小值为0.求最大的m（m>1）,使得存在,只要，就有2018-2019学年陕西省西安市高新一中 高一第一学期期中考试数学试题数学答案参考答案 1．B 【解析】，集合 ，则 .故选B. 2．D【解析】在A 中，当01x ＜＜时，1y ＜，所以集合A 到集合B 不成映射，故选项A 不成立； 在B 中，12x ≤≤时，1y ＜，所以集合A 到集合B 不成映射，故选项B 不成立；在C 中01x ≤≤，时，任取一个x 值，在02y ≤≤内，有两个y 值与之相对应，所以构不成映射，故选C 不成立；在D 中，01x ≤≤，时，任取一个x 值，在02y ≤≤内，总有唯一确定的一个y 值与之相对应，故选项D 成立． 故选D3．C 【解析】 【分析】令函数 ，则函数 是 上的单调增函数，且是连续函数，根据 ，可得函数的零点所在的区间为 ，由此可得方程 的解所在区间．【详解】令函数 ，则函数 是 上的单调增函数，且是连续函数. ∵ ，∴∴故函数 的零点所在的区间为 ∴方程 的解所在区间是故选C.【点睛】零点存在性定理：利用定理不仅要函数在区间 上是连续不断的曲线，且 ，还必须结合函数的图象与性质（如单调性、奇偶性）才能确定函数有多少个零点.4．C 【解析】 【分析】本题是条件开放题，根据已知点（1，0）和对称轴x=2，根据抛物线的对称性，探求二次函 数的性质． 【详解】A 、抛物线与x 轴两交点为（1，0），（3，0），故在x 轴上截得的线段长是2，正确；B 、图象过点（1，0），且对称轴是直线x=2时，图象必过（3，0）点，代入求得解析式即可得出与y 轴的交点可以是（0，3），正确．C 、顶点的横坐标应为对称轴，本题的顶点坐标与已知对称轴矛盾，错误；D 、因为图象过点（1，0），且对称轴是直线x=2，另一个对称点为（3，0），正确； 故答案为：C ． 【点睛】本题主要考查了二次函数的对称，函数图象上的点关于对称轴的对称点一定也在同一图象上． 5．D【解析】∵偶函数()f x 在0]∞-（，内单调递减，∴()f x 在0∞+（，）内单调递增， 则不等式()()1lg f f x -<等价于，∴1lgx >或1lgx <- ∴10x >或，∴不等式()()1lg f f x -<的解集是故选D.点睛：本题考查了函数的单调性与奇偶性的综合应用，在解对数不等式时注意对数的真数大于0，是个基础题；由于偶函数()f x 在0]∞-（，内单调递减故()f x 在0∞+（，）内单调递增，利用函数，从而解得x 的范围.6．D【解析】分析：利用指数函数与对数函数的单调性即可得出． 详解：∵0＜a ＜b ＜1，a b ∈（0，1），log b a ＞log b b=1，z=logb ＜0，则 的大小关系为 ．故选：D．点睛：利用指数函数对数函数及幂函数的性质比较实数或式子的大小，一方面要比较两个实数或式子形式的异同，底数相同，考虑指数函数增减性，指数相同考虑幂函数的增减性，当都不相同时，考虑分析数或式子的大致范围，来进行比较大小，另一方面注意特殊值的应用，有时候要借助其“桥梁”作用，来比较大小．7．B【解析】【分析】令f(x)=0得=0，所以，再作出函数与的图像得解.【详解】令f(x)=0得=0，所以，再作出函数与的图像,由于两个函数的图像只有一个交点，所以零点的个数为1.故答案为：B【点睛】(1)本题主要考查函数的零点问题，意在考查学生对这些知识的掌握水平和分析推理能力.(2)零点问题的处理常用的方法有方程法、图像法、方程+图像法.8．B【解析】由题意得，因为，则，所以函数表示以为周期的周期函数，又因为为奇函数，所以，所以，，，所以，故选B.9．A【解析】∵当x1≠x2时，＜0，∴f（x）是R上的单调减函数，∵f（x）=，，＞，∴＜＜＜＜，∴0＜a≤，故选：A．10．C【解析】当时，又是奇函数，画出函数的图象，由函数图象可知：，有个零点，其中有两个零点关于对称，还有两个零点关于对称，所以这四个零点的和为零，第五个零点是直线与函数，交点的横坐标，即方程的解，，故选C.【方法点睛】本题主要考查函数的图象与性质、函数的零点以及数形结合思想的应用，属于难题. 数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，.函数图象是函数的一种表达形式，它形象地揭示了函数的性质，为研究函数的数量关系提供了“形”的直观性．归纳起来，图象的应用常见的命题探究角度有：1、确定方程根的个数；2、求参数的取值范围；3、求不等式的解集；4、研究函数性质．11．【解析】试题分析：．考点：指数式与对数式的综合运算．12．，，【解析】【分析】应先将集合P化简，又S P，进而分别讨论满足题意的集合S，从而获得问题的解答.【详解】由已知P={﹣3，2}．当a=0时，S=∅，符合S P；当a≠0时，方程ax+1=0的解为x=﹣．为满足S P，可使﹣=﹣3或﹣=2，即：a=，或a=﹣．故所求的集合为{0，，﹣}．故答案为：，，【点睛】本题考查的是集合的包含关系判断以及应用问题．在解答的过程当中充分体现了集合元素的特性、分类讨论的思想．13．2【解析】【分析】根据函数奇偶性和对称性的关系求出函数的周期是4，结合函数的周期性和奇偶性进行转化求解即可．【详解】∵f（x）是奇函数，且f（1-x）=f（1+x），∴f（1-x）=f（1+x）=-f（x-1），f（0）=0，则f（x+2）=-f（x），则f（x+4）=-f（x+2）=f（x），即函数f（x）是周期为4的周期函数，∵f（1）=2，∴f（2）=f（0）=0，f（3）=f（1-2）=f（-1）=-f（1）=-2，f（4）=f（0）=0，则f（1）+f（2）+f（3）+f（4）=2+0-2+0=0，则f（1）+f（2）+f（3）+…+f（50）=12[f（1）+f（2）+f（3）+f（4）]+f（45）+f（46）=f（1）+f（2）=2+0=2，即答案为2.【点睛】本题主要考查函数值的计算，根据函数奇偶性和对称性的关系求出函数的周期性是解决本题的关键．14．(－∞，－)【解析】因为函数f(x)＝(a>0，a≠1)在区间(0，)内恒有f(x)>0，则f(x)的单调递增区间为(－∞，－)15．（1）；.（2）【解析】【分析】（1）先化简集合A和B,再求，. (2)由得，可得且,解不等式即得.【详解】(1)由3⩽3x⩽27,即3⩽3x⩽33,∴1⩽x⩽3,∴A=[1,3].由log2x<1,可得0<x<2,∴B=(0,2).∴ ∩ =[1,2).所以=.（2）由得，可得且解得.综上所述：a的取值范围是.【点睛】本题主要考查集合的化简与运算，考查集合的关系，意在考查学生对这些知识的掌握水平和分析推理能力.16．（1）；（2）2.【解析】【分析】（1）利用指数幂的运算性质即可得出；（2）利用对数的运算性质即可得出．【详解】（1）．。

2020-2021学年陕西省西安市高新一中八年级（上）期中数学试卷一、填空题（每小题3分，共30分）1．（3分）如图中的一张脸，小明说：“如果我用（0，2）表示左眼，用（2，2）表示右眼”，那么嘴的位置可以表示成（）A．（0，1）B．（2，1）C．（1，0）D．（1，﹣1）2．（3分）下列各图象中，不表示y是x的函数的是（）A．B．C．D．3．（3分）下列四组点中，在同一个正比例函数图象上的一组点是（）A．（2，5），（﹣4，10）B．（2，5），（﹣1，10）C．（2，﹣5），（4，﹣10）D．（﹣2，5），（1，﹣10）4．（3分）如图所示，点E在AC的延长线上，下列条件中能判断BD∥AC的是（）A．∠3＝∠A B．∠D＝∠DCEC．∠1＝∠2D．∠A+∠ACD＝180°5．（3分）直线y＝kx的图象如图所示，则函数y＝（1﹣k）x﹣k的图象大致是（）A．B．C．D．6．（3分）如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝120°，∠AOF的度数是（）A．20°B．30°C．40°D．60°7．（3分）如图，直线l1、l2的交点坐标可以看作方程组（）的解．A．B．C．D．8．（3分）点P（﹣a，a+2）一定不在第（）象限．A．一B．二C．三D．四9．（3分）如图，在四边形ABCD中，AB＝8，BC＝1，∠DAB＝30°，∠ABC＝60°，四边形ABCD的面积为5，则AD的长为（）A．B．2C．2D．310．（3分）若直线l1经过点（0，3），直线l2经过点（5，2），且l1与l2关于x轴对称，则l1与l2的交点坐标为（）A．（﹣2，0）B．（2，0）C．（﹣3，0）D．（3，0）二、填空题（每小题3分，共21分）11．（3分）命题“﹣a一定表示一个负数”是命题．（填“真”或“假”）12．（3分）在△ABC中，∠A：∠B：∠C＝3：4：5，则∠C等于．13．（3分）若点M（﹣7，m）、N（﹣8，n）都在函数y＝﹣x+1的图象上，则m和n的大小关系是．14．（3分）把直线y＝﹣2x﹣1向右平移2个单位后得到直线AB，则直线AB的表达式为．15．（3分）把长方形AB′CD沿对角线AC折叠，得到如图所示的图形，已知∠BAO＝40°，则∠ACD＝．16．（3分）在平面直角坐标系中，有点A（a，1），点B（﹣2，b），当线段AB∥y轴，且AB＝3时，则a﹣b＝．17．（3分）如图，在平面直角坐标系xOy中，已知点A（1，0），点C是y轴上的动点，线段CA绕着点C逆时针旋转90°至线段CB，连接BO，则BO的最小值是．三、解答题（共69分）18．（6分）如图，在平面直角坐标系中，△ABC的三个顶点都在格点上．（1）写出A、B、C三点的坐标；（2）画出△ABC关于x轴对称的△A1B1C1．19．（6分）尺规作图如图，△ABC中，∠B＝2∠C，在AC边上找一点P，使PB＝PC．（保留作图痕迹，不写作法）20．（7分）如图，在△ABC中，∠B＝40°，∠C＝60°，点D，E分别在边BC，AC上，且DE∥AB，若∠CAD＝25°，求∠ADE的度数．21．（8分）在平面直角坐标系中，点A是x轴上一点，点B是y轴上一点，若线段OA＝1，∠ABO＝30°．（1）则A点的的坐标是，B点的坐标是；（2）以线段AB为边，在平面直角坐标系中作等边△ABC，求出C点坐标．22．（10分）如图，直线l交x轴于A（﹣4，0），交y轴于B（0，6），C（m，3）是直线l上的一点．（1）求直线AB，OC的表达式；（2）在直线AB上找一点P，使S△OCP＝S△OAB，求出点P的坐标．23．（10分）在△ABC中，点E，点F分别是边AC，AB上的点，且AE＝AF，连接BE，CF交于点D，∠ABE＝∠ACF．（1）求证：△BCD是等腰三角形．（2）若∠A＝40°，BC＝BD，求∠BEC的度数．24．（10分）为了提高饮水质量，越来越多的居民选择家用净水器，光明商场计划从生产厂家购进甲、乙两种型号的家用净水器，甲型号净水器进价为160元/台，乙型号净水器进价为280元/台，经过协商沟通，生产厂家拿出了两种优惠方案：第一种优惠方案：甲、乙两种型号净水器均按进价的8折收费；第二种优惠方案：甲型号净水器按原价收费，乙型号净水器的进货量超过10台后超过的部分按进价的6折收费．光明商场只能选择一种优惠方案，已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍，设光明商场购进乙型号净水器x台，选择第一种优惠方案所需费用为y1元，选择第二种优惠方案所需要费用为y2元．（1）分别求出y1、y2与x的关系式；（2）光明商场计划购进乙型号净水器40台，请你为光明商场选择合适的优惠方案，并说明理由．25．（12分）如图，一次函数y＝x+2的图象与x，y轴分别交于A，B两点，点C与点A关于y轴对称．动点P，Q分别在线段AC，AB上（点P与点A，C不重合），且满足∠BPQ＝∠BAO．（1）点A的坐标为，点B的坐标为，线段BC的长度＝；（2）当点P在什么位置时，△APQ≌△CBP？说明理由；（3）当△PQB为等腰三角形时，求点P的坐标．2020-2021学年陕西省西安市高新一中八年级（上）期中数学试卷试题解析一、填空题（每小题3分，共30分）1．解：如图，嘴的位置可以表示成（1，0）．故选：C．2．解：A、根据图象知给自变量一个值，故A选项是函数，B、根据图象知给自变量一个值，故B选项是函数，C、根据图象知给自变量一个值，故C选项不是函数，D、根据图象知给自变量一个值，故D选项是函数，故选：C．3．解：A、∵≠，∴两点不在同一个正比例函数图象上；B、∵，∴两点不在同一个正比例函数图象上；C、∵＝，∴两点在同一个正比例函数图象上；D、∵≠，∴两点不在同一个正比例函数图象上．故选：C．4．解：A、由∠3＝∠A不能判断BD∥AC；B、∵∠D＝∠DCE，故本选项符合题意；C、∵∠1＝∠7，故本选项不合题意；D、∵∠A+∠ACD＝180°，故本选项不合题意．故选：B．5．解：∵直线y＝kx的图象经过第二、四象限，∴k＜0，∴1﹣k＞4，﹣k＞0，∴函数y＝（1﹣k）x﹣k的图象经过第一、二、三象限．故选：B．6．解：∵CD∥AB，∠D＝120°，∴∠AOD+∠D＝180°，∴∠AOD＝60°，∠DOB＝120°，∵OE平分∠BOD，∴∠DOE＝60°，∵OF⊥OE，∴∠FOE＝90°，∴∠DOF＝90°﹣60°＝30°，∴∠AOF＝∠AOD﹣∠DOF＝60°﹣30°＝30°．故选：B．7．解：设l1的解析式为y＝kx+b，∵图象经过的点（1，2），﹣2），∴，解得：，∴l4的解析式为y＝2x﹣2，可变形为3x﹣y＝2，设l2的解析式为y＝mx+n，∵图象经过的点（﹣2，0），1），∴，解得：，∴l5的解析式为y＝x+4，可变形为x﹣2y＝﹣2，∴直线l8、l2的交点坐标可以看作方程组的解．故选：A．8．解：当a＞0时，﹣a＜0，∴点P（﹣a，a+2）在第二象限；当a＜0时，﹣a＞0，也可能为负，∴点P（﹣a，a+2）可能在第一象限；∴点P（﹣a，a+2）可能在第一、二；不可能在第三象限，故选：C．9．解：如图，延长AD，∵∠DAB＝30°，∠ABC＝60°，∴∠E＝90°，又∵AB＝8，∠DAB＝30°，∴BE＝AB＝4BE＝5，∴CE＝3，∵四边形ABCD的面积为5，∴×AE×BE﹣，∴DE＝2，∴AD＝3，故选：C．10．解：设直线l2的解析式为y＝kx+b，∵直线l1经过点（6，3），l2经过点（8，2）1与l2关于x轴对称，∴两直线相交于x轴上，点（0，﹣3）在直线l3上，把（0，﹣3）和（7，得，解得：，故直线l3的解析式为：y＝x﹣3，令y＝0，则x＝6，即l1与l2的交点坐标为（4，0）．故选：D．二、填空题（每小题3分，共21分）11．解：当a＝0时，﹣a＝0，∴命题“﹣a一定表示一个负数”是假命题，故答案为：假．12．解：∵在△ABC中，∠A：∠B：∠C＝3：4：7，∴设∠A＝3x，∠B＝4x，∵∠A+∠B+∠C＝180°，∴8x+4x+5x＝180°，∴x＝15°，∴∠C＝3x＝75°，故答案为：75°．13．解：∵k＝﹣＜2，∴y随x的增大而减小，又∵﹣7＞﹣8，∴m＜n．故答案为：m＜n．14．解：把直线y＝﹣2x﹣1向右平移5个单位后得到直线AB，则直线AB的表达式为：y＝﹣2（x﹣2）﹣5．故答案为y＝﹣2x+3．15．解：∵四边形AB'CD是矩形∴AD∥B'C，∠B'＝900∴∠1＝∠2，∵翻折后∠1＝∠2，∴∠6＝∠3．∵翻折后∠B＝∠B'＝90°，∠BAO＝40°，∴∠AOC＝∠B+∠BAO＝130°，∴∠2＝∠2＝25°，∴∠BAC＝∠BAO+∠3＝65°，∵CD∥AB′，∴∠ACD＝∠CAB′＝∠CAB＝65°，故答案为：65°．16．解：∵当线段AB∥y轴，点A（a，b）的横坐标相同，∴a＝﹣2，∵AB＝3，∴|b﹣8|＝3，∴b﹣1＝7或b﹣1＝﹣3，∴b＝2或b＝﹣2．∴a﹣b＝﹣2﹣2＝﹣6，或a﹣b＝﹣2﹣（﹣5）＝0，故答案为：﹣6或3．17．解：设C（0，m），垂足为点M，∴∠BMC＝90°，∴∠MCB+∠B＝90°，∵线段CA绕着点C按逆时针方向旋转90°至线段CB，∴∠BAC＝90°，CB＝CA，∴∠MCB+∠ACO＝90°，∴∠B＝∠ACO，∵∠AOC＝90°，∴△AOC≌△CMB（AAS），∴MC＝OA，MB＝OC，∵点C（0，m），6），∴点B的坐标为（m，m+1），∴点B的运动轨迹是直线y＝x+1，∵直线Y＝x+4交x轴于E（﹣1，0），6），∴OE＝OF＝1，EF＝，过点O作OT⊥EF于T．则OT＝，根据垂线段最短可知，当点B与点T重合时，最小值为，故答案为：．三、解答题（共69分）18．解：（1）A（2，4），6），3）；（2）如图，△A1B4C1为所作．19．解：如图，点P即为所求．20．解：在△ABC中，∠BAC+∠B+∠C＝180°，∵∠B＝40°，∠C＝60°，∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣40°﹣60°＝80°，∵∠BAD＝∠BAC﹣∠CAD，∠CAD＝25°，∴∠BAD＝80°﹣25°＝55°，∵DE∥AB，∴∠ADE＝∠BAD，∴∠ADE＝55°．21．解：（1）在Rt△AOB中，∵∠ABO＝30°，∴AB＝2OA＝2，∴OB＝＝＝，∴A（﹣1，0），）；故答案为（﹣1，0），）；（2）如图，作A点关于y轴的对称点C，∴OA＝OC＝1，∴AB＝AC，而∠BAC＝60°，∴△ABC为等边三角形，此时C点坐标为（1；把B点向左平移3个单位得到C′点，则BC′＝BA＝2，∵BC′∥OA，∴∠ABC′＝∠BAO＝60°，∴△ABC′为等边三角形，此时C′点坐标为（﹣2，），综上所述，C点坐标为（1，）．22．解：（1）设直线AB的表达式为y＝kx+b（k≠0），∵点A（﹣4，2），6）在直线AB上，∴，∴，∴直线AB的表达式为y＝x+6，∵C（m，3）是直线l上的一点，∴m+6＝3，解得：m＝﹣2，∴C（﹣2，2），设直线OC的表达式为：y＝nx（n≠0），把C（﹣2，7）代入得：﹣2n＝3，∴n＝﹣，∴直线OC的表达式为：y＝﹣x；（2）∵S△OCP＝S△OAB，∴S△OCP＝×＝6，设P（x，x+7），分两种情况：①当点P在第一象限时，过P作PD⊥x轴于D，∵C（﹣2，3），∴OE＝3，CE＝3，∴S△OCP＝（3+＝8，解得：x＝，∴P（，2）；②当点P在第三象限时，同理得：P（﹣；综上，点P的坐标为P（，﹣1）．23．（1）证明：∵AE＝AF，∠A＝∠A，∴△ABE≌△ACF（AAS），∴AB＝AC，∠ABE＝∠ACF，∴∠ABC＝∠ACB，∴∠ABC﹣∠ABE＝∠ACB﹣∠ACF，即∠DBC＝∠DCB，∴△BCD是等腰三角形；（2）解：∵AB＝AC，∠A＝40°，∴∠ABC＝（180°﹣40°）＝70°，∵BD＝BC，∴∠BDC＝∠BCD，∵∠DBC＝∠DCB，∴△DBC是等边三角形，∴∠DBC＝60°，∴∠ABE＝10°，∴∠BEC＝∠A+∠ABE＝50°．24．解：（1）由题意可得，y1＝（280x+160×1.2x）×0.8＝416x，y4＝160×1.5x+280×10+280×（x﹣10）×3.6＝408x+1120，即y1，y8与x之间的函数关系式分别为：y1＝416x，y2＝408x+1120；（2）当x＝40时，y6＝16640元，y2＝17440元，∵y2＞y8，∴选择第一种优惠方案．25．解：（1）∵y＝x+3，∴当x＝0时，y＝2，当y＝7时，x＝﹣4，即点A的坐标是（﹣4，8），2），∵C点与A点关于y轴对称，∴C的坐标是（4，5），∴OA＝4，OC＝4，由勾股定理得：BC＝＝2．故答案为：（﹣6，0），2），7．（2）当P的坐标是（2﹣4，△APQ≌△CBP，理由是：∵OA＝4，P（4，0），∴AP＝6+2﹣8＝2，∵∠BPQ＝∠BAO，∠BAO+∠AQP+∠APQ＝180°，∠APQ+∠BPQ+∠BPC＝180°，∴∠AQP＝∠BPC，∵A和C关于y轴对称，∴∠BAO＝∠BCP，在△APQ和△CBP中，，∴△APQ≌△CBP（AAS），∴当P的坐标是（7﹣4，△APQ≌△CBP；（3）分为三种情况：①当PB＝PQ时，由（2）知，∴PB＝PQ，即此时P的坐标是（5﹣4；②当BQ＝BP时，则∠BPQ＝∠BQP，∵∠BAO＝∠BPQ，∴∠BAO＝∠BQP，而根据三角形的外角性质得：∠BQP＞∠BAO，∴此种情况不存在；③当QB＝QP时，则∠BPQ＝∠QBP＝∠BAO，即BP＝AP，设此时P的坐标是（x，8），∵在Rt△OBP中，由勾股定理得：BP2＝OP2+OB5，∴（x+4）2＝x5+22，解得：x＝﹣，即此时P的坐标是（﹣，0）．∴当△PQB为等腰三角形时，点P的坐标是（2，0）或（﹣．。

2023年陕西省西安市雁塔区高新唐南中学中考模拟物理试题（二）(word版)一、单选题(★★) 1. 下列估测的物理量中，基本符合实际情况的是（）A．小明从教学楼一楼爬上四楼做功的功率约为2WB．家用小汽车汽油机的效率可以达到95%C．教室里一盏日光灯正常工作电流约为0.2AD．对人体安全的电压为36V(★★) 2. 图甲是一种磁悬浮地球仪摆件，地球仪内部装有磁铁，底座内部装有如图乙所示的电磁铁。

下列说法正确的是（）A．电磁铁周围存在着磁场B．地球仪利用异名磁极间相互排斥的原理工作C．图乙中，利用安培定则可判断电磁铁上端是N极D．图乙中，将电源正、负极对调后，电磁铁磁极方向不变(★★★) 3. 关于信息传递，下列说法正确的是（）A．倒车雷达是利用微波进行定位的B．手机间通话是通过超声波传递信息的C．光纤通信是利用电流传递信息的D．金属容器对电磁波有屏蔽作用(★★) 4. 如图，弹簧测力计下悬挂一小条形磁铁，使弹簧测力计沿着水平放置的大条形磁铁的左端 N 极开始，向右端 S 极处逐渐移动时，弹簧测力计示数将（）A．逐渐增大B．逐渐减小C．先减小后增大D．先增大后减小(★★) 5. 下列情况中不属于防止电热危害的是（）A．电视机的后盖有许多孔B．家电长时间停用，隔段时间应通电一次C．电动机外壳有许多散热片D．电脑主板的CPU上有小风扇(★★) 6. 如图是正常家庭电路的一部分，下列说法正确的是（）A．导线B与大地之间的电压为220VB．测电笔先后插入插座的左右插孔，氖管都发光C．电冰箱的插头插入三孔插座能使电冰箱的金属外壳接地D．灯泡和开关的位置可以互换(★★★) 7. 如图甲、乙分别是小明家上月初和上月末的电能表的表盘，表盘上“1600imp/（kW•h）”表示用电器每消耗1kW·h的电能，指示灯闪烁1600次。

下列说法正确的是（）A．指示灯闪烁32次，电路中消耗的电能为0.02JB．小明家上月消耗的电能为911kW·hC．小明家干路中的电流不得超过10AD．指示灯闪烁次数越多，电能表所在电路消耗的电能越多(★★) 8. 电冰箱在设计电路时，当冷冻室温度高于设定温度时，压缩机会以输入总功率正常工作，当冷冻室温度低于设定温度时，则压缩机停止运作，一般家庭每12h压缩机工作2.5h.如表格所示是某小型号电冰箱的铭牌，根据铭牌内容，则下列选项错误的是（）A．该冰箱正常工作电压是220VB．一般家庭该电冰箱每经过24h，消耗电能0.62kW·hC．电冰箱除了压缩机工作消耗电能，还有其他部件消耗电能D．该电冰箱停止工作一天，一定节省电能2.4kW·h(★★★) 9. 如图甲是一种常见的手电筒，发光元件由2个发光二极管并联组成，每个发光二极管正常工作时的电流均为30mA。

西安高新唐南中学数学轴对称填空选择（提升篇）（Word版含解析）一、八年级数学全等三角形填空题（难）1．如图，已知点I是△ABC的角平分线的交点．若AB＋BI＝AC，设∠BAC＝α，则∠AIB＝______（用含α的式子表示）【答案】1206α︒-【解析】【分析】在AC上截取AD=AB，易证△ABI≌△ADI，所以BI=DI，由AB＋BI＝AC，可得DI=DC，设∠DCI=β，则∠ADI=∠ABI=2β，然后用三角形内角和可推出β与α的关系，进而求得∠AIB.【详解】解：如图所示，在AC上截取AD=AB，连接DI，点I是△ABC的角平分线的交点所以有∠BAI=∠DAI，∠ABI=∠CBI，∠ACI=∠BCI，在△ABI和△ADI中，AB=ADBAI=DAIAI=AI⎧⎪∠∠⎨⎪⎩∴△ABI≌△ADI（SAS）∴DI=BI又∵AB＋BI＝AC，AB+DC=AC∴DI=DC∴∠DCI=∠DIC设∠DCI=∠DIC=β则∠ABI=∠ADI=2∠DCI=2β在△ABC 中，∠BAC+2∠ABI+2∠DCI=180°，即42180ββ︒++=a ，∴180=3066β︒︒=--a a 在△ABI 中，180︒∠=-∠-∠AIB BAI ABI121802αβ︒=-- 1=23160028αα︒︒⎛⎫--- ⎪⎝⎭ =1206α︒-【点睛】本题考查全等三角形的判定和性质，以及三角形角度计算，利用截长补短构造全等三角形是解题的关键.2．如图，∠ACB ＝90°，AC ＝BC ，点C(1，2)、A(－2，0)，则点B 的坐标是__________.【答案】(3，－1)【解析】分析：过C 和B 分别作CD ⊥OD 于D ，BE ⊥CD 于E ，利用已知条件可证明△ADC ≌△CEB ，再由全等三角形的性质和已知数据即可求出B 点的坐标．详解：过C 和B 分别作CD ⊥OD 于D ，BE ⊥CD 于E ，∵∠ACB=90°，∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°，∴∠CAD=∠BCE ，在△ADC和△CEB中，∠ADC=∠CEB=90°；∠CAD=∠BCE，AC=BC，∴△ADC≌△CEB(AAS)，∴DC=BE，AD=CE，∵点C的坐标为(1,2),点A的坐标为(−2,0)，∴AD=CE=3，OD=1，BE=CD=2，∴则B点的坐标是(3,−1).故答案为(3,−1).点睛：本题主要考查了全等三角形的判定与性质，解题关键在于结合坐标、图形性质和已经条件.3．如图,C为线段AE上一动点(不与A． E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论：①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°，一定成立的有________（填序号）【答案】①②③⑤【解析】【分析】①根据全等三角形的判定方法，证出△ACD≌△BCE，即可得出AD=BE．③先证明△ACP≌△BCQ，即可判断出CP=CQ，③正确；②根据∠PCQ=60°，可得△PCQ为等边三角形，证出∠PQC=∠DCE=60°，得出PQ∥AE，②正确．④没有条件证出BO=OE，得出④错误；⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°，⑤正确；即可得出结论．【详解】解：∵△ABC和△CDE都是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∴∠ACB+∠BCD=∠DCE+∠BCD，∴∠ACD=∠BCE，在△ACD和△BCE中，AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△BCE（SAS），∴AD=BE，结论①正确．∵△ACD≌△BCE，∴∠CAD=∠CBE，又∵∠ACB=∠DCE=60°，∴∠BCD=180°-60°-60°=60°，∴∠ACP=∠BCQ=60°，在△ACP和△BCQ中，ACP BCQCAP CBQ AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△BCQ（AAS），∴CP=CQ，结论③正确；又∵∠PCQ=60°，∴△PCQ为等边三角形，∴∠PQC=∠DCE=60°，∴PQ∥AE，结论②正确．∵△ACD≌△BCE，∴∠ADC=∠AEO，∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°，∴结论⑤正确．没有条件证出BO=OE，④错误；综上，可得正确的结论有4个：①②③⑤．故答案是：①②③⑤．【点睛】此题是三角形综合题目，考查了全等三角形的判定和性质的应用、等边三角形的性质和应用、平行线的判定；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．4．已知在△ABC 中,两边AB、AC的中垂线，分别交BC于E、G．若BC＝12，EG＝2，则△AEG的周长是________．【答案】16或12．【解析】【分析】根据线段垂直平分线性质得出AE=BE，CG=AG，分两种情况讨论：①DE和FG的交点在△ABC内，②DE和FG的交点在△ABC外．【详解】∵DE，FG分别是△ABC的AB，AC边的垂直平分线，∴AE=BE，CG=AG．分两种情况讨论：①当DE和FG的交点在△ABC内时，如图1．∵BC=12，GE=2，∴AE+AG=BE+CG=12+2=14，△AGE的周长是AG+AE+EG=14+2=16．②当DE和FG的交点在△ABC外时，如图2，△AGE的周长是AG+AE+EG= BE+CG+EG=BC=12．故答案为：16或12．【点睛】本题考查了线段垂直平分线性质，注意：线段垂直平分线上的点到线段两个端点的距离相等．5．如图，在△ABD中，∠BAD＝80°，C为BD延长线上一点，∠BAC＝130°，△ABD的角平分线BE与AC交于点E，连接DE，则∠DEB＝_____．【答案】40°【解析】【分析】做辅助线，构建角平分线的距离，根据角平分线的性质和逆定理可得：EF=EG=EH，设∠DEG=y，∠GEB=x，根据三角形内角和定理可得：∠GEA=∠FEA=40°，∠FEB=∠HEB，列方程为2y+x=80-x,y+x=40,可得结论：∠DEB＝40°.【详解】如图，过E作EF⊥AB于F，EG⊥AD于G，EH⊥BC于H，∵BE平分∠ABD∴EH=EF∵∠BAC＝130°，∠BAD＝80°∴∠FAE=∠CAD=50°∴EF=EG∴EG=EH∴ED平分∠CDG∴∠HED=∠DEG设∠DEG=y，∠GEB=x，∵∠EFA=∠EGA=90°∴∠GEA=∠FEA=40°∵∠EFB=∠EHB=90°，∠EBH=∠EBF∴∠FEB=∠HEB∴2y+x=80-x,2y+2x=80y+x=40即∠DEB＝40°.故答案为：40°.【点睛】本题考查三角形内角和定理和角平分线的性质，正确作辅助线是解题的关键.6．如图，四边形ABCD是正方形，直线l1、l2、l3分别过A、B、C三点，l1∥l2∥l3，若l1与l2之间的距离为4，l2与l3之间的距离为5，则正方形的边长为______．【答案】41【解析】解：过B作直线BF⊥l3于F，交直线l1于点E．∵l1∥l3，∴∠AEB=∠BFC=90°，∴BE=4，BF=5．∵ABCD是正方形，∴AB=BC，∠ABC=90°，∴∠ABE+∠CBF=90°．∵∠ABE+∠BAE=90°，∴∠BAE=∠CBF．在△ABE和△BCF中，∵∠BAE=∠CBF，∠AEB=∠BFC，AB=BC，∴△ABE≌△BCF，∴AE=BF=5．在Rt△AEB中，AB=22=41．故答案为41．54AE BE=22点睛：本题考查了全等三角形的性质和判定，正方形的性质的应用，解答本题的关键是能正确作出辅助线，并进一步求出△ABE≌△BCF，难度适中．7．如图，Rt△ABC中，AB=AC，∠BAC=90°，BE⊥CE，垂足是E，BE交AC于点D，F是BE 上一点，AF⊥AE，且C是线段AF的垂直平分线上的点，AF=22，则DF=________.【答案】3.【解析】【分析】由题意可证的△ABF≌△ACE,可得△AEF为等腰直角三角形，取AF的中点O，连接CO交BE与点G，连接AG，可得△AGF, △AGE,△CEG均为等腰直角三角形，可得AG平行等于CE，可得四边形AGCE为平行四边形，可得FD的长.【详解】解：如图Rt△ABC中，AB=AC，∠BAC=90°，∴∠ABC=∠ACB=45°，又∠BAC=90°，BE⊥CE，∠DAE为∠BAC与EAF的公共角∴∠BAF=∠CAE,∠ABC=∠ACB=45°, BE⊥CE∴∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°，∴∠ABF=∠ACE，在△ABF与△ACE中，有AB ACBAF CAEABF ACE=⎧⎪∠=∠⎨⎪∠=∠⎩，∴△ABF≌△ACE，∴AE=AF, △AEF为等腰直角三角形, 取AF的中点O，连接CO交BE与点G，连接AG,C是线段AF的垂直平分线上的点，易得△AGF, △AGE,△CEG均为等腰直角三角形，AF=22∴AG=GE=CE=FG=2,又AG⊥BE,CE⊥BE,可得AG∥CE,∴四边形AGCE为平行四边形，∴GD=DE=1,∴DF=FG+GD=2+1=3.【点睛】本题主要考查三角形全等及性质，综合性强，需综合运用所学知识求解.8．如图，在△ABC 中，∠ABC =50°，∠ACB =60°，点E 在BC 的延长线上，∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ，连接AD ，以下结论：①∠BAC =70°；②∠DOC =90°；③∠BDC =35°；④∠DAC =55°，其中正确的是__________．（填写序号）【答案】①③④【解析】【分析】根据三角形内角和定理、角平分线的定义、三角形外角的性质、角平分线的性质解答即可．【详解】解：∵∠ABC =50°，∠ACB =60°，∴∠BAC =180°﹣50°﹣60°=70°，①正确；∵BD 是∠ABC 的平分线，∴∠DBC =12∠ABC =25°，∴∠DOC =25°+60°=85°，②错误； ∠BDC =60°﹣25°=35°，③正确；∵∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ，∴AD 是∠BAC 的外角平分线，∴∠DAC =55°，④正确．故答案为①③④．【点睛】本题考查的是角平分线的定义和性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．9．如图所示，在平行四边形ABCD 中，2AD AB =，F 是AD 的中点，作CE AB ⊥，垂足E 在线段上，连接EF 、CF ，则下列结论2BCD DCE ①∠=∠；EF CF =②；3DFE AEF ③∠=∠，2BEC CEF SS =④中一定成立的是______ .(把所有正确结论的序号都填在横线上)【答案】②③【解析】分析：由在平行四边形ABCD中，AD=2AB，F是AD的中点，易得AF=FD=CD，继而证得①∠DCF=12∠BCD；然后延长EF，交CD延长线于M，分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF（ASA），得出对应线段之间关系，进而得出答案．详解：①∵F是AD的中点，∴AF=FD，∵在▱ABCD中，AD=2AB，∴AF=FD=CD，∴∠DFC=∠DCF，∵AD∥BC，∴∠DFC=∠FCB，∴∠DCF=∠BCF，∴∠DCF=12∠BCD，即∠BCD=2∠DCF；故此选项错误；②延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A=∠MDF，∵F为AD中点，∴AF=FD，在△AEF和△DFM中，A FDMAF DFAFE DFM∠∠⎧⎪⎨⎪∠∠⎩＝＝＝，∴△AEF≌△DMF（ASA），∴FE=MF，∠AEF=∠M，∵CE⊥AB，∴∠AEC=90°，∴∠AEC=∠ECD=90°，∵FM=EF，∴FC=FM，故②正确；③设∠FEC=x，则∠FCE=x，∴∠DCF=∠DFC=90°-x，∴∠EFC=180°-2x，∴∠EFD=90°-x+180°-2x=270°-3x，∵∠AEF=90°-x，∴∠DFE=3∠AEF，故此选项正确．④∵EF=FM，∴S△EFC=S△CFM，∵MC＞BE，∴S△BEC＜2S△EFC故S△BEC=2S△CEF错误；综上可知：一定成立的是②③，故答案为②③．点睛：此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识，得出△AEF≌△DME是解题关键．10．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形，∠ADC=30°，若CD=6，BD=6.5，则AD=_________．【答案】2.5【解析】解：以CD为边向外作出等边三角形DCE，连接AE，∵∠ADC=30°，∴∠ADE=90°，在△ACE 与△BCD中，∵AC=BC，∠ACE=∠BCD，CE=DC，∴△ACE≌△BCD，∴BD=AE=6.5，∴AD2+DE2=AE2，∴AD3+62=6.52，∴AD=2.5．故答案为：2.5．二、八年级数学全等三角形选择题（难）11．在△ABC与△DEF中，下列各组条件，不能判定这两个三角形全等的是（）A．AB＝DE，∠B＝∠E，∠C＝∠F B．AC＝DE，∠B＝∠E，∠A＝∠FC．AC＝DF，BC＝DE，∠C＝∠D D．AB＝EF，∠A＝∠E，∠B＝∠F【答案】B【解析】利用全等三角形的判定定理，分析可得：A、AB=DE，∠B=∠E，∠C=∠F可利用AAS证明△ABC与△DEF全等；B、∠A=∠F，∠B=∠E，AC=DE，对应边不对应，不能证明△ABC与△DEF全等；C、AC=DF，BC=DE，∠C=∠D可利用ASA证明△ABC与△DEF全等；D、AB=EF，∠A=∠E∠B=∠F可利用SAS证明△ABC与△DEF全等；故选：D．点睛：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．12．如右图，在△ABC中，点Q，P分别是边AC，BC上的点，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四个结论：①AP平分∠BAC；②AS=AR；③BP=QP；④QP∥AB．其中一定正确的是( )A．①②③B．①③④C．①②④D．②③④【答案】C【解析】试题解析：∵PR⊥AB于点R，PS⊥AC于点S，且PR=PS，∴点P在∠BAC的平分线上，即AP平分∠BAC，故①正确；∴∠PAR=∠PAQ，∵AQ=PQ，∴∠APQ=∠PAQ，∴∠APQ=∠PAR，QP AB∴，故④正确；在△APR与△APS中,AP AP PR PS=⎧⎨=⎩，(HL)APR APS∴≌，∴AR=AS，故②正确；△BPR和△QSP只能知道PR=PS,∠BRP=∠QSP=90∘，其他条件不容易得到，所以，不一定全等.故③错误.故选C.13．已知OD平分∠MON，点A、B、C分别在OM、OD、ON上(点A、B、C都不与点O重合)，且AB=BC, 则∠OAB与∠BCO的数量关系为（）A．∠OAB+∠BCO=180°B．∠OAB=∠BCOC．∠OAB+∠BCO=180°或∠OAB=∠BCO D．无法确定【答案】C【解析】根据题意画图，可知当C处在C1的位置时，两三角形全等，可知∠OAB=∠BCO；当点C处在C2的位置时，根据等腰三角形的性质和三角形的外角的性质，∠OAB+∠BCO=180°.故选C.14．如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（）A．①②③B．①②④C．①③④D．②③④【答案】C【解析】已知BD为△ABC的角平分线，根据角平分线的定义可得∠ABD=∠CBD，在△AB D和△EB C 中，BD＝BC，∠ABD＝∠CBD，BE＝BA，由SAS可判定△ABD≌△EBC，即可得①正确；根据已知条件，无法证明AC=2CD，②错误；已知BD为△ABC的角平分线，BD=BC，BE=BA，可得∠BCD=∠BDC=∠BAE=∠BEA，再由∠BCE=∠BDA，∠BCE=∠BCD+∠DCE，∠BDA=∠DAE+∠BEA，∠BCD=∠BEA，可得∠DCE=∠DAE，所以AE=EC；再由△ABD≌△EBC，可得AD=EC，所以AD=AE=EC，即③正确；由△ABD ≌△EBC ，可得∠BCE =∠BDA ，所以∠BCE +∠BCD =∠BDA +∠BDC =180°，④正确.故选C.点睛：本题考查了全等三角形的判定及性质、等腰三角形的的性质、三角形外角的性质，本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键．15．如图在ABC △中，P ，Q 分别是BC 、AC 上的点，作PR AB ⊥，PS AC ⊥，垂足分别是R ，S ，AQ PQ =，PR PS =，下面三个结论：①AS AR =；②PQ AB ∥；③BRP △≌CSP △．其中正确的是（）．A ．①②B ．②③C ．①③D ．①②③ 【答案】A【解析】连接AP ，由题意得，90ARP ASP ∠=∠=︒，在Rt APR 和Rt APS 中，AP APPR PS =⎧⎨=⎩，∴△APR ≌()APS HL ，∴AS AR =，故①正确．BAP SAP ∠=∠，∴2SAB BAP SAP SAP ∠=∠+∠=∠，在AQP △中，∴AQ PQ =，∴QAP APQ ∠=∠，∴22CQP QAP APQ QAP SAP ∠=∠+∠=∠=∠，∴PQ AB ∥，故②正确；=，在Rt BRP和Rt CSP中，只有PR PS不满足三角形全等的条件，故③错误．故选A．点睛：本题主要考查三角形全等的判定方法以及角平分线的判定和平行线的判定，准确作出辅助线是解决本题的关键.16．在边长为1的正方形网格中标有A、B、C、D、E、F六个格点，根据图中标示的各点位置，与△ABC全等的是（）A．△ACF B．△ACEC．△ABD D．△CEF【答案】C【解析】【分析】利用勾股定理先分别求得△ABC的各边长以及各选项中三角形的各边长，再根据三角形全等的判定方法进行判定即可得.【详解】在△ABC中，AB=22+=10，BC=2231+=2，AC=22，11A、在△ACF中，AF=22+=5≠10，5≠2，5≠22，则△ACF与△ABC不全21等，故不符合题意；B、在△ACE中，AE=3≠10，3≠2，3≠22，则△ACE与△ABC不全等，故不符合题意；C、在△ABD中，AB=AB，AD=2=BC，BD=22=AC，则由SSS可证明△ACE与△ABC全等，故符合题意；D、在△CEF中，CF=3≠10，3≠2，3≠22，则△CEF与△ABC不全等，故不符合题意，故选C.【点睛】本题考查了勾股定理以及全等三角形的判定，熟练掌握勾股定理以及全等三角形的判定方法是解题的关键.17．如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为（）A．2 B．3 C．4 D．5【答案】C【解析】【分析】可延长DE至F，使EF=BC，利用SAS可证明△ABC≌△AEF，连AC，AD，AF，再利用SSS证明△ACD≌△AFD，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求解即可．【详解】延长DE至F，使EF=BC，连AC，AD，AF，在△ABC与△AEF中，=90AB AEABC AEFBC EF⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABC≌△AEF（SAS），∴AC=AF，∵AB=CD=AE=BC+DE，∠ABC=∠AED=90°，∴CD=EF+DE=DF，在△ACD与△AFD中，AC AFCD DFAD AD⎧⎪⎨⎪⎩＝＝＝，∴△ACD≌△AFD（SSS），∴五边形ABCDE的面积是：S=2S△ADF=2×12•DF•AE=2×12×2×2=4．故选C.【点睛】本题主要考查了全等三角形的判定及性质以及三角形面积的计算，正确作出辅助线，利用全等三角形把五边形ABCDE的面积转化为两个△ADF的面积是解决问题的关键．18．如图，在等腰直角△ABC中，∠ACB=90°，点O为斜边AB的中点，点D、E分别在直角边AC、BC上，且∠DOE=90°，DE交OC于点P，则下列结论：①图中全等三角形有三对；②△ABC的面积等于四边形CDOE面积的倍；③DE2+2CD•CE=2OA2；④AD2+BE2=2OP•OC．正确的有（）个．A．1 B．2 C．3 D．4【答案】C【解析】【分析】结论（1）正确．因为图中全等的三角形有3对；结论（2）错误．由全等三角形的性质可以判断；结论（3）正确．利用全等三角形和等腰直角三角形的性质可以判断．结论（4）正确．利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断．【详解】结论（1）正确，理由如下：图中全等的三角形有3对，分别为△AOC≌△BOC，△AOD≌△COE，△COD≌△BOE．由等腰直角三角形的性质，可知OA=OC=OB，易得△AOC≌△BOC．∵OC⊥AB，OD⊥OE，∴∠AOD=∠COE．在△AOD与△COE中，∴△AOD≌△COE（ASA），同理可证：△COD≌△BOE．结论（2）错误．理由如下：∵△AOD≌△COE，∴S△AOD=S△COE，∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=S△ABC即△ABC的面积等于四边形CDOE的面积的2倍．结论（3）正确，理由如下：∵△AOD≌△COE，∴CE=AD，∴CD+CE=CD+AD=AC=OA，∴（CD+CE）2=CD2+CE2+2CD•CE=DE2+2CD•CE=2OA2；结论（4）正确，理由如下：∵△AOD≌△COE，∴AD=CE；∵△COD≌△BOE，∴BE=CD．在Rt△CDE中，由勾股定理得：CD2+CE2=DE2，∴AD2+BE2=DE2．∵△AOD≌△COE，∴OD=OE，又∵OD⊥OE，∴△DOE为等腰直角三角形，∴DE2=2OE2，∠DEO=45°．∵∠DEO=∠OCE=45°，∠COE=∠COE，∴△OEP∽△OCE，∴，即OP•OC=OE2．∴DE2=2OE2=2OP•OC，∴AD2+BE2=2OP•OC．综上所述，正确的结论有3个，故选C．【点睛】本题是几何综合题，考查了等腰直角三角形、全等三角形、相似三角形和勾股定理等重要几何知识点．难点在于结论（4）的判断，其中对于“OP•OC”线段乘积的形式，可以寻求相似三角形解决问题．19．如图，已知等腰Rt△ABC和等腰Rt△ADE，AB=AC=4，∠BAC=∠EAD=90°，D是射线BC 上任意一点，连接EC．下列结论：①△AEC△ADB；②EC⊥BC ；③以A、C、D、E为顶点的四边形面积为8；④当BD=时，四边形AECB的周长为10524++;⑤当BD=32B时,ED=5AB；其中正确的有（）A．5个 B．4个 C．3 个 D．2个【答案】B【解析】解：∵∠BAC =∠EAD =90°，∴∠BAD =∠CAE ，∵AB =AC ，AD =AE ，∴△AEC ≌△ADB ，故①正确； ∵△AEC ≌△ADB ，∴∠ACE =∠ABD =45°，∵∠ACB =45°，∴J IAO ECB =90°，∴EC ⊥BC ，故②正确；∵四边形ADCE 的面积=△ADC 的面积+△ACE 的面积=△ADC 的面积+△ABD 的面积=△ABC 的面积=4×4÷2=8．故③正确；∵BD =2，∴EC =2，DC =BC -BD =422-=32，∴DE 2=DC 2+EC 2，=()()22322+=20，∴DE =25，∴AD =AE =252=10.∴AECB 的周长=AB +DC +CE +AE =442210+++=45210++，故④正确；当BD =32BC 时，CD =12BC ，∴DE =221322BC BC ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=102BC =52AB ．故⑤错误． 故选B ．点睛：此题是全等三角形的判定与性质的综合运用，熟练掌握等腰直角三角形的性质是解答此题的关键．20．如图，AC ⊥BE 于点C ，DF ⊥BE 于点F ，且BC ＝EF ，如果添上一个条件后，可以直接利用“HL ”来证明△ABC ≌△DEF ，则这个条件应该是( )A ．AC ＝DEB ．AB ＝DEC ．∠B ＝∠ED ．∠D ＝∠A【答案】B【解析】在Rt △ABC 与Rt △DEF 中，直角边BC ＝EF ，要利用“HL”判定全等，只需添加条件斜边AB=DE.故选：B.21．如图，△ABC 中，∠ABC=45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，DH ⊥BC 于H ，交BE 于G ．下列结论：①BD=CD ；②AD+CF=BD ；③CE=12BF ；④AE=BG ．其中正确的是A ．①②B ．①③C ．①②③D ．①②③④【答案】C【解析】【分析】根据∠ABC=45°，CD⊥AB可得出BD=CD，利用AAS判定Rt△DFB≌Rt△DAC，从而得出DF=AD，BF=AC．则CD=CF+AD，即AD+CF=BD；再利用AAS判定Rt△BEA≌Rt△BEC，得出CE=AE=12AC，又因为BF=AC所以CE=12AC=12BF，连接CG．因为△BCD是等腰直角三角形，即BD=CD．又因为DH⊥BC，那么DH垂直平分BC．即BG=CG．在Rt△CEG中，CG是斜边，CE是直角边，所以CE<CG．即AE<BG．【详解】解：∵CD⊥AB,∠ABC=45°，∴△BCD是等腰直角三角形.∴BD=CD.故①正确；在Rt△DFB和Rt△DAC中，∵∠DBF=90°−∠BFD,∠DC A=90°−∠EFC，且∠BFD=∠EFC，∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°，BD=CD，∴△DFB≌△DAC.∴BF=AC；DF=AD.∵CD=CF+DF，∴AD+CF=BD；故②正确；在Rt△BEA和Rt△BEC中.∵BE平分∠ABC，∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°，∴Rt△BEA≌Rt△BEC.∴CE=AE=12 AC.又由(1)，知BF=AC，∴CE=12AC=12BF；故③正确；连接CG.∵△BCD是等腰直角三角形，∴BD=CD.又DH⊥BC，∴DH 垂直平分BC.∴BG=CG.在Rt △CEG 中，∵CG 是斜边，CE 是直角边，∴CE<CG.∵CE=AE ，∴AE<BG.故④错误.故选C.【点睛】本题考查了等腰直角三角形、等腰三角形的判定与性质、全等三角形的判定与性质.此类问题涉及知识点较多，需要对相关知识点有很高的熟悉度.22．如图，在等腰△ABC 中，90ACB ︒∠=，8AC =，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =,连接DE 、DF 、EF 在此运动变化的过程中，下列结论：(1)DEF 是等腰直角三角形；(2)四边形CDFE 不可能为正方形，（3）DE 长度的最小值为4；（4）连接CF ，CF 恰好把四边形CDFE 的面积分成1：2两部分，则CE =13或143其中正确的结论个数是A ．1个B ．2个C ．3个D ．4个【答案】A【解析】【分析】 连接CF ，证明△ADF ≌△CEF ，根据全等三角形的性质判断①，根据正方形的判定定理判断②，根据勾股定理判断③，根据面积判断④．【详解】连接CF ，∵△ABC 是等腰直角三角形，∴∠FCB=∠A=45 ，CF=AF=FB ；∵AD=CE ，∴△ADF ≌△CEF(SAS)；∴EF=DF ，∠CFE=∠AFD ；∵∠AFD+∠CFD=90∘，∴∠CFE+∠CFD=∠EFD=90∘，又∵EF=DF∴△EDF 是等腰直角三角形(故(1)正确).当D. E 分别为AC 、BC 中点时,四边形CDFE 是正方形(故(2)错误).由于△DEF 是等腰直角三角形，因此当DE 最小时，DF 也最小；即当DF ⊥AC 时,DE 最小,此时142DF BC == .∴DE =故(3)错误).∵△ADF ≌△CEF ，∴S △CEF =S △ADF∴S 四边形CDFE =S △AFC ,∵CF 恰好把四边形CDFE 的面积分成1：2两部分∴S △CEF ：S △CDF =1:2 或S △CEF ：S △CDF =2:1即S △ADF ：S △CDF =1:2 或S △ADF ：S △CDF =2:1当S △ADF ：S △CDF =1:2时，S △ADF=13S △ACF =111684323⨯⨯⨯= 又∵S △ADF =1422AD AD ⨯⨯= ∴2AD=163∴AD=83(故(4)错误).故选：A.【点睛】本题考查了全等三角形，等腰直角三角形，以及勾股定理，掌握全等三角形，等腰直角三角形，以及勾股定理是解题的关键.23．如图，在正方形ABCD 中，AC 为对角线，E 为AB 上一点，过点E 作 EF∥AD，与AC 、DC 分别交于点G ，F ，H 为CG 的中点，连结DE 、 EH 、DH 、FH ．下列结论：①EG=DF；②△EHF≌△DHC；③∠AEH+∠ADH=180°；④若23AE AB =，则313DHC EDH SS =．其中结论正确的有（ ）A．1个B．2个C．3个D．4个【答案】D【解析】分析：①根据题意可知∠ACD=45°，则GF=FC，则EG=EF-GF=CD-FC=DF；②由SAS证明△EHF≌△DHC即可；③根据△EHF≌△DHC，得到∠HEF=∠HDC，从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°；④若AEAB=23，则AE=2BE，可以证明△EGH≌△DFH，则∠EHG=∠DHF且EH=DH，则∠DHE=90°，△EHD为等腰直角三角形，过H点作HM垂直于CD于M点，设HM=x，则DM=5x，26x，CD=6x，则S△DHC=12×HM×CD=3x2，S△EDH=12×DH2=13x2．详解：①∵四边形ABCD为正方形,EF∥AD，∴EF=AD=CD,∠ACD=45°,∠GFC=90°，∴△CFG为等腰直角三角形，∴GF=FC，∵EG=EF−GF，DF=CD−FC，∴EG=DF，故①正确；②∵△CFG为等腰直角三角形，H为CG的中点，∴FH=CH,∠GFH=12∠GFC=45°=∠HCD，在△EHF和△DHC中，EF=CD；∠EFH=∠DCH；FH=CH，∴△EHF≌△DHC(SAS)，故②正确；③∵△EHF≌△DHC(已证)，∴∠HEF=∠HDC，∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF−∠HDC=∠AEF+∠ADF=180°，故③正确；④∵AEAB=23，∴AE=2BE，∵△CFG为等腰直角三角形，H为CG的中点，∴FH=GH,∠FHG=90°，∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD，在△EGH和△DFH中，EG=DF ；∠EGH=∠HFD ；GH=FH ，∴△EGH ≌△DFH(SAS)，∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,∴△EHD 为等腰直角三角形，如图，过H 点作HM ⊥CD 于M ，设HM=x,则DM=5x,DH=26x ，CD=6x ，则S △DHC =12×HM×CD=3x 2,S △EDH =12×DH 2=13x 2， ∴3S △EDH =13S △DHC ，故④正确；故选D. 点睛：本题考查了相似三角形的判定与性质，全等三角形的判定与性质，正方形的性质，解题关键在于根据题意熟练的运用相关性质.24．如图，在四边形ABCD 中，//AB CD .不能判定ABD CDB ∆≅∆的条件是（ ）A ．AB CD =B ．AD BC = C ．//AD BC D ．A C ∠=∠【答案】B【解析】【分析】根据已知条件，分别添加选项进行排查，即可完成解答；注意BD 是公用边这个条件.【详解】解：A.若添加AB=CD,根据AB ∥CD ，则∠ABD=∠CDB ，依据SAS 可得△ABD ≌△CDB ，故A 选项正确；B.若添加AD=BC,根据AB ∥CD ，则∠ADB=∠CBD ，不能判定△ABD ≌△CDB ，故B 选项错误；C.若添加//AD BC ，则四边形ABCD 是平行四边形，能判定△ABD ≌△CDB ，故C 选项正确；D.若添加∠A=∠C ，根据AB ∥CD ，则∠ABD=∠CDB ，且BD 公用，能判定△ABD ≌△CDB ，故D 选项正确；故选：B.【点睛】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边.25．如图，Rt△ACB中，∠ACB=90°，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB=135°；②BF=BA；③PH=PD；④连接CP，CP平分∠ACB，其中正确的是（）A．①②③B．①②④C．①③④D．①②③④【答案】D【解析】分析：根据三角形内角和定理以及角平分线定义判断①；根据全等三角形的判定和性质判断②③；根据角平分线的判定与性质判断④．详解：在△ABC中，∵∠ACB=90°，∴∠BAC+∠ABC=90°，又∵AD、BE分别平分∠BAC、∠ABC，∴∠BAD+∠ABE=（∠BAC+∠ABC）=45°，∴∠APB=135°，故①正确．∴∠BPD=45°，又∵PF⊥AD，∴∠FPB=90°+45°=135°，∴∠APB=∠FPB，又∵∠ABP=∠FBP，BP=BP，∴△ABP≌△FBP，∴∠BAP=∠BFP，AB=FB，PA=PF，故②正确．在△APH和△FPD中，∵∠APH=∠FPD=90°，∠PAH=∠BAP=∠BFP，PA=PF，∴△APH≌△FPD，∴PH=PD，故③正确．∵△ABC的角平分线AD、BE相交于点P，∴点P到AB、AC的距离相等，点P到AB、BC的距离相等，∴点P到BC、AC的距离相等，∴点P在∠ACB的平分线上，∴CP平分∠ACB，故④正确．故选D．点睛：本题考查了角平分线的判定与性质，三角形全等的判定方法，三角形内角和定理．掌握相关性质是解题的关键．26．如图所示，点A、B分别是∠NOP、∠MOP平分线上的点，AB⊥OP于点E，BC⊥MN 于点C，AD⊥MN于点D，下列结论错误的是( )A．AD＋BC＝AB B．与∠CBO互余的角有两个C．∠AOB＝90°D．点O是CD的中点【答案】B【解析】【分析】根据角平分线上的点到角的两边距离相等可得AD=AE，BC=BE，利用角平分线的定义和平角的性质可得到∠AOB的度数，再利用“HL”证明Rt△AOD和Rt△AOE全等，根据全等三角形对应边相等可得OD=OE，同理可得OC=OE，然后求出∠AOB=90°，然后对各选项分析判断即可得解．【详解】∵点A，B分别是∠NOP，∠MOP平分线上的点，∴AD=AE，BC=BE．∵AB=AE+BE，∴AB=AD+BC，故A选项结论正确；与∠CBO互余的角有∠COB，∠EOB，∠OAD，∠OAE共4个，故B选项结论错误；∵点A、B分别是∠NOP、∠MOP平分线上的点，∴∠AOE=12∠EOD，∠BOC=12∠MOE，∴∠AOB=12(∠EOD+∠MOE)=12×180°=90°，故C选项结论正确；在Rt△AOD和Rt△AOE中，AO AOAD AE=⎧⎨=⎩，∴Rt△AOD≌Rt△AOE（HL），∴OD=OE，同理可得OC=OE，∴OC=OD=OE，∴点O是CD的中点，故D选项结论正确．故选B．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，余角的定义，熟记各性质并准确识图是解题的关键．27．如图，点B，F，C，E在同一条直线上，点A，D在直线BE的两侧，AB∥DE，BF＝CE，添加一个适当的条件后，仍不能使得△ABC≌△DEF（）A．AC＝DF B．AC∥DF C．∠A＝∠D D．AB＝DE【答案】A【解析】【分析】根据AB∥DE证得∠B＝∠E，又已知BF＝CE证得BC＝EF，即已具备两个条件：一边一角，再依次添加选项中的条件即可判断.【详解】∵AB∥DE，∴∠B＝∠E，∵BF＝CE，∴BF+FC＝CE+FC，∴BC＝EF，若添加AC＝DF，则不能判定△ABC≌△DEF，故选项A符合题意；若添加AC∥DF，则∠ACB＝∠DFE，可以判断△ABC≌△DEF（ASA），故选项B不符合题意；若添加∠A＝∠D，可以判断△ABC≌△DEF（AAS），故选项C不符合题意；若添加AB＝DE，可以判断△ABC≌△DEF（SAS），故选项D不符合题意；故选：A．【点睛】此题考查三角形全等的判定定理，熟练掌握定理，并能通过定理去判断条件是否符合全等是解决此题的关键.28．如图，Rt△ACB中，∠ACB=90°，∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P，分别交AC和BC的延长线于E，D，过P作PF⊥AD交AC的延长线于点H，交BC的延长线于点F，连接AF交DH于点G，则下列结论：①∠APB=45°；②PF=PA；③BD﹣AH=AB；④D G=AP+GH，其中正确的是（）A．1 B．2 C．3 D．4【答案】C【解析】【分析】①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP，再根据角平分线的定义∠ABP=12∠ABC，然后利用三角形的内角和定理整理即可得解；②先求出∠APB=∠FPB，再利用“角边角”证明△ABP和△FBP全等，根据全等三角形对应边相等得到AB=BF，AP=PF；③根据直角的关系求出∠AHP=∠FDP，然后利用“角角边”证明△AHP与△FDP全等，根据全等三角形对应边相等可得DF=AH；④根据PF⊥AD，∠ACB=90°，可得AG⊥DH，然后求出∠ADG=∠DAG=45°，再根据等角对等边可得DG=AG，再根据等腰直角三角形两腰相等可得GH=GF，然后求出DG=GH+AF，有直角三角形斜边大于直角边，AF＞AP，从而得出本小题错误.【详解】解：①∵∠ABC的角平分线BE和∠BAC的外角平分线，∴∠ABP=12∠ABC，∠CAP=12（90°+∠ABC）=45°+12∠ABC，在△ABP中，∠APB=180°-∠BAP-∠ABP，=180°-（45°+12∠ABC+90°-∠ABC）-12∠ABC，=180°-45°- 12∠ABC-90°+∠ABC-12∠ABC，=45°，故本小题正确；②∵PF⊥AD，∠APB=45°（已证），∴∠APB=∠FPB=45°，∵∵PB 为∠ABC 的角平分线，∴∠ABP=∠FBP ，在△ABP 和△FBP 中，APB FPB PB PBABP FBP ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABP ≌△FBP （ASA ），∴AB=BF ，AP=PF ；故②正确；③∵∠ACB=90°，PF ⊥AD ，∴∠FDP+∠HAP=90°，∠AHP+∠HAP=90°，∴∠AHP=∠FDP ，∵PF ⊥AD ，∴∠APH=∠FPD=90°，在△AHP 与△FDP 中，90AHP FDP APH FPD AP PF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△AHP ≌△FDP （AAS ），∴DF=AH ，∵BD=DF+BF ，∴BD=AH+AB ，∴BD-AH=AB ，故③小题正确；④∵PF ⊥AD ，∠ACB=90°，∴AG ⊥DH ，∵AP=PF ，PF ⊥AD ，∴∠PAF=45°，∴∠ADG=∠DAG=45°，∴DG=AG ，∵∠PAF=45°，AG ⊥DH ，∴△ADG 与△FGH 都是等腰直角三角形，∴DG=AG ，GH=GF ，∴DG=GH+AF ，∵AF ＞AP ，∴DG=AP+GH 不成立，故本小题错误，综上所述①②③正确．故选:C.【点睛】本题考查了直角三角形的性质，全等三角形的判定，以及等腰直角三角形的判定与性质，等角对等边，等边对等角的性质，综合性较强，难度较大，做题时要分清角的关系与边的关系.29．程老师制作了如图1所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题，操作学具时，点Q 在轨道槽AM 上运动，点P 既能在以A 为圆心、以8为半径的半圆轨道槽上运动，也能在轨道槽QN 上运动，图2是操作学具时，所对应某个位置的图形的示意图．有以下结论：①当∠PAQ=30°，PQ=6时，可得到形状唯一确定的△PAQ②当∠PAQ=30°，PQ=9时，可得到形状唯一确定的△PAQ③当∠PAQ=90°，PQ=10时，可得到形状唯一确定的△PAQ④当∠PAQ=150°，PQ=12时，可得到形状唯一确定的△PAQ其中所有正确结论的序号是( )A ．②③B ．③④C ．②③④D ．①②③④【答案】C【解析】【分析】分别在以上四种情况下以P 为圆心，PQ 的长度为半径画弧，观察弧与直线AM 的交点即为Q 点，作出PAQ ∆后可得答案．【详解】如下图，当∠PAQ=30°，PQ=6时，以P 为圆心，PQ 的长度为半径画弧，弧与直线AM 有两个交点，作出PAQ ∆，发现两个位置的Q 都符合题意，所以PAQ ∆不唯一，所以①错误．如下图，当∠PAQ=30°，PQ=9时，以P 为圆心，PQ 的长度为半径画弧，弧与直线AM 有两个交点，作出PAQ ∆，发现左边位置的Q 不符合题意，所以PAQ ∆唯一，所以②正确．如下图，当∠PAQ=90°，PQ=10时，以P 为圆心，PQ 的长度为半径画弧，弧与直线AM 有两个交点，作出PAQ ∆，发现两个位置的Q 都符合题意，但是此时两个三角形全等，所以形状相同，所以PAQ ∆唯一，所以③正确．如下图，当∠PAQ=150°，PQ=12时，以P 为圆心，PQ 的长度为半径画弧，弧与直线AM 有两个交点，作出PAQ ∆，发现左边位置的Q 不符合题意，所以PAQ ∆唯一，所以④正确．综上：②③④正确．故选C ．【点睛】本题考查的是三角形形状问题，为三角形全等来探索判定方法，也考查三角形的作图，利用对称关系作出另一个Q 是关键．30．如图，等边△ABC 的边AB 上一点P ，作PE ⊥AC 于E ，Q 为BC 延长线上的一点，当PA =CQ 时，连接PQ 交AC 于点D ，下列结论中不一定正确的是（ ）。

长安一中、高新一中、交大附中、师大附中、西安中学高2013届第一次模拟考试数学（文）试题第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合M={x|一3<x<3，x ∈Z ），N={x|x<1}，则M N= A ．{|3x x -<<1} B ．{|02}x x <<C ．{-3，-2，-1，0,1）D ．{-2，一1，0）【答案】D【解析】因为集合M={x|一3<x<3，x ∈Z}={-2，-1,0,1,2，}，N={x|x<1}，所以M N={-2，一1，0}。

2．已知直线a 和平面α，那么a//α的一个充分条件是 A ．存在一条直线b ，a//b 且b ⊂α B ．存在一条直线b ，a ⊥b 且b ⊥α C ．存在一个平面β，a ⊂β∥且α//βD ．存在一个平面β，α//β且α//β【答案】C【解析】A ．存在一条直线b ，a//b 且b ⊂α，错误，a 可能在平面α内； B ．存在一条直线b ，a ⊥b 且b ⊥α，错误，a 可能在平面α内； C ．存在一个平面β，a ⊂β，且α//β，正确，此为面面垂直的性质定理；D ．存在一个平面β，α//β且α//β，错误。

3．如果数列321121,,,,,n n a a a a a a a - …是首项为1，公比为2-的等比数列，则a 5等于A ．32B ．64C ．—32D ．—64【答案】A【解析】因为数列321121,,,,,n n a a a a a a a -…是首项为1，公比为2-的等比数列，所以3524112341,2,2,22,4a a a aa a a a a =====，以上几式相乘得：532a =。

4．设实数x ，y 满足11,11x y x y -≤+≤⎧⎨-≤-≤⎩则点（x,y ）在圆面2212x y +≤内部的概率为A ．8πB ．4π C ．34π D ．2π 【答案】B【解析】约束条件11,11x y x y -≤+≤⎧⎨-≤-≤⎩的可行域是边长为2的正方形，所以正方形的面积为 2.圆2212x y +=正好在正方形的内部，且其面积为2π，所以其概率为224ππ=。

2015年西安中考考试具体安排2015年西安中考考试考试时间：2015年全省统一的初中毕业学业考试时间为6月27日至28日。

中考各科具体考试时间如下：考试日期考试时间（北京时间）科目6月28日上午8:30-11:00 语文（星期日）下午14:00-16:00 数学16:50-18:30 思想品德与历史6月27日上午8:30-10:30 英语（星期六）下午14:00-16:00 物理与化学（备注：英语听力考试，8:20广播提示，8:30-8:50播送正式听力试题。

）2015年西安中考时间：6月27日至28日昨日从省教育厅发出的关于做好2015年陕西省初中毕业学业考试工作的通知中获悉，2015年中考基本保持原有的方式、统考科目和分值，考试时间为6月27日至28日。

考试科目仍为7科5卷据悉，2015年全省统一组织的初中毕业学业考试科目为语文、数学、英语、物理与化学、思想品德与历史，共7科5卷。

思想品德与历史实行开卷笔试，其他科目均为闭卷笔试。

语文为一卷制，其他科目为两卷制。

英语听力试题播放采用以广播为主、磁带为辅的办法进行。

在规定时间内，由陕西声媒广告文化传播有限责任公司新闻广播AM693、FM106.6同时向全省播放英语听力试题。

要求各地在拟设考点的学校提前试收上述两个频率的节目。

若收听效果不好，可用磁带播放。

磁带播放时间要与广播同步，从8:20开始先播送提示语，接着播送正式听力试题。

体育统一考试占35分学业考试以分数阅卷、以等级方式呈现。

考试成绩分A（优秀）、B（良好）、C（合格）、D（不合格）四个等级。

必要时，各等级下可设若干个二级等级（不宜过多），以便于高中招生时的实际操作。

学业成绩达到C等级以上（含C等级）为初中学生毕业要求。

继续实施体育考试。

体育考试成绩总分为50分，记入初中毕业学业考试总分，其中平时考核成绩占15分（体育课成绩9分，《国家学生体质健康标准》测试成绩6分）；统一考试成绩占35分。

陕西西安市高新区高新一中2024-2025学年八年级上学期收心考试英语试题一、单项选择1．My best friend Mary is ________ outgoing girl and we all like ________.A．a; she B．an; her C．the; she D．/ her2．She ________ hens and pigs with her ________ last Sunday night.A．fed; children B．feed; children C．feed; child D．fed; childs3．________ the teachers in their school is about 200 and half of them are ________ teachers.A．A number of; women B．A number of; womanC．The number of; women D．The number of; woman4．—This dress is too long, please give me ________ one.—Sure, madam. Give ________ back to me and try on this one.A．other; one B．other; it C．another; it D．another; one5．I think this film is ________. I am very ________ in it.A．interesting; interest.B．interested; interested C．interested; interestD．interesting; interested6．— Tim, I heard your father is a teacher. Can you tell me ________?— Well, he has short hair and wears glasses.A．what he is like B．what does he look likeC．what is he like D．what he looks like7．There are different ________ animals in the zoo, and I think the tigers are ________ scary.A．kinds of; kind of B．kinds of; a kind of C．kind of; a kind of D．kind of; kind of 8．— Susan, let’s go to the park to fly a kite after school.— Sorry. I have to go ________ home after school. It’s one of my family ________.A．easily; rule B．straight; rules C．easily; rules D．straight; rule 9．—I like the ________ named the English World very much.—Me, ________. I have read it for many years.A．game; too B．program; also C．movie; also D．magazine; too10．The little boy ________ into the river. A man quickly ________ towards him and saved him.A．fell; swim B．fall; swim C．fell; swam D．fall; swam二、完形填空Weekend is always fun time for students. Last Saturday, it was 11 sunny day and the air was clean. In the morning, Bob had a quick breakfast and went to the park with his mother. They 12 a walk in it. They stayed there 13 one hour and went back home at nine. It was quite hot, so Bob went to the 14 pool with his friend. They had a great time 15 in the water. At about twelve, they went to a small restaurant. There were some specials and they tasted 16 . They ate 17 . When they went out of the restaurant, it rained hard outside. But 18 , they had an umbrella and they didn’t get wet (淋湿).In the afternoon, Bob’s cousin Helen came to 19 house. They went to a science museum by bus. It took them about half an hour 20 there. It was interesting. They learned about robots at the museum. They left the museum at four o’ clock. They were tired but happy. It was a good weekend for Bob.11．A．an B．the C．a D．/12．A．take B．takes C．took D．to take13．A．at B．in C．about D．for14．A．swim B．swimming C．swam D．swims 15．A．plays B．to play C．playing D．played 16．A．well B．good C．bad D．badly17．A．a lot B．a lot of C．lots of D．a lots 18．A．lucky B．luckily C．unlucky D．unluckily 19．A．he B．himself C．him D．his20．A．get B．gets C．to get D．gettingMrs. White has a son. His name is Sam. The young man begins to 21 in a post office in a big city this autumn. He asks his mother to visit the city. The old woman is 22 and catches a train. Soon she gets to the city, 23 she doesn’t know where the post office is. She begins to 24 it. At a bus stop, she asks an old man, “Excuse me, sir. 25 canI get to the post office, please?”“We have about forty post offices in our city,” says the old man. “Which one do you want to go?” The old woman gives Sam’s 26 to him and the old man says, “Walk along this street and take the fourth turning on the left. The post office is just there.”Mrs. White 27 the old man and soon finds her son. They’re very happy. A week later, the old woman goes to the zoo. She sees many 28 . But after that she can’t find the way again. At the same bus stop, she meets the 29 old man and she asks the same question again.“Oh!” the old man calls out. “Are you 30 looking for your son?”21．A．work B．teach C．study D．live 22．A．beautiful B．afraid C．happy D．shy23．A．and B．but C．or D．so24．A．look at B．look for C．look like D．look after 25．A．Where B．Why C．When D．How 26．A．address B．number C．picture D．message 27．A．loses B．dresses C．thanks D．forgets 28．A．plants B．animals C．vegetables D．noodles 29．A．same B．different C．right D．wrong 30．A．often B．usually C．always D．still三、阅读理解Unlike other people, my Olympic heroes are not Olympic champions (冠军). They are just the people who do everyday things for the Olympics. They work every day, but they are not as popular as champions. They are Olympic volunteers (志愿者).These people aren’t the great stars of sports. They just want to do something for the Olympics by helping the Olympic Games go well. With their help, the Olympic Games can be successful (成功的). The stars of the Games are like beautiful boats on the sea, but the volunteers are the wind, and no one sees them. If there is no wind, the boats can’t move and no one want to watch them. The volunteers bring the wind of life to the players.The volunteers may never win medals (奖牌), but they always do their best in each game. Some would think the volunteer work is boring and meaningless. But in my eyes, they are also very important, and I really admire them. They are my Olympic heroes.31．Who is the writer’s Olympic hero?A．The champions.B．The players.C．The volunteers.D．The other people.32．The writer thinks that Olympic volunteers are like ________.A．the stars B．the wind C．the boat D．the sea33．What does the writer think of the volunteer work?A．Boring and meaningless.B．Easy and fun.C．Boring and easy.D．Important and helpful.34．What does the underlined word “admire” in Paragraph 3 mean in Chinese?A．敬佩B．评价C．放弃D．忽视35．Which of the followings can be the best title of the passage?A．The Olympic Games B．The Olympic ChampionsC．The Stars of the Games D．My Olympic Heroes根据短文内容，从短文后的选项中选出能填入空白处的最佳选项。