
w支持向量机: Maximum Margin Classifier
by pluskid, on 2010-09-08, in Machine Learning84 comments
支持向量机即Support Vector Machine,简称SVM 。我最开始听说这头机器的名号的时候,一种神秘感就油然而生,似乎把Support 这么一个具体的动作和Vector 这么一个抽象的概念拼到一起,然后再做成一个Machine ,一听就很玄了!
不过后来我才知道,原来SVM 它并不是一头机器,而是一种算法,或者,确切地说,是一类算法,当然,这样抠字眼的话就没完没了了,比如,我说SVM 实际上是一个分类器(Classifier) ,但是其实也是有用SVM 来做回归(Regression) 的。所以,这种字眼就先不管了,还是从分类器说起吧。
SVM 一直被认为是效果最好的现成可用的分类算法之一(其实有很多人都相信,“之一”是可以去掉的)。这里“现成可用”其实是很重要的,因为一直以来学术界和工业界甚至只是学术界里做理论的和做应用的之间,都有一种“鸿沟”,有些很fancy 或者很复杂的算法,在抽象出来的模型里很完美,然而在实际问题上却显得很脆弱,效果很差甚至完全fail 。而SVM 则正好是一个特例——在两边都混得开。
好了,由于SVM 的故事本身就很长,所以废话就先只说这么多了,直接入题吧。当然,说是入贴,但是也不能一上来就是SVM ,而是必须要从线性分类器开始讲。这里我们考虑的
是一个两类的分类问题,数据点用x来表示,这是一个n维向量,而类别用y来表示,可以取1 或者-1 ,分别代表两个不同的类(有些地方会选0 和 1 ,当然其实分类问题选什么都无所谓,只要是两个不同的数字即可,不过这里选择+1 和-1 是为了方便SVM 的
推导,后面就会明了了)。一个线性分类器就是要在n维的数据空间中找到一个超平面,其方程可以表示为
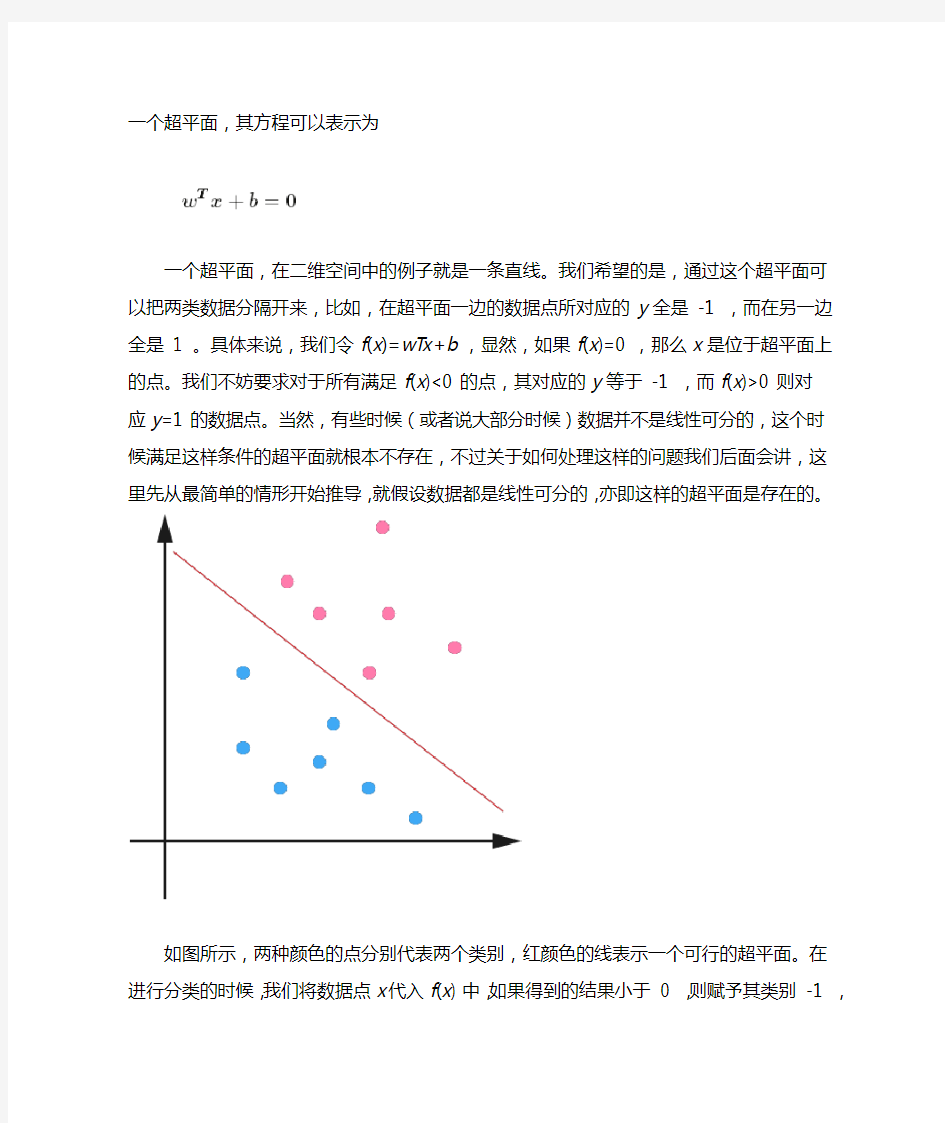
一个超平面,在二维空间中的例子就是一条直线。我们希望的是,通过这个超平面可以把两类数据分隔开来,比如,在超平面一边的数据点所对应的y全是-1 ,而在另一边全是 1 。具体来说,我们令f(x)=w T x+b,显然,如果f(x)=0,那么x是位于超平面上的点。我们不妨要求对于所有满足f(x)<0的点,其对应的y等于-1 ,而f(x)>0则对
应y=1的数据点。当然,有些时候(或者说大部分时候)数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在,不过关于如何处理这样的问题我们后面会讲,这里
先从最简单的情形开始推导,就假设数据都是线性可分的,亦即这样的超平面是存在的。
如图所示,两种颜色的点分别代表两个类别,红颜色的线表示一个可行的超平面。在进行分类的时候,我们将数据点x代入f(x)中,如果得到的结果小于0 ,则赋予其类别-1 ,
如果大于0 则赋予类别1 。如果f(x)=0,则很难办了,分到哪一类都不是。事实上,对于f(x)的绝对值很小的情况,我们都很难处理,因为细微的变动(比如超平面稍微转一个
小角度)就有可能导致结果类别的改变。理想情况下,我们希望f(x)的值都是很大的正数或者很小的负数,这样我们就能更加确信它是属于其中某一类别的。
从几何直观上来说,由于超平面是用于分隔两类数据的,越接近超平面的点越“难”分隔,因为如果超平面稍微转动一下,它们就有可能跑到另一边去。反之,如果是距离超平面很远的点,例如图中的右上角或者左下角的点,则很容易分辩出其类别。
实际上这两个Criteria 是互通的,我们定义functional margin 为γ?=y(w T x+b)=yf(x),
注意前面乘上类别y之后可以保证这个margin 的非负性(因为f(x)<0对应于y=?1的那些点),而点到超平面的距离定义为geometrical margin 。不妨来看看二者之间的关系。如图所示,对于一个点x,令其垂直投影到超平面上的对应的为x0,由于w是垂直于超平面的一个向量(请自行验证),我们有
又由于x0是超平面上的点,满足f(x0)=0,代入超平面的方程即可算出
不过,这里的γ是带符号的,我们需要的只是它的绝对值,因此类似地,也乘上对应的类别y即可,因此实际上我们定义geometrical margin 为:
显然,functional margin 和geometrical margin 相差一个∥w∥的缩放因子。按照我们前面的分析,对一个数据点进行分类,当它的margin 越大的时候,分类的confidence 越大。对于一个包含n个点的数据集,我们可以很自然地定义它的margin 为所有这n个点
的margin 值中最小的那个。于是,为了使得分类的confidence 高,我们希望所选择的hyper plane 能够最大化这个margin 值。
不过这里我们有两个margin 可以选,不过functional margin 明显是不太适合用来最大化的一个量,因为在hyper plane 固定以后,我们可以等比例地缩放w的长度和b的值,这样可以使得f(x)=w T x+b的值任意大,亦即functional margin γ?可以在hyper plane 保持不变的情况下被取得任意大,而geometrical margin 则没有这个问题,因为除上了∥w∥这个分母,所以缩放w和b的时候γ?的值是不会改变的,它只随着hyper plane 的
变动而变动,因此,这是更加合适的一个margin 。这样一来,我们的maximum margin classifier 的目标函数即定义为
当然,还需要满足一些条件,根据margin 的定义,我们有
其中,根据我们刚才的讨论,即使在超平面固定的情况下,γ?的值也可以随着∥w∥的变化而变化。由于我们的目标就是要确定超平面,因此可以把这个无关的变量固定下来,固定的方式有两种:一是固定∥w∥,当我们找到最优的γ?时γ?也就可以随之而固定;二是反过来固定γ?,此时∥w∥也可以根据最优的γ?得到。处于方便推导和优化的目的,我们选择第二种,令γ?=1,则我们的目标函数化为:
通过求解这个问题,我们就可以找到一个margin 最大的classifier ,如下图所示,中间的红色线条是Optimal Hyper Plane ,另外两条线到红线的距离都是等于γ?的:
到此为止,算是完成了Maximum Margin Classifier 的介绍,通过最大化margin ,我们使得该分类器对数据进行分类时具有了最大的confidence (实际上,根据我们说给的一个数据集的margin 的定义,准确的说,应该是“对最不confidence 的数据具有了最大的
confidence”——虽然有点拗口)。不过,到现在似乎还没有一点点Support Vector Machine 的影子。很遗憾的是,这个要等到下一次再说了,不过可以先小小地剧透一下,如上图所示,我们可以看到hyper plane 两边的那个gap 分别对应的两条平行的线(在高维空间中也应该是两个hyper plane)上有一些点,显然两个hyper plane 上都会有点存在,否则我们就
可以进一步扩大gap ,也就是增大γ?的值了。这些点呢,就叫做support vector ,嗯,先说这么多了。
支持向量机: Support Vector
by pluskid, on 2010-09-10, in Machine Learning49 comments
本文是“支持向量机系列”的第二篇,参见本系列的其他文章。
上一次介绍支持向量机,结果说到Maximum Margin Classifier ,到最后都没有说“支持向量”到底是什么东西。不妨回忆一下上次最后一张图:
可以看到两个支撑着中间的gap 的超平面,它们到中间的separating hyper plane 的距离
相等(想想看:为什么一定是相等的?),即我们所能得到的最大的geometrical margin γ?。而“支撑”这两个超平面的必定会有一些点,试想,如果某超平面没有碰到任意一个点的话,那么我就可以进一步地扩充中间的gap ,于是这个就不是最大的margin 了。由于在n维向量空间里一个点实际上是和以原点为起点,该点为终点的一个向量是等价的,所以这些“支撑”的点便叫做支持向量。
很显然,由于这些supporting vector 刚好在边界上,所以它们是满足y(w T x+b)=1(还记得我们把functional margin 定为 1 了吗?),而对于所有不是支持向量的点,也就是在“阵地后方”的点,则显然有y(w T x+b)>1。事实上,当最优的超平面确定下来之后,这
些后方的点就完全成了路人甲了,它们可以在自己的边界后方随便飘来飘去都不会对超平面产生任何影响。这样的特性在实际中有一个最直接的好处就在于存储和计算上的优越性,例如,如果使用100 万个点求出一个最优的超平面,其中是supporting vector 的有100 个,那么我只需要记住这100 个点的信息即可,对于后续分类也只需要利用这100 个点而不
是全部100 万个点来做计算。(当然,通常除了K-Nearest Neighbor 之类的Memory-based Learning算法,通常算法也都不会直接把所有的点记忆下来,并全部用来做后续inference 中的计算。不过,如果算法使用了Kernel 方法进行非线性化推广的话,就会遇到这个问题了。Kernel 方法在下一次会介绍。)
当然,除了从几何直观上之外,支持向量的概念也会从其优化过程的推导中得到。其实上一次还偷偷卖了另一个关子就是虽然给出了目标函数,却没有讲怎么来求解。现在就让我们来处理这个问题。回忆一下之前得到的目标函数:
这个问题等价于(为了方便求解,我在这里加上了平方,还有一个系数,显然这两个问题是等价的,因为我们关心的并不是最优情况下目标函数的具体数值):
到这个形式以后,就可以很明显地看出来,它是一个凸优化问题,或者更具体地说,它是一个二次优化问题——目标函数是二次的,约束条件是线性的。这个问题可以用任何现成的QP (Quadratic Programming)的优化包进行求解。所以,我们的问题到此为止就算全部解决了,
于是我睡午觉去了~
啊?呃,有人说我偷懒不负责任了?好吧,嗯,其实呢,虽然这个问题确实是一个标准的QP 问题,但是它也有它的特殊结构,通过Lagrange Duality变换到对偶变量(dual variable) 的优化问题之后,可以找到一种更加有效的方法来进行求解——这也是SVM 盛行的一大原因,通常情况下这种方法比直接使用通用的QP 优化包进行优化要高效得多。此外,在推导过
程中,许多有趣的特征也会被揭露出来,包括刚才提到的supporting vector 的问题。
关于Lagrange duality 我没有办法在这里细讲了,可以参考Wikipedia 。简单地来说,通过给每一个约束条件加上一个Lagrange multiplier,我们可以将它们融和到目标函数里去(参见高数中的带约束条件的求极值问题,使用拉格朗日数乘法)
然后我们令
容易验证,当某个约束条件不满足时,例如y i(w T x i+b)<1,那么我们显然有θ(w)=∞(只
要令αi=∞即可)。而当所有约束条件都满足时,则有θ(w)=12∥w∥2,亦即我们最初要最小化的量。因此,在要求约束条件得到满足的情况下最小化12∥w∥2实际上等价于直接最小化θ(w)(当然,这里也有约束条件,就是αi≥0,i=1,…,n),因为如果约束
条件没有得到满足,θ(w)会等于无穷大,自然不会是我们所要求的最小值。具体写出来,我们现在的目标函数变成了:
这里用p?表示这个问题的最优值,这个问题和我们最初的问题是等价的。不过,现在我们来把最小和最大的位置交换一下:
当然,交换以后的问题不再等价于原问题,这个新问题的最优值用d?来表示。并,我们
有d?≤p?,这在直观上也不难理解,最大值中最小的一个总也比最小值中最大的一个要大
吧!总之,第二个问题的最优值d?在这里提供了一个第一个问题的最优值p?的一个下界,在满足某些条件的情况下,这两者相等,这个时候我们就可以通过求解第二个问题来间接地求解第一个问题。具体来说,就是要满足KKT 条件,这里暂且先略过不说,直接给结论:我们这里的问题是满足KKT 条件的,因此现在我们便转化为求解第二个问题。
首先要让L关于w和b最小化,我们分别令?L/?w和?L/?b等于零:
带回L得到:
此时我们得到关于dual variable α的优化问题:
如前面所说,这个问题有更加高效的优化算法,不过具体方法在这里先不介绍,让我们先来看看推导过程中得到的一些有趣的形式。首先就是关于我们的hyper plane ,对于一个数
据点x进行分类,实际上是通过把x带入到f(x)=w T x+b算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们得到,因此
这里的形式的有趣之处在于,对于新点x的预测,只需要计算它与训练数据点的内积即可
(这里??,??表示向量内积),这一点至关重要,是之后使用Kernel 进行非线性推广的基本前提。此外,所谓Supporting Vector 也在这里显示出来——事实上,所有非Supporting
Vector 所对应的系数α都是等于零的,因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。
为什么非支持向量对应的α等于零呢?直观上来理解的话,就是这些“后方”的点——正如我们之前分析过的一样,对超平面是没有影响的,由于分类完全有超平面决定,所以这些无关的点并不会参与分类问题的计算,因而也就不会产生任何影响了。这个结论也可由刚才的推导中得出,回忆一下我们刚才通过Lagrange multiplier 得到的目标函数:
注意到如果x i是支持向量的话,上式中红颜色的部分是等于0 的(因为支持向量的functional margin 等于1 ),而对于非支持向量来说,functional margin 会大于1 ,因
此红颜色部分是大于零的,而αi又是非负的,为了满足最大化,αi必须等于0 。这也就是这些非Supporting Vector 的点的悲惨命运了。
嗯,于是呢,把所有的这些东西整合起来,得到的一个maximum margin hyper plane classifier 就是支持向量机(Support Vector Machine),经过直观的感觉和数学上的推导,为什么叫“支持向量”,应该也就明了了吧?当然,到目前为止,我们的SVM 还比较弱,只能处理线性的情况,不过,在得到了dual 形式之后,通过Kernel 推广到非线性的情况就
变成了一件非常容易的事情了。不过,具体细节,还要留到下一次再细说了。
支持向量机: Kernel
by pluskid, on 2010-09-11, in Machine Learning60 comments
本文是“支持向量机系列”的第三篇,参见本系列的其他文章。
前面我们介绍了线性情况下的支持向量机,它通过寻找一个线性的超平面来达到对数据进行分类的目的。不过,由于是线性方法,所以对非线性的数据就没有办法处理了。例如图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
对于这个数据集,我可以悄悄透露一下:我生成它的时候就是用两个半径不同的圆圈加上了少量的噪音得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如
果用X1和X2来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别
为Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,那么显然,上面的方程在新的坐标系下可以写作:
∑i=15a i Z i+a6=0
关于新的坐标Z,这正是一个hyper plane 的方程!也就是说,如果我们做一个映
射?:R2→R5,将X按照上面的规则映射为Z,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是Kernel 方法处理非线性问题的基本思想。
再进一步描述Kernel 的细节之前,不妨再来看看这个例子映射过后的直观例子。当然,我没有办法把5 维空间画出来,不过由于我这里生成数据的时候就是用了特殊的情形,具体
来说,我这里的超平面实际的方程是这个样子(圆心在X2轴上的一个正圆):
a1X21+a2(X2?c)2+a3=0
因此我只需要把它映射到Z1=X21, Z2=X22, Z3=X2这样一个三维空间中即可,下图(这是一个gif 动画)即是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:
现在让我们再回到SVM 的情形,假设原始的数据时非线性的,我们通过一个映射?(?)将其映射到一个高维空间中,数据变得线性可分了,这个时候,我们就可以使用原来的推导来进行计算,只是所有的推导现在是在新的空间,而不是原始空间中进行。当然,推导过程也
并不是可以简单地直接类比的,例如,原本我们要求超平面的法向量w,但是如果映射之
后得到的新空间的维度是无穷维的(确实会出现这样的情况,比如后面会提到的Gaussian Kernel ),要表示一个无穷维的向量描述起来就比较麻烦。于是我们不妨先忽略过这些细节,直接从最终的结论来分析,回忆一下,我们上一次得到的最终的分类函数是这样的:
f(x)=∑i=1nαi y i?x i,x?+b
现在则是在映射过后的空间,即:
f(x)=∑i=1nαi y i??(x i),?(x)?+b
而其中的α也是通过求解如下dual 问题而得到的:
maxαs.t.,∑i=1nαi?12∑i,j=1nαiαj y i y j??(x i),?(x j)?αi≥0,i=1,…,n∑i=1nαi y i=0
这样一来问题就解决了吗?似乎是的:拿到非线性数据,就找一个映射?(?),然后一股脑把原来的数据映射到新空间中,再做线性SVM 即可。不过若真是这么简单,我这篇文章的标题也就白写了——说了这么多,其实还没到正题呐!其实刚才的方法稍想一下就会发现有问题:在最初的例子里,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维,那么我们会得到19 维的新空间
(验算一下?),这个数目是呈爆炸性增长的,这给?(?)的计算带来了非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。所以就需要Kernel 出马了。
不妨还是从最开始的简单例子出发,设两个向量x1=(η1,η2)T和x2=(ξ1,ξ2)T,而?(?)即是到前面说的五维空间的映射,因此映射过后的内积为:
??(x1),?(x2)?=η1ξ1+η21ξ21+η2ξ2+η22ξ22+η1η2ξ1ξ2
另外,我们又注意到:
(?x1,x2?+1)2=2η1ξ1+η21ξ21+2η2ξ2+η22ξ22+2η1η2ξ1ξ2+1
二者有很多相似的地方,实际上,我们只要把某几个维度线性缩放一下,然后再加上一个常数维度,具体来说,上面这个式子的计算结果实际上和映射
φ(X1,X2)=(2√X1,X21,2√X2,X22,2√X1X2,1)T
之后的内积?φ(x1),φ(x2)?的结果是相等的(自己验算一下)。区别在于什么地方呢?一个是映射到高维空间中,然后再根据内积的公式进行计算;而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果。回忆刚才提到的映射的维度爆炸,在前一种方法已经无法计算的情况下,后一种方法却依旧能从容处理,甚至是无穷维度的情况也没有问题。
我们把这里的计算两个向量在映射过后的空间中的内积的函数叫做核函数(Kernel Function) ,例如,在刚才的例子中,我们的核函数为:
κ(x1,x2)=(?x1,x2?+1)2
核函数能简化映射空间中的内积运算——刚好“碰巧”的是,在我们的SVM 里需要计算的地方数据向量总是以内积的形式出现的。对比刚才我们写出来的式子,现在我们的分类函数为:
∑i=1nαi y iκ(x i,x)+b
其中α由如下dual 问题计算而得:
maxαs.t.,∑i=1nαi?12∑i,j=1nαiαj y i y jκ(x i,x j)αi≥0,i=1,…,n∑i=1nαi y i=0
这样一来计算的问题就算解决了,避开了直接在高维空间中进行计算,而结果却是等价的,实在是一件非常美妙的事情!当然,因为我们这里的例子非常简单,所以我可以手工构造出
对应于φ(?)的核函数出来,如果对于任意一个映射,想要构造出对应的核函数就很困难了。
最理想的情况下,我们希望知道数据的具体形状和分布,从而得到一个刚好可以将数据映射成线性可分的?(?),然后通过这个?(?)得出对应的κ(?,?)进行内积计算。然而,第二步
通常是非常困难甚至完全没法做的。不过,由于第一步也是几乎无法做到,因为对于任意的数据分析其形状找到合适的映射本身就不是什么容易的事情,所以,人们通常都是“胡乱”
选择映射的,所以,根本没有必要精确地找出对应于映射的那个核函数,而只需要“胡乱”
选择一个核函数即可——我们知道它对应了某个映射,虽然我们不知道这个映射具体是什么。由于我们的计算只需要核函数即可,所以我们也并不关心也没有必要求出所对应的映射的具
体形式。
当然,说是“胡乱”选择,其实是夸张的说法,因为并不是任意的二元函数都可以作为核函数,所以除非某些特殊的应用中可能会构造一些特殊的核(例如用于文本分析的文本核,注意其实使用了Kernel 进行计算之后,其实完全可以去掉原始空间是一个向量空间的假设了,只要核函数支持,原始数据可以是任意的“对象”——比如文本字符串),通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:
?多项式核κ(x1,x2)=(?x1,x2?+R)d,显然刚才我们举的例子是这里多项式核的一
个特例(R=1,d=2)。虽然比较麻烦,而且没有必要,不过这个核所对应的映射实
际上是可以写出来的,该空间的维度是(m+dd),其中m是原始空间的维度。
?高斯核κ(x1,x2)=exp(?∥x1?x2∥22σ2),这个核就是最开始提到过的会将原始空
间映射为无穷维空间的那个家伙。不过,如果σ选得很大的话,高次特征上的权重
实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;
反过来,如果σ选得很小,则可以将任意的数据映射为线性可分——当然,这并不
一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通
过调控参数σ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
?线性核κ(x1,x2)=?x1,x2?,这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来
了。
最后,总结一下:对于非线性的情况,SVM 的处理方法是选择一个核函数κ(?,?),通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。
此外,略微提一下,也有不少工作试图自动构造专门针对特定数据的分布结构的核函数,感兴趣的同学可以参考,比如NIPS 2003 的Cluster Kernels for Semi-Supervised Learning 和ICML 2005 的Beyond the point cloud: from transductive to semi-supervised learning 等。
实验2分类预测模型——支持向量机SVM 一、 实验目的 1. 了解和掌握支持向量机的基本原理。 2. 熟悉一些基本的建模仿真软件(比如SPSS 、Matlab 等)的操作和使用。 3. 通过仿真实验,进一步理解和掌握支持向量机的运行机制,以及其运用的场景,特别是 在分类和预测中的应用。 二、 实验环境 PC 机一台,SPSS 、Matlab 等软件平台。 三、 理论分析 1. SVM 的基本思想 支持向量机(Support Vector Machine, SVM ),是Vapnik 等人根据统计学习理论中结构风险最小化原则提出的。SVM 能够尽量提高学习机的推广能力,即使由有限数据集得到的判别函数,其对独立的测试集仍能够得到较小的误差。此外,支持向量机是一个凸二次优化问题,能够保证找到的极值解就是全局最优解。这希尔特点使支持向量机成为一种优秀的基于机器学习的算法。 SVM 是从线性可分情况下的最优分类面发展而来的,其基本思想可用图1所示的二维情况说明。 图1最优分类面示意图 图1中,空心点和实心点代表两类数据样本,H 为分类线,H1、H2分别为过各类中离分类线最近的数据样本且平行于分类线的直线,他们之间的距离叫做分类间隔(margin )。所谓最优分类线,就是要求分类线不但能将两类正确分开,使训练错误率为0,而且还要使分类间隔最大。前者保证分类风险最小;后者(即:分类间隔最大)使推广性的界中的置信范围最小,从而时真实风险最小。推广到高维空间,最优分类线就成为了最优分类面。 2. 核函数 ω
支持向量机的成功源于两项关键技术:利用SVM 原则设计具有最大间隔的最优分类面;在高维特征空间中设计前述的最有分类面,利用核函数的技巧得到输入空间中的非线性学习算法。其中,第二项技术就是核函数方法,就是当前一个非常活跃的研究领域。核函数方法就是用非线性变换 Φ 将n 维矢量空间中的随机矢量x 映射到高维特征空间,在高维特征空间中设计线性学习算法,若其中各坐标分量间相互作用仅限于内积,则不需要非线性变换 Φ 的具体形式,只要用满足Mercer 条件的核函数替换线性算法中的内积,就能得到原输入空间中对应的非线性算法。 常用的满足Mercer 条件的核函数有多项式函数、径向基函数和Sigmoid 函数等,选用不同的核函数可构造不同的支持向量机。在实践中,核的选择并未导致结果准确率的很大差别。 3. SVM 的两个重要应用:分类与回归 分类和回归是实际应用中比较重要的两类方法。SVM 分类的思想来源于统计学习理论,其基本思想是构造一个超平面作为分类判别平面,使两类数据样本之间的间隔最大。SVM 分类问题可细分为线性可分、近似线性可分及非线性可分三种情况。SVM 训练和分类过程如图2所示。 图2 SVM 训练和分类过程 SVM 回归问题与分类问题有些相似,给定的数据样本集合为 x i ,y i ,…, x n ,y n 。其中, x i x i ∈R,i =1,2,3…n 。与分类问题不同,这里的 y i 可取任意实数。回归问题就是给定一个新的输入样本x ,根据给定的数据样本推断他所对应的输出y 是多少。如图3-1所示,“×”表示给定数据集中的样本点,回归所要寻找的函数 f x 所对应的曲线。同分类器算法的思路一样,回归算法需要定义一个损失函数,该函数可以忽略真实值某个上下范围内的误差,这种类型的函数也就是 ε 不敏感损失函数。变量ξ度量了训练点上误差的代价,在 ε 不敏感区内误差为0。损失函数的解以函数最小化为特征,使用 ε 不敏感损失函数就有这个优势,以确保全局最小解的存在和可靠泛化界的优化。图3-2显示了具有ε 不敏感带的回归函数。 o x y 图3-1 回归问题几何示意图 o x y 图3-2 回归函数的不敏感地
支持向量机(SVM )原理及应用 一、SVM 的产生与发展 自1995年Vapnik (瓦普尼克)在统计学习理论的基础上提出SVM 作为模式识别的新方法之后,SVM 一直倍受关注。同年,Vapnik 和Cortes 提出软间隔(soft margin)SVM ,通过引进松弛变量i ξ度量数据i x 的误分类(分类出现错误时i ξ大于0),同时在目标函数中增加一个分量用来惩罚非零松弛变量(即代价函数),SVM 的寻优过程即是大的分隔间距和小的误差补偿之间的平衡过程;1996年,Vapnik 等人又提出支持向量回归 (Support Vector Regression ,SVR)的方法用于解决拟合问题。SVR 同SVM 的出发点都是寻找最优超平面(注:一维空间为点;二维空间为线;三维空间为面;高维空间为超平面。),但SVR 的目的不是找到两种数据的分割平面,而是找到能准确预测数据分布的平面,两者最终都转换为最优化问题的求解;1998年,Weston 等人根据SVM 原理提出了用于解决多类分类的SVM 方法(Multi-Class Support Vector Machines ,Multi-SVM),通过将多类分类转化成二类分类,将SVM 应用于多分类问题的判断:此外,在SVM 算法的基本框架下,研究者针对不同的方面提出了很多相关的改进算法。例如,Suykens 提出的最小二乘支持向量机 (Least Square Support Vector Machine ,LS —SVM)算法,Joachims 等人提出的SVM-1ight ,张学工提出的中心支持向量机 (Central Support Vector Machine ,CSVM),Scholkoph 和Smola 基于二次规划提出的v-SVM 等。此后,台湾大学林智仁(Lin Chih-Jen)教授等对SVM 的典型应用进行总结,并设计开发出较为完善的SVM 工具包,也就是LIBSVM(A Library for Support Vector Machines)。LIBSVM 是一个通用的SVM 软件包,可以解决分类、回归以及分布估计等问题。 二、支持向量机原理 SVM 方法是20世纪90年代初Vapnik 等人根据统计学习理论提出的一种新的机器学习方法,它以结构风险最小化原则为理论基础,通过适当地选择函数子集及该子集中的判别函数,使学习机器的实际风险达到最小,保证了通过有限训练样本得到的小误差分类器,对独立测试集的测试误差仍然较小。 支持向量机的基本思想:首先,在线性可分情况下,在原空间寻找两类样本的最优分类超平面。在线性不可分的情况下,加入了松弛变量进行分析,通过使用非线性映射将低维输
支持向量回归简介 人类通过学习,从已知的事实中分析、总结出规律,并且根据规律对未来 的现象或无法观测的现象做出正确的预测和判断,即获得认知的推广能力。在对智能机器的研究当中,人们也希望能够利用机器(计算机)来模拟人的良好学习能力,这就是机器学习问题。基于数据的机器学习是现代智能技术中的重要方面,机器学习的目的是通过对已知数据的学习,找到数据内在的相互依赖关系,从而获得对未知数据的预测和判断能力,在过去的十几年里,人工神经网络以其强大的并行处理机制、任意函数的逼近能力,学习能力以及自组织和自适应能力等在模式识别、预测和决策等领域得到了广泛的应用。但是神经网络受到网络结构复杂性和样本复杂性的影响较大,容易出现“过学习”或低泛化能力。特别是神经网络学习算法缺乏定量的分析与完备的理论基础支持,没有在本质上推进学习过程本质的认识。 现有机器学习方法共同的重要理论基础之一是统计学。传统统计学研究的是样本数目趋于无穷大时的渐近理论,现有学习方法也多是基于此假设。但在实际问题中,样本数往往是有限的,因此一些理论上很优秀的学习方法实际中表现却可能不尽人意。 与传统统计学相比, 统计学习理论(Statistical Learning Theory 或SLT ) 是一种专门研究小样本情况下机器学习规律的理论Vladimir N. Vapnik 等人从六、七十年代开始致力于此方面研究,到九十年代中期,随着其理论的不断发展和成熟[17] ,也由于神经网络等学习方法在理论上缺乏实 质性进展, 统计学习理论开始受到越来越广泛的重视。 统计学习理论是建立在一套较坚实的理论基础之上的,为解决有限样本学习问题提供了一个统一的框架。它能将很多现有方法纳入其中,有望帮助解决许多原来难以解决的问题(比如神经网络结构选择问题、局部极小点问题)等;同时, 在这一理论基础上发展了一种新的通用学习方法—支持向量机(Support Vector Machine 或SVM ) ,它已初步表现出很多优于已有方法的性能。一些学者认为,SVM 正在成为继神经网络研究之后新的研究热点,并将有力地推动机 器学习理论和技术的发展。 支持向量机(SVM )是一种比较好的实现了结构风险最小化思想的方法。它的机器学习策略是结构风险最小化原则为了最小化期望风险,应同时最小化经验风险和置信范围) 支持向量机方法的基本思想: (1 )它是专门针对有限样本情况的学习机器,实现的是结构风险最小化:在对给定的数据逼近的精度与逼近函数的复杂性之间寻求折衷,以期获得最好的推广能力; (2 )它最终解决的是一个凸二次规划问题,从理论上说,得到的将是全局最优解,解决了在神经网络方法中无法避免的局部极值问题; (3 )它将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性决策函数来实现原空间中的非线性决策函数,巧妙地解决了维数问题,并保证了有较好的推广能力,而且算法复杂度与样本维数无关。 目前,SVM 算法在模式识别、回归估计、概率密度函数估计等方面都有应用,且算法在效率与精度上已经超过传统的学习算法或与之不相上下。
实验报告 实验名称:机器学习:线性支持向量机算法实现 学员:张麻子学号: *********** 培养类型:硕士年级: 专业:所属学院:计算机学院 指导教员: ****** 职称:副教授 实验室:实验日期:
一、实验目的和要求 实验目的:验证SVM(支持向量机)机器学习算法学习情况 要求:自主完成。 二、实验内容和原理 支持向量机(Support V ector Machine, SVM)的基本模型是在特征空间上找到最佳的分离超平面使得训练集上正负样本间隔最大。SVM是用来解决二分类问题的有监督学习算法。通过引入了核方法之后SVM也可以用来解决非线性问题。 但本次实验只针对线性二分类问题。 SVM算法分割原则:最小间距最大化,即找距离分割超平面最近的有效点距离超平面距离和最大。 对于线性问题: 假设存在超平面可最优分割样本集为两类,则样本集到超平面距离为: 需压求取: 由于该问题为对偶问题,可变换为: 可用拉格朗日乘数法求解。 但由于本实验中的数据集不可以完美的分为两类,即存在躁点。可引入正则化参数C,用来调节模型的复杂度和训练误差。
作出对应的拉格朗日乘式: 对应的KKT条件为: 故得出需求解的对偶问题: 本次实验使用python 编译器,编写程序,数据集共有270个案例,挑选其中70%作为训练数据,剩下30%作为测试数据。进行了两个实验,一个是取C值为1,直接进行SVM训练;另外一个是利用交叉验证方法,求取在前面情况下的最优C值。 三、实验器材 实验环境:windows7操作系统+python 编译器。 四、实验数据(关键源码附后) 实验数据:来自UCI 机器学习数据库,以Heart Disease 数据集为例。 五、操作方法与实验步骤 1、选取C=1,训练比例7:3,利用python 库sklearn 下的SVM() 函数进
金融观察?一 基于机器学习的股票分析与预测模型研究① 姚雨琪 摘一要:近年来?随着全球经济与股市的快速发展?股票投资成为人们最常用的理财方式之一?本文研究的主要目标是利用机器学习技术?应用Python编程语言构建股票预测模型?对我国股票市场进行分析与预测?采用SVM与DTW构建股票市场的分析和预测模型?并通过Python编程进行算法实现? 本文对获取到的股票数据进行简单策略分析?选取盘中策略作为之后模型评估的基准线?分别选取上证指数二鸿达兴业股票二鼎汉股票数据利用已构建的支持向量机和时间动态扭曲模型在Python平台上进行预测分析?结果表明?对于上证指数而言?支持向量机预测下逆向策略更优?对于鸿达兴业股票和鼎汉股票而言?支持向量机预测下正向策略更优?基于时间动态扭曲算法的预测方法对于特定的股票有较高的精度和可信度?研究结论表明将机器学习运用于股票分析与预测可以提高股票价格信息预测的效率?保证对海量数据的处理效率?机器学习过程可以不断进行优化模型?使得预测的可信度和精度不断提高?机器学习技术在股票分析方面有很高的研究价值? 关键词:机器学习?股票预测?Python?SVM?DTW 中图分类号:F830.91一一一一一一文献标识码:A一一一一一一文章编号:1008-4428(2019)02-0123-02 一一一二引言 国外股票市场的股票分析预测开始得很早?研究者们将各种数学理论二数据挖掘技术等应用到股票分析软件中?并通过对历史交易数据的研究?从而得到股票的走势规律?近年来?由于现实中工作与研究的需要?机器学习的研究与应用在国内外越来越重视?机器学习可以在运用过程中依据新的数据不断学习优化?完善预测模型?将机器学习应用于股票市场的预测?从股票的历史数据中挖掘出隐藏在数据中的重要信息?这样既能够为股民们对股价预测研究提供理论支撑?又能够为公司的领导层提供决策支持?基于此?本文选择机器学习在股票分析中的应用作为研究方向?在机器学习及股票分析相关理论基础上?使用Python开发工具?并分别运用支持向量回归及时间动态扭曲进行预测? 二二相关技术与理论 (一)机器学习 机器学习是融合多领域技术的交叉学科?主要包括概率论与数理统计二微积分二线性代数二算法设计等多门学科?通过计算机相关技术自动 学习 实现人工智能?(二)股票分析方法 1.基本面分析 基本面分析指的是在分析股票市场供应和需求关系的相关因素(如宏观经济二政策导向二财务状况以及经营环境等)基础上确定股票的实际价格?从而预测股票价格的趋势?2.技术面分析 技术面分析指的是对股票图样趋势来分析和研究?来判断价格的走势? (三)基于Python的经典机器学习模型 1.支持向量机(SVM) 该模型最初用于分类?其最终目标是引入回归估计?建立回归估计函数G(x)?其中回归值与目标值之间的差值小于μ?同时保证该函数的VC维度最小?线性或非线性函数G(x)的回归问题可以转化为二次规划问题?并且获得的最优解是唯一的? 2.动态时间扭曲(DTW) 这是衡量时间序列之间的相似性的方法?并可以用在语音识别领域以判断两段声音是否表达了同一个意思?三二股票预测模型的构建 (一)确定初始指标 1.基于支持向量机确定指标 施燕杰(2005)利用支持向量机进行股票分析与预测?在多次反复尝试基础上提出了一系列的指标作为预测模型的输入向量?该指标能够有效地预测未来股价波动情况?本文在结合自身研究的基础上?对以上施燕杰提出的指标进行改进?在原有的指标基础上添加7日平均开盘价和7日平均收盘价?去除了成交额保留了成交量?最终建立如表1所示的20个初选指标? 表1一初选指标 变量X1X2X3X4X5X6X7X8X9X10含义 今日 开盘价 昨日 开盘价 前日 开盘价 7日平均 开盘价 今日 最高价 昨日 最高价 前日 最高价 7日平均 最高价 今日 最低价 昨日 最低价变量X11X12X13X14X15X16X17X18X19X20含义 前日 最低价 7日平均 最低价 今日 收盘价 昨日 收盘价 前日 收盘价 7日平均 收盘价 今日 成交量 昨日 成交量 前日 成交量 7日平均 成交量一一本文主要是进行股票分析与预测?因此在综合考虑各个 价格指标的基础上?本文选择选定时间段的下一日收盘价作为模型的输出向量? 2.基于动态时间扭曲确定指标 根据往常研究经验?我们将时间序列数据分成不同的期间?每个期间长度为5日?以每个时间段相邻每日收盘价涨跌率变化趋势为初始指标?选择时间序列期间下一日的收盘价与期间内最后一日收盘价涨跌率作为模型的输出向量?(二)选择样本 1.实验对象 本文在分别在主板市场二中小板市场和创业板市场中采取随机抽样的方法各随机选择一只股票数据作为研究对象?分别是上证指数二鸿达兴业股票二鼎汉股票? 2.样本规模 我们选取了2011年至2017年间上证指数1550条数据?2015年至2017年的鸿达兴业股票532条数据二鼎汉股票572 321 ①基金项目:江西财经大学第十三届科研课题立项?编号xskt18345?
支持向量机数据分类预测 一、题目——意大利葡萄酒种类识别 Wine数据来源为UCI数据库,记录同一区域三种品种葡萄酒的化学成分,数据有178个样本,每个样本含有13个特征分量。50%做为训练集,50%做为测试集。 二、模型建立 模型的建立首先需要从原始数据里把训练集和测试集提取出来,然后进行一定的预处理,必要时进行特征提取,之后用训练集对SVM进行训练,再用得到的模型来预测试集的分类。 三、Matlab实现 3.1 选定训练集和测试集 在178个样本集中,将每个类分成两组,重新组合数据,一部分作为训练集,一部分作为测试集。 % 载入测试数据wine,其中包含的数据为classnumber = 3,wine:178*13的矩阵,wine_labes:178*1的列向量 load chapter12_wine.mat; % 选定训练集和测试集 % 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集 train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)]; % 相应的训练集的标签也要分离出来 train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)]; % 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集 test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)]; % 相应的测试集的标签也要分离出来 test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)]; 3.2数据预处理 对数据进行归一化: %% 数据预处理 % 数据预处理,将训练集和测试集归一化到[0,1]区间 [mtrain,ntrain] = size(train_wine); [mtest,ntest] = size(test_wine); dataset = [train_wine;test_wine]; % mapminmax为MATLAB自带的归一化函数 [dataset_scale,ps] = mapminmax(dataset',0,1); dataset_scale = dataset_scale';
3.支持向量机(回归) 3.1.1 支持向量机 支持向量机(SVM )是美国Vapnik 教授于1990年代提出的,2000年代后成为了很受欢迎的机器学习方法。它将输入样本集合变换到高维空间使得其分离性状况得到改善。它的结构酷似三层感知器,是构造分类规则的通用方法。SVM 方法的贡献在于,它使得人们可以在非常高维的空间中构造出好的分类规则,为分类算法提供了统一的理论框架。作为副产品,SVM 从理论上解释了多层感知器的隐蔽层数目和隐节点数目的作用,因此,将神经网络的学习算法纳入了核技巧范畴。 所谓核技巧,就是找一个核函数(,)K x y 使其满足(,)((),())K x y x y φφ=,代 替在特征空间中内积(),())x y φφ(的计算。因为对于非线性分类,一般是先找一个非线性映射φ将输入数据映射到高维特征空间,使之分离性状况得到很大改观,此时在该特征空间中进行分类,然后再返会原空间,就得到了原输入空间的非线性分类。由于内积运算量相当大,核技巧就是为了降低计算量而生的。 特别, 对特征空间H 为Hilbert 空间的情形,设(,)K x y 是定义在输入空间 n R 上的二元函数,设H 中的规范正交基为12(),(),...,(), ...n x x x φφφ。如果 2 2 1 (,)((),()), {}k k k k k K x y a x y a l φφ∞ == ∈∑ , 那么取1 ()() k k k x a x φφ∞ ==∑ 即为所求的非线性嵌入映射。由于核函数(,)K x y 的定义 域是原来的输入空间,而不是高维的特征空间。因此,巧妙地避开了计算高维内 积 (),())x y φφ(所需付出的计算代价。实际计算中,我们只要选定一个(,)K x y ,
支持向量机非线性回归通用MA TLAB源码 支持向量机和BP神经网络都可以用来做非线性回归拟合,但它们的原理是不相同的,支持向量机基于结构风险最小化理论,普遍认为其泛化能力要比神经网络的强。大量仿真证实,支持向量机的泛化能力强于BP网络,而且能避免神经网络的固有缺陷——训练结果不稳定。本源码可以用于线性回归、非线性回归、非线性函数拟合、数据建模、预测、分类等多种应用场合,GreenSim团队推荐您使用。 function [Alpha1,Alpha2,Alpha,Flag,B]=SVMNR(X,Y,Epsilon,C,TKF,Para1,Para2) %% % SVMNR.m % Support Vector Machine for Nonlinear Regression % All rights reserved %% % 支持向量机非线性回归通用程序 % GreenSim团队原创作品,转载请注明 % GreenSim团队长期从事算法设计、代写程序等业务 % 欢迎访问GreenSim——算法仿真团队→https://www.doczj.com/doc/e615094098.html,/greensim % 程序功能: % 使用支持向量机进行非线性回归,得到非线性函数y=f(x1,x2,…,xn)的支持向量解析式,% 求解二次规划时调用了优化工具箱的quadprog函数。本函数在程序入口处对数据进行了% [-1,1]的归一化处理,所以计算得到的回归解析式的系数是针对归一化数据的,仿真测 % 试需使用与本函数配套的Regression函数。 % 主要参考文献: % 朱国强,刘士荣等.支持向量机及其在函数逼近中的应用.华东理工大学学报 % 输入参数列表 % X 输入样本原始数据,n×l的矩阵,n为变量个数,l为样本个数 % Y 输出样本原始数据,1×l的矩阵,l为样本个数 % Epsilon ε不敏感损失函数的参数,Epsilon越大,支持向量越少 % C 惩罚系数,C过大或过小,泛化能力变差 % TKF Type of Kernel Function 核函数类型 % TKF=1 线性核函数,注意:使用线性核函数,将进行支持向量机的线性回归 % TKF=2 多项式核函数 % TKF=3 径向基核函数 % TKF=4 指数核函数 % TKF=5 Sigmoid核函数 % TKF=任意其它值,自定义核函数 % Para1 核函数中的第一个参数 % Para2 核函数中的第二个参数 % 注:关于核函数参数的定义请见Regression.m和SVMNR.m内部的定义 % 输出参数列表 % Alpha1 α系数 % Alpha2 α*系数 % Alpha 支持向量的加权系数(α-α*)向量
支持向量机简介 摘要:支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以求获得最好的推广能力 。我们通常希望分类的过程是一个机器学习的过程。这些数据点是n 维实空间中的点。我们希望能够把这些点通过一个n-1维的超平面分开。通常这个被称为线性分类器。有很多分类器都符合这个要求。但是我们还希望找到分类最佳的平面,即使得属于两个不同类的数据点间隔最大的那个面,该面亦称为最大间隔超平面。如果我们能够找到这个面,那么这个分类器就称为最大间隔分类器。 关键字:VC 理论 结构风险最小原则 学习能力 1、SVM 的产生与发展 自1995年Vapnik 在统计学习理论的基础上提出SVM 作为模式识别的新方法之后,SVM 一直倍受关注。同年,Vapnik 和Cortes 提出软间隔(soft margin)SVM ,通过引进松弛变量i ξ度量数据i x 的误分类(分类出现错误时i ξ大于0),同时在目标函数中增加一个分量用来惩罚非零松弛变量(即代价函数),SVM 的寻优过程即是大的分隔间距和小的误差补偿之间的平衡过程;1996年,Vapnik 等人又提出支持向量回归 (Support Vector Regression ,SVR)的方法用于解决拟合问题。SVR 同SVM 的出发点都是寻找最优超平面,但SVR 的目的不是找到两种数据的分割平面,而是找到能准确预测数据分布的平面,两者最终都转换为最优化问题的求解;1998年,Weston 等人根据SVM 原理提出了用于解
1、问题的背景股票市场具有高收益与高风险并存的特性,人们一直都希望能够掌握其运行规律,并进行分析与预测。但是由于股票市场受到很多市场因素和非市场的影响,而且这些因素之间又有相互作用,因此要想建立一个模型来描述其内部相互作用的机理是非常困难的。从而这也成为证券分析研究领域的一个难题。股票价格的变化是非线性和时变的,支持向量机在股票分析中的应用 杨明海 信阳师范学院数学科学学院 464000 因此这些时间序列数据都是带有噪声的不稳定随机数据,从而使得用传统的统计方法来研究股票市场的运行规律已经不尽如人意。随着计算机科学的发展,把机器学习方法用在金融工程领域已经取得了很大的进展[1]。 当前很多模型的建立都要假定股票价 格序列具有某些非线性特征,这些假设或多或少的带有一些主观性。对于这类数据的预测很多研究者采用神经网络等方法来 做,但神经网络方法有着难以克服的一些 缺点,其网络结构需要事先指定或应用启 发式算法在训练过程中修正,这些启发式算法很难保证网络结构是最优的。另外神经网络易过学习和陷入局部最优的缺点也极大地限制其在实际中的应用。而支持向量机(SVM )它克服了神经网络的一些缺 点,如过学习,维数灾难,易陷入局部最优 等。而且支持向量机在实现金融时间序列 的预测[2]方面已有了一些探索性的研究,并在应用中取得了不错的表现。 2、支持向量机 20世纪60年代末,V a p n i k 和 Cervonenkis 建立了现代意义上的统计学习 理论[3],即是目前人们所称的V C 维理 论。1979年,在统计学习理论的VC 维理论 和结构风险最小化(SRM)准则的基础上, Vapnik 等人提出了一种新的机器学习算法 ——支持向量机(SVM)方法。支持向量机 方法根据有限样本的信息在模型的复杂性 (基于VC 维,即对特定训练集的训练精度)和学习能力(即由训练出的机器对测试数 据的识别能力)之间寻求最佳折衷,期望获 得最好的推广能力。大量的研究表明,作为 一种解决模式识别问题和非线性函数的回 归估计、预测等问题的新技术,SVM 无论 在模型拟合效果还是模型推广能力方面都 表现出了良好的性质。因此,它成为目前机 器学习领域的一个热门研究课题。当前对 SVM 的研究集中在训练算法的设计和应用 上。 支持向量机可以归结为解决一个二次规划问题(Quadratic Programming, QP ) [4]: 给定输入空间中训练样本:(1) SVM 是要得到下面的决策函数: (2)其中k(x i ,x j )是核函数,是每个样本对应的Lagrange 乘子,b 是阈值,是下面QP 问题的解:其中(核函数矩阵)是一个N ×N 的半正定矩阵,C 是正则化参数。 由于其坚实的理论基础,良好的泛化性能,简洁的数学形式,直观的几何解释 等特点,它在许多实际问题的应用中取得 了成功。本文用支持向量机方法对中国A 股市场深沪两市的部分部分股票进行分类 研究。 3、数值计算结果及分析3.1 实验数据由股票分析软件广发证券(至强版)下载了深沪股市几个交易日的数据,预处理如下: DATA1:选取2009年1月6号的1296只股票,以量比,换手率,内外比为因子,将涨幅大于一个百分点的股票归为+1类,跌幅大于一个百分点的归为-1类。将数据随机化后,选取1000个进行训练,296个进行测试。DATA2:选取2008年12月29号沪深两市共1192只股票,以每笔换手率,涨速,量比,总换手率,内外比,振幅为因子,将涨幅大于1.5个百分点的股票归
第卷第期农业水土工程研究进展课程论文V ol. Supp. . 2015年11月Paper of agricultural water and soil engineering progress subject Nov.2015 1 支持向量机(SVM)在作物需水预测中的应用研究综述 (1.中国农业大学水利与土木工程学院,北京,100083) 摘要:水资源的合理配置对于社会经济的发展具有重要意义。而在农业水资源的优化配置中常常需要提供精确的作物需水信息才能接下来进行水量的优化配置。支持向量机是基于统计学习理论的新型机器学习方法,因为其出色的学习性能,已经成为当前机器学习界的研究热点。但是目前对支持向量机的研究与应用大多集中在分类这一功能上,而在农业水资源配置中的应用又大多集中于预测径流量,本文系统介绍了支持向量机的理论与一些应用,并对支持向量机在作物需水预测的应用进行了展望。 关键词:作物需水预测;统计学习理论;支持向量机; 中图分类号:S16 文献标志码:A 文章编号: 0引言 作物的需水预测是农业水资源优化配置的前提和基础之一。但目前在解决数学模型中需要输入有预期的预测精度的数据时还是会遇到困难。例如,当大量的用水者的用水需求作为优化模型的输入时,预测精度太低时优化结果可能会出现偏差。此外,不确定性也存在于水的需求中,水需求受到一些影响因子和系统组成的影响(即人类活动,社会发展,可持续性要求以及政策法规),这不仅在不确定性因子间相互作用过程中使得问题更为复杂,也使得决策者在进行水资源分配过程中的风险增加。所以,准确的预测对水资源的需求对制定有效的水资源系统相关规划很重要。而提高需水量预测精度一直是国内外学术界研究难点和热点。 支持向量机(Support V ector Machine,SVM)是根据统计学理论提出的一种新的通用学习方法,该方法采用结构风险最小化准则(Structural Risk Minimization Principle),求解二次型寻优问题,从理论上寻求全局最优解,较好地兼顾了神经网络和灰色模型的优点[1][2],克服了人工神经网络结构依赖设计者经验的缺点,具有对未来样本的较好的泛化性能,较好解决了高维数、局部极小等问题[3]。目前,SVM已成功的应用于分类、函数逼近和时间序列预测等方面,并在水科学领域中取得了一些成果,Liong[4]已将SVM应用于水文预报,周秀平等[5]已将SVM应用于径流预测,王景雷等[6]亦已将SVM应用于地下水位预报。而需水预测问题本身也可以看作是一种对需水量及其影响因子间的复杂的非线性函数关系的逼近问题,但将SVM应用于作物需水预测的研究尚处于起步阶段。本文简要介绍支持向量机并对其研究进展进行综述,最后对未来使用支持向量机预测作物需水量进行展望。 收稿日期:修订日期:1支持向量机 1.1支持向量机国内外研究现状 自 1970 年以来,V apnik[1,2]等人发展了一种新的学习机——支持向量机。与现有的学习机包括神经网络,模糊学习机,遗传算法,人工智能等相比,它具有许多的优点:坚实的理论基础和较好的推广能力、强大的非线性处理能力和高维处理能力。因此这种学习方法有着出色的学习性能,并在许多领域已得到成功应用,如人脸检测、手写体数字识别、文本自动分类、非线性回归建模与预测、优化控制数据压缩及时间序列预测等。 1998年,Alex J. Smola[7]系统地介绍了支持向量机回归问题的基本概念和求解算法。Drucher[8]将支持向量机回归模型同基于特征空间的回归树和岭回归的集成回归技术bagging做了比较;Alessandro verri[9]将支持向量机回归模型同支持向量机分类模型和禁忌搜索(basic pursuit denoising)作了比较,并且给出了贝叶斯解释。通过分析得出了如下结论:支持向量机回归模型由于不依赖于输入空间的维数,所以在高维中显示出了其优越性。为了简化支持向量机,降低其复杂性,已有了一些研究成果。比如,Burges[10]提出根据给定的支持向量机生成缩减的样本集,从而在给定的精度下简化支持向量机,但生成缩减样本集的过程也是一个优化过程,计算比较复杂;1998年Scholkopf[11]等人在目标函数中增加了参数v以控制支持向量的数目,称为v-SVR,证明了参数v与支持向量数目及误差之间的关系,但支持向量数目的减少是以增大误差为代价的。Suykens等人[12]1999年提出的最小二乘支持向量机(LS-SVM)算法具有很高的学习效率,对大规模数据可采用共轭梯度法求解;田盛丰[13]等人提出了LS-SVM与序贯最优化算法(SMO)的混合算法。 1.2支持向量机在水资源领域研究现状
3.3 支持向量回归机 SVM 本身是针对经典的二分类问题提出的,支持向量回归机(Support Vector Regression ,SVR )是支持向量在函数回归领域的应用。SVR 与SVM 分类有以下不同:SVM 回归的样本点只有一类,所寻求的最优超平面不是使两类样本点分得“最开”,而是使所有样本点离超平面的“总偏差”最小。这时样本点都在两条边界线之间,求最优回归超平面同样等价于求最大间隔。 3.3.1 SVR 基本模型 对于线性情况,支持向量机函数拟合首先考虑用线性回归函数 b x x f +?=ω)(拟合n i y x i i ,...,2,1),,(=,n i R x ∈为输入量,R y i ∈为输出量,即 需要确定ω和b 。 图3-3a SVR 结构图 图3-3b ε不灵敏度函数 惩罚函数是学习模型在学习过程中对误差的一种度量,一般在模型学习前己经选定,不同的学习问题对应的损失函数一般也不同,同一学习问题选取不同的损失函数得到的模型也不一样。常用的惩罚函数形式及密度函数如表3-1。 表3-1 常用的损失函数和相应的密度函数 损失函数名称 损失函数表达式()i c ξ% 噪声密度 ()i p ξ ε -不敏感 i εξ 1 exp()2(1) i εξε-+ 拉普拉斯 i ξ 1 exp()2 i ξ- 高斯 212 i ξ 21 exp()22i ξπ -
标准支持向量机采用ε-不灵敏度函数,即假设所有训练数据在精度ε下用线性函数拟合如图(3-3a )所示, ** ()()1,2,...,,0 i i i i i i i i y f x f x y i n εξεξξξ-≤+??-≤+=??≥? (3.11) 式中,*,i i ξξ是松弛因子,当划分有误差时,ξ,*i ξ都大于0,误差不存在取0。这时,该问题转化为求优化目标函数最小化问题: ∑=++?=n i i i C R 1 ** )(21 ),,(ξξωωξξω (3.12) 式(3.12)中第一项使拟合函数更为平坦,从而提高泛化能力;第二项为减小误差;常数0>C 表示对超出误差ε的样本的惩罚程度。求解式(3.11)和式(3.12)可看出,这是一个凸二次优化问题,所以引入Lagrange 函数: * 11 ****1 1 1()[()] 2[()]() n n i i i i i i i i n n i i i i i i i i i i L C y f x y f x ωωξξαξεαξεξγξγ=====?++-+-+-+-+-+∑∑∑∑ (3.13) 式中,α,0*≥i α,i γ,0*≥i γ,为Lagrange 乘数,n i ,...,2,1=。求函数L 对ω, b ,i ξ,*i ξ的最小化,对i α,*i α,i γ,*i γ的最大化,代入Lagrange 函数得到对偶形式,最大化函数:
2007,43(5)ComputerEngineeringandApplications计算机工程与应用 1问题的提出 航空公司在客舱服务部逐步实行“费用包干”政策,即:综合各方面的因素,总公司每年给客舱服务部一定额度的经费,由客舱服务部提供客舱服务,而客舱服务产生的所有费用,由客舱服务部在“费用包干额度”中自行支配。新的政策既给客舱服务部的管理带来了机遇,同时也带来了很大的挑战。通过“费用包干”政策的实施,公司希望能够充分调用客舱服务部的积极性和主动性,进一步改进管理手段,促进新的现代化管理机制的形成。 为了进行合理的分配,必须首先搞清楚部门的各项成本、成本构成、成本之间的相互关系。本文首先对成本组成进行分析,然后用回归模型和支持向量机预测模型对未来的成本进行预测[1-3],并对预测结果的评价和选取情况进行了分析。 2问题的分析 由于客舱服务部的特殊性,“费用包干”政策的一项重要内容就集中在小时费的重新分配问题上,因为作为客舱乘务员的主要组成部分—— —“老合同”员工的基本工资、年龄工资以及一些补贴都有相应的政策对应,属于相对固定的部分,至少目前还不是调整的最好时机。乘务员的小时费收入则是根据各自的飞行小时来确定的变动收入,是当前可以灵活调整的部分。实际上,对于绝大多数员工来说,小时费是其主要的收入部分,因此,用于反映乘务人员劳动强度的小时费就必然地成为改革的重要部分。 现在知道飞行小时和客万公里可能和未来的成本支出有关系,在当前的数据库中有以往的飞行小时(月)数据以及客万公里数据,并且同时知道各月的支出成本,现在希望预测在知道未来计划飞行小时和市场部门希望达到的客万公里的情况下的成本支出。 根据我们对问题的了解,可以先建立这个部门的成本层次模型,搞清楚部门的各项成本、成本构成、成本之间的相互关系。这样,可以对部门成本支出建立一个层次模型:人力资源成本、单独预算成本、管理成本,这三个部分又可以分别继续分层 次细分,如图1所示。 基于支持向量机回归模型的海量数据预测 郭水霞1,王一夫1,陈安2 GUOShui-xia1,WANGYi-fu1,CHENAn2 1.湖南师范大学数学与计算机科学学院,长沙410081 2.中国科学院科技政策与管理科学研究所,北京100080 1.CollegeofMath.andComputer,HunanNormalUniversity,Changsha410081,China 2.InstituteofPolicyandManagement,ChineseAcademyofSciences,Beijing100080,China E-mail:guoshuixia@sina.com GUOShui-xia,WANGYi-fu,CHENAn.Predictiononhugedatabaseontheregressionmodelofsupportvectormachine.ComputerEngineeringandApplications,2007,43(5):12-14. Abstract:Asanimportantmethodandtechnique,predictionhasbeenwidelyappliedinmanyareas.Withtheincreasingamountofdata,predictionfromhugedatabasebecomesmoreandmoreimportant.Basedonthebasicprincipleofvectormachineandim-plementarithmetic,apredictionsysteminfrastructureonanaircompanyisproposedinthispaper.Lastly,therulesofevaluationandselectionofthepredictionmodelsarediscussed. Keywords:prediction;datamining;supportvectormachine;regressionmodel 摘要:预测是很多行业都需要的一项方法和技术,随着数据积累的越来越多,基于海量数据的预测越来越重要,在介绍支持向量机基本原理和实现算法的基础上,给出了航空服务成本预测模型,最后对预测结果的评价和选取情况进行了分析。 关键词:预测;数据挖掘;支持向量机;回归模型 文章编号:1002-8331(2007)05-0012-03文献标识码:A中图分类号:TP18 基金项目:国家自然科学基金(theNationalNaturalScienceFoundationofChinaunderGrantNo.10571051);湖南省教育厅资助科研课题(theResearchProjectofDepartmentofEducationofHunanProvince,ChinaunderGrantNo.06C523)。 作者简介:郭水霞(1975-),女,博士生,讲师,主要研究领域为统计分析;王一夫(1971-),男,博士生,副教授,主要研究领域为计算机应用技术,软件工程技术;陈安(1970-),男,副研究员,主要研究领域为数据挖掘与决策分析。 12
支持向量机算法推导及其分类的算法实现 摘要:本文从线性分类问题开始逐步的叙述支持向量机思想的形成,并提供相应的推导过程。简述核函数的概念,以及kernel在SVM算法中的核心地位。介绍松弛变量引入的SVM算法原因,提出软间隔线性分类法。概括SVM分别在一对一和一对多分类问题中应用。基于SVM在一对多问题中的不足,提出SVM 的改进版本DAG SVM。 Abstract:This article begins with a linear classification problem, Gradually discuss formation of SVM, and their derivation. Description the concept of kernel function, and the core position in SVM algorithm. Describes the reasons for the introduction of slack variables, and propose soft-margin linear classification. Summary the application of SVM in one-to-one and one-to-many linear classification. Based on SVM shortage in one-to-many problems, an improved version which called DAG SVM was put forward. 关键字:SVM、线性分类、核函数、松弛变量、DAG SVM 1. SVM的简介 支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度,Accuracy)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好的推广能力。 对于SVM的基本特点,小样本,并不是样本的绝对数量少,而是与问题的复杂度比起来,SVM算法要求的样本数是相对比较少的。非线性,是指SVM擅长处理样本数据线性不可分的情况,主要通过松弛变量和核函数实现,是SVM 的精髓。高维模式识别是指样本维数很高,通过SVM建立的分类器却很简洁,只包含落在边界上的支持向量。