第三章 马尔科夫过程
第一节 随机过程的概念
1、 随机系数
必然事件
自然界中出现的事件分为 不可能事件
随机事件
事物的变化过程 必然过程
随机过程
(1) 必然过程:有确定的变化形式,可以用精确的数学关系式来描述。如
()()sin m u t U t ω= ()()sin m i t I t ω?=+
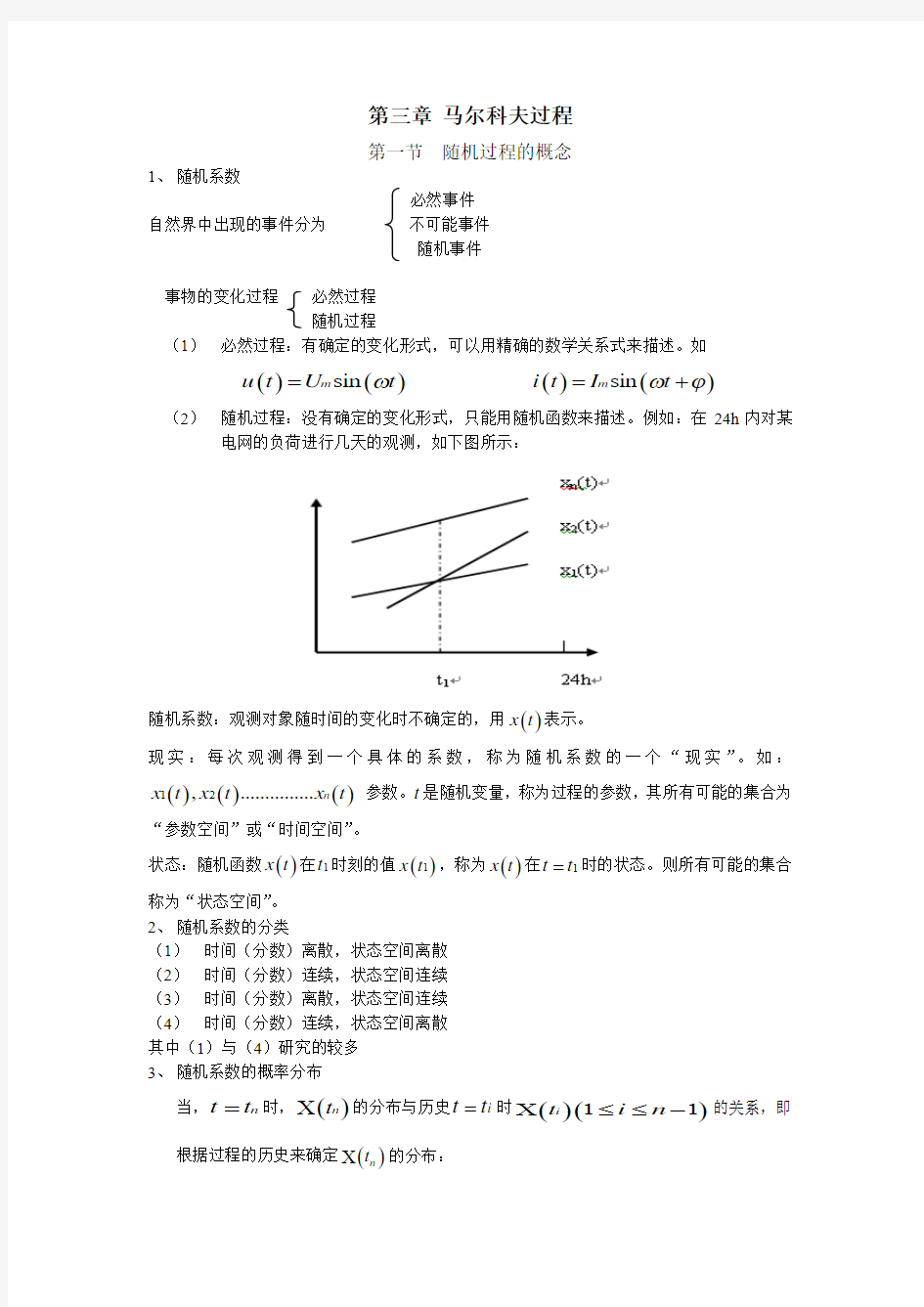
(2) 随机过程:没有确定的变化形式,只能用随机函数来描述。例如:在24h 内对某
电网的负荷进行几天的观测,如下图所示:
随机系数:观测对象随时间的变化时不确定的,用()x t 表示。
现实:每次观测得到一个具体的系数,称为随机系数的一个“现实”。如:
()()()12,...............n x t x t x t 参数。t 是随机变量,称为过程的参数,其所有可能的集合为
“参数空间”或“时间空间”。
状态:随机函数()x t 在1t 时刻的值()1x t ,称为()x t 在1t t =时的状态。则所有可能的集合称为“状态空间”。 2、 随机系数的分类
(1) 时间(分数)离散,状态空间离散 (2) 时间(分数)连续,状态空间连续 (3) 时间(分数)离散,状态空间连续 (4) 时间(分数)连续,状态空间离散 其中(1)与(4)研究的较多 3、 随机系数的概率分布
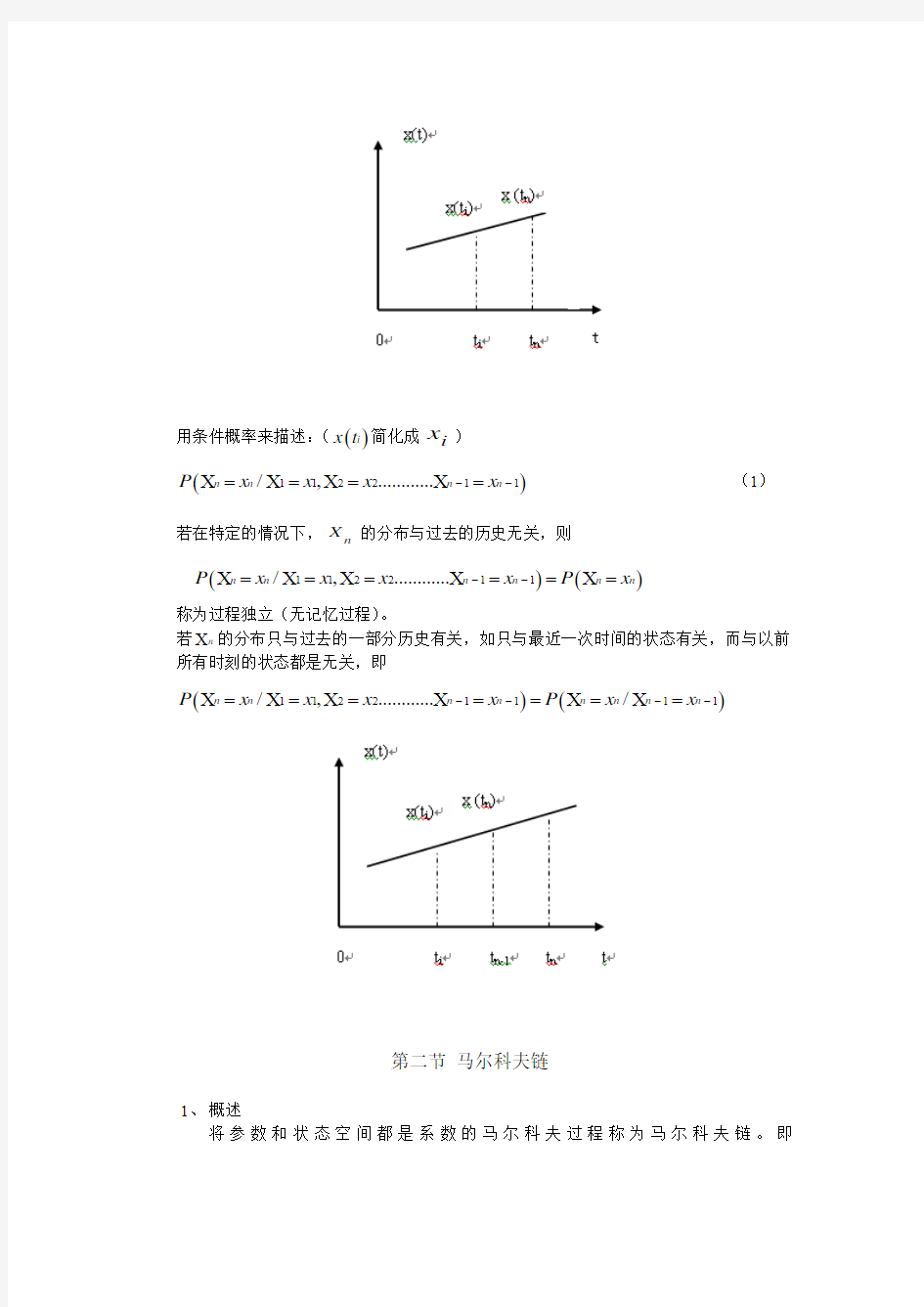
当,n t t =时,()n t X 的分布与历史i t t =时()()11i t i n X ≤≤-的关系,即
根据过程的历史来确定()n t X 的分布:
用条件概率来描述:(()i x t 简化成i x )
()112211/,............n n n n P x x x x --X =X =X =X = (1)
若在特定的情况下,n X 的分布与过去的历史无关,则
()()112211/,............n n n n n n P x x x x P x --X =X =X =X ==X =
称为过程独立(无记忆过程)。
若n X 的分布只与过去的一部分历史有关,如只与最近一次时间的状态有关,而与以前所有时刻的状态都是无关,即
()()11221111/,............/n n n n n n n n P x x x x P x x ----X =X =X =X ==X =X =
第二节 马尔科夫链
1、 概述
将参数和状态空间都是系数的马尔科夫过程称为马尔科夫链。即
()11/n n n n P x x --X =X =为n X 的概率分布,表明:n X 只与1n -X 有关。
为了方便,将现在的状态记为i ,未来时刻的状态记为j ,则上式可写成
()1/n n ij P j i P -X =X ==(从状态i 转移到状态j )
条件概率ij P 称为过程从状态i 过渡到状态j 的转移概率。若ij P =常数,则称此马尔科夫链式是时间齐次的,ij P 是在一步中完成从状态i 转移到状态j 的概率,称为一步转移概率。
若从i 到j 转移需要在m 步内完成,则m 步转移概率为:
()()0(/)/m ij n m n m P P j i P j i +=X =X ==X =X =
例3-1:某人练习射击,如果他未击中,下次击中的概率有1/2。但若第一次击中(而提高了信心),则下一次击中的概率就会增到3/4。现设他第一次击中失败,求第3.、3、4、5次击中的概率是多少?
解:这是一个具有双状态的离散马尔科夫过程。 “0”——成功,“1”——失败,两状态之间的转移可用图3-2表示
图3—2 状态转移图
图3—3 过渡特性
()()1111
10.375
2224
1113
00.625
2224
P P =?+?==?+?= (第二步)
总结:
(1) 设第0步的状态为1;
(2) 经有限步后的状态概率见表3—1;
(3) 图3—3的曲线描述了状态概率的过渡特性;
(4) 当步数增大时,状态概率趋于某一稳定值,且与初始状态无关。 2、转移矩阵和转移方程 接例3—1(射击)
转移概率()0,1ij P i j ==可写成矩阵形式(两状态)
:
0001'1011344122ij P P P P P P 1?? ?? ????===??????
1????
????
若状态数为n 时,一步转移概率的矩阵形式:
11121'1
2n ij n n nn P P P P P P P P ? ??
??
????==????
?? ??? 'P —是状态转移的概率矩阵,简称“转移矩阵”。 ij P —称为从状态i 到状态j 的一步转移概率。
因此:0,,1,2,,ij P i j n ≥=?
1
1,1,2,,
n
ij
j P
i n ===?∑ 即:每行1ij P =∑,i j →的所有状态概率之和 二步转移概率: ()2''''2P P P P ==
m 步转移概率:()
()()'1
n
m u r
ij
ik kj k P P P ==∑,式中u r m += n —为可能的状态数(参见射击图) 称为马尔科夫方程或状态转移方程
m 步转移矩阵:()''m m P P =
设某一系统或元件具有n 个状态,则其初始状态概率用一个概率向量()'0P 表示:
()[]'120,,,n P P P P =?
则m 步后的状态概率向量:()()()'''0m P m P P =
()'P m —m 步后系统的状态概率行向量
()'m
P — 一步转移矩阵的m 次方
在例3—1中
(1) 一步转移矩阵为:
()
00011''
10113/41/2P P P
P P
P 1/4????
===????
1/2 ???? (2) 二步转移矩阵为:
()2
''23/43/411/161/21/25/8P P 1/4 1/4 5/16??????===?????? 1/2 1/2 3/8 ??????
若给定过程从初始状态“1”出发,则初始状态的概率向量:
()[][]'010,01P P P ==
两步后的状态概率向量:
()[][][][]''211/16201015/80.6255/8P P 5/16??
= = = 3/8= 0.375?? 3/8 ??
说明:当初始状态为“1”时经两步后,处于“0”的概率为5/8=0.625,处于“1”
的概率为3/8=0.375。
(3) 当在第6、12步后,转移矩阵
()6'P 0.6667 0.3333??=??0.6665 0.3333?? ()
12'P 0.6667 0.3333??=??0.6665 0.3333??
即12m =时,'P 中的每一行都趋于同一稳定的转移概率向量
[]0.6666α= 0.3333
再增大m 值时,此值不变,无论初始状态是“0”,还是“1”。
[]'01ααα=
根据上述特点,下面关系成立:
()1'''P αα=
即:稳态下,再转一步,不变!
(4) 直接求稳定状态的转移概率 由于:()1'
''P α
α=
则:[][]01013/41/2αααα 1/4??
= ??
1/2 ??
010111
042
11
042
αααα-
+= -=
上述两式相同,故取其中一个等式 又因为 011αα+=
联立解得:
012
0.66673
1
0.3333
3
αα=
===
第三节 时间连续、状态离散的马尔科夫过程
1、概述
令1,n n t t t t t -==+?,则转移概率可表示:
()()()
(),ij P X t t j t i P t t +?=∣X ==??
(3—3) 若ij P 与t 无关,而只与过渡时间t ?有关,则为“齐次马尔科夫过程”,则式(3—3)可写成:
()()()
()(),ij ij ij P X t t j t i P t t P t q t +?=∣X ==?=?=? (3—4)
和
()()()
()()1,11n
ii ii ij i j j i
P X t t i t i P t t P t q t q t =≠+?=∣X ==?=?=-?=-?∑ (3—5)
式中:()ij
P t ?——在t ?内从状态i 转移到状态j 的概率
()ii P t ? ——在t ?内从i 转移到状态i 的概率
ij q 、i q ——转移出度(常数)
上式可用图3—4来表示:
图3—4 状态转移图
则:()()1ii ij j i
P t P t ≠?+?=∑,1
n
i ij j j i
q q t =≠=?∑
2、转移矩阵和转移出度矩阵
设λ为元件故障率,μ为故障修复率,则双态马尔科夫模型:
图3—5
此处转移出度:ij q λ=或μ,为常数 转移(概率)矩阵:
()()()()()()0001'
1011110101ij P t P t P t P t P t P t t
t t t λλλλμμμμ????
???=?= ?
??????-??-??????==+ ? ? ?
?-?-??????
()''P t E A t ?=+?
'A λλμμ-??
= ?-?? 称为“转移出度矩阵”
3、无条件状态概率
系统在t 时处于状态i 的概率可表示:
()()()i P t P t i =X =
()i P t 称为无条件状态概率 在t t +?时处于状态i 的概率:
()()()()()i i ii j ji j i
P t t P t P t P t P t ≠+?=?+?∑ (3—7)
即:()()()()1i i i j ji j i
P t t P t q t P t q t ≠+?=-?+?∑
ji q 为j 到i 的转移出度
上式两边减()i P t ,再除以
t ?得: ()()
()()i i i i j ji j i
P t t P t P t q P t q t ≠+?-=-+?∑
0t ?→时:
()()()/i i i j ji j i
P t P t q P t q ≠=-+∑
同理可得:
()()()/j j j j ij i j
P t P t q P t q ≠=-+∑
写成矩阵:
()()()()//
i
ij
i j
i j i
j ji j j i
q q
P t P t P t P t q q ≠≠??- ????? = ?????- ???
∑∑ 即
()()/'P t P t A = (3—9)
式(3—9)称为状态方程,也是一个矩阵微分方程,其解:
()()'
''0A t P t P e = (3—10)
'2
'
'2
2!
A t
t e
E At A =+++? (3—11)
4、应用示例
图3—5为双态马尔科夫模型,具有“0”和“1”两种状态。需求无条件概率
()0P t 和()1P t ,即t 时的状态概率。 将'A λλμ
μ-??
=
?-??
代入式(3—11) ∵ ()2
''A λμA =-+ ()()
1
1
''1n n n A λμ--A =-+
1)()()
''1
1t A t
e
E e A λμλμ
-+=+-+
2)设初始状态为“0”的概率为1,为“1”的概率为0,即0t =时,设备正常工作。
()()()[]'01000P P P = =1 0????
将1)、2)代入状态方程(3—10)式中可得:
()()[]()()
()()''
'
'1
01,t A t
t t P t P e
E e A e e λμλμλμλμμλλμλμλμλμλμ-+-+-+??==1 0+-??
+??
??
=+-??++++??
(3—12)
其中:()()()()01,t t P t e P t e λμλμμλλμλμ
λμ
λμ
λμ
-+-+=
+
=
-
++++
5、长期状态概率
当t →∞时,式(3—12)可得稳定状态概率:
0P μλμ
=
+ (正常运行)
1P λλμ
=
+ (故障) (3—13)
与初态()'0p 无关。 令 01
T λ
=
(平均工作时间) 11
T μ
=
(平均修复时间) 代入(3—13)可得:
001
T P T T =
+
1
101
T P T T =
+ (3—14) 6、求稳定状态概率的其他方法
从状态方程:()()/'P t P t A =出发,当t ?→∞ 时
()''0P t A = (3—15)
0—全0的向量
()'P t —稳态概率向量,()[]'12n P t P P P = ? 又 ∵ 11n
i i P ==∑ (3—16)
由式(3—15)、(3—16)可求得稳态状态概率。 例如,前例的条件求01P P
∵ [][]01P P λλμμ-??
0 0= ?-??
∴ 010P P λμ-+=
010P P λμ-= 又∵ 011P P += 可得:
01
P P μ
λμ
λλμ
=
+=+ 结果与式(3—13)相同