当前位置：文档之家› 三角函数逼近快速算法(正余弦)

三角函数逼近快速算法(正余弦)

原文出自：

http://lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/

里面提到了查表，采用查表并配合插值；以及泰勒级数

看过第一篇的文章后，大呼过瘾！原文作者的思路非常简捷，有趣，偶英语比较差，欢迎指正，废话不多说看文章

原文出处：

https://www.doczj.com/doc/e49550323.html,/forums/showthread.php?t=5784

http://lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/

在某些情况下我们需要一些更高效的且近似于标准值的sin 和cos函数。

有时候我们并需要过高的精度，这时C语言中自带的三角函数（sinf() 和cosf() f）计算的精度超出了我们所需要的精度要求，所以其效率很低。我们真正需要的是间于精度和效率的一个折中的方案。众所周知的取近似值的方法是：泰勒级数（和著名的马克劳林级数）

代码是：

x - 1/6 x^3 + 1/120 x^5 - 1/5040 x^7 + ...

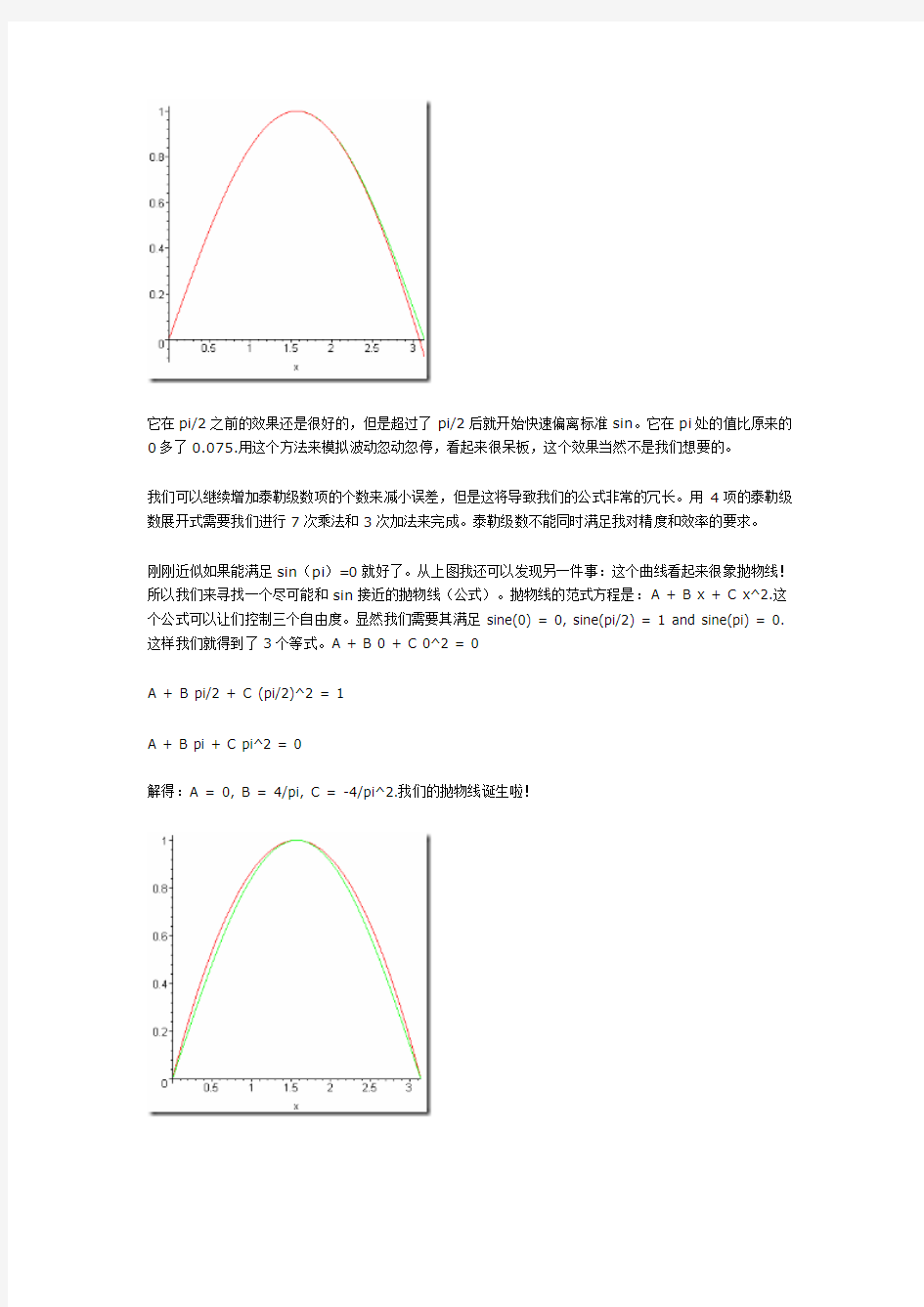
我们绘制了下图:

绿线是标准的sin函数，红线是4项泰勒级数展开式。这个近似值的效果看起来还不错，但是如果你仔细观察后会发现

它在pi/2之前的效果还是很好的，但是超过了pi/2后就开始快速偏离标准sin。它在pi处的值比原来的0多了0.075.用这个方法来模拟波动忽动忽停，看起来很呆板，这个效果当然不是我们想要的。

我们可以继续增加泰勒级数项的个数来减小误差，但是这将导致我们的公式非常的冗长。用4项的泰勒级数展开式需要我们进行7次乘法和3次加法来完成。泰勒级数不能同时满足我对精度和效率的要求。

刚刚近似如果能满足sin（pi）=0就好了。从上图我还可以发现另一件事：这个曲线看起来很象抛物线！所以我们来寻找一个尽可能和sin接近的抛物线（公式）。抛物线的范式方程是：A + B x + C x^2.这个公式可以让们控制三个自由度。显然我们需要其满足sine(0) = 0, sine(pi/2) = 1 and sine(pi) = 0. 这样我们就得到了3个等式。A + B 0 + C 0^2 = 0

A +

B pi/2 +

C (pi/2)^2 = 1

A +

B pi +

C pi^2 = 0

解得：A = 0, B = 4/pi, C = -4/pi^2.我们的抛物线诞生啦！

貌似这个的误差看起来比泰勒级数还要遭。其实不是的！这种方法的最大误差是0.056.（译者：而且这种近似值没有误差积累）而且这个近似值的绘制出的波动是光滑的，而且只需要3次乘法和一次加法。不过它还不够完美。下图是[-pi, pi] 之间的图像：

显然我们至少需要它在1个完整的周期内都符合我们要求。但是我们可以看出，我们缺少的另一半是原抛物线的一个映射。它的公式是：4/pi x + 4/pi^2 x^2。所以我们可以直接这样写：

Code:

if(x > 0) { y = 4/pi x - 4/pi^2 x^2; } else { y = 4/pi x + 4/pi^2 x^2; }

添加一个条件分支不是一个好的方法。它会让程序渐渐的变慢。但是观察一下我们模拟的和标准的图像是多么的接近啊！观察上面两式子，只是中间的一项正负号不同，我的第一个单纯的想法是可以提取x的正负号来消除分支，即使用：x / abs(x)。除法的代价是非常大的，我们来观察一下现在的公式：4/pi x - x / abs(x) 4/pi^2 x^2。将除法化简后我们得到：4/pi x - 4/pi^2 x abs(x).所以只需要多一步运算我们就得到了我们需要的sin逼近值！下图是结果

接下来我们要考虑cos。有基础的三角公理可以知道：cos(x) = sin(pi/2 + x).把x多加一个pi/2就可以搞定了？事实上它的某一部分不是我们期望得到的。

我们需要做的就是当x > pi/2时―跳回‖。这个可以由减去2 pi来实现。

Code:

x += pi/2;

if(x > pi) // Original x > pi/2 { x -= 2 * pi; // Wrap: cos(x) = cos(x - 2 pi)}

y = sine(x);

又出现了一个分支，我们可以用逻辑―与‖来消除它，像是这样：

x -= (x > pi) & (2 * pi);

Code:

x -= (x > pi) & (2 * pi);

注意这并不是c的源代码。但是这个应该可以说明它是怎么样运行的。当x > pi是false 时，逻辑―与‖（&）运算后得到的是0，也就是（x-=0）大小没有改变，哈哈完美的等价!我会给读这篇文章的读者留一些关于这个练习。虽然cos 比sin需要多一些运算，但是相比之下貌似也没有更好方法可以让程序更快了。现在我们的最大误差是0.056 ，四项泰勒级数展开式每一次都会有一点点误差。再来看看我们sin函数：

现在是不是不能继续提升精准度了呢？当前的版本已经可以满足大多度sin函数的应用了。但是对一些要求更高一些的程序现在做的还够。

仔细观察图像，你会注意到我们的近似值总是比真实值大，当然除了0，pi/2 和pi。所以我们要做的就是在不改变这些点（0，pi/2 和pi）的情况下，将函数再―按下去‖一些。解决方法是利用抛物线的平方。看起来就像这样：

注意它保持着原来那些关键点，不同的是它比真实的sin函数值更低了。所以我们可以用一个加权的平均值来使两个函数更接近。

Code:

Q (4/pi x - 4/pi^2 x^2) + P (4/pi x - 4/pi^2 x^2)^2

利用Q + P = 1. 你可以灵活的控制绝对误差或相对误差。别急我来告诉你取不同的极限结果时Q，P的值。绝对误差的最佳权值是：Q = 0.775, P = 0.225 ；相对误差的最佳权值是：Q = 0.782，P = 0.218 。让我们来看一下结果的图像。

红线呢？它几乎被绿线完全覆盖了，这足以证明我们的近似十分完美。最大误差是0.001，50倍的提升！这个公式看起来很长，但是括号里面的公式最终得到的值是相同的，也就是说括号里的只需要被计算一次。事实上在原来的基础上只是增加了额外的2次乘法和2次加法就可以得到现在的结果。

先别高兴的太早，我们还要―制造‖一个负号出来。我们需要增加一个abs()运算。最终的c代码是：

Code:

float sine(float x)

{

const float B = 4/pi;

const float C = -4/(pi*pi);

float y = B * x + C * x * abs(x);

#ifdef EXTRA_PRECISION // const float Q = 0.775;

const float P = 0.225;

y = P * (y * abs(y) - y) + y;

// Q * y + P * y * abs(y)

#endif }

所以我们仅仅是需要多加5次乘法和3次加法就可以完成了。如果我们忽略abs()这个仍然是比4项泰勒级数展开式快，更精准！Cos只需要相应的变换一下x就可以了。

(译者注：后面是汇编程序，不翻译了)

part2

我选取了最小误差的情况，用as3运行后发现提升了14倍，而且仍然是非常精准。不过你必须直接使用它，不能把它放到一个函数中，因为每调用一次额外的函数调用会削减执行效率，最终你会得到一个比Math.sin() 和Math.cos()效率更差的结果。还有这里会用到的三角定理：

cos(x) = sin(x + pi/2)

cos(x - pi/2) = sin(x)

下载: fastTrig.as.

可以清楚到对比结果，现在你可以用这个替换Math.sin() 和Math.cos()了

哇哦！！！几乎是相同的精准度（14倍速度提升）

//always wrap input angle to -PI..PI

if (x< -3.14159265)

x+= 6.28318531;

else

if (x> 3.14159265)

x-= 6.28318531;

//compute sine

if (x< 0)

sin= 1.27323954 * x+ .405284735 * x* x;

else

sin= 1.27323954 * x- 0.405284735 * x* x;

//compute cosine: sin(x + PI/2) = cos(x)

x+= 1.57079632;

if (x> 3.14159265)

x-= 6.28318531;

if (x< 0)

cos= 1.27323954 * x+ 0.405284735 * x* x

else

cos= 1.27323954 * x- 0.405284735 * x* x;

}

High precision sine/cosine (~8x faster)

//always wrap input angle to -PI..PI

if (x< -3.14159265)

x+= 6.28318531;

else

if (x> 3.14159265)

x-= 6.28318531;

//compute sine

if (x< 0)

{

sin= 1.27323954 * x+ .405284735 * x* x;

if (sin< 0)

sin= .225 * (sin*-sin- sin) + sin;

else

sin= .225 * (sin* sin- sin) + sin;

}

else

{

sin= 1.27323954 * x- 0.405284735 * x* x;

if (sin< 0)

sin= .225 * (sin*-sin- sin) + sin;

else

sin= .225 * (sin* sin- sin) + sin;

}

//compute cosine: sin(x + PI/2) = cos(x)

x+= 1.57079632;

if (x> 3.14159265)

x-= 6.28318531;

if (x< 0)

{

cos= 1.27323954 * x+ 0.405284735 * x* x;

if (cos< 0)

cos= .225 * (cos*-cos- cos) + cos;

else

cos= .225 * (cos* cos- cos) + cos;

}

else

{

cos= 1.27323954 * x- 0.405284735 * x* x;

if (cos< 0)

cos= .225 * (cos*-cos- cos) + cos;

else

cos= .225 * (cos* cos- cos) + cos;

}

Fast and accurate sine/cosine approximation

July 18, 2007 on 2:31 pm | In Actionscript | 50 Comments

Trigonometric functions are costly operations and can slow down your application if they are extensively used. There are two reasons why: First, Math.sin() is a function, and thus needs a function call which simple eats up some time. Second, the result is computed with much more precision than you would ever need in most situations.

Most often you just want the periodic wave-like characteristics of the sine or cosine, which can be approximated in various ways. One common way of making it faster is to create a lookup-table by computing the sine at discrete steps and storing the result in an array. For example:

var sineTable:Array = [];

for (var i:int = 0; i < 90; i++)

{

sineTable[i] = Math.sin(Math.PI/180 * i)

}

Due to the symmetry of the sine wave, it's sufficient to compute one quadrant only (0..pi/2), and the other 3/4's of the circle can be computed by shifting and wrapping the input value. The biggest drawback is that the values are stored at a fixed resolution and so the result is not very accurate. This can be enhanced with linear interpolation:

x = 22.5;

y = sineTable[int(x)] + (sineTable[int(x + .5)] - sineTable[int(x)]) / 2;

Much better, but yet the error exists. It also involves accessing array elements which m akes the code rather slow. Another technique uses taylor series approximation:

sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...

Like with the lookup-table, evaluating this term is costly.

After searching for alternatives, I finally found a fantastic solution using a quadratic curve which blows everything away in terms of performance and accuracy. For a detailed derivation, please follow the link because I won't go into it.

I did minor optimizations to figure out what AS3 likes most, and arrived at som e code that can be up to 14x faster, while still being very accurate. However, you have to use it directly - do not place the code inside a function, because the additional function call sweeps out the performance gain, and you are left with an approximation that is actually slower compared to a native Math.sin() or Math.cos() call. Also note that cos(x) = sin(x + pi/2) or cos(x - pi/2) = sin(x), so computing the cosine is just of matter adding pi/2 to the input value.

Download source: fastTrig.as.

Below is a simple visualization to show you the quality of the approximation. The high precision version can replace the Math.sin() and Math.cos() calls in nearly all situations.

Low precision sine/cosine (~14x faster)

//always wrap input angle to -PI..PI

if (x < -3.14159265)

x += 6.28318531;

else

if (x > 3.14159265)

x -= 6.28318531;

//compute sine

if (x < 0)

sin = 1.27323954 * x + .405284735 * x * x;

else

sin = 1.27323954 * x - 0.405284735 * x * x;

//compute cosine: sin(x + PI/2) = cos(x)

x += 1.57079632;

if (x > 3.14159265)

x -= 6.28318531;

if (x < 0)

cos = 1.27323954 * x + 0.405284735 * x * x

else

cos = 1.27323954 * x - 0.405284735 * x * x;

}

High precision sine/cosine (~8x faster)

//always wrap input angle to -PI..PI

if (x < -3.14159265)

x += 6.28318531;

else

if (x > 3.14159265)

x -= 6.28318531;

//compute sine

if (x < 0)

{

sin = 1.27323954 * x + .405284735 * x * x;

if (sin < 0)

sin = .225 * (sin *-sin - sin) + sin;

else

sin = .225 * (sin * sin - sin) + sin;

}

else

{

sin = 1.27323954 * x - 0.405284735 * x * x;

if (sin < 0)

sin = .225 * (sin *-sin - sin) + sin;

else

sin = .225 * (sin * sin - sin) + sin;

}

//compute cosine: sin(x + PI/2) = cos(x)

x += 1.57079632;

if (x > 3.14159265)

x -= 6.28318531;

if (x < 0)

{

cos = 1.27323954 * x + 0.405284735 * x * x;

if (cos < 0)

cos = .225 * (cos *-cos - cos) + cos;

else

cos = .225 * (cos * cos - cos) + cos;

}

else

{

cos = 1.27323954 * x - 0.405284735 * x * x;

if (cos < 0)

cos = .225 * (cos *-cos - cos) + cos;

else

cos = .225 * (cos * cos - cos) + cos;

}

50 COMMENTS ?

RSS feed for comments on this post.TrackBack URI

1. Nice find, though I think I‘d have to be in a real optim ization bind before I replaced all my sin/cos calls with all that stuff. :)

Comment by Keith Peters— July, 18 2007 #

2. Once again, incredible post.

There is an error in the link. The good link is :

http://lab.polygonal.de/wp-content/articles/fast_trig/fastTrig.as :

//1.27323954 = 4/pi

//0.405284735 =-4/(pi^2)

/********************************************************* * low precision sine/cosine

*********************************************************/

//always wrap input angle to -PI..PI

if (x < -3.14159265)

x += 6.28318531;

else

if (x > 3.14159265)

x -= 6.28318531;

//compute sine

if (x < 0)

sin = 1.27323954 * x + .405284735 * x * x;

else

sin = 1.27323954 * x - 0.405284735 * x * x;

//compute cosine: sin(x + PI/2) = cos(x)

x += 1.57079632;

if (x > 3.14159265)

x -= 6.28318531;

if (x < 0)

cos = 1.27323954 * x + 0.405284735 * x * x

else

cos = 1.27323954 * x - 0.405284735 * x * x;

}

/********************************************************* * high precision sine/cosine

*********************************************************/

//always wrap input angle to -PI..PI

if (x < -3.14159265)

x += 6.28318531;

else

if (x > 3.14159265)

x -= 6.28318531;

//compute sine

if (x < 0)

{

sin = 1.27323954 * x + .405284735 * x * x;

if (sin < 0)

sin = .225 * (sin *-sin - sin) + sin; else

sin = .225 * (sin * sin - sin) + sin; }

else

{

sin = 1.27323954 * x - 0.405284735 * x * x;

if (sin < 0)

sin = .225 * (sin *-sin - sin) + sin; else

sin = .225 * (sin * sin - sin) + sin; }

//compute cosine: sin(x + PI/2) = cos(x)

x += 1.57079632;

if (x > 3.14159265)

x -= 6.28318531;

if (x < 0)

{

cos = 1.27323954 * x + 0.405284735 * x * x

if (cos < 0)

cos = .225 * (cos *-cos - cos) + cos; else

cos = .225 * (cos * cos - cos) + cos; }

else

{

cos = 1.27323954 * x - 0.405284735 * x * x;

if (cos < 0)

cos = .225 * (cos *-cos - cos) + cos;

else

cos = .225 * (cos * cos - cos) + cos;

}

Comment by Jerom e— July, 18 2007 #

3. thank you, fixed now.

Comment by Michael— July, 18 2007 #

4. Woah, that‘s sick! Thanks for sharing, I always stopped at the first step :/

Comment by Mr.doob— July, 19 2007 #

5. Awesome! Let‘s see how PV3D can benefit from that! ;-)

Comment by Ralph Hauwert— July, 19 2007 #

6. The article on DevMaster mentions that you should avoid branching, especially in loops. I wonder if the sam e problem applies to AS3? Is there a speed improvement if you replace the branches by binary logic twists?

Comment by Patrick — July, 20 2007 #

7. Hi, it didn‘t work for m e (the author also says that this is not valid C code at all) Binary & converts the result to an integer. Only this works:

x -= int(x > y) && z;

But the code above is a lot slower than the pure if..else stateme nts.

Comment by Michael— July, 20 2007 #

8. Nice work Michael – this one goes a long way back. I th ink it may have been in Hart‘s

?Computer Approximations.‘

One thing I‘ve found helpful when working with compilers that don‘t support function inlining is to use the C preprocessor or awk or something similar to do all my debugging with library calls and then have the tool replace them with inline approximations going into production.

Another benefit of having inline code is that you can combine the sin or cos computation with whatever equation it‘s used in and realize additional gains by having the trig function result immediately available in a register.

regards,

- jim

Comment by Jim Armstrong— July, 20 2007 #

9. hey cool I didn‘t know there is even a whole book about approximations only ;-) talking about preprocessors, what IDE do you use ? I was trying to integrate the C preprocessor into FlashDevelop, but failed at configuring make or ant to use it.

Comment by Michael— July, 21 2007 #

10. Michael:

Another classic is Cody‘s ?A Software Manual for the Elementary Functions‘. There is a relatively new book by Muller –?Elementary Functions: Algorithms and Implementation‘, but I haven‘t read it yet.

I‘ve given up on direct integration of other tools to any IDE –don‘t have the bandwidth to work out all the issues, so I run awk or another text processor directly on the .AS files — very old school.

Best of luck in your continued (and superb) efforts!

regards,

- jim

Comment by Jim Armstrong— July, 22 2007 #

11. Hey thanks for the reference!

Doing University and making a blog isn‘t easy but shortly som e content will popout =D

Comment by Eduardo— August, 9 2007 #

12. [...] Fast and accurate sine/cosine approximation More code optimization to do

sine/cosine operations without using the Math class. [...]

Pingback by ? Blog Archive ? Links: Mathematical themes with Actionscript https://www.doczj.com/doc/e49550323.html,—August, 26 2007 #

13. [...] Fast and accurate sine/cosine approximation [...]

Pingback by ??a€o?¨???￡?? BLOG ? Blog Archive ?

as3?|a€￠???¤??a€??¤?????￥?‘a€―— September, 19 2007 #

14. Here‘s a modified fixed-point version that performs better :

https://www.doczj.com/doc/e49550323.html,/entry/26

Comment by Nicolas— November, 12 2007 #

15. I‘ev tested this in AS2, and it‘s not faster. So this optimisation trick is ONLY for AS3. Just to let you know.

Comment by JP— January, 8 2008 #

16. Thanks. This post was useful and more accurate than using an MS-Excell trendline function (2nd degree). Made minor changes that should speed things up since addition is cheaper than mult usually. This is the c code:（注：我本人已经亲自测试过OK,性能很好---tang）double sin(double rad){

double sine;

if (rad < 0)

sine = rad*(1.27323954 + .405284735 * rad);

else

sine = rad*(1.27323954 – 0.405284735 * rad);

if (sine < 0)

sine = sine*(-0.225 * (sine + 1) + 1);

else

sine = sine*(0.225 * (sine – 1) + 1);

return sine;

}

Comment by DYessick— January, 28 2008 #

17. @DYessick: I tried your version in AS3 and there is no noticeable difference unfortunately. Probably due to the weirdness of AS3.

Overall the high precision approximation gives a nice boost though, although it is closer to ~6.7 faster on my tests. This could depend on a variety of factors I imagine, not least of all your processor architecture.

Comment by brainclog— February, 4 2008 #

18. [...] polygonal labs ?￠a???? Fast and accurate sine/cosine approximation (tags: optimization math) [...]

Pingback by fcicq's https://www.doczj.com/doc/e49550323.html, ? Blog Archive ? links for 2008-02-09— February, 9 2008 #

19. You wrote:

―[...] it?￠a??a…￠s sufficient to compute one quadrant only (0..pi), and the other

3/4?￠a??a…￠s [...]‖

But …1/4 of 2pi is pi/2 and not pi, so a quadrant is (0..pi/2), i‘m wrong ?

Greg

Comment by Gregoire — March, 4 2008 #

20. thanks greg, you are right. i have fixed the article.

Comment by Michael— March, 5 2008 #

21. More over, you can use a Quadrant but an Octant is sufficient due to the symetry (x y, -x y, -x -y, x -y, y x, -y x, -y -x, y -x)

Comment by Passault Gr????goire — March, 18 2008 #

22. This is about 50% slower than using Math.cos(); ive found…I don‘t get it? I‘m not using it in a function either.

Comment by ColbyCheeze— April, 12 2008 #

23. always compile in release mode and use the release player (not the debug version) for doing benchmarks.

Comment by Michael— April, 12 2008 #

24. That makes a difference? Damn I didn‘t know that…I‘ll have to go find my release player, haven‘t even used that thing in forever.

Comment by ColbyCheeze— April, 14 2008 #

25. [...] Fast and accurate sine/cosine approximation [...]

Pingback by https://www.doczj.com/doc/e49550323.html, - New Media Development Blog ? Blog Archive ? Som e ActionScript 3.0 Optimizations— August, 11 2008 #

26. [...] Fast and accurate sine/cosine approximation [...]

Pingback by Optimizations links | JADBOX: Web Application Musings— August, 11 2008 #

27. This may be a bit outdated – I think Adobe took pretty harsh to your approximation genius and generated a super fast trig table…

Compiling using the Flex 3.2 SDK, I get these results…

iterations: 1,000,000

algorithm: FastMath [ high-quality approximation ]

angle: 1.302888286613767

FastMath.sin( 1.302888286613767 ) = 0.9643253756148902

– Time: 475 ms

…

iterations: 100,000

algorithm: Math [ flash ]

angle: 1.302888286613767

Math.sin( 1.302888286613767 ) = 0.9643267785343497

– Time: 167 ms

…

Can anyone else confirm this? Thanks!

Comment by Matt Bolt— January, 2 2009 #

28. I also made a mistake when typing the last post….The iterations for the Math.sin() test were also = 1,000,000 – *not* 100,000.

Comment by Matt Bolt— January, 2 2009 #

29. hi matt,

I cannot confirm this. make sure you are using the mxmlc compiler with debug=false and run the swf inside a release player. otherwise you get misleading results. with the Flex3.2 SDK the high quality approximation is now almost exactly 10x faster on my machine.

Comment by Michael— January, 3 2009 #

30. [...] Optimización de operaciones con seno y

coseno http://lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/ [...]

Pingback by Rendimiento y Optimización de AS3 | ?y por qué no?— January, 23 2009 #

31. Thanks alot, this really helps. But I was wondering if anyone could tell me where the numbers 0.405284735 and 0.225 came from?

Comment by Chris — January, 28 2009 #

32. Hi,

I know this is outdated, but these results may help somebody – these tests were done in Flash Lite 2.0 on a Nokia 6121 (I will test on more phones)

Calculating both sin and cos of 100 angles using Math.sin and Math.cos

= 6216 ms

Calculating the same thing using FastMath inline

= 4685 ms

In Flash Lite FastMath is around 25-30% faster

Just a note (it says this in the post too) that wrapping FastMath in a function call negates the speed increase, and you get the same results as just using Math.sin/cos.

Comment by Peter— February, 7 2009 #

33. And sorry ?of 100 angles‘ should be ?of 1000 angles‘…

Comment by Peter— February, 7 2009 #

34. [...] Fast and accurate sine and cosine approximation [...]

Pingback by Fast and accurate sine and cosine approximation — Some Random Dude—February, 21 2009 #

35. for sin, radians 0 <= x <= pi

temp = x * 2 / pi = x * 0.636619…

sin = temp * ( 2 – temp )

sin = sin * ( 0.225 * ( sin – 1 ) + 1 )

without refinement step, maximum error is 0.056 at +- 0.47

with refinement, maximum error is 0.001 at +- 1.38

for degrees, swap pi with 90

Comment by Eric Cole — February, 22 2009 #

36. sorry, swap pi with 180, so temp = x / 90

Comment by Eric Cole — February, 22 2009 #

37. [...] in January I saw this blog post by Michael Baczynski over at http://lab.polygonal.de/. The blog post describes a technique for fast [...]

Pingback by Low Precision Sine and Cosine— March, 21 2009 #

38. [...] a big fan of Polygonal Labs, and Michael has numerous posts such as this one that deal with fast approximation algorithms. This is another good one from his Actionscript [...]

Pingback by Actionscript Optimization ? The Algorithmist— March, 27 2009 #

39. [...] polygonal labs ? Fast and accurate sine/cosine approximation [...]

Pingback by polygonal labs ? Fast and accurate sine/cosine approximation — Some Random Dude— March, 27 2009 #

40. [...] Fast sin/cosine approximation [...]

Pingback by Flash and the art of optimization ? whitenoise— June, 19 2009 #

41. [...] polygonal labs – Fast and accurate sine/cosine approximation [...]

Pingback by sine approximation with fixed point math ? console-dev.de— July, 6 2009 #

42. Hi

i want draw sine curve same as above but i need text insted of pixel

Comment by Sweety — December, 1 2009 #

43. [...] os usamos intensam ente como por exemplo em sistem as de partículas. Por isso uma leitura a este post do Michael Baczynski é [...]

Pingback by Comunidade Portuguesa de Rich Internet Applications? Blog Archive ?

Introdu??o ao seno e coseno com Actionscript— January, 26 2010 #

44. [...] os usamos intensam ente como por exemplo em sistem as de partículas. Por isso uma leitura a este post do Michael Baczynski é [...]

高中数学必备知识点正弦与余弦定理和公式

三角函数正弦与余弦的学习，在数学中只要记住相关的公式即可。日常考试正弦和余弦的相关题目一般不会很难，是很多数学基础不是很牢的同学拿分的好题目。但对于有些同学来说还是很难拿分，那是为什么呢？首先，我们要了解下正弦定理的应用领域在解三角形中，有以下的应用领域：（1）已知三角形的两角与一边，解三角形（2）已知三角形的两边和其中一边所对的角，解三角形（3）运用a：b：c=sinA：sinB：sinC解决角之间的转换关系直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦正弦定理在△ABC中，角A、B、C所对的边分别为a、b、c，则有 a/sinA=b/sinB=c/sinC=2R（其中R为三角形外接圆的半径）其次，余弦的应用领域余弦定理余弦定理是揭示三角形边角关系的重要定理，直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。正弦定理的变形公式 (1) a=2RsinA, b=2RsinB, c=2RsinC; (2) sinA : sinB : sinC = a : b : c; 在一个三角形中，各边与其所对角的正弦的比相等，且该比值都等于该三角形外接圆的直径已知三角形是确定的，利用正弦定理解三角形时，其解是唯一的；已知三角形的两边和其中一边的对角，由于该三角形具有不稳定性，所以其解不确定，可结合平面几何作图的方法及“大边对大角，大角对大边”定理和三角形内角和定理去考虑解决问题 (3)相关结论： a/sinA=b/sinB=c/sinC=(a+b)/(sinA+sinB)=(a+b+c)/(sinA+sinB+sinC) c/sinC=c/sinD=BD=2R（R为外接圆半径）（4）设R为三角外接圆半径，公式可扩展为：a/sinA=b/sinB=c/sinC=2R,即当一内角为90°时，所对的边为外接圆的直径。灵活运用正弦定理，还需要知道它的几个变形sinA=a/2R,sinB=b/2R,sinC=c/2R asinB=bsinA,bsinC=csinB,asinC=csinA （5）a=bsinA/sinB sinB=bsinA/a 正弦、余弦典型例题 1．在△ABC中，∠C=90°，a=1，c=4，则sinA 的值为 2．已知α为锐角，且，则α的度数是（） A．30° B．45° C．60° D．90° 3．在△ABC中，若，∠A，∠B为锐角，则∠C的度数是（） A．75° B．90° C．105° D．120° 4．若∠A为锐角，且，则A=（） A．15° B．30° C．45° D．60° 5.在△ABC中，AB＝AC＝2，AD⊥BC，垂足为D，且AD＝，E是AC中点， EF⊥BC，垂足为F，求sin∠EBF的值。

关于正弦函数和余弦函数的计算公式(终审稿)

关于正弦函数和余弦函数的计算公式文稿归稿存档编号：[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-

cos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotαsin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanα cot（π＋α）＝cotα sin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（2π－α）＝－sinαcos（2π－α）＝cosα tan（2π－α）＝－tanαcot（2π－α）＝－cotαsin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanα

正弦定理和余弦定理

正弦定理和余弦定理高考风向 1.考查正弦定理、余弦定理的推导；2.利用正、余弦定理判断三角形的形状和解三角形；3.在解答题中对正弦定理、余弦定理、面积公式以及三角函数中恒等变换、诱导公式等知识点进行综合考查．学习要领 1.理解正弦定理、余弦定理的意义和作用；2.通过正弦、余弦定理实现三角形中的边角转换，和三角函数性质相结合． 1．正弦定理：a sin A ＝b sin B ＝c sin C ＝2R ，其中R 是三角形外接圆的半径．由正弦定理可以变形：(1)a ∶b ∶c ＝sin_A ∶sin_B ∶sin_C ；(2)a ＝2R sin_A ，b ＝2R sin_B ，c ＝2R sin_C ；(3)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝ c 2R 等形式，解决不同的三角形问题． 2．余弦定理：a 2＝b 2＋c 2－2bc cos_A ，b 2＝a 2＋c 2－2ac cos_B ，c 2＝a 2＋b 2－2ab cos_C ．余弦定理可以变形： cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 2 2ab . 3． S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ＝abc 4R ＝1 2 (a ＋b ＋c )·r (r 是三角形内切圆的半径)，并可由此计算R 、 r . 4．在△ABC 中，已知a 、b 和A 时，解的情况如下： [1．在三角形中，大角对大边，大边对大角；大角的正弦值也较大，正弦值较大的角也较大，即在△ABC 中，A >B ?a >b ?sin A >sin B ；tanA+tanB+tanC=tanA·tanB·tanC ；在锐角三角形中，cos A

三角函数正弦定理和余弦定理

(文）已知ΔABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量(,)m a b =， (sin ,sin )n B A =，(2,2)p b a =-- . (1)若m //n ，求证：ΔABC 为等腰三角形； (2)若m ⊥p ，边长c = 2，角ΔABC 的面积 . 答案：证明：（1）//,sin sin ,m n a A b B ∴=u v v Q 即22a b a b R R ? =? ，其中R 是三角形ABC 外接圆半径，a b =. ABC ∴?为等腰三角形（2）由题意可知//0,(2)(2)0m p a b b a =-+-=u v u v 即 a b ab ∴+= 由余弦定理可知， 2 2 2 4()3a b ab a b ab =+-=+- 2()340ab ab --=即4(1)ab ab ∴==-舍去. 11 sin 4sin 223 S ab C π ∴==??= 来源：09年高考上海卷题型：解答题，难度：中档

(文）在ABC ?中，A C AC BC sin 2sin ,3,5=== （Ⅰ）求AB 的值。（Ⅱ）求)4 2sin(π - A 的值。答案：（1）解：在ABC ? 中，根据正弦定理， A BC C AB sin sin = ，于是522sin sin ===BC A BC C AB （2）解：在ABC ? 中，根据余弦定理，得AC AB BC AC AB A ?-+=2cos 2 22 于是A A 2cos 1sin -== 5 5，从而5 3sin cos 2cos ,54cos sin 22sin 22=-== =A A A A A A 10 2 4 sin 2cos 4 cos 2sin )4 2sin(= -=- π π π A A A 来源：09年高考江西卷题型：解答题，难度：容易在⊿ABC 中，,A B 为锐角，角,,A B C 所对应的边分别为,,a b c ，且

关于正弦函数和余弦函数的计算公式

关于正弦函数与余弦函数的计算公式同角三角函数的基本关系式倒数关系: 商的关系: 平方关系: tanα·cotα＝1 sinα·cscα＝1 cosα·secα＝1 sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα sin2α＋cos2α＝1 1＋tan2α＝sec2α 1＋cot2α＝csc2α 诱导公式 sin(－α)＝－sinα cos(－α)＝cosα tan(－α)＝－tanα cot(－α)＝－cotα sin(π/2－α)＝cosα cos(π/2－α)＝sinα tan(π/2－α)＝cotα cot(π/2－α)＝tanα sin(π/2＋α)＝cosα cos(π/2＋α)＝－sinα tan(π/2＋α)＝－cotα cot(π/2＋α)＝－tanα sin(π－α)＝sinα cos(π－α)＝－cosα tan(π－α)＝－tanα cot(π－α)＝－cotα sin(π＋α)＝－sinα cos(π＋α)＝－cosα tan(π＋α)＝tanα cot(π＋α)＝cotα sin(3π/2－α)＝－cosα cos(3π/2－α)＝－sinα tan(3π/2－α)＝cotα cot(3π/2－α)＝tanα sin(3π/2＋α)＝－cosα

cos(3π/2＋α)＝sinα tan(3π/2＋α)＝－cotα cot(3π/2＋α)＝－tanα sin(2π－α)＝－sinα cos(2π－α)＝cosα tan(2π－α)＝－tanα cot(2π－α)＝－cotα sin(2kπ＋α)＝sinα cos(2kπ＋α)＝cosα tan(2kπ＋α)＝tanα cot(2kπ＋α)＝cotα (其中k∈Z) 两角与与差的三角函数公式万能公式 sin(α＋β)＝sinαcosβ＋cosαsinβ sin(α－β)＝sinαcosβ－cosαsinβ cos(α＋β)＝cosαcosβ－sinαsinβ cos(α－β)＝cosαcosβ＋sinαsinβ tanα＋tanβ tan(α＋β)＝—————— 1－tanα·tanβ tanα－tanβ tan(α－β)＝—————— 1＋tanα·tanβ 2tan(α/2) sinα＝—————— 1＋tan2(α/2) 1－tan2(α/2) cosα＝—————— 1＋tan2(α/2) 2tan(α/2) tanα＝—————— 1－tan2(α/2) 二倍角的正弦、余弦与正切公式三倍角的正弦、余弦与正切公式sin2α＝2sinαcosα

解三角形题型5正、余弦定理判断三角形形状(供参考)(新)

解三角形题型5：正、余弦定理判断三角形形状 1、（2013·陕西高考文科·Ｔ9）设△ABC 的内角A , B , C 所对的边分别为a, b, c , 若 cos cos sin b C c B a A +=, 则△ABC 的形状为 ( ) A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不确定 2、（2010上海文数）18.若△ABC 的三个内角满足sin :sin :sin 5:11:13A B C =，则△ABC （A ）一定是锐角三角形. （B ）一定是直角三角形. （C ）一定是钝角三角形. (D)可能是锐角三角形，也可能是钝角三角形. 3、如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．由增加的长度决定 4、在△ABC 中，已知2a b c =+，2 sin sin sin A B C =，试判断△ABC 的形状。 5、在△ABC 中，已知C B A sin cos sin 2=,那么△ABC 一定是 ( ) A ．直角三角形 B ．等腰三角形 C ．等腰直角三角形 D ．正三角形 6、A 为ΔABC 的一个内角,且sinA+cosA= 12 7 , 则ΔABC 是______三角形. 7、在△ABC 中，若c C b B a A sin cos cos = =，则△ABC 是（） A ．有一内角为30°的直角三角形 B ．等腰直角三角形 C ．有一内角为30°的等腰三角形 D ．等边三角形 8、若(a+b+c)(b+c －a)=3abc,且sinA=2sinBcosC, 那么ΔABC 是（） A ．直角三角形 B ．等边三角形 C ．等腰三角形 D ．等腰直角三角形 9、（2010辽宁文数17）在ABC ?中，a b c 、、分别为内角A B C 、、的对边，且2sin (2)sin (2)sin a A b c B c b C =+++ （Ⅰ）求A 的大小；（Ⅱ）若sin sin 1B C +=，试判断ABC ?的形状. 10、在ABC ?中，已知2222()sin()()sin()a b A B a b A B +?-=-?+,判断该三角形的形状。 11、在ΔABC 中,求分别满足下列条件的三角形形状： ①B=60°,b 2=ac ； ②b 2tanA=a 2tanB ； ③sinC= B A B A cos cos sin sin ++④ (a 2－b 2)sin(A+B)=(a 2+b 2)sin(A －B).

三角函数值的计算

第一章直角三角形的边角关系 2. 30°，45°，60°角的三角函数值一、学生知识状况分析学生的知识技能基础：本节课前学生已经学习了正切、正弦、余弦的定义。学生活动经验基础：在相关知识的学习过程中，学生已经经历了一些统计活动，解决了一些简单的现实问题，感受到了数据收集和处理的必要性和作用，获得了从事统计活动所必须的一些数学活动经验的基础；同时在以前的数学学习中学生已经经历了很多合作学习的过程，具有了一定的合作学习的经验，具备了一定的合作与交流的能力。二、教学任务分析本节课教学目标如下：知识与技能： 1．经历探索30°、45°、60°角的三角函数值的过程，能够进行有关的推理，进一步体会三角函数的意义。 2．能够进行30°、45°、60°角的三角函数值的计算 3．能够根据30°、45°、60°的三角函数值说明相应的锐角的大小过程与方法：经历探索30°、45°、60°角的三角函数值的过程，发展学生观察、分析、发现的能力。情感态度与价值观：培养学生把实际问题转化为数学问题的能力。教学重点：能够进行30°、45°、60°角的三角函数值的计算；能够根据30°、45°、60°的三角函数值说明相应的锐角的大小教学难点：三角函数值的应用三、教学过程分析本节课设计了六个教学环节：复习巩固、活动探究、讲解新课、知识应用、

A C B b a c 小结与拓展、作业布置。第一环节复习巩固活动内容：如图所示在 Rt △ABC 中，∠C=90°。（1）a 、b 、c 三者之间的关系是， ∠A+∠B= 。（2）sinA= ，cosA= ， tanA= 。 sinB= ，cosB= ，tanB= 。（3）若A=30°，则 c a = 。活动目的：复习巩固上一节课的内容第二环节活动探究活动内容： [问题]为了测量一棵大树的高度，准备了如下测量工具：①含30°和60°两个锐角的三角尺；②皮尺.请你设计一个测量方案，能测出一棵大树的高度. 我们组设计的方案如下：让一位同学拿着三角尺站在一个适当的位置B 处，使这位同学拿起三角尺，她的视线恰好和斜边重合且过树梢C 点，30°的邻边和水平方向平行，用卷尺测出AB 的长度，BE 的长度，因为DE=AB ，所以只需在Rt △CDA 中求出CD 的长度即可. 我们前面学习了三角函数的定义，如果一个角的大小确定，那么它的正切、正弦、余弦值也随之确定，如果能求出30°的正切值，在上图中，tan30°

三角函数之正余弦定理

教师寄语：天才=1％的灵感+99％的血汗 1 戴氏教育中高考名校冲刺教育中心【我生命中最最最重要的朋友们，请你们认真听老师讲并且跟着老师的思维走。学业的成功重在于考点的不断过滤，相信我赠予你们的是你们学业成功的过滤器。谢谢使用！！！】主管签字：________ §3.6 正弦定理和余弦定理一、考点、热点回顾 2014会这样考 1.考查正弦定理、余弦定理的推导；2.利用正、余弦定理判断三角形的形状和解三角形；3.在解答题中对正弦定理、余弦定理、面积公式以及三角函数中恒等变换、诱导公式等知识点进行综合考查．复习备考要这样做 1.理解正弦定理、余弦定理的意义和作用；2.通过正弦、余弦定理实现三角形中的边角转换，和三角函数性质相结合．基础知识.自主学习 1．正弦定理：a sin A ＝b sin B ＝c sin C ＝2R ，其中R 是三角形外接圆的半径．由正弦定理可以变形：(1)a ∶b ∶c ＝sin_A ∶sin_B ∶sin_C ；(2)a ＝2R sin_A ，b ＝2R sin_B ，c ＝2R sin_C ；(3)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c 2R 等形式，以解决不同的三角形问题． 2．余弦定理：a 2＝b 2＋c 2－2bc cos_A ，b 2＝a 2＋c 2－2ac cos_B ，c 2＝a 2＋b 2－2ab cos_C ．余弦定理可以变形：cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 2 2ab . 3． S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ＝abc 4R ＝1 2 (a ＋b ＋c )·r (r 是三角形内切圆的半径)，并可由此计算R 、r . 4．在△ABC 中，已知a 、b 和A 时，解的情况如下： A 为锐角 A 为钝角或直角图形关系式 a ＝b sin A b sin A b 解的个数一解两解一解一解