确定有穷自动机的最小化问题探讨

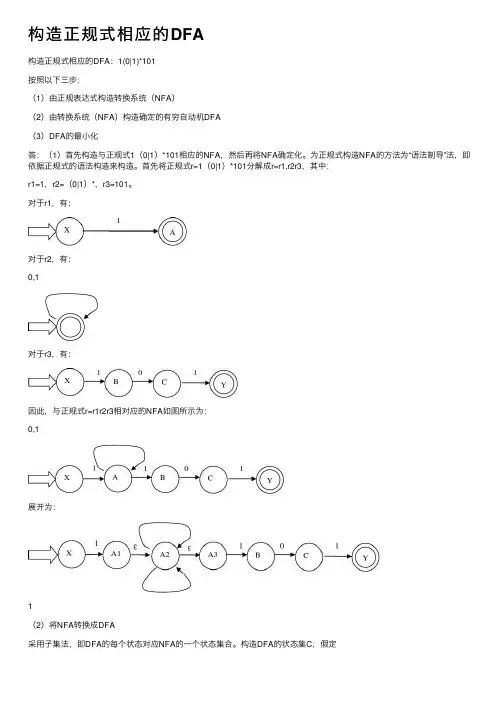
构造正规式相应的DFA
构造正规式相应的DFA：1(0|1)*101
按照以下三步：
（1）由正规表达式构造转换系统（NFA）
（2）由转换系统（NFA）构造确定的有穷⾃动机DFA
（3）DFA的最⼩化
答：（1）⾸先构造与正规式1（0|1）*101相应的NFA，然后再将NFA确定化。

为正规式构造NFA的⽅法为“语法制导”法，即依据正规式的语法构造来构造。

⾸先将正规式r=1（0|1）*101分解成r=r1,r2r3，其中：
r1=1，r2=（0|1）*，r3=101。

对于r1，有：
对于r2，有：
0,1
对于r3，有：
因此，与正规式r=r1r2r3相对应的NFA如图所⽰为：
0,1
展开为：
1
（2）将NFA转换成DFA
采⽤⼦集法，即DFA的每个状态对应NFA的⼀个状态集合。

构造DFA的状态集C，假定
DFA的状态转换图
1
（3）化简DFA：分割法，把DFA的状态集分成⼀些不想交的⼦集，使得不同的两⼦集的状态是可区别的，同⼀⼦集的状态是等价的。

⾸先，将状态分成两个⼦集：⼀个由终态组成，⼀个由⾮态组成：{T0，T1，T2，T3，T4} {T5}
{T0，T1，T2，T3} {T4} {T5}
{ T0，T1，T2} {T3} {T4} {T5}
{T0} {T1，T2} {T3} {T4} {T5}
在等价状态⼦集{T1，T2}中选状态T2做代表，消去其他状态T1，把从消去状态T1射出和
射⼊的弧都引到代表状态T2上，得到化简后的DFA：。

第三章习题参考解答3.1 构造自动机A，使得①②③当从左至右读入二进制数时，它能识别出读入的奇数；④它识别字母表{a, b}上的符号串，但符号串不能含两个相邻的a，也不含两个相邻的b；⑤它能接受字母表{0, 1}上的符号串，这些符号串由任意的1、0和随后的任意的11、00对组成。

⑥它能识别形式如±dd*⋅ d*E ±dd的实数，其中，d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。

3.2 构造下列正规表达式的DFSA：① xy*∣yx*y∣xyx；② 00∣(01)*∣11；③ 01((10∣01)*(11∣00))*01；④ a(ab*∣ba*)*b。

3.3 消除图3.24所示自动机的空移。

bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。

xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式，试证明① e∣e=e；② {{e}}={e}；③ {e}=ε∣e{e}；④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。

3.6 构造下面文法G[Z]的自动机，指明该自动机是不是确定的，并写出它相应的语言： G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中，f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。

试对此NDFSA确定化。

3.8 设文法G[〈单词〉]：〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。

DFA（确定的有穷自动机）的化简1. 实验内容输入一个DFA M,输出一个与之等价的最小化的DFA M’，设计并实现将NFA确定化为DFA的子集构造算法，输入非确定有限（穷）状态自动机，输出确定化的有限（穷）状态自动机编写一个程序，将一个非确定有限自动机转换为确定有限自动机。

2. 实验设计分析2.1 实验设计思路首先输入边集找到状态与边的关系，然后输入终结点，这样一个没有简化的NFA图就表示出来了，然后利用求闭包的方式求move集合，画出状态转化图，重命名后进行集合划分，再次重新画出状态转换矩阵，输出简化后的DFA。

2.2 实验算法（1）构造具有两个组的状态集合的初始划分I：接受状态组 F 和非接受状态组Non-F。

（2）对I采用下面所述的过程来构造新的划分I-new.For I 中每个组G doBegin当且仅当对任意输入符号a,状态s和读入a后转换到I的同一组中；/*最坏情况下，一个状态就可能成为一个组*/用所有新形成的小组集代替I-new中的G;end（3）如果I-new=I，令I-final=I,再执行第（4）步，否则令I=I=new,重复步骤（2）。

（4）在划分I-final的每个状态组中选一个状态作为该组的代表。

这些代表构成了化简后的DFA M＇状态。

令s是一个代表状态，而且假设：在DFA M 中，输入为a时有从s到t转换。

令t所在组的代表是r,那么在M’中有一个从s到r的转换，标记为a。

令包含s0的状态组的代表是M’的开始状态，并令M’的接受状态是那些属于F的状态所在组的代表。

注意,I-final的每个组或者仅含F中的状态，或者不含F中的状态。

（5）如果M’含有死状态（即一个对所有输入符号都有刀自身的转换的非接受状态d）,则从M’中去掉它；删除从开始状态不可到达的状态；取消从任何其他状态到死状态的转换。

2.3 实验流程1. 输入NFA各边信息（起点条件[空为*] 终点），以#结束2. 输入终态3. 求e-clouse闭包,将结点移入相应的闭包集合，并重新排序4. 输出状态转换矩阵，转换成DFA并重命名5. 执行DFA最简化6. 重命名DFA，输出最简化DFA状态转换矩阵2.4 实验的基本技术设计方案实验中含有一些数据结构的知识，假设I是NFA M状态集K的一个子集（即I∈K），则定义ε-closure（I）为：若Q∈I，则Q∈ε-closure（I）；若Q∈I，则从Q出发经过任意条ε弧而能到达的任何状态Q’，则Q’∈ε-closure（I）。

有穷自动机状态极小化方法及正则语言判定优化王晓峰【摘要】引入了等价性原则,定义等价关系的商集合∑*/～B,通过对商集合的有限性判断,来判定正则语言,大大简化了正则语言判定的步骤,并在有穷自动机的状态集上引入了等价关系,对等价状态进行压缩,构造出与其等价的最小有穷自动机,同时降低了有穷自动机状态的复杂性.【期刊名称】《广西民族大学学报（自然科学版）》【年(卷),期】2008(014)003【总页数】4页(P81-84)【关键词】自动机;正则语言;等价关系;终结一致;商集合【作者】王晓峰【作者单位】贵州大学,计算机科学与技术学院,贵州,贵阳,550025【正文语种】中文【中图分类】TP3010 引言自动机理论是计算机科学研究的重要分支之一，在编译技术，遗传算法，模式识别，密码学，人工智能等方面有着广泛的应用，几乎所有的有限状态系统都可以用有穷自动机来描述[1].自动机给出了一种计算模型，可以用来识别语言，控制过程等[2].本文引入了等价关系，通过等价类，构造出极小化有穷自动机，降低了自动机的复杂性和存储空间.同时，在等价关系上引入了商集合Σ*/～B的有关概念，通过Σ*/～B的有限性，证明一个语言是否为正则语言(正则语言的代数判定定理).这个定理在某些方面比泵引理更为方便，简化了判定正则语言的步骤.最后，通过举例，说明使用泵引理和代数判定定理判定正则语言的方法，并给出了他们的优劣点.1 基本概念定义1[3]：形如M=(Q, Σ,δ ,q0 ，F ) 的一个五元组称为一台确定性的有穷自动机(DFA)[4]，其中：Q是一个有穷集，称为状态集；Σ是一个有穷集，称为字母表；δ是一个函数，称为状态转移函数；δ：Q×Σ→ Q；q0是起始状态，q0∈Q；F是终结状态集，F ⊆Q；这里通过δ诱导出δ*：Q×Σ*→ Q,若ω∈Σ*，则δ*(q，ω)=p，表示经过|ω|步到达状态p.由δ归纳定义δ*如下：δ*(q，λ)=q；δ*(q，ωa)=δ(δ*(q，ω)，a).定义2[5]：(1)设M是一台DFA，定义：L(M)={ω∈Σ*|δ*(q0，ω)∈F}表示为M 所接受的语言；(2)B⊆Σ* ，若存在一台DFA的M，使L(M)=B，称B是DFA可接受的语言，称B为正则语言；定义3[6](语言的等价)：设M1和M2为两台DFA，若L(M1)=L(M2)，则称M1与M2等价，即M1识别的语言与M2识别的语言是一致的.记|M1|为M1中的状态数，若|M1|≤|M2|，且M1与M2等价，称M1比M2简单.定义4：对于所有的ω∈Σ*，如果δ*(p，ω)∈F意味着δ*(q，ω)∈F或者δ*(p，ω)∉F意味着δ*(q，ω)∉F，称这样的p和q为终结一致；反之，若存在符号串ω∈Σ*使得δ*(p，ω)∈F且δ*(q，ω)∉F，或者，反之亦然，那么状态p和q不是终结一致的，称ω是p和q不是终结一致的证据.在Q上引入二元关系R：(p,q)∈R⟺p与q终结一致.可以验证R是一个等价关系. 引理1：对于给定的DFA，M=(Q, Σ,δ,q0 ，F )，Q上的终结一致关系R是等价关系；记(p,q)∈R为p～q；若pq，即存在ω∈Σ*，使得p与q关于ω不是终结一致的.引理2(泵引理)：[7](判定正则语言的必要条件) 设L是无穷的正则语言.那么一定存在某个正整数m，满足，任意w∈L，|w|≥m，可以分解成w=xyz，其中：|xy|≤m，|y|≥1，对于所有的i=0，1，2，…，满足wi=xyiz也属于L.2 有穷自动机中的状态压缩(极小化)问题我们已经知道,自动机是一个五元组, M=(Q, Σ,δ,q0 ，F ),一台自动机假如可以停机,那么它必须从起始状态q0出发经过一系列中间状态(Q中的状态),最后到达结束状态(F中的状态)[8].在实现过程中,一般情况下,中间状态越少,所用步数也就越少.因此,能否采用一种算法(方式)将一台已知的自动机当中的“冗余状态”归并掉,从而减少中间状态,进而提高效率.根据定义4及引理1,我们可以实现自动机的最小化,也就是说,对于任意给出的自动机,我们可以构造出与之等价的状态数最少的自动机,而且这个自动机是唯一的.下面我们通过例子来说明具体的构造过程.例1：有穷自动机M=<Q,Σ,δ,q0,F>,其中Q={A,B,C,D,E,F,G,H},Σ={0,1},q0=A,F={C},如图1所示.图1 有穷自动机构造终结等价关系的算法-填表法：p，q∈Q，若p～q，则在表中对应的栏打√；若pq，则在表中对应的栏打×；具体构造如下：状态A和B，则存在ω=“01”，使得δ*(A，ω)∈F且δ*(B，ω)∉F,根据引理1，有AB，故在A和B所对应的栏打×；状态A和C，则存在ω=“1”，使得δ*(A，ω)∉F且δ*(C，ω)∈F,所以有AC，故在A和C所对应的栏打×；状态A和D，则存在ω=“0”，使得δ*(A，ω)∉F且δ*(D，ω)∈F,所以有AD，故在A和D所对应的栏打×；状态A和E，则对ω∈Σ*，使得定义4成立,根据引理1，有A～E，故在A和E所对应的栏打√；同理，有AF, AG, AH, BC, BD, BE, BF, BG, B～H, CD, CE, CF, CG, CH, DE, D～F, DG, DH, EF, EG, EH, FG, FH, GH,所以对应的终结一致等价表如图2所示：图2 终结一致等价图根据表1，把终结一致的状态进行归并，作为新的状态，即：{A,E},{B,H},{D,F},{C},{G}为新的状态，根据新的状态，画出对应的有穷自动机如图3所示：图3 新状态下的有穷自动机可以验证，图3和图1所对应的有穷自动机是等价的；那么图3是不是极小的，唯一的与图1等价的有穷自动机呢？回答是肯定的.证明：10(极小性) 假设图3不是图1的极小化有穷自动机，那么根据定义4及引理1，在图3中一定存在终结一致的状态，根据极小化的构造过程，将其归并；事实上，在图3中，归并任何两个状态，将导致与图1所表示的有穷自动机不等价；故图3是图1所对应的极小化有穷自动机；20(唯一性) 假设极小化有穷自动机是不唯一的,根据上述极小化有穷自动机的构造过程，也就是说至少还存在状态对{p,q},在存在某个串ω的情况下，使得δ*(p,ω)和δ*(q,ω)恰有一个被接受,即状态p和q不是终结一致的,但根据上述构造过程，不可能出现这种情况，因为，上述构造过程实质上是一个满射，不会漏掉不是终结一致的状态p和q.那么这种情况可能出现在图3中，根据引理1，终结一致关系R是等价关系，则必然导致图3中的某个状态归并，这与图3是极小化有穷自动机相矛盾；所以图3是唯一的；证毕.3 正则语言的代数判定方法定义5[9]：已知B⊆Σ*，由B定义Σ*上的一个二元关系～B，对x，y∈Σ*；x～By⟺∀z∈Σ*，xz与yz是B一致的；即：∀z∈Σ*，xz∈B且yz∈B或xz∉B且yz∉B，x与y是B一致的.可以验证，～B是Σ*上的一个等价关系.定义6 (商集合)：Σ*/～B={[x]|x∈Σ*}，其中[x]表示x所在的等价类对应的状态. 定理1(正则语言的代数判定定理)：给定B⊆Σ*，由B诱导出等价关系～B，则B 是正则语言⟺Σ*/～B有限.证明：(⟺)假定B是正则语言，则存在一台有穷自动机M=(Q, Σ,δ ,q0 ，F )，不妨假定M是一台极小化自动机，对每一个q∈Q，定义xq∈Σ*，δ*(q0，xq)=q；记Q={q1，q2，…，qn}，对应定义xq1，xq2，…，xqn；由于B=L(M)，对于任何x∈Σ*，若δ*(q0，x)=q，则x～Bxq；即：∀x∈Σ*，存在qi∈Q，使得x～Bxqi，由n有限，则Σ*/～B有限，即：|Σ*/～B|≤n；(⟺)设有一台DFA M=(Q, Σ,δ ,q0 ，F )，Σ*/～B有限，令Q=Σ*/～B,q0=[ε]，F={[x]| x∈B},δ([x],a)=[xa]；证毕.例如：B={0，00，000，…}=0*，Σ*={0,1}*；由定义5可知：[ε]={ε，0,00,000,…}=0*，[1]={1，10，11，…}；只有两个等价类[ε]和[1].有穷自动机的转换图如图4所示.故：B是正则语言.图4 有穷自动机的转换图我们知道，判断一个语言是正则语言，可以通过正则表达式、自动机或泵引理来判定；我们只给出无穷语言的泵引理，尽管有穷语言也是正则语言，但是因为泵自动生成无穷集合，所以不能按照上面引理，抽出相应的符号串，这个引理对于有穷语言依然成立，但是没什么意义.泵引理中的m要比最长的符号串的长度还大，所以不能够抽出符号串.泵引理是判定正则语言的必要条件，因此使用时，一般先作出假设，即某个语言是正则语言，然后验证满足引理的条件，但使用泵引理是很讲究技巧性的，使用起来往往是不容易的，并且在有些方面也存在不足.为此我们利用自动机中的等价性原则，得出了正则语言的代数判定定理，即通过商集合Σ*/～B的有限性来判定是否为正则语言，使用此定理在某些方面比泵引理更为方便.下面我们通过举例来说明使用正则语言的代数判定定理来判定正则语言：例2：对于语言A={0n1n|n>0},判断其是否是正则语言.证明:10 我们使用泵引理：假设A是正则语言，那么泵引理一定成立.我们不知道m的值，但是不论它取什么值，我们都可以取n=m.因此，子串y一定仅包含a.假设|y|=k.那么，根据泵引理，取i=0获得的符号串就是w0=am-kbm，显然，这个符号串不属于A.这与泵引理矛盾，因此，假设不成立，A不是正则语言.20 我们使用代数判定定理：假设m，n是正整数,当m<n时，0m1n∉A或者是含有子串10的串也不属于A.根据定义5、定义6及定理1，所有这样的串属于～B的同一个等价类；同时我们注意到，对于0m和0n，当m≠n时，它们不在同一个关于～B的等价类中，这样我们得到关于～B的无穷多个等价类，因此Σ*/～B无限.所以,语言A不是正则语言.证毕.例3：证明语言L={anbl|n≠l}不是正则语言.证明：10 我们使用泵引理：假设A是正则语言，那么泵引理一定成立.这里我们需要灵活的使用泵引理，选择具有n=l+1或n=l+2的符号串都不行，因为总会找到一种分解方式，使我们无法抽出不属于该语言的符号串.我们必须更有创造力才行.我们令n=m！，l=(m+1)！.如果选出长度k<n的y，我们抽取i次，得到具有m！+(i-1)k=(m+1)！，就可以推出和泵引理矛盾的结论.这个等式总是有可能成立的，因为并且k≤m.等式右侧是整数，因此我们成功的推出和泵引理相矛盾；由此，我们看出，使用泵引理是需要一定技巧的，这给我们的使用带来困难.20 我们使用代数判定定理：注意到，根据定义5、定义6及定理1，an和am，当m≠n时，它们不在同一个关于～B的等价类中，这样我们得到关于～B的无穷多个等价类，因此Σ*/～B无限.所以,语言L不是正则语言.证毕.通过上面的例子可以看出，使用正则语言的代数判定定理比使用泵引理更为简单.4 结语综上所述，我们通过定义等价关系，对有穷自动机的状态进行压缩，构造出与之等价的极小化有穷自动机，提出了一整套构造极小化自动机的方法.同时，引入了商集合Σ*/～B的概念，通过Σ*/～B的有限性，来判定一个语言是否是正则语言，这将大大简化了我们判定正则语言的步骤.下一步的任务是，我们争取总结出上下文无关语言的相关理论，形成一套比较完整的有关形式化语言判定的理论体系. [参考文献]【相关文献】[1]韩光辉.有限自动机的最小化理论[J].江汉大学学报, 2005,33(4): 14-16.[2]秦永彬,许道云. 有穷自动机中的等价性与等价归并算法[J].济南大学学报, 2006，(4).[3]Peter Linz. An Introduction to Formal Languages and Automata[M]. China Machine Press,2004.[4]Rabin M O,Scott D.Finite automata and their decision problems[J].IBM J Res Develop,1959，3:114-125.[5]Michael Sipser. Introduction to the Theory of Computation Second Edition[M].China Machine Press,2007.[6]SYu, G Rozenberg,A Salomaa.Handbook of Formal Languages[J].SpringerBerlin,1997(1):41-110.[7]叶瑞芬,沈百英.关于正则语言的泵引理[J].华东理工大学学报,1994,20(5):654-656.[8]John E.Hopcroft Rajeev Movwani Jeffrey D.Ullman. Introduction to Automata Theory,Languages,and Computation[M].China Machine Press,2007.[9]蒋宗礼,姜守旭.形式语言与自动机[M].北京：清华大学出版社,2003.。