一. 异面直线所成角的求法
1、正确理解概念
(1)在异面直线所成角的定义中,空间中的点O 是任意选取的,异面直线a 和b 所成角的大小,与点O 的位置无关。
(2)异面直线所成角的取值范围是(0°,]
90? 2、熟练掌握求法
(1)求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解,整个求解过程可概括为:一作二证三计算。
(2)求异面直线所成角的步骤:
①选择适当的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊点。 ②求相交直线所成的角,通常是在相应的三角形中进行计算。
③因为异面直线所成的角θ的范围是0°<θ≤90°,所以在三角形中求的角为钝角时,应取它的补角作为异面直线所成的角。
3、“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。
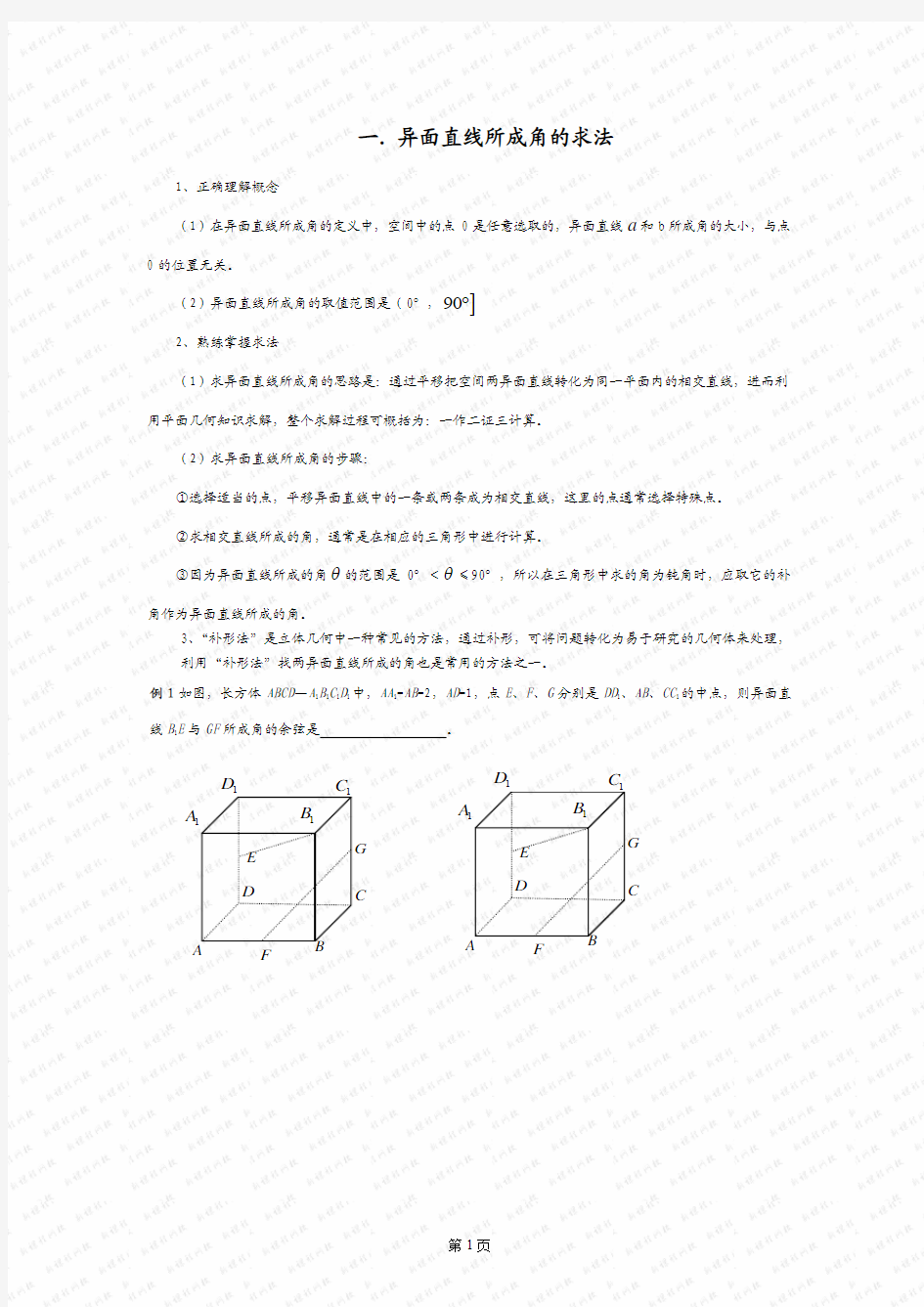
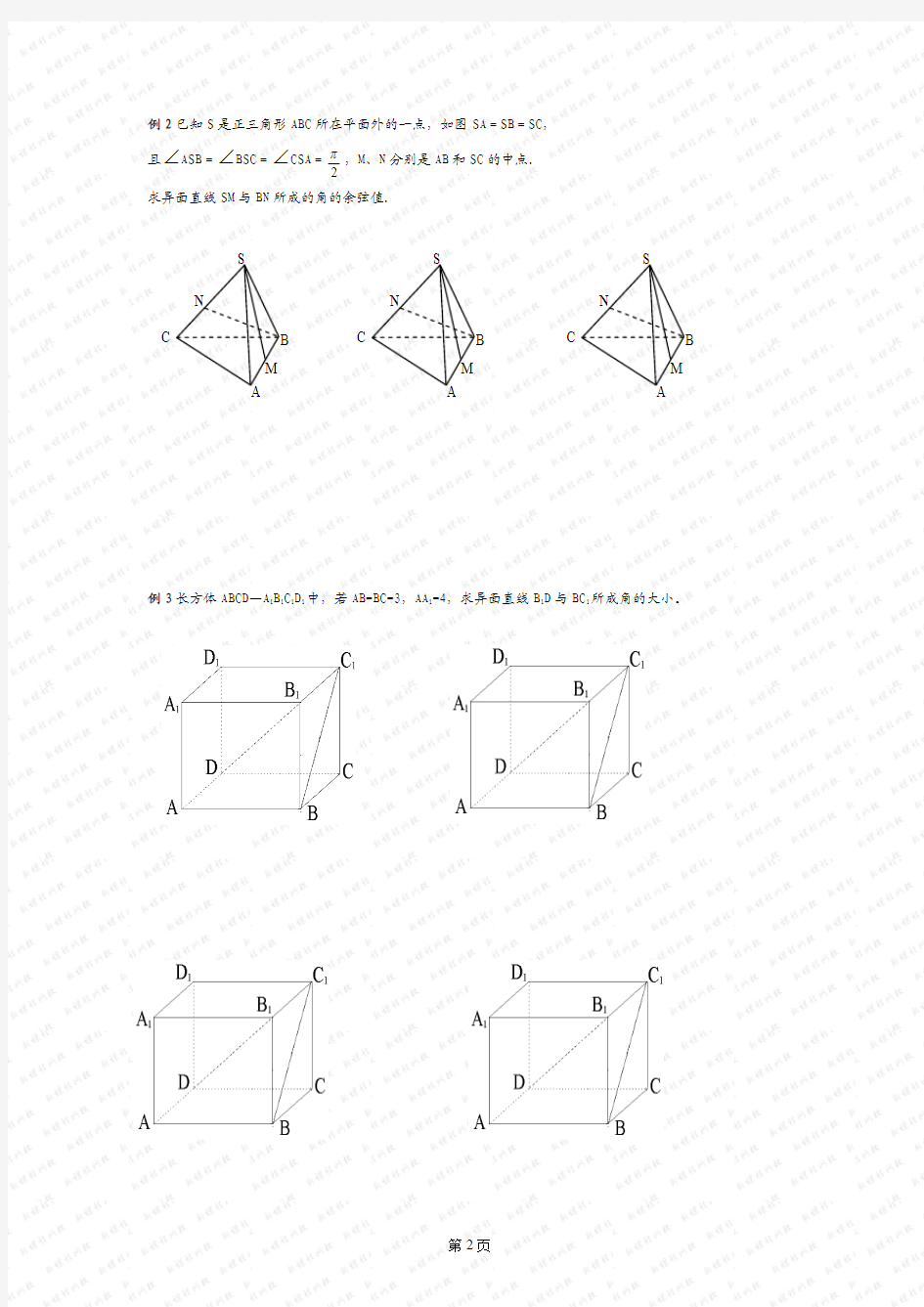
例1如图,长方体ABCD —A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点E 、F 、G 分别是DD 1、AB 、CC 1的中点,则异面直线B 1E 与GF 所成角的余弦是 。
E
F
1
A 1
B 1
C 1
D A
B
C D
G
E
F
1
A 1
B 1
C 1
D A
B
C
D
G
例2已知S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC , 且∠ASB =∠BSC =∠CSA =
2
π
,M 、N 分别是AB 和SC 的中点. 求异面直线SM 与BN 所成的角的余弦值.
例3长方体ABCD —A 1B 1C 1D 1中,若AB=BC=3,AA 1=4,求异面直线B 1D 与BC 1所成角的大小。
B M A
N
C S
B M A
N
C
S
B M A
N
C
S
例4如图,PA ⊥平面ABC ,90ACB ∠=?且PA AC BC a ===,则异面直线PB 与AC 所成角
的正切值等于_____.
练习:
1.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( )
3
1032()
()
()
()
2
10
5
5
A B C D
2.如图,A 1B 1C 1—ABC 是直三棱柱(三侧面为矩形),∠BCA=90°,点D 1、F 1 分别是A 1B 1、A 1C
1BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是
( ) 3013015()
()
()
()
10
2
15
10
A B C D 3.正方体ABCD —A 1B 1C 1D 1中,直线BC 1与AC
(A)相交且垂直 (B)相交但不垂直 (C)异面且垂直 (D)异面但不垂直 4.设a 、b 、c 是空间中的三条直线,下面给出四个命题:
①如果a ⊥b 、b ⊥c ,则a ∥c ;
②如果a 和b 相交,b 和c 相交,则a 和c 也相交;
③如果a 、b 是异面直线,c 、b 是异面直线,则a 、c 也是异面直线; ④如果a 和b 共面,b 和c 共面,则a 和
c
(第2题)
F 1 A
B
C D 1 C 1
A 1
B 1
B
1
(第1题)
A 1
A
B C 1
D 1
C
D M
N
N M
F
E
D
C
B A
( )
(A)4 (B)3 (C)2 (D)1 (E)0 5.如果直线l 和n 是异面直线,那么和直线l 、n 都垂直的直线 (A)不一定存在 (B)总共只有一条 (C)总共可能有一条,也可能有两条 (D)
6.如图,四面体SABC 的各棱长都相等,如果E 、F 分别为SC 、AB 的中点,那么异面直线EF 与SA 所成的角等于
(A)90° (B)60° (C)45° (D)30°
7.右图是正方体的平面展开图,在这个正方体中, ① BM 与ED 平行; ②CN 与BE 是异面直线; ③CN 与BM 成
60角;④DM 与BN 垂直.
以上四个命题中,正确命题的序号是 ( ) (A )① ② ③ (B )② ④ (C )③ ④ (D )② ③ ④
8.如图,四面体ABCD 中,AC ⊥BD,且AC =4,BD =3,M 、N 分别是AB 、CD 的中点,则求MN 和BD 所成角的
正切值为 。
9.异面直线a 、b 成60°,过空间一点P 的直线c 与a 、b 成角都为60°,则这样的直线c 有 条。 10.异面直线a 、b 成60°,直线c ⊥a ,则直线b 与c 所成的角的范围为 ( ) (A )[30°,90°] (B )[60°,90°] (C )[30°,60°] (D )[60°,120°]
11.如图,正三棱柱的九条棱都相等,三个侧面都是正方形,M 、N 分别是BC 和A 1C 1MN 与AB 1所
成角的余弦值。
12.如图,四面体ABCD 中,E 为AD 中点,若AC =CD =DA =8,AB =BD =5,BC =7,求BE 与AC 所成角的余弦值。
F
A
B C
E S (第6题)
A B C
D
M (第8题)
N
4 3 8
A B
C
D
E
(第12题)
7
8
5
4
4
5 (第11题)
M
A
B
C
N
C 1
A 1
B 1
二.共面、共线、共点问题
共点问题:
证明线共点,就是要证明这些直线都过其中两条直线的交点.解决此类问题的一般方法是:先证其中两条直线交于一点,再证该点也在其他直线上. 共线问题:
证明点共线,常常采用以下两种方法:①转化为证明这些点是某两个平面的公共点,然后根据公理3证得这些点都在这两个平面的交线上;②证明多点共线问题时,通常是过其中两点作一直线,然后证明其他的点都在这条直线上. 共面问题:
证明空间的点、线共面问题,通常采用以下两种方法:①根据已知条件先确定一个平面,再证明其他点或直线也在这个平面内;②分别过某些点或直线作两个平面,证明这两个平面重合.
1.如图所示,在正方体ABCD —A 1B 1C 1D 1中,E 为AB 中点,F 为A 1A 的中点. 求证:(1)E 、C 、D 1、F 四点共面;(2)CE 、D 1F 、DA 三线共点。
2.如图,∥,,,,求证:、、AB CD AB B CD D AC E B E ααα===D 三点共线。
练习:
1. 共点的四条直线最多能确定 个平面。
2. 空间四点中,若任意三点不共线,那么经过三点的平面有 个。
3. 已知平面
αβαβ 平面,点、,点且,=∈∈?=l A B C C l AB l R ,设过A 、B 、C 三
点的平面为
γ
,则
βγ
是( )
A. 直线AC
B. 直线BC
C. 直线CR
D. 以上全错
4. 已知△ABC 三边AB 、BC 、CA 分别交平面α于P 、Q 、R ,求证:P 、Q 、R 共线。
A B
C D A 1
B 1
C 1
D 1 A
B C
D P
Q
O
A B C D A 1
B 1
C 1
D 1 M N
A B C D
A 1
B 1
C 1
D 1
M N
E F
A B
C D A 1
B 1
C 1
D 1
E F
G 5. 如果△ABC 和△A 1B 1C 1不在同一平面内,且AA 1、BB 1、CC 1两两相交,求证:三直线AA 1、BB 1、CC 1交于一
点。
三.平行问题
1、“线//线”的证明: (1)平行四边形法: 如图,在正方体1111ABCD A B C D -中, 由11AB DC D C ,
得四边形11ABC D 为平行四边形,于是11//BC AD ;
(2)中位线法:如图,四棱锥的底面ABCD 为平行四边形,
点Q 是PC 的中点,则由OQ 是△PAC 的中位线,得到OQ//PA ;
(3)“线//面”平行法:如图,若11//B C 平面ABCD,
过11B C 的平面交平面ABCD 于MN,则11//B C MN ;
(4)“面//面”法:如图,若平面1111//A B C D 平面ABCD,
平面α与平面
1111A B C D 、平面ABCD 分别交于EF 、MN,
则有EF // MN;
(5)“平行线分线段成比例定理的推论”:
平行于三角形一边的直线截其它两边(或两边的延长线), 所得的对应线段成比例。 如图,在正方体
1111ABCD A B C D -中,E ,F 分别为面对角
A B C
D P
Q
O
A B C D A 1
B 1
C 1
D 1 M N
A
B C D A 1
B 1
C 1
D 1
M
N
A
B
C D
A B`
C D E F A
B
C D A
B`
C
D E
F
线D 1B 1,A 1B 上的动点,且D 1E= A 1F ,则
111,D E A F
EB FB
= 111D E A E
EB EG
=
又
,故11A E A F EG FB =,所以EF//GB 。
2、“线//面”的证明: (1)“线//线”法:
如图,Q 为PC 的中点,则//OQ AP ,所以//OQ 平面PAD ;
(2)“面//面”法: 如图,若
1111//A B C D 平面ABCD,直线MN 在平面1111A B C D ,
则MN //平面ABCD ; 3、“面//面”的证明:
“线//面”法:如图,在平面
1111A B C D 上找到两条相交直线
MN 、1MC 均平行于平面ABCD,则有平面1111A B C D //平面ABCD ;
例题分析:
1.αα//,//b a ,则a 与b 的位置关系( )
A .平行
B .异面
C .相交
D .以上情况均有可能
2.a ,b 是两条不相交的直线,则过直线b 且平行于a 的平面( )
A .有且只有一个
B .至少有一个
C .至多有一个
D .以上答案都不对
3、已知正方体ABCD-A`B`C`D`中,E ,F 分别是A`B`,B`C`的中点。求证:EF ∥面AD`C 。
A 11
E D 1
C 1
B 1
D
C
B
A
A 11
E
D 1
C 1
B 1
D
C
B
A
4、如图,已知矩形ABCD 所在平面外一点P ,E 、F 分别是AB, PC 的中点 , 求证:EF ∥平面P AD ; 5. 如图,四棱锥P -ABCD 的底面是正方形,点E 、F 分别为棱AB 、PD 的中点。 求证:AF ∥平面PCE ;
6、如图,在正方体1111ABCD A BC D -中,E 是1AA 的中点,求证:1//AC 平面
BDE 。
7. 如图,在底面为平行四边形的四棱锥P ABCD -
中,点E 是PD 的中点. 求证:PB ∥平面AEC .
E F
B
A
C
D
P C B
D A P E
F
C
B D
A P
E
F
E
F
B A
C
D
P
B 1
A 1
D 1C 1
B
A D C
P Q
_ P
_ B
_ A
_ N
_ M _ E
_ D
_ C _ P
_ B
_ A
_ N
_ M _ E
_ D
_ C _ P
_ B
_ A
_ N
_ M _ E
_ D
_ C B 1
A 1
D 1
C 1
B
A D
C
P
Q
8.已知正四棱锥P —ABCD ,M 、N 分别是P A 、BD 上的点,且PM ∶MA =BN ∶ND =5∶8,求证:直线MN ∥平面PBC ;
9、正方体ABCD-A 1B 1C 1D 1,P 、Q 分别是正方形AA 1D 1D 和A 1B 1C 1D 1的中心。求证PQ ∥平面DD 1C 1C ;;
10.已知正三棱柱ABC -A 1B 1C 1,D 为AC 中点。求证:直线AB 1∥平面C 1DB ;
11.如图:已知A 1B 1C 1-ABC 是正三棱柱,D 是AC 中点.证明:AB 1∥平面DBC 1;
A 1
C 1
C B
A
B 1 D
B C A
D A 1 B 1
C 1
A 1
C 1
C
B
A
B 1 D
B C A D A 1 B 1
C 1
12.如图,在斜三棱柱
111C B A ABC -中,
E 、
F 分别是棱A A C B 111、的中点,证明E A 1∥平面FC B 1
13.如图,在四棱锥ABCD
P -中,四边形ABCD 是平行四边形,E 是PC 的三等分点,F 是PB 的中点,
求证:AF ∥面BDE ;
14、如图PA ⊥平面ABCD ,四边形ABCD 是矩形,E 、F 分别是AB ,PD 的中点。求证:AF//平面PCE ;
F E
C 1
B 1
A 1C
B
A
F
E
P
D
C
B
A
F E
C 1
B 1
A 1C
B
A
F
E
P
D
C
B
A
G
F
P
A
E
B
C
H
15.如图,平面EFGH 分别平行于AB CD ,,H G F E ,,,分别在AD AC BC BD ,,,上,且
a CD =,
b AB =,AB CD ⊥.(1)求证:EFGH 是矩形;(2)求当点E 在什么位置时,EFGH
的面积最大.
16.如图,在四棱锥S ABCD -中,2SA AB ==,22SB SD ==,底面 ABCD 是菱形,且60ABC ∠=?,E 为CD 的中点.侧棱SB 上是否存在点F , 使得//CF 平面SAE ?并证明你的结论.
S
A
B
C
D
E
17.如图,四棱锥P —ABCD 中,底面ABCD 为梯形,AD//BC ,P A =AB =BC =
.2
1
AD 在棱PD 上是否存在一点E ,使CE ∥平面P AB ?若存在,请确定E 点的位置;若不存在,请说明理由.
18.如图,在长方体1111ABCD A BC D 中,
E 为1CC 的中点. (1)求证:1//AC 平面BDE ;
(2)判断并证明,点F 在棱1DD 上什么位置时,平面1//AC F 平面BDE .
异面直线所成的角求法 总结加分析 TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】
异面直线所成的角 一、平移法: 常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。 直接平移法 1.在空间四边形ABCD 中,AD =BC =2,E ,F 分别为AB 、CD 的中点,EF = 3 ,求AD 、BC 所成角的大小. 解:设BD 的中点G ,连接FG ,EG 。在△EFG 中 EF = 3 FG =EG =1 ∴∠EGF=120° ∴AD 与BC 成60°的角。 2.正?ABC 的边长为a ,S 为?ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分别是SC 和AB 的中点.求异面直线SA 和EF 所成角. 答案:45° 3.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA = 2 π ,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值. 证明:连结CM ,设Q 为CM 的中点,连结QN 则QN∥SM ∴∠QNB 是SM 与BN 所成的角或其补角
A B C D A 1 B 1 C 1 D 1 E F 连结BQ ,设SC =a ,在△BQN 中 BN = a 25 NQ =2 1SM = 4 2 a BQ = a 4 14 ∴COS∠QNB= 5 10 2222= ?-+NQ BN BQ NQ BN 4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA=90°,M 、N 分别是A 1B 1和A 1C 1的中点,若 BC =CA =CC 1,求BM 与AN 所成的角. 解:连接MN ,作NG∥BM 交BC 于G ,连接AG , 易证∠GNA 就是BM 与AN 所成的角. 设:BC =CA =CC 1=2,则AG =AN = 5 ,GN =BM = 6 , cos∠GNA= 10 30 5 62556= ??-+。 5.如图,在正方体1111D C B A ABCD -中,E 、F 分别是1BB 、CD 的中点.求AE 与F D 1所 成的角。 证明:取AB 中点G ,连结A 1G ,FG , 因为F 是CD 的中点,所以GF ∥AD , 又A 1D 1∥AD ,所以GF ∥A 1D 1, 故四边形GFD 1A 1是平行四边形,A 1G∥D 1F 。 设A 1G 与AE 相交于H ,则∠A 1HA 是AE 与D 1F 所成的角。
A B C S E F A B C D D 1 C 1 B 1 A 1 M N N M F E D C B A 高二数学练习(二) 一、选择题 1.分别和两条异面直线都相交的两条直线一定是 ( ) (A )不平行的直线 (B )不相交的直线 (C )相交直线或平行直线 (D )既不相交又不平行直线 2.已知EF 是异面直线a 、b 的共垂线,直线l ∥EF ,则l 与a 、b 交点的个数为 ( ) (A )0 (B )1 (C )0或1 (D )0,1或2 3.两条异面直线的距离是 ( ) (A )和两条异面直线都垂直相交的直线 (B )和两条异面直线都垂直的直线 (C )它们的公垂线夹在垂足间的线段的长 (D )两条直线上任意两点间的距离 4.设a, b, c 是空间的三条直线,下面给出三个命题:① 如果a, b 是异面直线,b, c 是异面直线,则a, c 是异面直线;② 如果a, b 相交,b, c 也相交,则a, c 相交;③ 如果a, b 共面,b, c 也共面,则a, c 共面.上述命题中,真命题的个数是 ( ) (A )3个 (B )2个 (C )1个 (D )0个 5.异面直线a 、b 成60°,直线c ⊥a ,则直线b 与c 所成的角的范围为 ( ) (A )[30°,90°] (B )[60°,90°] (C )[30°,60°] (D )[60°,120°] 6.如图:正四面体S -ABC 中,如果E ,F 分别是SC ,AB 的中点,那么异面直线EF 与SA 所成的角等于 ( ) (A )90°(B )45°(C )60°(D )30° 7.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 和N 分别为A 1B 1和的 中点,那么直线AM 与CN 所成角的余弦值是 ( ) (A )23(B )1010(C )5 3(D )54 8.右图是正方体的平面展开图,在这个正方体中, ①BM 与ED 平行; ②CN 与BE 是异面直线; ②③CN 与BM 成ο60角;④DM 与BN 垂直. 以上四个命题中,正确命题的序号是 ( ) (A )①②③ (B )②④ (C )③④ (D )②③④ 9.梯形ABCD 中AB//CD ,AB ?平面α,CD ?平面α,则直线CD 与平面α内的直线的位置关系只能是 ( )(A )平行 (B )平行和异面 (C )平行和相交 (D )异面和相交 10.在空间四边形ABCD 中,E 、F 分别为AB 、AD 上的点,且AE :EF =AF :FD =1 :4,又H 、G 分别为BC 、CD 的中点,则 ( ) (A )BD//平面EFGH 且EFGH 是矩形 (B )EF//平面BCD 且EFGH 是梯形 (C )HG//平面ABD 且EFGH 是菱形 (D )HE//平面ADC 且EFGH 是平行四边形 二、填空题 11.如图,在正三角形ABC 中,D 、E 、F G ,H ,I ,J 分别为AF ,AD ,BE ,DE DE ,EF ,DF 折成三棱锥以后,GH 与IJ 12.在四面体ABCD 中,若AC 与BD 成60°角,且AC =BD =a ,则连接AB 、BC 、CD 、DA 的中点的四边形面积为 .
如何求异面直线所成的角 立体几何在中学数学中有着重要的地位,求异面直线所成的角是其中重的内容之一,也是高考的热点,求异面直线所成的角常分为三个步骤:作→证→求。其中“作”是关键,那么如何作两条异面直线所成的角呢?本文就如何求异面直线所成的角提出了最常见的几种处理方法。 Ⅰ、用平移法作两条异面直线所成的角 一、端点平移法 例1、在直三棱柱111C B A ABC -中,090CBA ∠=,点D ,F 分别是11A C ,11A B 的中点,若 1AB BC CC ==,求CD 与AF 所成的角的余弦值。 解:取BC 的中点E ,连结EF ,DF , //DF EC Q 且DF EC = ∴四边形DFEC 为平行四边形 //EF DC ∴ EFA ∴∠(或它的补角)为CD 与AF 所成的角。 设2AB =, 则EF = AF = EA = 故2222EF FA EA EFA EF FA +-∠==g arccos 10 EFA ∴∠= 二、中点平移法 例2、在正四面体ABCD 中, M ,N 分别是BC ,AD 的中点,求AM 与CN 所成的角的余弦值。 解:连结MD ,取MD 的中点O ,连结NO , Q O 、N 分别MD 、AD 为的中点, ∴NO 为DAM ?的中位线, ∴//NO AM , ONC ∴∠(或它的补角)为AM 与CN 所成的角。 设正四面体ABCD 的棱长为2 ,则有2NO = ,CN = ,2CO =, 故2222 cos 23 NO CN CO ONC NO CN +-∠= =g 2 arccos 3 ONC ∴∠= 1 B D C
异面直线所成的角的求法 法一:平移法 在正方体 ABCD A i B i C i D i 中,求下列各对异面直线所成的角。 恵,求直线AB 与CD 所成的角。 习题1?在空间四边形ABCD 中,AD = BC = 2, E, F 分别为AB 、CD 的中点,EF =为, 求AD 、BC 所成角的大小. 例1: (1) AA 1 与 BC ; (2) DD 1 与 AB ; (3) A i B 与 A C 。 法二: 例2: 求直线AB 与MN 所成的角。 中位线 在空间四边形 ABCD 中,AB = CD ,且AB CD ,点M 、N 分别为BC 、AD 的中点, 变式:在空间四边形 ABCD 中,点M 、N 分别为 BC 、AD 的中点,AB = CD = 2,且 MN =
正 ABC 的边长为a , S 为 ABC 所在平面外的一点,SA = SB = SC = a, E , F 分别 是SC 和AB 的中点.求异面直线 SA 和EF 所成角. S 是正三角形 ABC 所在平面外的一点,如图 SA = SB = SC ,且 ASB = BSC = CSA = - , M 、N 分别是AB 和SC 的中点.求异面直线 SM 与BN 所成的角的 余弦值. 如图,在直三棱柱 ABC — A i B i C i 中,/ BCA = 90° M 、N 分别是 A i B i 和A i C i 的中 点, 若BC = CA = CC i ,求BM 与AN 所成的角. 5.如图1 — 28的正方体中,E 是A D 勺中点 (1) 图中哪些棱所在的直线与直线 BA 成异面直线? (2) 求直线 (3) 求直线 (4) 求直线 2. 3. 4 . BA 和CC 所成的角的大小; AE 和CC 所成的角的正切值; AE 和BA 所成的角的余弦值 B A (图 1— 28)
1.如图,在正方体1111ABCD A B C D -中,异面直线1A D 与1BC 所成的角为 A .30° B .45° C .60° D .90° 【答案】D 【解析】 试题分析:如图所示,连接B 1C , 则B 1C ∥A 1D ,B 1C ⊥BC 1,∴A 1D ⊥BC 1,∴A 1D 与BC 1所成的角为90°. 故选:D . 考点:异面直线及其所成的角 2.已知平行六面体ABCD - A 1B 1C 1D 1中,底面ABCD 是边长为1的正方形,AA 1=2,∠A 1AB =∠A 1AD =120°,则异面直线AC 1与A 1D 所成角的余弦值( ) A . 3 .7 C .5 D .5 【答案】B 【解析】 试题分析:设向量 1,,AB a AD b AA c === ,则11 ,AC a b c AD b c =++=- ,11AC A D ∴== 111111cos ,AC A D AC A D AC A D ?<>== 。 考点:空间向量的集合运算及数量积运算。 3.正方体1111ABCD A BC D -中,,,,E F G H 分别是1AA , AB ,1BB ,11B C 的中点,则直线EF 与GH 所成的角是( ) A .30° B .45° C .60° D .90°
【答案】C 【解析】 试题分析:由三角形中位线可知11,EF A B GH BC ,所以异面直线所成角为11A BC ∠,大小为60° 考点:异面直线所成角 4.在正方体1111ABCD A BC D -中,E 是11B C 的中点,则异面直线1DC 与BE 所成角的余弦值为( ) A . 5 .5.5 10 - D .5- 【答案】B 【解析】 试题分析:取BC 中点F ,连结1,FD FC ,则1 D CF ∠为异面直线所成角,设边长为2 ,11C F DC DF ∴== 1cos 5 DC F ∴∠= 考点:异面直线所成角 5.如图,正四棱柱ABCD A B C D ''''-中(底面是正方形,侧棱垂直于底面),3AA AB '=,则异面直线A B '与AD '所成角的余弦值为( ) A 、910 B 、45 C 、710 D 、3 5 【答案】A 【解析】 试题分析:连结'BC ,异面直线所成角为''A BC ∠,设1AB = ,在'' A BC ?中 ''''AC A B BC ===''9 cos 10 A BC ∴∠= 考点:异面直线所成角 6.点P 在正方形ABCD 所在平面外,PA ⊥平面ABCD ,AB PA =,则PB 与AC 所 成的角是 A .?60 B .?90 C .?45 D .?30 【答案】A 【解析】 试题分析:作出空间几何体如下图所示:设正方形的边长为2,
异面直线所成的角的两种求法 初学立几的同学,遇到的第一个难点往往便是求异面直线所成的角。难在何处?不会作! 下面介绍两种求法 一.传统求法--------找、作、证、求解。 求异面直线所成的角,关键是平移点的选择及平移面的确定。 平移点的选择:一般在其中一条直线上的特殊位置,但有时选在空间适当位置会更简便。 平移面的确定:一般是过两异面直线中某一条直线的一个平面,有时还要根据平面基本性质将直观图中的部分平面进行必要的伸展,有时还用“补形”的办法寻找平移面。 例1 设空间四边形ABCD ,E 、F 、G 、H 分别是AC 、BC 、DB 、DA 的中点,若AB =122,CD =4 2,且四边形EFGH 的面积为12 3, 求AB 和CD 所成的角. 解? 由三角形中位线的性质知,HG∥AB,HE∥CD, ∴ ∠EHG 就是异面直线AB 和CD 所成的角. ∵? EFGH 是平行四边形,HG =2 1 AB =62, H G F E D C B A
HE =2 1 ,CD =23, ∴? S EFGH =HG·HE·sin∠EHG=126 sin∠EHG,∴ 12 6sin∠EHG=123. ∴? sin∠EHG= 2 2 ,故∠EHG=45°. ∴? AB 和CD 所成的角为45° 注:本例两异面直线所成角在图中已给,只需指出即可。 例2.点A 是BCD 所在平面外一点,AD=BC ,E 、F 分别是AB 、CD 的中点,且EF=2 2 AD ,求异面直线AD 和BC 所成的角。(如图) 解:设G 是AC 中点,连接DG 、FG 。因D 、F 分别是AB 、CD 中点,故EG∥BC 且EG= 2 1 BC ,FG∥AD,且FG=2 1 AD ,由异面直线所成角定义可知EG 与FG 所成锐角或直角为异面直线AD 、BC 所成角,即∠EGF 为 所求。由BC=AD 知EG=GF=2 1 AD ,又EF=AD ,由余弦定理可得cos∠EGF=0,即∠EGF=90°。 注:本题的平移点是AC 中点G ,按定义过G 分别作出了两条异面直线的平行线,然后在△EFG 中求角。通常在出现线段中点时,常取另一线段中点,以构成中位线,既可用平行关系,又可用线段的倍半关系。 例3.已知空间四边形ABCD 中,AB=BC=CD=DA=DB=AC,M 、N 分别为BC 、AD 的中点。 求:AM 与CN 所成的角的余弦值; A B C G F E D
一. 异面直线所成角的求法 1、正确理解概念 (1)在异面直线所成角的定义中,空间中的点O 是任意选取的,异面直线a 和b 所成角的大小,与点O 的位置无关。 (2)异面直线所成角的取值范围是(0°,] 90? 2、熟练掌握求法 (1)求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几何知识求解,整个求解过程可概括为:一作二证三计算。 (2)求异面直线所成角的步骤: ①选择适当的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊点。 ②求相交直线所成的角,通常是在相应的三角形中进行计算。 ③因为异面直线所成的角θ的范围是0°<θ≤90°,所以在三角形中求的角为钝角时,应取它的补角作为异面直线所成的角。 3、“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。 例1如图,长方体ABCD —A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点E 、F 、G 分别是DD 1、AB 、CC 1的中点,则异面直线B 1E 与GF 所成角的余弦是 。 E F 1 A 1 B 1 C 1 D A B C D G E F 1 A 1 B 1 C 1 D A B C D G
例 2 已知 S 是正三角形ABC所在平面外的一点,如图SA=SB=SC, 且∠ASB=∠BSC=∠CSA= 2 π ,M、N分别是AB和SC的中点. 求异面直线SM与BN所成的角的余弦值. 例3长方体ABCD—A1B1C1D1中,若AB=BC=3,AA1=4,求异面直线B1D与BC1所成角的大小。 B M A N C S B M A N C S B M A N C S
异面直线及其所成的角填空题基础题1.doc 参考答案与试题解析 一.填空题(共30小题) 1.(2015?松江区一模)在正四棱柱ABCD﹣A1B1C1D1中,BC1与平面ABCD所成的角为60°,则BC1与AC所成的角为arccos(结果用反三角函数表示). 来源:2015年上海市松江区高考数学一模试卷(文科) 难度:0.80 考点:异面直线及其所成的角. 专题:计算题;空间位置关系与距离;空间角. 分析:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.由于CC1⊥平面ABCD,则∠C1BC=60°,设正四棱柱ABCD﹣A1B1C1D1中的底面边长为a,侧棱长为b,即b=a,再由余弦定理,即可得到. 解答:解:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.设正四棱柱ABCD﹣A1B1C1D1中的底面边长为a,侧棱长为b, 则由于CC1⊥平面ABCD,则∠C1BC=60°,
即有tan60°=,即b=a, 在△BA1C1中,BC1=BA1==2a,A1C1=a, cos∠BC1A1==. 则BC1与AC所成的角为arccos. 故答案为:arccos. 点评:本题考查空间的直线和平面所成的角,异面直线所成的角的求法,考查运算能力,属于基础题. 2.(2015?浦东新区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为arccos. 来源:2015年上海市浦东新区高考数学一模试卷 难度:0.80 考点:异面直线及其所成的角.
异面直线所成的角 一、平移法: 常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。 直接平移法 1.在空间四边形ABCD 中,AD =BC =2,E ,F 分别为AB 、CD 的中点,EF =3,求AD 、BC 所成角的大小. 解:设BD 的中点G ,连接FG ,EG 。在△EFG 中 EF =3 FG =EG =1 ∴∠EGF=120° ∴AD 与BC 成60°的角。 2.正?ABC 的边长为a ,S 为?ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分别是SC 和 AB 的中点.求异面直线SA 和EF 所成角. 答案:45° 3.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2 π ,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值. 证明:连结CM ,设Q 为CM 的中点,连结QN 则QN∥SM ∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ,设SC =a ,在△BQN 中 BN = a 25 NQ =2 1SM = 4 2a BQ = a 4 14 ∴COS∠QNB=5 10 2222= ?-+NQ BN BQ NQ BN 4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA=90°,M 、N 分别是A 1B 1和A 1C 1的中点,若BC = CA =CC 1,求BM 与AN 所成的角. 解:连接MN ,作NG∥BM 交BC 于G ,连接AG , 易证∠GNA 就是BM 与AN 所成的角. 设:BC =CA =CC 1=2,则AG =AN =5,GN =BM =6 , cos∠GNA= 10 305 62556=??-+。 B M A N C S
3 3 如何求异面直线所成的角 立体几何在中学数学中有着重要的地位,求异面直线所成的角是其中重的内容之一,也 是高考的热点,求异面直线所成的角常分为三个步骤:作 证 求。其中“作”是关键,那 么如何作两条异面直线所成的角呢?本文就如何求异面直线所成的角提出了最常见的几种处 理方法。 I 、用平移法作两条异面直线所成的角 、端点平移法 例1、在直三棱柱 ABC A 1B 1C 1中, CBA 900 ,点D , F 分别是 AQ , A ,B i 的中点,若 AB BC CC i ,求CD 与AF 所成的角的余弦值。 解:取BC 的中点E ,连结EF ,DF , QDF//EC 且 DF EC 四边形DFEC 为平行四边形 EF // DC EFA (或它的补角)为CD 与AF 所成的角。 设 AB 2,则 EF 76,AF 730 arccos 10 、中点平移法 例2、在正四面体ABCD 中, 解:连结MD ,取MD 的中点0,连结NO , Q O 、N 分别MD 、AD 为的中点, NO 为DAM 的中位线, NO//AM , ONC (或它的补角)为AM 与CN 所成的角。 広 J 7 设正四面体ABCD 的棱长为2,则有NO —,CN 73, CO — 2 2 皿 NO 2 CN 2 CO 2 故 cos ONC ----------------- 2NOgCN 2 ONC arccos-故EFA EF 2 FA 2 EA 2 2EFgFA 730 10 75,EA 45 M , N 分别是BC, AD 的中点,求AM 与CN 所成的角的余弦值。 EFA A l A D
异面直线及其夹角 教学目标:: 知识目标:1、掌握异面直线的概念,会画空间两条异面直线的图形, 会判断两直线是否为异面直线。 2、掌握异面直线所成角的概念及异面直线垂直的概念,能 求出一些较简单的异面直线所成的角 能力目标:在问题解决过程中,培养学生的实验观察能力、空间想能 力象、逻辑思维能力、分析问题、解决问题的能力。 教学重点、难点: 重点:异面直线所成角的概念, 能求出一些较简单的异面直线所成的角。 难点:异面直线所成角的定义, 如何作出异面直线所成的角。 教学准备:多媒体课件 教学课时:二课时 教学过程: 第一课时 一、导入新课 1.引导学生观察立交桥上的车辆为什么能畅通无阻? 两条道路所在的直线不在同一平面内。它们既不平行也不相交,这样的两条直线有什么特点呢? 2.请学生做一个小实验,拿两支笔在空间中你能摆出几种位置关系? 有3种:平行、相交、不平行也不相交的两条直线(对于这样的两条直线以前我们没有学习过,那么它们之间有什么特点和关系呢?)。(板书课题) 二、新课讲解 前面我们学习过平行线,相交线,它们是同一平面内两条直线的位置关系,通过前面的实验和动画的观察,在空间还存在另一种两条直线的位置关系(不平行也不相交)。我们给它一个新的名称“异面直线”。 1 异面直线的定义:不同在任何.. 一个平面内的两条直线叫异面直线。 2.两条异面直线的性质:既不平行,也不相交。(如前面我们所说的两个例子,同学们还能找出具有这种性质的两条直线吗?)找两位学生说说他们所找的情况。 3.空间两条异面直线的画法。 如何用图形来表示两条异面直线,通常怎么样画?(老师板演,同时让学生总结其特点) 这三种表示方法有一个共同的特点,就是用平面来衬托,离开平面的衬托,不同在任何一个平面的特征难以体现。(今后我们也可以不用平面来衬托) 同学们想一想如果这样表示两条异面直线行吗?为什么? a b a b b a
异面直线所成角的几种求法 异面直线所成角的大小,是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的。因此,通常我们要求异面直线所成的角会要求学生通过平移直线,形成角,然后在某个三角形中求出角的方法来得到异面直线所成角的大小。在这一方法中,平移直线是求异面直线所成角的关键,而如何平移直线要求学生有良好的空间观和作图能力。 一、向量法求异面直线所成的角 例1:如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是相邻两侧面BCC 1B 1及CDD 1C 1的中心。求A 1E 和B 1F 所成的角的大小。 解法一:(作图法)作图关键是平移直线,可平移其中一条直线,也可平移两条直线 到某个点上。作法:连结B 1E ,取B 1E 中点G 及A 1B 1中点H , 连结GH ,有GH//A 1E 。过F 作CD 的平行线RS ,分别交CC 1、DD 1于点R 、S ,连结SH ,连结GS 。 由B 1H//C 1D 1//FS ,B 1H=FS ,可得B 1F//SH 。在△GHS 中,设正方体边长为a 。GH=a (作直线GQ//BC 交BB 1于点Q ,46连QH ,可知△GQH 为直角三角形),HS=a (连A 1S ,可知△HA 1S 为直角三角形),2 6GS=a (作直线GP 交BC 于点P ,连PD ,可知四边形GPDS 为直角梯形)。426∴Cos ∠GHS=。6 1所以直线A 1E 与直线B 1F 所成的角的余弦值为。61解法二:(向量法)分析:因为给出的立体图形是一个正方体, 所以可以在空间建立直角坐标系,从而可以利用点的坐标表示出空间中每一个向量,从而可以用 向量的方法来求出两条直线间的夹角。 以B 为原点,BC 为x 轴,BA 为y 轴,BB 1为z 轴,设BC 长度为2。 B A C D F E B 1A 1D 1C 1 G H S R P Q 1
第二节 异面直线所成角的计算 1.定义: 直线a 、b 是异面直线,经过空间一交O ,分别a ?范围: 例1 如图,正方形ABCD 所在平面与正方形ABEF 所在平面成60ο角,求异面直线AD 与BF 所成角的余弦值. 分析:1.求异面直线所成的角常作出所成角的平面图形. 作法有: ①平移法:在异面直线的一条上选择“特殊点”,作另一条直线平行线或利用中位线.②补形法: 把空间图形补成熟悉的几何体, 其目的在于容易发现两条异面直线的关系. 2.解立几计算题要先作出所求的角,并要有严格的推理论证过程,还要有合理的步骤. 小结:求异面直线所成角的方法: 变式一:已知四棱锥ABCD P -中,底面ABCD 是正方形,各侧棱与底面边长相等,求异面直线PD 与AC 所成角的余弦值。 变式二:如图,点M 是正方形ABCD 所在平面外的一点,且MA=MB=MC=MD=AB 2,求异面直线MC 与BD 所成角的余弦值。 例2 设M 、N 是直角梯形ABCD 两腰的中点,DE ⊥AB 于E (如图).现将△ADE 沿DE 折起,使二面角AEB ∠=45°,此时点A 在平面BCDE 内的射影恰为点B ,则M 、N 的连线与AE 所成角的大小等于_________. 例3 空间四边形ABCD 中,对角线8AC =,6BD =,,M N 分别为,AB CD 的中点,且5MN =,求异面直线,AC BD 所成的角。 变式:在空间四边形ABCD 中,4BD =,6AC =,且AC BD ⊥,,M N 分 别为,AB CD 的中点,求MN 及MN 与BD 所成角的正切值。 1、两条直线,与平面α所成的角相等,则直线a ,b 的位置关系是 (A)平行 (B)相交 (C)异面 (D) 以上均有可能. 2、设棱长为1的正方体ABCD-A 1B 1C 1D 1中,M 、N 分别为AA 1和BB 1的中点,则直线CM 和D 1N 所成角的正弦值为 . 3、已知a 、b 是一对异面直线,且a 、b 成60o 角,则在过空间任意点P 的所有直线中,与a 、b 均成60o 角的直线有 条. 4、异面直线a 、b 互相垂直,c 与a 成30o 角,则c 与b 所成角的范围是 . 5、.如图,ABCD 是正方形,PD ⊥平面ABCD,PD=AD,则PA 与BD 所成的角的 度数为 6、 长方体ABCD -A 1B 1C 1D 1中,AB=AA 1=2cm ,AD=1cm , (1)求异面直线A 1C 1与BD 1所成的角的余弦值。 (2)若M 、N 分别是BC 、11C A 的中点,求异面直线M A 1与CN 所成角的余弦值。 A C B D A B M D A C B F E 1 A 1
构造异面直线所成角的几种方法 异面直线所成角的大小,是由空间任意一点分别引它们的平行线所成的锐角(或直角)来定义的.准确选定角的顶点,平移直线构造三角形是解题的重要环节.本文举例归纳几种方法如下,供参考. 一、抓异面直线上的已知点 过一条异面直线上的已知点,引另一条直线的平行线(或作一直线并证明与另一直线平行),往往可以作为构造异面直线所成角的试探目标. 例1(2005年全国高考福建卷)如图,长方体ABCD —A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点E 、F 、G 分别是DD 1、AB 、CC 1的中点,则异面直线A 1E 与GF 所成的角是( ) 二、抓异面直线(或空间图形)上的特殊点 考察异面直线上的已知点不凑效时,抓住特殊点(特别是中点)构造异面直线所成角是一条有效的途径. 例2(2005年全国高考浙江卷)设M 、N 是直角梯形ABCD 两腰的中点,DE ⊥AB 于E (如图).现将△ADE 沿DE 折起,使二面角A -DE -B 为45°,此时点A 在平面BCDE 内的射影恰为点B ,则M 、N 的连线与AE 所成角的大小等于_________. 三、平移(或构造)几何体 有些问题中,整体构造或平移几何体,能简化解题过程. 例3(2005年全国高考天津卷)如图,PA ⊥平面ABC ,90ACB ∠=?且 PA AC BC a ===,则异面直线PB 与AC 所成角的正切值等于_____. 1. 解:连B 1G ,则A 1E ∥B 1G ,知∠B 1G F 就是异面直线A 1E 与GF 所成的角.在 △B 1GF 中,由余弦定理,得 cos B 1GF =2221112B G GF B F B G GF +-= ?=0, 故∠ B 1 G F = ,应选(D). 2评注:本题是过异面直线FG 上的一点G ,作B 1G ,则A 1E ∥B 1G ,知∠B 1G F 就是所求的 角,从而纳入三角形中解决. 解:取AE 中点G, 连结GM 、BG ∵GM ∥ED ,BN ∥ED ,GM =21ED ,BN =2 1 ED . ∴ GM ∥BN ,且GM =BN . ∴BNMG 为平行四边形,∴MN//BG ∵A 的射影为B . ∴AB ⊥面BCDE . P B C A
异面直线所成的角 一.例题与课堂练习 题1.在空间四边形ABCD 中,AD =BC =2,E ,F 分别为AB 、CD 的中点,EF =3 , 求AD 、BC 所成角的大小. 题2.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2 π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值. 题3.正?ABC 的边长为a ,S 为?ABC 所在平面外的一点,SA =SB =SC =a ,E ,F 分 别是SC 和AB 的中点.求异面直线SA 和EF 所成角. 题4.如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA=90°,M 、N 分别是A 1B 1和A 1C 1的中点, 若BC =CA =CC 1,求NM 与AN 所成的角. 题5.如图,在正方体1111D C B A ABCD -中,E 、F 分别是1BB 、CD 的中点. 求AE 与F D 1所成的角。 题6.如图1—28的正方体中,E 是A′D′的中点 (1)图中哪些棱所在的直线与直线BA′成异面直线? (2)求直线BA′和CC′所成的角的大小; (3)求直线AE 和CC′所成的角的正切值; (4)求直线AE 和BA′所成的角的余弦值 【说明】(1)如图1—29,单独画出△A?BF,使图中线段与角的数量关系较直观 图中清楚,使计算更为方便和准确,这是立体几何中常用的重要方法; (2)解法中用余弦定理求cos∠A?BF,其实有更简单方法,请找出简单方法 (3)如果用余弦定理求出角的余弦值为负数,应如何写答案? B M A N C S A C B N M A C B B? (图 1- A? A B C? D? C D F E
- 总 1.如图,在正方体1111ABCD A B C D 中,异面直线1A D 与1BC 所成的角为 A .30 B .45 C .60 D .90 【答案】D 【解析】 试题分析:如图所示,连接B 1C , 则B 1C ∥A 1D ,B 1C ⊥BC 1,∴A 1D ⊥BC 1,∴A 1D 与BC 1所成的角为90°. 故选:D . 考点:异面直线及其所成的角 2.已知平行六面体ABCD - A 1B 1C 1D 1中,底面ABCD 是边长为1的正方形,AA 1=2,∠A 1AB =∠A 1AD =120°,则异面直线AC 1与A 1D 所成角的余弦值( ) A 6 B 14 C 15 D 10【答案】B 【解析】 试题分析:设向量1,,AB a AD b AA c ===,则11,AC a b c A D b c =++=-, 112,7AC A D ∴==, 11111114 cos ,7 AC A D AC A D AC A D ?<>= =。 考点:空间向量的集合运算及数量积运算。 3.正方体1111ABCD A B C D -中,,,,E F G H 分别是1AA ,AB ,1BB ,11B C 的中点,则直线EF 与GH 所成的角是( )
A .30° B .45° C .60° D .90° 【答案】C 【解析】 试题分析:由三角形中位线可知11,EF A B GH BC ,所以异面直线所成角为11A BC ∠, 大小为60° 考点:异面直线所成角 4.在正方体1111ABCD A B C D -中,E 是11B C 的中点,则异面直线1DC 与BE 所成角的余弦值为( ) A B C .5 10- D . 【答案】B 【解析】 试题分析:取BC 中点F ,连结1,FD FC ,则1DC F ∠为异面直线所成角,设边长为2 , 11C F DC DF ∴== =1cos 5 DC F ∴∠= 考点:异面直线所成角 5.如图,正四棱柱ABCD A B C D ''''-中(底面是正方形,侧棱垂直于底面),3AA AB '=,则异面直线A B '与AD '所成角的余弦值为( ) A 、910 B 、45 C 、710 D 、3 5 【答案】A 【解析】 试题分析:连结'BC ,异面直线所成角为''A BC ∠,设1AB = ,在'' A BC ?中''''AC A B BC ===''9 cos 10 A BC ∴∠= 考点:异面直线所成角 6.点P 在正方形ABCD 所在平面外,PA ⊥平面ABCD ,AB PA =,则PB 与AC 所成的角是 A .?60 B .?90 C .?45 D .?30 【答案】A 【解析】
一.选择题 1.没有公共点的两条直线的位置关系是( ) (A)平行 (B)异面 (C)平行或异面 (D)不能确定 2.分别在两相交平面内的两条直线的位置关系是( ) (A)异面 (B)平行 (C)平行或异面 (D)平行或异面或相交 3.两条异面直线指的是( ) (A)在空间不相交的两条直线(B)某一平面内的一条直线和这个平面外的一条直线 (C)分别位于两个不同平面的两条直线 (D)不同在任一平面内的两条直线 4.a 、b 是异面直线,b 、c 也是异面直线,那么a 、c 的位置是( ) (A)异面 (B)异面或平行 (C)异面或相交 (D)相交、平行或异面 5.说出正方体中各对线段的位置关系: (1) AB 和CC 1; (2)A 1C 和BD 1; (3)A 1A 和CB 1; (4)A 1C 1和CB 1; (5)A 1B 1和DC ; (6)BD 1和DC. 答案:1(C);2(D);3(D);4(D).5.(2)相交,(5)平行,其余异面; 6.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( ) 3 1032() () () ()2 10 5 5 A B C D 答案:(D),取AB 中点M ,CC 1中点N ,连B 1E 和B 1F ; 7.如图,A 1B 1C 1—ABC 是直 三棱柱(三侧面为矩形),∠BCA=90°,点D 1、F 1 分别是A 1B 1、A 1C 1的中点若BC=CA=CC 1,则 BD 1与AF 1所成角的余弦值是( ) 3013015() () () () 2 A B C D 答案:(A),延长B 1A 1至M ,使A 1M =A 1D 1,连MA ,取AB 中点N . 8.正方体ABCD —A 1B 1C 1D 1中,直线BC 1与AC (A)相交且垂直 (B)相交但不垂直 (C)异面且垂直 (D)异面但不垂直 9.设a 、b 、c 是空间中的三条直线,下面给出四个命题: ①如果a⊥b、b⊥c,则a∥c; ②如果a 和b 相交,b 和c 相交,则a 和c 也相交; ③如果a 、b 是异面直线,c 、b 是异面直线,则a 、c 也是异面直线; ④如果a 和b 共面,b 和c 共面,则a 和c 也共面 在上述四个命题中,真命题的个数是( ) (A)4 (B)3 (C)2 (D)1 (E)0 10.如果直线l 和n 是异面直线,那么和直线l 、n 都垂直的直线 B 1 (第6题) A 1 C 1 D 1 C D (第7题) F 1 A B C D 1 C 1 A 1 B 1 B 1 (第6题) A 1 A B C 1 D 1 C D M N
异面直线所成角的求法 内蒙古杭锦后旗奋斗中学 刘 宇 例:长方体ABCD —A 1B 1C 1D 1中,若AB=BC=3,AA 1=4,求异面直线B 1D 与BC 1所成角的大小。 选题意图,通过该题,让学生进一步理解异面直线所成角的概念,熟练掌握异面直线所成角的求法。 分析:构造三角形找中位线,然后利用中位线的性质,将异面直线所成的角转化为平面问题,解三角形求之。 解法一:如图①连结B 1C 交BC 1于0,过0点作OE ∥DB 1,则∠BOE 为所求的异面直线DB 1与BC 1所成的角。连结EB ,由已知有 B 1B C 1=5,BE=2,∴c o s ∠BOE=170 ∴∠BOE=cos arc 170 解法二:如图②,连DB 、AC 交于O 点,过O 点作OE ∥DB 1,过E 点作EF ∥C 1B ,则∠OEF 或其补角就是两异面直线所 成的角,过O 点作OM ∥DC ,连结MF 、OF 。则 ,cos ∠OEF=,∴异面直线B 1D 与 BC 1所成的角为cos arc 170 解法三:如图③,连结D 1B 交DB 1于O ,连结D 1A ,则四边形ABC 1D 1为平行四边形。在平行
四边形ABC1D1中过点O作EF∥BC1交AB、D1C1于E、F,则∠DOF或其补 ,cos∠角就是异面直线DB1与BC1所成的角。在△ADF中DF= 2 DOF=cos arc 解法四:如图④,过B1点作BE∥BC1交CB的延长线于E点。 则∠DB1E就是异面直线DB1与BC1所成角, 连结DE交AB于M, cos∠DB1 ∴∠DB1E=cos arc 解法五:如图⑤,在平面D1DBB1中过B点作BE∥DB1交D1B1的延长线于E,则∠C1BE就是异面直线DB1与BC1所成的角,连结C1E,在△B1C1E 中,∠C E=135°,C1 cos∠C1C1BE=cos arc 分析:在已知图形外补作一个相同的 几何体,以例于找出平行线。 解法六:如图⑥,以四边形ABCD为上底补接 一个高为4的长方体ABCD-A2B2C2D2,连结D2B,则 DB1∥D2B,∴∠C1BD2或其补角就是异面直线DB1与 BC1所成的角,连C1D2,则△C1D2C2为Rt△,cos∠ C1BD2=
考点30: 异面直线所成的角 【考纲要求】 1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题. 2.了解向量方法在研究立体几何问题中的应用. 【命题规律】 异面直线的知识是高考的热点问题,选择、填空、解答题都有可能进行考查.预计2018年的高考对本知识的考查空间向量的应用,仍然是以简单几何体为载体解决线线问题. 【典型高考试题变式】 (一)空间直线与直线夹角的问题 例1.【2017全国3卷(理)】a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60角时,AB 与b 成30角; ②当直线AB 与a 成60角时,AB 与b 成60角; ③直线AB 与a 所称角的最小值为45; ④直线AB 与a 所称角的最小值为60; 其中正确的是________.(填写所有正确结论的编号) 【答案】② ③ 【解析】由题意知,a ,b ,AC 三条直线两两相互垂直,画出图形如图. 不妨设图中所示正方体边长为1,故1AC =,2AB = 边AB 以直线AC 为旋转轴旋转,则A 点保持不变,B 点的运动轨迹是以C 为圆心,1为半径的圆.以C 为坐标原点,以CD 为x 轴正方向,CB 为y 轴正方向, CA 为z 轴正方向建立空间直角坐标系.则(1,0,0)D ,(0,0,1)A , 直线a 的方向单位向量(0,1,0)=a ,1=a .B 点起始坐标为(0,1,0), 直线b 的方向单位向量(1,0,0)=b ,1=b .设B 点在运动过程中的坐标()cos ,sin ,0B θθ',
空间角 1、异面直线所成角的求法一是几何法,二是向量法。异面直线所成的角的范围:(0, ] 2 几何法求异面直线所成角的思路是:通过平移把空间两异面直线转化为同一平面内的相交直线,进而利用平面几 何知识求解。基本思路是选择合适的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的 点。常见三种平移方法:直接平移:中位线平移(尤其是图中出现了中点):补形平移法:“补形法”是立体几何中 一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是 常用的方法之一。 例 1 在正方体ABCD A B C D 中,E是AB的中点, // (1)求 BA与 CC夹角的度数 . // (2)求 BA与 CB夹角的度数. (3)求 A/ E 与 CB/夹角的余弦值. 例 2:长方体 ABCD— A1B1C1D1中,若 AB=BC=3, AA1=4,求异面直线 B1D 与 BC1所成角的余弦值。 直接平移:常见的利用其中一个直线 a 和另一个直线 b 上的一个已知点,构成一个平面,在此平面内做直线 a 的 平行线。 解法一:如图④,过B1点作 BE∥ BC1交 CB的延长线于 E 点。 则∠ DBE 就是异面直线DB 与 BC 所成角,连结 DE交 AB于 M, DE=2DM=3 5, 1 1 1 1 7 34 cos ∠DBE= 170 解法二:如图⑤,在平面D1DBB1中过 B 点作 BE∥ DB1交 D1B1的延长线于E,则∠ C1BE就是异面直线DB1与 BC1所成的 角,连结 C1E,在△ B1C1E 中, ∠ C1B1E=135°, C1E=3 5 7 34 , cos ∠C1BE= 170 课堂思考: 1. 如图, PA矩形ABCD,已知PA=AB=8,BC=10,求AD与PC所成角的余切值为。