【全国大联考】【河南(新课标Ⅰ)】河南省信阳市2017-2018学年高三上学期期末质量检测化学试题(解析版)
- 格式:doc
- 大小:1.38 MB
- 文档页数:18

2017-2018学年河南省八市联考高三(上)第一次质检物理试卷一、选择题1. 下列有关质点的说法中正确的是()A. 只有质量和体积都极小的物体才能视为质点B. 研究一列火车过铁路桥经历的时间时,可以把火车视为质点C. 研究自行车的运动时,因为车轮在不停地转动,所以在任何情况下都不能把自行车作为质点D. 虽然地球很大,还在不停地自转,但是在研究地球的公转时,仍然可以把它视为质点【答案】D【解析】A项:质量大的物体也可以看成是质点,比如在研究地球绕太阳的运动时,地球就可以看成是质点,所以并不是只有质量和体积都极小的物体才能视为质点,所以A错误;B项:研究一列火车过铁路桥经历的时间时,火车的长度相对于桥来说是不能忽略的,所以不能把火车看成质点,所以B错误;C项:研究自行车的形状对分析的问题没有影响时就可以看成是质点,比如研究人骑自行车运动一段距离的时间的时候,就可以看成质点,所以C错误;D项:虽然地球很大,还在不停地自转,但是地球的体积相对于和太阳之间的距离来说是很小的,所以在研究地球的公转时,仍然可以把它视为质点,所以D正确。
点晴:本题考查学生物体能看成质点的条件:当物体的形状和大小对研究问题的影响可忽略时,物体可看成质点。
2. 甲物体以乙物体为参考系是静止的,甲物体以丙物体为参考系是运动的,那么,以乙物体为参考系,丙物体()A. 一定是静止的B. 一定是运动的C. 有可能是运动的,也有可能是静止的D. 条件不足,无法判断【答案】B【解析】试题分析:一个物体相对于另一个物体位置发生了改变,则这个物体就相对于另一个物体发生了运动.甲物体以乙物体为参考系是静止的,甲物体以丙物体为参考系是运动的;丙物体以乙物体为参考系,丙物体一定是运动的.解:甲物体以乙物体为参考系是静止的,说明甲相对于乙的位置没有改变.甲物体以丙物体为参考系是运动的,说明甲相对于丙的位置是改变的,则以乙物体为参考系,丙物体的位置一定是改变的,即丙物体一定是运动的.故选B【点评】本题考查对参考系的理解能力.根据物体间的位置是否改变来判断物体是否运动.3. 下列关于速度的说法正确的是()A. 速度是描述物体位置变化的物理量B. 速度方向就是物体运动的方向C. 位移方向和速度方向一定相同D. 匀速直线运动的速度方向是可以改变的【答案】B【解析】试题分析:速度是描述物体运动快慢的物理量,A错误;速度方向就是物体运动的方向,B正确;位移方向和速度方向可能相同可能相反可能不在一条直线上,C错误;匀速直线运动是速度不变的运动,D正确。

全国大联考2017-2018学年高三第四次联考•理综卷(化学部分)一、选择题7.2015年夏,台湾的“彩色派对”所用的彩色粉末由纯人然玉米粉制成,彩色粉末的主要成分是A.蛋白质B.淀粉C.油脂D.纤维素8.设A N 表示阿伏加德罗常数的数值,下列说法正确的是 A. 14g 由2N 和2213H C 组成的混合物所含的电子数为7A NB.标准状况下,11.2L NO 与11.2 L 2O 混合后所含的分子数小于0.75A NC.常温下,1L PH=3的Al 2(SO 4)3溶液中,水电离出的H +数目为10-3A ND.在100mL 1 mol • L -5Na 2S02溶液与1.12 L(标准状况)CL 2的反应中,•还原剂失电子0.2A N 9.X 、Y 、Z 、W 为原子序数依次增大的短周斯元素,相关信息如图所示。
下列判断正确的是A.原子半径:r(W)>r(Z) >r(Y)B.含Y 元素的盐溶液一定显酸性C.最高价铖化物对应水化物的酸性:Z >WD. X 、W 分别形成的简单气态氢化物可反应生成离子化合物 10.下列实验操作、现象和结论均正确的是11.只含C、H、0三种元素的有机物W,其蒸气的密度是NH2的6倍(相同条件下),取一定量的有机物W完全燃烧,生成CO2和H2O的质量比为22:9,则W能发生水解反应的结构(不考虑立体结构) 共有A.11种B. 10种C.9种D.8种12.一种熔融碳酸盐燃料电池的工作原理如图。
下列有关该电池的说法不正确...的是A.电流方向:由B极经用电器流向A极B.电极B上发生的电极反应为2CO2+O2+4e2CO CO2C.电池工作时,K+、Na+向电极B移动D.若消耗电极B上的O2 33.6L(标准状况),则至少需要1moL CH4参加反应13.已知:常温下浓度为0.1 moL• L-的下列溶液的pH如下表。
下列有关说法正确的是A.根据上表,NaF的水解程度比CH3COONa的大B.同体积、同pH的两种酸溶液消耗同浓度NaOH的体积:HF>CH3COOHC.向100mL 0.1 mol • L-1 CH3COONa溶液中通入224mL HF气体(标准状况): c(CH3CXX)H) +c(H+)=c(OH-)+c(F-)D.若将0.05 mol HC1缓慢地通入1 LO.1 moL• L-Na2S溶液中,则溶液中离子浓度大小为: c(Cl-)>c(HS-) >c(OH-)c(S2-) >c(H+)第Ⅱ卷(—)必考题26. (14分)焦亚硫酸钠(Na2S2O5)和硫代硫酸钠(Na2S2O3)在工业上有广泛的应用,例如焦亚硫酸钠是常用的食品抗氧化剂之一。

全国名校大联考2017~2018学年度高三第四次联考语文考生注意:1.本试卷满分150分,考试时间150分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上,选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;主观题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答。
超出答题区域......。
书写的答案无效.......。
在试题卷............、草稿纸上作答无效4.本卷命题范围:高考范围。
一.现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
汉字是世界上起源最早的文字之一,传承数千年,从未中断,为世界各国文化源流所仅见,见证了中华民族光辉灿烂的文化。
以汉字的独特性为基础,在儒释道思想的浸润下,中国书法成为具有丰富文化含量的独特艺术形式。
与中国画相比,书法以汉字为基础,思想性、抽象性都让它与中国传统文化有着更为紧密、直接的关系。
哲学家、艺术家熊秉明认为,实际上中国书法处于中国传统文化的核心部分,因为中国文化的核心在于哲学,而要使哲学精神的抽象落到现实生活,书法正起了桥梁的作用。
书法家沈鹏则强调书法的艺术性,他认为书法作为一门艺术,在本质上不给人知识,因此它在文化中无法担当核心的重负。
书法是纯形式的艺术,形式即其内容。
历史地看,书法的发展过程实际上就是书法风格的发展史。
近代以来,西方各种文化思潮的进入,挤压了中国传统文化的生存空间。
汉字、书法中的文化精神不断消减,很多书法工作者丧失了对文化传承的兴趣和能力,这是书法传承和发展面临的最大问题。
书法既是艺术,更是文化,它是一种真正地对人、社会、国家、民族和整个人类有滋养作用的艺术。
这滋养的力量正来源于中国传统文化思想的共同涵养。
作为中国传统文化主要源流的儒释道思想给书法的传承与发展打上了深刻的烙印,儒家给了书法中正平和,道家则让书法飘逸超迈,佛家赋予它空灵玄远。

8 .2017-2018学年河南省天一大联考高三 (上)10月段考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个 选项中,有且只有一项符合题目要求■1 - (5 分)已知向量:-,::>.匚,若二;则 m=( )A .- 4 B. 4C.- 3 D . 32. (5分)函数f (x ) =x+lnx - 3的零点位于区间( ) A . (0,1) B. (1,2) C. (2,3) D. (3,4)3. (5分)已知等比数列{a n }的前n 项和为S n ,若氏=3, S 6=28S 3,则a 3=( ) A . B. — C. 3D . 9934. (5分)将函数f (x ) =3sin (5x+©)的图象向右平移——个单位后关于y 轴对 称,贝U ©的值可以是( )A .5. (5分)已知m >n >0,则下列说法错误的是((■yx+l )_2<x=C0(5分)已知函数f (x ) = ] ,若关于x 的方程f (x )- kA .:「1 一 B.'.'77 n+1计 1 C.6. Ef —■一in 2+l n^+1(5分)已知等差数列{a n }的前n 项和为S n ,若S 6=4a 2,氏=3,则a 10=(A . 7.-3 B . 3 C. - 6 D . 6(5分)已知函数「一宀,若a v- 2, b >2,则“(a )>f (b )” “+b v 0”的(充分不必要条件 B.必要不充分条件 C. 充要条件D. 既不充分也不必要条件第1页(共16页)8 .第2页(共16页)(x+2) =0有3个实数根,则实数k 的取值范围是()9. (5分)已知sin a= (a€ [竺,2询),若金(牛卩)=2,则tan (时B )=52cos P( ) A .B.丄C. -D .-丄136136 x+l^y10.(5 分)已知实数x, y 满足' x<3 ,若z=mx+y 的最大值为10,则m=( )A . 1B . 2 C. 3D . 411. (5 分)已知数列{a n }满足 a 1= - 1, a n +1=| 1 - a n |+ 2a n +1,其前 n 项和为 S n ,则下列说法正确的个数为()①数列{a n }是等差数列;②a n =3n -2:③S n =」1 2A . 0B . 1C. 2D . 3212 . (5分)已知m , n €( 0, +^).若m 』+2 .则当迎-+2n 2-亘-2取得最小 n 2m n值时,m+n=( ) A . 2 B . 4 C. 6D . 8二、填空题:本大题共4小题,每小题5分,共20分. 13 . (5分)不等式2x 2- 9x+9>0的解集为 _______ .14 . (5分)已知实数a € (-3, 1), b €(*, *),贝唸的取值范围是 _______ . 15 . (5分)若函数-:.I - ■在(1, +x )上单调递增,则实数 m 的取x值范围是 ______ .16 . ( 5分)在△ ABC 中,角 A , B , C 的对边分别为a , b , c ,若- -.i^',且・ '记h 为AC 边上的高,贝U h 的取值范围 为 .三、解答题:本大题共6小题,共70分■解答应写出必要的文字说明或推理、验 算过程.17. (10分)已知数列{a n }的首项为 a i =1,且 a n +i =2 (a n +1) (n € N *). (1) 求数列{a n }的通项公式; (2)若.•,求数列] —.:的前n 项和T n.18. (12分)在厶ABC中,角A, B, C的对边分别为a, b, c,且a=4「, D在线段AC上,/ DBC=".4(1)若厶BCD的面积为24,求CD的长;(2)若:II.—,且c=12 .」上,求CD的长.2 319・(12分)已知向量_c.uzr;. l.__二二工,IT.(1)若m=4,求函数f (x)=- ‘的单调递减区间;(2)若向量一「满足:|, , . ' . ',求m的值.5 220. (12分)已知等比数列{a n}的前n项和为:一,等差数列{b n}的前5项和为30, b7=14.(1)求数列{a n}, {b n}的通项公式;(2)求数列{a n?b n}的前n项和T.21. (12分)已知函数]・J(1)讨论函数f (x)的单调性;(2)已知点M (1 , 0),曲线丫=f(x)在点P (X0, y°) (- Kx°w 1)处的切线l与直线x=1交于点”,求厶OMN (O为坐标原点)的面积最小时x o的值,并求出面积的最小值.22. (12 分)已知函数十;| 一・.I. J 1■:.e(1)若m=1,求曲线y=f (x)在(2, f (2))处的切线方程;(2)探究函数F (x) =xf (x)的极值点的情况,并说明理由.20仃-2018学年河南省天一大联考高三(上) 10月段考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求■1 - (5分)已知向量...’.匸-二,若-:■,则m=( )A.- 4B. 4C.- 3D. 3【解答】解:根据题意,向量【..【—一「.,若'—,则■? =2X( - 6) + (- 3) m=0,解可得m=- 4,故选:A.2. (5分)函数f (x) =x+lnx- 3的零点位于区间( )A. (0,1)B. (1,2)C. (2,3)D. (3,4)【解答】解:函数f (x) =x+lnx-3, (x>0)••• f'(x) =1+,可得f'(x)>0, f (x)为增函数,Xf (1) =1+0 - 3=- 2v 0,f (2) =2+ln2 - 3=ln2- 1v0,f (3) =3+ln3 - 3=In3>0,••• f (2) f (3)v0,所以f (x)的零点所在区间为(2, 3),故选B;3.(5分)已知等比数列{a n}的前n项和为S n,若a s=3, S6=28S3,则a3=( )A.丄B.丄C. 3D. 99 3【解答】解:若q=1时,a 5=3, --a i =3,6a i =28a i ,显然不成立, ••• qM 1, 由 a 5=3, S 6=28S 3,q 4=3I.' : ,十 ---- 28 X ------------------1-ql~q解得 q=3, a i = •,,■w Ia 3= 1 x 9=, 1:: 故选:B=3sin (5x+ ©)的图象向右平移——个单位后关于y 轴对称,则©的值可以是( A .B :【解答】解:将函数f (x ) =3sin (5x+ ©)的图象向右平移丄个单位, 4得到:y=3sin[5 (x -三)+©]=3sin (5x -昱匚 + ©),44得到的图象关于y 轴对称, 则:©-□=「: — (k € Z ),当 k =-2时,©=- ■: 故选:D .5. (5分)已知m >n >0,则下列说法错误的是( m 〉n n+1 irrfl可得*4.(5分)将函数f (x ) 解得:© =k(k € Z ),A .d 「D .亠.••一in +1 n +1【解答】解:根据对数函数的单调性可得 A 正确, ■/ m >n >0,/• m+1 > n+1 ••• m (m+1)> n (n+1), •••」匚> ,故B 正确,n+1 itrl-1根据幕函数的单调性可得 C 正确, 门 _「:.「-:•- “厂:= I 1 : 1n 2+l (w 2+l) (n £+l) (m 2+l) (n^ + 1)v 1 - mn 与0无法比较大小, 故D 错误,故选:D .6. (5分)已知等差数列{a n }的前n 项和为S n ,若S 6=4a 2,氏=3,则a io =( )A .- 3 B. 3C. - 6 D . 6【解答】解:设等差数列{a n }的公差为d ,v S 6=4a 2,氏=3,• 6a i^^d=4 (a i +d ), a i +2d=3,2解得 ai=2, d=-土7 7贝U a io= — — x 9= — 3. 77故选:A .7. (5 分)已知函数| ,若 a v- 2, b >2,则 “f a )>f (b ) 是 “+b v 0” 的( ) A .充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件【解答】解:由2|x| - 4>0,解得x >2或X V- 2,关于原点对称. 又f (- x ) =f (x ).可得函数f (X )在定义域内为偶函数.对于D,1m 2+ lx >2时,f (x ) =5x- ---------------- 在(2, +x)上单调递增.V2(x-2)••• a+b v 0? 2v b v- a? f (b )v f (- a ) =f (a ),••• “f(a )> f (b ) ”是 “+b v 0” 的充要条件.故选:C.(x+2) =0有3个实数根,则实数k 的取值范围是( )A . (°,」B (°,:;) C (0, 1)° (°,「【解答】解:在同一坐标系中画出分段函数 y=f (x )的图象与y=k (x+2)的图象,由图可知:当k €( 0,k AQ )时,分段函数f (x )的图象与y=k (x+2)的图象有 三个交占 ---- I 八、、) A (0, 1),Q (-2,0),实数k 的取值范围是(0,]). 故选:D .(5分)已知sin a=(妖[竽,2n),若畔严=2,则tan (幵)=8. (5分)已知函数f (x )=若关于x 的方程f (x )- k9.A .B ・C.13D .136-2<x<0【解答】解:t sin a = 2( a€ [ ,2 n ),「• cos a== i 2 口 =—,二 tan 口=门°5 2 birL5 cos _ ■•.mg 卩)•"詐3in0=sin +cos a ?tan ^_^_ +3tan B =2 cos P cos P 5 5••• tan B==,贝U tan ( a +B3故选:A .x+l 》y10. (5 分)已知实数x , y 满足' x<3,若z=mx+y 的最大值为10,则m=( )L y-1^0A . 1 B. 2 C. 3 D . 4x+l^y【解答】解:由实数x , y 满足x <3 ,作出可行域如图,L y-l>0易知 A (3, 1), B (3, 4), C (0, 1). 化目 标函数 z=mx+y 为y=_ mx+z ,当直线z=mx+y 经过B 点时,取得最大值10; • 10=3m+4,解得 m=2. 故选:B.幷5 4 3 1 1K :1 1 1 h / 1 1 ■ 壬-4-3亠1 o 12345 口-1 7-3 JI--4 -5—11. (5 分)已知数列{a n }满足 a 1= _ 1, a n +1 =| 1 _ a n |+ 2a n +1,其刖 n 项和为 S , 则下列说法正确的个数为()第8页(共16页)=-ri : - ■.:1-tan*^ ・ tan①数列{an是等差数列;②外=3n「2:③s n=…A. 0B. 1C. 2D. 3【解答】解:数列{a n}满足a i=- 1, a n+i=| 1 —a n|+2a n+1, 可得a2=| 1 - a i |+ 2a i +1=2 - 2+1=1,03=| 1 —a2|+ 2a2+1=0+2+1=3,a4=| 1 —a3|+ 2a3+1=2+6+1=9,则a4 —a3=6, a3 —a2=2,即有a4 —a3 工a3 —a2,则数列{a n}不是等差数列,故①不正确;a n=3n—2,不满足a1 = —1,故②不正确;若满足n=1时,a1=S = —1,但n=2 时,a2=S2 —S1=" —(—1) =1,2当n >2 时,a n=0—Si-1='—'=3n—2, n>2, n€ N* .代入a n+1 =| 1 —a n |+ 2a n+1,左边=3n —1,右边=3n —2—1+2?3n—2+1=3n —1,则a n+1 =| 1 —a n|+ 2a n+1 "恒成立.故③正确.故选:B.212. (5分)已知m, n€( 0, +^).若m』+2.则当%+2n2——取得最小n 2 m n值时,m+n=( )A. 2B. 4C. 6D. 8【解答】解:m, n€(0, +x).若m= +2.则m= >0,解得n> 1.+2n 2- 1 -二=「1+2n 2=f (n ).n n (n -i ) z(n-1 ) 3 令 f ' (n )> 0,解得 n >2,可得n=2, m=4时,f (n )取得最小值时,m+n=6. 故选:C.二、填空题:本大题共4小题,每小题5分,共20分.13. ( 5 分)不等式 2x 2- 9x+9> 0 的解集为 (-X ,_)u ( 3,+*)2【解答】解:不等式2x 2- 9x+9>0, 即为(x -3) (2x - 3)> 0, 解得x >3或x v ,2解集为(-x , )U ( 3, +x ).故答案为:(-X ,_)U ( 3, +X ).214. (5分)已知实数a € (- 3, 1), b €(£,〔),则至的取值范围是(-12,84 b8)_.【解答】解::b €(£, g ), ••丄 €( 4, 8),34 b•- a € (-3, 1), •「€(- 12, 8). b 故答案为:(-12, 8).15. (5分)若函数:.| <J 「在(1, +x )上单调递增,则实数z 值范围是」 ,+x ).【解答】解:•••函数•・:・’:.•■在(1 , +X )上单调递增, •「■: - - , > 0 在(1 , +X )上恒成立,则「+2n2— - :: = :Im n (n -i )(n-1 )m 的取即m》二一在(1, +X)上恒成立,令g (x)=' 贝u g(x)=」,’,2x3当 x €( 1,它)时,g' (x )> 0,当 x €(2, +x )时,g f(x )v 0,2 2故当x=时,g (x )取最大值一,227 故实数m 的取值范围是[一,+x), 27故答案为:[丄,+x ).2716 . ( 5分)在△ ABC 中,角 A , B , C 的对边分别为a , b , c ,若 'I. ,且J ■■■;二,记h 为AC 边上的咼,则h 的取值范围为(0, _L. 【解答】解:,二 sinBcosC=2sinAcosB sinCcosB 即 sinBcosC+sinCcosB=2sinAcosB ••• sin (B+C ) =2sinAcosEB 即 sinA=2sinAcosB ••• cosB= , • B= .23 T 5AB J acsinB= bh ,222 2• a +c =ac+3> 2ac ,• 0v ac < 3. • 0v h < .2故答案为:(0 ,].二三、解答题:本大题共6小题,共70分■解答应写出必要的文字说明或推理、验 算过程.17. (10分)已知数列{a n }的首项为 a 1=1,且 a n +1=2 (a n +1) (n € N *). (1)求数列{a n }的通项公式;• h =.,由余弦定理可得 cosB=L 2 5(2)若;_「.一,求数列 「;的前n 项和T n .n 23b n b r^l【解答】解:(1)数列{a n }的首项为a i =1,且a n +i =2 (a n +1) (n € N *). 则:a n +i +2=2 (a n +2),所以:{a n +2}是以3为首项,2为公比的等比数列. 则:.—-…, 解得:1 : ,十 +2(2)由于. =n ,则:11 1 八」・卅rrHn \+1 '所以:丁_■ ・• +「 11 n 丄2 2 3n n+1解得:|1 n 1n 丄n+1 n+118. (12分)在厶ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a=4「,D 在 线段 AC 上,,DBC=:.(1) 若厶BCD 的面积为24,求CD 的长;(2) 若「一』.——■,且 c=12_. i.wd 二,求 CD 的长.£J解得:BD=12,在△ BCD 中, CD 2=BC 2+BD 2 - 2BC?BD?cos4°即 CD 2=32+BD 2- 8BD,故 Cg2+144- 8X 12, 解得:CD=4:;(2)v tanA±,且 A €(0, n),故 sinA =」、° , cosA =*° ,31010 由题意得^ =,即「-= 二,解得:sinC=丄,sinA sinCsinC10IF•- C €( 0,今),cosC 響, ••• sin / BDC=sin (C+二)=二',45在厶BCD 中,由正弦定理得 =sinZDBC slnZBDC 解得:CD=2 二.【解答】解:(1)由S A BC 』?BD?=24,19. (12分)已知向量.. cosi, sin^ f b-(2sinK, m)•(1) 若m=4,求函数f (x) =•-的单调递减区间;(2) 若向量满足'' . . . A . :ii, T•,求m 的值.【解答】解:(〔)向量-J- . , ■.I.:.•'•函数 f (x)= ・:=4sinxcosxnmsin x=2sin2x—当m=4 时,可得 f (x)=2sin2x— 2cos2x+2=2 sin (2x —一)+2. 4JT ,3兀-■■=■. 亠一一,w x w丄^ +k n8 8•函数f (x) = ■-'的单调递减区间为[;:.i ],k€乙4 8⑵由一=「",戸2cosK-2sinx=z"即5,丄si n^K-irnO:x€(0, 一)由sin2x+cos2x=1曰- 3 4可得sinx= ,cosx=.55那么m=sin2x= .2520. (12分)已知等比数列{a n}的前n项和为一],等差数列{g}的前5项W-和为30,b7=14.(1) 求数列{a n}, {b n}的通项公式;(2) 求数列{a n?b n}的前n项和T.【解答】解:("等比数列的前n项和为*=!,••• n>2时,心—5 n=1时,a i=Si=1对于上式也成立.•-a n=3n「1.设等差数列{b n}的公差为d, •••前5项和为30,b7=14.二5b i+ ;|=30,b i+6d=14,2联立解得:b1=d=2.b n=2+2 ( n - 1) =2n.(2) a n b n=2n?3n-1.• T i=2 (1+2X 3+3X 32+・・+n?3n-1),3T n=2[ 3+2 X 32+-+ (n - 1) ?3n-1 +n?3n],-2T n=2 (1+3+32+-+3n-1)- 2n?3n= . . :- 2n?3n,解得:G=J肓厂苗+ - .21. (12分)已知函数-..< ..(1)讨论函数f (x)的单调性;(2)已知点M (1 , 0),曲线丫=f(x)在点P (x o, y o) (- Kx o< 1)处的切线l与直线x=1交于点”,求厶OMN (0为坐标原点)的面积最小时x0的值,并求出面积的最小值.【解答】解:(1)由题意得:f'(x) =e x-x,令m (x) =e x- x, 故m (x) =e x- 1,令m (x) =0,解得:x=0,故m (x)在(-x, 0)递减,在(0, +x)递增,故[m (x) ]min=m (0) =1,故e x-x>0,即f'(x)>0, 故函数f (x)在R递增;(2)由题意,切线I的斜率为f'( X。

全国名校大联考2017~2018学年度高三第二次联考第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{}2,1,3,4U =--,集合{}1,3B =-,则U B =ð( ) A .{}1,3- B .{}2,3- C .{}2,4- D .∅ 2.命题“()1,x ∀∈+∞,2log 1x x =-”的否定是( )A .()1,x ∀∈+∞,2log 1x x ≠-B .()1,x ∃∈+∞,2log 1x x ≠-C .()1,x ∃∈+∞,2log 1x x =-D .()1,x ∀∉+∞,2log 1x x ≠- 3.若sin 02πθ⎛⎫+<⎪⎝⎭,cos 02πθ⎛⎫-> ⎪⎝⎭,则θ是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角4.已知平面向量,a b r r的夹角为60°,(a =r ,1b =r ,则a b +=r r ( )A .2 B..4 5.若将函数2sin 2y x =的图象向左平移12π个单位长度,则平移后图象的对称轴为( ) A .()26k x k ππ=-∈Z B .()26k x k ππ=+∈Z C .()212k x k ππ=-∈Z D .()212k x k ππ=+∈Z 6.设函数()()3,1,log 24,1,xaa x f x x x ⎧≤⎪=⎨+>⎪⎩且()16f =,则()2f =( )A .1B .2C .3D .6 7.已知()0,απ∈且4sin 5α=,则tan 4πα⎛⎫-= ⎪⎝⎭( ) A .17±B .7±C .17-或7-D .17或7 8.已知()cos17,cos 73AB =︒︒uu u r ,()2cos 77,2cos13BC =︒︒uu u r,则ABC ∆的面积为( )A .2B .1C .2 9.函数()f x 有4个零点,其图象如下图,和图象吻合的函数解析式是( )A .()sin lg f x x x =-B .()sin lg f x x x =-C .()sin lg f x x x =-D .()sin lg f x x x =- 10.已知,,a b c 分别是ABC ∆的三个内角所对的边,满足cos cos cos a b cA B C==,则ABC ∆的形状是( )A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形 11.某新建的信号发射塔的高度为AB ,且设计要求为:29米AB <<29.5米.为测量塔高是否符合要求,先取与发射塔底部B 在同一水平面内的两个观测点,C D ,测得60BDC ∠=︒,75BCD ∠=︒,40CD =米,并在点C 处的正上方E 处观测发射塔顶部A 的仰角为30°,且1CE =米,则发射塔高AB =( )A .()1米 B .()1米 C .()1米 D .()1米12.设向量,,a b c r r r满足2a b ==r r ,2a b ⋅=-r r ,(),60a c b c --=︒r r r r ,则c r 的最大值等于( )A .4B .2C .1第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知函数()xf x a b =+()0,1a a >≠的定义域和值域都是[]1,0-,则ba = .14.若动直线x a =与函数()sin f x x =和()cos g x x =的图象分别交于,M N 两点,则MN 的最大值为 .15.已知函数()y f x =是定义在R 上的奇函数,当0x <时,()2f x x =-+,那么不等式()10f x +<的解集是 .16.已知ABC ∆的三边垂直平分线交于点O ,,,a b c 分别为内角,,A B C 的对边,且()222c b b =-,则AO BC ⋅uuu r uu u r的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知函数()xm f x a =(,m a 为常数,0a >且1a ≠)的图象过点()2,4A ,11,2B ⎛⎫- ⎪⎝⎭. (1)求实数,m a 的值; (2)若函数()()()11f xg x f x -=+,试判断函数()g x 的奇偶性,并说明理由.18.在锐角ABC ∆中,内角,,A B C 的对边分别是,,a b c ,且()cos sin20B C A ++=. (1)求A ;(2)若6a =ABC ∆的面积为3,求b c -的值. 19.如图,在ABC ∆中,3B π=,2BC =,点D 在边AB 上,AD DC =,DE AC ⊥,E为垂足.(1)若BCD ∆AB 的长;(2)若ED =,求角A 的大小.20.已知向量()2,sin m α=u r ,()cos ,1n α=-r ,其中0,2πα⎛⎫∈ ⎪⎝⎭,且m n ⊥u r r .(1)求sin 2α和cos 2α的值;(2)若()sin αβ-=,且0,2πβ⎛⎫∈ ⎪⎝⎭,求角β.21.设函数()sin 1f x x x =++.(1)求函数()f x 的值域和函数的的单调递增区间; (2)当()135f α=,且263ππα<<时,求2sin 23πα⎛⎫+ ⎪⎝⎭的值. 22.已知向量2sin ,cos 33x x a k ⎛⎫= ⎪⎝⎭r ,cos ,3x b k ⎛⎫=- ⎪⎝⎭r ,实数k 为大于零的常数,函数()f x a b =⋅r r ,x ∈R ,且函数()f x的最大值为12.(1)求k 的值;(2)在ABC ∆中,,,a b c 分别为内角,,A B C 所对的边,若2A ππ<<,()0f A =,且a =,求AB AC ⋅uu u r uu u r的最小值.2017~2018学年度高三第二次联考·数学(理科)参考答案一、选择题1-5:CBBCB 6-10:CCADC 11、12:AA 二、填空题13.4 14.{}0x x > 16.2,23⎛⎫- ⎪⎝⎭三、解答题17.解:(1)把()2,4A ,11,2B ⎛⎫- ⎪⎝⎭的坐标代入()x m f x a=, 得214,12ma m a -⎧=⎪⎪⎨⎪=⎪⎩,解得1m =,12a =.(2)()g x 是奇函数. 理由如下:由(1)知()2xf x =,所以()()()121121x xf xg x f x --==++. 所以函数()g x 的定义域为R .又()2122221222x x x x xx x xg x -----⋅--==+⋅+()2121x x g x -=-=-+, 所以函数()g x 为奇函数.18.解:(1)因为()cos sin20B C A ++=, 所以cos 2sin cos 0A A A -+=,即1sin 2A =. 又因为ABC ∆为锐角三角形,所以1sin 2A =,所以30A =︒. (2)因为1sin 32ABC S bc A ∆==,所以12bc =. 又因为2222cos a b c bc A =+-,所以2239b c -=+-2239b c +=.故b c -==15==.19.解:(1)∵BCD ∆,3B π=,2BC =,∴12sin 233BD π⨯⨯⨯=,∴23BD =. 在BCD ∆中,由余弦定理可得CD ===∴AB AD BD CD BD =+=+23=+=.(2)∵DE =,∴sin DE CD AD A ===. 在BCD ∆中,由正弦定理可得sin sin BC CDBDC B=∠.∵2BDC A ∠=∠,∴2sin 2A =,∴cos A =, ∴4A π=.20.解:(1)∵m n ⊥u r r,∴2cos sin 0αα-=,即sin 2cos αα=.代入22cos sin 1αα+=,得25cos 1α=,且0,2πα⎛⎫∈ ⎪⎝⎭,则cos α=,sin α=则sin 22sin cos ααα==42555⨯=. 2cos 22cos 1αα=-=132155⨯-=-.(2)∵0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,∴,22ππαβ⎛⎫-∈-⎪⎝⎭.又()sin 10αβ-=,∴()cos 10αβ-=∴()sin sin βααβ=--=⎡⎤⎣⎦()()sin cos cos sin ααβααβ---=5105102-=. 因0,2πβ⎛⎫∈ ⎪⎝⎭,得4πβ=.21.解:(1)依题意()sin 1f x x x =++2sin 13x π⎛⎫=++ ⎪⎝⎭. 因为22sin 23x π⎛⎫-≤+≤ ⎪⎝⎭,则12sin 133x π⎛⎫-≤++≤ ⎪⎝⎭.即函数()f x 的值域是[]1,3-. 令22232k x k πππππ-+≤+≤+,k ∈Z ,解得52+266k x k ππππ-+≤≤,k ∈Z ,所以函数()f x 的单调递增区间为52+266k k ππππ⎡⎤-+⎢⎥⎣⎦,,k ∈Z .(2)由()132sin 135fπαα⎛⎫=++= ⎪⎝⎭,得4sin 35πα⎛⎫+= ⎪⎝⎭.因为263ππα<<,所以23ππαπ<+<时,得3cos 35πα⎛⎫+=- ⎪⎝⎭. 所以2sin 2sin 233ππαα⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭2sin cos 33ππαα⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭432425525-⨯⨯=-. 22.解:(1)由题意,知()2sin ,cos cos ,333x x x f x a b k k ⎛⎫⎛⎫=⋅=⋅- ⎪ ⎪⎝⎭⎝⎭r r 2sin cos cos 333x x x k k =-21cos123sin 232xxk k +=-⋅=22sin cos 2332k x x k ⎛⎫--=⎪⎝⎭22332x x k⎫-⎪⎪⎝⎭2sin 2342x k π⎛⎫=-- ⎪⎝⎭. 因为x ∈R ,所以()f x的最大值为)12k =1k =. (2)由(1)知,()212342x f x π⎛⎫=-- ⎪⎝⎭, 所以()210342A f A π⎛⎫=--= ⎪⎝⎭,化简得2sin 34A π⎛⎫-=⎪⎝⎭因为2A ππ<<,所以25123412A πππ<-<,则2344A ππ-=,解得34A π=.因为222cos 2b c a A bc+-==22402b c bc +-=,所以2240b c ++=,则2240b c +=2bc ≥,所以(202bc ≤=-.则3cos 4AB AC AB AC π⋅==uu u r uuu r uu u r uuur (2012-≥, 所以AB AC ⋅uu u r uu u r的最小值为(201.。

12专题03破译三角函数图像变换问题、单选题1.【湖北省咸宁市2018届高三重点高中11月联考】若函数f x =cos2x , g x ]=sin j 2x -石【答案】【解析】/(+COS 2JC :+sin I 2x —— =cos2x4JT曲线 严 列乂)向左平移壬个单位长度后的解折式为:6本题选择E 选项.2•【山西省芮城中学 2018届高三期中】函数 f (x ) = Asin (G0x + W )(其中A A O ,申 <:丄)的图象过点2,0 ,—, -1,如图所示,为了得到 g x ;=cos2x 的图象,则只要将 f x 的图象()312曲线B .曲线y 二g x 向左平移 C .曲线 y = f x 向右平移 D .曲线 丄个单位长度后得到曲线6■JT个单位长度后得到曲线6—个单位长度后得到曲线12—个单位长度后得到曲线126丿即/(x )+^(x) =A. 向右平移二个单位长度6B. 向右平移个单位长度1233【答案】D+ 卩= --- 2A H (A:E Z) — +2lac(k e Z) 23It和八、 .K-(P — — > J (x) = SID I 2x4-—C.向左平移'个单位长度 6D.向左平移个单位长度12【解析】12 3TSJD3it71 1C — cos2x — sin 2无+—2 3二肚2 "12点睛:已知函数 y=Asi nicx 」‘LB (A -0,八>0)的图象求解析式 (1)y max — y min y max yminA, B =一 2由函数的周期T 求co ,T = 利用“五点法”中相对应的特殊点求:.【广东省执信中学 2017-2018学年高二上学期期中】将函数 y=Sin j 2x ' 的图象向右平移 一个单位2长度,所得图象对应的函数■: 7 二■: 7 二A 在区间[,]上单调递减B 在区间[,]上单调递增12 12 12 12J [ JEJ [ J [C.在区间^-,-]上单调递减D在区间[wy 上单调递增【答案】B兀【解析】将函数向右平移个单位长度得:((y =sin 2 x 一一J T(二 sin I 2x- 3 ,所以当7 2 二二二时,2x ,—12 3IL 2 24 •【陕西省西安市长安区2018届高三上学期质量检测】把函数.的图象上个点的横坐标缩短到原61 TI来的(纵坐标不变),再将图象向右平移个单位,那么所得图象的一个对称中心为23A B.c D (%)4【答案】D【解析】根据题意函数尸血时勺)的图象上个点的横坐标缩短到原来的k纵坐标不知,可得厂血伍昇6 2I创再将團象向右平移*单位,可得:V J sin|2 (x)+ -] = sin —)- ~cos2x^3 3 6 22K ■- + kn*2可得:x«- + -kn, kE疋"4 2当k・0时,可得对称中点为(:0).4故选ZZf x二cosi2x • 的图象,只需将函数I 6丿g x 二sin2x 的图象()A向左平移一个单位6C. 向左平移二个单位3【答案】A B向右平移一个单位6D向右平移少个单位3,所以函数单调递增,故选 B.125.【山东省莱芜市2018届高三上学期期中】要得到函数f x i = sin 「x ■ ' (其中)的图象如图2所示,为了得到 y 二cos 「x 的图象,只需把 y 二f x 的图象上所有点()【解析】g x 二 sin2x =cos所以向左平移n 二26 个单位,选A2 66 •【辽宁省沈阳市交联体2018届高三上学期期中】函数C.向左平移二个单位长度6【答案】AT 7 7T更jr 【解析】根据函数的^m-=—4 122九"所以:T^JL9<D=——=2>当沪彳时,函数fyr jr即:/ ( —) =sin (2x — +<p) =0.解得所以:f (x) =sin( 2x+ —).要得到y=cos2x的图象只需将函数 f (x) =sin(2x< )向左平移.个单位长度,3 12n 兀即y=sin (2x+ + ) =cos2x.6 3故选:A.点睛:已知函数y=Asi n[cx」‘LB(A 0^ 0)的图象求解析式(1 )2■:人=涯沁,ymin.(2)由函数的周期T求,T =2 2 ⑷利用“五点法”中相对应的特殊点求:.【豫西南部分示范性高中2017-2018年高三年级第一学期联考】已知函数f X =sin 2x,为得到B.向右平移.个单位长度12D.向右平移二个单位长度6A向左平移.个单位长度123A 向左平移二个单位长度 B.向左平移.个单位长度612C.向右平移二个单位长度D.向右平移二个单位长度612【答案】A【解析】函数 g x 二 cosi2x sin ;2xsin 12x —• I 6丿 126丿 J 3丿函数f (x )=s in ”2x +工1= sin |2 " x +丄1+》=sin " 2x +2兀】=g ( x ),是向左平移了工个单位长 2 V 3丿 [16丿3 一 V 3丿“丿 6度。

2017~2018学年度全国名校大联考高三第四次联考英语试卷(附答案)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How does the woman suggest going to New York?A.By plane.B.By train. C. By car2.When will the man leave?A.On September 3rd.B.On September 12th. C. On September 13th 3.What does the woman think of the trip?A.It’s disappointing.B.It’s fantastic. C. It’s dull4.What are the speakers talking about?A.Preparing for a meeting.B.Fixing a copying machine.C.Using a copying machine.5.How long did the woman wait alter work yesterday?A.One hour.B.Two hours.C.Three hours.第二节(共15小题;每小题1.5分,满分22.5分)听下而5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6.Where does the conversation probably take place?A.In a hotel.B.In a schoo1.C.In a shop.7.When will the pool open?A.At six o’clock tomorrow morning.B.At five o‘clock in the afternoon.C.At eighto’clock in the evening.听笫7段材料,同答第8拿10题。

2017-2018学年河南省信阳市高二(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的1.“∀x∈R,3x>2x”的否定是()A.∀x∈R,3x≤2x B.∀x∉R,3x<2xC.∃x0∈R,3x0≤2x0 D.∃x0∉R,3x0<2x02.用秦九韶算法求多项式f(x)=2x6﹣x2+2在x=2015时的值,需要进行乘法运算和加减法次数分别是()A.6,2 B.5,3 C.4,2 D.8,23.“x≠1”是“x2+2x﹣3≠0”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.如果甲、乙在围棋比赛中,甲不输的概率为60%,甲获胜的概率为50%,则甲、乙和棋的概率为()A.50% B.40% C.20% D.10%5.已知双曲线﹣=1(a>0,b>0)的一条渐近线经过点(3,),则双曲线的离心率为()A.B.2 C.或2 D.或26.“辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为()A.0 B.1 C.9 D.187.抛物线C:y2=4x的焦点为F,准线l与x轴交于点K,点A在C上,若△AFK的面积为4,则||=()A.6 B.5 C.4 D.38.已知一组数据2(x1﹣1),2(x2﹣1),…,2(x2015﹣1)的平均数为6,标准差为4,则新数据x1,x2,…,x2015的平均数与标准差分别为()A.4,1 B.3,2 C.4,2 D.3,19.运行下面程序,输出的结果是()A.47 B.48 C.102 D.12310.在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为()A.B.C.D.11.如图所示正方体ABCD﹣A1B1C1D1,设M是底面正方形ABCD内的一个动点,且满足直线C1D与直线C1M所成的角等于30°,则以下说法正确的是()A.点M的轨迹是圆的一部分B.点M的轨迹是椭圆的一部分C.点M的轨迹是双曲线的一部分D.点M的轨迹是抛物线的一部分12.点B,F分别是椭圆+=1(a>b>0)的上顶点与左焦点,过F作x轴的垂线与椭圆交于第二象限的一点P,H(,0)(c为半焦距),若OP∥BH(O为坐标原点),则椭圆的离心率为()A.B.C.D.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填在答题卡的相应位置13.先对112名学生随机地从1~112编号,用系统抽样方法抽取一个容量为16的样本,按编号平均分成16组(1~7,8~14,15~21,…,106~112),若第12组抽到的编号为82,则第4组中抽出的编号为.14.已知抛物线C:y2=8x的焦点F与双曲线E:﹣=1(a>0,b>0)的一个焦点重合,C的准线与E交于A,B,若||=6,则E的方程为.15.若八进制数等于二进制数,则a=,b=.16.在平面直角坐标系xOy中,从区域Ω:内随机抽取一点P,则P点到坐标原点的距离大于的概率为.三、解答题:本大题共5小题,满分60分,解答应写出文字说明,证明过程或演算步骤. 17.p:对任意实数x,都有x2+2ax+a≥0恒成立;q:x﹣4y﹣a=0与抛物线x2=4y有交点,若“¬(p∨q)”为假,“p∧q”为假,求实数a的取值范围.18.登山运动是一项有益身心健康的活动,但它受山上气温的限制.某登山爱好者为了了解某山上气温y(℃)与相应山高x(km)之间的关系,随机统计了5次山上气温与相应山高,如下表:气温y(℃)18 16 10 4 2山高(km) 2.6 3 3.4 4.2 4.8(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程:=bx+;(2)若该名登山者携带物品足以应对山上﹣2.4℃的环境,试根据(1)中求出的线性回归方程预测,这名登山者最高可以攀登到多少千米处?(参考公式:=,=﹣)19.如图,在侧棱和底面垂直的三棱柱ABC﹣A1B1C1中,AB=1,AC=,BC=2,AA1=,点P为CC1的中点.(1)求证:A1C⊥平面ABP;(2)求平面ABP与平面A1B1P所成二面角的正弦值.20.某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.(1)求身高分别在区间[165,170),[170,175),[175,180)的人数,并将频率分布直方图补充完整;(2)用分层抽样的方法从身高在区间[155,160),[170,175),[175,180)中抽取7人,现在从这抽出的7人中再抽取2人进行问卷调查,求身高在区间[170,175)中至少有1人进行问卷调查的概率.21.已知点A(1,0),点P是圆F:(x+1)2+y2=20上一动点,线段AP的垂直平分线交FP 于点M,记点M的轨迹为曲线C.(1)求曲线C的方程;(2)已知点B(0,),D(﹣4,0),若直线l:y=kx+与曲线C有两个不同的交点G 和H,是否存在常数k,使得向量(+)⊥(O为坐标原点)?如果存在,求出k的值;如果不存在,请说明理由.请考生在22题、23题、24题三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑[选修4-1:几几何证明选讲]22.如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.(1)证明:AD2=AB•DP;(2)若PD=3AB=3,BQ=,求弦CD的长.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,曲线C1的方程为+y2=1,以坐标原点为极点,x轴正半轴为极轴,并取相同的单位长度建立坐标系,曲线C2的极坐标方程为2ρ=sinθ.(1)写出曲线C1的参数方程,并求出C2的直角坐标方程;(2)若P,Q分别是曲线C1,C2上的动点,求||的取值范围.[选修4-5:不等式选讲]24.已知函数f(x)=2|x﹣1|﹣|x﹣a|,a>0.(1)当a=2时,求不等式f(x)≤1的解集;(2)若不等式f(x)≤5在区间[2,+∞)上有解,求a的取值范围.2015-2016学年河南省信阳市高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的1.“∀x∈R,3x>2x”的否定是()A.∀x∈R,3x≤2x B.∀x∉R,3x<2xC.∃x0∈R,3x0≤2x0 D.∃x0∉R,3x0<2x0【考点】的否定.【分析】利用全称的否定是特称写出结果即可.【解答】解:因为全称的否定是特称,所以,“∀x∈R,3x>2x”的否定是:∃x0∈R,3x0≤2x0.故选:C.2.用秦九韶算法求多项式f(x)=2x6﹣x2+2在x=2015时的值,需要进行乘法运算和加减法次数分别是()A.6,2 B.5,3 C.4,2 D.8,2【考点】秦九韶算法.【分析】由秦九韶算法的原理,可以把多项式f(x)=2x6﹣x2+2变形计算出乘法与加法的运算次数.【解答】解:∵f(x)=(((((2x)x)x)x﹣1)x)x+2,∴乘法要运算6次,加减法要运算2次.故选:A.3.“x≠1”是“x2+2x﹣3≠0”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】x2+2x﹣3≠0,解得x≠1,﹣3.即可判断出结论.【解答】解:x2+2x﹣3≠0,解得x≠1,﹣3.∴“x≠1”是“x2+2x﹣3≠0”的必要不充分条件.故选:B.4.如果甲、乙在围棋比赛中,甲不输的概率为60%,甲获胜的概率为50%,则甲、乙和棋的概率为()A.50% B.40% C.20% D.10%【考点】n次独立重复试验中恰好发生k次的概率.【分析】由条件利用互斥事件的概率加法公式,求得甲、乙和棋的概率.【解答】解:甲不输的概率,即甲获胜或甲与乙和棋的概率为60%,而甲获胜的概率为50%,故甲、乙和棋的概率为60%﹣50%=10%,故选:D.5.已知双曲线﹣=1(a>0,b>0)的一条渐近线经过点(3,),则双曲线的离心率为()A.B.2 C.或2 D.或2【考点】双曲线的简单性质.【分析】求出双曲线的渐近线方程,推出ab关系,然后求解离心率.【解答】解:双曲线﹣=1(a>0,b>0)的一条渐近线经过点(3,),可得,即,可得,解得e=.故选:A.6.“辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为()A.0 B.1 C.9 D.18【考点】程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的a,b,y的值,当y=0时满足条件y=0,退出循环,输出b的值为9.【解答】解:模拟执行程序框图,可得a=243,b=45y=18,不满足条件y=0,a=45,b=18,y=9不满足条件y=0,a=18,b=9,y=0满足条件y=0,退出循环,输出b的值为9.故选:C.7.抛物线C:y2=4x的焦点为F,准线l与x轴交于点K,点A在C上,若△AFK的面积为4,则||=()A.6 B.5 C.4 D.3【考点】抛物线的简单性质.【分析】可求出焦点F(1,0),准线l:x=﹣1,从而得到|KF|=2,这样根据△AFK的面积为4便可得到△AFK底边KF的高为4,从而得出点A的坐标为(4,4),根据两点间距离公式便可得出的值.【解答】解:如图,焦点F(1,0),准线l:x=﹣1;∴|KF|=2;∵S△AFK=4;∴△AFK底边KF上的高为4,即A点的纵坐标为4;∴A点的横坐标为4;∴A(4,4);∴.故选:B.8.已知一组数据2(x1﹣1),2(x2﹣1),…,2(x2015﹣1)的平均数为6,标准差为4,则新数据x1,x2,…,x2015的平均数与标准差分别为()A.4,1 B.3,2 C.4,2 D.3,1【考点】众数、中位数、平均数;极差、方差与标准差.【分析】利用平均数和方差公式的计算公式求解.【解答】解:∵数据2(x1﹣1),2(x2﹣1),…,2(x2015﹣1)的平均数为6,设数据数据x1,x2,…,x2015的平均数为a,则2a﹣2=6,解得:a=4,∵数据2(x1﹣1),2(x2﹣1),…,2(x2015﹣1)的标准差是4,设数据数据x1,x2,…,x2015的标准差是b,则22b4=162,解得:b=2故选:C.9.运行下面程序,输出的结果是()A.47 B.48 C.102 D.123【考点】伪代码.【分析】根据题意,模拟程序语言的运行过程,即可得出程序运行后输出的结果.【解答】解:模拟程序的运行过程,如下;A=2,B=1,A<18,A=2+1=3,B=3+1=4;A<18,A=3+4=7,B=7+4=11;A<18,A=7+11=18,B=18+11=29;A≥18,终止循环,输出C=18+29=47.故选:A.10.在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为()A.B.C.D.【考点】古典概型及其概率计算公式.【分析】先由甲同学所得评分的众数为84,则80+x=84,即x=4,再分别求出甲,乙的平均数,根据条件得到y的范围,根据概率公式计算即可.【解答】解:由茎叶图可知,甲的评分得分为:75,80,84,80+x,93,乙的评分得分为:73,82,80+x,80+y,90,由甲同学所得评分的众数为84,则80+x=84,即x=4,甲的平均分为×(75+80+84+84+93)=83.2,乙的平均分为×(73+82+84+80+y+90)=81.8+,∵甲同学所得评分的平均数不大于乙同学所得评分的平均数,∴83.2≤81.8+,解得y≥7,∵0≤y<10∴甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为=,故选:A.11.如图所示正方体ABCD﹣A1B1C1D1,设M是底面正方形ABCD内的一个动点,且满足直线C1D与直线C1M所成的角等于30°,则以下说法正确的是()A.点M的轨迹是圆的一部分B.点M的轨迹是椭圆的一部分C.点M的轨迹是双曲线的一部分D.点M的轨迹是抛物线的一部分【考点】棱柱的结构特征.【分析】由题意,设正方体的棱长为1,建立坐标系,利用直线C1D与直线C1M所成的角等于30°,可得cos30°=,化简即可得出结论.【解答】解:由题意,设正方体的棱长为1,建立坐标系,M(x,y,0),(0≤x≤1,0≤y ≤1),则=(0,﹣1,﹣1),=(x,y﹣1,﹣1),∵直线C1D与直线C1M所成的角等于30°,∴cos30°=,化简可得,∴点M的轨迹是椭圆的一部分,故选:B.12.点B,F分别是椭圆+=1(a>b>0)的上顶点与左焦点,过F作x轴的垂线与椭圆交于第二象限的一点P,H(,0)(c为半焦距),若OP∥BH(O为坐标原点),则椭圆的离心率为()A.B.C.D.【考点】椭圆的简单性质.【分析】依题意,可求得P(﹣c,),利用HB∥OP求得c2=ab,再利用椭圆的性质即可求得答案.【解答】解:依题意,作图如下:∵F(﹣c,0)是椭圆的左焦点,PF⊥OF,∴P(﹣c,),∴直线OP的斜率k=;又H(,0),B(0,b),∴直线HB的斜率k′=.∵HB∥OP,∴,∴c2=ab,又b2=a2﹣c2,∴c4=a2b2=a2(a2﹣c2),∴e4+e2﹣1=0,∴e2=,则e=,故选:B.二、填空题:本大题共4个小题,每小题5分,共20分,把答案填在答题卡的相应位置13.先对112名学生随机地从1~112编号,用系统抽样方法抽取一个容量为16的样本,按编号平均分成16组(1~7,8~14,15~21,…,106~112),若第12组抽到的编号为82,则第4组中抽出的编号为26.【考点】系统抽样方法.【分析】由总体容量及组数求出间隔号,即可求出第4组中抽出的编号.【解答】解:总体为112个个体,依编号顺序平均分成16个小组,则间隔号为7,所以在第4组中抽取的号码为82﹣(12﹣4)×7=26.故答案为:26.14.已知抛物线C:y2=8x的焦点F与双曲线E:﹣=1(a>0,b>0)的一个焦点重合,C的准线与E交于A,B,若||=6,则E的方程为x2﹣=1.【考点】抛物线的简单性质;双曲线的简单性质.【分析】求出抛物线C:y2=8x的焦点F(2,0),准线方程为x=﹣2,利用抛物线C:y2=8x 的焦点F与双曲线E:﹣=1(a>0,b>0)的一个焦点重合,得a2+b2=4①,x=﹣2时,y=3,代入,可得﹣=1②,由①②解得a,b,即可求出E的方程.【解答】解:抛物线C:y2=8x的焦点F(2,0),准线方程为x=﹣2,∵抛物线C:y2=8x的焦点F与双曲线E:﹣=1(a>0,b>0)的一个焦点重合,∴a2+b2=4①x=﹣2时,y=3,代入,可得﹣=1②,由①②解得a=1,b=,∴E的方程为x2﹣=1.故答案为:x2﹣=1.15.若八进制数等于二进制数,则a=7,b=1.【考点】进位制.【分析】由题意知1×82+8×2+a=1×26+b×24+1×22+2+1,从而解得.【解答】解:由题意知,1×82+8×2+a=1×26+b×24+1×22+2+1,即64+16+a=64+16b+7,故b=1,a=7,故答案为:7,1.16.在平面直角坐标系xOy中,从区域Ω:内随机抽取一点P,则P点到坐标原点的距离大于的概率为1﹣.【考点】几何概型;简单线性规划.【分析】作出不等式组对应的平面区域,由几何概型的公式可知概率即为面积之比,易得答案.【解答】解:作出不等式组对应的平面区域如图,(△AOB内部),则P点到坐标原点的距离大于的部分为△AOB内圆外部分,则B(1,1),△AOB的面积S==1,扇形的面积S==,则△AOB内圆外部分的面积S=1﹣,则对应的概率P==1﹣,故答案为:1﹣.三、解答题:本大题共5小题,满分60分,解答应写出文字说明,证明过程或演算步骤. 17.p:对任意实数x,都有x2+2ax+a≥0恒成立;q:x﹣4y﹣a=0与抛物线x2=4y有交点,若“¬(p∨q)”为假,“p∧q”为假,求实数a的取值范围.【考点】复合的真假.【分析】分别求出p,q为真时的a的范围,通过讨论p,q的真假,求出a的范围即可.【解答】解:若p是真,则△=(2a)2﹣4a≤0,解得:0≤a≤1,若q是真,则,得:x2﹣x+a=0有实数解,∴△=(﹣1)2﹣4a≥0,解得:a≤,由¬(p∨q)”为假,“p∧q”为假,得p,q一真一假,p真q假时,<a≤1,p假q真时,a<0,综上,a∈(﹣∞,0)∪(,1].18.登山运动是一项有益身心健康的活动,但它受山上气温的限制.某登山爱好者为了了解某山上气温y(℃)与相应山高x(km)之间的关系,随机统计了5次山上气温与相应山高,如下表:气温y(℃)18 16 10 4 2山高(km) 2.6 3 3.4 4.2 4.8(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程:=bx+;(2)若该名登山者携带物品足以应对山上﹣2.4℃的环境,试根据(1)中求出的线性回归方程预测,这名登山者最高可以攀登到多少千米处?(参考公式:=,=﹣)【考点】线性回归方程.【分析】(1)根据回归系数公式计算回归系数,得到回归方程;(2)把y=﹣2.4代入回归方程求出x的估计值.【解答】解:(1)=×(2.6+3+3.4+4.2+4.8)=3.6,=(18+16+10+4+2)=10.=(﹣1)×8+(﹣0.6)×6+(﹣0.2)×0+0.6×(﹣6)+1.2×(﹣8)=﹣24.8.=(﹣1)2+(﹣0.6)2+(﹣0.2)2+0.62+1.22=3.2.∴==﹣7.75,=10﹣(﹣7.75)×3.6=37.9.∴y关于x的线性回归方程是=﹣7.75x+37.9.(2)当y=﹣2.4时,有﹣2.4=﹣7.75x+37.9,解得x=5.2.所以这名登山者最高可以攀登到5.2千米处.19.如图,在侧棱和底面垂直的三棱柱ABC﹣A1B1C1中,AB=1,AC=,BC=2,AA1=,点P为CC1的中点.(1)求证:A1C⊥平面ABP;(2)求平面ABP与平面A1B1P所成二面角的正弦值.【考点】二面角的平面角及求法;直线与平面垂直的判定.【分析】(1)推导出AA1⊥AB,AB⊥AC,从而AB⊥A1C,再推导出A1C⊥AP,由此能证明A1C⊥平面ABP.(2)以A为坐标原点,以AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出平面ABP与平面A1B1P所成二面角的正弦值.【解答】证明:(1)在侧棱和底面垂直的三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∵AB⊂平面ABC,∴AA1⊥AB,∵AB=1,AC=,BC=2,AA1=,点P为CC1的中点,∴BC2=AB2+AC2,∴AB⊥AC,又AA1∩AC=A,∴AB⊥A1C,在矩形ACC1A1中,A1C==3,AP==,在Rt△A1CA中,sin∠A1CA==,在Rt△PAC中,cos=,∴sin∠A1CA=cos∠PAC,∴∠PAC+∠A1CA=90°,∴A1C⊥AP,∵AP∩AB=A,∴A1C⊥平面ABP.解:(2)由(1)知AB⊥AC,AA1⊥AB,AA1⊥AC,以A为坐标原点,以AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),A1(0,0,),C(0,,0),P(0,,),=(1,0,0),,设平面A1B1P的法向量为=(x,y,z),则,令y=1,得=(0,1,),由(1)知平面ABP的一个法向量为=(0,﹣,),∴cos<>===,∴sin<>==.即平面ABP与平面A1B1P所成二面角的正弦值为.20.某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.(1)求身高分别在区间[165,170),[170,175),[175,180)的人数,并将频率分布直方图补充完整;(2)用分层抽样的方法从身高在区间[155,160),[170,175),[175,180)中抽取7人,现在从这抽出的7人中再抽取2人进行问卷调查,求身高在区间[170,175)中至少有1人进行问卷调查的概率.【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图.【分析】(Ⅰ)先求出身高在区间[165,180]的频率,由此能求出身高分别在[165,170),[170,175),[175,180]的人数,并能将频率分布直方图补充完整.(Ⅱ)应从区间[155,160),[170,175),[175,180]内分别抽取的人数分别为1人,4人,2人,身高在区间[170,175)中至少有1人进行问卷调查的对立事件是身高在区间[170,175)中没有人进行问卷调查,由此利用对立事件概率计算公式能求出身高在区间[170,175)中至少有1人进行问卷调查的概率.【解答】解:(Ⅰ)身高在区间[165,180]的频率为1﹣5×(0.01+0.07)=0.6,设身高在区间[165,170),[170,175),[175,180)内的频率分别为a,b,c,由题意得,解得a=0.3,b=0.2,c=0.1,∴身高分别在[165,170),[170,175),[175,180]的人数为60,40,20.将频率分布直方图补充完整,如右图.(Ⅱ)身高在[155,160),[170,175),[175,180]的人数分别为10,40,20,∴应从区间[155,160),[170,175),[175,180]内分别抽取的人数分别为1人,4人,2人,现在从这抽出的7人中再抽取2人进行问卷调查,基本事件总数n==21,身高在区间[170,175)中至少有1人进行问卷调查的对立事件是身高在区间[170,175)中没有人进行问卷调查,∴身高在区间[170,175)中至少有1人进行问卷调查的概率:p=1﹣=.21.已知点A(1,0),点P是圆F:(x+1)2+y2=20上一动点,线段AP的垂直平分线交FP 于点M,记点M的轨迹为曲线C.(1)求曲线C的方程;(2)已知点B(0,),D(﹣4,0),若直线l:y=kx+与曲线C有两个不同的交点G 和H,是否存在常数k,使得向量(+)⊥(O为坐标原点)?如果存在,求出k 的值;如果不存在,请说明理由.【考点】椭圆的简单性质.【分析】(1)求得F(﹣1,0),圆F的半径,运用垂直平分线的性质和椭圆的定义,即可得到所求轨迹方程;(2)将直线y=kx+代入椭圆4x2+5y2=20,设G(x1,y1),H(x2,y2),运用韦达定理和判别式,假设(+)⊥,运用向量垂直的条件:数量积为0,解方程可得k,即可判断.【解答】解:(1)由题意可得F(﹣1,0),圆F的半径为2,|MF|+|MA|=|MF|+|MP|=|FP|=2>|FA|=2,由椭圆的定义可得,M的轨迹为以F,A为焦点,长轴长为2的椭圆,即有a=,c=1,b==2,则曲线C的方程为+=1;(2)将直线y=kx+代入椭圆4x2+5y2=20,可得(4+5k2)x2+10kx+5=0,①设G(x1,y1),H(x2,y2),可得x1+x2=﹣,+=(x1+x2,y1+y2),y1+y2=k(x1+x2)+2=,由B(0,),D(﹣4,0),可得=(﹣4,﹣),若(+)⊥,即有(+)•=0,即有﹣4(x2+x1)﹣(y1+y2)=0,可得﹣4•(﹣)﹣=0,解得k=,当k=时,方程①的判别式为500k2﹣20(4+5k2)=0不满足题意.故不存在这样的常数k,使得(+)⊥.请考生在22题、23题、24题三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑[选修4-1:几几何证明选讲]22.如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.(1)证明:AD2=AB•DP;(2)若PD=3AB=3,BQ=,求弦CD的长.【考点】与圆有关的比例线段.【分析】(1)由已知条件推导出△DAP∽△ABD,从而,由此能证明AD2=AB•DP.(2)推导出DQ=3,QA=,PA=2,由此能求出CD.【解答】证明:(1)∵AB∥CD,∴∠QAB=∠ADB,∵QA是⊙O的切线,∴∠QAB=∠ADB,∴∠APD=∠ADB,又PA是⊙O的切线,∴∠PAD=∠DBA,∴△DAP∽△ABD,∴,∴AD2=AB•DP.解:(2)∵AB∥CD,且PD=2AB,∴,由BQ=,知DQ=3,∵QA是⊙O的切线,∴QA2=QB=6,∴QA=,由,知PA=2,又PA是⊙O的切线,∴PA2=PD•PC,即24=3PC,解得PC=8,∴CD=8﹣3=5.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,曲线C1的方程为+y2=1,以坐标原点为极点,x轴正半轴为极轴,并取相同的单位长度建立坐标系,曲线C2的极坐标方程为2ρ=sinθ.(1)写出曲线C1的参数方程,并求出C2的直角坐标方程;(2)若P,Q分别是曲线C1,C2上的动点,求||的取值范围.【考点】椭圆的简单性质.【分析】(1)由椭圆性质能示出曲线C1的参数方程;由ρ2=x2+y2,y=ρsinθ,能求出C2的直角坐标方程.(2)设P(),曲线C2的圆心为C2,由C2(0,),由此利用两点间距离公式能求出|PQ|的取值范围.【解答】解:(1)∵在直角坐标系xOy中,曲线C1的方程为+y2=1,∴曲线C1的参数方程为,α为参数,∵曲线C2的极坐标方程为2ρ=sinθ,由2ρ=sinθ,得2ρ2=ρsinθ,∴,∴C2的直角坐标方程式x2+(y﹣)2=.(2)设P(),曲线C2的圆心为C2,由(1)知C2(0,),∴|PF2|====,当sinα=1时,|PC2|取最小值,此时|PQ|min==,当sinα=﹣时,|PC2|取得最大值,此时|PQ|max=+=,综上知,|PQ|的取值范围为[,].[选修4-5:不等式选讲]24.已知函数f(x)=2|x﹣1|﹣|x﹣a|,a>0.(1)当a=2时,求不等式f(x)≤1的解集;(2)若不等式f(x)≤5在区间[2,+∞)上有解,求a的取值范围.【考点】绝对值不等式的解法;分段函数的应用.【分析】(1)通过讨论x的范围得到不等式组,解出即可;(2)法一:求出f(x)的分段函数,通过讨论a的范围,求出f(x)的最小值,从而求出a的范围即可;法二:求出f(x)的分段函数,通过讨论x的范围得到关于a的不等式组,求出a的范围即可.【解答】解:(1)a=2时,f(x)≤1可化为2|x+1|﹣|x﹣2|﹣1≤0,∴或或,解得:﹣5≤x≤,故不等式的解集是:{x|﹣5≤x≤};(2)法一:由a>0,得f(x)=,要使不等式f(x)≤5在区间[2,+∞)上有解,则f(x)在区间[2,+∞)上的最小值f(x)min≤5,当0<a<2时,f(x)min=4+a≤5,解得:0<a≤1,a≥2时,f(x)min=8﹣a≤5,解得:a≥3,∴a的范围是(0,1]∪[3,+∞);法二:由a>0,得f(x)=,要使不等式f(x)≤5在区间[2,+∞)上有解,只需3x+2﹣a≤5,﹣1<x<a①或x+2+a≤5,x≥a②在[2,+∞)有解,由①得:x≤1+,﹣1<x<a,即,即a≥3,由②式得:x≤3﹣a,x≥a,要使②式在区间[2,+∞)有解,则,即0<a≤1,综上,a的范围是(0,1]∪[3,+∞).。

2017-2018学年高三第四次联考•理综卷(物理部分)二、选择题:14.一个带电粒子在匀强磁场中做匀速圆周运动,如果磁感应强度的大小变为原来的2倍,则 A.粒子的速率加倍,周期减半 B.粒子的角速度加倍,轨道半径减半 C.粒子的速率不变,加速度减半D.粒子的速率不变,周期不变15.如图所示,一根导线制成的等腰直角三角形线框ABC 以速度υ匀速穿过宽度为2L 的匀强磁场,线框AB 边的长度为 2L,AB 两端的电压AB U 随线框位移变化关系图象正确的是16.如图所示,理想变压器原、副线圈匝数比为m 1:m 2 = 4:1,原线圈回路中的电阻A 与副线圈回路中的负载电阻B 的阻值相等。
a 、b 端加一定交变电压后,下列说法中正确的是A.两电阻的电功率之比P A :PB b ==1:1,两电阻两端电压之比 Ua:Ub ==4:1B.两电阻的电功率之比P A :P B = 1:1,两电阻两端电压之比U A :U B = l:4C.两电阻的电功率之比P A :P B = 1:16,两电阻两端电压之比U A :U B = 4:1D.两电阻的电功率之比P A :P B = 1:16,两电阻两端电压之比U A :U B =1:417.如图甲所示,DO 是水平的,AB 是斜面,一个物体从高为h 的斜面体的顶端A 以初速度0υ开始沿AB 滑下,当物体到达B 点时速度大小也为0υ。
如果把图甲中的斜面改为动摩擦因数相同的曲面AC,如图乙所示,相同的物体从高为h 的斜面体的顶端A 以初速度0υ。
开始沿AC 滑下,当物体到达C 点时速度大小也为0υ。
现让同样的物体以20υ的速度分别从顶端A开始沿AB 、AC 滑下,若沿斜面到达B 点时速度大小为1υ,沿曲面到达C 点时速度大小为2υ,则它们速度大小关系是A. 1υ = 20υ>2υB. 1υ=20υ=2υC. 1υ=2υ<20υD. 1υ>2υ>20υ18.静止的城市绿化洒水车,由横截面积为S 的水龙头喷嘴水平喷出水流,水流从射出喷嘴到落地经历的时间为t 水流落地点和喷嘴连线与水平地面间的夹角为θ,忽略空气阻力(重力加速度g 取10 m/s 2), 以下说法正确的是 A.水流射出喷嘴时的速度大小为以θtan gB.水流落地时的速度大小为θtan 2gtC.水流落地时位移大小为θtan 2gtD.空中水柱的水量(体积)为θtan 22Sgt19.如图所示,A 、B 是等量异种电荷连线上的两点,ABCD 是关于两电荷连线的垂直平分线对称的矩形,则关于A 、B 、C 、D 各点的电场强度大小A E 、B E 、C E 、D E 及各点的电势A ϕ、B ϕ、C ϕ、D ϕ的说法正确的是A. A ϕ>D ϕ>C ϕ>B ϕB. A E =B E <C E =D EC.若电子由A 点运动到C 点,电场力做负功D.若电子由B 点运动到D 点,电场力做负功20.如图甲所示,一物块在水平拉力的作用下由静止开始运动,物块速度与时间关系的t -υ图象如图乙 所示,已知物块的质量kg ,物块与水平面间的动摩擦因数2.0=μ,重力加速度g 取10 m/s 2,则A.物块在位移x=1m 时约速度大小为2m/sB.物玦在前2s 时间内受到的拉力大小为4NC.物块在后2s 时间内受到的拉力做功为25JD.物块在t=ls 时受到的拉力的功率为6W21.随着我国探月三步走计划的实现,中华儿女到月球上去旅游不再是梦想,将来有一天你会成功登上月球。
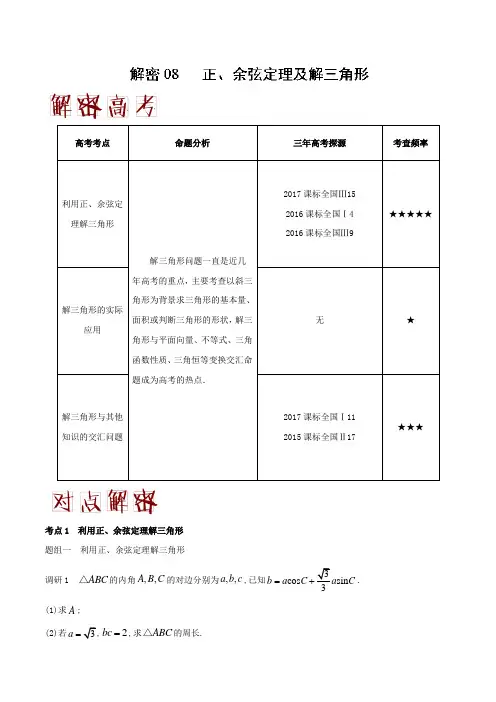
考点1 利用正、余弦定理解三角形 题组一 利用正、余弦定理解三角形调研1 ABC △的内角,,A B C 的对边分别为,,a b c ,已知cos sin 3b a C a C =+. (1)求A ;(2)若a =2bc =,求ABC △的周长.【解析】(1)cos sin b a C C =,,sin sin cos sin B A C A C ∴=+由正弦定理得, sin cos cos sin sin cos sin A C A C A C A C ∴+=,tan A =即()0πA ∈又,,∴π3A =. (2)22π,32cos3b c bc =+-由余弦定理得,()233b c bc +-=即, 2bc =又,3b c ∴+=,故3ABC △的周长为.调研2 如图,ABC △中,角,,A B C 的对边分别为,,a b c ,cb=.(1)求角B 的大小;(2)点D 为边AB 上的一点,记BDC θ∠=,若ππ,2,2CD AD a θ<<===,求sin θ与b 的值. 【解析】(1)c b =,sin sin CB =, 因为sin 0C >,所以sin tan cos B B B ==因为0πB <<,所以π6B =. (2)在BCD △中,因为sin sin sin CD BC a B BDC θ==∠,所以25sin sin B BDC=∠,所以sin θ=,因为θ为钝角,所以ADC ∠为锐角,所以()cos cos πADC θ∠=-==在ADC △中,由余弦定理,得2222cos(π)5425b AD CD AD CD θ=+-⨯-=+-=,所以b =☆技巧点拨☆利用正、余弦定理解三角形的关键是利用定理进行边角互化.即利用正弦定理、余弦定理等工具合理地选择“边”往“角”化,还是“角”往“边”化.若想“边”往“角”化,常利用“a =2R sin A ,b =2R sin B ,c =2R sin C ”;若想“角”往“边”化,常利用sin A =a 2R ,sin B =b 2R ,sin C =c 2R ,cos C =a 2+b 2-c 22ab等.题组二 与三角形面积有关的问题调研3 如图,在ABC △中,点D 在边AB 上,CD ⊥BC ,AC =53,CD =5,BD =2AD .(1)求AD 的长; (2)求ABC △的面积.【解析】(1) 在ABC △中,因为BD =2AD ,设AD =x (x >0),所以BD =2x .在BCD △中,因为CD ⊥BC ,CD =5,BD =2x ,所以cos ∠CDB =CD BD =52x.在ACD △中,因为AD =x ,CD =5,AC =53,所以cos ∠ADC =AD 2+CD 2-AC 22×AD ×CD =.因为∠CDB +∠ADC =π,所以cos ∠ADC =-cos ∠CDB ,=-52x ,解得x =5.所以AD 的长为5.(2)由(1)求得AB =3x =15,BC =4x 2-25=5 3. 所以cos ∠CBD =BCBD =32, 从而sin ∠CBD =12.所以S △ABC =12×AB ×BC ×sin∠CBA =12×15×53×12=7534.题组三 三角形形状的判断调研4 ABC △中,角,,A B C 的对边分别是,,a b c ,且cos sin a C C b c =+. (1)求A ;(2)若2,a ABC =△试判断此三角形的形状.【解析】(1)由正弦定理及cos sin a C C b c =+得,sin cos sin sin sin A C A C B C =+,即()sin cos sin sin sin A C A C A C C =++sin cos sin sin A C A C C -=,∵sin 0C >,()1cos 1sin 302A A A -=⇒-︒=, ∵0180A <<︒︒,∴3030150A ︒-︒<-<︒, ∴303060A A -=︒⇒=︒︒.(2)1sin 42S bc A bc ===, 由余弦定理得:2222cos a b c bc A =+-=()23b c bc +-()241242b c b c b c ⇒=+-⇒+=⇒==, ∵60A =︒,∴60B C ==︒, 故ABC △是等边三角形.☆技巧点拨☆判断三角形的形状有以下几种思路:(1)转化为三角形的边来判断,可简记为“化角为边”; (2)转化为角的三角函数(值)来判断,可简记为“化边为角”.提醒:在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免造成漏解.考点2 解三角形的实际应用 题组 解三角形的实际应用调研1 某新建的信号发射塔的高度为AB ,且设计要求为:29米AB <<29.5米.为测量塔高是否符合要求,先取与发射塔底部B 在同一水平面内的两个观测点,C D ,测得60BDC ∠=︒,75BCD ∠=︒,40CD =米,并在点C 处的正上方E 处观测发射塔顶部A 的仰角为30°,且1CE =米,则发射塔高AB =A .()1米B .()1米C .()1米D .()1米【答案】A【解析】画出草图,如图所示,在BDC △中,45DBC ∠=︒,由正弦定理得sin sin BDCBC CD DBC∠=⨯=∠;在AEF △中,30AEF ∠=︒,所以tan30AF EF =︒=米,所以11)AB AF =+=米.选A .☆技巧点拨☆高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形或者在空间构造三棱锥,再依据条件利用正、余弦定理解其中的一个或者几个三角形,从而求出所需测量物体的高度.调研2 海中一小岛C 的周围()8nmile 内有暗礁,海轮由西向东航行至A 处测得小岛C 位于北偏东75︒,航行8nmile 后,于B 处测得小岛C 在北偏东60︒(如图所示).(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.(2)如果有触礁的危险,这艘海轮在B 处改变航向为东偏南(0αα>)方向航行,求α的最小值.附:tan752︒=+【解析】(1)如图1,过点作直线AB 的垂线,交直线AB 于点D .由已知得15,30,15A CBD ACB ∠=︒∠=︒∠=︒, 所以8nmile AB BC ==,所以在Rt BCD △中,sin CD AB CBD =⋅∠=184nmile 2⨯=.又48<,所以海轮有触礁的危险.(2)如图2,延长CD 至E ,使()8nmile CE =,故()12nmile DE =,由(1)得tan30CDBD ==︒,所以tan 2DE DBE BD ∠===因为tan752︒=所以tan152︒==.即tan tan15DBE ∠=︒,所以15DBE ∠=︒. 故海轮应按东偏南15°的方向航行.☆技巧点拨☆解决此类问题的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.解题时应认真审题,结合图形去选择正、余弦定理,这是最重要的一步.考点3 解三角形与其他知识的交汇问题 题组一 解三角形与三角恒等变换相结合调研1 在ABC △中,,,a b c 分别为角,,A B C 的对边,已知7,2c ABC =△又tan tan A B +)tan tan 1.A B =-(1)求角C 的大小; (2)求a b +的值.【解析】(1)因为)tan tan tan tan 1,A B A B +=-所以()tan A B +=tan tan 1tan tan A BA B+=-又因为,,A B C 为ABC △的内角,所以2π,3A B +=所以π.3C =(2)由1sin 22ABC S ab C ==△及π,3C =得6,ab =又()2222221cos 222a b c ab a b c C ab ab +--+-===,7,2c =所以11.2a b +=题组二 解三角形与平面向量相结合调研2 如图,在ABC △中,已知点D 在边BC 上,且0AD AC ⋅=,sin 3BAC ∠=,AB =BD =.(1)求AD 的长; (2)求cos C .【解析】(1)因为0,AD AC ⋅=所以,AD AC ⊥所以πsin sin cos ,2BAC BAD BAD ⎛⎫∠=+∠=∠⎪⎝⎭即cos 3BAD ∠=. 在ABD △中,由余弦定理,可知2222cos BD AB AD AB AD BAD =+-⋅⋅∠, 即28150,AD AD -+=解得5,AD =或3AD =. 因为,AB AD >所以3AD =. (2)在ABD △中,由正弦定理,可知,sin sin BD ABBAD ADB=∠∠又由cos 3BAD ∠=可知1sin ,3BAD ∠=所以sin sin 3AB BAD ADB BD ∠∠==.因为π,2ADB DAC C C ∠=∠+=+所以cos C =.1.(2017-2018学年陕西省西安中学高三上学期期中考试)已知ABC △中,,则A.B.C.D.【答案】A△中,角的对边分别为,若2.(2017-2018学年广东省百校联盟高三第二次联考)在ABC,且,则A.B.C.D.【答案】B【解析】因为,所以.因为,且,所以由余弦定理可知,,解得,即.故选B.△中,内角的3.(2017-2018学年天津市静海县第一中学高三12月学生学业能力调研考试)在ABC△的面积为对边分别为,若,则ABCA.3 B.C.D.【答案】C4.(2017-2018学年广东省珠海市珠海二中、斗门一中高三上学期期中考试)如图,从气球上测得正前方的河流的两岸,的俯角分别为,,此时气球的高是,则河流的宽度等于A.m B.mC.m D.m【答案】C【解析】如图,由题意得,,,所以,,所以.选C.5.(2018届广东省揭阳市高三学业水平期末考试)ABC△的内角A、B、C的对边分别为a、b、c,已知ABC△的面积为a=2,b=3,则sinaAA.B.C.D.或【答案】D6.(2017-2018学年福建省厦门外国语学校高三上学期第三次阶段考试)在ABC△中,分别为内角的对边, 且,则A.B.C.D.【答案】B【解析】因为,且,所以两式相减可得==,因为,所以,则2π3A=,此时,则b=c,所以,故选B.7.(2017-2018学年广西柳州市高三毕业班上学期摸底联考)在锐角ABC△中,角所对的边分别为若则角等于__________.【答案】8.(2017-2018学年全国18名校大联考高三第二次联考)已知()cos17,cos73AB=︒︒,()2cos77,2cos13BC=︒︒,则ABC△的面积为__________.【解析】由题意得1c AB==,2a CB==,·BC BA=2cos77cos172cos13cos73-︒︒-︒︒=()2cos77cos17sin77sin17-︒︒+︒︒=()2cos 7717-︒-︒=1-;而·cos BC BA AB CB B ==2cos B =1-,解得1cos 2B =-,所以sin B =所以ABC △的面积1sin 2S ac B ==. 9.(2018届河南省中原名校高三上学期第五次联考)已知ABC △中,π2A =,角A B C 、、所对的边分别为a b c 、、,点D 在边BC 上,1AD =,且BD =2,DC BAD ∠=2DAC ∠,则sin sin BC=__________. 【解析】由π2A =及2BAD DAC ∠=∠可得BAD ∠=π,3DAC ∠=π6, 由2BD DC =,令,2DC x BD x ==则,因为1AD =,在ADC △中,由正弦定理可得1πsin sin 6x C =,所以sin C =12x,在ABD △中,πsin3sin 2B x ==所以sin sin B C 10.(2017-2018学年河南省漯河市高级中学高三上学期第四次模拟考试)如图,为了测量河对岸A B 、两点之间的距离,观察者找到一个点C ,从点C 可以观察到点A B 、;找到一个点D ,从点D 可以观察到点A C 、;找到一个点E ,从点E 可以观察到点B C 、.并测量得到一些数据:2CD =,CE =45D ∠=︒,105ACD ∠=︒,48.19ACB ∠=︒,75BCE ∠=︒,60E ∠=︒,则A B 、两点之间的距离为__________.(其中cos48.19︒取近似值23)11.(2017-2018学年广西贵港市高三上学期12月联考)在ABC △中,,,a b c 分别是内角,,A B C 的对边,且()3cos ,sin cos cos sin 05B A B c A B =--⋅=. (1)求边b 的值;(2)求ABC △的周长的最大值.【答案】(1) 1b =;1.【解析】(1)由()sin cos cos sin 0A B c A B --⋅=得sin cos cos sin sin A B A B c B +=.∴sin sin C c B =,即sin sin CB c=. 由正弦定理得sin sin B Cb c=,故1b =. (2)由余弦定理得22262cos 15a cb ac B ac +=+=+.∴()22161611552a c a c ac +⎛⎫+=+≤+ ⎪⎝⎭,∴a c +≤所以当a c =时, ABC △1.12.(2017-2018学年河南省郑州市高中毕业年级第一次质量预测)在ABC △中,角,,A B C 的对边分别为,,a b c ,且2cos 2c B a b =+.(1)求角C ;(2)若ABC △的面积为S =,求ab 的最小值. 【答案】(1)2π3;(2) 12.13.(2017-2018学年皖江名校12月份高三大联考)在ABC △中,设内角,,A B C 的对边分别为,,a b c ,向量()cos ,sin A A =m ,向量)sin ,cos ,2A A =+=n m n .(1)求角A 的大小;(2)若b =且c =,求ABC △的面积.【答案】(1) π4;(2)16. 【解析】(1)2+m n =()()22cos sin sin cos A AA A ++=)4cos sin 4A A +-=+π4cos 4A ⎛⎫+⎪⎝⎭, ππ44cos 4,cos 0,44A A ⎛⎫⎛⎫∴++=∴+= ⎪ ⎪⎝⎭⎝⎭又()0,πA ∈,∴ππ42A +=,则π4A =.(2)由余弦定理得2222cos a b c bc A =+-,即()222π2cos4a =+-⨯,解得a =∴8c =,∴18162ABC S =⨯=△. 14.(2018届民族大学附属中学高三上学期期末考试)ABC △的内角A 、B 、C 所对的边分别为,,a b c ,且sin sin a A b B +=sin sin .c C B(1)求角C ;(2)πcos 4A B ⎛⎫-+ ⎪⎝⎭的最大值. 【答案】(1)π4;(2) 2.15.(2017-2018学年山东省枣庄市第三中学高三一调模拟考试)设()f x =π1cos sin .22222x x x ⎫⎛⎫++-⎪ ⎪⎭⎝⎭(1)求()f x 的单调递增区间;(2)在ABC △中,,,a b c 分别为角,,A B C 的对边,已知π1,32f A a ⎛⎫+=-= ⎪⎝⎭求ABC △面积的最大值.【答案】(1) 2ππ2π,2π,33k k k ⎡⎤-++∈⎢⎥⎣⎦Z ;1.(2016新课标全国Ⅰ文科)ABC △的内角A 、B 、C 的对边分别为a 、b 、c.已知a =2c =,2cos 3A =,则b=A BC .2D .3【答案】D【解析】由余弦定理得3222452⨯⨯⨯-+=b b ,解得3=b (31-=b 舍去),故选D. 【名师点睛】本题属于基础题,考查内容单一,根据余弦定理整理出关于b 的一元二次方程,再通过解方程求b .运算失误是基础题失分的主要原因,请考生切记!2.(2017新课标全国Ⅰ文科)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin sin (sin cos )0B A C C +-=,a =2,c C =A .π12 B .π6 C .π4D .π3【答案】B3.(2017新课标全国Ⅲ文科)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b c =3,则A =_________. 【答案】75°4.(2015新课标全国Ⅱ文科)ABC △中,D 是BC 上的点,AD 平分∠BAC ,BD =2DC . (I )求sin sin BC∠∠ ;(II )若60BAC ∠=,求B ∠. 【解析】(I )由正弦定理得sin sin AD BD B BAD =∠∠,sin sin AD DCC CAD=∠∠,因为AD 平分BAC ∠,2BD DC =,所以sin 1sin 2B DC C BD ∠==∠.(II )因为180(),60C BAC B BAC ∠=-∠+∠∠=,所以1sin sin()sin(60)cos sin 22C BAC +B +B B B ∠=∠∠=∠=∠+∠. 由(I )知2sin sin B C ∠=∠,所以tan B =∠,30B =∠. 【名师点睛】三角形中的三角变换常用到诱导公式,如sin()sin ,cos()cos A B C A B C +=+=-,tan()tan A B C +=-就是常用的结论.另外,利用正弦定理或余弦定理处理条件中含有边或角的等式,常考虑对其实施“边化角”或“角化边”.。

2017-2018学年 高三数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.集合{}2|,M y y x x R ==-∈,{}22|2,N x x y x R =+=∈,则M N ⋂=( ) A .()(){}1,1,1,1--- B .{}1- C .[]1,0- D.⎡⎤⎣⎦2.命题:p “0x R ∃∈,使得200310x x -+≥”,则命题p ⌝为( )A .x R ∀∈,都有2310x x -+≤B .x R ∀∈,都有2310x x -+<C .0x R ∃∈,使得200310x x -+≤D .0x R ∃∈,使得200310x x -+<3.已知函数()ln(1)xf x e x =++的图像在()()0,0f 处的切线与直线40x ny -+=垂直,则n 的值为()A .B .C .D .4.已知向量()2,1a =,()1,3b =,则向量2a b -与a 的夹角为( ) A . B . C. D .5.在《张丘建算经》有一道题:“今有女子不善织布,逐日所织的布同数递减.初日织五尺,末一日织一尺,计织三十日,问共织布几何?”()A .30尺B .60尺 C.90尺 D .120尺6.已知命题:p “()0,x ∀∈+∞,ln 43x x +≥”;命题:q “()00,x ∃∈+∞,001842x x +≤”.则下列命题为真命题的是() A .()p q ⌝∧ B .p q ∧ C.()p q ∨⌝ D .()()p q ⌝∧⌝ 7.已知函数()sin 0,02y x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示,则,ωϕ的值分别是()A .1,26π B .1,6π C.1,3π D .1,23π8.若等比数列{}n a 的前项和为n S ,且23S =,663S =,则5S =() A .33- B .15 C.31 D .33-或319.已知实数,x y 满足12724y x x x y ⎧≥⎪⎪≤⎨⎪-≥⎪⎩,则23z x y =-的最小值为( )A .32-B .16- C.10- D .6-10.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为()A.)91π++.)928π+-C.)92π++.)918π++-11.定义在实数集R 上的函数()f x ,满足()()()22f x f x f x =-=-,当[]0,1x ∈时,()2x f x x =⋅.则函数()()lg g x f x x =-的零点个数为()A .99B .100 C.198 D .200 12.已知函数()f x 的定义域为R ,()'fx 为函数()f x 的导函数,当[)0,x ∈+∞时,()'2sin cos 0x x f x ->且x R ∀∈,()()cos 21f x f x x -++=.则下列说法一定正确的是()A .15324643f f ππ⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭ B .15344643f f ππ⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭C.3134324f f ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭ D .1332443f f ππ⎛⎫⎛⎫-->- ⎪ ⎪⎝⎭⎝⎭第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知函数()[](]213,3,030,3x x f x x ⎧-+∈-⎪=∈,则()33f x -=⎰ . 14.如图,已知ABC ∆中,D 为边BC 上靠近B 点的三等分点,连接AD ,E 为线段AD 的中点,若CE mAB nAC =+,则m n += .15.已知三棱锥A BCD -中,AB CD ==,BC AD ==,AC BD ==则三棱锥A BCD -的外接球的表面积为 .16.已知定义在()0,+∞的函数()()41f x x x =-,若关于x 的方程()()()2320f x t f x t +-+-=有且只有3个不同的实数根,则实数t 的取值集合是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分10分)如图,D 是ABC ∆内一点,角,,A B C 的对边分别是,,a b c ,且满足2D B ∠=∠,1cos 3D ∠=-,2AD =,ACD ∆的面积是.(1)求线段AC 的长;(2)若BC =,求线段AB 的长.18. (本小题满分12分)在一次水下考古活动中,某一潜水员需潜水50米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为x 米/分钟,每分钟用氧量为21100x 升;②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.3升;③返回水面时,平均速度为12x 米/分钟,每分钟用氧量为0.32升.潜水员在此次考古活动中的总用氧量为y 升. (1)如果水底作业时间是10分钟,将y 表示为x 的函数;(2)若[]6,10x ∈,水底作业时间为20分钟,求总用氧量y 的取值范围; (3)若潜水员携带氧气13.5升,请问潜水员最多在水下多少分钟(结果取整数)? 19. (本小题满分12分)已知函数()2332cos 2sin cos 232f x x x x ππ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭. (1)求函数()f x 的单调递减区间; (2)将函数()f x 的图象向右平移3π个单位长度,得到函数()g x 的图像,求当0,2x π⎡⎤∈⎢⎥⎣⎦时,函数()g x 的值域.20. (本小题满分12分) 已知数列{}n a 满足137a =,1341n n n a a a +=+,n N *∈. (1)求证:数列12n a ⎧⎫-⎨⎬⎩⎭是等比数列,并且求出数列{}n a 的通项公式; (2)求数列n n a ⎧⎫⎨⎬⎩⎭的前n 项和n S .21. (本小题满分12分)已知正三棱柱'''ABC A B C -如图所示,其中G 是BC 的中点,,D E 分别在线段AG ,'AC上运动,使得//DE 平面''BCC B ,F 是'BB 上的一点,且''284CC BC B F ===. (1)求证:''C F B D ⊥;(2)求二面角'''A B C C --的余弦值; (3)求线段DE 的最小值.22. (本小题满分10分) 已知函数()21ln 2f x x m x =-. (1)求函数()f x 的极值;(2)若1m ≥,试讨论关于x 的方程()()21f x x m x =-+的解的个数,并说明理由.试卷答案一、选择题1-5:DBDCC 6-10:AADBD 11、12:BB1.【解析】由2y x =-,x R ∈得0y ≤,所以集合(],0M ∈-∞,由222x y +=,x R ∈得N ⎡=⎣,所以M N ⎡⎤⋂=⎣⎦,故选D .3.【解析】依题意得,()'11x f x e x =++,所以()'0112f =+=.显然0n ≠,直线40x ny -+=的斜率为1n ,所以121n⋅=-,解得2n =-,故选D . 4. 【解析】依题意得,()23,1a b -=-,所以向量2a b -与a 的夹角的余弦值为()2102a b a a b a-⋅==-2a b -与a 的夹角为45,故选C . 6. 【解析】取12x =,可知ln 43x x +<,故命题p 为假命题;当00x >时,001842x x +≥=,当且仅当014x =时等号成立,故名气q 为真命题.所以()p q ⌝∧为真命题,p q ∧、()p q ∨⌝、()()p q ⌝∧⌝为假命题,故选A .7.【解析】由图像知,224433T ππππω⎛⎫=+==⎪⎝⎭,解得12ω=.当23x π=时,1y =,所以12sin 123πϕ⎛⎫⨯+=⎪⎝⎭,所以122,232k k Z ππϕπ⨯+=+∈,当0k =时,6πϕ=.故选A .9. 【解析】作出不等式组所表示的平面区域如下图阴影部分所示,观察可知,当直线23z x y =-过点(7,10)C 时,z 有最小值,最小值为16-.故选B .10. 【解析】由三视图可知,该几何体是由一个四棱锥和一个圆锥拼接而成,故()()221233489182S πππ⎫=⨯⨯⨯⨯-+⨯=++-⎪⎪⎭.故选D .11. 【解析】()f x 是偶函数图像关于直线1x =对称,周期是2,画图可得. 12. 【解析】令()()2sin F x x f x =-,则()()''sin 2F x x fx =-.因为当[)0,x ∈+∞时,()'2sin cos 0x x f x ->,即()'sin 2x f x >,所以()()''sin 20F x x f x =->,所以()()2sin F x x f x =-在[)0,x ∈+∞上单调递增.又x R ∀∈,()()cos 21f x f x x -++=,所以()()22sin f x f x x -+=,所以()()()()2222sin sin 2sin sin x f x x x f x x f x ⎡⎤---=-+=+-⎣⎦,故()()2sin F x x f x =-为奇函数,所以()()2sin F x x f x =-在R 上单调递增,所以5463F F ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭.即15344643f f ππ⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭,故选B . 二、填空题13.964π+14.12- 15.77π 16.{2,5- 13. 【解析】分部积分,第一部分公式法,第二部分几何意义 14. 【解析】依题意得,()11213333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+,故112115223336CE CA AE CA AD AC AB AC AB AC ⎛⎫=+=+=-++=- ⎪⎝⎭,151362m n +=-=-.15. 【解析】因为该三棱锥的对棱两两相等,所以可构造长、宽、高分别是6,4,5的长方形,如图所示,三棱锥A BCD -的外接球即为所构造的长方体的外接球,所以所求外接球的半径R ==A BCD -的外接球的表面积为224477S R πππ==⋅=.16. 【解析】作出()f x 图像,研究关于y 的二次方程()2320y t y t +-+-=根的分步.设()()232g y y t y t =+-+-,当2t =时,0y =,1y =显然符合题意.2t <时,一正一负根,()()00,10g g <<,方程的根大于1,()()()2220fx t f x t +-+-=只有1根;2t >时,两根同号,只能有一个正根在区间()0,1,而()()02,1240g t g t =-=->,对称轴()30,12ty -=∈,13t <<,05t ∆=⇒=±5t =-.所以取值集合中两个实数值. 三、解答题17.(本小题满分10分)解:(1)由1cos 3D ∠=-,sin D ∠=1sin 2ACD S AD CD D ∆=⨯⨯∠= 6CD ∴=……3分在ACD ∆中由余弦定理2222cos 48AC AD CD AD CD D =+-⋅∠=AC ∴=……5分(2)由已知21cos cos 212sin 3D B B ==-=-sin B ∴∠= ……7分在ABC ∆中,AC BC =,由正弦定理()sin sin 2sin sin AB AB AB ACACB B D Bπ==∠=∠-∠=所以8AB =……10分(也可以用等腰三角形求线段AB 的一半) 18.(本小题满分12分) 解:(1)依题意下潜时间50x 分钟,返回时间100x分钟, 250100100.30.32100x y x x∴=⨯+⨯+⨯整理得()32302x y x x∴=++>……4分 (2)由(1)同理得[]()326146,102x y x x∴=++≥∈函数在[]6,8x ∈是减函数,[]8,10x ∈是增函数所以潜水员最多在水下18分钟. ……12分19.(本小题满分12分)解:依题意,()2332cos 2sin cos 232f x x x x ππ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭2111cos 22cos cos cos 2cos cos 222x x x x x x x x ⎛⎫=+-=++- ⎪ ⎪⎝⎭1cos 213cos 22cos 2222223x x x x x x π+⎛⎫=+-==+ ⎪⎝⎭. ……3分 (1)令()3222232k x k k Z πππππ+≤+≤+∈,解得()71212k x k k Z ππππ+≤≤+∈, 即函数()f x 的单调递减区间为()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.……6分(2)将函数()f x 的图像向右平移3π个单位长度,得到函数23y x π⎛⎫=- ⎪⎝⎭的图象,()23g x x π⎛⎫=-+ ⎪⎝⎭的图象. ……9分因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以22,333x πππ⎡⎤-∈-⎢⎥⎣⎦,所以sin 23x π⎛⎫- ⎪⎝⎭⎡⎤∈⎢⎥⎣⎦,所以()g x ∈即函数()g x 的值域为.……12分20.(本小题满分12分)解:(1)由137a =,13,41n n n a a n N a *+=∈+ 所以141114333n n n n a a a a ++==+……2分 即1111223n n a a +⎛⎫-=- ⎪⎝⎭所以数列12na -是以13为首项,13为公比的等比数列111112333n nn a -⎛⎫⎛⎫∴-== ⎪ ⎪⎝⎭⎝⎭……4分 所以数列{}n a 的通项公式为3,231nn na n N *=∈⨯+……6分 (2)23n n n nn a =+……7分 设231123133333n n n n n T --=+++++ 则234111231333333n n n n n T +-=+++++ 两式相减得231121111111333333233n n n n n n n T ++⎛⎫=++++-=--⎪⎝⎭ 所以332443n nnT +=-⨯……10分 又22462n n n ++++=+所以2323434n n n S n n +=-+++⨯(或写成其它等价形式)……12分 21.(本小题满分12分)解:(1)如图,连接'B G ,因为G 是BC 的中点,所以AG GC ⊥,所以AG ⊥平面''BB C C .因为'C F ⊂平面''BB C C ,所以'AG C F ⊥. ……2分因为'''C B B GBB ∠=∠,且''''14B F BG BC B B ==,所以'''C B FB BG ∆∆,所以''B GC F ⊥.因为'AG B G G ⋂=,所以'C F ⊥平面'AB G .因为'B D ⊂平面'AB G ,所以''C F B D ⊥. ……4分(2)如图,以G 为坐标原点,GB 、GA 所在直线分别为x 轴、z 轴,建立空间直角坐标系,则,()0,0,0G ,()1,0,0B ,()'1,4,0B,('0,A ,()1,0,0C -,(A .所以(''B A =-,()'2,4,0B C =--. 设平面''A B C 的法向量为(),,m x y z =,则'''00m B A m B C ⎧⋅=⎪⎨⋅=⎪⎩,即0240x x y ⎧-+=⎪⎨--=⎪⎩,令2z =,得x y ⎧=⎪⎨=⎪⎩,则平面''A B C的一个法向量为()2. ……6分又平面''B CC 的一个法向量为()0,0,1n =, 所以所求二面角的余弦值为219cos ,m nm n m n ⋅==……8分 (3)由题意,可设()(0,0,0D k k ≤≤,()'01CE CA λλ=≤≤,由('1,CA =,得(),4CE λλ=,又()1,0,0C -,所以()1,4E λλ-,所以 ()1,4DE k λλ=--.易知(GA =为平面''BCC B 的一个法向量.因为//DE 平面''BCC B ,所以0DE GA ⋅=k =,(DE λ==,……11分 又因为221161721171717λλλ⎛⎫-+=-+ ⎪⎝⎭, 所以当117λ=时,线段DE . ……12分22.(本小题满分12分)解:(1)依题意得,()2'm x m f x x x x -=-=,()0,x ∈+∞, 当0m ≤时,()'0f x >,故函数()f x 在()0,+∞上单调递增,()f x 无极值;……2分当0m >时,()'fx =, 令()'0fx >,得0x <<()f x 单调递减, 令()'0f x >,得x >,函数()f x 单调递增,故函数()f x有极小值()1ln 22mm f m m =-=-. ……5分 综上所述,当0m ≤时,函数()f x 无极值;当0m >时,函数()f x 有极小值()1ln 2m m -,无极大值.(2)令()()()()22111ln 2F x f x x m x x m x m x =-++=-++-,0x >,问题等价于求()F x 函数的零点个数. ……7分易得()()()'11x x m m F x x m x x --=-++-=-. ①若1m =,则()'0Fx ≤,函数()F x 为减函数, 注意到()3102F =>,()4ln 40F =-<,所以()F x 有唯一零点;……9分 ②若1m >,则当01x <<或x m >时,()'0F x <,当1x m <<时,()'0F x >,所以函数()F x 在()0,1和(),m +∞上单调递减,在()1,m 上单调递增,注意到()1102F m =+>,()22ln(22)0F m m m +=-+<,所以()F x 有唯一零点. ……11分综上,若1m ≥,函数()F x 有唯一零点,即方程()()21f x x m x =-+有唯一解. ……12分。
天一大联考2017-2018学年高中毕业班阶段性测试(三)数学(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2*|60A x N x x =∈-≤,{}0,2,6B =,则A B = ( )A .{}2,6B .{}3,6C .{}0,2,6D .{}0,3,62.已知i 是虚数单位,若复数1b iz ai-=+为纯虚数(a ,b R ∈),则||z =( )A .1B C .2D .33.如图是一边长为8的正方形苗圃图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍.若在正方形图案上随机取一点,则该点取自白色区域的概率为( )A .64πB .32π C .16π D .8π4.已知函数()f x x =0a >)的最小值为2,则实数a =( ) A .2B .4C .8D .165.已知数列{}n a 满足212222n n n a a a ++=⋅,261036a a a ++=,581148a a a ++=,则数列{}n a 前13项的和等于( )A .162B .182C .234D .3466.用1a ,2a ,…,10a 表示某培训班10名学员的成绩,其成绩依次为85,68,95,75,88,92,90,80,78,87.执行如图所示的程序框图,若分别输入i a 的10个值,则输出的1ni -的值为( )A .35B .13C .710D .797.如图画出的是某几何体的三视图,则该几何体的体积为( )A .16B .32C .48D .608.已知0x >,0y >,0z >,且411y z x+=+,则x y z ++的最小值为( ) A .8B .9C .12D .169.将函数()|sin cos |22x x f x =-向左平移6π个单位长度,则所得函数的一条对称轴是( ) A .6x π=B .4x π=C .3x π=D .23x π=10.已知点(1,,)Q m -,P 是圆C :22()(24)4x a y a -+-+=上任意一点,若线段PQ 的中点M 的轨迹方程为22(1)1x y +-=,则m 的值为( ) A .1B .2C .3D .411.已知四棱锥P ABCD -则该四棱锥外接球的表面积为( ) A .18πB .323π C .36π D .48π12.已知过抛物线C :28y x =的焦点F 的直线l 交抛物线于P ,Q 两点,若R 为线段PQ 的中点,连接OR 并延长交抛物线C 于点S ,则||||OS OR 的取值范围是( ) A .(0,2) B .[2,)+∞C .(0,2]D .(2,)+∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.71(5)2x y -的展开式中25x y 的系数是 .(用数值作答) 14.已知实数x ,y 满足20,240,32120,x y x y x y ++≥⎧⎪+-≤⎨⎪--≤⎩则43y z x +=+的取值范围为 .15.如图,在等腰梯形ABCD 中,122AD BC AB DC ====,点E ,F 分别为线段AB ,BC 的三等分点,O 为DC 的中点,则cos ,FE OF <>=.16.已知过点(0,1)-与曲线323()62a f x x x x =-+-(0x >)相切的直线有且仅有两条,则实数a 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知等差数列{}n a 的前3项分别为1,a ,b ,公比不为1的等比数列{}n b 的前3项分别为4,22a +,31b +.(1)求数列{}n a 与{}n b 的通项公式; (2)设21)n n n c a =-,求数列{}n c 的前n 项和n S .18.在ABC ∆中,内角A ,B ,C 的对边分别是a ,b ,c,满足222222()tan )a c b B b c a +-=+-.(1)求角A ;(2)若ABC ∆的面积为32,求22(cos bc A ac B a b-+-的值. 19.某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:(1)请根据以上数据,用最小二乘法求水上摩托使用率y 关于年份代码x 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?附:回归直线方程为 y bxa =+ ,其中1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑ , a y bx =- .20.如图,已知四棱锥P ABCD -的底面为直角梯形,//AD BC ,90ADC ∠=︒,且22AD BC CD ==,PA PB PD ==.(1)求证:平面PAD ⊥平面ABCD ;(2)设45PAD ∠=︒,求二面角B PD C --的余弦值.21.如图,已知F 为椭圆C :22221(0)x y a b a b+=>>的右焦点,1B ,2B ,A 为椭圆的下、上、右三个顶点,2B OF ∆与2B OA ∆(1)求椭圆C 的标准方程;(2)试探究在椭圆C 上是否存在不同于点1B ,2B 的一点P 满足下列条件:点P 在y 轴上的投影为Q ,PQ 的中点为M ,直线2B M 交直线0y b +=于点N ,1B N 的中点为R ,且MOR ∆.若不存在,请说明理由;若存在,求出点P 的坐标. 22.已知函数()ln ()f x x mx m R =-∈. (1)讨论()f x 的单调性;(2)若方程()0f x =存在两个不同的实数根1x ,2x ,证明:12()2m x x +>.天一大联考2017-2018学年高中毕业班阶段性测试(三)数学(理科)答案一、选择题1-5:AADBB 6-10:CABCD 11、12:CD 二、填空题 13.52532-14.2(,2][,)32-∞-+∞ 15.12- 16.(2,)+∞ 三、解答题17.解:(1)由题意,得221,(22)4(31),a b a b =+⎧⎨+=+⎩解得1,1a b =⎧⎨=⎩(舍去)或3,5,a b =⎧⎨=⎩ 所以数列{}n a 的公差为2d =,通项公式为12(1)21n a n n =+-=-,即21n a n =-, 数列{}n b 的公比为2q =,通项公式为11422n n n b -+=⋅=. (2)由(1)得211(21)(21)2121n c n n n n ==--+-+,所以1111112(1)()()133521212121n nS n n n n =-+-++-=-=-+++….18.解:(1)∵222222()tan )a c b B b c a +-+-,∴由余弦定理,得2cos tan cos ac B B A =,即cos tan cos a B B A =.由正弦定理与同角三角函数基本关系,得sin sin cos cos cos BA B B A B⋅=,∴tan A =3A π=.(2)∵ABC ∆的面积为32,∴13sin 232bc π=,即bc =∴(cos cos bc A ac B A ac B -+=-+22222222b c a a c b ac bc ac+-+-=-+⋅22a b =-,∴22(cos 1bc A ac Ba b -+=-.19.解:(1)由表格数据,得 3.5x =,16y =,61371i ii x y==∑,∴61622166i ii i i x y x ybx x==-=-∑∑ 3716 3.516217.5-⨯⨯==,∴ 162 3.59a=-⨯=, ∴水上摩托使用率y 关于年份代码x 的线性回归方程为 29y x =+.当8x =时, 28925y =⨯+=,故预测该娱乐场2018年水上摩托的使用率为25%. (2)由频率估计概率,结合条形图知Ⅰ型水上摩托每辆可使用1年、2年、3年和4年的概率分别为0.2,0.3,0.3,0.2,∴每辆Ⅰ型水上摩托可产生的纯利润期望值1(0.81)0.2(20.81)0.3(30.81)0.3(40.81)0.21E ξ=-⨯+⨯-⨯+⨯-⨯+⨯-⨯=(万元). 由频率估计概率,结合条形图知Ⅱ型水上摩托每辆可使用1年、2年、3年和4年的概率分别为0.1,0.2,0.4和0.3,∴每辆Ⅱ型水上摩托可产生的纯利润期望值2(0.8 1.2)0.1(20.8 1.2)0.2(30.8 1.2)0.4(40.8 1.2)0.3 1.12E ξ=-⨯+⨯-⨯+⨯-⨯+⨯-⨯=(万元).20.(1)证明:如图,分别取AD ,AB 的中点O ,G ,连接OB ,OP ,OG ,PG , 则四边形OBCD 为正方形, ∴OA OB =,∴OG AB ⊥. 又PA PB =,∴PG AB ⊥, ∴AB ⊥平面POG ,∴AB PO ⊥. ∵PA PD =,∴PO AD ⊥.又∵AB 与AD 为平面ABCD 内的两条相交直线,∴PO ⊥平面ABCD . 又PO ⊂平面PAD ,∴平面PAD ⊥平面ABCD .(2)解:由(1)知,以{},,OB OD OP为一组正交基底,建立如图所示的空间直角坐标系Oxyz ,∵45PAD ∠=︒,则由PO AD ⊥,知PO OA OB OD ===.令1OA OB OD ===,则(0,0,1)P ,(1,0,0)B ,(1,1,0)C ,(0,1,0)D ,∴(1,0,1)PB =- ,(0,1,1)PD =- ,(1,0,0)CD =-.设平面PBD 的法向量为1111(,,)n x y z =,则由11,,n PB n PD ⎧⊥⎪⎨⊥⎪⎩ ,得110,0,n PB n PD ⎧⋅=⎪⎨⋅=⎪⎩即11110,0,x z y z -=⎧⎨-=⎩取11x =,得1(1,1,1)n = . 又设平面PCD 的法向量为2222(,,)n x y z =,则由22,,n CD n PD ⎧⊥⎪⎨⊥⎪⎩ 得220,0,n CD n PD ⎧⋅=⎪⎨⋅=⎪⎩即2220,0,x y z -=⎧⎨-=⎩取21y =,得2(0,1,1)n = ,∴121212cos ,||||n n n n n n ⋅<>===⋅, 又二面角B PD C --为锐角, ∴二面角B PD C --21.解:(1)由已知,得221212B OF B OAbcS c S a ab ∆∆===.又c =2a =,结合222a b c =+,解得1b =,∴椭圆C 的标准方程为2214x y +=. (2)设00(,)P x y (00x ≠),则0(0,)Q y ,∴220014x y +=,00(,)2x M y . 又∵2(0,1)B ,∴直线2B M 的方程为002(1)1y y x x -=+. ∵00x ≠,∴01y ≠,令1y =-,得0(,1)1x N y --. 又∵1(0,1)B -,则00(,1)2(1)x R y --,||MR == 直线MR 的方程为0000()22x xy y x y -=--,即00220yy x x +-=, ∴点O 到直线MR的距离为1d ==,∴1||1210MOR S MR d ∆=⋅==解得027y =,代入椭圆方程,得0x =, ∴存在满足条件的点P,其坐标为2(,)77±. 22.解:(1)函数()f x 的定义域为(0,)+∞,11'()mx f x m x x-=-=. 当0m ≤时,'()0f x >,∴()f x 在区间(0,)+∞上单调递增.当0m >时,由'()0f x >,得10x m <<,∴()f x 在区间1(0,)m上单调递增, 由'()0f x <,得1x m >,∴()f x 在区间1(,)m+∞上单调递减.(2)由方程()0f x =存在两个不同的实数根1x ,2x ,可设120x x >>, ∵1()0f x =,2()0f x =,∴11ln 0x mx -=,22ln 0x mx -=,∴1212ln ln ()x x m x x -=-,∴1212ln ln x x m x x -=-.要证12()2m x x +>,只需证121212ln ln 2x x x x x x ->-+,等价于1122122()ln x x x x x x ->+, 设121x t x =>,上式转化为2(1)ln (1)1t t t t ->>+, 设2(1)()ln 1t g t t t -=-+,22(1)'()0(1)t g t t t -=>+, ∴()g t 在(1,)+∞上单调递增, ∴()(1)0g t g >=,∴2(1)ln 1t t t ->+,∴12()2m x x +>.。
2017-2018学年 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集R U =,集合{}120|<<=x x A ,{}0log |3>=x x B ,则()=B C A U ( ) A .{}1|>x x B .{}0|>x x C .{}10|<<x x D .{}0|<x x 【答案】D考点:集合的运算.2.下列有关的说法错误的是( )A .“若012=-x ,则1=x ”的逆否为:“若1≠x ,则012≠-x ” B .“1=x ”是“0232=+-x x ”的充分不必要条件C .若集合{}044|2=++=x kx x A 中只有一个元素,则1=kD .对于R x p ∈∃:,使得012<++x x ,则R x p ∈∀⌝::p ⌝,均有012≥++x x【答案】C 【解析】试题分析:“若012=-x ,则1=x ”的逆否为:“若1≠x ,则012≠-x ”,正确;当1=x ,能得到0232=+-x x ,但0232=+-x x ,得到1=x 或2=x ,故正确;当0=k 时,方程0442=++x kx 只有一个根,故错误,对于R x p ∈∃:,使得012<++x x ,则R x p ∈∀⌝::p ⌝,均有012≥++x x ,正确,故答案为C.考点:1、四种的关系;2、充分条件、必要条件.3.已知函数()⎪⎩⎪⎨⎧≥+<+=1,1,122x ax x x x f x ,若()[]a f f 40=,则实数a 等于( )A .9B .2C .21D .54 【答案】B考点:分段函数的应用.4.已知9.0log 8.0=a ,9.0log 1.1=b ,9.01.1=c ,则c b a ,,的大小关系为( ) A .c b a << B .b c a << C .c a b << D .b a c << 【答案】C 【解析】试题分析:8.0log 9.0log 1log 8.08.08.0<<,因此10<<a ,1log 9.0log 1.11.1<,因此0<b ,11.11.109.0=>,1>c ,因此c a b <<,故答案为C.考点:指数函数和对数函数性质.5.已知数列{}n a 为等比数列,满足274=+a a ,892-=⋅a a ,则131a a +的值为( ) A .7 B .17 C .217- D .17或217- 【答案】D 【解析】试题分析: 274=+a a ,892-=⋅a a ,∴274=+a a ,874-=⋅a a ,所以⎩⎨⎧=-=4274a a 或⎩⎨⎧-==2474a a当⎩⎨⎧=-=4274a a 时,17131=+a a ;当⎩⎨⎧-==2474a a ,217131-=+a a ,故答案为D.考点:等比数列的性质.6.在ABC ∆中,若点D 满足2=,则=( ) A .3231+ B .3235- C .3132- D .3132+ 【答案】D【解析】试题分析:由2=,得()-=-2,因此+=23,因此3132+=,故答案为D. 考点:平面向量的应用.7.已知函数()1122+++=x x x x f ,若()32=a f ,则()a f -( )A .32 B .32- C .34 D .34- 【答案】C考点:偶函数的应用.8.函数()193cos 3-⋅=x x x x f 的图象大致为( )A .B .C .D . 【答案】D 【解析】试题分析:函数的定义域{}0|≠x x ,由于()193cos 3-⋅=x x xx f ,()()193cos 3--⋅=-∴--x x x x f x x x 913cos 3-=()x f -=,因此函数()193cos 3-⋅=xx xx f 是奇函数,所以排除A ,当x 从大于0的方向接近0时,0>y ,排除B ;当x 无限接近∞+时,y 接近于0,故选D. 考点:1、函数的奇偶性;2、函数的图象. 9.已知534sin =⎪⎭⎫⎝⎛-πα,则()απ2sin +等于( ) A .257-B .257C .259D .2516【答案】A考点:1、三角函数的倍角公式;2、三角函数的化简求值. 10.已知函数()23ln 212+-=x x x f 在其定义域内的一个子区间()1,1+-a a 内不是单调函数,则实数a 的取值范围是( ) A .⎪⎭⎫ ⎝⎛-23,21 B .⎪⎭⎫⎝⎛-45,43 C .⎪⎭⎫ ⎝⎛23,1 D .⎪⎭⎫⎢⎣⎡23,1【答案】D 【解析】试题分析:因为函数()23ln 212+-=x x x f 在区间()1,1+-a a 上不单调,所以 ()xx x x x f 2142122-=-='在区间()1,1+-a a 上有零点,由()0='x f ,得21=x ,则⎪⎩⎪⎨⎧+<<-≥-121101a a a ,得231<≤a ,故答案为D. 考点:函数的单调性与导数的关系.11.对任意实数a ,b 定义运算 “⊗”:⎩⎨⎧<-≥-=⊗1,1,b a a b a b b a ,设()()()x x x f +⊗-=412,若函数()k x f y +=有三个零点,则k 的取值范围是( )A .[)1,2-B .[]1,0C .[)0,2-D .()1,2-【答案】A 【解析】试题分析:当--12x ()x +41≥时,3≥x 或1≤x ;当--12x ()x +41<时,31<<x ,()⎩⎨⎧<<-≤≥+=∴31,113,42x x x x x x f 或,图象如图所示,若函数()k x f y +=有三个零点可转化为()x f y =与k y -=有三个不同的交点,由图可知12,21k k -<-≤∴-≤<,故答案为A.考点:1、函数的零点;2、函数图象的应用.12.设()x f 是定义在R 上的函数,其导函数为()x f ',若()()1<'-x f x f ,()20160=f ,则不等式()12015+⋅>xe xf (其中e 为自然对数的底数)的解集为( )A .()()+∞∞-,00,B .()+∞,0C .()+∞,2015D .()()+∞∞-,20150, 【答案】B考点:1、构造新函数;2、函数的单调性与导数的关系.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.求值:_____167sin 73sin 13cos 17sin 0000=+ . 【答案】21 【解析】 试题分析:=+0000167sin 73sin 13cos 17sin 000013sin 73sin 13cos 73cos +2160cos 0==. 考点:两角差的余弦公式.14.设函数()x f 在()+∞,0内可导,且()1213++=xxex e f ,则()______1='f .【答案】27考点:求导数值.15.已知点()1,1-A ,()2,1B ,()1,2--C ,()4,3D ,则向量在方向上的投影为_____.【答案】223. 【解析】试题分析:()1,2=,()5,5=,向量在方向上的投影为==⋅θcos 2232515=,故答案为223. 考点:1、向量的坐标运算;2、投影的求法.16.若函数()⎪⎩⎪⎨⎧≤+⎪⎭⎫⎝⎛->+=1,2321,log x x a x a x x f a 为R 上的增函数,则实数a 的取值范围是____. 【答案】63<≤a .【解析】考点:分段函数的单调性.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)已知n S 是等差数列{}n a 的前n 项和,且π86=S ,273a a =. (1)求数列{}n a 的通项公式;(2)设n n a b cos =,n T 是数列{}n b 的前n 项和,求2015T 的值. 【答案】(1)63ππ+=n a n ;(2)2015T 23-=.考点:1、等差数列的基本运算;2、数列求和. 18.(本小题满分12分)设:P 函数()⎪⎭⎫⎝⎛+-=16lg 2a x ax x f 的值域为R ;:q 不等式a x x <-93对一切R x ∈均成立.(1)如果p 是真,求实数a 的取值范围;(2)如果“q p ∨”为真,且“q p ∧”为假,求实数a 的取值范围. 【答案】(1)20≤≤a ;(2)410≤≤a 或2>a .②由⎪⎩⎪⎨⎧≥⨯->016410aa a ,得⎩⎨⎧≤≤->220a a ,20≤<∴a 因此所求实数a 的取值范围20≤≤a(2)q 是真,不等式a x x <-93对一切R x ∈均成立,令x t 3=,2t t y -=,0>t ,当21=t , 414121max =-=y ,41>∴a若“q p ∨”为真,且“q p ∧”为假,则q p ,一真一假①若p 真q 假,则⎪⎩⎪⎨⎧≤≤≤4120a a ,得410≤≤a ②若p 假q 真,则⎪⎩⎪⎨⎧>><4120a a a 或,得2>a 综上,实数a 的取值范围410≤≤a 或2>a . 考点:1、逻辑连结词;2、集合的运算.19、(本小题满分12分)已知向量⎪⎭⎫ ⎝⎛=43,sin x a ,()1,cos -=x b .(1)当b a //时,求x x 2sin cos 2-的值;(2)设函数()()x f ⋅+=2,已知在ABC ∆中,内角A 、B 、C 的对边分别为a 、b 、c ,若3=a ,2=b ,36sin =B ,求当30π≤≤x 时,()()⎪⎭⎫ ⎝⎛++=62cos 4πA x f x g 的取值范围.【答案】(1)58;(2)⎥⎦⎤⎢⎣⎡--212,123.(2)()()b b a x f ⋅+=221cos 2cos sin 22++=x x x 2342sin 2+⎪⎭⎫ ⎝⎛+=πx 由正弦定理得362sin sin 3==B b A ,得22sin =A 4π=∴A 或43π=A ,a b > ,4π=∴A 因此()()⎪⎭⎫⎝⎛++=62cos 4πA x f x g 2142sin 2-⎪⎭⎫ ⎝⎛+=πx30π≤≤x ,1211424πππ≤+≤∴x , 2122142sin 2123-≤-⎪⎭⎫ ⎝⎛+≤-∴πx 即()∈x g ⎥⎦⎤⎢⎣⎡--212,123. 考点:1、同角三角函数的基本关系;2、三角函数的化简;3、求三角函数的值域. 20.(本小题满分12分)已知函数()n mx x x x f +++=232131以()a ,0为切点的切线方程是022=-+y x .(1)求实数m ,n 的值; (2)若方程()b x x f +=2在⎥⎦⎤⎢⎣⎡-3,23上有两个不等实根,求实数b 的取值范围. 【答案】(1)2,2=-=n m ;(2)619411<≤b 或2134≤<-b .由方程b x x x =+--22213123在⎥⎦⎤⎢⎣⎡-3,23上有两个不等实根,得619411<≤b 或2134≤<-b故方程b x x x =+--22213123在⎥⎦⎤⎢⎣⎡-3,23上有两个不等实根,实数b 的取值范围619411<≤b 或2134≤<-b . 考点:1、导数的几何意义;2、导数与函数的单调性、极值;3、函数与方程. 21.(本小题满分12分)已知函数()ax xx x f ++=1ln . (1)若函数()x f 在[)+∞,1上是单调函数,求实数a 的取值范围; (2)已知函数()xx x g 1+=,对于任意[]e x ,11∈,总存在[]e x ,12∈,使得()()21x g x f ≤成立,求正实数a 的取值范围.【答案】(1)0≥a 或41-≤a ;(2)ea 110-≤<.(2)()x f a ≤恒成立()min x f a ≤⇔.试题解析:(1)()a x x x f +-='211221x x ax -+=,[)+∞∈,1x ,由于函数()x f 在[)+∞,1上是单调函数,()0≥'∴x f 或()0≤'x f 对任意[)+∞∈,1x 恒成立, 即012≥-+x ax 或012≤-+x ax 对任意[)+∞∈,1x 恒成立,x x a 112-≥∴或xx a 112-≤对任意[)+∞∈,1x 恒成立 令x t 1=,由于[)+∞∈,1x ,(]1,0∈∴t ,设()t t t h -=241212-⎪⎭⎫ ⎝⎛-=t因此()041≤≤-t h ,所以实数a 的取值范围为0≥a 或41-≤a(2)由(1)知,当0>a 时,函数()x f 在[]e ,1上为增函数, 故()()()e f x f f ≤≤1,即()eae x f a 111++≤≤+ ()222111xx x x g -=-=' ,∴当[]e x ,1∈,()0≥'x g ,所以函数()x g 在[]e ,1上是单调递增函数()()()e g x g g ≤≤∴1,即()ee x g 12+≤≤对任意[]e x ,11∈,总存在[]e x ,12∈,使得()()21x g x f ≤成立, 可知()()max 2max 1x g x f ≤,所以e ae 11++e e 1+≤,即ea 11-≤,故所求正实数a 的取值范围ea 110-≤<.考点:1、函数的导数;2、函数的应用;3、恒成立的问题. 22.(本小题满分12分)已知函数()()x a a x x a x f 22321ln +-+=()R a ∈,()x x x x x g --=222ln 3.(1)判断()x g 在区间[]4,2上单调性;(2)若2≥a ,函数()x f 在区间[]4,2上的最大值为()a G ,求()a G 的解析式,并判断()a G 是否有最大值和最小值,请说明理由(参考数据:7.02ln 69.0<<).【答案】(1)()x g 在区间[]4,2上单调递增;(2)()⎪⎩⎪⎨⎧>+--≤≤--=)4(8442ln 2)42(21ln 23233a a a a a a a a a a G ;()a G 有最小值,没有最大值.试题解析:(1)证明:()x x x x x g --=222ln 3 ,()1ln 6--='∴x x x x g设()1ln 6--=x x x x h ,则()5ln 6+='x x h ,∴当42<<x 时,()0>'x h ,()x h ∴在区间()4,2上单调递增 ()()012ln 432>-=h ,∴当42<<x 时,()()02>>h x h , ()x g ∴在区间[]4,2上单调递增(1)()()x a a x x a x f 22321ln +-+= ,()()23a a x xa x f +-+='∴,()+∞∈,0x ,即()()()x a x a x x f --=', 2≥a ,2a a <∴,当x 变化时,函数()()x f x f ',变化情况如下表:因此当42≤≤a 时,42≥a ,()x f 在区间[]4,2上的最大值()2332ln a a a a a f --= 当4>a 时,()x f 在区间[]4,2上的最大值为()8442ln 2423+--=a a a f即()⎪⎩⎪⎨⎧>+--≤≤--=)4(8442ln 2)42(21ln 23233a a a a a a a a a a G考点:1、判断函数的单调性;2、求函数的解析式和最值.。
绝密★启用前试卷类型:全国卷天一大联考 2017—2018学年高中毕业班阶段性测试(三)化学考生注意:1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在答題卡上的指定位置。
2.回答选择题时,选出每小題答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H-1 C-12 O-16 S-32 Fe-56 Cu-64一、选择题:本题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.化学与生活息息相关。
下列各“剂”在应用过程中表现还原性的是A.臭氧柜里臭氧作餐具的“消毒剂”B.热纯碱溶液常作厨房的“洗涤剂”C.活性铁粉在食品袋中作“去氧剂”D.小苏打常作制糕点的“起泡剂”2.葡萄糖无氧呼吸生成物为乳酸(C3H6O3)。
等质量的乳酸分别与足量的钠、碳酸氢钠溶液完全反应,产生气体体积之比为1∶1(同温同压)。
乳酸的结构简式可能是A.CH3OCH2COOH B.CH3CH(OH)COOH C.CH3COOCH2OH D.HCOOCH2OCH33.下列有关说法正确的是A.Mg(HCO3)2、NaHSO3和(NH4)3PO4都是酸式盐B.BaSiO3、HC1O4和Na2S都是强电解质C.蛋白质溶液和淀粉溶液的分散质直径都小于1nmD.CH2Cl2、C6H6和CH4O表示的物质都是纯净物4.下列各组离子中因发生氧化还原反应而不能大量共存的是A.无色透明溶液中:Fe3+、NH4+、SO42-、Cl-B.Ba(AlO2)2溶液中:K+、Mg2+、HCO3-、NO3-C.能使酚酞变红色的溶液中:Na+、Ba2+、Cl-、Br-D.pH=0的溶液中:Na+、K+、S2-、SO32-5.硫代硫酸钠溶液与氯气能发生反应:Na2S2O3+4Cl2+5H2O=2NaCl+6HCl+2H2SO4。
【试卷整体分析】
考试范围:必考内容难度:一般
【题型考点分析】
河南省信阳市2017-2018学年高三上学期期末质量检测
化学试题
第I卷(选择题)
1.《本草经集注》中记载了区别硝石(KNO3)和朴消(Na2SO4):“以火烧之,紫青烟起,乃真硝石也”,这是运用了硝石的
A.焰色反应B.氧化性C.还原性D.不稳定性
【答案】A
【解析】钾的焰色反应是紫色,用火烧硝石(KNO3),是钾的焰色反应,故选A。
2.设N A为阿伏加德罗常数的值。
下列说法正确的是( )
A.136g熔融的KHSO4中含有2N A个阳离子
B.40gH218O与40gD2O所含的中子数均为20N A
C.1molFe分别与足量的稀硫酸和稀硝酸反应转移电子数均为2N A
D.标准状况下,22.4LNO和11.2LO2混合后气体的分子总数为N A
【答案】B
【解析】A.硫酸氢钾在熔融状态下只能电离为钾离子和硫酸氢根,故136g硫酸氢钾即1mol硫酸氢钾在熔融状态下含N A个阳离子,故A错误;B.H218O与D2O相对分子质量均为20,且分子内中子数均为10,则40g所含的中子数均为20N A,故B正确;C.Fe与足量稀硫酸反应生成FeSO4,与足量稀硝酸反应生成Fe(NO3)3,故C错误;D.NO和O2混合后要生成NO2,且还存在NO2N2O4,则标准状况下,22.4LNO和11.2LO2混合后气体的分子总数小于N A,故D错误;故答案为C。
学@科网
3.水溶液中能大量共存的一组离子是
A.Na+、Al3+、Cl﹣、CO32﹣B.H+、Na+、Fe2+、MnO4﹣
C.K+、NH4+、OH﹣、SO42﹣D.K+、Ca2+、Cl﹣、NO3﹣
【答案】D
【解析】Al3+和CO32﹣之间发生双水解并相互促进水解进行到底,生成沉淀和气体,不能大量共存,A错误;MnO4﹣、Fe2+在H+存在条件下,发生氧化还原反应,不能大量共存,B错误;NH4+与OH﹣之间反应生成一水合氨,不能大量共存,C错误;K+、Ca2+、Cl﹣、NO3﹣四种离子间相互不反应,能够大量共存,D正确;正确选项D。
点睛:Al3+与CO32﹣、HCO3-、S2-、AlO2-等发生双水解反应,且进行到底生成氢氧化铝沉淀,所以Al3+。