无限循环小数
- 格式:doc
- 大小:24.00 KB
- 文档页数:1

无限小数不一定是循环小数,循环小数一定是无限小数.√.考点:小数的读写、意义及分类.专题:小数的认识.分析:从小数点后某一位开始不断地重复出现的一个或一节数字的无限小数叫做循环小数,如2.66…,4.2323…等;无限小数只是位数无限,包括循环小数和不循环的无限小数,所以循环小数一定是无限小数,无限小数不一定是循环小数.解答:解:由分析可知,“无限小数不一定是循环小数,循环小数一定是无限小数”,这种说法是正确的;故答案为:√.点评:此题考查了学生对循环小数和无限小数意义的理解与区分,无限小数的范围大于循环小数的范围.2.97171…是无限小数也是循环小数.√.考点:小数的读写、意义及分类.分析:要知道2.97171…是不是无限小数和循环小数,就必须对无限小数和循环小数的概念与特征有准确的理解与掌握.无限小数是一种位数无限的小数;循环小数是位数无限而且从某一位起,后面某一位或某几位数字重复出现的小数.解答:解:小数2.97171…,位数是无限的,同时出现了循环节71,所以2.97171…是无限小数也是循环小数.故答案为:√.点评:此题考查了无限小数和循环小数的概念,只要掌握了概念与特征,就能做到准确判断循环小数是无限小数中的一种√.考点:小数的读写、意义及分类.分析:要想正确判断此题的正误,首先要弄清无限小数与循环小数之间的关系:无限小数包括无限循环小数和无限不循环小数.解答:解:因为小数分为无限小数和有限小数;而无限小数又分为循环小数和无限不循环小数;所以,循环小数属于无限小数.故答案为:√.点评:此题考查了循环小数和无限小数的概念,以及它们之间的包含关系循环小数一定是无限小数,无限小数不一定是循环小数.√.(判断对错)考点:小数的读写、意义及分类.分析:从小数点后某一位开始不断地重复出现的一个或一节数字的无限小数,叫做循环小数,如2.66…,4.2323…等;无限小数只是位数无限,包括循环小数和不循环的无限小数,所以循环小数一定是无限小数,无限小数不一定是循环小数.解答:解:循环小数一定是无限小数,无限小数不一定是循环小数;这种说法是正确的.故答案为:√.点评:此题考查了学生对循环小数和无限小数概念的理解与区别,无限小数的范围大于循环小数的范围下列各数是循环小数的是A,是无限小数的是ABA.1.070707…B.6.282828C.3.1415926…考点:小数的读写、意义及分类.专题:小数的认识.分析:无限小数是一种位数无限的小数;循环小数是位数无限而且从某一位起,后面某一位或某几位数字重复出现的小数.解答:解:1.070707…是循环小数;1.070707…和3.1415926…是无限小数.故选:A,AB.点评:题考查了无限小数和循环小数的概念,只要掌握了概念与特征,就能做到准确判17.878787,17.8765…,17.87,17.888…中17.878787,17.87是有限小数,17.8765…,17.888…是无限小数,17.888…是循环小数.考点:小数的读写、意义及分类.专题:小数的认识.分析:根据循环小数、有限小数和无限小数的概念将这些数直接分类.解答:解:17.878787,17.8765…,17.87,17.888…中,17.878787,17.87是有限小数,17.8765…,17.888…是无限小数,17.888…是循环小数.故答案为:17.878787,17.87;17.8765…,17.888…;17.888….点评:此题考查辨识循环小数、有限小数和无限小数,关键是明白它们的概念小数分为有限小数、循环小数和无限小数.错误.(判断对错)考点:小数的读写、意义及分类.专题:小数的认识.分析:根据小数的分类,小数可分为有限小数和无限小数;有限小数的小数部分的位数是有限的,无限的小数的小数部分的位数是无限的,且循环小数的位数也是无限的,所以循环小数也是无限小数;据此判断即可.解答:解:因为小数可分为有限小数和无限小数,循环小数也是无限小数;所以小数可分为有限小数、循环小数和无限小数,说法错误;故答案为:错误.点评:此题主要考查小数的分类以及循环小数和无限小数关系小数0.3535是纯循环小数.错误.考点:分数的意义、读写及分类.分析:纯循环小数是无限小数,而小数0.3535是有限小数,由此进行判断即可.解答:解:小数0.3535是纯循环小数.故答案为:错误.点评:此题考查纯循环小数的辨识,纯循环小数是无限小数下面各数,哪些是有限小数,哪些是无限小数,哪些是循环小数?2.11、11632.32474747…、1.178953…、9.999、0.0897897…、10.932457…、0.63636363…、1.24568555.考点:小数的读写、意义及分类.专题:小数的认识.分析:根据小数的分类,小数可分为有限小数和无限小数;有限小数的小数部分的位数是有限的,无限的小数的小数部分的位数是无限的,一个无限小数的小数部分有一个或几个依次不断重复出现的数字,这样的小数就叫做循环小数,据且循环小数的位数也是无限的,所以循环小数也是无限小数;据此判断即可.解答:解:有限小数:2.11、9.999、1.24568555;无限小数:11632.32474747…、1.178953…、0.0897897…、10.932457…、0.63636363…;循环小数有:11632.32474747…、0.0897897…、0.63636363….点评:此题主要考查小数的分类以及循环小数和无限小数关系.有限循环小数小数,并没有有限循环小数这种说法。


小数的循环小数与无限不循环小数小数是我们日常生活中经常遇到的数的一种表现形式,可以表示小于1的部分。
然而,小数在其内部又可以分为循环小数和无限不循环小数。
本文将介绍这两种类型的小数,以及它们的特点和应用。
1. 循环小数循环小数是指小数部分中有一个或多个数字序列循环出现的小数。
例如,1/3可以表示为0.3333...,其中数字3永远循环出现。
这种循环可以是一个数字、多个数字或整个小数部分。
循环小数可以用有限表示法来表示,也可以用无限循环线上加数字循环的方式表示。
有限表示法是指当循环节是一个数字时,可以直接使用该数字表示循环小数。
例如,1/6可以表示为0.1666,循环节为6。
无限循环线上加数字循环的表示法则是将循环节用一条横线覆盖,并在上方标注循环数字。
例如,1/7可以表示为0.142857,循环节为142857,可以写为0.142857上有一条横线,循环数字为142857。
循环小数有一些有趣的数学性质。
例如,循环小数可以通过除法算法或计算机程序转化为分数形式。
此外,循环小数还可以用连分数形式表示,其中每个循环节数字可以表示为一个分数。
循环小数还与数论中的周期性问题有关,在一些数学证明中有重要应用。
2. 无限不循环小数无限不循环小数是指小数部分中没有任何数字序列重复出现的小数。
例如,π(圆周率)和e(自然对数的底数)就是无限不循环小数的例子,它们的小数部分包含无限多个数字,并且没有重复的循环节。
无限不循环小数具有无穷无尽的数字序列,因此无法用有限表示法表示。
我们通常会使用近似值来表示无限不循环小数,例如π可以使用3.14或3.14159作为近似值。
然而,这些近似值只能精确到一定的小数位数,无法完全表示无限不循环小数的真实值。
无限不循环小数在科学和工程领域有广泛的应用。
例如,π在几何学中用于计算圆的周长和面积,e在金融学和概率论中用于计算复利和概率分布。
综上所述,小数可以分为循环小数和无限不循环小数两种类型。

循环小数简写循环小数是一种数学表示方式,它可以用来表示无限不循环的小数。
它的出现是为了解决无法用有限的数字来表示无限的小数的问题。
循环小数的表达方式也有很多种,主要是分为简写循环小数和完整写法两种。
简写的循环小数是用一个最短的表达式来表示一个无限小数,像是 0.1212121212…写为 0.12(12),(12)表示这个小数从第二位一直循环到末尾。
而完整写法则是将无限循环的小数转换为有限的分数来表示,例如 0.1212121212…可以转换为 12/99 。
由于完整写法需要将小数转换成分数,所以它一般只用来处理比较简单的小数,而简写循环小数则可以用来表示比较复杂的循环小数。
简写循环小数的表达方式有几种。
第一种是将循环小数的数字用括号括起来表示,例如 0.1212121212…写为 0.12(12) 。
如果由于要表达的循环小数的小数位数十分多,可以省略多余的数字,像是0.1212121212…写为 0.12(1),或者 0.123456789…写为 0.123(4)。
第二种是将循环小数写成分数形式,例如 0.1212121212…写为12/99,或者 0.123456789…写为 123/999。
第三种是将循环小数写成分子/分母的形式,例如0.1212121212…写为 12/999,或者 0.123456789…写为 123/9999。
最后,还可以用数学符号来表示循环小数。
例如,0.1212121212…以用 0.12∞表示, 0.123456789…以用 0.123∞表示,0.1212121212…以用 12/99∞表示,而 0.123456789…以用 123/999∞表示。
数学中经常使用循环小数,它可以用来表示一些比较复杂的概率,例如不同概率出现的概率,即=3.1415…。
循环小数还可以用来表示数学等式中的不确定系数,例如,用 0.1212121212…表示 a + b = c 中的 a b,因为 a b是不确定的系数。

证明分数一定是小数或无限循环小数分数一定是小数或无限循环小数。
要证明这一点,我们可以从两个方面进行论证:一方面,使用数学语言和推理来证明;另一方面,使用直观的例子来说明。
首先,我们可以使用数学语言来进行证明。
假设有一个分数a/b,其中a和b是整数,b不等于0。
如果a/b是一个有限小数,那么我们可以将其表示为m个数字的形式:a/b = d1d2d3...dm,其中d1, d2,d3, ..., dm是十进制数字。
我们可以假设这些数字的最高位是d1,最低位是dm。
我们可以将这个有限小数转化为分数的形式:a/b = d1 *10^(m-1) + d2 * 10^(m-2) + ... + dm-1 * 10 + dm。
换句话说,我们可以将有限小数表示为一个分数,这个分数的分子是一个整数,分母是一个整数。
然而,我们可以推出一个矛盾的结论:如果分数a/b是一个有限小数,那么我们可以找到一个整数n,使得a/b=n。
但是,这与我们最初的假设矛盾,即a和b是整数,b不等于0,且a/b是一个非整数。
因此,我们可以断定,分数一定是一个无限循环小数或者是一个无限不循环小数。
由于我们可以找到许多这样的例子,进一步显示了分数可能是无限循环小数或小数。
这是因为在十进制系统中,我们只有有限数量的数字来表示分数,因此无法精确表示无限个数字。
因此,我们只能使用一个数字或一个无限循环的数字来代表分数。
综上所述,分数一定是小数或无限循环小数。
这个结论可以通过数学语言和推理来证明,也可以通过直观的例子进行说明。
无论从理论上还是实际观察到的现象中,我们都可以得出这样的结论。

循环小数有限小数无限小数教学内容:小学数学五年级上册第40页信息窗3第2课时教学目标:1.通过感受生活中的循环现象,初步认识循环小数、有限小数和无限小数,能用循环小数表示除法的商,并能正确区分有限小数和无限小数.2. 培养学生的分析能力、分类能力和概括能力,提高学生解决简单实际问题的能力。
3.在自主探索与合作交流的过程中,培养数学的极限思想.4.丰富学生积极的数学情感,感受数学与生活的密切联系.教学重难点:教学重点:理解循环小数,有限小数和无限小数的意义,会用循环小数表示除法的商教学难点:会用循环小数表示除法的商,将循环小数和相似的数进行大小比较,会区分有限小数和无限小数。
教具、学具:教师准备:多媒体课件学生准备:计算器一、创设情境,提出问题1.故事引入:上课之前,老师给你讲个故事:“从前有座山,山上有座庙,庙里有个老和尚, 老和尚对小和尚说,从前有座山,山上有座庙,庙里有个老和尚, 老和尚对小和尚说,从前……”哪位同学能接着往下讲?同学讲了多遍,突然停住了“:这个故事讲不完。
”老师问“:为什么呢?”学生答到“:这个故事总是不断地重复说这几句话。
” 教师顺势引导“:在数学王国里,就有一种小数,它有着和这个故事一样的特点,具体是什么老师先不告诉你们,让我们一起到数字王国里去找到它,认识它吧。
”二、自主学习,小组探究。
出示信息窗3的问题1.独立列算式并尝试计算:350÷6= 。
并要求先用竖式计算,有发现的话再用计算器验证。
2.思考:计算过程中你遇到了什么困难?你有什么新发现?3.小组讨论:把你的困难和发现在小组内交流一下,看能否找到解决问题的方法,并总结一下大家的发现。
老师倾听学生的讨论,对有困难的组适当加以点拨,但以听为主,放手让学生自主发现学习,同时对学生对知识的理解程度做到心中有数。
根据学生的回答板书:350÷6=58.3333333……首先找学生说一下他们的发现预设:百分位出现3之后就一直在循环。

无限循环小数化分数
等比数列法:无限循环小数,先找其循环节,然后将其展开为一等比数列、求出前n 项和、取极限、化简。
套公式法:纯循环,用9做分母,有多少个循环数就几个9,比如0.3,3的循环就是9分之3,0.654,654的循环就是999分之654, 0.9,9的循环就是9分之9(1),以此类推。
例:0.…… 1的循环,我们可以设此小数为x,可得:
10x-x=1.……-0.……
9x=1
x=1/9
例:0........=1
设x=0.......
10x-x=9......-0......
9x=9
x=1
关于这方面,还可以运用音速的科学知识予以证明。
套公式法混循环
基准:把混循环小数0.˙化成分数:
解:0.˙
=[(/)+8/)]
=/(+)+8/
=[(/)-(/)]+(8/)
=(/)+[(8/)-(/)]
=(/)-(22/)
=/
=/。
纯循环小数
将氢铵循环小数重写成分数,分子就是一个循环节的`数字共同组成的数;分母各位数字都就是9,9的个数与循环节中的数字的个数相同。
例如:0....=1/9、0....=/。

循环小数的知识循环小数是数学中一个重要的概念,它常常出现在除法运算或计算无理数时。
循环小数指的是一个无限不循环的小数,即小数部分存在一定的规律重复出现的情况。
本文将从循环小数的定义、性质以及应用等方面进行介绍。
一、循环小数的定义循环小数是指小数部分存在一定的规律重复出现的无限小数。
它可以用一个带括号的数字串表示,括号中的数字表示循环的部分。
例如,0.3333...可以表示为0.(3),0.142857142857...可以表示为0.(142857)。
循环小数可以用有限小数表示,例如1/3=0.3333...可以表示为1/3=0.3。
二、循环小数的性质1. 循环小数是无理数。
循环小数是无限不循环的,它不能被有限小数表示,所以它是无理数。
2. 循环小数可以通过有理数表示。
循环小数可以通过一个有限小数和一个无限循环小数相加得到。
例如,0.25=0.2+0.05,其中0.2是有限小数,0.05是无限循环小数。
3. 循环小数可以通过分数表示。
循环小数可以通过一个整数和一个循环节相除得到。
例如,1/3=0.3333...,其中1是整数,3是循环节。
4. 循环小数可以通过无理数表示。
循环小数可以通过一个无理数和一个无限循环小数相加得到。
例如,π=3.1415926535...可以表示为3+0.1415926535...,其中3是无理数,0.1415926535...是无限循环小数。
三、循环小数的应用1. 循环小数的除法运算。
循环小数可以通过长除法进行计算,找到循环节的规律,从而将循环小数转化为有限小数。
2. 循环小数的近似计算。
循环小数可以通过截断或近似计算得到一个有限小数,使得计算更加简便。
3. 循环小数的转化。
循环小数可以通过分数转化为有理数,或者通过无理数转化为无限循环小数。
4. 循环小数的应用于几何学。
循环小数可以用于计算圆周率、黄金分割等几何学中的问题。
循环小数是指小数部分存在一定的规律重复出现的无限小数。

无限循环小数化分数(原创实用版)目录1.无限循环小数的概念2.无限循环小数与分数的关系3.如何将无限循环小数化为分数4.实例解析正文1.无限循环小数的概念无限循环小数是指小数部分有一段数字或数字序列不断重复出现的小数。
例如,1/3 = 0.3333...,其中 3 无限循环重复出现。
无限循环小数是一种特殊的小数,它在数学中有着广泛的应用。
2.无限循环小数与分数的关系无限循环小数与分数有着密切的关系。
可以证明,每一个无限循环小数都可以表示为一个分数,反之亦然。
例如,0.6666...可以表示为 2/3,而 1/3 可以表示为 0.3333...,这为无限循环小数的研究和应用提供了便利。
3.如何将无限循环小数化为分数为了将无限循环小数化为分数,我们可以采用一种名为“进位制”的方法。
具体操作如下:(1)将无限循环小数的循环部分用一个字母(如 x)表示,得到一个新的小数,例如 0.3333...可以表示为 0.x。
(2)将新小数乘以 10^n,其中 n 表示循环部分的位数。
例如,如果循环部分有两位,那么 n=2,乘以 10^2=100。
(3)将乘积减去原数,即 100x - x = 99x。
(4)化简得到的分数,即将分子和分母同时除以它们的最大公约数。
通过以上步骤,我们可以将无限循环小数化为一个分数。
4.实例解析以 0.6666...为例,循环部分有两位,即 n=2。
按照上述方法,我们可以得到:(1)0.66 = 0.6666...(2)0.66 × 100 = 66(3)66 - 0.66 = 65.34(4)65.34 可以化为最简分数 13/2。

无限小数的概念无限小数,指的是在小数点后有无限位小数的数。
在数学中,我们可以通过循环小数和无理数来表示无限小数。
无限小数在生活和自然界中也存在很多实例,比如圆周率π、黄金分割比等等。
一、循环小数循环小数是指小数点后有一段长度为n的小数,该小数段在数列中不断重复。
举例来说,1/3=0.33333...中的小数0.3无限循环出现,可以表示为0.3(3)。
1.循环小数的表示循环小数可以用如下方式来表示:a0.a1 a2 a3 ... an (b1 b2 ...bm)其中a0表示最高位整数,ai表示小数部分的第i位数字,(b1 b2 ...bm)表示小数部分循环节的长度为m的数字串。
2.循环小数的性质循环小数有以下性质:(1)一个不为零的有理数的小数部分,要么是有限小数,要么是循环小数。
(2)循环小数是有理数。
(3)一个有理数的小数部分是循环节为n的循环小数(n>0),当且仅当其既约分数是形如k/(10^n - 1)的形式。
3.循环小数的变换循环小数可以通过如下方式变换:(1)去循环节:如果一个小数是循环小数,则可以通过减去其循环节部分,将其变为有限小数。
例如0.142857142857...可以变为0.142857,并且这两个小数相等。
(2)扩大倍数:如果一个小数是循环小数,则可以通过乘以一个整数k,将其变为有限小数。
例如1/7=0.142857142857...可以变为2/14=0.285714,并且这两个小数相等。
二、无理数无理数是指不能表示为有限小数或循环小数的数。
无理数不能表示成两个整数之比。
无理数可以由无限小数来定义和表示。
1.无理数的表示无理数可以通过连分数的形式来表示:a0 + 1 / (a1 + 1 / (a2 + 1 / (a3 +...其中a0为整数部分,a1,a2,a3,...为连分数的部分(系数),1/a1,1/a2,1/a3,...为连分数的余数。
2.无理数的性质无理数有以下性质:(1)无理数不是有理数。
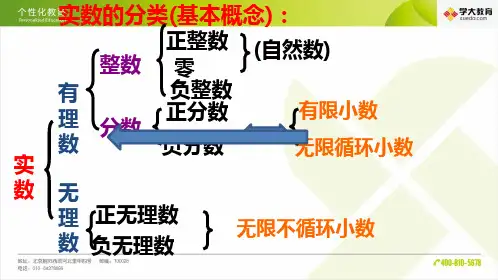
专题: 循环小数
1. 关于无限小数的定义
1) 无限循环小数是满足以下条件的无限小数:
(1) 从小数部分的某一位起,由一个数字或者有限个数字构成循环节;
(2) 循环节内数字,不再构成循环;
(3) 循环节依次不断地重复无数次出现;
(4) 若循环节后面还有数字则忽略不计。
2) 无限不循环小数由以下两种无限小数构成:
(1) 从小数部分的任何一位起,都不存在循环节的无限小数;
(2) 从小数部分的某一位起,由无限个数字构成循环节,并且循环节内数字不再构成循环的无限小数。
2. 循环小数化成分数
1) 纯循环小数化成分数
(1) 分子是由一个循环节的数字构成的数;
(2) 分母各位数字都是9,而且9的个数等于循环节中的数字的个数。
2) 混循环小数化成分数
(1) 分子是由不循环部分的数字,和一个循环节的数字连接在一起构成的数,减去不循环部分数字构成的数;
(2) 分母的前几位数字是9,后面几位数字是0,且9的个数与循环节的数位相同,0的个数与不循环部分的数位相同。
3. 循环小数的不唯一性
1) 根据无限循环小数的定义可知,使用无限循环小数表示有理数的缺点在于数的表示方式具有不唯一性。
2) 无限循环小数的不唯一性的实例
4. 循环小数的应用
1) 有理数的“分数形式”的定义
(1) 有理数是一个整数a和一个非零整数b的比,写作ba,又称作分数。
(2) 有理数是能表示成分数的数,或整数和分数统称有理数。
2) 有理数的“小数形式”的定义
(1) 有理数由有限小数和无限循环小数组成。
(2) 无限不循环小数称为无理数。