欧几里得与欧几里得几何 亚历山大里亚的欧几里得(约公元前330年—前275年),古希腊数学家,被称为“几何之父”。他活跃于托勒密一世(公元前323年-前283年)时期的亚历山大里亚,他最著名的著作《几何原本》是欧洲数学的基础,提出五大公设,发展欧几里得几何,被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。 欧几里得是古希腊著名数学家、欧氏几何学的开创者。欧几里得生于雅典,当时雅典就是古希腊文明的中心。浓郁的文化气氛深深地感染了欧几里得,当他还是个十几岁的少年时,就迫不及待地想进入“柏拉图学园”学习。他在有攀滋入学园之后,便全身心地沉潜在数学王国里。他潜心求索,以继器粕拉图的学术为奋斗目标,除此之外,他哪儿也不去,什么也不干。熬翻阅和研究了柏拉图的所有著作和手稿,可以说,连柏拉图的亲传攀擎也没有谁能像他那样熟悉柏拉图的学术思想、数学理论。经过对柏拉图思想的深入探究,他得出结论:图形是神绘制的,所有一切籀象的逻辑规律都体现在图形之中。因此,对智慧的训练,就应该从戡图形为主要研究对象的几何学开始。他确实领悟到了柏拉图思想的要旨,并开始沿着柏拉图当年走过的道路,把几何学的研究作为自醺羽主要任务,并最终取得了世人敬仰的成就。 最早的几何学兴起于公元前7年的古埃及,后经古希腊等人传到古希腊的都城,又借毕达哥拉斯学派纂糯典。在欧几里得以前,人们已经积累了许多几何学的知识,然黔这些知识当中,存在一个很大的缺点和不足,就是缺乏系统性。大多数是片断、零碎的知识,公理与公理之问、证明与证明之间并没有什么很强的联系性,更不要说对公式和定理进行严格的逻辑论证和说明。因此,随着社会经济的繁荣和发展,特别是随着农林畜牧业的发展、土地开发和利用的增多,把这些几何学知识加以条理化和系统化,成为一整套可以自圆其说、前后贯通的知识体系,已经是刻不容缓,成为科学进步的大势所趋。欧几里得通过早期对柏拉图数学思想,尤其是几何学理论系统而周详的研究,已敏锐地察觉到了几何学理论的发展趋势。他下定决心,要在有生之年完成这一工作。为了完成这一重任,欧几里得不辞辛苦,长途跋涉,从爱琴海边的雅典古城,来到尼罗河流域的埃及新埠—亚历山大城,为的就是在这座新兴的,但文化蕴藏丰富的异域城市实现自己的初衷。在此地的无数个日日夜夜里,他一边收集以往的数学专著和手稿,向有关学者请教,一边试着著书立说,阐明自己对几何学的理解,哪怕是尚肤浅的理解。经过欧几里得忘我的劳动,终于在公元前300年结出丰硕的果实,这就是几经易稿而最终定形的《几何原本》一书。这是一部传世之作,几何学正是有了它,不仅第一次实现了系统化、条理化,而且又孕育出一个全新的研究领域——欧几里得几何学,简称欧氏几何。 不朽的平面几何学著作 《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作。传到今天的欧几里得著作并不多,然而我们却可以从这部书详细的写作笔调中,看出他真实的思想底蕴。 全书共分13卷。书中包含了5条“公理”、5条“公设”、23个定义和467个命题。在每一卷内容当中,欧几里得都采用了与前人完全不同的叙述方式,即先提出公理、公设和定义,然后再由简到繁地证明它们。这使得全书的论述更加紧凑和明快。而在整部书的内容安排上,也同样贯彻了他的这种独具匠心的安排。它由浅到深,从简至繁,先后论述了直边形、圆、比例论、相似形、数、立体几何以及穷竭 法等内容。其中有关穷竭法的讨论,成为近代微积分思想的来源。仅仅从这些卷帙的内容安排上,我们就不难发现,这部书已经基本囊括了几何学从公元前7世纪的古埃及,一直到公元前4世纪——欧几里得生活时期——前后总共400多年的数学发展历史。这其中,颇有代表性的便是在第1卷到第4卷中,欧几里得对直边形和圆的论述。正是在这几卷中,他总结和发挥了前人的思维成果,巧妙地论证了毕达哥拉斯定理,也称“勾股定理”。即在一直角三角形中,斜边上的正方形的面积等于两条直角边上的两个正方形的面积之和。他的这一证明,从此确定了勾股定理的正确性并延续了2000多年。《几何原本》是一部在科学史上千古流芳的巨著。它不仅保存了许多古希腊
Koller 教授把决策作为一种单独的模块进行讲解,但我认为,决策和推理本质上是一样的,都是在假设已知CPD或者势函数的情况下对模型给出结论。 1、决策==逐利 决策的基本思想很intuitive,并且非常有用。在赌博行为中,最后获得的钱与硬币的正反,赌注的大小有关。硬币的正反显然是随机变量,而赌注的大小却是决策量。显而易见的是,决策的最终目的是使得某个期望最大化。再举一个视觉中的例子,对于双目配准算法而言,左相机对应右相机的像素可以认为是随机变量。但是否将两个像素配在一起却可以认为是一个决策(假设像素一一对应,如果甲配了乙就不能配丙了,希望配准的最终结果是尽可能正确的)。故决策的数学表达为: 其中,P(X|A)表示在给定决策下,随机变量X的概率。U(x,a)表示给定决策下,x发生所获得的收益。简单的决策如图所示:
2、决策的方法 显然从上面的分析可知,我们要做的决策就是使得期望最大化的那个。换一个角度来看,如果每次的决策都是未知的,决策取决于已知信息,决策影响最终结果,如果决策也是随机变量,我们应该把获利最多的那个决策组作为我们所需采取的决策库。换而言之,凡事应有a,b,c三策,不同的策略对应不同的情况。显然,我们所需要采取的策略取决于已知的信息(Action的父节点)。而策略组本身就是一个随机变量。 如图所示,如果变量真实值无法观测,只能通过一个传感器(survey)来进行推测时,决策应该取决于S的值。S的值又和其所有父节点(M)的值相关。MEU表示所选择的策略。
显然,我们需要P(S)deta(F|S)U(F,M),然后P(S)需要对P(M,S)进行边际获得。故表达式如上。带入数据发现
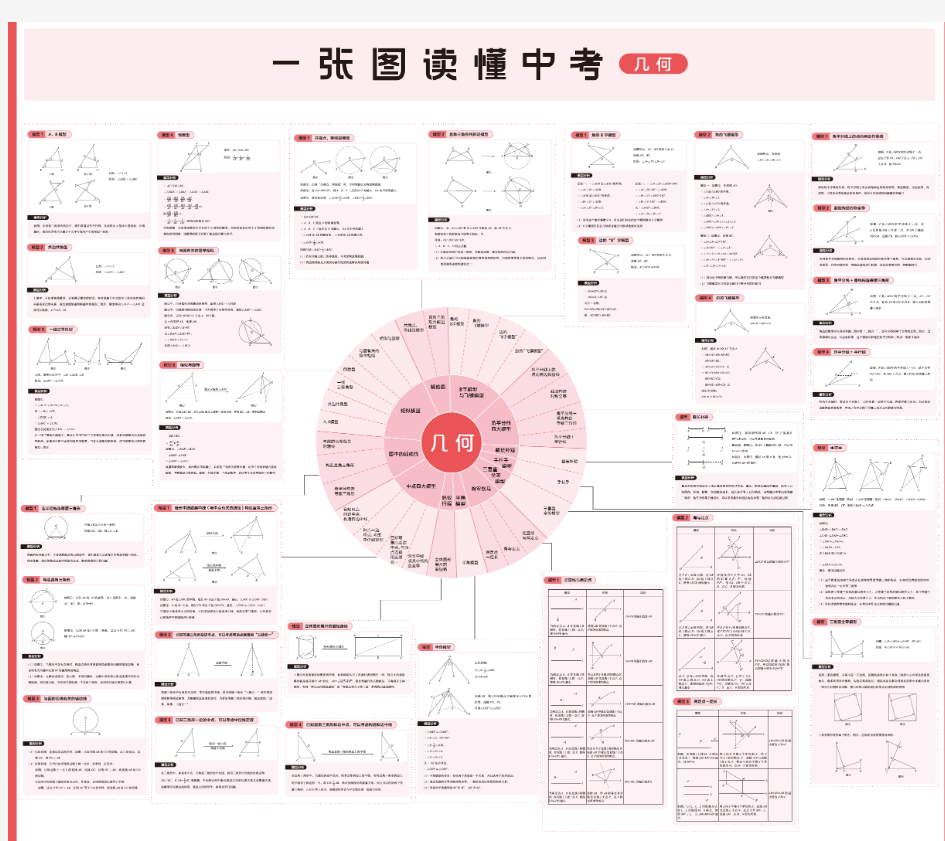
初中几何常见九大模型解析(完美版) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
初中几何常见九大模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有;③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) 模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE;②; ③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③
?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②;③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导? 模型四:角含半角模型90° (1)角含半角模型90°-1 ?条件:①正方形;②; ?结论:①;②的周长为正方形周长的一半; 也可以这样: ?条件:①正方形;② ?结论:
欧几里得几何与非欧几何 摘要:欧几里得的《几何原本》奠定了几何学发展的基础, 随着逻辑推理的理论发展, 非欧几何在艰难中产生发展起来;其中少不了欧几里得、罗巴切夫斯基与黎曼在几何学上的巨大贡献,且两者几何学之间存在着严密的辩证关系。 关键词:欧几里得几何、几何原本、非欧几何、辩证关系 欧氏几何是人类创立的第一个完整的严密的(相对而言) 科学体系。它于公元前三世纪由古希腊数学家欧几里得完成,后来经历了两千多年的发展,对科学和哲学的影响是极其深远的。十九世纪二十年代,几何学发展史上出现了新的转折点,德国数学家高斯、匈牙利数学家亚·鲍耶和俄国数学家罗巴切夫斯基分别在1824年、1825年1826年各自独立地创立了非欧几何,其中以罗巴切夫斯基所发表的内容最完善,因此取名为罗氏几何学。1854年,德国数学家黎曼创立了黎曼几何。十九世纪末,德国数学家阂可夫斯基发展了黎曼几何,创立了四维空时几何学。1915年,爱因斯坦利用非欧几何——四维空间几何学作为工具创立了广义相对论, 不久广义相对论连同非欧几何为天文观察等科学实践所证实。从此,人们确认非欧几何是人类发现的伟大的自然科学真理。 一、欧几里得几何的发展 (一)古希腊前期几何学的发展为欧几里得几何的产生奠定了基础 在欧几里得时代以前,数学家与学者们就已经获得许多几何方面的成果,但大多数是零星的,有的对部分内容也作过一些整理加工,但不系统。面对前人留下的材料以及一些证明方法,欧几里得认真进行了总结、提练、筛选,以及分析、综合、归纳、演绎,集前人工作之大成,系统整理加工成巨著《几何原本》,所以说古希腊前期的几何学的发展为欧几里得几何的产生奠定了基础。 最早研究几何的一批人是爱奥尼亚学派,它的创始人是泰勒斯,据传他曾用一根已知长度的杆子,通过同时测量竿影和金字塔影之长,求出了金字塔的高度。人也把数学之成为抽象理论和有些定理演绎证明归功于他,如圆被直径二等分,等腰三角形两底角相等,两直线相交对顶角相等,两角及夹边对应相等的两个三角形全等,内接于半圆的角是直角等的论证。 对几何从经验上升到理论作出重要贡献的有毕达哥拉斯学派。他们注意研究抽象的数学概念,尤其对整数的性质有出色的研究。雅典的巧辩学派以著名的三等分任意角、化圆为方和倍立方三大难题为其研究中心。 柏拉图是那个时代影响最大的哲学家。柏拉图及其后继者把数学概念看作抽象图。柏拉图说数学概念不依赖于经验而自有其实在性。它们只能为人所发现,并非为人所发明或塑造。他是第一个把严密推理法则加以系统化的人,希腊人最早坚持数学里必须用演绎推理作求证的唯一方法,并使数学有别于所有其他知识领域或研究领域。柏拉图学派的最重要发现是圆锥曲线。还对不可公度量作过一些研究。这些都为欧几里得的研究开辟了道路。 欧多克斯是古希腊时代最大的数学家,他在数学上的第一个大贡献是关于比
软件学报ISSN 1000-9825, CODEN RUXUEW E-mail: jos@https://www.doczj.com/doc/df1493124.html, Journal of Software,2013,24(11):2476?2497 [doi: 10.3724/SP.J.1001.2013.04486] https://www.doczj.com/doc/df1493124.html, +86-10-62562563 ?中国科学院软件研究所版权所有. Tel/Fax: ? 概率图模型研究进展综述 张宏毅1,2, 王立威1,2, 陈瑜希1,2 1(机器感知与智能教育部重点实验室(北京大学),北京 100871) 2(北京大学信息科学技术学院智能科学系,北京 100871) 通讯作者: 张宏毅, E-mail: hongyi.zhang.pku@https://www.doczj.com/doc/df1493124.html, 摘要: 概率图模型作为一类有力的工具,能够简洁地表示复杂的概率分布,有效地(近似)计算边缘分布和条件分 布,方便地学习概率模型中的参数和超参数.因此,它作为一种处理不确定性的形式化方法,被广泛应用于需要进行 自动的概率推理的场合,例如计算机视觉、自然语言处理.回顾了有关概率图模型的表示、推理和学习的基本概念 和主要结果,并详细介绍了这些方法在两种重要的概率模型中的应用.还回顾了在加速经典近似推理算法方面的新 进展.最后讨论了相关方向的研究前景. 关键词: 概率图模型;概率推理;机器学习 中图法分类号: TP181文献标识码: A 中文引用格式: 张宏毅,王立威,陈瑜希.概率图模型研究进展综述.软件学报,2013,24(11):2476?2497.https://www.doczj.com/doc/df1493124.html,/ 1000-9825/4486.htm 英文引用格式: Zhang HY, Wang LW, Chen YX. Research progress of probabilistic graphical models: A survey. Ruan Jian Xue Bao/Journal of Software, 2013,24(11):2476?2497 (in Chinese).https://www.doczj.com/doc/df1493124.html,/1000-9825/4486.htm Research Progress of Probabilistic Graphical Models: A Survey ZHANG Hong-Yi1,2, WANG Li-Wei1,2, CHEN Yu-Xi1,2 1(Key Laboratory of Machine Perception (Peking University), Ministry of Education, Beijing 100871, China) 2(Department of Machine Intelligence, School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China) Corresponding author: ZHANG Hong-Yi, E-mail: hongyi.zhang.pku@https://www.doczj.com/doc/df1493124.html, Abstract: Probabilistic graphical models are powerful tools for compactly representing complex probability distributions, efficiently computing (approximate) marginal and conditional distributions, and conveniently learning parameters and hyperparameters in probabilistic models. As a result, they have been widely used in applications that require some sort of automated probabilistic reasoning, such as computer vision and natural language processing, as a formal approach to deal with uncertainty. This paper surveys the basic concepts and key results of representation, inference and learning in probabilistic graphical models, and demonstrates their uses in two important probabilistic models. It also reviews some recent advances in speeding up classic approximate inference algorithms, followed by a discussion of promising research directions. Key words: probabilistic graphical model; probabilistic reasoning; machine learning 我们工作和生活中的许多问题都需要通过推理来解决.通过推理,我们综合已有的信息,对我们感兴趣的未 知量做出估计,或者决定采取某种行动.例如,程序员通过观察程序在测试中的输出判断程序是否有错误以及需 要进一步调试的代码位置,医生通过患者的自我报告、患者体征、医学检测结果和流行病爆发的状态判断患者 可能罹患的疾病.一直以来,计算机科学都在努力将推理自动化,例如,编写能够自动对程序进行测试并且诊断 ?基金项目: 国家自然科学基金(61222307, 61075003) 收稿时间:2013-07-17; 修改时间: 2013-08-02; 定稿时间: 2013-08-27
欧几里得的故事 言传身教 欧几里得大约生于公元前325年,他是古希腊数学家,他的名字与几何学结下了不解之缘,他因为编著《几何原本》而闻名于世,但关于他的生平事迹知道的却很少,他是亚历山大学派的奠基人。早年可能受教于柏拉图,应托勒密王的邀请在亚历山大授徒,托勒密曾请教欧几里得,问他是否能把证明搞得稍微简单易懂一些,欧几里得顶撞国王说:“在几何学中是没有皇上走的平坦之道的。”他是一位温良敦厚的教育家。 另外有一次,一个学生刚刚学完了第一个命题,就问:“学了几何学之后将能得到些什么?”欧几里得随即叫人给他三个钱币,说:“他想在学习中获取实利。”足见,欧几里得治学严谨,反对不肯刻苦钻研投机取巧的思想作风。 在公元前6世纪,古埃及、巴比伦的几何知识传入希腊,和希腊发达的哲学思想,特别是形式逻辑相结合,大大推进了几何学的发展。在公元前6世纪到公元前3世纪期间,希腊人非常想利用逻辑法则把大量的、经验性的、零散的几何知识整理成一个严密完整的系统,到了公元前3世纪,已经基本形成了“古典几何”,从而使数学进入了“黄金时代”。柏拉图就曾在其学派的大门上书写大型条幅“不懂几何学的人莫入”。欧几里得的《几何原本》正是在这样一个时期,继承和发扬了前人的研究成果,取之精华汇集而成的。 《几何原本》 欧氏《几何原本》推论了一系列公理、公设,并以此作为全书的起点。共13卷,目前中学几何教材的绝大部分都是欧氏《几何原本》的内容。 勾股定理在欧氏《几何原本》中的地位是很突出的,在西方,勾股定理被称作毕达哥拉斯定理,但是追究其发现的时间,在我国和古代的巴比伦、印度都比毕达哥拉斯早几百年,所以我们称它勾股定理或商高定理。在欧氏《几何原本》中,勾股定理的证明方法是:以直角三角形的三条边为边,分别向外作正方形,然后利用面积方法加以证明,人们非常赞同这种巧妙的构思,因此目前中学课本中还普遍保留这种方法。 据说,英国的哲学家霍布斯一次偶然翻阅欧氏的《几何原本》,看到勾股定理的证明,根本不相信这样的推论,看过后十分惊讶,情不自禁地喊道: “上帝啊,这不可能”,于是他就从后往前仔细地阅读了每个命题的证明,直到公理和公设,最终还是被其证明过程的严谨、清晰所折服。 欧氏《几何原本》的部分内容与早期智人学派研究三个著名几何作图问题有关,特别是圆内接正多边形的作图方法。欧氏的《几何原本》只把用没有刻度的直尺画直线,用圆规画圆列为公理,限定了“尺规”作图。于是几何作图就出现了“可能”与“不可能”的情况。在这里欧几里得只给出了正三、四、五、六、十五边形的作法,加上连续地二等分弧,可以扩展到正2n、3(2n)、5(2n)、15(2n)边形。因此,我们可以想象欧几里得一定还尝试
概率图模型中的推断 王泉 中国科学院大学网络空间安全学院 2016年11月
?推断问题回顾 ?精确推断:信念传播 –信念传播算法回顾 –信念传播在HMM中的应用?近似推断:吉布斯采样–吉布斯采样算法回顾 –吉布斯采样在LDA中的应用
?推断问题回顾 ?精确推断:信念传播 –信念传播算法回顾 –信念传播在HMM中的应用?近似推断:吉布斯采样–吉布斯采样算法回顾 –吉布斯采样在LDA中的应用
?已知联合概率分布 P x 1,?,x n ,估计 –x Q 问题变量;x E 证据变量;x Q ∪x E =x 1,?,x n P R =1 P R =0 0 P R =1G =1= ? P B =0.001 P E =0.002 P A B ,E =0.95 P A B ,?E =0.94 P A ?B ,E =0.29 P A ?B ,?E =0.001 P J A =0.9 P J ?A =0.05 P M A =0.7 P M ?A =0.01 P B =1E =0,J =1=? P x Q x E =x Q ,x E x E
?已知联合概率分布 P x 1,?,x n ,估计 –x Q 问题变量;x E 证据变量;x Q ∪x E =x 1,?,x n P x Q x E =x Q ,x E x E 观测图片 y i 原始图片 x i y ?=argmax P y x 朴素贝叶斯 x ?=argmax P x y 图像去噪
?精确推断:计算P x Q x E的精确值 –变量消去 (variable elimination) –信念传播 (belief propagation) –计算复杂度随着极大团规模的增长呈指数增长,适用范围有限?近似推断:在较低的时间复杂度下获得原问题的近似解–前向采样 (forward sampling) –吉布斯采样 (Gibbs sampling) –通过采样一组服从特定分布的样本,来近似原始分布,适用范围更广,可操作性更强
欧几里德《几何原本》与公里化思想 班级:314数教3班姓名:余燕红学号:49 【摘要】欧几里得《几何原本》产生的历史背景、主要内容以及所包含的公理化思想促进了几何学的发展, 对数学的发展也有着重大的影响. 【关键词】欧几里得;《几何原本》;公理化思想 一、欧几里得 “几何无王者之道”, 说出这句话的人正是古希腊数学家欧几里得(公元前 330 ~公元前275), 他是论证几何的集大成者, 关于他的生平我们了解的甚少, 根据有限的记载推断,欧几里得早年就学于雅典, 在公元前 300年左右, 应托勒密王的邀请到亚历山大城教学.他 写过不少数学、天文、光学和音乐方面的著作, 现存的有《原本》(Elements)、《数据》(Data)、《论剖分》(OnDivisions)、《现象》 (Phaenomena)、《光学》(Optic)和《镜面反射》(Catoptrica)等, 在这些著作当中, 最著名的莫过于《原本》了, 根据早期的翻译, 我们也称之为《几何原本》. 二、《几何原本》 1.历史起源:最早的几何学兴起于公元前 7世纪的古埃及, 由古希腊数学家泰勒斯迈出了 论证数学的第一步, 之后毕达哥拉斯又进行了发展.在欧几里得之前, 已经积累了许多的几何知识, 但是这些知识缺乏系统性, 大多数都是片断的、零散的知识, 公理与公理之间、证明与证明之间没有很强的联系性, 更没有对公式和定理进行严格的和逻辑的证明.随着对几何知识的使用越来越多, 就迫切将这些知识条理化和系统化, 使其成为一套可以自圆其说、前后贯通的知识体系.欧几里得通过早期对柏拉图数学思想, 尤其是几何理论系统周详的研究, 敏锐地观察到了几何学理论的发展趋势, 所以, 他背负着这一重任来到文化丰富的亚历山大 城, 在这里, 他一边收集以往的数学专著和手稿, 并不断地向有关学者请教, 一边试着著书立说, 阐述自己对几何学的理解, 哪怕是尚肤浅的理解, 经过他的努力, 终于在公元前300年, 几经易稿最终写成《几何原本》一书. 2.内容框架:“《几何原本》共分 13卷, 包括 5条公理、5条公设、119个定义和 465条命题.”第Ⅰ卷给出了一些最基本的定义, 如点、线、面、圆等等, 并给出了 5条公理和 5条公设.欧几里得以这些基本定义、公设和公理作为全书推理的出发点, 第Ⅰ, Ⅱ, Ⅲ, Ⅳ和Ⅵ卷包含了平面几何的一些基本内容, 如全等形、平行线、多边形、圆、毕达哥拉斯定理、初等作图及相似形等;第Ⅱ, Ⅵ卷中涉及“几何代数”的内容;第Ⅴ卷讲比例论;第Ⅶ , Ⅷ , Ⅸ卷是关于数论的内容, 其中陈述了求两数最大公因子的辗转相除法, 即著名的欧几里得算法;第Ⅹ卷讨论不可公度量;而最后三卷主要是立体几何的内容.这是一本集前人思想和欧几里得个人创造于一体的不朽之作, 几何学正是因为有了它, 不仅第一次实现了系统化、条理化, 而且又孕育出一个全新的研究领域———欧几里得几何学, 简称“欧式几何学”. 三、公理化思想及其发展 “欧几里得《几何原本》可以说是数学史上的第一座理论丰碑, 它最大的功绩就是它确立了数学中的演绎范式.这种范式要求一门学科中的每一个命题必须是在它之前已建立的一些命题的逻辑结论, 而所有这样的推理链的共同出 发点, 是一些基本定义和被认为是不证自明的基本原理———公设或公理, 这就是后来所谓的公理化思想.”它的目的就是把数学表达成为一个演绎系统, 其出发点就是一组基本概念和公理.很显然, 欧几里得在前人研究的基础上, 以 5条公设和 5条公理, 运用
【模型1】倍长 1、倍长中线; 2、倍长类中线; 3、中点遇平行线延长相交 【模型2】遇多个中点,构造中位线 1、直接连接中点; 2、连对角线取中点再相连 【例1】在菱形ABCD和正三角形BEF中,/ ABC = 60° G是DF的中点,连接GC、GE . (1)如图1,当点E在BC边上时,若AB = 10, BF = 4,求GE的长; (2)如图2,当点F在AB的延长线上时,线段GE、GC有怎样的数量和位置关系,写出你的猜想,并给予证明; (3)如图3,当点F在CB的延长线上时,(2)问中的关系还成立吗?写出你的猜想,并给予证明. 易证明△ CHG CEG,贝U GE =涣羌 中点模型 【解答】 (1)延长EG交CD于点H 注意G的两端点D、E 所在的直线DC // FE A C E
易证明△ BCE ◎△ FIE,则△ CEI是等边三角形,GE = . 3 GC,且GE丄GC 【例2】如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE= AF,/ DAE =Z BAF. (1)求证:CE= CF; (2)若/ ABC = 120°点G是线段AF的中点,连接DG、EG,求证:DG丄EG. 【解答】 (1) 证明△ ABEADF 即可; (2) 延长DG与AB相交于点H,连接HE,证明△ HBE◎△ EFD即可 (2)延长CG交AB于点I,
【例3】如图,在凹四边形 CD交EF于H点,求证:/ ABCD中,AB= CD, E、F分别为BC、AD的中点,BA交EF延长线于G点, /_ BGE=Z CHE. 【解答】 取BD中点可证,如图所示: E
第12卷第1期 数 学 教 育 学 报 Vol.12, No.1 2003年2月 JOURNAL OF MATHEMATICS EDUCATION Feb., 2003 收稿日期:2002–11–10 基金项目:本文得到国家自然科学基金委员会天元基金和华诚基金的支持 作者简介:齐民友(1930—),男,安徽芜湖人,武汉大学教授,主要从事偏微分方程研究. 中国人眼中的欧几里得《几何原本》 齐民友 (武汉大学 数学学院,湖北 武汉 430072) 摘要:《几何原本》由意大利传教士利玛窦在16世纪末传入中国,全书共15卷.利玛窦与徐光启合作将《原本》前6卷翻译成中文.1856年,李善兰与英国人伟烈亚力合作,将全书15卷译成中文.西方数学传入中国伴随着尖锐的斗争.数学不仅仅是一种技术意义下的“工具”,而是与我国固有文化极不相同的一种文化. 关键词:《几何原本》;数学方法论;文化 中图分类号:G40–055 文献标识码:A 文章编号:1004–9894(2003)01–0001–06 海森伯在《物理学与哲学》一书中这样说[1]:“今天,当人们谈到现代物理学时,首先就想到原子武器.……并且都心悦诚服地承认物理学对一般政治形势的影响比以往任何时期都要大.但是,现代物理学的政治方面真的是它的最重要的方面吗?……每个工具都带有用来创造它的那种精神.因为每个国家和政治集团,不管它的地理位置和文化传统如何,都必须以某种方式关心这种新武器,所以,现代物理学的精神必将渗透到许多人的心灵之中,并以各种不同方式和老传统联系起来.”对于某些地区和某种文化传统,它“将同本地文化的宗教基础和哲学基础发生冲突.……这种冲突可能引起全新的、难以预料的发展”.现代数学在中国的传播和发展过程恰好证实了这个论断.这一过程是漫长而且充满冲突的.欧几里得《几何原本》传入中国就是一个例证. 1 “几何原本”的传入 欧几里得的《几何原本》是意大利传教士耶苏 会士利玛窦(1552—1610)传入中国的.利玛窦曾受教于克拉维乌斯(1537—1612,著名数学家,耶苏会士,曾受教皇格里高里十三世之命,主持了Gregory历的制订,完成了主要的计算工作).根据教皇保罗二世当时向东方派遣传教士的决定,他于1582年(一说为1581年)来到澳门,次年到达广东肇庆.但是,他遇到的是一个不友好的环境.原来,明皇朝一直实行严厉的闭关锁国的政策.后因经济方面的原因有所松动.传教士来华也多起来了.但对他们的活动的真实目的及其对于中国人民 可能的影响,朝廷仍抱有极大的疑虑.因此,直到1600年他才获准进入北京.当时,他向皇帝献上了贡物:其中有圣经、圣像、时钟、世界地图,据说还有圣骨.但是,这反而引起了更深的怀疑.据明史记载,当时即有官员说,基督教义已属无稽之谈,教徒升天又何来遗骨留在人世?但是,诸如地图,时钟等等,却引起了不少读书人的兴趣.传教士们为了在中国传播天主教义,力图找到中国人能够接受的方式.利玛窦曾向教皇报告,认为接近中国人的最好的,甚至是唯一的方法就是向中国人传授西方数学.正是在这种背景下开始了欧几里得《几何原本》的翻译. 时至16世纪末,传统的中国数学已经衰落了,许多古算典籍甚至已经失传了.但是当时手工业、冶金工业、商业以及原始的银行业,却都有了相当的发展.这就需要数学有相应的发展.毫不偶然,《几何原本》的著名中译者徐光启(1562—1633)出身于商人家庭,最终官至大学士,终身关心农业、防洪、灌溉、乃至国防.另一方面,历法问题在中国各皇朝中又有特殊的重要性.天文异象如日月蚀,彗星出现等等,被看作灾难,如政变、篡权的先兆.自古以来,各朝各代,常设钦天监,其负责人(钦天监正)需就天文异象的出现向皇帝作秘密报告.因此,历法问题不仅关乎农业,更关系到皇朝的命运.明代沿用元代大统历与回回历,因年代久远,误差甚大,修正历法,乃成急务,但精通历法人才难得.1596年9月22日日蚀即有误报.时利玛窦在南昌按西法准确预报了这次日蚀,因此名声大振.许多人去向他学习西方历法.他以Clavius
小学平面几何五大模型 一、 共角定理 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E分别是, AB AC上的点如图⑴(或D在BA的延长线上,E在AC上),则:():() S S AB AC AD AE =?? △△ 证明:由三角形面积公式S=1/2*a*b*sinC可推导出 若△ABC和△ADE中, ∠BAC=∠DAE 或∠BAC+∠DAE=180°, 则 ADE ABC S S ? ? = AE AD AC AB ? ? 二、等积模型 ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如下图 12 :: S S a b = ③夹在一组平行线之间的等积变形,如右图 ACD BCD S S= △△ ; 反之,如果 ACD BCD S S = △△ ,则可知直线AB平行于CD. ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. b a S2 S1 D C B A
三、蝶形定理 1、任意四边形中的比例关系(“蝶形定理”): ①1243::S S S S =或者1324S S S S ?=? ②()()1243::AO OC S S S S =++ 速记:上×下=左×右 蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面 可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 2、梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. 四、相似模型 (一)金字塔模型 (二) 沙漏模型 G F E A B C D A B C D E F G ①AD AE DE AF AB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:. 相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; A B C D O b a S 3 S 2 S 1S 4 S 4 S 3 S 2 S 1O D C B A
概率图模型介绍与计算 01 简单介绍 概率图模型是图论和概率论结合的产物,它的开创者是鼎鼎大名的Judea Pearl,我十分喜欢概率图模型这个工具,它是一个很有力的多变量而且变量关系可视化的建模工具,主要包括两个大方向:无向图模型和有向图模型。无向图模型又称马氏网络,它的应用很多,有典型的基于马尔科夫随机场的图像处理,图像分割,立体匹配等,也有和机器学习结合求取模型参数的结构化学习方法。严格的说他们都是在求后验概率:p(y|x),即给定数据判定每种标签y的概率,最后选取最大的后验概率最大的标签作为预测结果。这个过程也称概率推理(probabilistic inference)。而有向图的应用也很广,有向图又称贝叶斯网络(bayes networks),说到贝叶斯就足以可以预见这个模型的应用范围咯,比如医疗诊断,绝大多数的机器学习等。但是它也有一些争议的地方,说到这就回到贝叶斯派和频率派几百年的争议这个大话题上去了,因为贝叶斯派假设了一些先验概率,而频率派认为这个先验有点主观,频率派认为模型的参数是客观存在的,假设先验分布就有点武断,用贝叶斯模型预测的结果就有点“水分”,不适用于比较严格的领域,比如精密制造,法律行业等。好吧,如果不遵循贝叶斯观点,前面讲的所有机器学习模型都可以dismiss咯,我们就通过大量数据统计先验来弥补这点“缺陷”吧。无向图和有向图的例子如(图一)所示: 图一(a)无向图(隐马尔科夫)(b)有向图 概率图模型吸取了图论和概率二者的长处,图论在许多计算领域中扮演着重要角色,比如组合优化,统计物理,经济等。图的每个节点都可看成一个变量,每个变量有N个状态(取值范围),节点之间的边表示变量之间的关系,它除了
初中几何常见九大模型解析模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?】 ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?` ?结论: ?右图中①; ?②延长AC交BD于点E,必有
(2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ' ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形) 模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE;②;③ ?证明提示: ①作垂直,如图,证明; - ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?<
?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明为等 边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?' ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①;②;③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导 ? 模型四:角含半角模型90°
欧几里得 亚历山大里亚的欧几里得(约公元前330年—前275年),古希腊数学家,被称为“几何之父”。他活跃于托勒密一世(公元前323年-前283年)时期的亚历山大里亚,他最著名的著作《几何原本》是欧洲数学的基础,提出五大公设,发展欧几里得几何,被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品,是几何学欧几里得的一生 的奠基人欧几里得(Euclid)是古希腊著名数学家、欧氏几何学的开创者。欧几里得生于雅典,当时雅典就是古希腊文明的中心。浓郁的文化气氛深深地感染了欧几里得,当他还是个十几岁的少年时,就迫不及待地想进入“柏拉图学园”学习。 一天,一群年轻人来到位于雅典城郊外林荫中的“柏拉图学园”。只见学园的大门紧闭着,门口挂着一块木牌,上面写着:“不懂几何者,不得入内! ”这是当年柏拉图亲自立下的规矩,为的是让学生们知道他对数学的重视,然而却把前来求教的年轻人给闹糊涂了。有人在想,正是因为我不懂数学,才要来这儿求教的呀,如果懂了,还来这儿做什么?正在人们面面相觑,不知是退、是进的时候,欧几里得从人群中走了出来,只见他整了整衣冠,看了看那块牌子,然后果断地推开了学园大门,头也没有回地走了进去。 “柏拉图学园”是柏拉图40岁时创办的一所以讲授数学为主要内容的学校。在学园里,师生之间的教学完全通过对话的形式进行,因此要求学生具有高度的抽象思维能力。数学,尤其是几何学,所涉及对象就是普遍而抽象的东西。它们同生活中的实物有关,但是又不来自于这些具体的事物,因此学习几何被认为是寻求真理的最有效的途径。
柏拉图甚至声称:“上帝就是几何学家。”遂一观点不仅成为学园的主导思想,而且也为越来越多的希腊民众所接受。人们都逐渐地喜欢上了数学,欧几里得也不例外。他在有幸进入学园之后,便全身心地沉潜在数学王国里。他潜心求索,以继承柏拉图的学术为奋斗目标,除此之外,他哪儿也不去,什么也不干,熬夜翻阅和研究了柏拉图的所有著作和手稿,可以说,连柏拉图的亲传弟子也没有谁能像他那样熟悉柏拉图的学术思想、数学理论。经过对柏拉图思想的深入探究,他得出结论:图形是神绘制的,所有一切现象的逻辑规律都体现在图形之中。因此,对智慧训练,就应该从图形为主要研究对象的几何学开始。他确实领悟到了柏拉图思想的要旨,并开始沿着柏拉图当年走过的道路,把几何学的研究作为自己的主要任务,并最终取得了世人敬仰的成就。欧几里得是希腊亚历山大大学的数学教授。著名的古希腊学者阿基米德,是他“学生的学生”——卡农是阿基米德的老师,而欧几里得是卡农的老师。 欧几里得不仅是一位学识渊博的数学家,同时还是一位有“温和仁慈的蔼然长者”之称的教育家。在著书育人过程中,他始终没有忘记当年挂在“柏拉图学园”门口的那块警示牌,牢记着柏拉图学派自古承袭的严谨、求实的传统学风。他对待学生既和蔼又严格,自己却从来不宣扬有什么贡献。对于那些有志于穷尽数学奥秘的学生,他总是循循善诱地予以启发和教育,而对于那些急功近利、在学习上不肯刻苦钻研的人,则毫不客气地予以批评。在柏拉图学派晚期导师普罗克洛斯的《几何学发展概要》中,就记载着这样一则故事,说的是数学在欧几里得的推动下,逐渐成为人们生活中的一个时髦话题(这与当今社会截然相反),以至于当时亚里山大国王托勒密一世也想赶这一时髦,学点儿几何学。虽然这位国王见多识广,但欧氏几何却令他学的很吃力。于是,他问欧几里得“学习几何学有没有什么捷径可走?”,欧几里得笑到:“抱歉,陛下!学习数学和学习一切科学一样,是没有什么捷径可走
几何模型:一线三等 角模型
一线三等角模型 一.一线三等角概念 “一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。 二.一线三等角的分类 全等篇 同侧 锐角直角钝角 P 异侧 相似篇 A 同侧锐角直角钝角 异侧
三、“一线三等角”的性质 1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC ∽△BDE. 2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED ,则△AEC ≌△BDE. 3.中点型“一线三等角” 如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1 902 BOC BAC ∠=?+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”. 如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关, 1 902 BOC BAC ∠=?+∠这是内心的性质,反之未必是内心. 在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心. 5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 ) 图 3-5 其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题 四、“一线三等角”的应用
欧几里得的故事 如果要问,古往今来,在浩如烟海的科学著作中,发行最广、沿用时间最长的书是哪一部?肯定的回答是:欧几里得的《几何原本》。 欧几里得是公元前三世纪希腊数学家,他是我们现在所学的欧氏几何的创始人,历史上称之为“几何学之父”。 欧几里得把毕生的精力献给了科学事业。他一生刻苦钻研,治学严谨,他在科学事业上的伟大成就,正是通过自己的辛勤劳动换来的。因此,他始终反对那种不想付出辛勤劳动,而指望通过走捷径、投机取巧来取得成绩的治学态度。下面的两个小故事很好地反映了他的这个性格。 曾经有一个聪明的年轻人提出要向欧几里得学习几何,欧几里得答应了他的要求。那个年轻人跟随欧几里得学习了一段时间后,产生了畏难怕苦的情绪,想打退堂鼓。有一次,他向欧几里得提了这么一个问题:欧几里得先生,我这么辛苦地学习几何学,在我学成之后,我会得到什么好处呢?欧几里得听了以后,没有直接批评他,而是幽默地对身边的侍者说:“快去拿三个金币给这位先生,因为他想在学习中获取实惠。”一席话把那个年轻人闹了个大红脸。 另一个故事说,当时统治埃及的托勒密国王为了赶时髦,想学一点几何学。他自命“天赋圣明”,认为对于天下无论什么事情,他都能一看就懂,一学就会。可当他翻阅了十三卷《几何原本》之后,皱起了眉头来。他转念一想,又自作聪明地认为,这类“繁琐说教”乃是专为凡夫俗子而设的,像他这般富有的天子,肯定另有一条捷径。于是他问欧几里得:“学习几何学除了看《几何原本》之外,有没有其他的捷径?”欧几里得笑道:“陛下,很抱歉。在学习科学的时候,国王和百姓都是一样的。科学上没有专供国王走的捷径。学习几何学,人人都要独立思考,就像种庄稼一样,不耕耘就不会有收获的。”从此之后,“几何无王者之道”就成为学习数学的箴言而流传至今。 【启示】欧几里得之所以成为伟大的数学家,是因为他勤奋工作。同样道理,我们要想取得好的学习成绩,也必须有刻苦钻研、锲而不舍的精神。如果像那个年轻人和国王一样,在学习中畏难怕苦、投机取巧,只会一事无成。