数学文卷·2014届四川省成都市高三第一次诊断性考试(2014.01)WORD版

2014年普通高等学校招生全国统一考试理科（四川卷）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的。

1．已知集合2{|20}A x x x =--≤，集合B 为整数集，则A B ⋂=（ ） A ．{1,0,1,2}- B ．{2,1,0,1}-- C ．{0,1} D ．{1,0}- 【答案】A【解析】{|12}A x x =-≤≤，B Z =，故A B ⋂={1,0,1,2}- 2．在6(1)x x +的展开式中，含3x 项的系数为（ ） A ．30 B ．20 C ．15 D ．10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3．为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上所有的点（ ）A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度 C ．向左平行移动1个单位长度 D ．向右平行移动1个单位长度【答案】A【解析】因为1sin(21)sin[2()]2y x x =+=+，故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4．若0a b >>，0c d <<，则一定有（ ） A ．a b c d > B ．a b c d < C ．a b d c > D ．a b d c< 【答案】D【解析】由1100c d d c<<⇒->->，又0a b >>，由不等式性质知：0a b d c ->->，所以a b d c< 5．执行如图1所示的程序框图，如果输入的,x y R ∈，则输出的S 的最大值为（ ）A ．0B ．1C ．2D ．3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时，函数2S x y =+2()22x y y y ≤+-≤-≤ ∴ S 的最大值为2.6．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（ ）A ．192种B ．216种C ．240种D ．288种 【答案】B【解析】当最左端为甲时，不同的排法共有55A 种；当最左端为乙时，不同的排法共有14C 44A 种。

试题分第Ｉ卷和第Ⅱ卷两部分。

满分150 分，考试时间150 分钟。

注意事项：1．答题前，务必将自己的姓名、考号准确无误地填写、填涂在答题卡规定的位置上；2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号；3．答题时，必须使用黑色签字笔，将答案规范、整洁地书写在答题卡规定的位置上； 4．所有题目必须在答题卡上作答，在试题卷上答题无效； 5．考试结束后将答题卡交回，不得折叠、损毁答题卡。

第Ｉ卷（选择题 50分）一、选择题（每题5分；共50分）1．已知集合{}2|20A x x x =->，}1|{≤=x x B ，=B A （ ）A ．[]0,1 B ．(]0,1 C ．(],0-∞ D ．.以上都不对2．0203sin 702cos 10--的值为（ ）A ．23B ．1C ．3D ．23．若一个几何体的三视图如右图所示，这个几何体可能是一个 ( )A ．棱台B ．棱锥C ．棱柱D ．圆柱 4．复数21i z -=（其中i 为虚数单位），则下列说法中正确的是（ ） A ．在复平面内复数z 对应的点在第一象限B ．复数z 的共轭复数主视图左视图俯视图122i z =--C ．若复数1z z b =+()b ∈R 为纯虚数，则12b =- D ．复数z 的模1||2z =5．已知命题:p ,x R ∃∈有32x x <成立；命题:q (0,)x ∀∈+∞，恒有1sin 2sin x x+≥成立，则下列命题为真命题的是（ ）A ．p q ∧B ．()p q ⌝∨ C．()p q ∧⌝D ．()()p q ⌝∧⌝6．函数错误！未找到引用源。

的图像因酷似汉字的“囧”字，而被称为“囧函数”。

则方程错误！未找到引用源。

的实数根的个数为（ ） A ．1 B ．2 C ．3 D ．4 7．已知数列{}na 的前n 项和2n S n n=-，正项等比数列{}n b 中，23b a =，2314(2,)n n n b b b n n N +-+=≥∈，则2log n b =（ ）A ．1n -B ．21n -C ．2n -D ．n8．若实数x 、y 满足⎪⎪⎩⎪⎪⎨⎧≤--≥+-≥≥0120100y x y x y x ，实数y x z -=3的最小值为 （ ）A ．1-B ．0C ．23D ．39．若A 、B 为锐角，满足sin cos()sin AA B B=+，则tan A 的最大值为（ ）A ．42B ．21C ．1D ．210．若存在区间],[n m ，使得函数()x f 定义域为],[n m 时，其值域为*)(],[N k kn km ∈，则称区间],[n m 为函数()x f 的“k 倍区间”．已知函数()x x x f sin 3+=，则()x f 的“5倍区间”的个数是 （ ） A ．0 B ．1 C ．2 D ．3第Ⅱ卷（非选择题，共100分）二、填空题（每小题5分，共25分）11．已知ABC ∆的三内角A 、B 、C 所对边长分别为是a 、b 、c ，设向量(,sin )m a b C =+，()3,sin sin n a c B A=+-，若m ∥n ，则角B 的大小为___________12．公差不为0的等差数列{}n a 的部分项123,,,k k k a a a ，构成等比数列，且123126,,k k k ===，则4k = .13．若两个正实数,x y 满足211x y+=，则y x 2+的最小值是 ． 14．已知函数)(x f y =定义域为),(ππ-，且函数)1(+=x f y 的图象关于直线1-=x 对称，当),0(π∈x 时，（其中)(x f '是)(x f 的导函数），若0.3(3),(log 3)a f b f π==，31(log )9c f =，则c b a ,,的大小关系是_____________15．给出下列命题：① 已知a 、b 为异面直线，过空间中不在a 、b 上的任意一点，可以作一个平面与a 、b 都平行；② 在二面角βα--l 的两个半平面α、β内分别有直线a 、b ，则二面角βα--l 是直二面角的充要条件是β⊥a 或α⊥b ；③已知异面直线a 与b 成060，分别在a 、b 上的线段AB 与CD 的长分别为4和2，AC 、BD 的中点分别为E 、F ，则3=EF ；④若正三棱锥的内切球的半径为1，则此正三棱锥的体积最小值38．则正确命题的编号是 。

第Ⅰ卷（共50分）一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集U ={1，2，3，4，5，6，7，8}，M ={1，3，5，7}，N ={5，6，7}，则()U C M N =( )A ．{5，7}B ．{2，4}C ．{1，3，5，6，7}D ．{2，4，8}2. 下列命题中的假命题是( ) A ．x ∀∈R ，120x ->B ．x *∀∈N ，2(1)0x ->C ．x ∃∈R ，lg 1x <D ．x ∃∈R ，tan 2x =3.12lg 2lg 25-的值为 ( ) A ．1B ．2C ．3D ．4【答案】B 【解析】试题分析：2112lg 2lglg(2)lg10022525-=÷==，故选B. 考点：对数与对数运算4.函数21()(1)sin f x x x =-的图象大致为5.△ABC 中，若2AD DB =，13CD CA CB λ=+，则λ=( )A ．13B ．23C ．23-D ．13-6.将函数()sin(2)()22f x x ππθθ=+-<<的图象向右平移(0)ϕϕ>个单位长度后得到函数()g x 的图象，若()f x 、()g x 的图象都经过点P ，则ϕ的值可以是( ) A ．53π B ．56π C ．2π D ．6π7.设数列{}n a 是首项大于零的等比数列，则“12a a <”是“数列{}n a 是递增数列”的( ) A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件8.若曲线12()f x x -=在点(,())a f a 处的切线与两条坐标轴围成的三角形的面积为18，则a = ( ) A ．64B ．32C ．16D ．8【答案】A9.一支人数是5的倍数且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人．则这只游行队伍的最少人数是( ) A ．1025B ．1035C ．1045D ．105510.定义在R 上的函数()f x 满足221,11(4)(),()log (|2|2),13x x f x f x f x x x ⎧-+-⎪+==⎨--+<⎪⎩≤≤≤，若关于x 的方程()0f x ax -=有5个不同实根，则正实数a 的取值范围是( )A ．11(,)43B ．11(,)64C．1(16)6-D．1(,86-【答案】D第Ⅱ卷（共100分）二、填空题（每题5分，满分25分，将答案填在答题纸上）11.复数22(56)(215)i m m m m +++--（i 是虚数单位）是纯虚数，则实数m 的值为 ．12.等比数列{}n a 中，若公比4q =，且前3项之和等于21，则该数列的通项公式n a = ．考点：等比数列的通项公式13.使不等式3log 14a<（其中01a <<）成立的a 的取值范围是 ．14.设()f x 是定义在R 上的奇函数，且当0x ≥时，2()f x x =，若对任意[,2]x a a ∈+，不等式()(31)f x a f x ++≥恒成立，则实数a 的取值范围是 ．【答案】(,5]-∞-15.已知集合22{()|()()()()}A f x f x f y f x y f x y x y =-=+⋅-∈R ，、，有下列命题： ①若1,0()1,0x f x x ⎧=⎨-<⎩≥，则()f x A ∈；②若()f x kx =，则()f x A ∈；③若()f x A ∈，则()y f x =可为奇函数； ④若()f x A ∈，则对任意不等实数12,x x ，总有1212()()0f x f x x x -<-成立．其中所有正确命题的序号是．（填上所有正确命题的序号）三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.）16.（本小满分12分）在一次数学统考后，某班随机抽取10名同学的成绩进行样本分析，获得成绩数据的茎叶图如下．（Ⅰ）计算样本的平均成绩及方差；（Ⅱ）现从80分以上的样本中随机抽出2名学生，求抽出的2名学生的成绩分别在[80,90)、[90,100]上的概率．17. （本小题满分12分）在△ABC中，角A、B、C的对边分别为a、b、c，设S为△ABC的面积，满足2224)S a b c=+-．(Ⅰ)求角C的大小；(Ⅱ)若tan21tanA cB b+=，且8AB BC=-，求c的值．18. （本小题满分12分）设等差数列{}n a 的前n 项和为n S ，且36a =，10110S =． （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列{}n b 前n 项和为n T ，且1n a n T =-，令()n n n c a b n *=∈N ．求数列{}n c 的前n 项和n R .试题解析：（Ⅰ）设等差数列{}n a 的公差为d ，19.（本小满分12分）已知函数321()43sin 32f x x x θ=-+，其中x ∈R ，(0,)θπ∈． (Ⅰ)若()f x '的最小值为34-，试判断函数()f x 的零点个数，并说明理由； (Ⅱ)若函数()f x 的极小值大于零，求θ的取值范围．因此，函数()f x 在sin 2x θ=处取得极小值3sin 11()sin 2432f θθ=-+， ··· 9分20.（本小满分12分）设平面向量),2cos )x x π=+a ，(2cos ,cos )x x =-b ，已知函数()f x m =⋅+a b 在[0,]2π上的最大值为6． （Ⅰ）求实数m 的值； （Ⅱ）若026()5f x =，0[,]42x ππ∈．求0cos 2x 的值．21.（本小满分14分）已知函数()(1)ln 15a f x x a x a x=++-+，322()23(2)664F x x a x x a a =-+++--，其中0a <且1a ≠-．(Ⅰ) 当2a =-，求函数()f x 的单调递增区间；(Ⅱ) 若1x =时，函数()F x 有极值，求函数()F x 图象的对称中心坐标；（Ⅲ）设函数2(()66(1))e ,1,()e (), 1.x F x x a x x g x f x x ⎧-+-⋅=⎨⋅>⎩≤ （e 是自然对数的底数），是否存在a 使()g x 在[,]a a -上为减函数，若存在，求实数a 的范围；若不存在，请说明理由．（2）当2a >-时，()m x 在[2,]a -上是增函数，在(,2],[,)a -∞-+∞是减函数，。

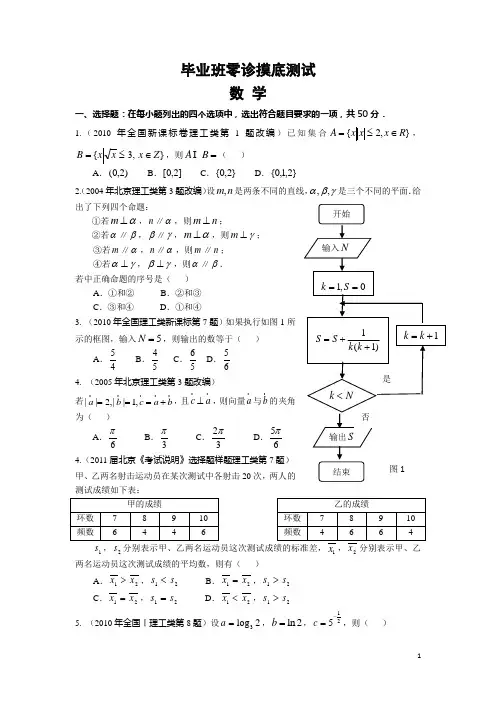
毕业班零诊摸底测试数 学一、选择题：在每小题列出的四个选项中，选出符合题目要求的一项，共50分． 1.（2010年全国新课标卷理工类第1题改编）已知集合},2{R x x x A ∈≤=，≤=x x B {,3}Z x ∈，则=B A （ ）A ．)2,0(B ．]2,0[C ．}2,0{D ．}2,1,0{2.（2004年北京理工类第3题改编）设n m ,是两条不同的直线，γβα,,是三个不同的平面．给出了下列四个命题：①若α⊥m ，n ∥α，则n m ⊥； ②若α∥β，β∥γ，α⊥m ，则γ⊥m ； ③若m ∥α，n ∥α，则m ∥n ； ④若γα⊥，γβ⊥，则α∥β． 若中正确命题的序号是（ ）A ．①和②B ．②和③C ．③和④D ．①和④3. （2010年全国理工类新课标第7题）示的框图，输入5=N ，则输出的数等于（ ）A ．45 B ．54 C ．56 D ．654. （2005年北京理工类第3题改编）若||2,||1,a b c a b ===+，且c a ⊥，则向量a 与b 为（ ）A ．6πB ．3πC ．32πD 4.（2011届北京《考试说明》选择题样题理工类第甲、乙两名射击运动员在某次测试中各射击20测试成绩如下表：1s ，2s 12两名运动员这次测试成绩的平均数，则有（ ）A ．>1x 2x ，<1s 2sB ．=1x 2x ，>1s 2sC ．=1x 2x ，=1s 2sD ．<1x 2x ，>1s 2s5. （2010年全国Ⅰ理工类第8题）设3log 2a =，ln 2b =，125c -=，则（ ）A ．a b c <<B ．b c a <<C ．c a b <<D ．c b a <<6. （2010年全国一理工类第4题）假设双曲线的渐近线与抛物线12+=x y 相切，则该双曲线的离心率为（ ）A ．3B ．2C ．5D ．67. （2011年全国理工类第6题）已知直二面角βα--l ，点α∈A ，l AC ⊥，C 为垂足，点β∈B ，l BD ⊥，D 为垂足．若2=AB ，1==BD AC ，则=CD （ ）A ．2B ．3C ．2D ．18. （2009年四川省理工类第6题）已知d c b a ,,,为实数，且d c >，则“b a >”是“d b c a ->-”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 9. （2011年北京理工类第7题改编）某四棱锥的三视图 如图2所示，该四棱锥的表面积是（ ）A ．32B ．21616+C ．48D ．23216+10. （2011届四川省成都市毕业班零诊第12题）已知F 1、F 2分别为椭圆2222x y a b+＝1(a ＞b ＞0)的左右焦点，经过椭圆上第二象限内任意一点P 的切线为l ，过原点O 作OM ∥l 交F 2P于点M ，则|MP |与a 、b 的关系是（ ）A ．|MP |＝aB ．|MP |＞aC ．|MP |＝bD ．|MP |＜b 二、填空题：把答案填在题中横线上，共25分．11.（2010年四川省理工类第3题改编）若变量y x ,满足约束条件⎪⎩⎪⎨⎧≥-≤-≤+,1,23,6x y x y x则=z y x 32+的最小值为 ；12.（2011年全国理工类第9题改编）如果)(x f 是周期为2的奇函数，当10≤≤x 时，)1(2)(x x x f -=，那么=-)25(f ；13.（2006年北京理工类第12题）在AB C ∆中，A ∠，B ∠，C ∠所对的边长分别是c b a ,,，若A sin ：B sin ：C sin 8:7:5=，则B ∠的大小是 ；14.（2010年全国一理工类第10题改编）已知函数()lg f x x =,若0<a<b,且()()f a f b =,则2a b +的取值范围是________________；15. （2012届四川省绵阳市一诊第16题）设函数)(x f 的定义域为R ，若存在常数0>A ，使得|||)(|x A x f ≤对一切实数x 均成立，则称)(x f 为“倍约束函数” ．现给出下列函数： ①x x f 3)(=； ②12)(2-=x x f ； ③xe xf =)(（其中e 为自然对数的底数）；图3④)(x f 是定义在实数集R 的奇函数，且对一切21,x x 均有)(5|)()(|2121x x x f x f -≤-. 其中是“倍约束函数”的是 ．（写出所有正确命题的序号） 三、解答题：解答应写出文字说明、演算步骤或证明过程，共75分．16.（2010年北京文史类第16题）已知}{n a 为等差数列，且63-=a ，08=a ．（Ⅰ）求}{n a 的通项公式；（Ⅱ）若等比数列}{n b 满足81-=b ，3212a a a b ++=，求}{n b 的前n 项和公式．17.（2009年四川理工类第17题改编）在ABC ∆中，,A B 为锐角，角,,A B C 所对应的边分别为,,a b c，且3cos 2,sin 5A B ==．（Ⅰ）求cos()A B +的值； （Ⅱ）若1a b +=-，求,,a b c 的值．18.（2011年四川省成都市高二上期末调研理第20题）如图3，直四棱柱1111D C B A ABCD -中（侧棱与底面垂直的棱柱叫直棱柱），底面ABCD 是边长为4的菱形，且60DAB ∠=，321=AA ，P 、Q 分别是棱11D A 和AD 的中点，R 为PB 的中点． （Ⅰ）求证：⊥QR 平面PBC ； （Ⅱ）求二面角R QC B --的余弦值．A 1D B ACB 1C 1D 1 P Q R19.（2013年四川省成都市高二上期末调研理第20题）已知函数2()21f x ax bx =++， （Ⅰ）若()f x 中的a ，b 是从区间[]1,3-中任取的两个不同的整数，求()f x 为二次函数且存在零点的概率；（Ⅱ）若[]1,3a ∈，[]2,2b ∈-，求[][](1)3(1)30f f -⋅--≤的概率．20. （2013届四川省高考《考试说明》解答题样题第39题）已知抛物线C ：)0(22>=p px y 经过点)4,2(，B A ,为抛物线C 上异于坐标原点O 的两个动点，且满足0OA OB ⋅=.（Ⅰ）求抛物线C 的方程；（Ⅱ）求证：直线AB 恒过定点(2,0)p ；（Ⅲ）若线段AB 的中垂线经过点(16,0)，求线段AB 的长．21.（2010年全国理工类新课标第21题改编） 设函数2()1x f x e x ax =---．（Ⅰ）若0a =，求()f x 的单调区间； （Ⅱ）求证：1xe x ≥+；（Ⅲ）若当0x ≥时()0f x ≥，求a 的取值范围．毕业班摸底测试数 学一、选择题：在每小题列出的四个选项中，选出符合题目要求的一项．1.（2010年全国理标卷类第1题改编）已知集合},2{R x x x A ∈≤=，≤=x x B {,3}Z x ∈，则=B A （ ）DA ．)2,0(B ．]2,0[C ．}2,0{D ．}2,1,0{2.（2004年北京理工类第3题改编）设n m ,是两条不同的直线，γβα,,是三个不同的平面．给出了下列四个命题：①若α⊥m ，n ∥α，则n m ⊥； ②若α∥β，β∥γ，α⊥m ，则γ⊥m ； ③若m ∥α，n ∥α，则m ∥n ； ④若γα⊥，γβ⊥，则α∥β． 若中正确命题的序号是（ ）AA ．①和②B ．②和③C ．③和④D ．①和④3. （2010年全国理工类新课标第7示的框图，输入5=N ，则输出的数等于（ ）A ．45 B ．54 C ．56 D ．654. （2005年北京理工类改编）若||2,||1,a b c a b ===+，且c a ⊥，则向量a 与b 为（ ）CA ．6πB ．3πC ．32πD 4.（2011年北京《考试说明》样题工类类第7题）甲、乙两名射击运动员在某次测试中各射击20测试成绩如下表：1s ，2s 12名运动员这次测试成绩的平均数，则有（ ）BA ．>1x 2x ，<1s 2sB ．=1x 2x ，>1s 2sC ．=1x 2x ，=1s 2sD ．<1x 2x ，>1s 2s5. （2010年全国一理工类第8题）设a=3log 2,b=In2,c=125-,则（ ）C A ．a<b<c B ．b<c<a C ．c<a<b D ．c<b<a6. （2010年全国一理工类第4题）假设双曲线的渐近线与抛物线12+=x y 相切，则该双曲线的离心率为（ ）CA ．3B ．2C ．5D ．67. （2011年全国理工类第6题）已知直二面角βα--l ，点α∈A ，l AC ⊥，C 为垂足，点β∈B ，l BD ⊥，D 为垂足．若2=AB ，1==BD AC ，则=CD （ ）CA ．2B ．3C ．2D ．18. （2009年四川省理工类第6题）已知d c b a ,,,为实数，且d c >，则“b a >”是“d b c a ->-”的（ ）BA ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 9. （2011年北京理工类第7题改编）某四棱锥的三视图 如图3所示，该四棱锥的表面积是（ ）BA ．32B ．21616+C ．48D ．23216+10. （2011届四川省成都市毕业班零诊第12题）已知F 1、F 2分别为椭圆2222x y a b+＝1(a ＞b ＞0)的左右焦点，经过椭圆上第二象限内任意一点P 的切线为l ，过原点O 作OM ∥l 交F 2P 于点M ，则|MP |与a 、b 的关系是（ ）AA ．|MP |＝aB ．|MP |＞aC ．|MP |＝bD ．|MP |＜b 二、填空题：把答案填在题中横线上．11.（2010年四川省理工类第3题改编）若变量y x ,满足约束条件⎪⎩⎪⎨⎧≥-≤-≤+,1,23,6x y x y x则=z y x 32+的最小值为 ；532min =+=z12.（2011年全国理工类第9题改编）如果)(x f 是周期为2的奇函数，当10≤≤x 时，)1(2)(x x x f -=，那么=-)25(f ；21-13.（2006年北京理工类第12题）在ABC ∆中，A ∠，B ∠，C ∠所对的边长分别是c b a ,,，若A sin ：B sin ：C sin 8:7:5=，则B ∠的大小是 ；3π 14.（2010年全国一理工类第10题改编）已知函数()lg f x x =,若0<a<b,且()()f a f b =,则2a b +的取值范围是________________；[3,)+∞15. （2012届四川省绵阳市2012届一诊第16题）设函数)(x f 的定义域为R ，若存在常数0>A ，使得|||)(|x A x f ≤对一切实数x 均成立，则称)(x f 为“倍约束函数”.现给出下列函数：①x x f 3)(=； ②12)(2-=x x f ； ③xe xf =)(（其中e 为自然对数的底数）；④)(x f 是定义在实数集R 的奇函数，且对一切21,x x 均有)(5|)()(|2121x x x f x f -≤-. 其中是“倍约束函数”的是 ．（写出所有正确命题的序号）①④ 三、解答题：解答应写出文字说明、演算步骤或证明过程．16. （2010年北京第16题）已知}{n a 为等差数列，且63-=a ，08=a ．（Ⅰ）求}{n a 的通项公式；（Ⅱ）若等比数列}{n b 满足81-=b ，3212a a a b ++=，求}{n b 的前n 项和公式． 解：（Ⅰ）设等差数列}{n a 的公差为d ．∵63-=a ，08=a ，∴⎩⎨⎧=+-=+.05,6211d a d a 解得101-=a ，2=d ．∴1222)1(10-=⨯-+-=n n a n ．（Ⅱ）设等比数列}{n b 的公比为q ．∵3212a a a b ++=24-=，81-=b ，∴=-q 824-，3=q ．∴数列}{n b 的前n 项和公式为)31(41)1(1n n n qq b S -=--=．17.（2009年四川理工类第17题改编）在ABC ∆中，,A B 为锐角，角,,A B C 所对应的边分别为,,a b c，且3cos 2,sin 5A B ==．（Ⅰ）求cos()A B +的值； （Ⅱ）若1a b +=-，求,,a b c 的值．解：（Ⅰ）A 、B为锐角，sin B =cos B ∴== 又23cos 212sin 5A A =-=，sin A ∴=cos 5A ==，cos()cos cos sin sin A B A B A B ∴+=-==（Ⅱ）由（Ⅰ）知34C π=,sin C ∴=由正弦定理sin sin sin a b c A B C ==得==，即a =，c =，1a b -=，1b -=，1b ∴=a ∴==18.（2011年四川省成都市高二上期末调研理第20题）如图9，在直四棱柱1111D C B A ABCD -中（侧棱与底面垂直的棱柱叫直棱柱），底面ABCD 是边长为4的菱形，且60DAB ∠=，321=AA ，P 、Q 分别是棱11D A 和AD 的中点，R 为PB 的中点． （Ⅰ）求证：⊥QR 平面PBC ； （Ⅱ）求二面角R QC B --的余弦值． 解：（Ⅰ）∵ABCD 为边长为4的菱形，且60DAB ∠=︒，Q 为AD 的中点， ∴AQ BQ ⊥．A 1DCB 1C 1D 1 P Q R以Q 为坐标原点建立如图10所示的空间直角坐标系Q xyz -． 图9∴(0,0,(0,(4,P B C R -． ∴(0,3,3),(0,23,23),(4,0,0)QR PB CB ==-=．0660,0QR PB QR CB =+-==，∴0,=⊥⊥．又B BCPB = ，∴QR ⊥平面PBC ． （Ⅱ）设平面RQC 的法向量为(,,)x y z =m ．由00040QRQC x ⎧=+=⎪⇒⎨=-+=⎪⎪⎩⎩m m ． 令1=y ，得1)=-m ．取平面QBC 的法向量为(0,01)=n ． 图10 ∴cos ,11<>==-m n ． ∵二面角R QC B --为锐角，∴二面角R QC B --的余弦值为11112． 19.（2013年四川省成都市高二上期末调研第20题）已知函数2()21f x ax bx =++， （Ⅰ）若()f x 中的a ，b 是从区间[]1,3-中任取的两个不同的整数，求()f x 为二次函数且存在零点的概率；（Ⅱ）若[]1,3a ∈，[]2,2b ∈-，求[][](1)3(1)30f f -⋅--≤的概率． 解：（Ⅰ）9()20P A =；（Ⅱ）7()8P B =． 20. （2013届四川省高考考试说明解答题样题第39题）已知抛物线C ：)0(22>=p px y 经过点)4,2(，B A ,为抛物线C 上异于坐标原点O 的两个动点，且满足0OA OB ⋅=.（Ⅰ）求抛物线C 的方程；（Ⅱ）求证：直线AB 恒过定点(2,0)p ；（Ⅲ）若线段AB 的中垂线经过点(16,0)，求线段AB 的长． 解：（Ⅰ）∵抛物线经过点)4,2(，∴4p =．∴抛物线方程为x y 82=． （Ⅱ）①当AB 斜率不存在时，)8,8(),8,8(-B A ，此时直线AB 过点)0,8(． ②当AB 斜率存在时，设),(),,(,:2211y x B y x A b kx y l AB +=．联立0)82(82222=+-+⇒⎩⎨⎧+==b x kb x k bkx y xy ．x A 1∴2121228,b bx x y y k k==．由0OA OB ⋅=且0≠b 得，k b 8-=．即直线过点)0,8( ∴直线AB 过定点)0,2(p ．（Ⅲ）①当AB 斜率不存在时，)8,8(),8,8(-B A ，此时16||=AB ．②当AB 斜率存在时，设),(),,(,:2211y x B y x A b kx y l AB +=，AB 中点坐标为),(00y x ． 由（Ⅱ），得800-=x y k ． 由21122288y x y x ⎧=⎪⇒⎨=⎪⎩2121218y y x x y y +=--，即04y k =． ∵16100-=-x y k ．解得1k =±．即:(8)AB l y x =±-． ∴108||=AB ． 综上，当AB 斜率不存在时，16||=AB ；当AB 斜率存在时，108||=AB ． 21.（2010年全国理工类新课标第21题改编） 设函数2()1x f x e x ax =---．（Ⅰ）若0a =，求()f x 的单调区间； （Ⅱ）求证：1xe x ≥+；（Ⅲ）若当0x ≥时()0f x ≥，求a 的取值范围．解：（Ⅰ）0a =时，()1x f x e x =--，'()1x f x e =-.当(,0)x ∈-∞时，'()0f x <；当(0,)x ∈+∞时，'()0f x >.故()f x 在(,0)-∞单调减少，在(0,)+∞单调增加．（Ⅱ）'()12x f x e ax =--由（Ⅰ）知1x e x ≥+，当且仅当0x =时等号成立. （Ⅲ）由（Ⅱ）问，故'()2(12)f x x ax a x ≥-=-，从而当120a -≥，即12a ≤时，'()0 (0)f x x ≥≥，而(0)0f =，于是当0x ≥时，()0f x ≥. 由1(0)x e x x >+≠可得1(0)x e x x ->-≠.从而当12a >时，'()12(1)(1)(2)x x x x x f x e a e e e e a --<-+-=--，故当(0,ln 2)x a ∈时，'()0f x <，而(0)0f =，于是当(0,ln 2)x a ∈时，()0f x <. 综合得a 的取值范围为1(,]2-∞.。

绵阳市高2011级第一次诊断性考试数学(文)参考解答及评分标准一、选择题：本大题共10小题，每小题5分，共50分．CBDDB AACAD二、填空题：本大题共5小题，每小题5分，共25分．11．912．56a 13．5 14．21()e e ， 15．m <0或m >2三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．解：（I ）x x x x f cos )3sin cos 3cos (sin 2)(ππ-= x x x 2cos 3cos sin -=2)2cos 1(32sin 21x x +-=1sin 222x x = 23)32sin(--=πx ，……………………………………………6分 ∴ ππ==22T ，即f (x )的最小正周期为π． …………………………………7分 （II ）由22πk π-≤23πx -≤22πk π+，可得12πk π-≤x ≤512πk π+，k ∈Z ， 由22πk π+≤23πx -≤322πk π+，可得512πk π+≤x ≤1112πk π+，k ∈Z ， 即函数f (x )的单调递减区间为5[]1212ππk πk π-+，，k ∈Z ， 单调递增区间为11[]1212ππk πk π5++，，k ∈Z ， ∴ f (x )在[5012π，]上是减函数，在[52ππ12，]上是增函数． ………………12分 17．解：（I ）设{a n }的公差为d ，则由题知⎩⎨⎧=+++=+，，4874143111d a d a d a 解得a 1=2，d =4． ……………………………………4分 ∴a n =2+4(n -1)=4n -2．…………………………………………………………6分 （II ）设{b n }的公比为q ，若q =1，则S 1=b 1，S 2=2b 1，S 3=3b 1，由已知312322S S S +=⨯，代入得8b 1=4b 1，而b 1≠0，故q =1不合题意．…………………………………………………………7分若q ≠1，则S 1=b 1，q q b S --=1)1(212，qq b S --=1)1(313，于是23111(1)(1)22311b q b q b q q--⨯⨯=+--， 整理得：4q 2=3q +q 3，解得q =0（舍去），q =1（舍去），q =3， ………10分∴ 8031)31(244=--⨯=S ． ………………………………………………………12分 18．解：（I ）∵21)(x a x x f -='， ∴ 由题意知(1)2f '=，即1-a =2，解得a =-1．于是f (1)=-1-2=-3，∴ -3=2×1+b ，解得b =-5． …………………………………………………6分 （II ）由题知ln 2a x x+-≥0对任意x >0恒成立，即a ≥2ln x x x -， 令 x x x x g ln 2)(-=，∴ x x x g ln 1)1(ln 2)(-=+-='． ………………………………………………8分 显然当0<x <e 时，0)(>'x g ，即得g (x )在(0，e )上是增函数，当x ≥e 时，()g x '≤0，即得g (x )在[)e +∞，上是减函数．∴ e e g x g ==)()(max ．∴ a ≥e ，即a 的最小值为e ．………………………………………………12分19．解：（I ）由已知A =2， 且有3)0sin(2=+⋅ϕω，即23sin =ϕ， 由|ϕ|<2π得3πϕ=．又∵ 最高点为(1，2)，∴ ，2)3sin(2=+πω 解得6πω=． ∴ )36sin(2ππ+=x y ．…………………………………………………………6分 （II ）∵ B 点的横坐标为3，代入函数解析式得2sin(3)63B ππy =⨯+=1，∴ 2)34(122=-+=BD ．…………………………………………………8分 在△BCD 中，设∠CBD =θ，则∠BDC =180º-120º-θ=60º-θ． 由正弦定理有)60sin(sin 120sin θθ-︒==︒BC CD BD ， ∴ θsin 362=CD ，)60sin(362θ-︒=BC ， …………………………………9分 ∴ )]60sin([sin 362θθ-︒+=+CD BC ]sin 21cos 23[sin 362θθθ-+=)3sin(362πθ+=． ∴ 当且仅当6πθ=时，折线段BCD 最长，最长为362千米．……………12分 20．解：（I ）由于f (1+x )=f (2-x )知函数f (x )关于23=x 对称， 即232=-b ，解得b =-3，于是 f (x )=x 2-3x +2．………………………………3分 22111()111x x x g x x x ⎧-≤-≥⎪=⎨--<<⎪⎩，或，，， 当x ≤-1，或x ≥1时，由f (x )≥g (x )有x 2-3x +2≥x 2-1，解得x ≤1，∴ 此时x 的范围为x ≤-1，或x =1．当-1<x <1时，由f (x )≥g (x )有x 2-3x +2≥1-x 2，解得x ≤12或x ≥1， ∴ 此时x 的范围为-1<x ≤21． ∴ 综上知，使不等式f (x )≥g (x )成立的x 的取值集合为{x |x ≤12或x =1}． ………………………………………………………………7分（II ）⎩⎨⎧<<-+≥-≤++=，，，或，1151132)(2x bx x x bx x x h 若b=0时，22311()51 1.x x x h x x ⎧+≤-≥=⎨-<<⎩，或，，显然h (x )>0恒成立，不满足条件． …………………………………………………………………9分若b ≠0时，函数ϕ(x )=bx +5在(0，1)上是单调函数，即ϕ(x )在(0，1)上至多一个零点，不妨设0<x 1<x 2<2．①如果0<x 1<1，1≤x 2<2时，则0)1()0(<ϕϕ，且(1)(2)h h ≤0，即50(5)(211)0b b b +<⎧⎨++≤⎩，，解得112-≤5b <-． 经检验211-=b 时，)(x h 的零点为1011，2（舍去），∴112-<5b <-． ②若1≤x 1<x 2<2时， 2(1)1(2)0124240h h b b ≥⎧⎪>⎪⎪⎨<-<⎪⎪->⎪⎩，，，，即⎪⎪⎩⎪⎪⎨⎧>-<-<<->+≥+，或，，，626248011205b b b b b 得：-5≤b <- ∴ 综上所述b的取值范围为112b -<<- ……………………………12分21．解：（I ）∵ )0(2)(<--='a a x e x f x ，∴ 当x ∈[-2，0]时，0)(>'x f ，即f (x )在[-2，0]上是增函数， ∴ 1)0()(max ==f x f ． …………………………………………………………4分 （II ）∵ 函数f (x )恰有两个不同的极值点x 1，x 2， ∴ 方程e x -2x -a =0有两个不同的零点x 1，x 2． 令h (x )=e x -2x -a ．①2)(-='x e x h ，当2ln <x 时，0)(<'x h ，h (x )是减函数； 当2ln >x 时，h '(x )>0，h (x )是增函数， ∴ )(x h 在x =ln2时取得最小值． ∴ x 1<ln2．………………………………………………………………………9分 ②∵ h (x 1)=0，即0211=--a x e x ， ∴ 121x e a x -=．于是21111211111)1()2()(x e x x x e x e x f x x x +-=⋅---=， ∴ )2()(111x e x x f -='．∵ x 1<ln2，∴ 120x e ->．∴ 当x 1<0时，0)(1<'x f ，f (x 1)是减函数； 当0≤x 1<ln2时，2()0f x '>，)(1x f 是增函数． ∴ f (x 1)在(-∞，ln2)上的最小值为f (0)=1，此时a =1．…………………14分。