Novel Architectures for P2P Applications the Continuous-Discrete Approach

离散傅里叶变换的算术傅里叶变换算法张宪超1，武继刚1，蒋增荣2，陈国良1（1.中国科技大学计算机科学与技术系，合肥230027；2.国防科技大学系统工程与数学系，长沙410073）摘要：离散傅里叶变换（DFT）在数字信号处理等许多领域中起着重要作用.本文采用一种新的傅里叶分析技术—算术傅里叶变换（AFT）来计算DFT.这种算法的乘法计算量仅为0（N）；算法的计算过程简单，公式一致，克服了任意长度DFT传统快速算法（FFT）程序复杂、子进程多等缺点；算法易于并行，尤其适合VLSI设计；对于含较大素因子，特别是素数长度的DFT，其速度比传统的FFT方法快；算法为任意长度DFT的快速计算开辟了新的思路和途径.关键词：离散傅里叶变换（DFT）；算术傅里叶变换（AFT）；快速傅里叶变换（FFT）中图分类号：TN917文献标识码：A文章编号：0372-2112（2000）05-0105-03An Algorithm for Computing DFT Using Arithmetic Fourier TransformZHANG Xian-chao1，WU Ji-gang1，JIANG Zeng-rong2，CHEN Guo-iiang1（1.Dept.of CompUter Science&Technology，Unio.of Science&Technology of China，Hefei230027，China；2.Dept.of System Engineering&Mathematics，National Unio.of Defense Technology，Changsha410073，China）Abstract：The Discrete Fourier Transform（DFT）piays an important roie in digitai signai processing and many other fieids.In this paper，a new Fourier anaiysis technigue caiied the arithmetic Fourier transform（AFT）is used to compute DFT.This aigorithm needs oniy0（N）muitipiications.The process of the aigorithm is simpie and it has a unified formuia，which overcomes the disadvantage of the traditionai fast method that has a compieX program containing too many subroutines.The aigorithm can be easiiy performed in paraiiei，especiaiiy suitabie for VLSI designing.For a DFT at a iength that contains big prime factors，especiaiiy for a DFT at a prime iength，it is faster than the traditionai FFT method.The aigorithm opens up a new approach for the fast computation of DFT.Key words：discrete Fourier transform（DFT）；arithmetic Fourier transform（AFT）；fast Fourier transform（FFT）!引言离散傅里叶变换（DFT）在数字信号处理等许多领域中起着重要作用.但DFT的计算量很大（N点DFT需0（N2）乘法和加法）.因此，DFT的快速计算问题非常重要.1965年，Cooiey 和Tukey开创了快速傅里叶变换（FFT）方法，使N点DFT的计算量从0（N2）降到0（N iog N），开辟了DFT的快速计算时代.但FFT的计算仍较复杂，且对不同长度的DFT其计算公式不一致，致使任意长DFT的FFT程序非常复杂，包含大量子进程.1988年，Tufts和Sadasiv［1］提出了一种用莫比乌斯反演公式（Mibius inversion formuia）计算连续函数的傅立叶系数的方法并命名为算术傅立叶变换（AFT）.AFT有许多良好的性质：其乘法量仅为0（N）；算法简单，并行性好，尤其适合VLSI设计.因此很快得到广泛关注，并在数字图像处理等领域得到应用.AFT已成为继FFT后一种新的重要的傅立叶分析技术［2~5］.根据DFT和连续函数的傅立叶系数的关系，可以用AFT 计算DFT.这种方法保持了AFT的良好性质，且具有公式一致性.大量实验表明，同直接计算相比，AFT方法可以将DFT的计算时间减少90%，对含较大素因子，特别是其长度本身为素数的DFT，它的速度比传统的FFT快.从而它为DFT快速计算开辟了新的途径."算术傅立叶变换本文采用文［3］中的算法.设A（t）为周期为T的函数，它的傅立叶级数只含有限项，即：A（t）=a0+!Nn=1a n cos2!f0t+!Nn=1b n sin2!f0t（1）其中：f0=1/T，a0=1T"TA（t）dt.令：B（2n，!）=12n!2n-1m=0（-1）m A（m2nT+!T），-1<!<1（2）则傅立叶系数a n和b n可以由下列公式计算：a n=!［N/n］l=1，3，5，…U（l）B（2nl，0）b n=!［N/n］l=1，3，5，…U（l）（-1）（l-1）/2B（2n，14nl），n=1，…，N（3）第5期2000年5月电子学报ACTA ELECTR0NICA SINICAVoi.28No.5May2000其中：!（l ）=I ，（-I ）r ，0{，l =I l =p I p 2…p r 3p 使p 2\l为莫比乌斯（M bioLS ）函数.这就是AFT ，其计算量为：加法：N 2+［N /2］+［N /3］+…+I -2N ；乘法：2N.AFT 需要函数大量的不均匀样本点，而在实际应用中，若计算函数前N 个傅立叶系数，根据奈奎斯特（NygLiSt ）抽样定律，只需在函数的一个周期内均匀抽取2N 个样本点.这时可以用零次插值解决样本不一致问题.文献［2、3］已作了详细的分析，本文不再重复.3DFT 的AFT 算法3.1DFT 的定义及性质定义1设X I 为一长度为N 的序列，它的DFT 定义为：Y I =Z N-II =0X I w II ，I =0，I ，…，N -I ；w =e -i 2!/N（4）性质1用记号X I 、=、Y I 表示序列Y I 为序列X I 的DFT ，G I 、=、H I ，则：pX I +gG I 、=、pY I +gH I （5）因此，一个复序列的DFT 可以用两个实序列的DFT 计算.故本文只讨论实序列DFT 的计算问题.性质2设X I 为一实序列，X I 、=、Y I ，则：Re Y I =Re Y N -I ，Im Y I =-Im Y N -I （Re Y I 和Im Y I 分别代表Y I 的实部和虚部）（6）因此，对N 点实序列DFT ，只需计算：Re Y I 和Im Y I （I =0，…，「N /2）.3.2DFT 的AFT 算法离散序列的DFT 和连续函数的傅立叶系数有着密切的联系.事实上，若序列X I 是一段区间［0，T ］上的函数A （t ）经过离散化后得到的，再设A （t ）的傅立叶级数只含前N /2项，即：A （t ）=a 0+Z「N /2-II =Ia I coS2!f 0t +Z「N /2-II =I6I Sin2!f 0t（7）则DFT Y I 和傅立叶系数的关系为：Re Y I =「N /2a I /2Im Y I =「N /26I /{2，I =0，…，「N /2（8）式（7）中函数代表的是一种截频信号.对一般函数，式（8）中的“=”要改为“匀”［7］.因此，序列X I 的DFT 可以通过函数A （t ）的傅里叶系数计算.对于一般给定序列X I ，注意到在任意一个区间上，经过离散后能得到序列X I 的函数有无穷多个.对所有这些插值函数，公式（8）都近似地满足（仅式（7）中的函数精确地满足式（8））［7］.AFT 的零次插值实现实质上就是用这些插值函数中的零次插值函数代替原来的函数进行计算的.而从AFT 的零次插值实现方法可知，用AFT 计算傅里叶系数，实际上参与计算的只是函数经离散化后得到的序列，而不必知道函数本身.因此，我们可以任取一个区间，在这个区间上，把序列X算（8）中的“傅里叶系数”，再通过式（8），就可以计算出序列的DFT .算法描述如下（采用［0，I ］区间）：for I =I to 「N /2for m =0to 2I -IB （2I ，0）：=B （2I ，0）+（-I ）mX［Nm /2I +0.5］B （2I ，I /4I ）：=B （2I ，I /4I ）+（-I ）mX［Nm /2I +N /4I +0.5］endforB （2I ，0）：=B （2I ，0）/2I B （2I ，I /4I ）：=B （2I ，I /4I ）/2I endforfor =0to N -I a 0：=a 0+X （ ）/N for I =I to 「N /2for I =I to［「N /2/I ］by 2a I ：=a I +!（I ）B （2II ，0）6I ：=6I +!（I ）（-I ）（K -I ）/2B （2II ，I /4II ）endforRe Y I ：=「N /2a I /2Re Y N -I ：=Re Y I Im Y I ：=「N /2a I /2Im Y N -I ：=-Im Y I endfor endfor图IDFT 的AFT 算法程序AFT 方法的误差主要是由零次插值引起的，大量实验表明，同FFT 相比，其误差是可以接受的（部分实验结果见附录）.4算法的性能4.1算法的程序DFT 的AFT 算法具有公式一致性，且公式简单，因此算法的程序也很简单（图I ）.图2DFT 的AFT 算法进程示意为便于比较，不妨看一下FFT 的流程.图3FFT 算法进程示意可以看出，FFT 的程序中包含大量子进程，且这些子程序都较复杂.其中素数长度DFT 的FFT 算法程序尤其复杂.因此，任意长DFT 的FFT 算法其程序是非常复杂的.4.2算法的计算效率AFT 方法把DFT 的乘法计算量从0（N 2）降到0（N ），它2电子学报2000年计算时间减少90%.当DFT的长度!为2的幂时，FFT比AFT 方法快"对一般长度的DFT，当!含较大素因子时，AFT方法比FFT快；当!的因子都较小时，AFT方法不如FFT快.当DFT长度!本身为一较大素数时，AFT方法比FFT快"附录中给出部分实验结果以便比较"特别指出，对素数长度DFT，FFT的计算过程非常复杂，很难在实际中应用.而AFT方法算法简单，提供了较好的素数长度DFT快速算法"表1是两种算法计算效率较详细的比较"表1长度52191197114832417FFT效率67.30%68.03%72.50%71.23%76.22% AFT方法效率91.39#91.78#91.63#91.81#91.83# 4.3算法的并行性AFT具有良好的并行性，尤其适合VLSI设计，已有许多VLSI设计方案被提出，并在数字图像处理等领域得到应用.DFT的AFT算法继承了AFT优点，同样具有良好的并行性"5结论和展望本文采用算术傅里叶变换（AFT）计算DFT.这种方法把AFT的各种优点引入DFT的计算中来，开辟了DFT快速计算的新途径.把AFT方法同FFT结合起来，还可以进一步提高DFT的计算速度"参考文献［1］ D.W.Tufts and G.Sadasiv.The arithmetic Fourier transform.IEEE ASSP Mag，Jan.1988：13~17［2］I.S.Reed，D.W.Tufts，Xiao Yu，T.K.Troung，M.T.Shih and X.Yin.Fourier anaiysis and signai processing by use of Mobius inversion for-muiar.IEEE Trans.Acoust.Speech Speech Processing，Mar，1990，38（3）：458~470［3］I.S.Reed，Ming Tang Shih，T.K.Truong，R.Hendon and D.W.Tufts.A VLSI architecture for simpiified arithmetic fourier transform aigo-rithm.IEEE Trans.Signai Processing，May，1993，40（5）：1122~1132［4］H.Park and V.K.Prasanna.Moduiar VLSI architectures for computing the arithmetic fourier transform.IEEE.Signai Processing，June，1993，41（6）：2236~2246［5］Lovine.F.P，Tantaratanas.Some aiternate reaiizations of the arithmetic Fourier transform.Conference on Signai，system and Computers，1993，（Cat，93，CH3312-6）：310~314［6］蒋增荣，曾泳泓，余品能.快速算法.长沙：国防科技大学出版社，1993［7］E.0.布赖姆.快速傅立叶变换.上海：上海科学技术出版社，1976附录：较详细的实验结果（机型：586微机，主频：166MHz单位：秒）2的幂长度长度AFT方法基-2FFT直接算法2560.005160.002400.115120.018600.004400.4410240.075800.01100 1.81素数长度长度AFT方法FFT直接算法5210.03790.14390.449710.13400.4400 1.6014830.3103 1.0904 3.7924170.8206 2.389910.75任意长度长度因子分解AFT方法FFT直接算法13462!6370.270.44 3.1429862!1483 1.26 2.1414.8235793!1193 1.81 1.9222.1646374637 3.0821.4237.4755742!3!929 4.45 2.4752.2964364!1609 5.94 3.5772.6278933!3!8778.96 1.92105.49最大相对误差长度AFT方法FFT1024实部 2.1939>10-2 2.3328>10-2虚部 2.1938>10-29.9342>10-2 2048实部 4.2212>10-3 1.1967>10-2虚部 6.1257>10-3 4.9385>10-2 4096实部 2.3697>10-3 6.0592>10-3虚部 2.0422>10-3 2.4615>10-3张宪超1971年生"1994年、1998年分别获国防科技大学学士、硕士学位"现在中国科技大学攻读博士学位"主要研究方向为信号处理的快速、并行计算等"武继刚1963年生"烟台大学副教授，现在中国科技大学攻读博士学位"主要研究方向为算法设计和分析等"3第5期张宪超：离散傅里叶变换的算术傅里叶变换算法。

THEORY OF MODELING AND SIMULATIONby Bernard P. Zeigler, Herbert Praehofer, Tag Gon Kim2nd Edition, Academic Press, 2000, ISBN: 0127784551Given the many advances in modeling and simulation in the last decades, the need for a widely accepted framework and theoretical foundation is becoming increasingly necessary. Methods of modeling and simulation are fragmented across disciplines making it difficult to re-use ideas from other disciplines and work collaboratively in multidisciplinary teams. Model building and simulation is becoming easier and faster through implementation of advances in software and hardware. However, difficult and fundamental issues such as model credibility and interoperation have received less attention. These issues are now addressed under the impetus of the High Level Architecture (HLA) standard mandated by the U.S. DoD for all contractors and agencies.This book concentrates on integrating the continuous and discrete paradigms for modeling and simulation. A second major theme is that of distributed simulation and its potential to support the co-existence of multiple formalisms in multiple model components. Prominent throughout are the fundamental concepts of modular and hierarchical model composition. These key ideas underlie a sound methodology for construction of complex system models.The book presents a rigorous mathematical foundation for modeling and simulation. It provides a comprehensive framework for integrating various simulation approaches employed in practice, including such popular modeling methods as cellular automata, chaotic systems, hierarchical block diagrams, and Petri Nets. A unifying concept, called the DEVS Bus, enables models to be transparently mapped into the Discrete Event System Specification (DEVS). The book shows how to construct computationally efficient, object-oriented simulations of DEVS models on parallel and distributed environments. In designing integrative simulations, whether or not they are HLA compliant, this book provides the foundation to understand, simplify and successfully accomplish the task.MODELING HUMAN AND ORGANIZATIONAL BEHAVIOR: APPLICATION TO MILITARY SIMULATIONSEditors: Anne S. Mavor, Richard W. PewNational Academy Press, 1999, ISBN: 0309060966. Hardcover - 432 pages.This book presents a comprehensive treatment of the role of the human and the organization in military simulations. The issue of representing human behavior is treated from the perspective of the psychological and organizational sciences. After a thorough examination of the current military models, simulations and requirements, the book focuses on integrative architectures for modeling theindividual combatant, followed by separate chapters on attention and multitasking, memory and learning, human decision making in the framework of utility theory, models of situation awareness and enabling technologies for their implementation, the role of planning in tactical decision making, and the issue of modeling internal and external moderators of human behavior.The focus of the tenth chapter is on modeling of behavior at the unit level, examining prior work, organizational unit-level modeling, languages and frameworks. It is followed by a chapter on information warfare, discussing models of information diffusion, models of belief formation and the role of communications technology. The final chapters consider the need for situation-specific modeling, prescribe a methodology and a framework for developing human behavior representations, and provide recommendations for infrastructure and information exchange.The book is a valuable reference for simulation designers and system engineers.HANDBOOK OF SIMULATOR-BASED TRAININGby Eric Farmer (Ed.), Johan Reimersma, Jan Moraal, Peter JornaAshgate Publishing Company, 1999, ISBN: 0754611876.The rapidly expanding area of military modeling and simulation supports decision making and planning, design of systems, weapons and infrastructure. This particular book treats the third most important area of modeling and simulation – training. It starts with thorough analysis of training needs, covering mission analysis, task analysis, trainee and training analysis. The second section of the book treats the issue of training program design, examining current practices, principles of training and instruction, sequencing of training objectives, specification of training activities and scenarios, methodology of design and optimization of training programs. In the third section the authors introduce the problem of training media specification and treat technical issues such as databases and models, human-simulator interfaces, visual cueing and image systems, haptic, kinaesthetic and vestibular cueing, and finally, the methodology for training media specification. The final section of the book is devoted to training evaluation, covering the topics of performance measurement, workload measurement, and team performance. In the concluding part the authors outline the trends in using simulators for training.The primary audience for this book is the community of managers and experts involved in training operators. It can also serve as useful reference for designers of training simulators.CREATING COMPUTER SIMULATION SYSTEMS:An Introduction to the High Level Architectureby Frederick Kuhl, Richard Weatherly, Judith DahmannPrentice Hall, 1999, ISBN: 0130225118. - 212 pages.Given the increasing importance of simulations in nearly all aspects of life, the authors find that combining existing systems is much more efficient than building newer, more complex replacements. Whether the interest is in business, the military, or entertainment or is even more general, the book shows how to use the new standard for building and integrating modular simulation components and systems. The HLA, adopted by the U.S. Department of Defense, has been years in the making and recently came ahead of its competitors to grab the attention of engineers and designers worldwide. The book and the accompanying CD-ROM set contain an overview of the rationale and development of the HLA; a Windows-compatible implementation of the HLA Runtime Infrastructure (including test software). It allows the reader to understand in-depth the reasons for the definition of the HLA and its development, how it came to be, how the HLA has been promoted as an architecture, and why it has succeeded. Of course, it provides an overview of the HLA examining it as a software architecture, its large pieces, and chief functions; an extended, integrated tutorial that demonstrates its power and applicability to real-world problems; advanced topics and exercises; and well-thought-out programming examples in text and on disk.The book is well-indexed and may serve as a guide for managers, technicians, programmers, and anyone else working on building simulations.HANDBOOK OF SIMULATION:Principles, Methodology, Advances, Applications, and Practiceedited by Jerry BanksJohn Wiley & Sons, 1998, ISBN: 0471134031. Hardcover - 864 pages.Simulation modeling is one of the most powerful techniques available for studying large and complex systems. This book is the first ever to bring together the top 30 international experts on simulation from both industry and academia. All aspects of simulation are covered, as well as the latest simulation techniques. Most importantly, the book walks the reader through the various industries that use simulation and explains what is used, how it is used, and why.This book provides a reference to important topics in simulation of discrete- event systems. Contributors come from academia, industry, and software development. Material is arranged in sections on principles, methodology, recent advances, application areas, and the practice of simulation. Topics include object-oriented simulation, software for simulation, simulation modeling,and experimental design. For readers with good background in calculus based statistics, this is a good reference book.Applications explored are in fields such as transportation, healthcare, and the military. Includes guidelines for project management, as well as a list of software vendors. The book is co-published by Engineering and Management Press.ADVANCES IN MISSILE GUIDANCE THEORYby Joseph Z. Ben-Asher, Isaac YaeshAIAA, 1998, ISBN 1-56347-275-9.This book about terminal guidance of intercepting missiles is oriented toward practicing engineers and engineering students. It contains a variety of newly developed guidance methods based on linear quadratic optimization problems. This application-oriented book applies widely used and thoroughly developed theories such LQ and H-infinity to missile guidance. The main theme is to systematically analyze guidance problems with increasing complexity. Numerous examples help the reader to gain greater understanding of the relative merits and shortcomings of the various methods. Both the analytical derivations and the numerical computations of the examples are carried out with MATLAB Companion Software: The authors have developed a set of MATLAB M-files that are available on a diskette bound into the book.CONTROL OF SPACECRAFT AND AIRCRAFTby Arthur E. Bryson, Jr.Princeton University Press, 1994, ISBN 0-691-08782-2.This text provides an overview and summary of flight control, focusing on the best possible control of spacecraft and aircraft, i.e., the limits of control. The minimum output error responses of controlled vehicles to specified initial conditions, output commands, and disturbances are determined with specified limits on control authority. These are determined using the linear-quadratic regulator (LQR) method of feedback control synthesis with full-state feedback. An emphasis on modeling is also included for the design of control systems. The book includes a set of MATLAB M-files in companion softwareMATHWORKSInitial information MATLAB is given in this volume to allow to present next the Simulink package and the Flight Dynamics Toolbox, providing for rapid simulation-based design. MATLAB is the foundation for all the MathWorks products. Here we would like to discus products of MathWorks related to the simulation, especially Code Generation tools and Dynamic System Simulation.Code Generation and Rapid PrototypingThe MathWorks code generation tools make it easy to explore real-world system behavior from the prototyping stage to implementation. Real-Time Workshop and Stateflow Coder generate highly efficient code directly from Simulink models and Stateflow diagrams. The generated code can be used to test and validate designs in a real-time environment, and make the necessary design changes before committing designs to production. Using simple point-and-click interactions, the user can generate code that can be implemented quickly without lengthy hand-coding and debugging. Real-Time Workshop and Stateflow Coder automate compiling, linking, and downloading executables onto the target processor providing fast and easy access to real-time targets. By automating the process of creating real-time executables, these tools give an efficient and reliable way to test, evaluate, and iterate your designs in a real-time environment.Real-Time Workshop, the code generator for Simulink, generates efficient, optimized C and Ada code directly from Simulink models. Supporting discrete-time, multirate, and hybrid systems, Real-Time Workshop makes it easy to evaluate system models on a wide range of computer platforms and real-time environments.Stateflow Coder, the standalone code generator for Stateflow, automatically generates C code from Stateflow diagrams. Code generated by Stateflow Coder can be used independently or combined with code from Real-Time Workshop.Real-Time Windows Target, allows to use a PC as a standalone, self-hosted target for running Simulink models interactively in real time. Real-Time Windows Target supports direct I/O, providing real-time interaction with your model, making it an easy-to-use, low-cost target environment for rapid prototyping and hardware-in-the-loop simulation.xPC Target allows to add I/O blocks to Simulink block diagrams, generate code with Real-Time Workshop, and download the code to a second PC that runs the xPC target real-time kernel. xPC Target is ideal for rapid prototyping and hardware-in-the-loop testing of control and DSP systems. It enables the user to execute models in real time on standard PC hardware.By combining the MathWorks code generation tools with hardware and software from leading real-time systems vendors, the user can quickly and easily perform rapid prototyping, hardware-in-the-loop (HIL) simulation, and real-time simulation and analysis of your designs. Real-Time Workshop code can be configured for a variety of real-time operating systems, off-the-shelf boards, and proprietary hardware.The MathWorks products for control design enable the user to make changes to a block diagram, generate code, and evaluate results on target hardware within minutes. For turnkey rapid prototyping solutions you can take advantage of solutions available from partnerships between The MathWorks and leading control design tools:q dSPACE Control Development System: A total development environment forrapid control prototyping and hardware-in-the-loop simulation;q WinCon: Allows you to run Real-Time Workshop code independently on a PC;q World Up: Creating and controlling 3-D interactive worlds for real-timevisualization;q ADI Real-Time Station: Complete system solution for hardware-in-the loopsimulation and prototyping.q Pi AutoSim: Real-time simulator for testing automotive electronic control units(ECUs).q Opal-RT: a rapid prototyping solution that supports real-time parallel/distributedexecution of code generated by Real-Time Workshop running under the QNXoperating system on Intel based target hardware.Dynamic System SimulationSimulink is a powerful graphical simulation tool for modeling nonlinear dynamic systems and developing control strategies. With support for linear, nonlinear, continuous-time, discrete-time, multirate, conditionally executed, and hybrid systems, Simulink lets you model and simulate virtually any type of real-world dynamic system. Using the powerful simulation capabilities in Simulink, the user can create models, evaluate designs, and correct design flaws before building prototypes.Simulink provides a graphical simulation environment for modeling dynamic systems. It allows to build quickly block diagram models of dynamic systems. The Simulink block library contains over 100 blocks that allow to graphically represent a wide variety of system dynamics. The block library includes input signals, dynamic elements, algebraic and nonlinear functions, data display blocks, and more. Simulink blocks can be triggered, enabled, or disabled, allowing to include conditionally executed subsystems within your models.FLIGHT DYNAMICS TOOLBOX – FDC 1.2report by Marc RauwFDC is an abbreviation of Flight Dynamics and Control. The FDC toolbox for Matlab and Simulink makes it possible to analyze aircraft dynamics and flight control systems within one softwareenvironment on one PC or workstation. The toolbox has been set up around a general non-linear aircraft model which has been constructed in a modular way in order to provide maximal flexibility to the user. The model can be accessed by means of the graphical user-interface of Simulink. Other elements from the toolbox are analytical Matlab routines for extracting steady-state flight-conditions and determining linearized models around user-specified operating points, Simulink models of external atmospheric disturbances that affect the motions of the aircraft, radio-navigation models, models of the autopilot, and several help-utilities which simplify the handling of the systems. The package can be applied to a broad range of stability and control related problems by applying Matlab tools from other toolboxes to the systems from FDC 1.2. The FDC toolbox is particularly useful for the design and analysis of Automatic Flight Control Systems (AFCS). By giving the designer access to all models and tools required for AFCS design and analysis within one graphical Computer Assisted Control System Design (CACSD) environment the AFCS development cycle can be reduced considerably. The current version 1.2 of the FDC toolbox is an advanced proof of concept package which effectively demonstrates the general ideas behind the application of CACSD tools with a graphical user- interface to the AFCS design process.MODELING AND SIMULATION TERMINOLOGYMILITARY SIMULATIONTECHNIQUES & TECHNOLOGYIntroduction to SimulationDefinitions. Defines simulation, its applications, and the benefits derived from using the technology. Compares simulation to related activities in analysis and gaming.DOD Overview. Explains the simulation perspective and categorization of the US Department of Defense.Training, Gaming, and Analysis. Provides a general delineation between these three categories of simulation.System ArchitecturesComponents. Describes the fundamental components that are found in most military simulations.Designs. Describes the basic differences between functional and object oriented designs for a simulation system.Infrastructures. Emphasizes the importance of providing an infrastructure to support all simulation models, tools, and functionality.Frameworks. Describes the newest implementation of an infrastructure in the forma of an object oriented framework from which simulation capability is inherited.InteroperabilityDedicated. Interoperability initially meant constructing a dedicated method for joining two simulations for a specific purpose.DIS. The virtual simulation community developed this method to allow vehicle simulators to interact in a small, consistent battlefield.ALSP. The constructive, staff training community developed this method to allow specific simulation systems to interact with each other in a single joint training exercise. HLA. This program was developed to replace and, to a degree, unify the virtual and constructive efforts at interoperability.JSIMS. Though not labeled as an interoperability effort, this program is pressing for a higher degree of interoperability than have been achieved through any of the previous programs.Event ManagementQueuing. The primary method for executing simulations has been various forms of queues for ordering and releasing combat events.Trees. Basic queues are being supplanted by techniques such as Red-Black and Splay trees which allow the simulation store, process, and review events more efficiently than their predecessors.Event Ownership. Events can be owned and processed in different ways. Today's preference for object oriented representations leads to vehicle and unit ownership of events, rather than the previous techniques of managing them from a central executive.Time ManagementUniversal. Single processor simulations made use of a single clocking mechanism to control all events in a simulation. This was extended to the idea of a "master clock" during initial distributed simulations, but is being replaced with more advanced techniques in current distributed simulation.Synchronization. The "master clock" too often lead to poor performance and required a great deal of cross-simulation data exchange. Researchers in the Parallel Distributed Simulation community provided several techniques that are being used in today's training environment.Conservative & Optimistic. The most notable time management techniques are conservative synchronization developed by Chandy, Misra, and Bryant, and optimistic synchronization (or Time Warp) developed by David Jefferson.Real-time. In addition to being synchronized across a distributed computing environment, many of today's simulators must also perform as real-time systems. These operate under the additional duress of staying synchronized with the human or system clock perception of time.Principles of ModelingScience & Art. Simulation is currently a combination of scientific method and artistic expression. Learning to do this activity requires both formal education and watching experienced practitioners approach a problem.Process. When a team of people undertake the development of a new simulation system they must follow a defined process. This is often re-invented for each project, but can better be derived from experience of others on previous projects.Fundamentals. Some basic principles have been learned and relearned by members of the simulation community. These have universal application within the field and allow new developers to benefit from the mistakes and experiences of their predecessors.Formalism. There has been some concentrated effort to define a formalism for simulation such that models and systems are provably correct. These also allow mathematical exploration of new ideas in simulation.Physical ModelingObject Interaction. Military object modeling is be divided into two pieces, the physical and the behavioral. Object interactions, which are often viewed as 'physics based', characterize the physical models.Movement. Military objects are often very mobile and a great deal of effort can be given to the correct movement of ground, air, sea, and space vehicles across different forms of terrain or through various forms of ether.Sensor Detection. Military object are also very eager to interact with each other in both peaceful and violent ways. But, before they can do this they must be able to perceive each other through the use of human and mechanical sensors.Engagement. Encounters with objects of a different affiliation often require the application of combat engagement algorithms. There are a rich set of these available to the modeler, and new ones are continually being created.Attrition. Object and unit attrition may be synonymous with engagement in the real world, but when implemented in a computer environment they must be separated to allow fair combat exchanges. Distributed simulation systems are more closely replicating real world activities than did their older functional/sequential ancestors, but the distinction between engagement and attrition are still important. Communication. The modern battlefield is characterized as much by communication and information exchange as it is by movement and engagement. This dimension of the battlefield has been largely ignored in previous simulations, but is being addressed in the new systems under development today.More. Activities on the battlefield are extremely rich and varied. The models described in this section represent some of the most fundamental and important, but they are only a small fraction of the detail that can be included in a model.Behavioral ModelingPerception. Military simulations have historically included very crude representations of human and group decision making. One of the first real needs for representing the human in the model was to create a unique perception of the battlefield for each group, unit, or individual.Reaction. Battlefield objects or units need to be able to react realistically to various combat environments. These allow the simulation to handle many situations without the explicit intervention of a human operator.Planning. Today we look for intelligent behavior from simulated objects. Once form of intelligence is found in allowing models to plan the details of a general operational combat order, or to formulate a method for extracting itself for a difficult situation.Learning. Early reactive and planning models did not include the capability to learn from experience. Algorithms can be built which allow units to become more effective as they become more experienced. They also learn the best methods for operating on a specific battlefield or under specific conditions.Artificial Intelligence. Behavioral modeling can benefit from the research and experience of the AI community. Techniques of value include: Intelligent Agents, Finite State Machines, Petri Nets, Expert and Knowledge-based Systems, Case Based Reasoning, Genetic Algorithms, Neural Networks, Constraint Satisfaction, Fuzzy Logic, and Adaptive Behavior. An introduction is given to each of these along with potential applications in the military environment.Environmental ModelingTerrain. Military objects are heavily dependent upon the environment in which they operate. The representation of terrain has been of primary concern because of its importance and the difficulty of managing the amount of data required. Triangulated Irregular Networks (TINs) are one of the newer techniques for managing this problem. Atmosphere. The atmosphere plays an important role in modeling air, space, and electronic warfare. The effects of cloud cover, precipitation, daylight, ambient noise, electronic jamming, temperature, and wind can all have significant effects on battlefield activities.Sea. The surface of the ocean is nearly as important to naval operations as is terrain to army operations. Sub-surface and ocean floor representations are also essential for submarine warfare and the employment of SONAR for vehicle detection and engagement.Standards. Many representations of all of these environments have been developed.Unfortunately, not all of these have been compatible and significant effort is being given to a common standard for supporting all simulations. Synthetic Environment Data Representation and Interchange Specification (SEDRIS) is the most prominent of these standardization efforts.Multi-Resolution ModelingAggregation. Military commanders have always dealt with the battlefield in an aggregate form. This has carried forward into simulations which operate at this same level, omitting many of the details of specific battlefield objects and events.Disaggregation. Recent efforts to join constructive and virtual simulations have required the implementation of techniques for cross the boundary between these two levels of representation. Disaggregation attempts to generate an entity level representation from the aggregate level by adding information. Conversely, aggregation attempts to create the constructive from the virtual by removing information.Interoperability. It is commonly accepted that interoperability in these situations is best achieved though disaggregation to the lowest level of representation of the models involved. In any form the patchwork battlefield seldom supports the same level of interoperability across model levels as is found within models at the same level of resolution.Inevitability. Models are abstractions of the real world generated to address a specific problem. Since all problems are not defined at the same level of physical representation, the models built to address them will be at different levels. The modeling an simulation problem domain is too rich to ever expect all models to operate at the same level. Multi-Resolution Modeling and techniques to provide interoperability among them are inevitable.Verification, Validation, and AccreditationVerification. Simulation systems and the models within them are conceptual representations of the real world. By their very nature these models are partially accurate and partially inaccurate. Therefore, it is essential that we be able to verify that the model constructed accurately represents the important parts of the real world we are try to study or emulate.Validation. The conceptual model of the real world is converted into a software program. This conversion has the potential to introduce errors or inaccurately represent the conceptual model. Validation ensures that the software program accurately reflects the conceptual model.Accreditation. Since all models only partially represent the real world, they all have limited application for training and analysis. Accreditation defines the domains and。

ANNA UNIVERSITYChennai-25.Syllabus for M.C.A. Master of Computer ApplicationsCA131 Computer Fundamentals and Programming Techniques 3 0 0 31 DIGITAL PRINCIPLES 9Boolean Logic - Number system - Gates - Combinational Logic - Multiplexers - Decoders - Sequential Logic - Counters - Shift Register.2 PERIPHERALS 9Semiconductor memories - Auxillary memory devices - I/O devices - Keyboard -Mouse - Modem - Computer display using CRT - Printers - Central Processing Unit.3 PROGRAM DEVELOPMENT METHODOLOGIES 9Top down approach - Stepwise refinement - Modularity - Pseudo code - Control structures - Sequence - Selection - Iteration - Recursion - Structured programming.4 INTRODUCTION TO C LANGUAGE 9Expression - Operators - Pointers - Arrays - Statements - Functions & Recursion - Preprocessor directives - Input output functions and file handling.5 POINTERS & FILE HANDLING 9Pointers -Linked List -Records - File handling.Total No of periods: 45References :1. Thomas C,Bartee,Computer Architecture and Logic Design,TMH 1997.2. Ghosh Dastidar, Computers and Computations - A Beginners guide Chattopadhyay and Sarkar,PHI,1999.3. Charles H.Roth.Jr,Foundations of Logic Design,IV Ed,Jaico Publishing House Mumbai 1999.4. Bian W.Kemighan and Dennis Ritchie,C Programming Language, PHI,1990.5. How to solve it by Computer,R.G.Dromey,PHI,New Delhi,1999.CA132 Data Structures and Algorithms 3 1 0 41 INTRODUCTION 12Introduction - Lists - Stacks - Queues - Linear data structure,Array and Linked lists - Implementation - Applications.2 TREES 13Trees - General and binary trees - Operations - Traversals - Search trees -Balanced trees.3 SORTING 12Sorting - Insertion sort - Quick sort - Merge sort - Heap sort - Sorting on several keys - External sorting.4 GRAPHS 11Graphs representation - Traversal - Topological tables and files - Sorting - Applications - Representation - Marking techniques - Files - Sequential - Index sequential - Random access organization - Implementation.5 ALGORITHM ANALYSIS AND DESIGN 12Algorithms - Time and sapace complexity - Sorting - Design techniques - Knapsack - Travaling salesman - Graph coloring - Squeezing.Total No of periods: 60References :1. Kruse R.L.,Leung BP.Tondo C.L,Data structures and program design in C,PHI,1995.2. Ellis Horowitz, Sahni & Dinesh Mehta Fundamental of data structures in C++,Galgotia,1999.3. Tanenbaum A.S,Langram Y.,Augestein M.J.,Data structures using C,PHI,1992.4. Jean Paul tremblay,Paul G.Sorenson,An Introduction to data structures with Application,Tata McGraw Hill,1995.5. Horowitz, Sahni, S.Rajasekaran, Computer Algorithms, Galgotia,2000.CA133 Data Base Management Systems 3 0 0 31 INTRODUCTION 9Historical prespective - Files versus database systems - Architecture - E-R model - Security and Integrity - Data models.2 RELATIONAL MODEL 9The relation - Keys - Constraints - Relational algebra and Calculus - Queries - Programming and triggers.3 DATA STORAGE 9Disks and Files - file organizations - Indexing - Tree structured indexing - Hash Based indexing.4 QUERY EVALUATION AND DATABASE DESIGN 9External sorting - Query evaluation - Query optimization - Schema refinement and normalization - Physical database design and tuning - Security.5 TRANSACTION MANAGEMENT 9Transaction concepts - Concurrency control - Crash recovery - Decision support - Case studies.Total No of periods: 45References :1. Raghu ramaKrishnan and Johannes gehrke, Database Management Systems, MC Graw Hill International Editions, 2000.2. C.J. Date, An Introduction to Database Systems, 7th Edition,Addision Wesley, 1997.3. Abraham Silberschatz, Henry.F.Korth and S.Sudharshan, Database system Concepts, 3rd Edition, Tata Mc Graw Hill,1997.CA134 Computer Architecture 3 0 0 31 INTRODUCTION TO DIGITAL DESIGN 6Gates to circuits - Combinational and sequential.2 COMPUTER ORGANIZATION 12Basics - Processor design - Instruction sets - addressing modes - ALU design - Control design - Hardwired control unit - Micro programmed control unit.3 MEMORY 9RAM - ROM - Cache memory - Associative memories - Virtual memory - Memory management.4 INPUT-OUTPUT ORGANIZATION 10Input - output organization - Programmed I/O - DMA - Interrupt - I/O hardware - Standard I/O interfaces - I/O devices - Storage devices.5 TRENDS IN ARCHITECTURE 8RISC Vs CISC - Parallel architectures - Pipelining - Case studies.Total No of periods: 45References :1. V.C.Hamacher, Z.G.Vraesic, S.G.Zaky, Computer Organization, Tata McGraw Hill,1996.2. Vincent P.Heuring,Harry F.Jordan, Computer systems Design and Architecturre, Addison Wesley,1999.3. John P.Hayes, Computer Architecture and Organisation, MC Graw Hill,3rd edition,1999.4. David A.Patterson and John L.Hennessy, Computer Organisation and Design, Harcourt asia PTE Ltd, 2nd edition 1999.MA154 Mathematical Foundation of Computer Science 3 1 0 41 LOGIC 12Statements - Connectives -Truth Tables - Normal forms - Predicate calculus - Inference Theory for Statement Calculus and Predicate Calculus - Automatic Theorem proving.2 COMBINATORICS 12Review of Permutation and Combination - Mathematical Induction - Pigeon hole principle - Principle of Inclusion and Exclusion - Recurrence relations.3 ALGEBRAIC STRUCTURES 12Semi group - Monoid - Groups (Definitions and Examples only) Cyclic group - Permutation groups (Sn and Dn ) - substructures - Homomorphism of semi group, monoid and groups - Cosets and Lagrange Theorem - Normal Subgroups - Rings and Fields (Definition and examples only)4 RECURSIVE FUNCTIONS 12Recursive functions - Primitive functions - computable and non-computable functions.5 LATTICES 12Partial order relation, poset - lattices, Hasse diagram - Boolean algebra.Total No of periods: 60References:1. Gersting J.L., Mathematical Structure for Computer Science, 3rd Edition W.H. Freeman and Co., 1993.2. Lidl and Pitz., Applied Abstract Algebra, Springer - Verlag, New York, 1984.3. K.H.Rosen, Discrete Mathematics and its Applications, Mc-Graw Hill Book Company,1999.4. /rosenCA135 Programming Lab 0 0 4 21 MS-DOS EDITOR COMMANDS 4Creating file (COPYCON, EDIT command etc ) - Directory related commands (MD,CD,RD) -Disk Related Commands (FDISK, FORMAT, DISKCOPY,XCOPY etc ) Other Commands.2 UNIX COMMANDS 4Basic Commands (cp,rm , ls, pwd,cat etc) - Basic Shell Programming - Advanced Shell Programming.3 BASIC C PROGRAMMING 4Simple programs using I/O (Entering Input Data, Writing Output data, gets and puts functions - operators - expressions.4 CONTROL STATEMENTS 4Implementation of programs using control statements (Branching Statements IF - BLOCK IF - NESTED IF - GOTO - SWITCH - WHILE - CONTINUE and etc..)5 FUNCTIONS 4Defining a function - accessing a function - Passing arguments to a function - Recursive function6 ARRAYS AND STRUCTURES 8Processing an array - passing Arrays to a function - Passing portion of an Array to a function - multidimenstional Arrays - Defining a structure - Accessing a structure.7 POINTERS 8Declaration and processing pointers - passing pointer to a function - Dynamic memory Allocation - Pointers and one dimensional array.8 FILE HANDLING 8Opening and Closing a Data file - Creating a Data file - Processing a Data file - Unformatted Data files.9 DATA STRUCTURES 12Stacks - Queues - Linked Lists - Trees - Sparse matrix Manipulations.10 GRAPHICS FUNCTION AND ANIMATION 4Line Primitives - 2D Geometrical object constructions, RST - Transformations - Animating Geometrical objects.Total No of periods: 60CA141 Computer Communication and Networks 3 1 0 41 INTRODUCTION 12Communication model - Data communications networking - Data transmission concepts and terminology - Transmission media - Data encoding -Data link control.2 NETWORK FUNDAMENTALS 12Protocol architecture - Protocols - OSI - TCP/IP - LAN architecture - Topologies - MAC - Ethernet, Fast ethernet, Token ring, FDDI, Wirelsee LANS - Bridges.3 NETWORK LAYER 12Network layer - Switching concepts - Circuit switching networks - Packet switching - Routing - Congestion control - X.25 - Internetworking concepts and X.25 architectural models - IP - Unreliable connectionless delivery - Datagrams - Routing IP datagrams - ICMP.4 TRANSPORT LAYER 12Transport layer - Reliable delivery service - Congestion control - connection establishment - Flow control - Transmission control protocol - User datagram protocol.5 APPLICATIONS 12Applications - Sessions and presentation aspects - DNS, Telnet, rlogin, FTP, SMTP - WWW - Security - SNMP.Total No of periods: 60References :1. Larry L.Peterson & Bruce S.Davie, Computer Networks - A systems Approach, 2nd edition, Harcourt Asia/Morgan Kaufmann, 2000.2. William Stallings, Data and Computer Communications, 5th edition, PHI,1997.CA142 System Software 3 0 0 31 INTRODUCTION 9Basic concepts - Machine structure - Typical architectures.2 ASSEMBLERS 9Funtions - Machine dependent and Machine independent assembler Features - Design and Implementation - Examples.3 LOADERS AND LINKERS 9Functions - Machine dependent and Machine independent loader features - Linkage editors - Dynamic linking - Bootstrap loaders - Implementation - Examples.4 MACRO PROCESSORS 9Functions - Features - Recursive macro expansion - General-purpose macro processors - Macro processing within language translators - Implementation - Examples.5 COMPILERS AND UTILITIES 9Introduction to compilers - Different phases of a compiler - Simple one pass compiler - Code optimization techniques - System software tools - Text editors - Interactive debugging systems.Total No of periods: 45References :1. Leland L.Beck, System Software - An Introduction to Systems Programming, 3rd Edition, Addison Wesley,1999.2. D.M.Dhamdhere, System Programming and Operating Systems, Tata Mc Graw Hill Company, 1993.3. A.U.Aho,Ravi Sethi and J.D.Ullman, Compilers Principles Techniques and Tools, Addison Wesley,1988.4. John J.Donovan, systems Programming, Tata Mc Graw Hill Edition,1991.CA143 Software Engineering 3 1 0 41 INTRODUCTION 12Software Engineering paradigms - Waterfall life cycle model, spiral model, prototype model, 4th Generation techniques - Planning - Cost estimation - Organization structure - Software project scheduling, Risk analysis and management - Requirements and specification - Rapid prototyping.2 SOFTWARE DESIGN 12Abstraction - Modularity - Software architecture - Cohesion,coupling - Various design concepts and notations - Real time and distributed system design - Documentation - Dataflow oriented design - Jackson system development - Designing for reuse - Programming standards.3 SOFTWARE METRICS 12Scope - classification of metrics - Measuring Process and Product attributes - Direct and indirect measures - Reliability - Software quality assurance - Standards.4 SOFTWARE TESTING AND MAINTENANCE 12Software testing fundamentals - Software testing strategies - Black box testing, White Box testing, System testing - Testing tools - Test case management - Software maintenance organzation - Maintenance report - Types of maintenance.5 SOFTWARE CONFIGURATION MANAGEMENT(scm) & CASE TOOLS 12 Need for SCM - Version control - SCM process - Software configuration items - Taxonomy - case repository - Features.Total No of periods: 60References :1. Roger S.Pressman, Software Engineering: A Practitioner Approach, 5th Edition, MCGraw Hill, 1999.2. Fairley, Software Engineering Concepts, McGraw Hill, 1985.3. Sommerville I., Software Engineering, 5th Edition, Addison Wesley, 1996.CA144 System Analysis and Design 3 0 0 31 INTRODUCTION 9System Concepts - Subsystems - Types of Systems - Systems and the System analyst - Business as a systems - Information systems - systems Lifecycle - Systems Development Stages - Role of system Analyst - Characeristics of System Analyst.2 SYSTEM PLANNING AND INVESTIGATION 9Approaches to system Development - Methods of Investigation - Recording the investigation feasibility assessment.3 SYSTEM DESIGN 9Analyzing user requirements - Logical system Definition - Physical Definition - Physical Design of Computer subsystem - File Design - Database Design - Output and Input Design - Computer Procedure Design - system security.Form Design - dialogue design - code design - system implementation - Changeover - Maintenance and review.4 PROJECT DOCUMENTATION 9Communitcation skills - Problems in communication written reports - Principles of report writing with structure - standard documentation - study Proposal - System Propposal - User system Specification - Program and Suit Specification - User Manual - Operational Manual - Test Data file - Changeover - Instructions - System audit report.5 MANAGEMENT INFORMATION SYSTEMS 9Introduction to MIS - Survey of IS Technology - Conceptual foundation - IS Requirements - Development - Implementation and Management of IS Resources.Total No of periods: 45References:1. James A Senn, Analysis and Design of Information Systems, McGraw Hill,1989.,2. Igor Gawryszkiewycz, Introduction to system analysis and design, PHI, New Delhi,2000.3. V.Rajaraman,Analysis and Design of information Systems, PHI, New Delhi,2000.CA145 Object Oriented Programming 3 0 0 31 OOP PARADIGM 5Comparison of programming paradigms - Key concepts of Object Oriented Programming - Object identification - Object Oriented design fundamentals - Object Oriented languages.2 INTRODUCTION TO C++ 10Comparison with C - Overview of C++ - Classes and Objects - Arrays, pointers,references and dynamic allocation.3 OVERLOADING 10Function Overloading - Copy constructors - Default arguments - Operator overloading.4 ADDITIONAL FEATURES 10Inheritance - Virtual functions - Polymorphisms - Templates - Exception handling - I/O stream - File I/O - STL5 DESIGN CONCEPTS 10Role of classes - Relationship between classes - Class interface - Components - Study of typical Object Oriented systems.Total No of periods: 45References :1. Herbert Schildt, C++ The complete References, III Edition, 1999.2. Bjame Stroustrup, The C++ Programming Language, Third Edition , Addison Wesley,2000.3. Stanley B.Lippman, Jove Lajoie, C++ Primer, III Edition, Addison Wesley,1998.4. Barkakati N, Object Oriented Programming in C++, PHI, 1995.CA146 Object Oriented Programming and DBMS Lab 0 0 4 21 CLASS 6Implementation of a class - constructor - destructor - friend class - friend functions - static member functions.2 OVERLOADING 6Implementation of overloading in functions and operators - unary and binary operators - other operators.3 INHERITANCE 6Implementation of Inheritance - simple - multilevel - multiple - hybrid.4 POLYMORPHISM 6Implementation of polymorphism - Virtual functions - Pure virtual functions.5 TEMPLATE, EXCEPTION HANDLING AND I/O STREAMS 6Implementation of class templates - exception handling - creation and manipulation of files.6 DATA DEFINITION AND UPDATION 4Creation of tables - Views - Insertion - Modification and deletion of elements.7 DATA CONTROL 4Usage of DCL commands.8 DATA RETRIEVAL 4Implementation of queries - sub queries - correlated sub queries.9 ADVANCED QUERIES 6Implementation of joins - Self - equi join - natural join - aggregate functions and set manipulation.10 HIGH - LEVEL CONSTRUCTS 6Implementation of PL / SQL - triggers - cursors and sub programs.11 DATABASE CONNECTIVITY 6Implementation of database connectivity through front - end tools - Generation of Reports.Total No of periods: 60CA231 Microprocessors and its Applications 3 0 2 41 INTRODUCTION 10Evolution of Microprocessors - Overview of 8- bit microprocessors - Limitations - Applications2 8086 MICROPROCESSOR 32Architecture of intel 8086 microprocessor - Addressing methods - Instruction set - Assembly language programming - Programming examples using MASM.3 8086 BASED SYSTEM DESIGN 11Intel 8086 signals and timing - MIN/MAX mode of operation - Memory and I/O system design using Intel 8086.4 INTERFACING CONCEPTS 14Programmable peripheral interface - Programmable communication interface - DMA controller - Timer - Interrupt controller - Keyboard/display controller.5 APPLICATIONS 8Applications using microcontrollers - Advanced microprocessors(Intel family)Total No of periods: 75References :1. Douglas. V.Hall, Microprocessors and Interfacing - Programming and Hardware, McGraw Hill International Edition,1986.2. Liu and Gibson, Microcomputer System,the 8086/8088 family,Prentice hall of india Pvt.Ltd.,1989.3. Gaonkar,R.S., Microprocessor Architecture, Programming and Applications with 8080/8085 A, Wiley Eastern Ltd, New Delhi,1991.4. Intel manuals.CA232 Operating Systems 3 1 0 41 INTRODUCTION 8Multiprogramming - Time sharing - Distributed system - Real time systems - I/O structure - Dual mod operation - Hardware protection - General system architecture - Operating system services - System calls - System programs - System design and implementation.2 PROCESS MANAGEMENT 11Process concept - Concurrent process - Scheduling concepts - CPU scheduling -Scheduling algorithms - Multiple processor scheduling.3 PROCESS SYCHRONIZATION 11Critical section - Synchronization harware - Semaphores,classical problem of synchronization - Interprocess communication - Deadlock - Characerization,Prevention, Avoidance, Detection.4 STORAGE MANAGEMENT 12Swapping, single and multiple partition allocation - Paging - Segmentation - Paged segmentation, Virtual memory - Demand paging - Page replacement and alogrithms - Thrashing - Secondary storage management - Disk structure - Free space management - Allocation methods - Disk scheduling - Performance and reliability improvements - Storage hierarchy.5 FILES AND PROCTECTION 18File system organization - File operations - Access methods - Consistency semantics - Directory structure organization - File protection - Implementation issues - Securtiy - Encryption - Case study - UNIX and Windows NT - Introduction to distributed OS design.Total No of periods: 60References :1. Silberschatz and Galvin, Operating System Concepts, 4th Edition, Addison Wesley Publishing co.,1995.2. Deital, An Introduction to OPerating systems, Addison Wesley Publishing Co., 1985.3. Milankovic.M., Operatin system Concepts and Design, 2nd Edition, McGraw Hill 1992.4. Madanick SE and Donovan JJ, Operating System, McGraw Hill, 1974.CA233 Object Oriented Analysis and Design 3 0 0 31 OBJECT ORIENTED DESIGN FUNDAMENTALS 9The objec model - Classes and Objects - Complexity - Classification - Notation - Process - Pragmatics - Binary and entity relationship - Object types - Object state - OOSD life cycle.2 OBJECT ORIENTED ANALYSIS 9Overview of object oriented analysis - Shaler/Mellor, Coad/Yourdon, Rumbagh,Booch - UML - Usecase - Conceptual model - Behaviour - Class - Analysis patterns - Overview - Diagrams - Agrregation.3 OBJECT ORIENTED DESIGN METHODS 9UML - Diagrams - Collaboration - Sequence - Class - Design patterns and frameworks - Comparison with other design methods.4 MANAGING OBJECT ORIENTED DEVELOPMENT 9Managing analysis and design - Evaluation testing - Coding - Maintenance - Metrics.5 CASE STUDIES IN OBJECT ORIENTED DEVELOPMENT 9Design of foundation class libraries - Object Oriented databases - Client/Server computing - Middleware.Total No of periods: 45References :1. Craig Larman, Applying UML and patterns, Addison Wesley,2000.2. The Unified Modeling Language User Guide, Grady Booch, James Rumbaugh, Ivar Jacobson, Addison - Wesley Long man, 1999, ISBN 0-201-57 168-4.3. Ali Bahrami, Object Oriented System Development, McGraw Hill International Edition, 1999.4. Fowler, Analysis Patterns, Addison Wesley,1996.5. Erich Gamna, Design Patterns, Addison Wesley, 1994.CA234 Unix and Network Programming 3 0 0 31 INTRODUCTION & FILE SYSTEM 9Overview of UNIX OS - File I/O - Files and directories - Standard I/O library - System data files and information.2 PROCESSES 9Environment of a UNIX process - Process control - Process relationships - Signals terminal I/O - Advanced I/O - threads.3 INTERPROCESS COMMUNICATION 9Introduction - Message passing - Synchronization - Shared memory.4 SOCKETS 9Introduction - TCP sockets - I/O multiplexing - Socket options - UDP sockets - Name and address conversions.5 APPLICATIONS 9Raw sockets - Debugging techniques - TCP echo client server - UDP echo client server - Ping - Trace route - Client server applications.Total No of periods: 45References :1. W.Richard Stevens, Advanced programming in the UNIX environment, Addison Wesley,1999.2. W.Richard Stevens, UNIX Network Programming Volume 1,2, Prentice Hall International,1998.CA235 Unix Lab 0 0 4 21 BASIC COMMANDS 8Learning an Editor, Knowing to use commands like ls,cp,rm,diff,rmdir,cat etc. Learning to write a make file, compiling C programs in Unix.2 IMPLEMENTATION OF SYSTEM CALLS RELATED TO FILE SYSTEM 8To use system calls - create,open,read, write, close, stat,fstat,lseek.3 PROCESS CREATION, EXECUTION 8Implementation of fork, exec system calls.4 PIPES 4Implementation of Inter process communication using pipes.5 SEMAPHORES 8Known to use semaphores. Solving synchronization problems.6 MESSAGE QUEUES 4Implementation of inter process communication using message Queues.7 SHARED MEMORY 4IPC using shared memory8 SOCKET PROGRAMMING - TCP SOCKETS 4Client server communication using TCP Sockets.9 SOCKET PROGRAMMING - UDP SOCKETS 4Client Server communication using UDP Scokets.10 APPLICATIONS USING TCP , UDP SOCKETS 8Application like File transfer , chat using TCP, UDP Sockets.Total No of periods: 60CA241 Internet Programming and Tools 3 1 0 41 BASIC INTERNET CONCEPTS 9History of Internet - Internet addressing - TCP/IP - DNS and directory services - Internet Resources - Applications - Electronic mail, Newgroups, UUCP, FTP, Telnet, Finger.2 WORLD WIDE WEB 5Overview - Hyper Text Markup Language - Uniform Resource Locators - Protocals - MIME Types - Browsers - Plug- ins - Net meeting and chat - Search Engines.3 SCRIPTING LANGUAGE 14Java Script programming -Dynamic HTML - Cascading style sheets - Object model and collections - Event model - Filters and Transitions - ActiveX controls - Multimedia - Client side scripting.4 JAVA 20Java fundamentals - IO Streaming - Object Serialization - Applications - Applets -Networking - Threading - Native Interfaces - Image Processing.5 ADVANCED JAVA 12Remote methods invocation - Multicasting - JDBC - Server side programming - Enterprise Applications - Automated Solutions.Total No of periods: 60References :1. D.Norton and H.Schildt, Java2 : the complete reference, TMH 2000.2. Internet & World wide Web How to program, Deitel & Deitel, Prentice Hall 2000.3. Java How to program,Deitel & Deitel, Prentice Hall 1999.4. Core Java Vol.1 and Vol. 2, Gary Cornell and Cay S.Horstmann, Sun Microsystems Press 1999.4. Active X source Book, Ted coombs,Jason Coombs and Don Brewer, John Wiley &sons 1996.1 INTRODUCTION 8Relational databases - ODBC - JDBC - Stored procedures - Triggers - Forms - Reports - Decision support - Databases - Servers2 PARALLEL AND DISTRIBUTED DATABASES 10Parallel databases - I/O parallelism - Interquery and Intraquery parallelism - Intra operation and Interoperation parallelism - Design of parallel databases - Distributed databases - Distributed data storage - Network transparency distributed query processing - Transaction model - Commit protocols - Coordinator selection - Concurrency control - Deadlock handling - Multidtabase systems.3 SPECIALIZED DATABASES 12Dedutive databases - Temporal and Spatial databases - Web databases - Multimedia databases.4 OBJECT ORIENTED DATABASES 10Objects - Storage - Retrieval - Query language - Object relational databases - Architecture - query processing.5 DATA WAREHOUSING AND DATA MINING 5Data Warehousing architecture - Implementation - Data mining - Rules - Clustering.Total No of periods: 45References :1. Ramez Eimasri, Shamkant, B.Navathe, Fundamentals of Database Systems, 3rd Edition, Addison Wesley,2000.2. Abraham Silberschatz, Henry.F.Korth and S.Sudharshan, Database System Concepts, McGraw Hill International Editions, 1997.3. Setrag Khosafian, Object Oriented Databases, John Wiley & Sons,1993.4. Gary W.Hanson and James V.Hanson, Database Management and Design, Prentice Hall of India Pvt Ltd.,1999.5. M.Tamer Ozsu and Patrick Valduriez, Principles of Distributed Database Systems, Prentice Hall International INC, 1999.1 WINDOWS PROGRAMMING 10Conceptual comparison of traditional programming paradigms - Overview of Windows programming - Data types - Resources - Windows messages - Device contexts - Document interface - Dynamic linking libraries - SDK(Software Development Kit) tools - Context help.2 VISUAL BASIC PROGRAMMING 10Form design - Overview - Programming fundamentals - VBX Controls - Graphics application - Animation - Interfacing - File system controls - Data control - Database applications.3 VISUAL C++ PROGRAMMING 10Frame work calsses - VC++ components - Resources - Event handling - Message dispatch system - Model and Modeless dialogs - Importing VBX controls - Document view architecture - Serialization - Multiple document interface - Splitter windows - Co-ordination between controls - Subclassing.4 DATABASE CONNECTIVITY 8Mini database applications - Embedding controls in view - Creating user defined DLL's - Dialog based applications - Dynamic data transfer functions - User interface classes - Database management with ODBC - Communicating with other applications - Object linking and embedding.5 BASICS OF GUI DESIGN 7Goals of user interface design - Three models - Visual interface design - File system - Storage and retrieval system - Simultaneous multiplatform development - Interoperability.Total No of periods: 45References :1. David Kruglinski J., Inside Visual C++, Microsoft Press , 1993.2. Microsoft Visual C++ and Visual Basic manuals.3. Petzoid, Windows Programming, Microsoft Press, 1992.4. Alan cooper, The Essentials of User Interface Design, IDG Books World Wide Inc., California, USA, 1995.5. Pappar and Murray,Visual C++: The Complete Reference, TMH,2000.CA244 Computer Graphics and Multimedia Systems 3 0 0 31 INTRODUCTION 9I/O devices - VGA card - Bresenham technique - DDA - Display files - Clipping algorithms - circle Drawing algorithms.2 2D TRANSFORMATIONS 9Two dimensional transformations - Interactive Input methods - Polygons - splines - Window viewport mapping.3 3D TRANSFORMATIONS 93D Concepts - Projections - Hidden surface and hidden line elimination - visualization and rendering - color models - Texture mapping - animation - morphing.4 OVERVIEW OF MULTIMEDIA 9Overview of hardware and software components - 2D and 3D graphics in multimedia - audio - video - Standards for multimedia authoring and designing - Multimedia project development.5 APPLICATIONS 9Multimedia Information system - MMDB - Image information system -Video conferencing concepts of virtual reality.Total No of periods: 45References :1. Foley J.D, Van Dam A, Feiner S.K, Hughes J.F, computer Principles and practice, Addison, Wesley publication company, 1993.2. Siamon J. Gibbs and Dionysios C. Tsichritzis, Multimedia programming, Addison, Wesley, 1995.3. Tom Vaughan, Multimedia - making it work, Osborne Mc Graw Hill, 1993.4. Hearn D and Baker M.P, Computer graphics 2nd edition PHI, New Delhi, 1995.5. John Villamil, Casanova and Leony Fernanadez, Eliar, Multimedia Graphics, PHI, 1998.。

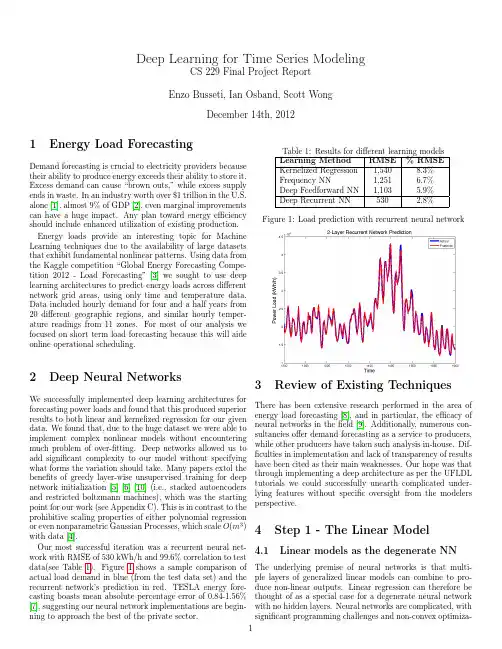
Deep Learning for Time Series ModelingCS 229Final Project Report Enzo Busseti,Ian Osband,Scott WongDecember 14th,20121Energy Load ForecastingDemand forecasting is crucial to electricity providers because their ability to produce energy exceeds their ability to store it.Excess demand can cause “brown outs,”while excess supply ends in waste.In an industry worth over $1trillion in the U.S.alone[1],almost 9%of GDP [2],even marginal improvements can have a huge impact.Any plan toward energy efficiency should include enhanced utilization of existing production.Energy loads provide an interesting topic for Machine Learning techniques due to the availability of large datasets that exhibit fundamental nonlinear ing data from the Kaggle competition “Global Energy Forecasting Compe-tition 2012-Load Forecasting”[3]we sought to use deep learning architectures to predict energy loads across different network grid areas,using only time and temperature data.Data included hourly demand for four and a half years from 20different geographic regions,and similar hourly temper-ature readings from 11zones.For most of our analysis we focused on short term load forecasting because this will aide online operational scheduling.2Deep Neural NetworksWe successfully implemented deep learning architectures forforecasting power loads and found that this produced superior results to both linear and kernelized regression for our given data.We found that,due to the huge dataset we were able to implement complex nonlinear models without encountering much problem of over-fitting.Deep networks allowed us to add significant complexity to our model without specifying what forms the variation should take.Many papers extol the benefits of greedy layer-wise unsupervised training for deep network initialization [5][6][10](i.e.,stacked autoencoders and restricted boltzmann machines),which was the starting point for our work (see Appendix C).This is in contrast to the prohibitive scaling properties of either polynomial regression or even nonparametric Gaussian Processes,which scale O (m 3)with data [4].Our most successful iteration was a recurrent neural net-work with RMSE of 530kWh/h and 99.6%correlation to test data(see Table 1).Figure 1shows a sample comparison of actual load demand in blue (from the test data set)and the recurrent network’s prediction in red.TESLA energy fore-casting boasts mean absolute percentage error of 0.84-1.56%[7],suggesting our neural network implementations are begin-ning to approach the best of the private sector.Table 1:Results for different learning models Learning Method RMSE %RMSE Kernelized Regression 1,5408.3%Frequency NN 1,251 6.7%Deep Feedforward NN 1,103 5.9%Deep Recurrent NN 530 2.8%Figure 1:Load prediction with recurrent neural network3Review of Existing TechniquesThere has been extensive research performed in the area of energy load forecasting [8],and in particular,the efficacy of neural networks in the field [9].Additionally,numerous con-sultancies offer demand forecasting as a service to producers,while other producers have taken such analysis in-house.Dif-ficulties in implementation and lack of transparency of results have been cited as their main weaknesses.Our hope was that through implementing a deep architecture as per the UFLDL tutorials we could successfully unearth complicated under-lying features without specific oversight from the modelers perspective.4Step 1-The Linear Model4.1Linear models as the degenerate NNThe underlying premise of neural networks is that multi-ple layers of generalized linear models can combine to pro-duce non-linear outputs.Linear regression can therefore be thought of as a special case for a degenerate neural network with no hidden layers.Neural networks are complicated,with significant programming challenges and non-convex optimiza-1tions,so we first wanted to establish that they really do pro-vide some worthwhile reward over simpler models.After considering some necessary state-space transforma-tions to our data (Appendix A)we implemented least squares regressions over a simple linear model.Unsurprisingly,this suffered from severe high bias as our model was far too sim-ple.Repeating this exercise for quadratic and cubic features we were still able to train over the whole dataset,but the problems of high bias remained still.4.2Scaling issues with large dataThis process of feature creation was wasteful as full polyno-mial expansion gave many features without statistical signifi-cance but still necessitated lengthy ing subset selection methods (such as forward/backward stepwise or the LASSO)and only expanding relevant variables helped weed these out.However,this was only computationally possible on smaller subsets of the data,which might cause us to lose valuable training information.To maintain most of the information of the dataset while facilitating more complex calculations,we implemented k-means clustering.Running the algorithm until convergence was prohibitively slow,however we found good results with some expedited ing different numbers of clus-ters and performing a naive “nearest centroid”classification wesaw improved results as we increased model complexity (Figure 2).We found that clustering was more effective using feature standardization (mean zero/unit variance).Figure 2:Cross validation of number of clusters using nearest neighbor4.3Kernel methods add model complexity In a final bid to add more model complexity,we implemented a kernelized local regression based upon squared exponential distance to centroids.We found that our results were im-proved by additionally considering the number of data points forming part of each cluster.Once again,computational expense proved to be our lim-iting factor and we were only able to complete the kernelized regression with 400clusters per geographic zone.This pro-duced disappointing results as the means over-simplified our dataset and our kernels were unable to scale to the necessary data sizes.5Step 2-Neural NetsNeural networks are a more principled way to add complexity on large datasets.We implemented feedforward networks to explore model parameters and then augmented these with recurrent structure to improve forecasting accuracy.We chose our model parameters through k-folds validation on our data,including:sample set size,feature engineering,anomaly filtering,training algorithms,and network topology.Due to the computationally intensive nature of this process,only feedforward networks were considered at this stage.Un-less otherwise stated,the networks were trained with 70%of the data,15%was used for validation stopping,and 15%for testing (chosen at random).This was repeated 10times per experiment to average out sample error.5.1Learning CurvesTo assess levels of bias and variance in a mid-sized feedfor-ward network (two hidden layers of 30and 10neurons,re-spectively),we trained the network with varying proportions of training data and examined the learning curves.Figure 3summarizes the results,once again demonstrating a high bias problem even with this complex neural network.This led us to focus our work on developing new features and incorporate increased model complexity.Figure 3:Learning curves show high bias5.2Feature EngineeringWhile neural networks have the benefit of being able to fit highly non-linear models,modeler insight of how to represent the data can be equally important.To determine the im-pact of feature engineering,we trained feedforward networks with additional hand engineered features (See Appendix A).2The features were introduced cumulatively,and10models were trained for each feature set.Figure4shows that humanadded features can make a significant difference in the overallperformance of the model.In particular,circular seasons andhours and the day of the week feature decreased RMS error3.5%and8.5%,respectively.That being said,models thatcan realize more complexity than the mid-sized network(i.e.,deeper networks and recurrent networks)have had even betterperformance,and demonstrate the power of deep learning.Figure4:Feature Engineering5.3Fourier transform NetworkTo exploit the strong periodicity of the data(see Figure1)we tried to predict the power loads in frequency space,usingModified Discrete Cosine Transforms(Appendix B).To per-form a discrete Fourier transform wefirst need tofix a timewindow size,l,to split the time series.A natural choice is24hours,because the daily pattern of power load variation andtemperature are very consistent.We also tried smaller timewindows,down to2hours.The transformed dataset is made of samples(ˆx(i),ˆy(i))whereˆx(i)is the transform of the i-th time window of thetemperature time series for all11zones,plus the date,andˆy(i)is the transform of the i-th time window of the powerloads time series.This reduces the number of samples by afactor l.Eachˆx(i)∈R11×l+1and eachˆy(i)∈R l.We used a network topology with two hidden layers,thefirst had the same number of nodes of the inputˆx(i)and thesecond the same of the outputˆy(i).To speed up computationand reduce risk of overfitting we applied PCA toˆx(i)andworked on thefirst95%of the total variance,significantlyreducing dimensionality.The resulting RMSE of the network for different sizes of thetime window of the transform are shown in Figure5.As weincrease the size of the time window we(1)reduce the numberof samples in the dataset and(2)increase the dimensionalityof each sample by∼l.The complexity of the model thusincreases while simultaneously the dataset becomes smaller.We expected better results from the Fourier transform net-work model than the non-transformed model,since it shouldhelp the networkfind repeating patterns,however this wasnot the case.This was in contrast to the more elementarytransforms in Figure4and Appendix A.Our conclusion wasthat,except for the most basic transforms,it is better to allowthe neural network tofind the nonlinear relationships itself.Figure5:The right axis shows RMSE of the network in trans-formed space with various sizes of the time window of thetransform.The left axis shows the number of samples in thedataset.Training stops when the backpropagation algorithmreaches a minimum or we complete1000iterations.Perfor-mance is evaluated against15%test data.5.4Anomaly FilteringLiterature[8]suggests thatfiltering time series data foranomalies may reduce error for neural networks.We use amixture of gaussians to estimate the least likely data,andlabel it as anomalous.Wefit ten through100multi-variategaussians to the data in18-dimensional feature space(fromFeature Engineering),and identified the lowest1%,5%,and10%likelihood data with“anomaly features.”Neural net-works were then trained in this new feature space,howeverthere was no discernible improvement in the generalizationerror of these models.Diving deeper into the data,Figure6shows the anomalousdata points identified by mixture of gaussians in red(em-bedded in2-D with PCA)and how it maps to the time se-ries.Mixture of gaussians identified peaks in demand in thesummer and winter,which were not particularly anomalous.Gaussian methods also failed to identify known outlier data,such as the huge power outages experienced on January5,2005(marked in green in Figure6).Although we might hopethese green points areflagged as outliers,they were actuallyprobable data points in the gaussian model,as you can see bymapping to thefirst two principal components.It is possiblethat alternative methods could provide modeling gains,butwe decided this was not worth pursuing.5.5Training algorithmNeural networks,and in particular deep neural networks,arenotoriously difficult to train due to their non-convex objectivefunctions.We examinedfive training algorithms to determinethe best and fastest solution.Levenberg-Marquardt(“LM”,a combined quasi-Newton and gradient ascent algorithm)was3Figure 6:AnomalyFilteringfound to converge fastest and almost always produce the best error.BFGS (quasi-Newton),Scaled Conjugate Gradient,and Conjugate Gradient with Polak-Ribire updates were all slower and had worse error than LM.LM with Bayesian Reg-ularization produced the lowest error with 2-layer networks (though,not with 4),butconvergence time was prohibitively long to be useful.Table 2summarizes RMS error for the different algorithms on different sized networks.Table 2:Training AlgorithmsRMSE Training Algorithm 2-Layer 4-Layer Levenberg-Marquardt 1,3921,263BFGS Quasi-Newton 1,5062,602Bayesian Regulation 1,2901,887Scaled Conjugate Gradient1,7811,681Conjugate Gradient1,5961,5935.6Recurrent Neural NetworksUsing a purely feedforward network we ignore some of the temporal structure time series data presents.In particular,this structure can be exploited through the use of recurrent neural networks where we explicitly construct a sequential representation of our data.Recurrent neural networks may have multiple types of feed-back loops.The two that were employed here were input delays and feedback delays.Each type of delay effectively in-creases the number of input nodes by providing the network with delayed information along with current information.In the case of input delays,multiple consecutive time steps of the input features are presented to the network simultane-ously.For feedback delays,the output of the model is pro-vided to input nodes,along with previous data.This can either be done with “open”loops,where the known output is provided as an input,or with “closed”loops,which con-nects the network output to the input directly.Here,we have trained and forecasted one-step-ahead with with open loops.To predict farther ahead,closed loops need to be used.Briefly experimenting with closed loops,error increased ∼10%due to “clipping”of peak and trough demand.5.7Network TopologyPerformance of the networks varies highly depending on the number of hidden layers and neurons per layer.Figure 7il-lustrates network performance as a function of complexity (number of weights).Feedforward network achieve near op-timal performance around 2,700weights (3-layers of 50,30,and 10neurons,respectively),with RMS error of 1,269.Ad-ditional complexity through more neurons did not improve performance,but deeper networks occasional produced bet-ter results (however,performance was erratic due to finding local-non-global optimum).Figure 7:Topology SelectionRecurrent neural networks performed drastically better for comparable complexity.All recurrent networks shown in Fig-ure 7are 2-layers –we experimented with deeper networks,however training time increased rapidly (i.e.,≥8hours per model).Best 2-layer results were achieved with 50and 25neurons per layer,respectively,one input tap delay,and one through 48hours of feedback tap delay (∼4,500weights).6ConclusionDeep neural networks are able to accurately gauge electricity load demand across our grid.It is clear from Table 1that recurrent neural networks outperformed all of our competing methods by a significant margin.We believe that,in general,deep learning architectures are well suited to the problems of power load forecasting since we have large availability of rel-evant data with complicated nonlinear underlying processes.We were disappointed with our output using competing nonlinear kernelized methods,and perhaps using pre-built SVM packages would have produced superior results.Due to their poor scaling properties we did not pursue our initial work in Gaussian process modeling.However,potential for sparse computational approximations might provide interesting fu-ture avenues of research [10][11].We believe that within deep learning,cutting edge techniques such as restricted boltzmann machines might allow us to train more complex models effi-ciently.4AppendixA Transformation of VariablesWithin our dataset,it was important to frame our feature variables in ways that were conducive to sensible models,and exploiting natural symmetries.For example,each training example was taken from one of 20distinct geographical zones.Since we had no idea,a priori,of how these zones relate wefound better results modeling zone z ∈R 20than naively z ∈{1,2,..,20}.On the other hand,much of the observed structure to the data was found to be periodic in nature (daily,weekly,sea-sonal).With that in mind we took care,particularly for our linear models,to reflect this a priori symmetry in our data.For variables with inherent symmetry present (hours:24,months:12etc)we transformed to polar coordinates via a (sin,cos)pair of variables to seek solutions of given period-icity.Figure 8:Transformation ofVariablesFigure 9:x →[y 1,y 2]=[sin (2πx ω),cos (2πxω)]we show x as a red dot mapped to y in blue.We can then fit the desired relationship as linear in R 2for the new circular y featuresB Frequency Space TransformMore generally,we might want to exploit the periodicity in the data (Figure1)when we are not sure about the exact period.For example,we know there are pattens around the work-ing day which might be more easily seen in the transformedFourier space.We implemented the Modified Discrete Cosine Transform (MDCT)[12]which performs a discrete transformover fixed size windows returning real coefficients and well-behaved edges.The time windows overlap by half of their length.For ex-ample in case of 24hours time windows the first sample starts at 0and ends at 24of the first day,the second sample from 12to 12of the second day,the third from 0to 24of the secondday,and so on.The original signal is recovered by summing the overlapping parts of each inverse transform (time-domain aliasing cancellation).It is well known that minimizing error in the frequency space is equivalent to the original problem.We were motivated by mp3compression,which uses similar techniques,to use this to express our data in a more efficient manner.CStacked Autoencoder Building on the literature [10]we trained feed forward neural networks with stacked autoencoders.Greedy layer-wise train-ing [5][6]has been shown to improve network performance in scenarios where large amounts of unlabeled data is avail-able,but minimal labeled data.While all of the data used in this paper are labeled,it was our hope that greedy layer-wise training would help avoid local-non-global minima in the optimization problem.However,results with this technique were discouraging,with no significant performance gain butadded computational complexity.References[1]/totalenergy/data/annual/pdf/sec3_11.pdf [2]/itable/error_NIPA.cfm[3]/c/global-energy-forecasting-competition-2012-load-foreca [4]Gaussian Processes for Machine Learning -Rasmussenand Williams [5]Y.Bengio,“Learning Deep Architectures for AI”,Foun-dations and Trends in Machine Learning ,vol 2.,no.1,2009.[6]Bengio,Y.,Lamblin,P.,Popovici,D.,&Larochelle,H.(2007).Greedy layer-wise training of deep networks.In Sch¨o lkopf,B.,Platt,J.,&Hoffman,T.(Eds.),Advances in Neural Information Processing Systems 19(NIPS’06),pp.153-160.MIT Press.[7]/[8]J.Connor,R.D.Martin,and L.E.Atlas,“Recurring Neu-ral Networks and Robust Time Series Prediction”,IEEE Transactions on Neural Networks ,vol.5,no.2,March 1994.[9]/ir/bitstream/1840.16/6457/1/etd.pdf[10]Hinton,G.E.,Osindero,S.,&Teh,Y.W.(2006).A fastlearning algorithm for deep belief nets.Neural computa-tion ,18(7),1527-1554.[11]/pdf/1106.5779v1.pdf .[12]Malvar,Henrique S.Signal processing with lapped trans-forms.Artech House,Inc.,1992.5。

深度增强学习方向论文整理责编：王艺一. 开山鼻祖DQNPlaying Atari with Deep Reinforcement Learning，V. Mnih et al., NIPS Workshop, 2013.Human-level control through deep reinforcement learning, V. Mnih et al., Nature, 2015.二. DQN的各种改进版本（侧重于算法上的改进）Dueling Network Architectures for Deep Reinforcement Learning. Z. Wang et al., arXiv, 2015.Prioritized Experience Replay, T. Schaul et al., ICLR, 2016.Deep Reinforcement Learning with Double Q-learning, H. van Hasselt et al., arXiv, 2015.Increasing the Action Gap: New Operators for Reinforcement Learning, M. G. Bellemare et al., AAAI, 2016.Dynamic Frame skip Deep Q Network, A. S. Lakshminarayanan et al., IJCAI Deep RL Workshop, 2016.Deep Exploration via Bootstrapped DQN, I. Osband et al., arXiv, 2016.How to Discount Deep Reinforcement Learning: Towards New Dynamic Strategies, V. Fran?ois-Lavet et al., NIPS Workshop, 2015.Learning functions across many orders of magnitudes，H Van Hasselt，A Guez，M Hessel，D SilverMassively Parallel Methods for Deep Reinforcement Learning, A. Nair et al., ICML Workshop, 2015.State of the Art Control of Atari Games using shallow reinforcement learningLearning to Play in a Day: Faster Deep Reinforcement Learning by Optimality Tightening（11.13更新）Deep Reinforcement Learning with Averaged Target DQN（11.14更新）三. DQN的各种改进版本（侧重于模型的改进）Deep Recurrent Q-Learning for Partially Observable MDPs, M. Hausknecht and P. Stone, arXiv, 2015.Deep Attention Recurrent Q-NetworkControl of Memory, Active Perception, and Action in Minecraft, J. Oh et al., ICML, 2016.Progressive Neural NetworksLanguage Understanding for Text-based Games Using Deep Reinforcement LearningLearning to Communicate to Solve Riddles with Deep Distributed Recurrent Q-NetworksHierarchical Deep Reinforcement Learning: Integrating TemporalAbstraction and Intrinsic MotivationRecurrent Reinforcement Learning: A Hybrid Approach四. 基于策略梯度的深度强化学习深度策略梯度：End-to-End Training of Deep Visuomotor PoliciesLearning Deep Control Policies for Autonomous Aerial Vehicles with MPC-Guided Policy SearchTrust Region Policy Optimization深度行动者评论家算法：Deterministic Policy Gradient AlgorithmsContinuous control with deep reinforcement learningHigh-Dimensional Continuous Control Using Using Generalized Advantage EstimationCompatible Value Gradients for Reinforcement Learning of Continuous Deep PoliciesDeep Reinforcement Learning in Parameterized Action SpaceMemory-based control with recurrent neural networksTerrain-adaptive locomotion skills using deep reinforcement learningCompatible Value Gradients for Reinforcement Learning of Continuous Deep PoliciesSAMPLE EFFICIENT ACTOR-CRITIC WITH EXPERIENCE REPLAY（11.13更新）搜索与监督：End-to-End Training of Deep Visuomotor PoliciesInteractive Control of Diverse Complex Characters with Neural Networks连续动作空间下探索改进：Curiosity-driven Exploration in DRL via Bayesian Neuarl Networks结合策略梯度和Q学习：Q-PROP: SAMPLE-EFFICIENT POLICY GRADIENT WITH AN OFF-POLICY CRITIC（11.13更新）PGQ: COMBINING POLICY GRADIENT AND Q-LEARNING（11.13更新）其它策略梯度文章：Gradient Estimation Using Stochastic Computation GraphsContinuous Deep Q-Learning with Model-based AccelerationBenchmarking Deep Reinforcement Learning for Continuous Control Learning Continuous Control Policies by Stochastic Value Gradients五. 分层DRLDeep Successor Reinforcement LearningHierarchical Deep Reinforcement Learning: Integrating Temporal Abstraction and Intrinsic MotivationHierarchical Reinforcement Learning using Spatio-Temporal Abstractions and Deep Neural NetworksStochastic Neural Networks for Hierarchical Reinforcement Learning –Authors: Carlos Florensa, Yan Duan, Pieter Abbeel （11.14更新）六. DRL中的多任务和迁移学习ADAAPT: A Deep Arc hitecture for Adaptive Policy Transfer from Multiple SourcesA Deep Hierarchical Approach to Lifelong Learning in MinecraftActor-Mimic: Deep Multitask and Transfer Reinforcement Learning Policy DistillationProgressive Neural NetworksUniversal Value Function ApproximatorsMulti-task learning with deep model based reinforcement learning （11.14更新）Modular Multitask Reinforcement Learning with Policy Sketches （11.14更新）七. 基于外部记忆模块的DRL模型Control of Memory, Active Perception, and Action in Minecraft Model-Free Episodic Control八. DRL中探索与利用问题Action-Conditional Video Prediction using Deep Networks in Atari GamesCuriosity-driven Exploration in Deep Reinforcement Learning viaBayesian Neural NetworksDeep Exploration via Bootstrapped DQNHierarchical Deep Reinforcement Learning: Integrating Temporal Abstraction and Intrinsic MotivationIncentivizing Exploration In Reinforcement Learning With Deep Predictive ModelsUnifying Count-Based Exploration and Intrinsic Motivation#Exploration: A Study of Count-Based Exploration for Deep Reinforcemen Learning（11.14更新）Surprise-Based Intrinsic Motivation for Deep Reinforcement Learning（11.14更新）九. 多Agent的DRLLearning to Communicate to Solve Riddles with Deep Distributed Recurrent Q-NetworksMultiagent Cooperation and Competition with Deep Reinforcement Learning十. 逆向DRLGuided Cost Learning: Deep Inverse Optimal Control via Policy OptimizationMaximum Entropy Deep Inverse Reinforcement LearningGeneralizing Skills with Semi-Supervised Reinforcement Learning （11.14更新）十一. 探索+监督学习Deep learning for real-time Atari game play using offline Monte-Carlo tree search planningBetter Computer Go Player with Neural Network and Long-term PredictionMastering the game of Go with deep neural networks and tree search, D. Silver et al., Nature, 2016.十二. 异步DRLAsynchronous Methods for Deep Reinforcement LearningReinforcement Learning through Asynchronous Advantage Actor-Critic on a GPU（11.14更新）十三：适用于难度较大的游戏场景Hierarchical Deep Reinforcement Learning: Integrating Temporal Abstraction and Intrinsic Motivation, T. D. Kulkarni et al., arXiv, 2016.Strategic Attentive Writer for Learning Macro-ActionsUnifying Count-Based Exploration and Intrinsic Motivation十四：单个网络玩多个游戏Policy DistillationUniversal Value Function ApproximatorsLearning values across many orders of magnitude十五：德州pokerDeep Reinforcement Learning from Self-Play in Imperfect-Information GamesFictitious Self-Play in Extensive-Form GamesSmooth UCT search in computer poker十六：Doom游戏ViZDoom: A Doom-based AI Research Platform for Visual Reinforcement LearningTraining Agent for First-Person Shooter Game with Actor-Critic Curriculum LearningPlaying FPS Games with Deep Reinforcement LearningLEARNING TO ACT BY PREDICTING THE FUTURE（11.13更新）Deep Reinforcement Learning From Raw Pixels in Doom（11.14更新）十七：大规模动作空间Deep Reinforcement Learning in Large Discrete Action Spaces十八：参数化连续动作空间Deep Reinforcement Learning in Parameterized Action Space十九：Deep ModelLearning Visual Predictive Models of Physics for Playing BilliardsJ. Schmidhuber, On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllersand Recurrent Neural World Models, arXiv, 2015. arXiv Learning Continuous Control Policies by Stochastic Value GradientsData-Efficient Learning of Feedback Policies from Image Pixels using Deep Dynamical ModelsAction-Conditional Video Prediction using Deep Networks in Atari GamesIncentivizing Exploration In Reinforcement Learning With Deep Predictive Models二十：DRL应用机器人领域：Trust Region Policy OptimizationTowards Vision-Based Deep Reinforcement Learning for Robotic Motion ControlPath Integral Guided Policy SearchMemory-based control with recurrent neural networksLearning Hand-Eye Coordination for Robotic Grasping with Deep Learning and Large-Scale Data CollectionLearning Deep Neural Network Policies with Continuous Memory StatesHigh-Dimensional Continuous Control Using Generalized Advantage EstimationGuided Cost Learning: Deep Inverse Optimal Control via PolicyOptimizationEnd-to-End Training of Deep Visuomotor PoliciesDeepMPC: Learning Deep Latent Features for Model Predictive ControlDeep Visual Foresight for Planning Robot MotionDeep Reinforcement Learning for Robotic ManipulationContinuous Deep Q-Learning with Model-based AccelerationCollective Robot Reinforcement Learning with Distributed Asynchronous Guided Policy SearchAsynchronous Methods for Deep Reinforcement LearningLearning Continuous Control Policies by Stochastic Value Gradients机器翻译:Simultaneous Machine Translation using Deep Reinforcement Learning目标定位：Active Object Localization with Deep Reinforcement Learning目标驱动的视觉导航：Target-driven Visual Navigation in Indoor Scenes using Deep Reinforcement Learning自动调控参数：Using Deep Q-Learning to Control Optimization Hyperparameters人机对话：Deep Reinforcement Learning for Dialogue GenerationSimpleDS: A Simple Deep Reinforcement Learning Dialogue System Strategic Dialogue Management via Deep Reinforcement Learning Towards End-to-End Learning for Dialog State Tracking and Management using Deep Reinforcement Learning视频预测：Action-Conditional Video Prediction using Deep Networks in Atari Games文本到语音：WaveNet: A Generative Model for Raw Audio文本生成：Generating Text with Deep Reinforcement Learning 文本游戏：Language Understanding for Text-based Games Using Deep Reinforcement Learning无线电操控和信号监控：Deep Reinforcement Learning Radio Control and Signal Detection with KeRLym, a Gym RL AgentDRL来学习做物理实验：LEARNING TO PERFORM PHYSICS EXPERIMENTS VIA DEEP REINFORCEMENT LEARNING（11.13更新）DRL加速收敛：Deep Reinforcement Learning for Accelerating the Convergence Rate（11.14更新）利用DRL来设计神经网络：Designing Neural Network Architectures using Reinforcement Learning（11.14更新）Tuning Recurrent Neural Networks with Reinforcement Learning （11.14更新）Neural Architecture Search with Reinforcement Learning（11.14更新）控制信号灯：Using a Deep Reinforcement Learning Agent for Traffic Signal Control（11.14更新）二十一：其它方向避免危险状态：Combating Deep Reinforcement Learning’s Sisyphean Curse with I ntrinsic Fear （11.14更新）DRL中On-Policy vs. Off-Policy 比较：On-Policy vs. Off-Policy Updates for Deep Reinforcement Learning（11.14更新）130+位讲师，16大分论坛，中国科学院院士陈润生、滴滴出行高级副总裁章文嵩、联想集团高级副总裁兼CTO芮勇、上交所前总工程师白硕等专家将亲临2016中国大数据技术大会，票价折扣即将结束，预购从速。

1Table Of Contents Digital Integrated Circuits—A Design Perspective (2nd Ed)Table of ContentsPREFACEPART I. THE FOUNDATIONSCHAPTER 1: INTRODUCTION1.1 A Historical Perspective1.2Issues in Digital Integrated Circuit Design1.3Quality Metrics of a Digital Design1.3.1Cost of an Integrated Circuit1.3.2Functionality and Robustness1.3.3Performance1.3.4Power and Energy Consumption1.4Summary1.5To Probe FurtherChapter 2: THE MANUFACTURING PROCESS2.1Introduction2.2Manufacturing CMOS Integrated Circuits2.2.1The Silicon Wafer2.2.2Photolithography2.2.3Some Recurring Process Steps2.2.4Simplified CMOS Process Flow2.3Design Rules — The Contract between Designer and Process Engineer 2.4Packaging Integrated Circuits2.4.1Package Materials2.4.2Interconnect Levels2.4.3Thermal Considerations in PackagingDIGITAL INTEGRATED CIRCUITS22.5Perspective — Trends in Process Technology2.5.1Short-Term Developments2.5.2In the Longer Term2.6Summary2.7To Probe FurtherDESIGN METHODOLOGY INSERT A: IC LAYOUTCHPATER 3: THE DEVICES3.1Introduction3.2The Diode3.2.1 A First Glance at the Diode — The Depletion Region3.2.2Static Behavior3.2.3Dynamic, or Transient, Behavior3.2.4The Actual Diode—Secondary Effects3.2.5The SPICE Diode Model3.3The MOS(FET) Transistor3.3.1 A First Glance at the Device3.3.2The MOS Transistor under Static Conditions3.3.3Dynamic Behavior3.3.4The Actual MOS Transistor—Some Secondary Effects3.3.5SPICE Models for the MOS Transistor3.4 A Word on Process Variations3.5Perspective: Technology Scaling3.6Summary3.7To Probe FurtherDESIGN METHODOLOGY INSERT B: CIRCUIT SIMULATION CHAPTER 4: THE WIRE4.1Introduction4.2 A First Glance4.3Interconnect Parameters — Capacitance, Resistance, and Inductance3Table Of Contents4.3.1Capacitance4.3.2Resistance4.3.3Inductance4.4Electrical Wire Models4.4.1The Ideal Wire4.4.2The Lumped Model4.4.3The Lumped RC model4.4.4The Distributed rc Line4.4.5The Transmission Line4.5SPICE Wire Models4.5.1Distributed rc Lines in SPICE4.5.2Transmission Line Models in SPICE4.6Perspective: A Look into the Future4.7Summary4.8To Probe FurtherPART II. A CIRCUIT PERSPECTIVEChapter 5: THE CMOS INVERTER5.1Introduction5.2The Static CMOS Inverter — An Intuitive Perspective5.3Evaluating the Robustness of the CMOS Inverter: The Static Behavior5.3.1Switching Threshold5.3.2Noise Margins5.3.3Robustness Revisited5.4Performance of CMOS Inverter: The Dynamic Behavior5.4.1Computing the Capacitances5.4.2Propagation Delay: First-Order Analysis5.4.3Propagation Delay from a Design Perspective5.5Power, Energy, and Energy-Delay5.5.1Dynamic Power Consumption5.5.2Static Consumption5.5.3Putting It All Together5.5.4Analyzing Power Consumption Using SPICEDIGITAL INTEGRATED CIRCUITS45.6Perspective: Technology Scaling and its Impact on the Inverter Metrics 5.7Summary5.8To Probe FurtherCHAPTER 6: DESIGNING COMBINATIONAL LOGIC GATES IN CMOS 6.1Introduction6.2Static CMOS Design6.2.1Complementary CMOS6.2.2Ratioed Logic6.2.3Pass-Transistor Logic6.3Dynamic CMOS Design6.3.1Dynamic Logic: Basic Principles6.3.2Speed and Power Dissipation of Dynamic Logic6.3.3Issues in Dynamic Design6.3.4Cascading Dynamic Gates6.4Perspectives6.4.1How to Choose a Logic Style?6.4.2Designing Logic for Reduced Supply Voltages6.5Summary6.6To Probe FurtherDESIGN METHODOLOGY INSERT C: HOW TO SIMULATE COMPLEX LOGIC GATESC.1Representing Digital Data as a Continuous EntityC.2Representing Data as a Discrete EntityC.3Using Higher-Level Data ModelsC.4To Probe FurtherDESIGN METHODOLOGY INSERT D: LAYOUT TECHNIQUES FOR COMPLEX GATES5Table Of ContentsCHAPTER 7: DESIGNING SEQUENTIAL LOGIC CIRCUITS7.1Introduction7.1.1Timing Metrics for Sequential Circuits7.1.2Classification of Memory Elements7.2Static Latches and Registers7.2.1The Bistability Principle7.2.2Multiplexer-Based Latches7.2.3Master-Slave Edge-Triggered Register7.2.4Low-Voltage Static Latches7.2.5Static SR Flip-Flops—Writing Data by Pure Force7.3Dynamic Latches and Registers7.3.1Dynamic Transmission-Gate Edge-triggered Registers7.3.2C2MOS—A Clock-Skew Insensitive Approach7.3.3True Single-Phase Clocked Register (TSPCR)7.4Alternative Register Styles*7.4.1Pulse Registers7.4.2Sense-Amplifier Based Registers7.5Pipelining: An approach to optimize sequential circuits7.5.1Latch- vs. Register-Based Pipelines7.5.2NORA-CMOS—A Logic Style for Pipelined Structures7.6Non-Bistable Sequential Circuits7.6.1The Schmitt Trigger7.6.2Monostable Sequential Circuits7.6.3Astable Circuits7.7Perspective: Choosing a Clocking Strategy7.8Summary7.9To Probe FurtherDIGITAL INTEGRATED CIRCUITS6 PART III. A SYSTEM PERSPECTIVECHAPTER 8: IMPLEMENTATION STRATEGIES FOR DIGITAL ICS 8.1Introduction8.2From Custom to Semicustom and Structured Array Design Approaches 8.3Custom Circuit Design8.4Cell-Based Design Methodology8.4.1Standard Cell8.4.2Compiled Cells8.4.3Macrocells, Megacells and Intellectual Property8.4.4Semi-Custom Design Flow8.5Array-Based Implementation Approaches8.5.1Pre-diffused (or Mask-Programmable) Arrays8.5.2Pre-wired Arrays8.6Perspective—The Implementation Platform of the Future8.7Summary8.8To Probe FurtherDESIGN METHODOLOGY INSERT E: CHARACTERIZING LOGIC AND SEQUENTIAL CELLSDESIGN METHODOLOGY INSERT F: DESIGN SYNTHESISCHAPTER 9: COPING WITH INTERCONNECT9.1Introduction9.2Capacitive Parasitics9.2.1Capacitance and Reliability—Cross Talk9.2.2Capacitance and Performance in CMOS9.3Resistive Parasitics9.3.1Resistance and Reliability—Ohmic Voltage Drop9.3.2Electromigration9.3.3Resistance and Performance—RC Delay9.4Inductive Parasitics7Table Of Contents9.4.1Inductance and Reliability— Voltage Drop9.4.2Inductance and Performance—Transmission Line Effects9.5Advanced Interconnect Techniques9.5.1Reduced-Swing Circuits9.5.2Current-Mode Transmission Techniques9.6Perspective: Networks-on-a-Chip9.7Chapter Summary9.8To Probe FurtherCHAPTER 10: TIMING ISSUES IN DIGITAL CIRCUITS10.1Introduction10.2Timing Classification of Digital Systems10.2.1Synchronous Interconnect10.2.2Mesochronous interconnect10.2.3Plesiochronous Interconnect10.2.4Asynchronous Interconnect910.3Synchronous Design — An In-depth Perspective10.3.1Synchronous Timing Basics10.3.2Sources of Skew and Jitter10.3.3Clock-Distribution Techniques10.3.4Latch-Based Clocking *10.4Self-Timed Circuit Design*10.4.1Self-Timed Logic - An Asynchronous Technique10.4.2Completion-Signal Generation10.4.3Self-Timed Signaling10.4.4Practical Examples of Self-Timed Logic10.5Synchronizers and Arbiters*10.5.1Synchronizers—Concept and Implementation10.5.2Arbiters10.6Clock Synthesis and Synchronization Using a Phase-Locked Loop10.6.1Basic Concept10.6.2Building Blocks of a PLL10.7Future Directions and Perspectives10.7.1Distributed Clocking Using DLLsDIGITAL INTEGRATED CIRCUITS810.7.2Optical Clock Distribution10.7.3Synchronous versus Asynchronous Design10.8Summary10.9To Probe FurtherDESIGN METHODOLOGY INSERT G: DESIGN VERIFICATIONCHAPTER 11: DESIGNING ARITHMETIC BUILDING BLOCKS11.1Introduction11.2Datapaths in Digital Processor Architectures11.3The Adder11.3.1The Binary Adder: Definitions11.3.2The Full Adder: Circuit Design Considerations11.3.3The Binary Adder: Logic Design Considerations11.4The Multiplier11.4.1The Multiplier: Definitions11.4.2Partial-Product Generation11.4.3Partial Product Accumulation11.4.4Final Addition11.4.5Multiplier Summary11.5The Shifter11.5.1Barrel Shifter11.5.2Logarithmic Shifter11.6Other Arithmetic Operators11.7Power and Speed Trade-off’s in Datapath Structures11.7.1Design Time Power-Reduction Techniques11.7.2Run-Time Power Management11.7.3Reducing the Power in Standby (or Sleep) Mode11.8Perspective: Design as a Trade-off11.9Summary11.10To Probe Further9Table Of ContentsCHAPTER 12: DESIGNING MEMORY AND ARRAY STRUCTURES12.1Introduction12.1.1Memory Classification12.1.2Memory Architectures and Building Blocks12.2The Memory Core12.2.1Read-Only Memories12.2.2Nonvolatile Read-Write Memories12.2.3Read-Write Memories (RAM)12.2.4Contents-Addressable or Associative Memory (CAM)12.3Memory Peripheral Circuitry12.3.1The Address Decoders12.3.2Sense Amplifiers12.3.3Voltage References12.3.4Drivers/Buffers12.3.5Timing and Control12.4Memory Reliability and Yield12.4.1Signal-To-Noise Ratio12.4.2Memory yield12.5Power Dissipation in Memories12.5.1Sources of Power Dissipation in Memories12.5.2Partitioning of the memory12.5.3Addressing the Active Power Dissipation12.5.4Data-retention dissipation12.5.5Summary12.6Case Studies in Memory Design12.6.1The Programmable Logic Array (PLA)12.6.2 A 4 Mbit SRAM12.6.3 A 1 Gbit NAND Flash Memory12.7Perspective: Semiconductor Memory Trends and Evolutions12.8Summary12.9To Probe FurtherDIGITAL INTEGRATED CIRCUITS10 DESIGN METHODOLOGY INSERT H: VALIDATION AND TEST OF MANUFACTURED CIRCUITSH.1IntroductionH.2Test ProcedureH.3Design for TestabilityH.3.1Issues in Design for TestabilityH.3.2Ad Hoc TestingH.3.3Scan-Based TestH.3.4Boundary-Scan DesignH.3.5Built-in Self-Test (BIST)H.4Test-Pattern GenerationH.4.1Fault ModelsH.4.2Automatic Test-Pattern Generation (ATPG)H.4.3Fault SimulationH.5To Probe FurtherINDEX。