当前位置：文档之家› 电磁场原理习题与解答(第2章)

电磁场原理习题与解答(第2章)

第二章习题答案

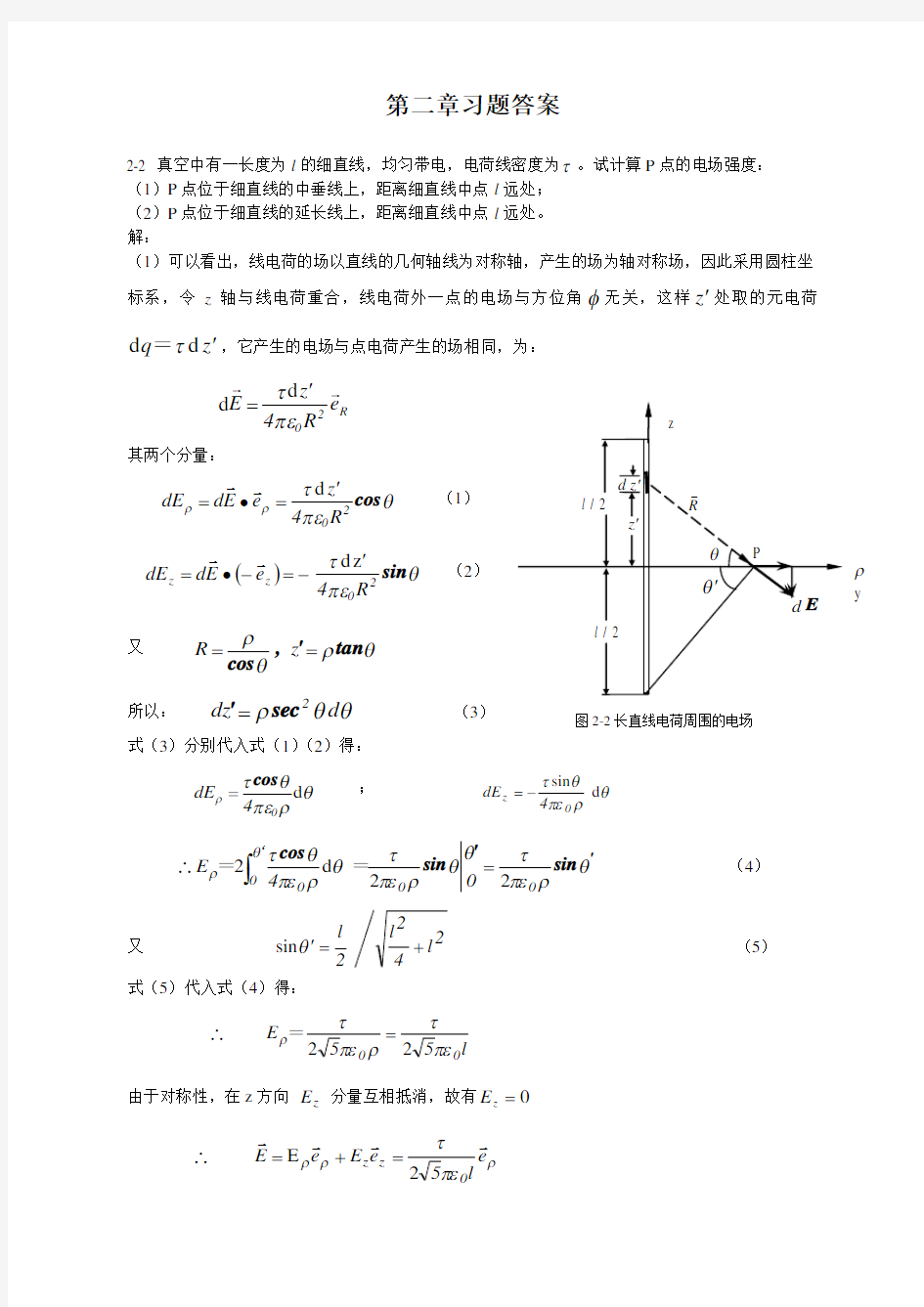
2-2 真空中有一长度为l 的细直线，均匀带电，电荷线密度为τ。试计算P 点的电场强度：（1）P 点位于细直线的中垂线上，距离细直线中点l 远处；（2）P 点位于细直线的延长线上，距离细直线中点l 远处。解：

（1）可以看出，线电荷的场以直线的几何轴线为对称轴，产生的场为轴对称场，因此采用圆柱坐标系，令z 轴与线电荷重合，线电荷外一点的电场与方位角φ无关，这样z '处取的元电荷

z q 'd d τ＝，它产生的电场与点电荷产生的场相同，为：

20e R

4z E πετ'=d d 其两个分量：

θπετρρcos 2

4z e E d dE '

=?=d （1） ()θπετsin 2

0z z R

4e E d dE z d '-=-?=

（2）又

θρθ

tan ',cos ==

z R

所以：

θθρd dz 2sec '= （3）

式（3）分别代入式（1）（2）得：

θρ

πεθ

τρd 04dE cos =

； θρπεθτd sin 0z 4dE -

= 'sin 'sin cos θρ

πετ

θθρπετθρ

πεθ

θρ000

004E 22d 2=?

∴＝

＝‘ （4）

又 2l 4

2l 2

l +='θsin （5）

式（5）代入式（4）得：

55E 00πετρπετρ22=∴

＝

由于对称性，在z 方向 z E 分量互相抵消，故有0=z E

ρρρπετ

e l

5e E e E 0z z 2E =

+=∴

d ρ

l / 2

z d '

图2-2长直线电荷周围的电场

l / 2

θ R

z '

θ'

（2）建立如图所示的坐标系

在x 处取元电荷dx dq τ=则它在P 点产生的电场强度为

20e R

4x d E d πετ'=

其在x 方向的分量为：

0x R 4x d dE πετ'

又 x l R -=

0x x l 4x d R

4x d dE )

-(''

∴

πετπετ

()l 3x l 4x l 4x d E 02

l 2

l 020x πετ

πετπετ='-?=''

--?

∴∴

∴////1)-( x 0x x x e l

3e E E

πετ=

=∴

2-3 真空中有一密度为m C n /2π的无限长线电荷沿y 轴放置，另有密度分别为2/1.0m C n 和2/1.0m C n -的无限大带电平面分别位于z=3m 和z=-4m 处。试求p 点（1，-7，2）的电场强度E 。

解：m z 3=和m z 4-=的带电平面产生的电场为()()

???

??>-<<<--=340341

.001或z z e E z ε

沿y 轴放置的线电荷产生的电场为

(

)(

)

m nV e z e x z x e z x z

e z x x y x E z x z x /111222202

222220

2++=???? ??++++=

επεπ

所以，p 点（1，-7，2）的电场强度为

()

V e e e e e E E E z x z x z /88.3359.2224

.000

1+=+++

=+=εε

应用叠加原理计算电场强度时，要注意是矢量的叠加。

2-4 真空中的两电荷的量值以及它们的位置是已知的，如题图2-4所示，试写出电位),θ?r （和电

场),(θr E

的表达式。

解：为子午面场，对称轴为极轴，因此选球坐标系，由点电荷产生的电位公式得：

y d x '

x '

021

0121r 4q r 4q p πεπε???+

+=)(

又 2

1)c o s 2(θrc c r r -+= ， 212

cos 2(θrd d r r -+=

()()θθθθθθe c e c r e c e c e r c r r r r r 1 sin cos sin cos +-=--=-=

()()θθθθθθe d e d r e d e d e r d r r r r r 2 sin cos sin cos +-=--=-=

2202

2201

0210121rc 2c r 4q rc 2c r 4q r 4q r 4q p )cos ()cos (θπεθπεπεπε???-++

-+=

+=∴)(

2301r 4r q r 4r q p E πεπε

+=11)( [][]??

????????-++-+-++-=23

22r 22322r 10rd 2d r e d e d r q rc 2c r e c e c r q 4)()()()(1θθθθθθπεθθcos sin cos cos sin cos

θθθθθπεθθθθπεe rc 2c r d q rc 2c r c q 41e rd 2d r d r q rc 2c r c r q 4123222232210r 23222232210 ????

????-++-++????

????-+-+-+-=)()

()()()()(cos sin cos sin cos cos cos cos

2-5解，

(1) 由静电感应的性质和电荷守恒原理，充电到U 0后将电源拆去，各极板带电情况如图（1）所示 03213

33U d

E d E d E U AB

=++=

E E E 0321===

301U

d E U U U DB CD AC ====

题图2-4

B C

+ - (1)

E 2E 3E +

+++

++++++--------------+

++++++-

----

--0σ+ 0σ-

()3

U U U U U DB CD CB BC -

=+-=-= C 、D 板无电荷

(2) 若将C 、D 板用导线联接，C 、D 两板的电荷将在电场作用下进行中和，一直到U CD =0，内侧正负电荷全部中和掉，其它部分的电荷由于电场的作用以及电荷守恒（这时电源已拆去）而都不变化，再断开联接线时也不会变化。电荷分布情况如图（2）所示。

02=E 0=CD U 3

301U

d E U U DB AC ===

320U U AB =；()300

U U U U DB

CB BC -=+-=-= 0

01εσ

=E ； d U 000εσ=

C 、

D 板有电荷

（3）由于在联接C 、D 板时有电源，电源的作用将强迫A 、B 板间的电压U AB =U 0；C 、D

板被短接强迫U CD =0，为满足U AB =U 0的条件，显然必须使3

1E E ',增大到31E E '',，也即相应的电荷密度应增大，如图（3）所示。由于电场力的作用，依次拆去电源与C 、D

板间联线时，情况不再变化。

='E 03133U d

E d E ='+' ； d

U E E 23031='=' 2

301U

d E U U DB AC ='==

0=CD U

()2

U U U U DB CB BC -

=+-=-= C 、D 板有电荷

（4）若在继（2）之后将A 、B 板短接，则A 、B 板成为一常电位系统，由于在（2）的情

况下，03

≠=

U U AB ，因此电荷将进行中和来达到0=AB U 的强制条件。而C 、D 板与外界没有导线联接，各自板上的总电荷保持不变，但会在内外两侧间发生电荷转移。达到0=AB U 后，一切电荷的转移都将停止，电荷分布如图（4）所示。

0σ+ 0σ- +

++++++-----

--+

++++++-

----

-A B C D +

- (2)

1E 02=E 3E A

C D 1E ''2

E ''3E ''+

++++

+++-----

---

+++-

--2σ-2

σ+A

- (3)

1E '02='E 3E '+

++++++

++++++-

-------

----

0131

εσ=''=''E E ， 0

εσ

=''E ()02

1=''+''+''=d

E E E U AB d U 00021εσσσ==+ 解得

d U E E 3031

=''='' d U E E 322012-=''-='' 9301U d E U U DB AC ='

'== ，923

U d

E U CB -=''=

2-6 半径为b 的无限长圆柱中，有体密度为0ρ的电荷，与它偏轴地放有一半径为a 的无限长圆柱空洞，两者轴线平行且距离为d ，如图2-6所示，求空洞内的电场强度。

解：由于空洞存在，电荷分布不具有对称性，由此产生的场亦无对称性，因此不能用高斯定律求解。这是可把空洞看作也充满0ρ，使圆柱体内无空洞，然后再令空洞中充满-ρ，并单独作用，分

别求出两种场的分布后叠加即可。设空洞内的电场强度为E

。

第一步 0ρ 单独作用，如图（b ）所示，由体密度为0ρ的电荷产生的电场强度为1E

，由高斯定

理

l l E q S D 200ρπρπρε=?

2d 11

S 11

＝

所以： ρερρe 2E 0

b ρ

(b )

0ρ

o ' y '

ρ'

( c)

图2-6

(a )

0ρ-

第二步 0ρ-单独作用产生的电场强度为2E

，如图（c ）所示。

l l E q S D 200ρπρρπε'-='???

2d 22

S 22

＝

ρερρ''-=e E 0

022

第三步将0ρ和0ρ-在空洞中产生的场进行叠加，即

()x 0

001e 2d e e 2E E E

ερρρερρρ='-'＝＋＝2 注：x e d d

=='-ρρ

2-7半径为 a 介电常数为ε的介质球内，已知极化强度 r e r

r P

k )(=（k 为常数）。试求：（1）极化电荷体密度p ρ和面密度p σ ；（2）自由电荷体密度ρ ；

（3）介质球内、外的电场强度E 。

解：(1) 2r r k e r k P -=???

??-?=-?=?? p ρ ， a

k r k e P a

r n =

===? p σ

（2）

因为是均匀介质，有

P E εE εD 0

+== 0

εεp E -=

∴

因此

P E εD 0

εεε-=

200r k

P D ?-=???

? ??-?=?=??εεεεεερ

(3) 球内电场，

()r 00

e r

εεk

εεp E

（ r < a ）

球外电场，由高斯定理：

=?a

r 4r k

dv q S d D πεεερ

ππ4a

k r 4D 0

εεε-=?

r 20e r a k D εεε-=

∴

， ()r 2

000e r

a k D E

εεεεε-== （ r > a ）或 0

p V

p 0p S

dV dV q q S d E ερ

εσρ

ρε???

+=?

2-8 具有两层同轴介质的圆柱形电容器，内导体的直径为2cm ，内层介质的相对介电常数31=r ε，外层的相对介电常数22=r ε，要使两层介质中的最大场强相等，并且内层介质所承受的电压和外层介质相等，问两层介质的厚度各为多少？

解：以圆柱心为坐标原点，径向为ρ轴，设单位长度上带电荷为τ，由高斯定理

l lD s d D ?==?→→?τπρ2，()312R R e D ≤≤=→→ρπρτ

ρ。()2100111

12R R e D D E r r ≤===≤→

→

→→

ρρεπετεεερ

()12002222

2R R e D

E r r ≤≤===→→

→

ρρεπετεεερ，ρεπετ→→=e R E r 10max 112，ρεπετ

→→=e R E r 20max 22

max 2max 11,2,3,121→

→====E E cm R r r εε cm R 5.12=∴

将电位参考点设在外导体上，即,0|3==R ρ? 则()32322ln 22

R R R e d E r R ≤≤=

???

??=?→

→

ρρπετρ?ρ

ρ ()3223221212ln 2ln 2|223

R R R R R e d E e d E R R

R ≤≤+=

+??? ??

=??? ?

?==→

→→→

??ρπετρπετ?ρρ?ρρρρρ， 3

221||||2211R R R R ====-=-ρρρρ???? ，

0ln 2ln 2ln 2ln 21

32232232121-=-+∴

R R

R R R R R R πετπετπετπετ 即 cm R 96.15.13/53==，所以，内cm R R 5.012=-，外cm R R 46.023=-

2-9 用双层电介质制成的同轴电缆如题图2-9所示，介电常数 014εε= , 022εε= 内、外导体

单位长度上所带电荷分别为τ和τ-

（1）求两种电介质中以及1R <ρ 和3R >ρ处的电场强度与电通密度；（2）求两种电介质中的电极化强度；（3）问何处有极化电荷，并求其密度。解：

(1)由高斯定理可得：

???

????><<<=)

R ()R (R π2)R (3311ρρρτρρ

0e 0D

电场强度 εD E =，故 ?????

????

?><<=<<=<=)

R ()R (R 4π2π)

R (R 8π2π)R (E 3320221011ρρρετρετρρ

ετρετρρρρρ

e e e 0

(2) 由 P E εD 0

+= ，得两种电介质中的电极化强度为

??????

?<<<<=-=)

R (R 4π)

R (R 8π33221ρρ

τρρ

τερρ

e e E D P 0

(3) 内、外导体圆柱表面上和两种电介质交界面上有极化电荷，它们分别是：

在1R =ρ处：

p π83)(R e P τσρ-=

-=?

在3R =ρ处： 3

R e P 4πp τ

σρ=

在2R =ρ处：:

21p π84ππ83)(R R R e P e P τ

τσρρ=

-+=??

2-10 有三块相互平行、面积均为S 的薄导体平板，A 、B 板间是厚度为d 的空气层，B 、C 板间则是厚度为d 的两层介质，它们的介电常数分别为1ε 和2ε，如题2-10所示。设A 、C 两板接地，B 板的电荷为Q ，忽略边缘效应，试求：（1）板间三区域内的电场强度；

（2）两介质交界面上的极化电荷面密度；（3） A 、C 板各自的自由电荷面密度。

解 (1) 在A 、C 板间的三介质区域内，分别为均匀电场，在Q 为正电荷时各电场方向如图所示，从而有

012001111

22E d E d E d

E s E s Q E E

εεεε=+??

+=??=?

从而解得

图2-9

A B

2n e 1n e

2ε

1ε

0ε

题图2-10

0221120010212010212010212()()()()

Q Q Q

E E E s s s εεεεεεεεεεεεεεεεεεεεεε+=

++++++及及（2）在两介质分界面上

()()[]

()()()

2120102101201

n 2

021012n 21n 1p

2p 1p S Q

E E e E D E D e P e P εεεεεεεεεεεεσσσ++-=

-=---=+=+=???

（3）在A 、C 板上的电荷面密度分别为 012120022010212010212()()()

A C Q Q

E E s s εεεεεσεσεεεεεεεεεεεεε-+-=-=

=-=

++++及

2-12 如题图2-12所示球形电容器中，对半地填充有介电常数分别为1ε和2ε两种均匀介质，两介质交界面是以球心为中心的圆环面。在内、外导体间施加电压U 时，试求：（1）电容器中的电位函数和电场强度；（2）内导体两部分表面上的自由电荷密度。解：（1）方法一：设内导体带电荷为Q ，外导体带电荷Q -，选球坐标，应用高斯定律

Q s d D S

由媒质分界面条件可知，在两种介质中2121D D E E

≠=,，所以

()Q s d E s d E s d E s d D s d D S S S S S =+=+=+?

?????1

21221121

εεεε

()Q E r =+212

π2εε ()

r e r Q

212π2εε+=

∴

（1）

令外导体为参考导体，则电位函数为

()

()???? ??-+=

+==?

??22121211ππ2222R r Q

r d r Q

l d E R r

R r

εεεε? （2） ()

()???

? ??-+=

??212121211ππ222

R R Q

r d r Q

l d E U R R R R εεεε

()

22121π2R R R UR Q

-=+∴

εε

将上式带入（1）（2）得

r 21221e r

1R R R UR E -=∴

， ?

??--=21221R 1r 1R R R UR ?

题图2-12

方法二：用静电场的边值问题求解，在均匀介质1和介质2中，电位分别满足拉普拉斯方程，并且边界面条件相同，所以可判断两个区域的电位函数相同，有

?===?==0

U 021R r R r 2???;

取球坐标系有

r r r

r r

r 12

2=??+

????

????=

?φ

θθ

?θ

θ??sin 1

)(sin sin 1

)(2

在两种介质中，?都与θ、φ无关，所以

r r r 12

2=????=

?)(2

上式的通解为 21c r

c +-

有边界条件解得： 1c ＝

2121R R U R R - 2c ＝2

12R R U

R -

所以 ???

? ??--=21221R 1r 1R R R UR ? ，r

21221e r

1R R R UR E

-=?-=? (2) 两种介质中的电位移矢量分别为

111E D ε=' ， 222E D

ε='

根据分界面条件 ()

12n D D e

-=?σ

对于本题，设媒质2为介质，媒质1为导体，因此有0D 1=

， n 2e D ?=σ

则内导体两部分表面上的自由电荷密度为

1n 111R R UR e R E -=

=?εεσ

)( ，

2n 122R R UR e R E -=

=?εεσ

)(

2-15 有三个同心导体球壳的半径分别是()321321,a a a a a a <<和，导体球壳之间是真空。已知球

壳2上的电量为q ，内球壳1与外球壳3均接地。求：（1）球壳2与内、外球壳之间的电场和电位分布

（2）内球壳1的外表面与外球壳3的内平面上的电荷面密度21σσ和。

解：内球壳外表面电荷密度为1σ，外球壳内表面电荷密度2σ。由高斯定律q s d D =?→

→?

得：

当

1a r a <<时，

→→

→→→

→

→===

∴=?

e r a D E e r

D a s d D r s 2

021101

121

11,41

εσεσπσ

()2

012122

112321011202111144,42

r q a D q a s d D a r a r a r a dr r a l d E s

a r a r πεσππσεσεσ?+=+=?<<-===→

→→→

→

???时，，当，()r a r a q

a dr r q a l d E a r

a r -+=+==??→

→

3012

120121223

34444πεσππεσπ?，又当2a r =时，21??=，即()()

232

3012

121201

144a a a a q a a a a a -+=-πεσπεσ 解得：()()

13212314a a a a q a a ---=πσ

在3a r =处，22σ=?→

→

p e n ()()2332122

12444a a a a q a a a a ---=-=∴ππσπσ 2-17 在半径分别为a 和b （b>a ）的同轴长圆柱形导体之间，充满密度为0ρ的空间电荷，且内、外筒形导体之间的电压为U ，如题图2-16所示。试用边值问题的方法求电荷区内的电位函数。解：圆柱形导体之间的电位满足泊松方程，对应的边值问题为

???????==-=?==0

U b a 02

ρρ??ερ?; 在圆柱形坐标中电位仅是ρ的函数，因此泊松方程有如下形式：

ερ

ρ?ρρρ?0-=???

? ???????12＝

上式的通解为

212

0c c 4++-=ρε

ρρ?ln

由给定的边界条件确定积分常数：

b U

a b c ln 4)

2201--=

ερ ， 0

200

22024ln ln ]4)([ερερb a

b b

U a b c +---

= 所以：02002200

2200

04b a

b b U 4a b a

b U

4a b 4ερερρερερρ?+????

??-----+-=ln ln ln ln )()

(

2-19 两平行导体平板，相距为d ，板的尺寸远大于d ，一板的电位为零，另一板电位为0V ，两板

题图2-16

间充满电荷，电荷体密度与距离成正比，即x x 0)(ρρ=。试求两板间的电位分布（注：x ＝0处板的电位为零）。

解：两平行导体平板间的电位满足泊松方程，忽略边缘效应，在直角坐标系对应的边值问题为

()??????

?==-=?==U

0x d x 0x 0

??ερ?;

上式泊松方程转化为：

002

2ερ?

x x

d d -= 其通解

210

06C x C x ++-=ερ?

由给定的边界条件确定积分常数：

0C 2= ， 0

0016ερd d U C +

= 所以：

x x d d x U )(6220

0-+=

ερ? 上式第一项为电源对电位函数的贡献，第二项为电荷)(x ρ的贡献。

2-20 在无限大接地导体平面两侧各有一点电荷1q 和2q ，与导体平面的距离为d ，求空间电位的分布。

解：因为是无限大接地导体，所以，当1q 单独作用时，接地导体对2q 相当于屏蔽作用，当2q 单独作用时，接地导体对1q 相当于屏蔽作用，所以：

1q 单独作用时产生的电位在1q 所在侧，设1r 和2r 分别为1q 和1q 的镜像到p 的距离，由镜像法得：

4442

011

011r r q r q r q -=

πεπεπε?＝

2q 单独作用时产生的电位在2q 所在侧，

设3r 和4r 分别为2q 和2q 的镜像到p 的距离，由镜像法得： )1

1(4444

3024

023

022r r q r q r q -=

πεπεπε?＝

)(x ρ

题图2-19

2-28 若将某对称的三芯电缆中三个导体相连，测得导体与铅皮间的电容为0.051F μ，若将电缆中的两导体与铅皮相连，它们与另一导体间的电容为0.037F μ，求：（1）电缆的各部分电容；（2）每一相的工作电容；

（3）若在导体1、2之间加直流电压100V ，求导体每单位长度的电荷量。解：三芯电缆的结构及各部分电容如图（a ）所示

（1）对应于两次测量的等值电容电路分别如图（b ）和图（c ）所示：

由图（b ）得：

051.030=C F μ，017.00=C F μ

由图（c ）得：

0370C C C 110.=++ F μ

01.0)017.0037.0(2

1=-?=

C F μ

图（a ）图（b ）

图（c ）图（d ）

图（e ）

（2）工作电容是指在一定的工作状态下的等值电容，在这里是指三相工作时一相的电容，等值

电容如图（d ）和（e ）所示：

所以，一相的工作电容为

047.03C 10=+=C C F μ

（3）若在导体1,2之间接一直流电压100V ，则从A, B 端看去的等效电容为：

0235.02

C ==C AB F μ

所以

35.21000235.0=?==AB AB AB U C q m C /μ

注：电缆是作为无限长来处理的，所以这里的电容均应理解为单位长度的电容。

2-31 一个由两只同心导电球壳构成的电容器，内球半径为a ，外球壳半径为b ，外球壳很薄，其厚度可略去不计，两球壳上所带电荷分别为+Q 和-Q ，均匀分布在球面上。求这个同心球型电容器的静电能量。

解：同心球形电容器的电容为： ()

a b ab

C -=

04πε

所以，同心球形电容器中的静电能量为

()ab

Q a b C Q W e 02

242121πε-=

2-32 空气中，相隔1cm 的两块平行导电平板充电到100V 后脱离电源，然后将一厚度为1mm 的绝缘导电片插入两极间，问：

（1）忽略边缘效应，导电片吸收了多少能量？这部分能量起到了什么作用？两板间的电压和电荷的改变量各为多少？最后存储在其中的能量多大？

（2）如果电压源一直与两平导电行板相连，重答前题。

解：设导电平板的面积为S 。两平行板间的间隔为d=1cm 。显然，绝缘导电片的厚度

mm d 110

δ。平板间的电压为V U 1000=。（1）忽略边缘效应，未插入绝缘导电片时 2002

000000002121,U d

S U C W U d S

U C q e εε==== 插入导电片后

00019

10910C d S d S C ==-=

εδε 002012110

2110921e e W C q C q W =??=?=

所以，导电片中吸收的能量为

J W W W e e e 701010425.410

-?==

- 这部分能量使绝缘导电片中的正、负电荷分离，在导电片进入极板间时，做机械工。

这是一常电荷系统，电荷守恒，各极板电荷量不变，0=?q 。而插入绝缘导电片后的电压为

V U C q C q U 9010

109010001==?== 所以电压的改变量为

V U U U 10001-=-=?

（2）如果电源一直连接着，则

000011001910910100,0q U C U C q V

U U U ==

====?

所以，电荷的改变量为

C q q q q 800110983.09

-?==-=? 而

020021119

102191021e e W U C U C W =?== 因此，导电片吸收的能量为

J W W W e e e 700110915.49

-?==

- 其作用同（1）。

2-33

解选取坐标系如图中所示。设液体上升的高度为h ，液面的面积为S （d ?a ），极板长度为l ，电场强度为

U E x 0

则静电能量密度为

22002

0e12121d U E w x εε== ， 22

02e22121d

U E w x εε==

静电能量为

()S z l d

U S z d U W -+=22

00e 2121εε

将两极板看作电容器，则电容为

()d

z l a d z a -+=εε0C 电容中储存的能量：

()

()S z l d

zS d U z l a d U z a d U U W -+=-+==22

022

002

0e 21212121C 21εεεε

空气与液体分界面上的电场力为：

ε, ρm

题 2-33 图 o

()S d

U W f const

u z 22

00e 21

εε-=??=

= ()z 2

0021

e f S d U εε-=

因为εε<0，所以静电力沿z 负方向，有将液体吸向空气的趋势。升高液体的重力为

()z m e f g S h g ρ=

由 g

f f = ()S h

g S d

U m 22

021ρεε=-? ()2

021gd U h m ρεε-=∴

电磁场理论习题及答案7.

习题： 1. 在3z m =的平面内，长度0.5l m =的导线沿x 轴方向排列。当该导线以速度 24x y m v e e s =+在磁感应强度22363x y z B e x z e e xz T =+-的磁场中移动时，求感应电动势。解：给定的磁场为恒定磁场，故导线中的感应电动势只能是导线在恒定磁场中移动时由洛仑兹力产生的。有 ()in v B dl ε=??? 根据已知条件，得 2233()|(24)(363)|z x y x y z z v B e e e x z e e xz ==?=+?+- 210854(1236)x y z e x e x e x =-++- x dl e dx = 故感应电动势为 0.5 20[10854(1236)]13.5in x y z x e x e x e x e dx V ε=-++-?=-? 2.长度为l 的细导体棒位于xy 平面内，其一端固定在坐标原点。当其在恒定磁场 0z B e B =中以角速度ω旋转时，求导体棒中的感应电动势。解：导体中的感应电动势是由洛仑兹力产生的，即 ()in v b dl ε=??? 根据已知条件，导体棒上任意半径r 处的速度为 v e r ωΦ= r dl e dr = 故感应电动势为 20000 1()()2 l l L in z r v b dl e r e B e dr B rdr B l V εωωωΦ=??=??==??? 3.试推出在线性、无耗、各向同性的非均匀媒质中的麦克斯韦方程。解：考察麦克斯韦方程中的参量，利用它们与电场强度E 和磁感应强度B 的

关系，将,,H B D E J E μεσ===代入即可，注意在非均匀媒质中,,μεσ是空间坐标的函数。考察麦克斯韦第一方程，有 11 ()B H B B μ μμ ??=?? =??+?? 2 1 1 B B μμ μ =- ??+?? D E J J t t ε ??=+=+?? 所以 E B B J t μμμε μ ?????=++ ? 而 ()D E E E εεερ??=??=??+??=，于是，微分形式的麦克斯韦方程用E 和B 表示为 E B B J t μμμε μ ?????=++ ? B E t ???=- ? 0B ??= E E εερ??+??= 对于无耗媒质，0σ=，因此有0J =。 4.试由麦克斯韦方程推导出电流连续性方程J t ρ???=-?。解：对麦克斯韦第一方程D H J t ???=+ ?两边取散度，得

电磁场与电磁波第二章课后答案

第二章静电场重点和难点电场强度及电场线等概念容易接受，重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程，即散度方程和旋度方程，并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。利用亥姆霍兹定理，直接导出真空中电场强度与电荷之间的关系。通过书中列举的4个例子，总结归纳出根据电荷分布计算电场强度的三种方法。至于媒质的介电特性，应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。讲解介质中静电场方程时，应强调电通密度仅与自由电荷有关。介绍边界条件时，应说明仅可依据积分形式的静电场方程，由于边界上场量不连续，因而微分形式的场方程不成立。关于静电场的能量与力，应总结出计算能量的三种方法，指出电场能量不符合迭加原理。介绍利用虚位移的概念计算电场力，常电荷系统和常电位系统，以及广义力和广义坐标等概念。至于电容和部分电容一节可以从简。重要公式真空中静电场方程：积分形式： ? = ?S S E 0 d εq ?=?l l E 0d 微分形式： ερ= ??E 0=??E 已知电荷分布求解电场强度： 1， )()(r r E ?-?=； ? ' '-'= V V d ) (41)(| r r |r r ρπε? 2， ? '''-'-'=V V 3 d |4) )(()(|r r r r r r E περ 3， ? = ?S S E 0 d εq 高斯定律

介质中静电场方程：积分形式： q S =?? d S D ?=?l l E 0d 微分形式： ρ=??D 0=??E 线性均匀各向同性介质中静电场方程：积分形式： ε q S = ?? d S E ?=?l l E 0d 微分形式： ε ρ= ??E 0=??E 静电场边界条件： 1， t t E E 21=。对于两种各向同性的线性介质，则 2 21 1εεt t D D = 2， s n n D D ρ=-12。在两种介质形成的边界上，则 n n D D 21= 对于两种各向同性的线性介质，则 n n E E 2211εε= 3，介质与导体的边界条件： 0=?E e n ； S n D e ρ=? 若导体周围是各向同性的线性介质，则 ε ρS n E = ； ε ρ? S n -=?? 静电场的能量：

电磁场复习题

《电磁场与电磁波基础》复习题一、填空题：（第一章）（第二章）（第三章）（第四章）（第五章）（第六章）（第一章） 1、直角坐标系下，微分线元表达式 z e y e x e l z y x d d d d ++= 面积元表达式 2、圆柱坐标系下，微分线元表达式z e e e l z d d d d ++=φρρφρ，面积元表达式z e l l e S z d d d d d φρρφρρ == z e l l e S z d d d d d ρφρφφ ==φρρφρd d d d d z z z e l l e S == 3、圆柱坐标系中，ρe 、e ? 随变量? 的变化关系分别是φρφ e e =??，ρφφe -e =?? 4、矢量的通量物理含义是矢量穿过曲面的矢量线的总和；散度的物理意义是矢量场中任意一点处通量对体积的变化率；散度与通量的关系是散度一个单位体积内通过的通量。 5、散度在直角坐标系 F z F y F x F V S d F F div Z Y X S V ??=??+??+??=??=?→?0lim 散度在圆柱坐标系 z F F F F div Z ??+??+??=φρρρρφρ1)(1 6、矢量微分算符（哈密顿算符）?在直角坐标系的表达式为 z z y y x x e e e ??+??+??=? 圆柱坐标系 z e z ??+??+??=? φρρφρe e 球坐标系分别 ? θθφθ??+??+??=?sin e e r e r r r 7、高斯散度定理数学表达式 ???=??V s S d F dV F ，本课程主要应用的两个方面分别是静电场的散度、恒定磁场的散度；

电磁场与电磁波课后习题及答案六章习题解答

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场 5cos mT z e t ω=B 之中，如题图所示。滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i. 解穿过导体回路abcda 的磁通为 5cos 0.2(0.7) cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==?=?-=--=+?g g B S e e 故感应电流为 11 0.35sin (12cos ) 1.75sin (12cos )mA in d i R R dt t t t t R ωωωωωωΦ = =-=-+-+E 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。解介质棒内距轴线距离为r 处的感应电场为 00 z r r r B φωω=?=?=E v B e e B e 故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X 极化电荷体密度为 200 00 11()()2()P rP r B r r r r B ρεεωεεω?? =-??=- =--??=--P 极化电荷面密度为 0000()()P r r r a e r a B σεεωεεω==?=-?=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为 220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=??=--=??=- 平行双线传输线与一矩形回路共面，如题图所示。设0.2a m =、0.1m b c d ===、7 1.0cos(210)A i t π=?，求回路中的感应电动势。

电磁场与微波技术(第2版)黄玉兰-习题答案

) 第一章证： 941(6)(6)50=0 A B A B A B A B =?+?-+-?=∴?∴和相互垂直和相互平行（1） 2 222 0.5 0.50.5 2222 0.5 0.5 0.5 2272(2)(2272)1 24 s Ax Ay Az A divA x y z x x y x y z Ads Ad dz dy x x y x y z dz ττ---????==++ ???=++=?=++=??? ??由高斯散度定理有 ?

（1）因为闭合路径在xoy 平面内，故有： 222()()8(2) (22)()2()8 x y z x y x z x s A dl e x e x e y z e dx e dy xdx x dy A dl S XOY A ds e yz e x e dxdy xdxdy A ds → →→ → ?=+++=+∴?=??=+=??=∴??因为在面内，所以，定理成立。。 (1) 由梯度公式

(2,1,3) |410410x y z x y z x y z u u u u e e e x y z e e e e e e ????=++???=++=++1 方向：（）（2）最小值为0，与梯度垂直证明 00u A ???=??= 书上p10 ，第二章

3343 sin 3sin 4q a V e wr qwr J V e a ρρ ρπθ θ ρπ= ==?=

''222 2' 30 222 ,40 =l l l dl d R Er R ez z ea a ez z ea a Er r z z a P ez z ea a E d z a ea π ρρα?ρα?πε===--= = +-=+? 用圆柱坐标系进行求解场点坐标为P(0,0,z).线电荷元可以视为点电荷，其到场点的距离矢量得所以点的电场强度为（）2' ' '0 3222 cos sin 0 20 l z ex ey ea d z E e z a π ???ραε+∴=∴=+?（）。 -

电磁场原理习题与解答

第五章习题答案 2sin ()2a vt a B dS N a k vt +-=+-? 5-2 如题图所示，一半径为a 的金属圆盘，在垂直方向的均匀磁场B 中以等角速度ω旋转，其轴线与磁场平行。在轴与圆盘边缘上分别接有一对电刷。这一装置称为法拉第发电机。试证明两电刷之间的电压为2 2ω Ba 。证明：，选圆柱坐标， ρφe vB e B e v B v E z ind =?= ?= 其中 φρωe v = 2 2 ω ρρωρερ ρa B d B e d e v B l d E a a l ind === =?? ???∴ 证毕 5-4 一同轴圆柱形电容器，其内、外半径分别为cm r 11=、cm r 42=，长度cm l 5.0=，极板间介质的介电常数为04ε，极板间接交流电源，电压为V t 10026000u πsin =。求 s t 0.1=时极板间任意点的位移电流密度。解法一：因电源频率较低，为缓变电磁场，可用求静电场方法求解。忽略边沿效应，电容器中的场为均匀场，选用圆柱坐标，设单位长度上内导体的电荷为τ，外导体电荷为τ-，因题图5-2 z v ρ

此有 ρρ πετe 2E 0 = 21r r <<ρ 1 200222 1 2 1 r r d dl E u r r r r ln πετρρπετ== = ? ? ? 1 202r r u ln =∴ πετ 所以 ρρe r r u E 1 2 ln = ， ρρ εe r r u D 1 2 ln = 2A/m ρ ρππρ ε ρ ε e t 10010026000r r e t u r r t D J 1 21 2d cos ln ln ?=??= ??= 当s t 1=时 2 5 12A/m 10 816100100260004108584ρρ ρ π πρ e e J d --?=????=.cos ln . 解法二：用边值问题求解，即 ?? ? ??=====?4 01u 02ρ?ρ?? 由圆柱坐标系有 0)(1=????ρ ? ρρρ (1) 解式(1)得 21ln c c +=ρ? 由边界条件得： 4 u c 1ln - = u c 2= u 4 u +- =∴ ρ?ln ln 所以 ρρπ?e 4 t 10026000E ln sin = -?=

电磁场理论习题及答案1

一． 1.对于矢量A u v，若A u v＝ e u u v x A＋y e u u v y A＋z e u u v z A， x 则： e u u v?x e u u v＝；z e u u v?z e u u v＝； y e u u v?x e u u v＝；x e u u v?x e u u v＝ z 2.对于某一矢量A u v，它的散度定义式为；用哈密顿算子表示为 3.对于矢量A u v，写出：高斯定理斯托克斯定理 4.真空中静电场的两个基本方程的微分形式为和 5.分析恒定磁场时，在无界真空中，两个基本场变量之间的关系为，通常称它为二.判断：（共20分，每空2分）正确的在括号中打“√”，错误的打“×”。 1.描绘物理状态空间分布的标量函数和矢量函数，在时间为一定值的情况下，它们是唯一的。（） 2.标量场的梯度运算和矢量场的旋度运算都是矢量。（） 3.梯度的方向是等值面的切线方向。（） 4.恒定电流场是一个无散度场。（） 5.一般说来，电场和磁场是共存于同一空间的，但在静止和恒定的情况下，电场和磁场可以独立进行分析。（） 6.静电场和恒定磁场都是矢量场，在本质上也是相同的。（）

7.研究物质空间内的电场时，仅用电场强度一个场变量不能完全反映物质内发生的静电现象。（） 8.泊松方程和拉普拉斯方程都适用于有源区域。（） 9.静电场的边值问题，在每一类的边界条件下，泊松方程或拉普拉斯方程的解都是唯一的。（） 10.物质被磁化问题和磁化物质产生的宏观磁效应问题是不相关的两方面问题。（）三.简答：（共30分，每小题5分） 1.用数学式说明梯无旋。 2.写出标量场的方向导数表达式并说明其涵义。 3.说明真空中电场强度和库仑定律。 4.实际边值问题的边界条件分为哪几类？ 5.写出磁通连续性方程的积分形式和微分形式。 6.写出在恒定磁场中，不同介质交界面上的边界条件。四.计算：（共10分）半径分别为a,b(a>b),球心距为c(c

《电磁场与电磁波》(陈抗生)习题解答选

《电磁场与电磁波》（陈抗生）习题解答第一章引言——波与矢量分析 1．1 .,,/)102102cos(1026300p y v k f E m V x t y y E E 相速度相位常数度，频率波的传播方向，波的幅的方向，，求矢量设 --?+?==ππ 解：m /V )x 102t 102cos(10y y E z E y E x E E 26300y 0z 0y 0x --?π+?π==++= ∴ 矢量E 的方向是沿Y 轴方向，波的传播方向是-x 方向；波的幅度 m /V 10E E 3y -== 。s /m 10102102k V ;102k ;MHZ 1HZ 1021022f 82 6P 266 =?π?π=ω=?π===π?π=πω=-- 1．2 写出下列时谐变量的复数表示（如果可能的话） )6sin()3sin()()6(cos 1)()5()2120cos(6)()4(cos 2sin 3)()3(sin 8)()2() 4cos(6)()1(πωπωωππωωωπ ω++ =-=- =-=-=+=t t t U t t D t t C t t t A t t I t t V （1）解： 4/)z (v π=? j 23234 sin j 64cos 6e 6V 4j +=π+π==π∴ （2）解：)2t cos(8)t (I π-ω-= 2 )z (v π-=? j 8e 8I j 2=-= π-∴

（3）解：） t cos 132 t sin 133 (13)t (A ω-ω= j 32e 13A 2)z ()2t cos(13)t (A 133cos )2(j v --==π-θ=?∴π-θ+ω== θπ-θ则则令（4）解：)2 t 120cos(6)t (C π-π= j 6e 6C 2j -==∴π (5)(6)两个分量频率不同，不可用复数表示 1．3由以下复数写出相应的时谐变量] )8.0exp(4)2 exp(3)3() 8.0exp(4)2(1)1(j j C j C j C +==+=π （1）解： t sin t cos j t sin j t cos )t sin j t )(cos j 1(e )j 1(t j ω-ω+ω+ω=ω+ω+=+ω t sin t cos )Ce (RE )t (C t j ω-ω==∴ω （2）解：)8.0t cos(4)e e 4(RE )Ce (RE )t (C t j 8.0j t j +ω===ωω （3）解：)8.0t (j )2t (j t j 8.0j j t j e 4e 3e )e 4e 3(Ce 2+ωπ+ωωω+=+=π 得：)t cos(3)8.0t cos(4)8.0t cos(4)2 t cos(3)Ce (RE )t (C t j ω-+ω=+ω+π+ω==ω 1．4 ] Re[,)21(,)21(000000**????++--=+++=B A B A B A B A z j y j x B z j y j x A ，，，求：假定解：1B A B A B A B A z z y y x x -=++=?

《电磁场与电磁波》经典例题

一、选择题 1、以下关于时变电磁场的叙述中，正确的是（） A 、电场是无旋场 B 、电场和磁场相互激发 C 、电场与磁场无关 2、区域V 全部用非导电媒质填充，当此区域中的电磁场能量减少时，一定是（） A 、能量流出了区域 B 、能量在区域中被消耗 C 、电磁场做了功 D 、同时选择A 、C 3、两个载流线圈之间存在互感，对互感没有影响的的是（） A 、线圈的尺寸 B 、两个线圈的相对位置 C 、线圈上的电流 D 、空间介质 4、导电介质中的恒定电场E 满足（） A 、0??=E B 、0??=E C 、??=E J 5、用镜像法求解电场边值问题时，判断镜像电荷的选取是否正确的根据是（） A 、镜像电荷是否对称 B 、电位方程和边界条件不改变 C 、同时选择A 和B 6、在静电场中，电场强度表达式为3(32)()y x z cy ε=+--+x y z E e e e ，试确定常数 ε的值是（） A 、ε=2 B 、ε=3 C 、ε=4 7、若矢量A 为磁感应强度B 的磁矢位，则下列表达式正确的是（） A 、=?B A B 、=??B A C 、=??B A D 、2=?B A 8、空气（介电常数10εε=）与电介质（介电常数204εε=）的分界面是0z =平面，若已知空气中的电场强度124= +x z E e e 。则电介质中的电场强度应为（） A 、1216=+x z E e e B 、184=+x z E e e C 、12=+x z E e e 9、理想介质中的均匀平面波解是（） A 、TM 波 B 、TEM 波 C 、TE 波 10、以下关于导电媒质中传播的电磁波的叙述中，正确的是（） A 、不再是平面波 B 、电场和磁场不同相 C 、振幅不变 D 、以T E 波的形式传播二、填空 1、一个半径为α的导体球作为电极深埋地下，土壤的电导率为 σ，略去地面的影响，则电极的接地电阻R = 2、内外半径分别为a 、b 的无限长空心圆柱中均匀的分布着轴向电流I ，设空间离轴距离为()r r a <的某点处，B= 3、自由空间中，某移动天线发射的电磁波的磁场强度

电磁场理论习题及答案_百度文库

习题 5.1 设x 0的半空间充满磁导率为的均匀介质，x 0的半空间为真空，今有线电流沿z轴方向流动，求磁感应强度和磁化电流分布。 5.2 半径为a的无限长圆柱导体上有恒定电流J均匀分布于截面上，试解矢势A 的微分方程，设导体的磁导率为 0，导体外的磁导率为。 5.3 设无限长圆柱体内电流分布，J azrJ0(r a)求矢量磁位A和磁感应B。5.4载有电流的细导线，右侧为半径的半圆弧，上下导线相互平行，并近似为向左侧延伸至无穷远。试求圆弧中心点处的磁感应强度。 5.5 两根无限长直导线，布置于x 1,y 0处，并与z轴平行，分别通过电流I 及 I，求空间任意一点处的磁感应强度B。 5.6 半径的磁介质球，具有磁化强度为M az(Az2 B) 求磁化电流和磁荷。 5.7已知两个相互平行，相隔距离为d，共轴圆线圈，其中一个线圈的半径为 a(a d)，另一个线圈的半径为b，试求两线圈之间的互感系数。

5.8 两平行无限长直线电流I1和I2，相距为d，求每根导线单位长度受到的安培力Fm。 5.9 一个薄铁圆盘，半径为a，厚度为b b a ，如题5.9图所示。在平行于z轴方向均匀磁化，磁化强度为M。试求沿圆铁盘轴线上、铁盘内、外的磁感应强度和磁场强度。 5.10 均匀磁化的无限大导磁媒质的磁导率为，磁感应强度为B，若在该

媒质内有两个空腔，，空腔1形状为一薄盘，空腔2像一长针，腔内都充有空气。试求两空腔中心处磁场强度的比值。 5.11 两个无限大且平行的等磁位面D、N，相距h， mD 10A， mN 0。其间充以两种不同的导磁媒质，其磁导率分别为 1 0， 2 2 0，分界面与等磁位面垂直，求媒质分界面单位面积受力的大小和方向。题5.11图 5.12 长直导线附近有一矩形回路，回路与导线不共面，如题5.12图 a 所示。证明：直导线与矩形回路间的互感为 M 0aln2 R2b R2 C22 b2 R2 题5.12图 a 5.13 一环形螺线管的平均半径r0 15cm，其圆形截面的半径a 2cm，铁芯的相对磁导率 r 1400，环上绕N 1000匝线圈，通过电流I 0.7A。（1）计算螺线管的电感；（2）在铁芯上开一个l0 0.1cm的空气隙，再计算电感（假设开口后铁芯的 r不变）；（3）求空气隙和铁芯内的磁场能量的比值。 5.14 同轴线的内导体是半径为a的圆柱，外导体是半径为b的薄圆柱面，其厚度可忽略不计。内、外导体间充有磁导率分别为 1和 2两种不同的磁介质，如题5.14图所示。设同轴线中通过的电流为I，试求：（1）同轴线中单位长度所储存的磁场能量；（2）单位长度的自感。 5.15 已知一个平面电流回路在真空中产生的磁场强度为

(川理工)电磁场与电磁波重要例题习题解读

电磁场与电磁波易考简答题归纳 1、什么是均匀平面电磁波？答：平面波是指波阵面为平面的电磁波。均匀平面波是指波的电场→ E 和磁场→ H 只沿波的传播方向变化，而在波阵面内→ E 和→ H 的方向、振幅和相位不变的平面波。 2、电磁波有哪三种极化情况？简述其区别。答：（1）直线极化，同相位或相差 180；2）圆极化，同频率，同振幅，相位相差 90或 270；（3）椭圆极化，振幅相位任意。 3、试写出正弦电磁场的亥姆霍兹方程（即亥姆霍兹波动方程的复数形式），并说明意义。答：0 02222=+?=+?→ →→ → H k H E k E ，式中μεω22 =k 称为正弦电磁波的波数。意义：均匀平面电磁波在无界理想介质中传播时，电场和磁场的振幅不变，它们在时间上同相，在空间上互相垂直，并且电场、磁场、波的传播方向三者满足右手螺旋关系。电场和磁场的分量由媒质决定。 4、写出时变电磁场中麦克斯韦方程组的非限定微分形式，并简述其意义。答：????????? ??=??=????-=????+=??→→ → →→ →→ρ εμμ εE H t H E t E J H )4(0)3()2()1( 物理意义：A 、第一方程：时变电磁场中的安培环路定律。物理意义：磁场是由电流和时变的电场激励的。 B 、第二方程：法拉第电磁感应定律。物理意义：说明了时变的磁场激励电场的这一事实。 C 、第三方程：时变电场的磁通连续性方程。物理意义：说明了磁场是一个旋涡场。 D 、第四方程：高斯定律。物理意义：时变电磁场中的发散电场分量是由电荷激励的。 5、写出麦克斯韦方程组的微分形式或积分形式，并简述其意义。答：（1）微分形式（2）积分形式物理意义：同第4题。 6、写出达朗贝尔方程，即非齐次波动方程，简述其意义。答：→→ → -=??-?J t A A μμε222 ，ερμε-=?Φ?-Φ?→ →222t 物理意义：→ J 激励→ A ，源ρ激励Φ，时变源激励的时变电磁场在空间中以波动方式传播，是时变源的电场辐射过程。 7、写出齐次波动方程，简述其意义。答：0 222=??-?→ → t H H με，022 2=??-?→ → t E E με 物理意义：时变电磁场在无源空间中是以波动方式运动，故称时变电磁场为电磁波，且电磁波的传播速度为： με υ1= p 8、简述坡印廷定理，写出其数学表达式及其物理意义。答：（1）数学表达式：①积分形式：??? ++?? =?-→ →τττστεμd E d E H t S d S S 222)2 1 21(，其中，→ →→?=H E S ，称为坡印廷矢量。 ???????????=??=????-=????+=??→→ →→→ →→ρD B t B E t D J H )4(0)3()2()1( ????? ??????=?=????-=????+=???????→→→ →→→→→→→→→→q S d D l d B S d t B l d E S d t D J l d H S S S l s l )4(0)3()2()()1(

电磁场二章习题解答(精品文档)

第二章习题解答 2.1 一个平行板真空二极管内的电荷体密度为42004 9 U d x ρε--=- ，式中阴极板位于0x =，阳极板位于x d =，极间电压为0U 。如果040V U =、1cm d =、横截面210cm S =，求：（1）0x =和x d =区域内的总电荷量Q ；（2）2x d =和x d =区域内的总电荷量Q '。解（1） 4323 000 4 d ()d 9 d Q U d x S x τ ρτε--==-=?? 11004 4.7210C 3U S d ε--=-? （2） 432002 4d ()d 9d d Q U d x S x τρτε--' '= = -=? ?11004(10.9710C 3U S d ε--=-? 2.2 一个体密度为732.3210C m ρ-=?的质子束，通过1000V 的电压加速后形成等速的质子束，质子束内的电荷均匀分布，束直径为2mm ，束外没有电荷分布，试求电流密度和电流。解质子的质量271.710kg m -=?、电量191.610C q -=?。由 2 1 mv qU = 得 61.3710v ==? m 故 0.318J v ρ== 2A m 26(2)10I J d π-== A 2.3 一个半径为a 的球体内均匀分布总电荷量为Q 的电荷，球体以匀角速度ω绕一个直径旋转，求球内的电流密度。解以球心为坐标原点，转轴（一直径）为z 轴。设球内任一点P 的位置矢量为r ，且r 与z 轴的夹角为θ，则P 点的线速度为 sin r φωθ=?=v r e ω 球内的电荷体密度为 3 43 Q a ρπ= 故 33 3sin sin 434Q Q r r a a φ φω ρωθθππ===J v e e 2.4 一个半径为a 的导体球带总电荷量为Q ，同样以匀角速度ω绕一个直径旋转，求球表面的面电流密度。解以球心为坐标原点，转轴（一直径）为z 轴。设球面上任一点P 的位置矢量为r ，且r 与z 轴的夹角为θ，则P 点的线速度为 sin a φωθ=?=v r e ω 球面的上电荷面密度为 2 4Q a σπ= 故 2 sin sin 44S Q Q a a a φφω σωθθππ===J v e e 2.5 两点电荷18C q =位于z 轴上4z =处，24C q =-位于y 轴上4y =处，求(4,0,0)处的电场强度。

电磁场理论复习题(题库+答案)

第1~2章矢量分析宏观电磁现象的基本规律 1. 设：直角坐标系中，标量场zx yz xy u ++=的梯度为A ，则 A = ，=??A 0 。 2. 已知矢量场 xz e xy e z y e A z y x ?4?)(?2+++= ，则在M （1，1，1）处=??A 9 。 3. 亥姆霍兹定理指出，若唯一地确定一个矢量场（场量为A ），则必须同时给定该场矢量的旋度及散度。 4. 写出线性和各项同性介质中场量D 、E 、B 、H 、J 所满足的方程（结构方程）：。 5. 电流连续性方程的微分和积分形式分别为和。 6. 设理想导体的表面A 的电场强度为E 、磁场强度为B ，则（a ）E 、B 皆与A 垂直。（b ）E 与A 垂直，B 与A 平行。（c ）E 与A 平行，B 与A 垂直。（d ）E 、B 皆与A 平行。答案：b 7. 设自由真空区域电场强度(V/m) )sin(?0βz ωt E e E y -= ，其中0E 、ω、β 为常数。则空间位移电流密度d J （A/m 2）为：（a ） )cos(?0βz ωt E e y - （b ） )cos(?0βz ωt ωE e y - （c ） )cos(?00βz ωt E ωe y -ε （d ） )cos(?0βz ωt βE e y -- 答案：c 8. 已知无限大空间的相对介电常数为4=εr ，电场强度 )(?)(?)(?y x e z x e z y e z y x +++++A ??A ??E J H B E D σ=μ=ε= , ,t q S d J S ??-=?? t J ?ρ?-=??

电磁场习题解读

静电例1、三个点电荷q1、q2、q3沿一条直线分布，已知其中任一点电荷所受合力均为零，且 q1=q3=Q ，求在固定q1、q3的情况下，将q2从o →∞,外力需作功A=? 解：由已知q1所受静电力例2、有两个点电荷带电量为nq 和-q （n>1),相距d,证明电势为零的等势面为一球面。证明：空间任一点电势整理可得：上式为球面方程：球心坐标球面半径例3、点电荷-q 位于圆心处，A 、B 、C 、D 位于同一圆周上的四点如图示。将q0从A 移至B 、C 、D 点，电场力的功。 A=0 例4. 已知: 是闭合曲面的一部分，面内无净电荷电场线穿过该闭合面，穿过部分的电场通量1?Φ，求:通过其余部分的电场通量2?Φ。解：由高斯定理 ?∑=?=ΦS i i e q S d E 0 ε ，00=Φ∴=∑e i i q ，12120?Φ-=Φ∴=?Φ+Φ∴ 例5、长为L,线电荷密度λ的两根均匀带电细棒，沿同一直线放置，两棒近端相距 a ，求两棒间的静电力。 q 2 x o d n n 1 (22 - 、 0、0） 04)2(42 0322031=+=a q q a q q f πεπε4412Q q q -=-=∴e A A -=∴)0(2--=o U q a Q q 0242πε-=a Q 028πε =q nq U U U -+=2 220 2220)(44z y d x q z y x nq ++--+ ++=πεπε0 =令 222222)(z y d x q z y x nq ++-=++∴[] 2222222)(z y x z y d x n ++=++-22222221()1(-=++--n nd z y d n n x 1 2-= n nd R S ?S ?

电磁场与电磁波课后习题及答案--第四章习题解答

习题解答如题图所示为一长方形截面的导体槽，槽可视为无限长，其上有一块与槽相绝缘的盖板，槽的电位为零，上边盖板的电位为 U ，求槽内的电位函数。解根据题意，电位(,)x y ?满足的边界条件为 ① (0,)(,)0y a y ??== ② (,0)0x ?= ③ 0(,)x b U ?= 根据条件①和②，电位(,)x y ?的通解应取为 1 (,)sinh( )sin()n n n y n x x y A a a ππ?∞ ==∑ 由条件③，有 01 sinh( )sin()n n n b n x U A a a ππ∞ ==∑ 两边同乘以 sin( ) n x a π，并从0到a 对x 积分，得到 00 2sin()d sinh()a n U n x A x a n b a a ππ== ? 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ? =? ? ? = ?，故得到槽内的电位分布 1,3,5, 41(,)sinh()sin() sinh()n U n y n x x y n n b a a a ππ?π π== ∑ 两平行无限大导体平面，距离为b ，其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。上板和薄片保持电位 U ，下板保持零电位，求板间电位的解。设在薄片平面上，从0=y 到 d y =，电位线性变化，0(0,)y U y d ?=。 ~ a > 题图

解应用叠加原理，设板间的电位为 (,)x y ?=12(,)(,)x y x y ??+ 其中， 1(,)x y ?为不存在薄片的平行无限大导体平面间（电压为 U ）的电位，即 10(,)x y U y b ?=；2(,)x y ?是两个电位为零的平行导体板间有导体薄片时的电位，其边界条件为： ① 22(,0)(,)0x x b ??== ② 2(,)0() x y x ?=→∞ ③ 002100(0)(0,)(0,)(0,)() U U y y d b y y y U U y y d y b d b ????-≤≤??=-=? ?-≤≤?? # 根据条件①和②，可设2 (,)x y ?的通解为 21(,)sin()e n x b n n n y x y A b π π?∞ -==∑ 由条件③有 00100(0)sin()() n n U U y y d n y b A U U b y y d y b d b π∞ =? -≤≤??=??-≤≤??∑ 两边同乘以 sin( ) n y b π，并从0到b 对y 积分，得到 0002211(1)sin()d ()sin()d d b n d U U y n y n y A y y y b b b b d b b ππ=-+-=??022sin() ()U b n d n d b ππ 故得到 (,)x y ?=0022 121sin()sin()e n x b n U bU n d n y y b d n b b π πππ∞-=+∑ 求在上题的解中，除开0U y 一项外，其他所有项对电场总储能的贡献。并按 2 02U W C e f =定出边缘电容。解在导体板（0=y ）上，相应于 2(,)x y ?的电荷面密度题图

工程电磁场复习题

一填空题 1. 麦克斯韦方程组的微分形式是：、、和。 2. 静电场的基本方程为：、。 3. 恒定电场的基本方程为：、。 4. 恒定磁场的基本方程为：、。 5. 理想导体（媒质2）与空气（媒质1）分界面上，电磁场边界条件为：、、和。 6. 线性且各向同性媒质的本构关系方程是：、、。 7. 电流连续性方程的微分形式为：。 8. 引入电位函数?是根据静电场的特性。 9. 引入矢量磁位A ? 是根据磁场的特性。 10. 在两种不同电介质的分界面上，用电位函数?表示的边界条件为：、。 11. 电场强度E ?的单位是，电位移D ?的单位是；磁感应强度B ? 的单位是，磁场强度H ? 的单位是。 12. 静场问题中，E ?与?的微分关系为：，E ? 与?的积分关系为：。 13. 在自由空间中，点电荷产生的电场强度与其电荷量q 成比，与观察点到电荷所在点的距离平方成比。 14. XOY 平面是两种电介质的分界面，分界面上方电位移矢量为z y x e e e D ????0001255025εεε++= C/m 2 ，相对介电常数为2，分界面下方相对介电常数为5，则分界面下方z 方向电场强度为__________，分界面下方z 方向的电位移矢量为_______________。 15. 静电场中电场强度z y x e e e E ? ??? 432++=，则电位?沿122333 x y z l e e e = ++v v v v 的方向导数为_______________，点A （1，2，3）和B （2，2，3）之间的电位差AB U =__________________。 16. 两个电容器1C 和2C 各充以电荷1Q 和2Q ，且两电容器电压不相等，移去电源后将两电容器并联，总的电容器储存能量为，并联前后能量是否变化。 17. 一无限长矩形接地导体槽，在导体槽中心位置有一电位为U 的无限长圆柱导体，如图所示。由于对称性，矩形槽与圆柱导体所围区域内电场分布的计算可归结为图中边界1Γ、2Γ、3Γ、4Γ和5Γ所围区域Ω内的电场计算。则在边界_____________上满足第一类边界条件，在边界_____________上满足第二类边界条件。 18. 导体球壳内半径为a ，外半径为b ，球壳外距球心d 处有一点电荷q ，若导体球壳接地，则球壳内表面的感应电荷总量为____________，球壳外表面的感应电荷总量为____________。

文档之家

电磁场原理习题与解答(第2章)

电磁场理论习题及答案7.

电磁场与电磁波第二章课后答案

最新电磁场与微波技术(第2版)黄玉兰-习题答案资料

电磁场复习题

电磁场与电磁波课后习题及答案六章习题解答

电磁场与微波技术(第2版)黄玉兰-习题答案

电磁场原理习题与解答

电磁场理论习题及答案1

《电磁场与电磁波》(陈抗生)习题解答选

《电磁场与电磁波》经典例题

电磁场理论习题及答案_百度文库

(川理工)电磁场与电磁波重要例题习题解读

电磁场二章习题解答(精品文档)

电磁场理论复习题(题库+答案)

电磁场习题解读

电磁场与电磁波课后习题及答案--第四章习题解答

最新电磁学第二章习题答案

工程电磁场复习题