当前位置：文档之家 › 第2章 随机信号分析复习

第2章 随机信号分析复习

  • 格式：ppt
  • 大小：1.06 MB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

第二章随机信号分析2.3.2平稳随机过程的各态历经性

第二章随机信号分析2.3.2平稳随机过程的各态历经性

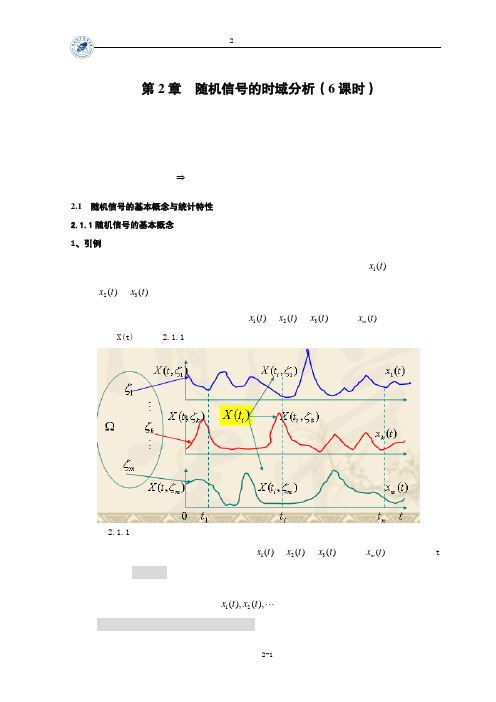
第二章随机信号分析2.3.2平稳随机过程的各态历经性
2.3.2 平稳随机过程的各态历经性( 遍历性)：
均值遍历过程
令：为的实现（样函数），其时间平均值为：
一般情况,不同样函数的时间平均值不一样, 是一个随机变量. 若的数学期望( 统计平均值) 与其样函数的时间平均值以概率为一相等, 即:;则称为均值遍历过程。

自相关遍历过程
样函数的时间平均自相关函数为:
若则称为自相关遍历过程。

若的均值和自相关均为遍历的，则称为宽遍历随机过程。

若的所有统计平均特性和其样函数所有相应的时间平均特性以概率为一相等, 则称为严遍历过程或窄义遍历过程. 本章仅限于研究宽遍历过程.如果不加特别说明,遍历过程即指宽遍历过程. 不难看出,遍历过程必定是平稳过程,但平稳过程不一定是遍历过程。

若是平稳高斯过程, 且；: 则是遍历过程. 对于遍历过程,只要根据其一个样函数,便可得到其数字特征。

随机信号分析第2章--随机信号

随机信号分析第2章--随机信号
18
例1.1 随机信号U(t)的一维概率密度函数为
f (u,t)
1
A0
exp
u2 A0
不同时刻的随机变量彼此统计独立，求其n维
概率密度函数。
解：t1,t2 ,,tn 时刻，随机变量 X (t1), X (t2 ),, X (tn ) 统计独立，则
f (u1, u2 ,, un;t1, t2 ,, tn ) f (u1;t1). f (u2;t2 ),, f (un;tn )
随机变量 0 与相位随机变量 ，以时间参量
t建立随机信号 W (t, s) Asin(0t )
，观察信号随参量t的各次过程，其样本函数 呈现出正弦函数规律。W (t) 称为正弦随机信 号。
无数个正弦样本函数组成了正弦随机信号，符合 定义2中对于随机信号的描述。
33
(1)均值
X (t) Esin(0t ) Esin 0t cos cos0t sin
12
基本概率特性
一、一维概率分布 随机信号 X (t) 在任意 t T 时刻的取值 X (t)
是一维随机变量。概率 PX (t) x 是取值 x ，时
刻 t 的函数，记做
F(x;t) PX (t) x
称为随机信号 X (t) 的一维概率分布函数。 若有F(x;t) 偏导数存在，则有
f (x;t) F(x;t) x
实随机变量 X (t) 与之对应，就称依赖于参量 t
的随机变量族X (t), t T 为实随机信号或随机
过程。
11
二、随机信号的分类 1.按时间参量来分类
时间连续的随机信号：时间t是连续的。 如：正弦随机信号，二进制传 输信号 时间离散的随机信号：时间t是离散的。 如：贝努里随机信号 2.按信号状态取值分类 取值连续的随机信号：X(t)值是连续的 如：正弦随机信号 取值离散的随机信号：X(t)值是离散的 如：贝努里随机信号，二进制传输信号 还有很多的分类方法

《随机信号分析基础》第2章 课件_随机信号时域分析

《随机信号分析基础》第2章 课件_随机信号时域分析

随机过程的一维统计特性具有普通随机变量的各种性质，区别在它们同时还是时间t 的函 数。“一维”只描述出随机过程在各个孤立时刻（任一时刻）的统计特性，没有反映各时刻之 间的内在联系 Þ 用“n 维”更为全面。 （2）二维分布
二维概率分布函数： X(t1)与 X(t2 ) ， FX (x1, x2;t1,t2 ) = FX (x1, x2 ) = P[X(t1) £ x1, X(t2 ) £ x2 ]
= E {X 2(t) - mX2 (t) - 2X(t)mX (t)} = E {X 2(t)} - mX2 (t)
【含义】 ① t2(t) ----随机信号在t 时刻取值相对于中心（均值）的偏离程度。 t(t)称为标准差。
② 若 X(t)为归一化阻抗下的电压或电流，则 E {X 2(t)}表示时刻t 上的瞬时总功率的统计平
若 n 阶偏导数存在，可有 n 维概率密度函数
fX (x1, x2,× × ×xn；t1,t2,× × ×tn )
=
¶FX (x1, x2,× × ×xn；t1,t2,× × ×tn ) ¶x1¶x2 × × × ¶xn
显然，n ­Þ 反映“内在联系”愈充分，也就越为完整地描述随机过程的全部统计特性。
2、定义 令随机试验的概率空间为 {W, F, P} ，若对于样本空间 W 中的任何一个样本点
xi Î W ，总有一个确知函数 xi = X(t, xi )，t Î T 与之对应，这样对于所有的 x Î W ，就可得 到一族关于t 的函数 X(t, x) ，称为随机信号。
族中的每一个函数称为该随机过程的样本函数。随机信号 X(t, x)常简记为 X(t)，对应的 样本函数简记为 x (t ) 。
2.1.3 随机过程的数字特征

第2章 随机信号的时域分析——fxm

第2章 随机信号的时域分析——fxm

mX (t ) E X (t ) xf X ( x; t )dx


图 2.1.4.1 随机信号的数学期望
【说明】 1
o
t T ，X(t)代表一随机变量，它的随机取值 x(t)(t 固定)，记为 X。
2o 由于 mX(t)是随机过程 X(t)的所有样本函数在 t 时刻所取的样本 x1 , x2 , , xn
第 2 章 随机信号的时域分析
第 2 章 随机信号的时域分析（6 课时）
在实际通信和信息系统中，将承载信息的、 随时间、 空间或其他几个参量变化的物理量 （如 声、光、电）抽象为信号，用确定时间函数来表示—确定信号。信号与系统等课程分析的就是 确定信号。而实际通信信号显然是不确定的，具有随机性，是随机信号。但正如前章所述，随 机并不意味着无规律，随机信号与随机变量一样，其特性服从某种统计规律，这就是本课程的 研究目的。 研究思路：统计规律用统计方法处理。因此完全可以借鉴随机变量的处理方法，但需要 考虑随机信号的时间函数特性！ 2.1 随机信号的基本概念与统计特性 2.1.1 随机信号的基本概念 1、引例 噪声电压——当对接收机的噪声电压作“单次”观察时，可以得到波形 x1 (t ) ，也可能得到 波形 x2 (t ) ， x3 (t ) 等等，每次观测的波形的具体形状，虽然事先不知道，但肯定为所有可能的 波形中的一个。而这些所有可能的波形集合 x1 (t ) ， x2 (t ) ， x3 (t ) ，…， xm (t ) ，…，就构成了 随机过程 X(t)。如图 2.1.1 所示。
图 2.1.1
噪声电压的起伏波形
说明：①样本函数：每次试验的结果： x1 (t ) ， x2 (t ) ， x3 (t ) ，…， xm (t ) ，都是时间 t

第二章 信号分析基础(随机信号和相关分析)090310

第二章 信号分析基础(随机信号和相关分析)090310

西安工业大学机电学院
2)互相关函数：
R xy ( ) lim
1 T 1 T
T

T
x ( t ) y ( t ) dt y ( t ) x ( t ) dt
0 T
或
R yx ( ) lim
T

0
x(t)
y(t)
西安工业大学机电学院
算法：令x(t)、y(t)二个信号之间产生时差τ，再相 乘和积分，就可以得到τ时刻二个信号的相关性。
0
正弦函数是一个零均值 一个周期内的平均值表 1 T0 T 0

T0
A sin( t ) sin[ ( t ) ] dt
2
0
2

, 令 t ＝ ，则 dt A
2
d

A
2
R xx ( )
2

2
sin sin( ) d
•集合平均：不是沿单个样本的时间轴进行，而是将集 合中所有样本函数对同一时刻ti的观测值取平均；（纵 向）
•时间平均：单个样本的时间历程进行平均；（横向）
西安工业大学机电学院
工程中很多随机信号具有各态历经性，由 于不可能观测足够多的样本函数来描述一 个随机过程，故工程中常以一个或几个有 限长度的样本记录来推断整个随机过程， 以时间平均来估计集合平均。这就使得信 号的分析处理简化了
围的面积为信号的平均
所以 S x ( ) 就是信号的功率谱密度
沿频率轴的分布，简称
西安工业大学机电学院
西安工业大学机电学院
西安工业大学机电学院
功率谱与传递函数、频率响应函数的关系
H ( ) S xy ( ) S x ( ) , S xy 输入输出互谱， S x 输入自谱

第二章随机信号分析基础习题

第二章随机信号分析基础习题

2.6
解:由图可得下表 ξ1 ξ2 ξ3
X(2) 3 X(6) 5
所以：
4 7
6 2
1 14 E[ X (6)] (5 7 2) ; 3 3 1 55 E[ X (2) X (6)] (3 5 4 7 6 2) ; 3 3
出现一个典型的错误：
1 13 E[ X (2)] (3 4 6) ; 3 3

2
0
cos( ot )d
由定义先求出均方值，就可以得到方差：
E[ X (t )] E[a cos (0t )] 2 1 cos(2 0 t 2 ) E[a ] 2 2 2 a a 2 cos(2 0t 2 )d 22 2 0 a 2
2.12 证明：
dX (t ) E[ X (t ) ] dt
X (t t ) X (t ) E[ X (t )lim ] t t 0
E[ X (t ) X (t t )] E[ X (t ) X (t )] lim t t 0
lim
t 0
RX (t , t t ) RX (t , t ) t
3、随机过程的数字特征 数学期望
m X (t ) E[ X (t )] x p X ( x; t )dx

2 X 2

2 ( t ) E [ X ( t )] x 均方值 p X ( x ; t )dx
2 2 ( t ) D [ X ( t )] E [{ X ( t ) m ( t )} ] 方差 X
第二章 随机信号概论
本章要点： 1、随机过程的概念 可理解为依赖于时间t的一族随机变量或 随机试验得到的一族时间t的函数。 2、随机过程的概率分布

2. 随机信号分析_随机信号的时域分析

X (t ) X (t1 ) 0 t1 X (t 2 ) t2 X (ti ) ti X (t n ) tn t
随机过程X(t)在任意n个时刻t1,t2,…,tn状态X(t1) ,X(t2) ,…,X(tn)构 成n维随机变量[ X(t1),X(t2),…,X(tn) ]，当t0,n ∞时的 n维随 机变量近似随机过程。因此，可以借用对n维随机变量的分析研 究来“替代”或“近似”对随机过程的分析研究。 一、随机过程的一维分布
E[ X (t )] x 2 f X ( x, t )dx
2

将t视为变量时，即为过程X (t)的均方值。 同理，过程X(t)的方差：
D[ X (t )] E{[ X (t ) mX (t )] } [ x mX (t )]2 f X ( x, t )dx X 2 (t )
t
确定信号——幅度、相位均随时间做 有规律的、已知的变化。可以用确定 的时间函数来描述。可以准确的与测 其未来的变化。 随机信号——幅度、相位均随时间做 无规律的、未知的、随机的变化。无 法用确定的时间函数来描述。无法准 确的与测其未来的变化。 t 但，随机信号的统计规律则是确定的。
因此，人们用统计学方法建立了随机信号的数学模型→随机过程。
整个时间段T上，任意两个时刻的状态的联合概率分布情况。
所以定义随机过程X(t) 二维分布函数：
FX ( x1 , x2 ; t1 , t 2 ) P{X (t1 ) x1 ; X (t 2 ) x2 }......... .........1 , t 2 T t
随机过程X(t) 二维概率密度：
§2.1
随机过程的基本概念
下面由一个试验实例来建立随机过程的概念。 举例： 在相同条件下，对同一雷达接收机的内部噪声电压（或电 流）经过大量的重复测试后，设观测 到的所有的可能结果有n种， 记录下n个不相同的波形。

随机信号分析第二章new


fo 0
2 fot
fo=2;
N=1000;
t=[-4.995:0.01:4.995];
F=fo*rand(N,1);
x=cos(2*pi*F*t);
plot(t,x);
xlabel('time, t');
ylabel('X(t)');
求解
X (t)
6
5
4
3
2
1
0
t1
1
1
X(t1) X(t2) Pi
1
5
1/4
2 2
2
4
1/4
3
6
2
1/4
3 4
3
1
1/4
4
t2
t
求解
RX (t1,t2 )
k1 k2 P{X (t1 ) k1, X (t2 ) k2}
k1, k2 X
k1 k2 Pi
i
1 (1 5 2 4 6 2 31) 7 4
相互正交
1. 若两个过程X (t)和Y (t)之间的互相关函数等于零，
则称X(t)和Y(t)之间相互正交
2. 随机过程X (t)的一维特征函数
X(u,t)=
-
pX(x;t)ejuxdx
E[exp( juX (t))]
同理可得二维、三维以至n维特征函数
随机序列及其统计特性
一个N点的随机序列可以看成是一个N维
FX(x1,x2,...,xn;t1,t2,...,tn ) =P{X(t1) x1,X(t2 ) x2,...,X(tn ) xn} pX(x1,x2,...,xn;t1,t2,...,tn ) = nFX(x1,x2,...,xn;t1,t2,...,tn )

第二章 信号分析基础(随机信号和相关分析)090310


西安工业大学机电学院
2.6 信号的
西安工业大学机电学院
R x ( ) 是实偶函数，故
S x ( ) 也是实偶函数
R x ( 0 ) lim
1 T
T
T

2 T 2
x ( t )dt
2



S x ( f )df 或
1 2



S x ( )d
功率， 功率谱
S x ( )曲线下面和频率轴所包
cos
0
2
∴Rxx(τ)不反映相位信息θ，只反映幅值。
西安工业大学机电学院
图例:
计算正弦波信号自相关函数，在τ＝0，π/2， π的自相关函数值情况
*

将不同时移τ的计算值标在图上，两点连 线，就可以得到信号的相关函数曲线。
*

*

西安工业大学机电学院
意义：
自相关函数是区别信号类型的一个非常有效的手段，
• 只要信号中有周期成分，自相关函数τ很大时都不衰减，带
有明显周 期性；
• 信号中不包含周期成分的随机信号，当τ稍大时，自相关函 数都趋于0 见书图2－27 正弦波：周期信号，自相关函数也为周期函数；
正弦波加随机噪声：自相关函数在τ很大时都不衰减；
宽带随机噪声：自相关函数很快衰减为零； 窄带随机噪声：自相关函数有较慢的衰减特性。
围的面积为信号的平均
所以 S x ( ) 就是信号的功率谱密度
沿频率轴的分布，简称
西安工业大学机电学院
西安工业大学机电学院
西安工业大学机电学院
功率谱与传递函数、频率响应函数的关系
H ( ) S xy ( ) S x ( ) , S xy 输入输出互谱， S x 输入自谱

通信原理与技术第2章-随机信号分析

第2章 随机信号分析本章教学要求：1、掌握平稳随机过程的概念和性质、高斯白噪声的性质。

2、理解高斯过程和窄带随机过程的基本内容，随机过程通过线性系统的基本描述。

3、了解随机变量和随机过程的概念及数学描述。

4、了解噪声的分类和特点。

§2.1 随机变量及其数学描述一、概率论的基本概念1．随机现象：在个别试验中其结果呈现出不确定性；在大量重复试验中其结果又具有统计规律性 的现象。

现象——投掷硬币、分子原子热运动、噪声概念——样本：随机现象的某次出现（观测、实验）。

事件：样本的结果。

样本空间：无穷多（大量）样本的全体（可能的试验结果）。

事件空间：结果的集合，可能无穷多，也可能只有少数几种。

2．概率（1）随机现象的规律性表现在样本的大量统计特性上。

大量样本的集体行为有规律：设N 次观测中事件A 出现了m A 次，A 发生的频率为A m N,当N 很大时，A m N有确定的比值。

（2）概率的定义：（1）任何随机事件的概率P(A)，其值介于 0≤P(A)≤1 之间。

（2）条件概率： P(A|B) 为事件B 已出现的条件下，事件A 出现的概率。

一般 P(A|B)≠P(A) ，但若B 与A 无关，则P(A|B)＝P(A) 。

（3）两事件之积的概率P(AB) 叫联合概率，它代表A 和B 同时出现的概率，故P(AB)＝P(BA)。

计算方法（公式）是： P(AB)= P(A) P(B|A) 或者＝P(B) P(A|B) P(A 1A 2……An)= P(A 1) P(A 2|A 1) P(A 3|A 1A 2)……P(A n |A 1A 2……A n-1) 于是便得到计算后验概率的公式：()()()()P A P B A P A B P B（4）两事件之和的概率P(A+B)代表A 或B 出现的概率（二者之一或共同），显然P(A+B)= P(A)+ P(B) - P(AB) 原因如图所示：（5）可能的事件全体A i （i=1,……n ），若为互斥、完备集合，则有归一化公式:1()1n ii P A ==∑同样，对条件概率有：1()1nii P AB ==∑对联合概率有：11()1n n iji j P A B===∑∑和1()()n i j j i P A B P B ==∑，1()()mi j i j P A B P A ==∑（6）全概率公式：若事件B 1，B 2，……，B n 两两互斥（B 1，……，B n 为S 的一个划分）P （B i ）> 0。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。