java实现一元线性回归算法
- 格式:doc
- 大小:42.50 KB
- 文档页数:14

用R软件实现一元线性回归一)理解一元线性回归,并会通过软件实现一元线性回归二)通过软件计算回归系数,会进行回归方差的显著性检验实验目的(三)掌握残差分析四)掌握回归系数的区间估计五)掌握预测和控制实验环境一、实验原理一)一元线性回归模型PC电脑1部,R软件y1x二)回归方程的显著性检验1.t检验2.F检验3.相关系数的显著性检验三)残差分析四)回归系数的区间估计五)预测1.单值预测2.区间预测二、实验内容及步骤案例3一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状,经过10周时间,收集了每周加班时间的数据和签发的新保单的数据,x为每周签发的新保单数据,y为每周加班时间(小时),数据见表2-1.表2-1每周加班工夫和签发的新保单的数据表周序号xy18253.522151.0310704.045502.054801.0713504.583251.596703.01012155.01.绘制散点图X Y<-c(3.5,1,4,2,1,4.5,1.5,3,5) 1plot(X,Y,main="每周加班工夫和签发的新保单的散点图")。
abline(lm(Y~X))成效分析:从图可发觉,每周加班工夫和签发的新保单成线性干系,因此能够斟酌一元线性模子。
2.求出回归方程,并对响应的方程做检修求出回归方程,并对相应方程做检验a<-lm(Y~X)summary(a)Call:lm(formula = Y ~ X)Residuals:Min1QMedian3QMax-0. -0....Coefficients:Estimate Std。
Error t value Pr(>|t|)(Intercept) 0.xxxxxxxx.xxxxxxxx.3390.745X0.xxxxxxxx.xxxxxxxx.4656.34e-05 ***2Signif。
codes:0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.485 on 7 degrees of freedomMultiple : 71.65 on 1 and 7 DF,p-value: 6.344e-05结果分析:从上述程序的输出结果可以看出回归方程通过了回归参数的检验与回归方程的检验,因此得到的回归方程为:Y0.xxxxxxx+0.xxxxxxxX3.参数估计confint(a)2.5 %97.5 %Intercept) -0.xxxxxxxx0 0.xxxxxxxx4#这里出现的是常数项置信区间X0.xxxxxxxx7 0.xxxxxxxx1#这里出现的是系数的置信区间4.预测预测N<-data.frame(X=260)#输入X=260NX1 260XXXXXXfitlwrupr1 1. -0.xxxxxxx 2.结果分析:由上述程序计算结果可得预测值与相应的预测区间为Y(260)0.241.069,2.374]平均值E(y)的置信区间计算如下:yconf yconffitlwrupr1 1. 0. 1.结果分析:平均值E(y)的置信区间为[1.069,1.692]5.残差分析残差分析残差e e3xxxxxxx.xxxxxxxx0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx7890.xxxxxxxx0.xxxxxxxx0.xxxxxxxx标准化残差ZRE<-e/1.319 ##计算回归a的标准化残差ZRExxxxxxx.xxxxxxxx0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx7890.xxxxxxxx0.xxxxxxxx0.xxxxxxxx学生化残差SRE<-rstandard(a) ##计算学生化残差SRExxxxxxx.xxxxxxxx0.xxxxxxxx -0.xxxxxxxx -0.xxxxxxxx -1.xxxxxxxx -1.xxxxxxxx7890.xxxxxxxx0.xxxxxxxx1.xxxxxxxx成效分析:能够看出,学生氏残差绝对值都小于2,因此模子吻合根本假定。


《土地利用规划学》一元线性回归分析学院:资源与环境学院班级:2013009姓名:x学号:201300926指导老师:x目录一、根据数据绘制散点图: (1)二、用最小二乘法确定回归直线方程的参数: (1)1)最小二乘法原理 (1)2)求回归直线方程的步骤 (3)三、回归模型的检验: (4)1)拟合优度检验(R2): (4)2)相关系数显著性检验: (5)3)回归方程的显著性检验(F 检验) (6)四、用excel进行回归分析 (7)五、总结 (15)一、根据数据绘制散点图:◎由上述数据,以销售额为y 轴(因变量),广告支出为X 轴(自变量)在EXCEL 可以绘制散点图如下图:◎从散点图的形态来看,广告支出与销售额之间似乎存在正的线性相关关系。
大致分布在某条直线附近。
所以假设回归方程为:x y βα+=二、用最小二乘法确定回归直线方程的参数: 1)最小二乘法原理年份 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 广告支出(万元)x 4.00 7.00 9.00 12.00 14.00 17.00 20.00 22.00 25.00 27.00销售额y7.00 12.00 17.00 20.00 23.00 26.00 29.00 32.00 35.00 40.00最小二乘法原理可以从一组测定的数据中寻求变量之间的依赖关系,这种函数关系称为经验公式。
考虑函数y=ax+b ,其中a,b 为待定常数。
如果Pi(xi,yi)(i=1,2,...,n )在一条直线上,则可以认为变量之间的关系为y=ax+b 。
但一般说来, 这些点不可能在同一直线上. 记Ei=yi-(axi+b),它反映了用直线y=ax+b 来描述x=xi ,y=yi 时,计算值y 与实际值yi 的偏差。
当然,要求偏差越小越好,但由于Ei 可正可负,所以不能认为当∑Ei=0时,函数y=ax+b 就好好地反应了变量之间的关系,因为可能每个偏差的绝对值都很大。

线性回归1. 代价函数最小化的方法: ● (批量)梯度下降法 ● 正归方程2. 梯度下降法先假设一个定点,然后按照一定的步长顺着这个点的梯度进行更新迭代下去,最后可以找到一个局部最优点,使代价函数在这个局部取得最小值量(vector)测价度注:1.是对θi的求偏导2.批量梯度下降的每一步都用到了所有的训练样本3.在多维问题中,要保证这些特征值都具有相近的维度,使得梯度下降算法更快的收敛.特征缩放公式:1.除以最大值2.3.学习率的选择:可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛通常可以考虑尝试些学习率:α=0.01,0.03,0.1,0.3,1,3,10 规可以一次性求出最优解①定义训练的参数(学习率训练次数打印步长)②输入训练集(定义占位符X = tf.placeholder("float")Y = tf.placeholder("float"))③随机生成w与b(初始化的方式很多种,方式不同可能会影响训练效果)④创建线性模型(pred = tf.add(tf.multiply(X, W), b))⑤用均方差计算training cost(cost = tf.reduce_sum(tf.pow(pred-Y,2))/(2*n_samples))⑥使用梯度下降进行优化(optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost))⑦变量初始化与创建图init = tf.global_variables_initializer()with tf.Session() as sess:sess.run(init)⑧开始训练Fit所有的训练数据设定每50次的打印内容⑨用测试集进行测试计算testing cost计算training cost 与testing cost之间的差值并输出⑩画图程序:import tensorflow as tfimport numpyimport matplotlib.pyplot as pltrng = numpy.random #产生随机数# Parameters(参数学习率训练次数打印步长)learning_rate = 0.01training_epochs = 1000display_step = 50# Training Datatrain_X = numpy.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1])train_Y=numpy.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,2.827,3.465,1.65,2.904,2.42,2.94,1.3])n_samples = train_X.shape[0]# tf Graph InputX = tf.placeholder("float")Y = tf.placeholder("float")# Set model weightsW = tf.Variable(rng.randn(), name="weight")b = tf.Variable(rng.randn(), name="bias")# Construct a linear modelpred = tf.add(tf.multiply(X, W), b)# Mean squared errorcost = tf.reduce_sum(tf.pow(pred-Y, 2))/(2*n_samples)# Gradient descentoptimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) # Initialize the variables (i.e. assign their default value)init = tf.global_variables_initializer()# Start trainingwith tf.Session() as sess:# Run the initializersess.run(init)# Fit all training datafor epoch in range(training_epochs):for (x, y) in zip(train_X, train_Y):sess.run(optimizer, feed_dict={X: x, Y: y})# Display logs per epoch stepif (epoch+1) % display_step == 0:c = sess.run(cost, feed_dict={X: train_X, Y:train_Y})print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(c), \"W=", sess.run(W), "b=", sess.run(b))plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')print("Optimization Finished!")training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})print("Training cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b), '\n')# Graphic displayplt.plot(train_X, train_Y, 'ro', label='Original data')plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')plt.legend()plt.show()# Testing exampletest_X = numpy.asarray([6.83, 4.668, 8.9, 7.91, 5.7, 8.7, 3.1, 2.1])test_Y = numpy.asarray([1.84, 2.273, 3.2, 2.831, 2.92, 3.24, 1.35, 1.03])print("Testing... (Mean square loss Comparison)")testing_cost = sess.run( tf.reduce_sum(tf.pow(pred - Y, 2)) / (2 * test_X.shape[0]),feed_dict={X: test_X, Y: test_Y}) print("Testing cost=", testing_cost)print("Absolute mean square loss difference:", abs(training_cost - testing_cost))plt.plot(test_X, test_Y, 'bo', label='Testing data')plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')plt.legend()plt.show()结果:5.非线性回归代码import tensorflow as tfimport numpy as npimport matplotlib.pyplot as plt # python中的画图工具包#利用numpy生成200个随机点,定义样本x_data=np.linspace(-0.5,0.5,200)[:,np.newaxis] #在-0.5-0.5范围内产生200个样本,增加维度(200行1列)noise=np.random.normal(0,0.02,x_data.shape)y_data=np.square(x_data)+noise#定义两个placeholderx=tf.placeholder(tf.float32,[None,1])y=tf.placeholder(tf.float32,[None,1])#定义神经网络中间层(10个神经元)Weights_L1=tf.Variable(tf.random_normal([1,10])) #给权值随机赋值,1代表一个输入,10代表中间层有10个神经元biases_L1=tf.Variable(tf.zeros([1,10])) #偏执层初始化为0Wx_plus_b_L1=tf.matmul(x,Weights_L1)+biases_L1 /信号的总和=输入*权值=偏执L1=tf.nn.tanh(Wx_plus_b_L1) # 激活函数(这里是双曲正切函数)#定义神经网络输出(一个神经元)Weights_L2=tf.Variable(tf.random_normal([10,1]))biases_L2=tf.Variable(tf.zeros([1,1])) #在输出时op只有一个所以bias 只有一个输入Wx_plus_b_L2=tf.matmul(L1,Weights_L2)+biases_L2prediction=tf.nn.tanh(Wx_plus_b_L2)#二次代价函数loss=tf.reduce_mean(tf.square(y-prediction))train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)#梯度下降法with tf.Session() as sess: #定义绘画sess.run(tf.global_variables_initializer()) #变量的初始化for _ in range(500): #进行训练,循环次数sess.run(train_step,feed_dict={x:x_data,y:y_data})#获得预测值prediction_value=sess.run(prediction,feed_dict={x:x_data}) #画图plt.figure()plt.scatter(x_data,y_data)plt.plot(x_data,prediction_value,'r-',lw=5)plt.show()1.定义占位符①placeholder (浮点型,[行,列]) 行不知道用None,列与输入的样本一致;②placeholder经常与feed一起使用,而feed类似于补丁形式,先以placeholder的形式给要输入的变量占位符,然后在run()的过程中给予feed_dict。

java 实现excel linest方法### Java实现Excel Linest方法在Java中,实现Excel文件的线性回归分析(Linest)通常需要借助一些外部库,如Apache POI和JFreeChart等,因为Java原生API并不直接支持此类高级统计分析。
以下是如何使用这些库在Java中实现类似Excel Linest功能的方法。
#### 导语线性回归是统计中的一种方法,用于评估两个或多个变量之间的关系。
在Excel中,`Linest`函数可以用来进行线性拟合,估算趋势线。
在Java中,我们可以通过以下步骤模拟这一过程。
#### 1.准备数据首先,需要准备或读取包含数据的Excel文件。
这里假设你已经有了两个数组,一个包含x轴数据,另一个包含y轴数据。
```javadouble[] xData = { /* x坐标数据*/ };double[] yData = { /* y坐标数据*/ };```#### 2.添加依赖在项目中,需要添加Apache POI和JFreeChart的依赖,以处理Excel文件和进行统计分析。
#### 3.实现线性回归使用JFreeChart库中的`SimpleRegression`类来执行线性回归分析。
```javaimport org.jfree.data.statistics.SimpleRegression;// 创建SimpleRegression对象SimpleRegression regression = new SimpleRegression();// 添加数据点for (int i = 0; i < xData.length; i++) {regression.addData(xData[i], yData[i]);}// 获取回归系数double intercept = regression.getIntercept();double slope = regression.getSlope();// 打印结果System.out.println("截距: " + intercept);System.out.println("斜率: " + slope);// 根据回归方程计算预测值double predictedY = intercept + slope * xValue;```#### 4.读取Excel文件如果你需要从Excel文件中读取数据,可以使用Apache POI。


一元线性回归模型教学设计一、教学目标通过本次教学,学生应该能够:1. 了解一元线性回归模型的基本概念和原理;2. 掌握一元线性回归模型的建立和求解方法;3. 能够运用一元线性回归模型解决实际问题;4. 培养学生的数据分析和模型建立能力。
二、教学内容1. 介绍一元线性回归模型的基本概念- 线性回归模型的基本思想- 回归方程和回归线的含义- 最小二乘法的原理2. 一元线性回归模型的建立和求解方法- 数据收集和变量选择- 模型建立和参数估计- 残差分析和模型检验3. 运用一元线性回归模型解决实际问题- 实际问题的建模方法- 数据处理和分析方法- 结果解释和模型评价三、教学过程1. 导入引入案例通过一个实际案例来引入一元线性回归模型的概念和应用,例如预测房价与房屋面积的关系。
2. 概念讲解- 介绍线性回归模型的基本思想和原理,以及回归方程和回归线的含义;- 解释最小二乘法的原理及其在一元线性回归模型中的应用。
3. 模型建立和参数估计- 数据收集和变量选择:讲解数据收集的方法和重要性,以及对自变量的选择;- 模型建立和参数估计:讲解如何建立一元线性回归模型并通过最小二乘法来估计模型的参数。
4. 残差分析和模型检验- 残差分析:讲解残差的概念及其在回归模型中的含义;- 模型检验:讲解常用的模型检验方法,如回归系数的显著性检验、模型拟合优度检验等。
5. 实际问题的建模和解决- 介绍实际问题的建模方法和步骤,包括数据处理、模型选择和参数估计;- 使用实际数据进行模型的建立和求解,分析结果并给出合理解释。
6. 教学案例练习提供多个一元线性回归的教学案例,供学生进行实践操作和分析讨论。
7. 总结归纳小结一元线性回归模型的基本概念、建立方法和应用步骤,提醒学生需要注意的问题和要点。
四、教学手段教学手段可以采用多种形式,如讲解、示范、案例分析、课堂练习、小组讨论等,通过多种形式的互动与合作,达到知识的传授和能力的培养。

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。

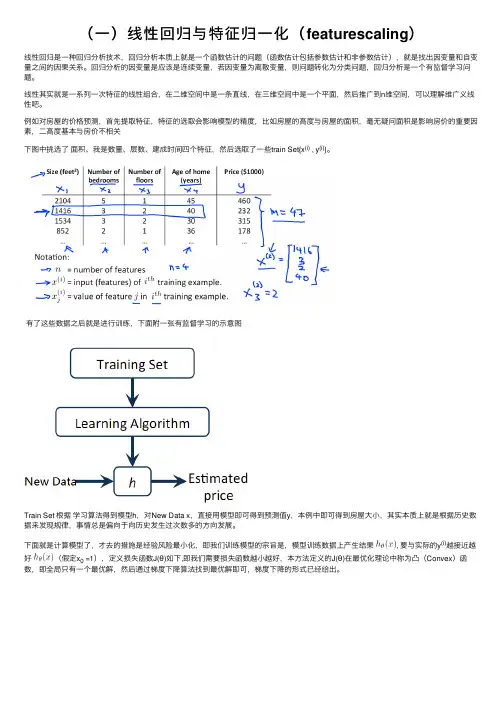
(⼀)线性回归与特征归⼀化(featurescaling)线性回归是⼀种回归分析技术,回归分析本质上就是⼀个函数估计的问题(函数估计包括参数估计和⾮参数估计),就是找出因变量和⾃变量之间的因果关系。
回归分析的因变量是应该是连续变量,若因变量为离散变量,则问题转化为分类问题,回归分析是⼀个有监督学习问题。
线性其实就是⼀系列⼀次特征的线性组合,在⼆维空间中是⼀条直线,在三维空间中是⼀个平⾯,然后推⼴到n维空间,可以理解维⼴义线性吧。
例如对房屋的价格预测,⾸先提取特征,特征的选取会影响模型的精度,⽐如房屋的⾼度与房屋的⾯积,毫⽆疑问⾯积是影响房价的重要因素,⼆⾼度基本与房价不相关下图中挑选了⾯积、我是数量、层数、建成时间四个特征,然后选取了⼀些train Set{x(i) , y(i)}。
有了这些数据之后就是进⾏训练,下⾯附⼀张有监督学习的⽰意图Train Set 根据学习算法得到模型h,对New Data x,直接⽤模型即可得到预测值y,本例中即可得到房屋⼤⼩,其实本质上就是根据历史数据来发现规律,事情总是偏向于向历史发⽣过次数多的⽅向发展。
下⾯就是计算模型了,才去的措施是经验风险最⼩化,即我们训练模型的宗旨是,模型训练数据上产⽣结果, 要与实际的y(i)越接近越好(假定x0 =1),定义损失函数J(θ)如下,即我们需要损失函数越⼩越好,本⽅法定义的J(θ)在最优化理论中称为凸(Convex)函数,即全局只有⼀个最优解,然后通过梯度下降算法找到最优解即可,梯度下降的形式已经给出。
梯度下降的具体形式:关于梯度下降的细节,请参阅局部加权回归有时候样本的波动很明显,可以采⽤局部加权回归,如下图,红⾊的线为局部加权回归的结果,蓝⾊的线为普通的多项式回归的结果。
蓝⾊的线有⼀些⽋拟合了。
局部加权回归的⽅法如下,⾸先看线性或多项式回归的损失函数“很明显,局部加权回归在每⼀次预测新样本时都会重新确定参数,以达到更好的预测效果。

一元线性回归模型案例一元线性回归模型是统计学中最基本、应用最广泛的一种回归分析方法,可以用来探究自变量与因变量之间的线性关系。
一元线性回归模型的数学公式为:y = β0 + β1x,其中y表示因变量,x表示自变量,β0和β1分别为截距和斜率。
下面以一个实际案例来说明一元线性回归模型的应用。
假设我们有一组数据,其中x表示一个房屋的面积,y表示该房屋的售价,我们想利用一元线性回归模型来预测房屋的售价。
首先,我们需要收集一组已知数据,包括房屋的面积和售价。
假设我们收集了10个不同房屋的面积和售价数据,如下所示:房屋面积(x)(平方米)售价(y)(万元)80 12090 130100 140110 150120 160130 170140 180150 190160 200170 210我们可以根据这组数据绘制散点图,横坐标表示房屋面积x,纵坐标表示售价y,如下所示:(插入散点图)接下来,我们可以利用最小二乘法来拟合一条直线,使其能够最好地拟合这些散点。
最小二乘法是一种最小化误差平方和的方法,可以得到最优的拟合直线。
根据一元线性回归模型的公式,可以通过计算拟合直线的斜率β1和截距β0来实现最小二乘法。
其中,斜率β1可以通过下式计算得到:β1 = n∑(xiyi) - (∑xi)(∑yi)n∑(xi^2) - (∑xi)^2截距β0可以通过下式计算得到:β0 = (1/n)∑yi - β1(1/n)∑xi通过带入已知数据,我们可以计算得到斜率β1和截距β0的具体值。
在本例中,计算结果如下:β1 ≈ 1.0667β0 ≈ 108.6667最后,利用得到的斜率β1和截距β0,我们可以得到一元线性回归模型的具体公式为:y ≈ 108.6667 + 1.0667x我们可以利用这个回归模型进行预测。
例如,如果有一个房屋的面积为130平方米,那么根据回归模型,可以预测该房屋的售价为170 + 108.6667 ≈ 278.6667万元。
java实现求解一元n次多项式Java实现求解一元n次多项式可以通过使用Java中的多项式类库来完成。
多项式类库提供了各种操作多项式的方法,包括求解多项式的根、求多项式的系数等。
在Java中,可以使用Apache Commons Math库中的Polynomial类来实现求解一元n次多项式的功能。
该类提供了多种方法来操作多项式,例如,可以使用getRoots()方法来求解多项式的根,使用getCoefficients()方法来获取多项式的系数等。
下面是一个使用Apache Commons Math库中的Polynomial类来求解一元n次多项式的示例代码:```javaimport mons.math3.analysis.polynomials.PolynomialFunction;public class PolynomialSolver {public static void main(String[] args) {double[] coefficients = {1.0, 2.0, 3.0, 4.0}; // 多项式系数PolynomialFunction polynomial = new PolynomialFunction(coefficients); // 创建多项式对象double[] roots = polynomial.getRoots(); // 求解多项式的根System.out.println("多项式的根为:");for (double root : roots) {System.out.println(root);}}}```在上面的示例代码中,我们首先定义了一个包含多项式系数的数组,然后创建了一个多项式对象,最后使用getRoots()方法求解多项式的根,并将结果输出到控制台上。
除了使用Apache Commons Math库中的Polynomial类之外,还可以使用其他的数学类库来实现求解一元n次多项式的功能,例如,JScience、JAMA等。
Python实现——⼀元线性回归(梯度下降法)2019/3/25⼀元线性回归——梯度下降/最⼩⼆乘法⼜名:⼀两位⼩数点的悲剧感觉这个才是真正的重头戏,毕竟前两者都是更倾向于直接使⽤公式,⽽不是让计算机⼀步步去接近真相,⽽这个梯度下降就不⼀样了,计算机虽然还是跟从现有语句/公式,但是在不断尝试中⼀步步接近⽬的地。
简单来说,梯度下降的⽬的在我看来还是要到达两系数的偏导数函数值为零的取值,因此,我们会从“任意⼀点”开始不断接近,由于根据之前最⼩⼆乘法的推导,可以说⽅差的公式应该算⼀个⼆次函数...?总之,这么理解的话就算只⽤中学知识也能知道在导数值为0时求得最⼤/⼩值。
那么就很简单了,我们让a,b⼀点点接近就可以了,⽽逼近的过程⼗分有趣,且巧妙。
当前点的导数值如果为正,说明该点的横坐标需要左移,⽽为负则需要右移(为0就胜利了),因此根据这个特性我们可以直接设定为以下python代码:a=a-n*get_pa(c,d)b=b-n*get_pb(c,d)其中,get_pa()以及get_pb()对应的分别为a或b求偏导数值,以a,b两个值为输⼊值,⽽n则是⾮常重要的调节系数,重要到让我⽆法正常运⾏程序,后⽂会着重提及。
运⽤到了正减,负增,通过减法实现,很巧妙【来⾃于Coursera的华盛顿⼤学“机器学习:回归”课程的想法接下来,还是先给出求⽅差,求偏导的函数。
求⽅差:def get_sqm(a,b):sqm=0for i in range(100):sqm=sqm+(cols2[i]-a-b*cols1[i])*(cols2[i]-a-b*cols1[i])return sqm求a,b的偏导:def get_pa(a,b):pa=0for i in range(100):pa=pa-2*(cols2[i]-a-b*cols1[i])return padef get_pb(a,b):pb=0for i in range(100):pb=pb-2*cols1[i]*(cols2[i]-a-b*cols1[i])return pb好像...也没有太多可说的?那就迫不及待的进⼊正题吧!来⾃于我被调节系数n折磨的⼀整个下午的怨念!其实主题的循环函数并不是那么难理解和构建,我很早就完成了:while abs(get_pa(a,b))>=10 and abs(get_pb(a,b))>=10 :c=ad=ba=a-n*get_pa(c,d)b=b-n*get_pb(c,d)print(get_sqm(a,b))偏导数的限制...我取了10...看起来很惊悚,但也是没办法,被吓得,只能松⼀点了。
Python实现——⼀元线性回归(最⼩⼆乘法)2019/3/24线性回归——最⼩⼆乘法公式法暂时⽤python成功做出来了图像,但是其中涉及到的公式还是更多的来⾃于⽹络,尤其是最⼩⼆乘法公式中的两个系数的求解,不过⽬前看了下书⾼数也会马上提及(虽然可能不会讲这两个公式),但是运⽤的知识其实还是⽬前能够接受的:偏导,⼆元⽅程。
乍⼀看其实也没什么,只是由于有了求和符号的⼲扰让计算显得复杂。
该博客中对其的推导看起来⽐较简洁容易接受,其中结尾公式的计算不难让⼈想到线性代数中的向量乘积运算,但是那样的表⽰⽅法我并不熟练,等到系统的学习线代后再深挖....吧。
总的来说:y=a+bx 便是我们的预测函数。
然⽽不同于以往的是变量变为了a与b两个系数,从这⾥也不难看到其实若是⼆次拟合也有⼀个好处那便是虽然x中含有⼆次项⽽系数中并没有,仍然是⼀次⽅程。
⽽我们所要做到的便是能够让这个函数在基于现有数据的参照下偏差最⼩,⽽偏差值的衡量我们将会⽤⽅差来表⽰,不选择简单的做差是由于做差势必会带来正负的区别,⽽由此⼜会导致偏差之间相互抵消,⽽若是加上绝对值的话⼜要涉及判断,因此⽅差成为了简单直接的⽅式。
之后的求解,简单来说就是分别对两个系数进⾏求偏导,在之后,我们再转换⼀下观念。
虽然我们⽬前来看是把系数当作了未知数,但是实际上这还是关于x,y的⽅程,对于x,y的⽅差,应视其为⼆次函数,也因此最⼩值的求解应该在导数0点取得。
(有待商榷,这只是我⽬前的理解)因此再分别对应回两个偏导为零继续求解,其中关于a的⽅程较为简单,⽽b则会⿇烦⼀点。
⽽在我的python实现中前两个库函数可能没有使⽤到修正:上两个函数应该为excel导⼊的函数,之前应该是忘了import xlrdimport xlwtimport matplotlib.pyplot as pltimport numpy as np此处则对应的是读取数据workbook=xlrd.open_workbook(r'1.xls')sheet=workbook.sheet_by_index(0)cols1=sheet.col_values(0) #获取第⼀列cols2=sheet.col_values(1) #获取第⼆列以下则是在为最后⼀步的公式提供准备每个参量,把单个值提前表⽰出来s1=0s2=0s3=0s4=0for i in range(n):s1 = s1 + cols1[i]*cols2[i]s2 = s2 + cols1[i]s3 = s3 + cols2[i]s4 = s4 + cols1[i]*cols1[i]最后这⾥就是公式的求解,相信就算没看前⾯推导,也能⼤概懂点其中每个量的相互关系以及上⾯所准备的参量的意义b = (s2*s3-n*s1)/(s2*s2-s4*n)a = (s3 - b*s2)/n最后便是作图,plt.scatter()绘制散点图,plt.plot是折线图,⽽np.linspace()则需要根据实际数据的情况进⾏合理取值plt.scatter(cols1,cols2,color = 'blue')x=np.linspace(0,100,1000)y=b*x+aplt.plot(x,y,color="red")plt.show()这个是我第⼀次成功运⾏后得出的图像(实验室提供的第⼀组数据)虽然可能更适合⼆次拟合?但是⼤概也是我的第⼀次成功尝试吧整体代码如下import xlrdimport xlwtimport matplotlib.pyplot as pltimport numpy as npworkbook=xlrd.open_workbook(r'2.xls')sheet=workbook.sheet_by_index(0)cols1=sheet.col_values(0) #获取第⼀列cols2=sheet.col_values(1) #获取第⼆列#plt.plot(cols1,cols2)n=100s1=0s2=0s3=0s4=0for i in range(n):s1 = s1 + cols1[i]*cols2[i]s2 = s2 + cols1[i]s3 = s3 + cols2[i]s4 = s4 + cols1[i]*cols1[i]b = (s2*s3-n*s1)/(s2*s2-s4*n) #最⼩⼆乘法获取系数的公式a = (s3 - b*s2)/n #最⼩⼆乘法获取系数的公式plt.scatter(cols1,cols2,color = 'blue')x=np.linspace(0,15,100)y=b*x+aplt.plot(x,y,color="red")plt.show()PS:谨记,利⽤excel导⼊数据的时候⼀定要记得检查表格中数据的类型,由于当时⼀开始表格内部的数并不是以数字存储的,读⼊的时候可能是以字符?⽂本?反正是不能正确显⽰,直接就是⼀个莫名其妙的y=x图像,惊了我都,⼀直以为是我代码错误,后来才觉察到。
一元线性回归方程中回归系数的几种确定方法
1、首先对方程进行变形,令为y= aX+ b,通过求解线性回归方程(即确定y 的值)可得出一元线性回归方程中各个自变量之间的关系。
2、再用线性代数知识将上式化成标准型(标准型在实际应用中是最常见的),这样就可以根据其他因素对它做出调整,从而确定出不同的回归系数。
3、对于非线性问题还有一种办法:即求解线性回归方程后,根据实验结果(如均值等)对原方程作出调整,然后对每次调整所产生的新的自变量x 和y 分别赋予相应的权重,则新的自变量对应的权重就构成了回归系数。
java实现一元线性回归算法 网上看一个达人用java写的一元线性回归的实现,我觉得挺有用的,一些企业做数据挖掘不是用到
了,预测运营收入的功能吗?采用一元线性回归算法,可以计算出类似的功能。直接上代码吧:
1、定义一个DataPoint类,对X和Y坐标点进行封装: package com.zyujie.dm; public class DataPoint { /** the x value */ public float x;
/** the y value */ public float y;
/** * Constructor. * * @param x * the x value * @param y * the y value */ public DataPoint(float x, float y) { this.x = x; this.y = y; } }
2、下面是算法实现回归线: /** * File : DataPoint.java * Author : zhouyujie * Date : 2012-01-11 16:00:00 * Description : Java实现一元线性回归的算法,回归线实现类,(可实现统计指标的预测) */ package com.zyujie.dm;
import java.math.BigDecimal; import java.util.ArrayList;
public class RegressionLine // implements Evaluatable { /** sum of x */ private double sumX;
/** sum of y */ private double sumY;
/** sum of x*x */ private double sumXX;
/** sum of x*y */ private double sumXY;
/** sum of y*y */ private double sumYY;
/** sum of yi-y */ private double sumDeltaY;
/** sum of sumDeltaY^2 */ private double sumDeltaY2;
/** 误差 */ private double sse;
private double sst; private double E; private String[] xy; private ArrayList listX; private ArrayList listY; private int XMin, XMax, YMin, YMax; /** line coefficient a0 */ private float a0;
/** line coefficient a1 */ private float a1;
/** number of data points */ private int pn;
/** true if coefficients valid */ private boolean coefsValid;
/** * Constructor. */ public RegressionLine() { XMax = 0; YMax = 0; pn = 0; xy = new String[2]; listX = new ArrayList(); listY = new ArrayList(); }
/** * Constructor. * * @param data * the array of data points */ public RegressionLine(DataPoint data[]) { pn = 0; xy = new String[2]; listX = new ArrayList(); listY = new ArrayList(); for (int i = 0; i < data.length; ++i) { addDataPoint(data[i]); } }
/** * Return the current number of data points. * * @return the count */ public int getDataPointCount() { return pn; }
/** * Return the coefficient a0. * * @return the value of a0 */ public float getA0() { validateCoefficients(); return a0; }
/** * Return the coefficient a1. * * @return the value of a1 */ public float getA1() { validateCoefficients(); return a1; } /** * Return the sum of the x values. * * @return the sum */ public double getSumX() { return sumX; }
/** * Return the sum of the y values. * * @return the sum */ public double getSumY() { return sumY; }
/** * Return the sum of the x*x values. * * @return the sum */ public double getSumXX() { return sumXX; }
/** * Return the sum of the x*y values. * * @return the sum */ public double getSumXY() { return sumXY; }
public double getSumYY() { return sumYY; } public int getXMin() { return XMin; }
public int getXMax() { return XMax; }
public int getYMin() { return YMin; }
public int getYMax() { return YMax; }
/** * Add a new data point: Update the sums. * * @param dataPoint * the new data point */ public void addDataPoint(DataPoint dataPoint) { sumX += dataPoint.x; sumY += dataPoint.y; sumXX += dataPoint.x * dataPoint.x; sumXY += dataPoint.x * dataPoint.y; sumYY += dataPoint.y * dataPoint.y;
if (dataPoint.x > XMax) { XMax = (int) dataPoint.x; } if (dataPoint.y > YMax) { YMax = (int) dataPoint.y; } // 把每个点的具体坐标存入ArrayList中,备用 xy[0] = (int) dataPoint.x + ""; xy[1] = (int) dataPoint.y + ""; if (dataPoint.x != 0 && dataPoint.y != 0) { System.out.print(xy[0] + ","); System.out.println(xy[1]);
try { // System.out.println("n:"+n); listX.add(pn, xy[0]); listY.add(pn, xy[1]); } catch (Exception e) { e.printStackTrace(); }
/* * System.out.println("N:" + n); System.out.println("ArrayList * listX:"+ listX.get(n)); System.out.println("ArrayList listY:"+ * listY.get(n)); */ } ++pn; coefsValid = false; }
/** * Return the value of the regression line function at x. (Implementation of * Evaluatable.) * * @param x * the value of x * @return the value of the function at x */ public float at(int x) {