牛顿迭代法解三元二次方程组(C++版)

求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。

它的基本思想是通过不断逼近
方程的解，使得逼近值与真实解的差距越来越小，最终得到方程的解。

下面介绍三种新的迭代法：牛顿迭代法，弦截法和切线法。

一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。

它的迭代公式为：
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解，f(x_n)表示在x_n处的函数值，f'(x_n)表示在x_n 处的导数值。

牛顿迭代法的优点是收敛速度快，通常是二阶收敛，但其缺点是需要计算函数的导数，如果导数计算困难或者导数为零的情况下，该方法可能不适用。

二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似，但其缺点是需要计算函数的导数，且对于初始逼近
解的选择比较敏感。

牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。

它们各自有着优点
和缺点，适用的领域和条件也不尽相同。

在实际问题中，需要根据具体情况选择合适的方
法来求解非线性方程。

二元非线性方程牛顿迭代法C++代码.小弟需要解一个二元非线性方程组，虽然说matlab的解法是一两个代码的事，但是我的情况是需要在C++ 里面实现。

由于自己不熟悉C++代码和牛顿迭代法的解法，小弟最近在网上找了一些资料。

发现很多有问题的例子，纯粹是在误导别人，浪费别人的时间。

于是小弟自己在看了解法(牛顿迭代法）的基础上,自己通过C++ 语言实现了一些简单方程组的解法，分享给给大家。

1. 非线性方程组的解法原理我在网上找了一个资料，应该是中南大学计算机学院的教程，如下：注意,他这里的例子第二个方程应该是，x1*x2＊x2+x1-10*x2+8经过观察，我发现其实对于2元方程来说：f(x1,x2）和g （x1，x2）。

牛顿迭代法里面的迭代量(Δx 1 和Δx 2) 可以如下表示.（我看到网上很多例子用矩阵来表示，我表示看不太懂，而且根据网上贴出来的程序,发现有错误。

而我发现对于2元方程来说，用下面的表示方法更直观，更简单。

2元方程并不需要再学习矩阵的相关知识。

）()()()221121211,,,x x x f x x x f x x f x ∂∂+∂∂-=∆ ()()()221121212,,,x x x g x x x g x x g x ∂∂+∂∂-=∆2。

代码(运行环境, VS 2010, WIN 7 64)// Nonlinear。

cpp ：Defines the entry point for the console application.//＃include "stdafx.h"＃include <math.h>＃include 〈iostream〉using namespace std；int _tmain(int argc，_TCHAR* argv[］){double x1，x2; //变量x1,x2;double x1_0，x2_0; //变量x1，x2迭代前的值double x1_1，x2_1; //变量x1，x2迭代后的值double delta_x1，delta_x2; //变量double function_F,function_G；//方程f（x1,x2）和g（x1，x2) double F_x1，F_x2; //方程f的偏导double G_x1,G_x2；//方程g的偏导double Error=1e—10；//给定的误差double Error_cout；//用来计算的误差int Steps；//运行步骤int Max_Steps=100000；//最大运行步骤x1 = 0.5;x2 = 0.5；//初始化初值x1_0 = x1;x2_0 = x2;for(Steps=1;Steps〈=Max_Steps；Steps++){// 方程组，f(x1，x2), g（x1,x2)function_F = x1_0*x1_0—10。

⽜顿迭代法求平⽅根迭代是数值分析中通过从⼀个初始估计出发寻找⼀系列近似解来解决问题（⼀般是解⽅程或者⽅程组）的过程，为实现这⼀过程所使⽤的⽅法统称为迭代法（Iterative Method）。

　⼀般可以做如下定义：对于给定的线性⽅程组x=Bx+f（这⾥的x、B、f同为矩阵，任意线性⽅程组都可以变换成此形式），⽤公式x(k+1）=Bx(k)+f（括号中为上标，代表迭代k次得到的x，初始时k=0)逐步带⼊求近似解的⽅法称为迭代法（或称⼀阶定常迭代法）。

如果k 趋向⽆穷⼤时limt(k)存在，记为x*，称此迭代法收敛。

显然x*就是此⽅程组的解，否则称为迭代法发散。

跟迭代法相对应的是直接法（或者称为⼀次解法），即⼀次性的快速解决问题，例如通过开⽅解决⽅程x +3= 4。

⼀般如果可能，直接解法总是优先考虑的。

但当遇到复杂问题时，特别是在未知量很多，⽅程为⾮线性时，我们⽆法找到直接解法（例如五次以及更⾼次的代数⽅程没有解析解，参见阿贝⽿定理），这时候或许可以通过迭代法寻求⽅程（组）的近似解。

最常见的迭代法是⽜顿法。

其他还包括最速下降法、共轭迭代法、变尺度迭代法、最⼩⼆乘法、线性规划、⾮线性规划、单纯型法、惩罚函数法、斜率投影法、遗传算法、模拟退⽕等等。

　利⽤迭代算法解决问题，需要做好以下三个⽅⾯的⼯作：确定迭代变量 在可以⽤迭代算法解决的问题中，⾄少存在⼀个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。

建⽴迭代关系式 所谓迭代关系式，指如何从变量的前⼀个值推出其下⼀个值的公式（或关系）。

迭代关系式的建⽴是解决迭代问题的关键，通常可以顺推或倒推的⽅法来完成。

对迭代过程进⾏控制 在什么时候结束迭代过程？这是编写迭代程序必须考虑的问题。

不能让迭代过程⽆休⽌地重复执⾏下去。

迭代过程的控制通常可分为两种情况：⼀种是所需的迭代次数是个确定的值，可以计算出来；另⼀种是所需的迭代次数⽆法确定。

对于前⼀种情况，可以构建⼀个固定次数的循环来实现对迭代过程的控制；对于后⼀种情况，需要进⼀步分析出⽤来结束迭代过程的条件。

解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象，其在实际应用中广泛存在，如物理学、工程学、经济学等领域。

求解非线性方程是一个具有挑战性的问题，因为这类方程往往没有简单的解析解，需要通过数值方法进行求解。

牛顿迭代法作为一种古老而有效的数值求解方法，对于求解非线性方程具有重要的应用价值。

本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。

我们将详细阐述牛顿迭代法的基本思想，包括其历史背景、数学原理以及收敛性分析。

我们将通过具体实例，展示牛顿迭代法的计算步骤和实际操作过程，以便读者能够更好地理解和掌握该方法。

我们将探讨牛顿迭代法在各个领域中的实际应用，包括其在物理学、工程学、经济学等领域中的典型应用案例，以及在实际应用中可能遇到的问题和解决方法。

通过本文的介绍，读者可以深入了解牛顿迭代法的基本原理和应用技巧，掌握其在求解非线性方程中的实际应用方法，为进一步的研究和应用提供有力支持。

二、牛顿迭代法的基本原理牛顿迭代法，又称为牛顿-拉夫森方法，是一种在实数或复数域上近似求解方程的方法。

其基本原理是利用泰勒级数的前几项来寻找方程的根。

如果函数f(x)在x0点的导数f'(x0)不为零，那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示，即：这就是牛顿迭代法的基本迭代公式。

给定一个初始值x0，我们可以通过不断迭代这个公式来逼近f(x)的根。

每次迭代，我们都用当前的近似值x0来更新x0，即：这个过程一直持续到满足某个停止条件，例如迭代次数达到预设的上限，或者连续两次迭代的结果之间的差小于某个预设的阈值。

牛顿迭代法的收敛速度通常比线性搜索方法快，因为它利用了函数的导数信息。

然而，这种方法也有其局限性。

它要求函数在其迭代点处可导，且导数不为零。

牛顿迭代法可能不收敛，如果初始点选择不当，或者函数有多个根，或者根是重根。

因此，在使用牛顿迭代法时，需要谨慎选择初始点，并对迭代过程进行适当的监控和调整。

实验二：迭代法求解方程组姓名：徐烨学号：08072105时间：2010-11-17一、实验目的利用jacobi 迭代法和gauss-seidei 迭代法求解线性方程组，利用newton 迭代法求解非线性方程组。

在求解过程中，利用这三种方法的迭代原理，根据迭代法的求解流程，写出三种迭代法的迭代格式，学习三种迭代法的原理和解题步骤，并使用matlab 软件求解方程。

在实验过程中，分别取不同的初值进行求解，并做结果分析，解怒同德方程来比较这三种迭代方法的利弊。

二、实验步骤newton 迭代法⒈newton 迭代原理考虑非线性方程f(x)=0，求解她的困难在于f 是非线性函数。

为克服这一困难，考虑它的线性展开。

设当前点为Xk, 在Xk 处的Taylor 展开式为f ()x ≈f ()()()k k k x x x f x -'+令上式右端为0.解其方程得到()()k k k k x f x f x x '-=+1 ⋅⋅⋅=1,0k 此式就称为Newton 公式。

2. newton 迭代法的matlab 实现function x=newton(fname,dfname,x0,e,N)%用途：牛顿迭代法解非线性方程组分f(x)=0%fname 和dfname 分别表示f(x)及其到函数的M 函数句柄或内嵌函数的表达式%x0为迭代初值，e 为精度%x 为返回数值解，并显示计算过程，设置迭代次数上线N 以防发散if nargin<5,N=500;endif nargin<4,e=le-4;endx=x0;x0=x+2*e;k=0;fprintf('It.no=%2d x%[2d]=%12.9f\n',k,k,x)while abs(x0-x)>e&k<Nk=k+1;x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);fprintf('It.no=%2d x[%2d]=%12.9f\n',k,k,x) endif k==N,fprintf('已达到迭代次数上限');end在试验中，我用这种方法求f(x)=x3-3*x-1=0的解①初值为2时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,2,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 1.888888889It.no= 2 x[ 2]= 1.879451567It.no= 3 x[ 3]= 1.879385245It.no= 4 x[ 4]= 1.879385242x =1.879385241571817e+000②初值为5时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,5,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 3.486111111It.no= 2 x[ 2]= 2.562343095It.no= 3 x[ 3]= 2.075046554It.no= 4 x[ 4]= 1.902660228It.no= 5 x[ 5]= 1.879777024It.no= 6 x[ 6]= 1.879385355It.no= 7 x[ 7]= 1.879385242x =1.879385241571826e+000③初值为8时，新建一个文件，输入：fun=inline('x^3-3*x-1');dfun=inline('3*x^2-3');x=newton(fun,dfun,8,0.5e-6)即可得此方程的解为：It.no= 0 xIt.no= 1 x[ 1]= 5.423280423It.no= 2 x[ 2]= 3.754505841It.no= 3 x[ 3]= 2.719579123It.no= 4 x[ 4]= 2.148629510It.no= 5 x[ 5]= 1.920654127It.no= 6 x[ 6]= 1.880593045It.no= 7 x[ 7]= 1.879386323It.no= 8 x[ 8]= 1.879385242It.no= 9 x[ 9]= 1.879385242x =1.879385241571817e+000gauss-seidel 实验过程1.gauss-seidel 迭代原理将方程组Ax=b （设n i a n ,2,1;0⋅⋅⋅=≠）化成等价方程组：)(1∑≠-=ij j i i i i x a b a x j i ),2,1(n i ⋅⋅⋅= 采用迭代格式： ⎪⎪⎭⎫ ⎝⎛--=∑∑-=+=++111111i j n i j k jij k j ij i ij k i x a x a b a x ()n i ⋅⋅⋅⋅=,2,1 2.gauss-seidel 迭代法的matlab 实现function x=jacobi(A,b,x0,emg,N)% A 是线性方程组的系数矩阵% b 是值向量% x0是迭代初始向量% N 是迭代上限，诺迭代次数大于>N,则迭代失败% emg 是控制精度% 用gauss-seidei 迭代法求解线性方程组Ax=b 的解%k 表示迭代次数%x 表示用迭代法求得的解线性方程组的近似解if nargin<5N=500;else N=N;endn=length(b);x1=zeros(n,1);x2=zeros(n,1);x1=x0;k=0;r=max(abs(b-A*x1));while r>emgfor i=1:nsum=0;for j=1:nif i~=jsum=sum+A(i,j)*x1(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Nwarning('迭代次数达到上限！');return;endendx=x1；在试验中，我用此方法求①A1=922282217 ，b=6810的线性方程组的解 新建一个文件，输入：A=[7 1 2;2 8 2;2 2 9];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=gaussseidel(A,b,x0,emg)可得此方程的解为：x =1.269406363593758e+0006.210045136516440e-0012.465753606121330e-001改变此初值为x0=[1 2 3]’时，可得此方程的解为：x =1.269406358870516e+0006.210045989420114e-0012.465753427083272e-001②A2=32-1-1-102-2-2-10 ，b=15.01的线性方程组的解 新建一个文件，输入：A=[10 -2 -2;-2 10 -1;-1 -2 3];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=gaussseidel(A,b,x0,emg)即可得此方程的解为：x =2.067226785332675e+0001.588235242744889e+0003.747899090274151e+000改变此初值为x0=[4 5 6]’时，可得此方程的解为：x =2.067226982320636e+0001.588235338736795e+0003.747899219931409e+000jacobi 迭代法的实验过程1.jacobi 迭代原理将方程组Ax=b （设n i a n ,2,1;0⋅⋅⋅=≠）化成等价方程组：)(1∑≠-=ij j i i i i x a b a x j i ),2,1(n i ⋅⋅⋅= 采用迭代格式:⎪⎪⎭⎫ ⎝⎛-=∑≠+111j k j ij i ii k i x a b a x ()n i ⋅⋅⋅=,2,1 2.Jacobi 迭代法的matlab 实现function x=jacobi(A,b,x0,emg,N)% A 是线性方程组的系数矩阵% b 是值向量% x0是迭代初始向量% N 是迭代上限，诺迭代次数大于>N,则迭代失败% emg 是控制精度% 用jacobi 迭代法求解线性方程组Ax=b 的解%k 表示迭代次数%x 表示用迭代法求得的解线性方程组的近似解if nargin<5N=500;else N=N;endn=length(b);x1=zeros(n,1);x2=zeros(n,1);x1=x0;k=0;r=max(abs(b-A*x1));while r>emgfor i=1:nsum=0;for j=1:nif i~=jsum=sum+A(i,j)*x1(j);endendx2(i)=(b(i)-sum)/A(i,i);endr=max(abs(x2-x1));x1=x2;k=k+1;if k>Nwarning('迭代次数达到上限！');return;endendx=x1；在实验中，我用此方法求①A1=922282217 ，b=6810的线性方程组的解，这样可以比 这两种方法的优越性新建一个文件，输入：A=[7 1 2;2 8 2;2 2 9];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=jacobi(A,b,x0,emg)即可得此方程的解为：x=1.269406606540146e+0006.210048051684348e-0012.465755635845312e-001改变此初值为x0=[1 2 3]’时，可得此方程的解为：x =1.269406576962693e+0006.210047721178078e-0012.465755330013612e-001②A2=32-1-1-102-2-2-10 ，b=15.01的线性方程组的解 新建一个文件，输入：A=[10 -2 -2;-2 10 -1;-1 -2 3];b=[10 8 6]';x0=[0 0 0]';emg=10^(-6);x=jacobi (A,b,x0,emg)即可得此方程的解为：x =2.067226548410933e+0001.588235036073759e+0003.747898577034409e+000改变此初值为x0=[4 5 6]’时，可得此方程的解为：x =2.067227297951090e+0001.588235601041707e+0003.747899852657807e+000三、实验分析由Jacobi 的迭代公式可以看到，在计算机上使用该法线性方程组时，x(m)分量必须保存到x(m+1)的分量全部复出后才不再需要。

迭代法和牛顿迭代法的优缺点及应用在数值计算和算法设计中，迭代法和牛顿迭代法是两种常见的数值优化方法。

它们可以很好地用于解决非线性方程组、最优化问题以及数学模型的求解等问题。

在实际应用中，它们的优缺点各有不同，可根据问题的特点选择适合的方法。

本文将对迭代法和牛顿迭代法的优缺点及应用进行分析。

一、迭代法1、迭代法的原理迭代法是一种通过不断逼近目标值的方法。

其思想是将一个原问题转化为一个递归求解的过程。

假设我们要求解一个方程f(x) = 0，可以利用如下公式进行迭代：$x_{n+1} = g(x_n)$其中，$g(x_n)$是一个递推公式，用来表示如何从$x_n$ 得到$x_{n+1}$。

通过不断迭代，可以逐渐逼近解。

当迭代次数足够多时，可以得到符合精度的解。

2、迭代法的优点（1）实现简单：迭代法的计算过程非常简单，只需要考虑递推公式即可。

（2）收敛速度较快：迭代法的收敛速度要比其他方法要快，尤其是在某些非线性问题中，迭代法表现出了其优异的收敛性。

（3）适用范围广：迭代法可以用于解决各种类型的数学问题，包括求解非线性方程组、求解最优化问题以及求解微积分方程等。

3、迭代法的缺点（1）收敛不稳定：由于迭代法只是通过不断逼近目标值的过程，收敛的速度和稳定性都受到了影响，可能存在发散的情况。

（2）初值选择的影响：迭代法在求解问题时，对于初值的选择需要非常慎重，因为不同的初值会得到不同的收敛结果。

（3）依赖递推公式：迭代法需要依赖于递推公式，当递推公式难以求解或者导数难以计算时，迭代法的效果可能会受到影响。

二、牛顿迭代法1、牛顿迭代法的原理牛顿迭代法是一种利用函数的一阶导数和二阶导数来逼近根的方法。

对于一个非线性方程f(x)=0，设其在$x_0$处的导数不为0，则可以用如下公式进行迭代：$x_{n+1} = x_n −\frac {f(x_n)}{f′(x_n)}$其中$f'(x_n)$是$f(x_n)$的一阶导数。

迭代法求解⽅程（组）的根⾸先，迭代法解⽅程的实质是按照下列步骤构造⼀个序列x0,x1,…,xn,来逐步逼近⽅程f(x)=0的解:1）选取适当的初值x0；2）确定迭代格式，即建⽴迭代关系，需要将⽅程f(x)=0改写为x=φ(x)的等价形式；3) 构造序列x0，x1，……，xn，即先求得x1=φ(x0)，再求x2=φ(x1)，……如此反复迭代，就得到⼀个数列x0， x1，……，xn，若这个数列收敛，即存在极值，且函数φ(x)连续，则很容易得到这个极限值,x*就是⽅程f(x)=0的根。

举个例⼦：求解⽅程： f(x) =x^3-x-1=0 在区间（1，1.5）内的根。

⾸先我们将⽅程写成这种形式：⽤初始根x0=1.5带⼊右端，可以得到这时，x0和x1的值相差⽐较⼤，所以我们要继续迭代求解，将x1再带⼊公式得直到我们我们得到的解的序列收敛，即存在极值的时候，迭代结束。

下⾯是这个⽅程迭代的次数以及每次xi的解（i=0,1,2....）我们发现当k=7和8的时候，⽅程的解已经不再发⽣变化了，这时候我们就得到了此⽅程的近似解。

1#define eps 1e-82int main()3 {4 x0=初始近似根；5do{6 x1=x0;7 x0=g(x1); //按特定的⽅程计算新的近似根8 }while(fabs(x0-x1)>eps);9 printf("⽅程的近似根是%f\n",x0);10 }注意：如果⽅程⽆解，算法求出的近似根序列就不会收敛，那么迭代过程就会变成死循环。

因此，在使⽤迭代算法前应先考察⽅程是否有解，并在算法中对迭代次数给予限制。

下⾯再写⼀个求解⽅程组的例⼦加深⼀下理解：算法说明：⽅程组解的初值X=（x0，x1，…，xn-1）,迭代关系⽅程组为：xi=gi(X)(i=0,1,…,n-1),w为解的精度,maxn为迭代次数。

算法如下：算法核⼼：1int main()2 {3for (i=0; i<n; i++)4 x[i]=初始近似根;5do6 {7 k=k+1;8for(i=0; i<n; i++）9 y[i]=x[i];10for(i=0; i<n; i++)11 x[i]=gi(X); //按特定的⽅程计算新的近似根12 c=0;13for(i=0; i<n; i++)14 c=c+fabs(y[i]-x[i]);//c要每次重新设初值为015 }while(c>eps and k<maxn );16for(i=0; i<n; i++)17 print("变量的近似根是"，x[i]);18 }选取初始向量精确度为1e-8，迭代次数为100求解代码如下：1 #include<iostream>2 #include<cstdio>3 #include<cstring>4 #include<cmath>5#define eps 1e-86using namespace std;7const int maxn=100;8double x[10],y[10];9int main()10 {11for(int i=1;i<=4;i++)12 x[i]=0;13int cnt=0;14double c=0;15do{16for(int i=1;i<=4;i++)17 y[i]=x[i];18for(int i=1;i<=4;i++)19 {20 x[1]=(6+x[2]-2*x[3])/10;21 x[2]=(25+x[1]+x[3]-3*x[4])/11;22 x[3]=(-11-2*x[1]+x[2]+x[4])/10;23 x[4]=(15-3*x[2]+x[3])/8;24 }25 c=0;26for(int i=1;i<=4;i++)27 c+=(fabs(y[i]-x[i]));28 }while(c>eps&&cnt<maxn);29for(int i=1;i<=4;i++)30 printf("x%d = %.4lf\n",i,x[i]);31 }运⾏结果如下：迭代法求解⽅程的过程是多样化的，⽐如⼆分逼近法求解，⽜顿迭代法等。

高次方程的求解方法在数学中，高次方程是指其最高次数大于等于2的多项式方程。

对于高次方程的求解是数学中的重要课题之一。

本文将介绍几种常见的高次方程求解方法。

一、一元高次方程的求解方法一元高次方程是指只含有一个未知数的高次方程。

下面将介绍二次方程和三次方程的求解方法。

1. 二次方程的求解方法二次方程是指最高次数为2的一元方程。

一般形式为：ax^2 + bx + c = 0，其中a、b、c为已知常数，而x为未知数。

求解二次方程的一种常见方法是使用求根公式。

根据二次方程的解法，可以得到求根公式为：x = (-b ± √(b^2-4ac))/(2a)。

当求根公式中的判别式(b^2-4ac)大于零时，方程有两个不相等的实数根；当判别式等于零时，方程有两个相等的实数根；当判别式小于零时，方程有两个共轭复数根。

2. 三次方程的求解方法三次方程是指最高次数为3的一元方程。

一般形式为：ax^3 + bx^2 + cx + d = 0。

求解三次方程的一种常见方法是使用牛顿迭代法。

该方法通过不断逼近，寻找多项式的根。

牛顿迭代法的迭代公式为：x(n+1) = x(n) - f(x(n))/f'(x(n))，其中x(n+1)为下一个近似解，x(n)为当前的近似解，f(x(n))为方程的多项式函数值，f'(x(n))为多项式函数的导数值。

二、多元高次方程的求解方法多元高次方程是指含有多个未知数的高次方程。

下面将介绍二元高次方程和三元高次方程的求解方法。

1. 二元高次方程的求解方法二元高次方程是指含有两个未知数的高次方程。

一般形式为：f(x, y) = 0。

求解二元高次方程可以采用消元法或者代入法。

消元法是通过将一个未知数用另一个未知数表示，从而减少方程的未知数个数。

代入法是将一个未知数的表达式代入到另一个方程中，从而求解方程的解。

2. 三元高次方程的求解方法三元高次方程是指含有三个未知数的高次方程。

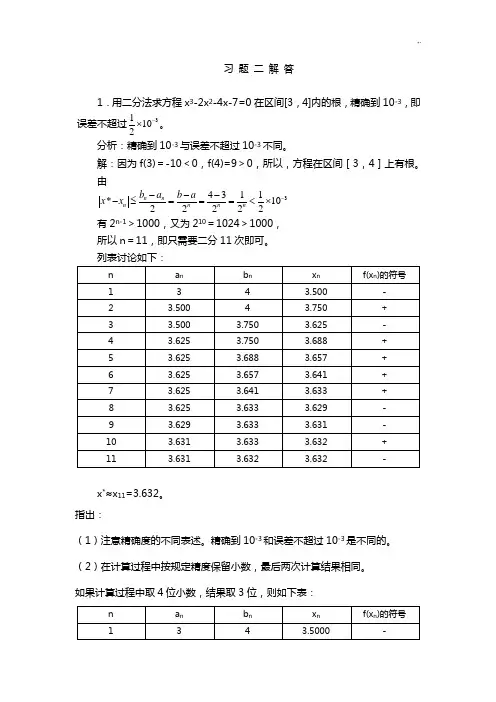
习 题 二 解 答1．用二分法求方程x 3-2x 2-4x-7=0在区间[3，4]内的根，精确到10-3，即误差不超过31102-⨯。

分析：精确到10-3与误差不超过10-3不同。

解：因为f(3)＝-10＜0，f(4)=9＞0，所以，方程在区间［3，4］上有根。

由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1＞1000，又为210＝1024＞1000， 所以n ＝11，即只需要二分11次即可。

x *≈x 11=3.632。

指出：（1）注意精确度的不同表述。

精确到10-3和误差不超过10-3是不同的。

（2）在计算过程中按规定精度保留小数，最后两次计算结果相同。

如果计算过程中取4位小数，结果取3位，则如下表：（3）用秦九韶算法计算f(x n )比较简单。

1*．求方程x 3-2x 2-4x-7=0的隔根区间。

解：令32247y x x x =---， 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时，有12223,x x =-=。

函数单调区间列表分析如下：因为214902150327(),()y y -=-<=-<，所以方程在区间223(,)-上无根； 因为21490327()y -=-<，而函数在23(,)-∞-上单调增，函数值不可能变号，所以方程在该区间上无根；因为2150()y =-<，函数在(2,+∞)上单调增，所以方程在该区间上最多有一个根，而(3)=-10<0,y(4)=9>0，所以方程在区间(3,4)有一个根。

所以，该方程有一个根，隔根区间是(3.4)。

2．证明1sin 0x x --=在[0,1]内有一个根，使用二分法求误差不大于41102-⨯的根，需要迭代多少次？分析：证明方程在指定区间内有一个根，就是证明相应的函数在指定区间有至少一个零点。

牛顿迭代法计算根号3牛顿迭代法是一种广泛应用于数学和科学计算中的方法，特别是求解方程根的微分方法，也是求解非线性方程的有效估计方式。

它的原理可以概括为，从一个初始猜测值开始，用迭代技术对待求根或零点的方程及其导数进行计算，每次迭代变化都与其初值有关，根据某种折中原则，不断改变初始猜测值，直至解取得满意的靠近精度或无限接近的精度。

本文将以求解根号3的牛顿迭代法为例，简要介绍牛顿迭代法的原理及几种求解方法。

求解根号3的牛顿迭代：牛顿迭代法的基本原理：牛顿迭代法的的基本原理即可以用x(n+1)=x(n)–y/y'的迭代步骤不断改变x的值，使其靠近真实的解，其中x(n)为第n步的迭代值，y=f(x)，y'=f'(x)。

首先，我们从任意一个非负数x(0)开始，然后按照公式x(n+1)=x(n)-y/y'计算出第二步的迭代值x(1)，依次类推计算出第三步、第四步……的迭代值，直至余数y小于设定值时，便可求出根号3。

牛顿迭代法计算根号3的步骤：第一步：计算f(x)的值，即被求的式子的值；第二步：计算f'(x)的值，即求出f(x)的导数；第三步：计算x(n+1)的值，即根号3的一个近似值，新的x的值；第四步：迭代，将第三步算出的x(n+1)代入第一步和第二步式子重新求解，来获得新的x(n+2)；第五步：重复第四步，直到x(n+2)与x(n+1)之间的差值满足预先设定的精度要求，即可求得根号3的近似值。

结论：牛顿迭代法是一种非常有用的数学计算方式，它可以有效的解决各种复杂的方程问题。

只要掌握了牛顿迭代法的基本原理，就可以使用这一计算方法来解决根号3的问题。