14-成像系统1-透镜的相位变换作用、透镜的傅里叶变换特性、课堂演示实验
- 格式:ppt
- 大小:1.15 MB
- 文档页数:40




傅里叶变换光学系统-实验报告————————————————————————————————作者: ————————————————————————————————日期:实验10 傅里叶变换光学系统实验时间:2014年3月20日 星期四一、 实验目的1. 了解透镜对入射波前的相位调制原理。
2. 加深对透镜复振幅、传递函数、透过率等参量的物理意义的认识。
3. 观察透镜的傅氏变换力图像,观察4f 系统的反傅氏变换的图像,并进行比较。
4. 在4f 系统的变换平面插入各种空间滤波器,观察各种试件相应的频谱处理图像。
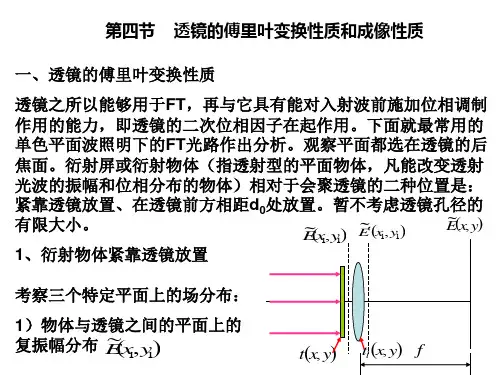
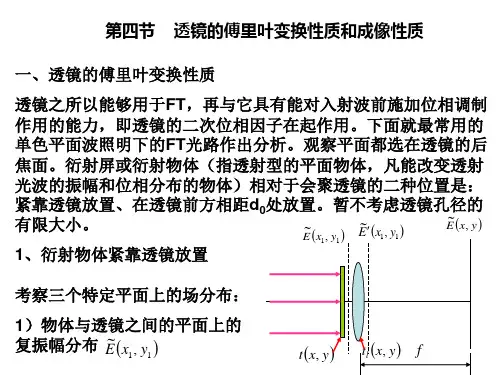
二、 实验原理1. 透镜的F T性质及常用函数与图形的关学频谱分析 透镜由于本身厚度的不同,使得入射光在通过透镜时,各处走过的光程差不同,即所受时间延迟不同,因而具有相位调制能力。
假设任意点入射光线在透镜中的传播距离等于改点沿光轴方向透镜的厚度,并忽略光强损失,即通过透镜的光波振幅分布不变,仅产生位相的变化,且其大小正比于透镜在该点的厚度。
设原复振幅分布为(,)L U x y 的光通过透镜后,其复振幅分布受到透镜的位相调制后变为(,)L U x y ':(,)(,)exp[(,)]L L U x y U x y j x y ϕ'= (1)若对于任意一点(x,y)透镜的厚度为(,)D x y ,透镜的中心厚度为0D 。
光线由该点通过透镜时在透镜中的距离为(,)D x y ,空气空的距离为0(,)D D x y -,透镜折射率为n,则该点的位相延迟因子(,)t x y 为:0(,)exp()exp[(1)(,)]t x y jkD jk n D x y =- (2)由此可见只要知道透镜的厚度函数(,)D x y 就可得出其相位调制。
在球面镜傍轴区域,用抛物面近似球面,并引入焦距f,有: 22012111(,)()()2D x y D x y R R =-+- (3)12111(1)()n f R R =-- (4) 220(,)exp()exp[()]2kt x y jknD jx y f=-+ (5) 第一项位相因子0exp()jknD 仅表示入射光波的常量位相延迟,不影响位相的空间分布,即波面形状,所以在运算过程中可以略去。




透镜傅里叶变换透镜傅立叶变换一、定义透镜傅立叶变换(Lens Fourier Transformation),是一种基于蒙特卡罗法(而不是傅立叶变换)的非线性变换,它利用光学镜头将光线聚集在非正弦函数中,从而将其转换为波形,生成新的函数,其中会出现极大的变化,有时被称为“大波形变换”。
二、原理透镜傅立叶变换是一种基于蒙特卡罗法的变换,它利用光学镜头将光线聚焦在一族非正弦函数中,从而转换成波形,看上去它们细微不同。
非正弦函数以一种分布变化的形式,把函数变成一种局部性。
透镜傅立叶变换是一种非线性变换,通过对数据进行非线性变换,可以把数据从某种特定的形式变换为另一种特定的形式。
它可以使数据和信号以新的方式展示出来,使得原本不能描述的特性可观察到,从而创造出新的信息。
三、应用1. 图像处理:利用透镜傅立叶变换,可以从图像中提取出特征和细节,这在图像压缩、模式识别、图像复原等方面具有重要的作用;2. 声音处理:透镜傅立叶变换可以精确定位和检测声音中的特定频率,从而实现音频处理;3. 量子计算:透镜傅立叶变换可以模拟量子里的特殊事件,从而帮助实现量子计算;4. 高斯投影:透镜傅立叶变换可以将几何图形映射到平行的高精度平面图上,从而实现高斯正变化;5. 光学成像:透镜傅立叶变换可以用来分析和估计光场的分布,以推导出小型微片、大型成像系统的行为。
四、优点1. 精确可控:透镜傅立叶变换对所处理数据的可控性非常强,变换的分布可以实时调节;2. 高效率:比起傅立叶变换,透镜傅立叶变换更加简单高效,一般来说比傅立叶变换快得多;3. 全面直观:透镜傅立叶变换可以更好地揭示数据背后潜在的一致性,能够全面直观地展示所传输的信息。
透镜的位相变换作用07094060 钱乔龙众所周知,平面波经过正透镜后变成会聚的球面波,平面波面变换成球面波面。
我们把透镜两个球面顶点上的切平面叫做它的输入面和输出面。
若一条光线在输入面上的(x , y ) 点入射,在相对的输出面上从近似相同的坐标处射出。
这就是说可以忽略了光线在透镜内部因折射而产生的垂轴平移,这样的透镜称为薄透镜。
透镜的厚度远小于两个球面的曲率半径时,都可以近似的看作薄透镜。
透镜一般是由光密物质构成的。
正透镜的中心区域厚,边缘区域薄。
线通过透镜时中心区域光学路程长,位相延迟大;边缘的光程短,位相延迟小,使光波的等相面改变了形状。
因而,一个薄透镜的作用只使入射光波的位相空间分布发生改变,是一种位相变换器。
如果略去透镜对光能量的吸收和反射损失,则透镜只改变入射光的空间位相分布。
因而它可以看作位相衍射屏。
透镜的位相变换作用可以用它的透射函数t (x , y ) 来表示。
考虑一个无吸收,无表面反射损失和无像差的薄透镜。
轴上一点物O到透镜的距离为d1。
在几何光学旁轴近似条件下,透镜将点O成像在I点处。
根据物像关系, I点到透镜顶点的距离d2=d1*f/(f-d1),其中f为透镜的焦距。
在透镜的两个顶点处,分别做参考平面p2和p3与之相切。
由于考虑的是薄透镜,故光线在p2面上的入射点与在p3面上的出射点可以用同一平面直角坐标(x ,y) 表示。
且由于 p2和p3两个平面相隔很近,可以认为这两个平面上对应的光振动,其振幅值是相等的。
若点物O发出一单位振幅的球面波,由菲涅耳近似,则在p2平面上的光场分布为下式:由于点物成像在I点,则入射球面波在透镜后p3平面上的光场,可以看成是以I为圆心,半径为d2的球面波,表示为如果以符号t 表示透镜对入射光场的作用因子则出射光场位相分布就等于因子t1乘以入射光场的位相分布。
则由上两式得:由于点O和点I之间是物象关系,所以物距d1和像距d2应满足透镜定律:。