Jitter Analysis_The dual-Dirac
- 格式:pdf
- 大小:275.89 KB
- 文档页数:16


第18卷 第6期 太赫兹科学与电子信息学报Vo1.18,No.6 2020年12月 Journal of Terahertz Science and Electronic Information Technology Dec.,2020 文章编号:2095-4980(2020)06-1003-07分布式相参雷达多脉冲积累相参参数估计方法王雪琦,涂刚毅,吴少鹏(中国船舶重工集团公司第七二四研究所,江苏南京 211106)摘 要:分布式相参雷达(DCAR)是目前国内外雷达领域的重要研究方向,精确的参数估计是实现其良好相参性能的前提和核心。
基于动目标模型,提出一种基于多脉冲积累的相参参数估计方法。
该方法通过对多脉冲信号进行快、慢时间匹配滤波处理,实现多脉冲相参积累;再利用互相关法进行相参参数估计。
仿真分析对比了不同脉冲个数和不同输入信噪比下的参数估计性能和相参性能,仿真结果表明,该方法具有可行性,且可以有效提高低信噪比情况下的参数估计性能和相参性能。
关键词:分布式相参;参数估计;动目标;多脉冲积累中图分类号:TN957.51文献标志码:A doi:10.11805/TKYDA2019182Coherent parameters estimation method for distributed coherent radarbased on multi-pulse accumulationWANG Xueqi,TU Gangyi,WU Shaopeng(No.724 Research Institute of CSIC,Nanjing Jiangshu 211106,China)Abstract:Distributed Coherent Aperture Radar(DCAR) is an important research direction in the field of radar at home and abroad. Accurate parameter estimation is the premise and core of good coherenceperformance. Based on the moving target model, a coherent parameter estimation method based onmulti-pulse accumulation is proposed. The method performs fast-time and slow-time match filtering formulti-pulse signals, and obtains the results of multi-pulse coherent accumulation. Then thecross-correlation method is utilized to estimate the coherent parameters. The performance of parameterestimation and correlation under different numbers of pulses and different input signal-to-noise ratios arecompared by simulation analysis. The simulation results show that the method is feasible and caneffectively improve the performance of parameter estimation and coherence in low signal-to-noise ratio.Keywords:distributed coherence;parameter estimation;moving target;multi-pulse accumulation分布式相参雷达(DCAR)因具有较好的探测性能、高角度分辨力、灵活性和机动性等一系列技术优势而成为目前国内外雷达领域研究热点[1-5]。


the dirac-delta sequence 术语概述及解释说明1. 引言1.1 概述在数学中,Dirac-Delta序列是一种特殊的函数序列,由英国物理学家保罗·狄拉克(Paul Dirac)于20世纪提出。
Dirac-Delta序列在数学分析、信号处理和物理学等领域广泛应用,它具有独特的性质和重要的应用价值。
1.2 文章结构本文将对Dirac-Delta序列进行详细的定义、性质与应用探讨,并分析Dirac序列与Dirac-Delta序列之间的关系。
文章结构如下所示:1. 引言2. 正文3. Dirac-Delta序列的定义与性质3.1 Dirac-Delta函数的引入3.2 Dirac-Delta序列的定义3.3 Dirac-Delta序列的性质与应用4. Dirac序列与Dirac-Delta序列之间的关系4.1 Dirac序列的定义与性质4.2 Dirac序列与Dirac-Delta函数的关系5. 结论通过以上结构,读者将逐步了解Dirac-Delta序列及其相关术语,并深入探讨其定义、性质以及应用方面。
1.3 目的本文旨在向读者介绍和解释Dirac-Delta序列这一重要的数学术语及其相关概念。
通过对其定义、性质与应用的详细说明,希望读者能够更加全面地理解和掌握该序列,在实际问题中能够正确运用并深化对其的认识。
同时,本文将分析Dirac序列与Dirac-Delta序列之间的关系,从而进一步拓展读者对于这两者的认知。
在阅读本文后,读者将能够清晰了解Dirac-Delta序列,并具备一定的基础来应用该概念解决实际问题。
希望本文能够为对数学有兴趣或从事相关领域研究的人士提供帮助,并推动更多关于Dirac-Delta序列的进一步研究和应用。
2. 正文正文部分将对Dirac-Delta序列的相关概念进行详细解释和说明。
首先,我们会介绍Dirac函数的引入,然后给出Dirac-Delta序列的定义,并讨论其性质和应用。

Maxim > App Notes > High-Speed Interconnect Oscillators/Delay Lines/Timers/CountersDec 10, 2004 Keywords: CLK jitter, clock jitter, phase noise, phase noise conversion, phase noise measurement, jittermeasurement, jitter and phase noise, phase noise calculation, timing errorAPPLICATION NOTE 3359Clock (CLK) Jitter and Phase Noise ConversionAbstract: This application note on clock (CLK) signal quality describes how to measure jitter and phase-noise, including period jitter, cycle-to-cycle jitter, and accumulated jitter. It describes the relationship between period jitter and phase-noise spectrum and how to convert the phase-noise spectrum to the period jitter.Clock (CLK) signals are required in almost every integrated circuit or electrical system. In today's world, digital data is processed or transmitted at higher and higher speeds, while the conversions between analog and digital signals are done at higher resolutions and higher data rates. These functions require engineers to pay special attention to the quality of clock signals.Clock quality is usually described by jitter or phase-noise measurements. The often-used jitter measurements are period jitter, cycle-to-cycle jitter, and accumulated jitter. Among these jitters, period jitter is most often encountered. Clock phase-noise measurement examines the spectrum of the clock signal.This article first briefly reviews the measurement setups for clock period jitter and phase noise. The relationship between the period jitter and the phase-noise spectrum is then described. Finally, a simple equation to convert the phase-noise spectrum to the period jitter is presented.Period Jitter and Phase Noise: Definition and MeasurementPeriod JitterPeriod jitter (J PER) is the time difference between a measured cycle period and the ideal cycle period. Due to its random nature, this jitter can be measured peak-to-peak or by root of mean square (RMS). We begin by defining the clock rising-edge crossing point at the threshold V TH as T PER(n), where n is the time domain index, as shown in Figure 1. Mathematically, we can describe J PER as:where T0 is the period of the ideal clock cycle. Since the clock frequency is constant, the random quantity J PERmust have a zero mean. Thus the RMS of J PER can be calculated by:where <•> is the expected operation. Figure 1 shows the relation between J PER and T PER in a clock waveform.Figure 1. Period jitter measurement.Phase-Noise SpectrumTo understand the definition of the phase-noise spectrum L(f), we first define the power spectrum density of a clock signal as S C(f). The S C(f) curve results when we connect the clock signal to a spectrum analyzer. The phase-noise spectrum L(f) is then defined as the attenuation in dB from the peak value of S C(f) at the clock frequency, f C, to a value of S C(f) at f. Figure 2 illustrates the definition of L(f).Figure 2. Definition of phase-noise spectrum.Mathematically, the phase-noise spectrum L(f) can be written as:Remember that L(f) presents the ratio of two spectral amplitudes at the frequencies, f C and f. The meaning of L(f) will be discussed in next section.Period Jitter (J PER) MeasurementThere are different instruments used to measure the period jitter. People most commonly use a high-precisiondigital oscilloscope to conduct the measurement. When the clock jitter is more than 5 times larger than the oscilloscope's triggering jitter, the clock jitter can be acquired by triggering at a clock rising edge and measuring it at the next rising edge. Figure 3 shows a splitter generating the trigger signal from the clock under test. This method eliminates the internal jitter from the clock source in the digital oscilloscope.Figure 3. Self-trigger jitter measurement setup.It is possible for the duration of scope trigger-delay to be longer than the period of a high-frequency clock. In that case, one must insert a delay unit in the setup that delays the first rising edge after triggering so that it can be seen on the screen.There are more accurate methods for measuring jitter. Most of these approaches use a post-sampling process of the data sampled from high-speed digital oscilloscopes to estimate the jitter according to the definitions in Equations 1 or 2. This post-sampling approach provides high-precision results, but it can only be performed with high-end digital oscilloscopes [2, 3].Phase-Noise Spectrum L(f) MeasurementAs Equation 3 showed above, L(f) can be measured with a spectrum analyzer directly from the spectrum, S C(f), of the clock signal. This approach, however, is not practical. The value of L(f) is usually larger than 100dBc which exceeds the dynamic range of most spectrum analyzers. Moreover, f C can sometimes be higher than the input-frequency limit of the analyzer. Consequently, the practical way to measure the phase noise uses a setup that eliminates the spectrum energy at f C. This approach is similar to the method of demodulating a passband signal to baseband. Figure 4 illustrates this practical setup and the signal-spectrum changes at different points in the test setup.Figure 4. Practical phase-noise measurement setup.The structure described in Figure 4 is typically called a carrier-suppress demodulator. In Figure 4, n(t) is the input to the spectrum analyzer. We will next show that by scaling down the spectrum of n(t) properly, we can obtain the dBc value of L(f).Relation between RMS Period Jitter and Phase NoiseUsing the Fourier series expansion, it can be shown that a square-wave clock signal has the same jitter behavior as its base harmonic sinusoid signal. This property makes the jitter analysis of a clock signal much easier. A sinusoid signal of a clock signal with phase noise can be written as:and the period jitter is:From Equation 4 we see that the sinusoid signal is phase modulated by the phase noise Θ(t). As the phase noise is always much smaller than π/2, Equation 4 can be approximated as:The spectrum of C(t) is then:where SΘ(f) is the spectrum of q(t). Using the definition of L(f), we can find:This illustrates that L(f) is just SΘ(f) presented in dB. This also explains the real meaning of L(f).We have now shown that the setup in Figure 4 enables the measurement of L(f). Furthermore, one can see that the signal C(t) is mixed with cos(2πf C t) and filtered by the lowpass filter. Thus, we can express the signal n(t) at the input of the spectrum analyzer as:The spectrum appears on the spectrum analyzer as:Therefore we can obtain the phase noise spectrum SΘ(f) and L(f):Then L(f) can be read in dBc directly from the spectrum of n(t) after scaled down by A²/4.From Equation 11, the mean square (MS) of Θ(t) can be calculated by:Following Equation 5 above, we finally show the relationship between the period jitter, J PER, and the phase noise spectrum, L(f), as:In some applications like SONET and 10Gb, engineers only monitor the jitter at a certain frequency band. In such acase, the RMS J PER within a certain band can be calculated by:Approximation of RMS J PER from L(f)The phase noise usually can be approximated by a linear piece-wise function when the frequency axis of L(f) is in log scale. In such a case, L(f) can be written as:where K-1 is the number of the pieces of the piece-wise function and U(f) is the step function. See Figure 5.Figure 5. A typical L(f) function.If we substitute L(f) shown in Equation 15 into Equation 14, we have:To illustrate this, the following table presents a piecewise L(f) function with f C = 155.52MHz.Table 1. Measurements of Function L(f).Frequency (Hz)101000300010000L(f) (dBc)-58-118-132-137Next we calculate the a i and b i by:The results are listed in Table 2.Table 2. Parameters to Present L(f) as a Piecewise Function.i1234f i (Hz)101000300010000a i (dBc/decade)-30-29.34-9.5N/Ab i (dBc)-58-118-132-137Substituting the Table 2 values into Equation 16, we get:The RMS jitter of the same clock measured by the setup in Figure 4 at the same band is 4.2258ps. Therefore, the proposed approximation approach for converting phase noise to jitter has proved quite accurate. In this example, the error is less than 4%.Equation 16 can also be used to estimate the required jitter limit when the phase-noise spectrum envelope is given.A simple spreadsheet file has been posted with the equation coded as an example.SummaryThis article demonstrates the exact mathematical relationship between jitter measured in time and the phase-noise measured in frequency. Many engineers concerned with signal integrity and system timing frequently question this relationship. The results presented here clearly answer the question. Based on that mathematical relationship, weproposed a method for estimating the period jitter from the phase-noise spectrum. Engineers can use this method to quickly establish a quantitative relationship between the two measurements, which will help greatly in the application or design of systems and circuits.Reference1. SEMI G80-0200, "Test Method for the Analysis of Overall Digital Timing Accuracy for Automated TestEquipment".2. Tektronix Application Note: "Understanding and Characterizing Timing Jitter"3. LeCroy White Paper: "The Accuracy of Jitter Measurements"4. David Chandler, "Phase Jitter-Phase Noise and VCXO," Corning Frequency Control Inc.Related PartsMAX9485:QuickView-- Full (PDF) Data Sheet-- Free SamplesMAX9486:QuickView-- Full (PDF) Data Sheet-- Free SamplesMAX9489:QuickView-- Full (PDF) Data SheetAutomatic UpdatesWould you like to be automatically notified when new application notes are published in your areas of interest? Sign up for EE-Mail™.Application note 3359: /an3359More InformationFor technical support: /supportFor samples: /samplesOther questions and comments: /contactAN3359, AN 3359, APP3359, Appnote3359, Appnote 3359Copyright © by Maxim Integrated ProductsAdditional legal notices: /legal。





AAbsolutely integrable 绝对可积Absolutely integrable impulse response 绝对可积冲激响应Absolutely summable 绝对可和Absolutely summable impulse response 绝对可和冲激响应Accumulator 累加器Acoustic 声学Adder 加法器Additivity property 可加性Aliasing 混叠现象All-pass systems 全通系统AM (Amplitude modulation ) 幅度调制Amplifier 放大器Amplitude modulation (AM) 幅度调制Amplitude-scaling factor 幅度放大因子Analog-to-digital (A-to-D) converter 模数转换器Analysis equation 分析公式(方程)Angel (phase) of complex number 复数的角度(相位)Angle criterion 角判据Angle modulation 角度调制Anticausality 反因果Aperiodic 非周期Aperiodic convolution 非周期卷积Aperiodic signal 非周期信号Asynchronous 异步的Audio systems 音频(声音)系统Autocorrelation functions 自相关函数Automobile suspension system 汽车减震系统Averaging system 平滑系统BBand-limited 带(宽)限的Band-limited input signals 带限输入信号Band-limited interpolation 带限内插Bandpass filters 带通滤波器Bandpass signal 带通信号Bandpass-sampling techniques 带通采样技术Bandwidth 带宽Bartlett (triangular) window 巴特利特(三角形)窗Bilateral Laplace transform 双边拉普拉斯变换Bilinear 双线性的Bilinear transformation 双线性变换Bit (二进制)位,比特Block diagrams 方框图Bode plots 波特图Bounded 有界限的Break frequency 折转频率Butterworth filters 巴特沃斯滤波器C“Chirp” transform algorithm“鸟声”变换算法Capacitor 电容器Carrier 载波Carrier frequency 载波频率Carrier signal 载波信号Cartesian (rectangular) form 直角坐标形式Cascade (series) interconnection 串联,级联Cascade-form 串联形式Causal LTI system 因果的线性时不变系统Channel 信道,频道Channel equalization 信道均衡Chopper amplifier 斩波器放大器Closed-loop 闭环Closed-loop poles 闭环极点Closed-loop system 闭环系统Closed-loop system function 闭环系统函数Coefficient multiplier 系数乘法器Coefficients 系数Communications systems 通信系统Commutative property 交换性(交换律)Compensation for nonideal elements 非理想元件的补偿Complex conjugate 复数共轭Complex exponential carrier 复指数载波Complex exponential signals 复指数信号Complex exponential(s) 复指数Complex numbers 复数Conditionally stable systems 条件稳定系统Conjugate symmetry 共轭对称Conjugation property 共轭性质Continuous-time delay 连续时间延迟Continuous-time filter 连续时间滤波器Continuous-time Fourier series 连续时间傅立叶级数Continuous-time Fourier transform 连续时间傅立叶变换Continuous-time signals 连续时间信号Continuous-time systems 连续时间系统Continuous-to-discrete-time conversion 连续时间到离散时间转换Convergence 收敛Convolution 卷积Convolution integral 卷积积分Convolution property 卷积性质Convolution sum 卷积和Correlation function 相关函数Critically damped systems 临界阻尼系统Crosss-correlation functions 互相关函数Cutoff frequencies 截至频率DDamped sinusoids 阻尼正弦振荡Damping ratio 阻尼系数Dc offset 直流偏移Dc sequence 直流序列Deadbeat feedback systems 临界阻尼反馈系统Decibels (dB) 分贝Decimation 抽取Decimation and interpolation 抽取和内插Degenerative (negative) feedback 负反馈Delay 延迟Delay time 延迟时间Demodulation 解调Difference equations 差分方程Differencing property 差分性质Differential equations 微分方程Differentiating filters 微分滤波器Differentiation property 微分性质Differentiator 微分器Digital-to-analog (D-to-A) converter 数模转换器Direct Form I realization 直接I型实现Direct form II realization 直接II型实现Direct-form 直接型Dirichlet conditions 狄里赫利条件Dirichlet, P.L. 狄里赫利Discontinuities 间断点,不连续Discrete-time filters 离散时间滤波器Discrete-time Fourier series 离散时间傅立叶级数Discrete-time Fourier series pair 离散时间傅立叶级数对Discrete-time Fourier transform (DFT)离散时间傅立叶变换Discrete-time LTI filters 离散时间线性时不变滤波器Discrete-time modulation 离散时间调制Discrete-time nonrecursive filters 离散时间非递归滤波器Discrete-time signals 离散时间信号Discrete-time systems 离散时间系统Discrete-time to continuous-time离散时间到连续时间转换conversionDispersion 弥撒(现象)Distortion 扭曲,失真Distribution theory(property)分配律Dominant time constant 主时间常数Double-sideband modulation (DSB) 双边带调制Downsampling 减采样Duality 对偶性EEcho 回波Eigenfunctions 特征函数Eigenvalue 特征值Elliptic filters 椭圆滤波器Encirclement property 围线性质End points 终点Energy of signals 信号的能量Energy-density spectrum 能量密度谱Envelope detector 包络检波器Envelope function 包络函数Equalization 均衡化Equalizer circuits 均衡器电路Equation for closed-loop poles 闭环极点方程Euler, L. 欧拉Euler’s relation欧拉关系(公式)Even signals 偶信号Exponential signals 指数信号Exponentials 指数FFast Fourier transform (FFT) 快速傅立叶变换Feedback 反馈Feedback interconnection 反馈联结Feedback path 反馈路径Filter(s) 滤波器Final-value theorem 终值定理Finite impulse response (FIR) 有限长脉冲响应Finite impulse response (FIR) filters 有限长脉冲响应滤波器 Finite sum formula 有限项和公式 Finite-duration signals 有限长信号 First difference 一阶差分 First harmonic components 基波分量 (一次谐波分量) First-order continuous-time systems 一阶连续时间系统 First-order discrete-time systems 一阶离散时间系统 First-order recursive discrete-timefilters一阶递归离散时间滤波器First-order systems 一阶系统 Forced response 受迫响应 Forward path 正向通路 Fourier series 傅立叶级数 Fourier transform 傅立叶变换 Fourier transform pairs 傅立叶变换对 Fourier, Jean Baptiste Joseph 傅立叶(法国数学家,物理学家) Frequency response 频率响应 Frequency response of LTI systems 线性时不变系统的频率响应 Frequency scaling of continuous-time Fourier transform 连续时间傅立叶变化的频率尺度(变换性质) Frequency shift keying (FSK) 频移键控 Frequency shifting property 频移性质 Frequency-division multiplexing (FDM) 频分多路复用 Frequency-domain characterization 频域特征 Frequency-selective filter 频率选择滤波器 Frequency-shaping filters 频率成型滤波器 Fundamental components 基波分量 Fundamental frequency 基波频率 Fundamental period 基波周期GGain 增益 Gain and phase margin 增益和相位裕度 General complex exponentials 一般复指数信号 Generalized functions 广义函数 Gibbs phenomenon 吉伯斯现象 Group delay 群延迟HHalf-sample delay 半采样间隔时延 Hanning window 汉宁窗 Harmonic analyzer 谐波分析议 Harmonic components 谐波分量Harmonically related 谐波关系Heat propagation and diffusion 热传播和扩散现象Higher order holds 高阶保持Highpass filter 高通滤波器Highpass-to-lowpass transformations 高通到低通变换Hilbert transform 希尔波特滤波器Homogeneity (scaling) property 齐次性(比例性)IIdeal 理想的Ideal bandstop characteristic 理想带阻特征Ideal frequency-selective filter 理想频率选择滤波器Idealization 理想化Identity system 恒等系统Imaginary part 虚部Impulse response 冲激响应Impulse train 冲激串Incrementally linear systems 增量线性系统Independent variable 独立变量Infinite impulse response (IIR) 无限长脉冲响应Infinite impulse response (IIR) filters 无限长脉冲响应滤波器Infinite sum formula 无限项和公式Infinite taylor series 无限项泰勒级数Initial-value theorem 初值定理Inpulse-train sampling 冲激串采样Instantaneous 瞬时的Instantaneous frequency 瞬时频率Integration in time-domain 时域积分Integration property 积分性质Integrator 积分器Interconnection 互联Intermediate-frequency (IF) stage 中频级Intersymbol interference (ISI) 码间干扰Inverse Fourier transform 傅立叶反变换Inverse Laplace transform 拉普拉斯反变换Inverse LTI system 逆线性时不变系统Inverse system design 逆系统设计Inverse z-transform z反变换Inverted pendulum 倒立摆Invertibility of LTI systems 线性时不变系统的可逆性Invertible systems 逆系统LLag network 滞后网络Lagrange, J.L. 拉格朗日(法国数学家,力学家)Laplace transform 拉普拉斯变换Laplace, P.S. de 拉普拉斯(法国天文学家,数学家)lead network 超前网络left-half plane 左半平面left-sided signal 左边信号Linear 线性Linear constant-coefficient difference线性常系数差分方程equationsLinear constant-coefficient differential线性常系数微分方程equationsLinear feedback systems 线性反馈系统Linear interpolation 线性插值Linearity 线性性Log magnitude-phase diagram 对数幅-相图Log-magnitude plots 对数模图Lossless coding 无损失码Lowpass filters 低通滤波器Lowpass-to-highpass transformation 低通到高通的转换LTI system response 线性时不变系统响应LTI systems analysis 线性时不变系统分析MMagnitude and phase 幅度和相位Matched filter 匹配滤波器Measuring devices 测量仪器Memory 记忆Memoryless systems 无记忆系统Modulating signal 调制信号Modulation 调制Modulation index 调制指数Modulation property 调制性质Moving-average filters 移动平均滤波器Multiplexing 多路技术Multiplication property 相乘性质Multiplicities 多样性NNarrowband 窄带Narrowband frequency modulation 窄带频率调制Natural frequency 自然响应频率Natural response 自然响应Negative (degenerative) feedback 负反馈Nonanticipatibe system 不超前系统Noncausal averaging system 非因果平滑系统Nonideal 非理想的Nonideal filters 非理想滤波器Nonmalized functions 归一化函数Nonrecursive 非递归Nonrecursive filters 非递归滤波器Nonrecursive linear constant-coefficient非递归线性常系数差分方程difference equationsNyquist frequency 奈奎斯特频率Nyquist rate 奈奎斯特率Nyquist stability criterion 奈奎斯特稳定性判据OOdd harmonic 奇次谐波Odd signal 奇信号Open-loop 开环Open-loop frequency response 开环频率响应Open-loop system 开环系统Operational amplifier 运算放大器Orthogonal functions 正交函数Orthogonal signals 正交信号Oscilloscope 示波器Overdamped system 过阻尼系统Oversampling 过采样Overshoot 超量PParallel interconnection 并联Parallel-form block diagrams 并联型框图Parity check 奇偶校验检查Parseval’s relatio n 帕斯伐尔关系(定理)Partial-fraction expansion 部分分式展开Particular and homogeneous solution 特解和齐次解Passband 通频带Passband edge 通带边缘Passband frequency 通带频率Passband ripple 通带起伏(或波纹)Pendulum 钟摆Percent modulation 调制百分数Periodic 周期的Periodic complex exponentials 周期复指数Periodic convolution 周期卷积Periodic signals 周期信号Periodic square wave 周期方波Periodic square-wave modulating signal 周期方波调制信号Periodic train of impulses 周期冲激串Phase (angle) of complex number 复数相位(角度)Phase lag 相位滞后Phase lead 相位超前Phase margin 相位裕度Phase shift 相移Phase-reversal 相位倒置Phase modulation 相位调制Plant 工厂Polar form 极坐标形式Poles 极点Pole-zero plot(s) 零极点图Polynomials 多项式Positive (regenerative) feedback 正(再生)反馈Power of signals 信号功率Power-series expansion method 幂级数展开的方法Principal-phase function 主值相位函数Proportional (P) control 比例控制Proportional feedback system 比例反馈系统Proportional-plus-derivative 比例加积分Proportional-plus-derivative feedback 比例加积分反馈Proportional-plus-integral-plus-比例-积分-微分控制differential (PID) controlPulse-amplitude modulation 脉冲幅度调制Pulse-code modulation 脉冲编码调制Pulse-train carrier 冲激串载波QQuadrature distortion 正交失真Quadrature multiplexing 正交多路复用Quality of circuit 电路品质(因数)RRaised consine frequency response 升余弦频率响应Rational frequency responses 有理型频率响应Rational transform 有理变换RC highpass filter RC 高阶滤波器RC lowpass filter RC 低阶滤波器Real 实数Real exponential signals 实指数信号Real part 实部Rectangular (Cartesian) form 直角(卡笛儿)坐标形式Rectangular pulse 矩形脉冲Rectangular pulse signal 矩形脉冲信号Rectangular window 矩形窗口Recursive (infinite impulse response)递归(无时限脉冲响应)滤波器filtersRecursive linear constant-coefficient递归的线性常系数差分方程difference equationsRegenerative (positive) feedback 再生(正)反馈Region of comvergence 收敛域right-sided signal 右边信号Rise time 上升时间Root-locus analysis 根轨迹分析(方法)Running sum 动求和SS domain S域Sampled-data feedback systems 采样数据反馈系统Sampled-data systems 采样数据系统Sampling 采样Sampling frequency 采样频率Sampling function 采样函数Sampling oscilloscope 采样示波器Sampling period 采样周期Sampling theorem 采样定理Scaling (homogeneity) property 比例性(齐次性)性质Scaling in z domain z域尺度变换Scrambler 扰频器Second harmonic components 二次谐波分量Second-order 二阶Second-order continuous-time system 二阶连续时间系统Second-order discrete-time system 二阶离散时间系统Second-order systems 二阶系统sequence 序列Series (cascade) interconnection 级联(串联)Sifting property 筛选性质Sinc functions sinc函数Single-sideband 单边带Single-sideband sinusoidal amplitude单边带正弦幅度调制modulationSingularity functions 奇异函数Sinusoidal 正弦(信号)Sinusoidal amplitude modulation 正弦幅度调制Sinusoidal carrier 正弦载波Sinusoidal frequency modulation 正弦频率调制Sliding 滑动Spectral coefficient 频谱系数Spectrum 频谱Speech scrambler 语音加密器S-plane S平面Square wave 方波Stability 稳定性Stabilization of unstable systems 不稳定系统的稳定性(度)Step response 阶跃响应Step-invariant transformation 阶跃响应不定的变换Stopband 阻带Stopband edge 阻带边缘Stopband frequency 阻带频率Stopband ripple 阻带起伏(或波纹)Stroboscopic effect 频闪响应Summer 加法器Superposition integral 叠加积分Superposition property 叠加性质Superposition sum 叠加和Suspension system 减震系统Symmetric periodic 周期对称Symmetry 对称性Synchronous 同步的Synthesis equation 综合方程System function(s) 系统方程TTable of properties 性质列表Taylor series 泰勒级数Time 时间,时域Time advance property of unilateral z-单边z变换的时间超前性质transformTime constants 时间常数Time delay property of unilateral z-单边z变换的时间延迟性质transformTime expansion property 时间扩展性质Time invariance 时间变量Time reversal property 时间反转(反褶)性Time scaling property 时间尺度变换性Time shifting property 时移性质Time window 时间窗口Time-division multiplexing (TDM) 时分复用Time-domain 时域Time-domain properties 时域性质Tracking system (s) 跟踪系统Transfer function 转移函数transform pairs 变换对Transformation 变换(变形)Transition band 过渡带Transmodulation (transmultiplexing) 交叉调制Triangular (Barlett) window 三角型(巴特利特)窗口Trigonometric series 三角级数Two-sided signal 双边信号Type l feedback system l 型反馈系统UUint impulse response 单位冲激响应Uint ramp function 单位斜坡函数Undamped natural frequency 无阻尼自然相应Undamped system 无阻尼系统Underdamped systems 欠阻尼系统Undersampling 欠采样Unilateral 单边的Unilateral Laplace transform 单边拉普拉斯变换Unilateral z-transform 单边z变换Unit circle 单位圆Unit delay 单位延迟Unit doublets 单位冲激偶Unit impulse 单位冲激Unit step functions 单位阶跃函数Unit step response 单位阶跃响应Unstable systems 不稳定系统Unwrapped phase 展开的相位特性Upsampling 增采样VVariable 变量WWalsh functions 沃尔什函数Wave 波形Wavelengths 波长Weighted average 加权平均Wideband 宽带Wideband frequency modulation 宽带频率调制Windowing 加窗zZ domain z域Zero force equalizer 置零均衡器Zero-Input response 零输入响应Zero-Order hold 零阶保持Zeros of Laplace transform 拉普拉斯变换的零点Zero-state response 零状态响应z-transform z变换z-transform pairs z变换对。
时钟抖动(ClockJitter)和时钟偏斜(ClockSkew)系统时序设计中对时钟信号的要求是⾮常严格的,因为我们所有的时序计算都是以恒定的时钟信号为基准。
但实际中时钟信号往往不可能总是那么完美,会出现抖动(Jitter)和偏移(Skew)问题。
所谓抖动(jitter),就是指两个时钟周期之间存在的差值,这个误差是在时钟发⽣器内部产⽣的,和晶振或者PLL内部电路有关,布线对其没有影响。
如下图所⽰:除此之外,还有⼀种由于周期内信号的占空⽐发⽣变化⽽引起的抖动,称之为半周期抖动。
总的来说,jitter可以认为在时钟信号本⾝在传输过程中的⼀些偶然和不定的变化之总和。
时钟偏斜(skew)是指同样的时钟产⽣的多个⼦时钟信号之间的延时差异。
它表现的形式是多种多样的,既包含了时钟驱动器的多个输出之间的偏移,也包含了由于PCB⾛线误差造成的接收端和驱动端时钟信号之间的偏移。
时钟偏斜指的是同⼀个时钟信号到达两个不同寄存器之间的时间差值,时钟偏斜永远存在,到⼀定程度就会严重影响电路的时序。
如下图所⽰:信号完整性对时序的影响,⽐如串扰会影响微带线传播延迟;反射会造成数据信号在逻辑门限附近波动,从⽽影响最⼤/最⼩飞⾏时间;时钟⾛线的⼲扰会造成⼀定的时钟偏移。
有些误差或不确定因素是仿真中⽆法预见的,设计者只有通过周密的思考和实际经验的积累来逐步提⾼系统设计的⽔平。
Clock skew 和Clock jitter 是影响时钟信号稳定性的主要因素。
很多书⾥都从不同⾓度⾥对它们进⾏了解释。
其中“透视”⼀书给出的解释最为本质:Clock Skew: The spatial variation in arrival time of a clock transition on an integrated circuit;Clock jitter: The temporal vatiation of the clock period at a given point on the chip;简⾔之,skew通常是时钟相位上的不确定,⽽jitter是指时钟频率上的不确定(uncertainty)。
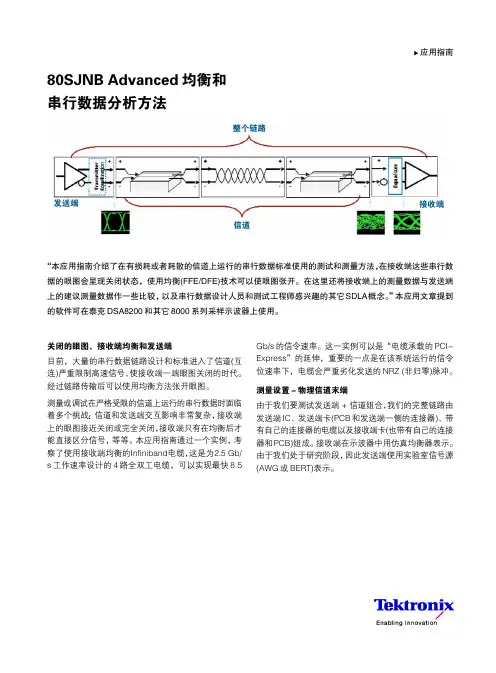
如何进行PCI-Express的一致性测试和分析泰克(中国)有限公司高级应用工程师 曾志摘要:PCI-Express串行标准越来越广泛地在计算机行业应用,作为芯片与芯片之间,系统与插卡之间,系统与系统之间的高速连接,由于不同设备可能由不同的厂商提供,为了保证设备之间可靠的互联互通,必须对其接口进行一致性测试。
同时高速串行信号容易对系统内部或者外部产生EMI辐射和干扰,PCIE标准定义了SSC(扩频时钟)来减少EMI,但是SSC如果使用不当的话也可能会影响接口互联的可靠性。
本文介绍如何根据PCIE的标准及其众多的子标准定义的测试规范和分析方法进行一致性测试,同时讨论如何对SSC(扩频时钟)进行验证和分析。
关键词:PCI-Express,PLL(锁相环),时钟恢复,眼图,抖动,模板,SSC(扩频时钟)。
引言:随着计算机及通讯设备的性能要求越来越高,传统的低速的并行总线如PCI等的数据吞吐量已经无法满足要求,PCI Sig组织联合了一线的芯片厂商和测试测量仪器厂商制定了PCI-Express Rev1.0的规范,将串行数据速率提高到2.5Gbps,数据带宽提高到32个Lane即80Gbps,而且明确要求对宣称支持该规范的芯片和接口进行一致性测试,在PCI-Express Rev1.0A的规范实施后,PCI Sig 又对规范进行了更新,Release了PCI-Express Rev1.1的规范,对抖动测试方法作了修改。
同时,对于PCI-Express在不同环境上的实现,又制定了相应的子规范,如Base,CEM,Express module,cable 等。
最近,PCI Sig组织在讨论和制定PCIE 2.0的规范,将数据速率提高到5Gbps.并制定了相应的眼图和抖动分析方法. PCI-Express规范的不同版本及其子规范有合起来有9个以上,往往使测试工程在对不同的PCIE实现选择何种标准无所适从。
一、在一致性测试中如何根据不同的标准选择相应的模板以及PLL模型进行眼图和抖动测量。
信号完整性分析基础系列之五--抖动的分类一、峰峰值抖动、均方根抖动过去多年来用于量化抖动的最常用的方法是峰峰值抖动(Peak-to-peak Jitter)和均方根抖动(Root-Mean-Square Jitter,抖动直方图或者抖动分布的1 或者RMS 值)。
但是由于随机抖动以及非固定抖动的存在,使得抖动的峰峰值随着观察样本数量的增加而增加,因此说峰峰值抖动参数用于衡量固有抖动会很有效,但是衡量随机性抖动却会出现很大误差;相同的道理,由于固有抖动及非高斯性抖动和噪声的存在,使得抖动的直方图或者分布图不呈现完全的高斯分布,因此统计得到的抖动的1σ或者RMS值不等于真实高斯分布的1 值。
峰峰值抖动和均方根抖动均是对某一类抖动的统计分析指标。
二、相位抖动、周期抖动、相邻周期间抖动由于时钟系统是数字电路系统非常关键的一部分,直接决定了数据信号发送和接收的成败,是整个系统的主动脉,因此时钟的抖动一直备受关注。
描述时钟系统的抖动参量一般分为三类,即相位抖动(Phase jitter)、周期抖动(Period jitter)、相邻周期间抖动(Cycle to cycle jitter).1、相位抖动在数字系统中,两个逻辑电平之间的切换通常伴随着快沿的出现,这些边沿在时序上的不稳定性就叫做相位抖动(phase jitter,有时也叫累积抖动,accumulated jitter,指实际边沿位置与理想边沿位置的偏差,以时间为单位,也可以换算成弧度,角度等);相位抖动是相位噪声在数字域的等效体现,它是离散量,因此只有当边沿存在时候才有定义。
理想边沿位置一般定义在数字信号一个比特位时间间隔的整数倍位置处。
如下图1 所示为某一不会直接使用时钟的边沿来保证时序关系,而是看周期的稳定性,也就是周期的抖动,有时候时钟周期越长,可能带来保持时间余量不足。
安捷伦⽰波器使⽤⽅法Jitter Analysis Techniques Using an Agilent Infiniium OscilloscopeProduct NoteIntroductionWith higher-speed clocking and data transmission schemes in the computer and communications industries, timing margins are becoming increasingly tight.Sophisticated techniques are required to ensure that timing margins are being met and to find the source of problems if they are not.This product note discussesvarious techniques for measuring jitter and points out theiradvantages and disadvantages. It describes how to set up an Agilent Infiniium oscilloscope to make effective jitter measure-ments and the accuracy of these measurements. Some of themeasurement techniques are only available on Agilent 54845A/B and 54846A/B oscilloscopes with version A.04.00 or later software.These measurement techniques are indicated as such in the text.Jitter FundamentalsJitter is defined as the deviation of a transition from its ideal time.Jitter can be measured relative to an ideal time or to another transition. Several factors can affect jitter. Since jitter sources are independent of each other,a system will rarely encounter a worst-case jitter scenario. Only when each independent jitter source is at its worst and is aligned with the other sources will this occur. As a result, jitter is statistical in nature. Predicting the worst-case jitter in a system can take time.Jitter can be broken down into two categories:Random jitter is uncorrelated jitter caused by thermal or other physical, randomprocesses. The shape of the jitter distribution is Gaussian.For example, a well-behaved phase lock loop (PLL) wanders randomly around its nominal clock frequency.?Deterministic or systematic jitter can be caused by inter-symbol interference,crosstalk, sub-harmonicdistortion and other spurious events such as power-supply switching. It is important to understand the nature of the jitter to help diagnose its cause and, if possible, correct it. Deterministic jitter is more easily reduced or eliminated once the source has been identified.Jitter Measurement TechniquesThis product note will discuss four methods that can be used to characterize jitter in a system:Infinite persistenceHistogramsMeasurement statisticsMeasurement functionsInfinite PersistenceAgilent’s Infiniium oscilloscopes present several different views of jitter. One way to measure jitter is to trigger on one waveform edge and look at another edge while infinite persistence is turned on. To use this technique, set up the scope to trigger on a rising or falling edge and set the horizontal scale to examine the next rising or falling edge. In the Display dialog box, set persistence to infinite.This technique measurespeak-to-peak jitter and does not provide information about jitter distribution. Infinite persistence is easy to set up and will acquire data quickly, giving you the best chance to see worst-case jitter. However, since the tails of the jitter distribution theoretically go on forever, it will take a long time to measure the worst-case, peak-to-peak jitter.It is important to understandtheerror sources of this measurement. This technique is subject to oscilloscope trigger jitter–the largest contributor to timingerror in an oscilloscope. Trigger jitter results from the failure to place the waveform correctly relative to when a trigger event occurs. Since the infinite persistence technique overlaps multiple waveform acquisitions onto the scope display, and each acquisition is subject to trigger jitter, the accuracy of this technique can be limited. If your jitter margins are being met using this technique, then more advanced measurement techniques are not necessary. This product note will discuss Infiniium’s timebase and trigger specifications in detail in alater section.HistogramsThis technique not only shows worst-case jitter, but also gives a perspective on jitter distribution. Histograms do not acquire infor-mation as quickly as infinite persistence since each acquisition must be counted in the histogram measurement.To set up a histogram, trigger on an edge and set the horizontalscale and position so that you canview the next rising or fallingedge. In the Histogram dialog box,turn on a horizontal histogramand set both Y window markersto the same voltage. For example,if a clock threshold is at 800 mV,set both Y markers to this voltage.Set the X markers to the left andright of the edge (figure 1). Figure 1. Histogram of edge showing bi-modal distribution23It is often possible to determine if the jitter is random or deter-ministic by the shape of the histogram. Random jitter will have a Gaussian distribution.Infiniium displays the percentage of points within mean +/- 1, 2,and 3 standard deviations to help in determining how Gaussian the distribution is. For a Gaussian distribution these values should be 68%, 95%, and 99.7%, respec-tively. Non-Gaussian distributions usually indicate that the jitter has deterministic components.This technique has the same limitation on accuracy as the infinite persistence technique.Multiple acquisitions contribute to the histogram and they all contain the oscilloscope trigger jitter mentioned above. Measurement StatisticsThe next method involvescomputing statistics on waveform measurement results. For example,the scope can measure the period of a waveform on successive acquisitions. Simply drag the period measurement icon to the waveform that is to be measured.The statistics will indicate the mean, standard deviation, and min and max of the period measurements. You can let the scope run for a while to determine the amount of clock jitter present. This measurement is not subject to trigger jitter because it is a delta-time or relative measure-ment. Even if the waveform is not placed correctly relative to the trigger, the edges are measuredaccurately relative to each other.Figure 2. Setting up a jitter measurementThis measurement is subject to the timebase stability of the instrument, which is typically very good. This is a valid measurement technique but is slow to gather statistical information. Since the scope acquires a waveform, makes a measurement, and then acquires a waveform at a later time, most clock periods are not measured.With this technique, it is impossible to see how the period jitter varies over short periods of time. For example, if you have spread-spectrum clocking, this measurement will lump the slowest and fastest periods together.The Agilent 54845A/B and54846A/B Infiniium oscilloscopes can compute statistics on every instance of a measurement in asingle acquisition. To enable this capability, select the Jitter tab,then check “Measure all edges” in the Measurement Definitions dia-log box (figure 2).For example, instead of only measuring the first period on every acquisition or trigger event,every period can be measured and statistics gathered. This greatly increases the speed at which statistics are gathered and reduces the overall time to make jitter measurements. Statistics are accumulated across allmeasurements in the acquisition and across acquisitions.Pressing “Clear Display” will reset the measurement statistics.This feature is useful if you are probing the clock at different locations and want to reset the measurements.It is important to set up the scope correctly to make effective jitter measurements. Set the vertical scale of the channel being measured to offer the largest waveform that will fit on screen vertically. This will make the most effective use of the scope’s A/D converter.The scope should be set toreal-time acquisition mode inthe Acquisition dialog box. Since equivalent-time sampling can combine samples from different acquisitions, the scope’s trigger jitter would adversely affect jitter measurements. The averaging function should be turned off since, again, this combines multiple acquisition data.You may want to set the scopeto its maximum memory depth. This will make the scope less responsive to operate, but the scope can make many measure-ments on a single acquisition. Since jitter measurements are statistical, many measurements are desirable. Taking many acquisitions of small records will give a more random selection but will take longer than fewer large acquisitions. Having extremely deep memory is not necessary to getting good jitter measurements. Normally, measurements aremade at 10%, 50%, and 90% of thewaveform amplitude. This isconvenient for quickly makingmeasurements; however, whenmaking measurements acrossacquisitions and combiningtheir statistics this is not thebest solution.In the Measurement Definitiondialog box, Thresholds tab, themeasurement thresholds shouldbe set to absolute voltages. Forexample, if you are makingcycle-cycle jitter or periodmeasurements, set the middlevoltage threshold to your clockthreshold. Set the upper andlower voltage thresholds toroughly +/- 10% of the signalamplitude in voltage. This willestablish a band around thethreshold that the edge must gothrough to be measured and willeliminate false edge detection.In addition to the period jitter measurement, the cycle-cycle jitter measurement uses the same technique. The cycle-cycle jitter measurement, available on Agilent 54845A/B and 54846A/B oscilloscopes, is the differenceof two consecutive period measurements.Pi – P(i-1), 2 ≤i ≤nWhereP is a period measurement and n is the number of periods inthe waveform.Cycle-cycle jitter is a measure of the short-term stability of a clock. It may be acceptable for the clock frequency to change slowly over time but not vary from cycle to cycle. For this measurement, every period in the acquisition is measured regardless of how the “Measure all edges” selection is set. In this case, the statistics represent all of the cycle-cycle jitter measurements in one acquisition, or all acquisitionsif the scope is running.If absolute clock stability is required, then a period measurement should be made. If your system can track with small changes in the clock frequency, then cycle-cycle jitter should be measured.Again, if your timing marginsare being met with thistechnique, more advancedtechniques are not necessary. Itis only fairly recently that tightertiming margins have causedengineers to need other jittermeasurement techniques.45Measurement FunctionAgilent 54845A/B and 54846A/B Infiniium oscilloscopes can plot measurement results correlated to the signal being measured. For example, if every period is meas-ured, as in the case above, the measurement function will plot period measurement results on the vertical axis, time-correlated to the waveform that the period measurement is measuring (figure 3).In this example, the secondperiod is slightly longer than the first. The third period is shorter than the second. Also notice that the lengths of the measurement function lines correspond to the period and their placement corresponds to channel 1 because we are measuring period on channel 1.Using this technique, the shape of the jitter is apparent. For example, with spread-spectrum clocking you can see the modulation frequency as the period gets progressively slower and faster. This allows you to see sinusoidal shapes or other patterns in the measurement function plot (figure 4). It is also possible to correlate poor jitter results with the source waveform that caused them. This can aid not only in your design but can also ensure that the scope is measuring appropriate voltage levels when gatheringjitter statistics.Figure 3. Measurement function on a few cyclesFigure 4. Measurement function on many cyclesTo turn on the measurement function, first turn on the desired measurement to track. Measurements that can be tracked with the measurement function are rise time, fall time, period, frequency, cycle-cycle jitter, + width, - width and duty cycle. The measurement function is enabled in the Waveform Math dialog box (figure 5). Select a function that is a different color than the channel you are measuring to make it easier to see. Set the function operator to “measurement.” Select the measurement you wish to track and turn on the measurement function. The math function now plots the measurement results on the vertical axis, time-correlated to the channel being measured. Only one measurement function can be enabled at a time; however, the function can beset to track any of the currently active measurements listed above.Set up the acquisition by selectingthe maximum memory depth inthe Acquisition dialog box. Turnoff averaging and Sin(X)/Xinterpolation in the Acquisitiondialog box. Set the sample rateso that you are getting at leastseveral sample points on theedges that you are measuring.Measurements are made on thedata that is windowed by thescreen. To see something slowerthat may be coupling into yourclock, for example, you will needto compress the channel data onthe screen.Now that the memory depth andsample rate are fixed, you canadjust the horizontal scale sothat all of the acquired data ison screen. In order to make fulluse of the A/D converter andseparate the waveforms on thedisplay, you may want to split thegrid into two parts. If you havea very dense waveform that isbeing measured, it will be nearlyimpossible to see the measurementfunction on top of it. Turn on thesplit grid in the Display dialog box. Figure 5. Setting up a measurement function6Sources of Measurement ErrorIn this section we will examine some of the principal sources of jitter measurement error. For best accuracy, the scope should be making measurements at the same temperature as when the scope was last calibrated. If the temperature has varied by more than 5 degrees, the softwareself-calibration should be performed again. The Calibration dialog box shows the change from the calibration temperature. Trigger JitterThe most common source of error across multiple acquisitions is trigger jitter. This is the error associated with placing the first point and all subsequent points of the waveform relative towhen the trigger occurs.For Infiniium models 54830B, 54831B, and 54832B, trigger jitter is 8 ps RMS. For the 54845A/B and 54846A/B, trigger jitter is8ps RMS. Figure 6 shows a 54845B measuring its trigger jitter using its own aux out signal. If the jitter is Gaussian, youcan convert RMS jitter topeak-to-peak jitter by multiplyingthe RMS jitter by 6. Trigger jitteris only relevant if you aremeasuring absolute times asopposed to relative times. Forexample, the histogram techniquedescribed above has this errorsource, but a period measurementdoes not since it is a delta-time orrelative measurement.Figure 6. Histogram of trigger jitterThis source of error can also bepresent in period measurementsif the scope is in equivalent time.In equivalent time, the scope maycombine data points from multipleacquisitions. The scope alsocombines points from multipleacquisitions in real-time averagingmode. If it is possible, jittermeasurements should be maderelative to other edges inreal-time, non-averaged mode.78Sources of Measurement Error (continued)Timebase StabilityInfiniium uses a highly stable crystal oscillator as a source for the sample clock. Errors resulting from instability of the timebase are the least significant. Timebase stability is not a specified quantity but is typically 5 ps RMS for the 54845 and 54846. For the 54830,54831, and 54832, it is typically 2ps RMS. These measurements were made at the sametemperature as the calibration.Vertical NoiseErrors in the vertical portion of the signal path including the A/D converter and preamplifier also contribute to the scope’s jitter.Any misplacement of thewaveform vertically will translate through the slew rate of the signal into time error (figure 7). If the slew rate of the signal atthe point of measurement issteep, then the vertical error will translate into a small time jitter.If the slew rate is slow, however,this can be the most significantsource of error.Figure 7. How vertical errors contribute to time errorsAliasing and InterpolationFrom the previous section, it is clear that the signal should have a high slew rate to alleviate vertical errors. However, this can lead to signal aliasing. If the signal is not sampled sufficiently, significant time errors will be present up to the sample interval. When the scope makes measurements, it interpolates the samples above and below the measurement threshold to get the time of the level crossing. If the interpolation filter is enabled, up to 16interpolated points may be placed between two adjacent acquisition samples. Beyond this, linearinterpolation is used to determine the threshold crossing times.However, samples will only be added if the record length is less than 16K samples.A Case StudyTo illustrate how to use the jitter analysis capability of an Agilent Infiniium oscilloscope, let’s examine a typical problem. You suspect that your power supply or another slower speed clock is coupling into the main clock on the board that you are designing. In order to understand how to eliminate the problem, you would like to know the frequency and wave shape of the signal that is coupling into your clock. Traditionally, you would use an FFT magnitude spectrum and look at the side bands from the fundamental. For example, in figure 8 we have acquired a long record of a number of clock pulses and computed the FFT magnitude with a waveform math function. After we zoom in on the fundamental frequency of the clock, you can see side bands.If we take the difference in frequency from the fundamental to the nearest side band, we can determine the frequency of the coupling signal. In this example, it is measured at 198 kHz. We can also notice the odd harmonics and guess that the coupling signal would not be a sine wave. The resolution of the FFT will not give us a great deal of accuracy in determining the frequency, and we can not really see the shape of the coupling signal.To solve this problem using thejitter analysis capability, we needto think about the problem in adifferent way. If a slower signalwere modulating a higherfrequency signal, then we wouldexpect the period of the higherfrequency signal to get slightlylonger, then slightly shorter, etc.,according to the slower signal(figure 8). The measurementfunction method described earlierin this product note could beused to plot how the periodchanges across the waveform.To set up the scope, acquirethe channel data with a longacquisition record in real-timeacquisition mode. Put all of thewaveform on screen by settingthe sample rate to manual andadjusting the time per division.This will allow you to see how theperiod varies across the entireacquisition. In the MeasurementDefinitions dialog box, Jitter tab,set the control to Measure AllEdges (figure 2). Now, turn ona period measurement. In theMath dialog box, turn on theMeasurement function and setto the period measurement. Figure 8. FFT of clock910A Case Study (continued)You can now see how the period measurement varies across the signal (figure 9). Adjust the time per division until you can see several periods of the slower speed signal in the measurement function. To measure the frequency, use the markers or simply drag the frequencymeasurement to the measurement function. Using this technique, we measure 197 kHz and we can see that the signal is a square wave.This confirms that another signal on the board is coupling into the clock. Armed with this knowledge,we are better equipped to find a solution.SummaryThis product note presents several methods for measuring jitter with Agilent’s Infiniium oscilloscopes. The following quick reference will help you choose the best method for a number of circumstances. Infinite PersistenceShows absolute time or edge jitter Works best when the jitter to be measured is greater than the scope’s jitter Sets up easily ?Acquires data quickly ?Measures only worst-case,peak-to-peak jitterFigure 9. Measurement function showing coupling signalHistogramsShows absolute time or edge jitter Works best when the jitter to be measured is greater than the scope’s jitter Shows a distribution of the jitterHelps determine if the jitter is random or deterministic Measures worst-case, peak-to-peak jitter Measures RMS jitterMeasurement StatisticsShows worst-case, peak-to-peak delta time or measurement jitter Sets up easily Measurement FunctionsShows how measurements vary as a function of timeShows the shape and frequency of a jitter source Helps determine if the jitter is random or deterministic/doc/e26170104431b90d6c85c778.htmlAgilent Technologies’ Test and Measurement Support, Services, and AssistanceAgilent Technologies aims to maximize the value you receive, while minimizing your risk and problems. We strive to ensure that you get the test and measurement capabilities you paid for and obtain the support you need. Our extensive support resources and services can help you choose the right Agilent products for your applications and apply them successfully. Every instrument and system we sell has a global warranty. Support is available for at least five years beyond the production life of the product. Two concepts underlie Agilent's overall support policy: "Our Promise" and "Your Advantage."Our PromiseOur Promise means your Agilent test and measurement equipment will meet its advertised performance and functionality. When you are choosing new equipment, we will help you with product information, including realistic performance specifications and practical rec-ommendations from experienced test engineers. When you use Agilent equipment, we can verify that it works properly, help with product operation, and provide basic measurement assistance for the use of specified capabilities, at no extra cost upon request. Many self-help tools are available.Your AdvantageYour Advantage means that Agilent offers a wide range of additional expert test and meas-urement services, which you can purchase according to your unique technical and business needs. Solve problems efficiently and gain a competitive edge by contracting with us for cal-ibration, extra-cost upgrades, out-of-warranty repairs, and on-site education and training, as well as design, system integration, project management, and other professional engineering services. Experienced Agilent engineers and technicians worldwide can help you maximize your productivity, optimize the return on investment of your Agilent instruments and sys-tems, and obtain dependable measurement accuracy for the life of those products./doc/e26170104431b90d6c85c778.html /find/emailupdatesGet the latest information on the productsand applications you select.By internet, phone, or fax, get assistance with all your test & measurement needsOnline assistance:/doc/e26170104431b90d6c85c778.html /find/assistPhone or FaxUnited States:(tel) 800 452 4844Canada:(tel) 877 894 4414(fax) 905 282 6495China:(tel) 800 810 0189(fax) 800 820 2816Europe:(tel) (31 20) 547 2323(fax) (31 20) 547 2390Japan:(tel) (81) 426 56 7832(fax) (81) 426 56 7840Korea:(tel) (82 2) 2004 5004(fax) (82 2) 2004 5115Latin America:(tel) (305) 269 7500(fax) (305) 269 7599Taiwan:(tel) 0800 047 866(fax) 0800 286 331Other Asia Pacific Countries:(tel) (65) 6375 8100(fax) (65) 6836 0252Email: tm_asia@/doc/e26170104431b90d6c85c778.htmlProduct specifications and descriptions in this document subject to change without notice. Agilent Technologies, Inc. 2002 Printed in USA October 15, 20025988-6109EN。
Jitter Analysis: The dual-DiracModel, RJ/DJ, and Q-Scale
White PaperThe dual-Dirac model is a tool for quickly estimating total jitter defined at a low bit error ratio, TJ(BER). Thedeterministic and random subcomponents of the jitter signal are separated within the context of the model toyield two quantities, root-mean-square random jitter (RJ) and a model-dependent form of the peak-to-peakdeterministic jitter, DJ(δδ). The total jitter of a system is
then estimated from RJ and DJ(δδ).
This paper provides a complete description of the dual-Dirac model, how it is used in technology standardsand a summary of how it is applied on different types oftest equipment. The Q-scale formulation is described indetail and is used to provide a simple visual description of the model’s features and to show how different implementations of the model can lead to different results. For an introduction to jitter analysis please see reference [1].
Section one is a short self-contained summary. The succeeding sections provide the complete reference material for understanding the summary. This format provides both the story-in-a-nutshell and the details-in-fullso that you can, hopefully, access the information youneed as quickly as possible – if you have comments or suggestions, accolades or criticisms, please send me anote: ransom_stephens@agilent.com.
31-December-2004
2three regions: at the crossing-point the distribution
is dominated by DJ, at time-delays farther from the crossing-point the distribution is increasingly dominated by RJ until, far from the crossing point, in the asymptoticlimit, the tails follow the Gaussian RJ distribution. Theasymptotic tails of the distribution usually cause errors at the level of BER < 10–8. The ideal way to determine
the behavior of the tails, and hence, TJ(BER) would be o deconvolve RJ and DJ. But without knowing the DJ distribution beforehand, there is no practical way todeconvolve the distribution
The dual-Dirac model, Figure 1, provides the simplest possible distribution: the crossing-point is separated intotwo Dirac-delta functions positioned at µLand µR, the
DJ dominated region, followed by an artificially abrupttransition to the RJ dominated tails. There are many ways to implement the dual-Dirac model, in all of themestimating TJ(BER) is a matter of describing the tails ofthe jitter distribution with the tails of two Gaussians ofwidth σseparated by a fixed amount DJ(δδ) ≡|µL– µR|:
The dual-Dirac model is a Gaussian approximation to the outer edges of the jitter distribution displaced by DJ(δδ).
Conceptually, think of DJ closing the eye a fixed amount,DJ(δδ), and the Gaussian RJ tails closing the eye an
amount that depends on the bit error ratio of interest.Once σand DJ(δδ) are measured the eye closure at anyBER can be estimated with:
TJ(BER)≅2QBERxσ+ DJ(δδ), (1)
where QBERis calculated from the complementary error
function, as given in Table 2. Since σis multiplied by 2 QBER, the accuracy of TJ(BER) depends first on theaccuracy of the RJ measurement, σ, and second on theaccuracy of the DJ(δδ) measurement.
1. What The dual-Dirac Approximation Is AndWhat It Is NotThe dual-Dirac model is universally accepted for its utilityin quickly estimating total jitter defined at a bit error ratio,TJ(BER), and for providing a mechanism for combiningTJ(BER) from different network elements. It relies on thefive assumptions given in Table 1.
Table 1: The dual-Dirac model assumptions.1.Jitter can be separated into two categories, random jitter (RJ) and deterministic jitter (DJ).2.RJ follows a Gaussian distribution and can be fully described in terms of a single relevant parameter, the rms value of the RJ distribution or, equivalently, the width of the Gaussian distribution, σ.3.DJ follows a finite, bounded distribution.4.DJ follows a distribution formed by two Dirac-delta functions. The time-delay separation of the two delta functions gives the dual-Dirac model-dependent DJ, as shown in Figure 1.5.Jitter is a stationary phenomenon. That is, a measurement of the jitter on a given system taken over an appropriate time interval will give the same result regardless of when that time interval is initiated.
A measurement of TJ(BER) at low BER can only be performed on a Bit Error Ratio Tester (BERT) and takesas long as is necessary to transmit about 10/BER bits2
(e.g., to measure TJ(10–12) would take about 70 minutes).The first two assumptions in Table 1, that jitter is causedby a combination of random and deterministic processeswhose distributions can be separated and that RJ followsa Gaussian, are standard industry-wide assumptions; they are the key to how the dual-Dirac model is used toestimate TJ(BER) from measurements of comparativelylow statistics.