
嘉兴市2020—2021学年第一学期期末检测
高三数学
满分150分,时间120分钟.
一?选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合{|lg(1)}A x y x ==-,{|13}B x x =-<<,则A B =( )
A. {|13}x x -<<
B. 3|}1{x x ≤<
C. {|23}x x <<
D. {|13}x x <<
2. 已知数列{}n a 满足13(N )n n a a n *
+=∈,且12a =,则123n a a a a +++???+=( )
A. 31n -
B. 3n
C. 131n --
D. 13n -
3. 已知,R x y ∈,则“||0x y +>”是“0x >”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件
4. 函数()1cos f x x x x ??
=-
???
(x ππ-≤≤且0x ≠)的图象可能为( ) A. B. C.
D.
5. 设,l m 是两条不同的直线,α是一个平面,则下列说法正确的是( ) A. 若//l α,m α?,则//l m
B. 若//l α,//m α,则//l m
C. 若l m ⊥,m α?,则l α⊥
D. 若l α⊥,//l m ,则m α⊥
6. 已知实数,x y 满足条件202035x y x y x y -≥??
+≥??+≤?
,则2z x y =+的最大值是( )
A. 0
B. 3
C. 4
D. 5
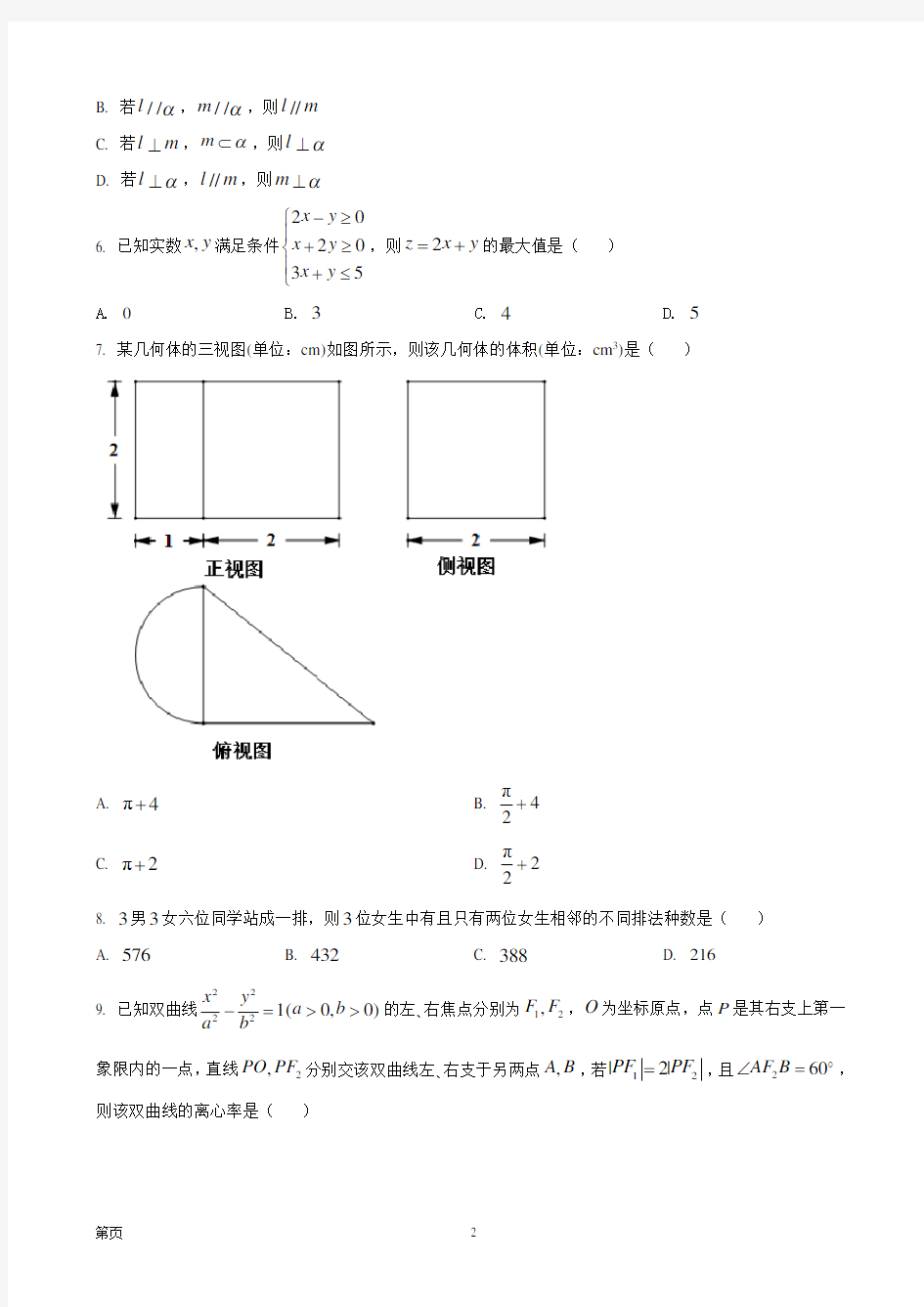
7. 某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm 3)是( )
A. π4+
B.
π42
+ C. π2+
D.
π22
+ 8. 3男3女六位同学站成一排,则3位女生中有且只有两位女生相邻的不同排法种数是( ) A. 576
B. 432
C. 388
D. 216
9. 已知双曲线22
221(0,0)x y a b a b
-=>>的左?右焦点分别为12,F F ,O 为坐标原点,点P 是其右支上第一
象限内的一点,直线2,PO PF 分别交该双曲线左?右支于另两点,A B ,若12|2|PF PF =,且260AF B ∠=?,则该双曲线的离心率是( )
A.
3
B.
2
C.
23
D.
5 10. 对任意0x >,若不等式2e ln e x
a x ax x
++≥恒成立(e 为自然对数的
底数),则正实数a 的取值范围是
( ) A. (0,e]
B. 2(0,e ]
C. 2[,e]e
D. 2
2[,e ]e
二?填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11. 已知复数2
1i
z =
+(其中i 虚数单位),则z =______;z =______.
12. 已知抛物线2(0)y mx m =≠的焦点为F ,准线方程为2x =-,点0(,4)P x 是抛物线上的一点,则实数m =___________,||PF =___________.
13. 已知△ABC 中,角,,A B C 所对的边分别为,,a b c ,4c =,π
3
A =
,且△ABC 的面积为3,则b =___________;cos C ___________.
14. 已知526
0126(1)(1)mx x a a x a x a x ++=+++???+.若25a =,则m =___________;
135a a a ++=___________.
15. 已知平面向量a 与b
夹角为120?,b 在a 上的投影是1-,且满足(2)(3)a b a b +⊥-,则
|2|a b +=___________.
16. 甲乙两人进行5局球赛,甲每局获胜的概率为
3
4
,且各局的比赛相互独立,已知甲胜一局的奖金为8元,设甲所获的奖金总额为X 元,则甲所获奖金总额的方差()D X =___________.
17. 如图,在多面体ABC DEF -中,已知棱,,AE BD CF 两两平行,AE ⊥底面DEF ,DE DF ⊥,四边形ACFE 为矩形,23AE DE DF BD ====,底面△DEF 内(包括边界)动点P 满足,AP BP 与底
面DEF 所成的角相等.记直线CP 与底面DEF 的所成角为θ,则tan θ的取值范围是
___________.
三?解答题:本大题共5小题,共74分.解答应写出文字说明?证明过程或演算步骤.
18. 在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知函数()2cos sin()(R)3
f x x x x π
=-∈.
(1)求5(
)12
f π
的值; (2)求函数()y f x =的单调递增区间. 19. 如图,四棱锥-P ABCD 中,△
PAD 为正三角形,//AB CD ,1
22
AD DC AB ==
=,23BC =,3PC =.
(1)求证:AD PC ⊥;
(2)求AB 与平面PAD 所成角的正弦值. 20. 已知数列{}n a 满足13
2
a =,112n n a a -=-,2n ≥,*n N ∈.
(1)证明:数列1
{}1
n a -为等差数列,并求数列{}n a 的通项公式; (2)若2n n n
a c n =
?,记数列{}n c 的前n 项和为n T ,求证:3
14
n T ≤<. 21. 已知中心在坐标原点的椭圆C ,其焦点分别为1(1,0)F -,2(1,0)F ,点226(3P -
为椭圆C 上一点.
(1)求椭圆C 的方程;
(2)过点(6,4)Q -的直线1l 与x 轴交于点(,0)T t ,由点(,0)T t 引另一直线2l 交椭圆C 于,A B 两点.是否存在实数t ,使得直线,,QA QT QB 的斜率成等差数列,若存在,求出t 的值;若不存在,说明理由. 22. 已知函数()(1)ln f x m x =+,2()g x mx x =+,m R ∈. (1)当0m =时,曲线()()()
()1a
x f x a R g x φ=+
-∈在2x =处的切线与直线210x y +-=平行,求函数()y x φ=在2
,e e ????上的最大值(e 为自然对数的底数);
(2)当1m =时,已知0a b <<,证明:()()4()()f a f b a
a b g a g b a b
->-+--.
嘉兴市2020—2021学年第一学期期末检测
高三数学
满分150分,时间120分钟.
一?选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合{|lg(1)}A x y x ==-,{|13}B x x =-<<,则A B =( )
A. {|13}x x -<<
B. 3|}1{x x ≤<
C. {|23}x x <<
D. {|13}x x <<
【答案】D
2. 已知数列{}n a 满足13(N )n n a a n *
+=∈,且12a =,则123n a a a a +++???+=( )
A. 31n -
B. 3n
C. 131n --
D. 13n -
【答案】A
3. 已知,R x y ∈,则“||0x y +>”是“0x >”的
( ) A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件
D. 既不充分也不必要条件 【答案】B 4. 函数()1cos f x x x x ??
=-
???
(x ππ-≤≤且0x ≠)的图象可能为( ) A. B.
C. D.
【答案】D
5. 设,l m 是两条不同的直线,α是一个平面,则下列说法正确的是( ) A. 若//l α,m α?,则//l m B. 若//l α,//m α,则//l m C. 若l m ⊥,m α?,则l α⊥ D. 若l α⊥,//l m ,则m α⊥ 【答案】D
6. 已知实数,x y 满足条件202035x y x y x y -≥??
+≥??+≤?
,则2z x y =+的最大值是( )
A. 0
B. 3
C. 4
D. 5
【答案】C
7. 某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm 3)是( )
A. π4+
B.
π42
+ C. π2+ D.
π22
+ 【答案】A
9. 已知双曲线22
221(0,0)x y a b a b
-=>>的左?右焦点分别为12,F F ,O 为坐标原点,点P 是其右支上第一
象限内的一点,直线2,PO PF 分别交该双曲线左?右支于另两点,A B ,若12|2|PF PF =,且260AF B ∠=?,则该双曲线的离心率是( )
A.
3 B.
2
C.
23
D.
5 【答案】A
10. 对任意0x >,若不等式2e ln e x
a x ax x
++≥恒成立(e 为自然对数的底数),则正实数a 的取值范围是
( ) A. (0,e] B. 2
(0,e ]
C. 2[,e]e
D. 2
2[,e ]e
【答案】B
二?填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
11. 已知复数2
1i
z =
+(其中i 为虚数单位),则z =______;z =______. 【答案】 (1). 1i + (2).
2
12. 已知抛物线2(0)y mx m =≠的焦点为F ,准线方程为2x =-,点0(,4)P x 是抛物线上的一点,则实数m =___________,||PF =___________. 【答案】 (1). 8 (2). 4
13. 已知△ABC 中,角,,A B C 所对的边分别为,,a b c ,4c =,π
3
A =
,且△ABC 3b =___________;cos C ___________.
【答案】 (1). 1 (2). 1315. 已知平面向量a 与b 的夹角为120?,b 在a 上的投影是1-,且满足(2)(3)a b a b +⊥-,则
|2|a b +=___________.
【答案】
72
16. 甲乙两人进行5局球赛,甲每局获胜的概率为
34
,且各局的比赛相互独立,已知甲胜一局的奖金为8元,设甲所获的奖金总额为X 元,则甲所获奖金总额的方差()D X =___________. 【答案】60
17. 如图,在多面体ABC DEF -中,已知棱,,AE BD CF 两两平行,AE ⊥底面DEF ,DE DF ⊥,四边形ACFE 为矩形,23AE DE DF BD ====,底面△DEF 内(包括边界)的动点P 满足,AP BP 与底面DEF 所成的角相等.记直线CP 与底面DEF 的所成角为θ,则tan θ的取值范围是___________.
【答案】31033,102????
三?解答题:本大题共5小题,共74分.解答应写出文字说明?证明过程或演算步骤.
18. 在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知函数()2cos sin()(R)3
f x x x x π
=-∈.
(1)求5(
)12
f π
的值; (2)求函数()y f x =的单调递增区间.
【答案】(123
-(2)π5[,],(Z)1212k k k πππ-+
∈. 19. 如图,四棱锥-P ABCD 中,△PAD 为正三角形,//AB CD ,1
22
AD DC AB ==
=,23BC =3PC =.
(1)求证:AD PC ⊥;
(2)求AB 与平面PAD 所成角的正弦值. 【答案】(1)证明见解析;(2)
3
4
. (1
)取AD 中点O ,连结
,,OP OC AC .因为1
22
AD DC AB ==
=,23BC =, 由平几及解三角形知识得()
2
22222423
22cos cos 2422AC AC BAC ACD AC
AC
+-+-∠=
=∠=
???? ,解得
2AC = ,所以60ADC ∠=?,
因此△ADC 为正三角形,故AD OC ⊥,又因为△
PAD 也是正三角形,
因此AD OP ⊥,又OC OP O =,所以AD ⊥平面POC ,而PC ?平面POC ,所以AD PC ⊥.
(2)方法一:
因为//AB CD ,所以AB 与平面PAD 所成角即CD 与平面PAD 所成角,记作θ. 由(1)得AD ⊥平面POC ,又AD ?平面PAD ,所以平面PAD ⊥平面POC , 平面PAD
平面POC PO =,故过点C 作CH ⊥平面PAD ,则垂足H 必在直线PO 上,
此时CDH θ=∠,在正△
PAD 中,3
32
PO AD =
=,而3OC =3PC =, 所以在△POC 中,由余弦定理可得120POC ∠=?,所以3
sin 602
CH OC =??=,又2CD =, 所以3sin sin 4CH CDH CD θ=∠=
=,所以AB 与平面PAD 所成角的正弦值为3
4
.
方法二:
由(1)知AD ⊥平面POC ,又AD ?平面ABCD ,所以平面POC ⊥平面ABCD , 平面POC
平面ABCD OC =.故过点O 作直线Oz OC ⊥,则Oz ⊥平面ABCD ,
又AD CO ⊥,故可如图建立空间直角坐标系.又1OD =,3OC =3OP =120POC ∠=?,可求
得各点坐标:(0,0,0)O ,(1,0,0)D ,3,0)C ,33(0,,)22
P -
, 设平面PAD 的一个法向量为(,,)n x y z =,则00n OD n OP ??=??=?,即(,,)(1,0,0)0
33
(,,)(0,)02x y z x y z ?=??
??-
=??, 故0
33
02x y z =???+=??,令1z =,故(0,3,1)n =,又(1,3,0)CD =, 记CD 与平面PAD 所成角为θ,则33sin cos ,22
4
||||
n CD n CD n CD θ?-===
=
??.
又因为//AB CD ,故AB 与平面PAD 所成角的正弦值为34
. 20. 已知数列{}n a 满足13
2
a =,112n n a a -=-,2n ≥,*n N ∈.
(1)证明:数列1
{}1
n a -为等差数列,并求数列{}n a 的通项公式; (2)若2n n n a c n =
?,记数列{}n
c 的前n 项和为n T ,求证:3
14
n T ≤<. 【答案】(1)证明见解析,2
1n n a n +=+;(2)证明见解析.
(1)当132a =时,因为112n n a a -=-,1111111n n n n a a a a -----=-=,
所以
1111111111111
1
11n n n n n n n a a a a a a a ---------=--==---,
所以数列1
{
}1n a -为首项为111
a -,公差为1的等差数列. 又132a =
,1121
a =-,所以
111n n a =+-,解得21n n a n +=+. (2)因为2
1
n n a n +=
+,所以1211(1)22(1)2n n n n n c n n n n -+=
=-?+??+?. 所以121n n n T c c c c -=++???++
1121111111
112222322(1)2(1)2n n n
n n n -=-
+-+???+-=-????+?+?, 即1
1(1)2
n n T n =-
+?,显然1n
T <,另一方面, 11111112
1(1)0(1)222(1)2(1)2n n n n n n n
n T T n n n n n n ---+-=-
--=-=>+???+??+?,
故数列{}n T 是递增数列,所以134n T T ≥=
,因此,3
14
n T ≤<. 21. 已知中心在坐标原点的椭圆C ,其焦点分别为1(1,0)F -,2(1,0)F ,点226
(,)3P -
为椭圆C 上一点.
(1)求椭圆C 的方程;
(2)过点(6,4)Q -的直线1l 与x 轴交于点(,0)T t ,由点(,0)T t 引另一直线2l 交椭圆C 于,A B 两点.是否存在实数t ,使得直线,,QA QT QB 的斜率成等差数列,若存在,求出t 的值;若不存在,说明理由.
【答案】(1)22
1
43
x y +=;(2)存在,23t =. 【解析】 【分析】
(1)根据条件算出153PF =
,27
3
PF =,然后利用抛物线定义求出答案即可;
(2)分直线2l 的斜率为零、直线2l 的斜率不为零两种情况讨论,当直线2l 斜率不为零时,可设直线2l 的方程为x ny t =+,11(,)A ny t y +,22(,)B ny t y +,由2QA QB QT k k k +=可得
21212(2128)(6)(64)()0nt n n y y t t n y y --+---+=,联立直线2l 的方程与椭圆的方程消元可得
12y y +,12y y ?,代入即可求解.
【详解】(1)设椭圆C 的方程为22
221(0)x y a b a b
+=>>,由题意可求得153PF =,273PF =
由椭圆定义可知122||||4a PF PF =+=,所以2a =,而1c =,故2223b a c =-=
故所求椭圆C 的方程为22
143
x y +=
(2)假设存在实数t ,使得直线,,QA QT QB 的斜率成等差数列,即满足2QA QB QT k k k += ①当直线2l 的斜率为零时,此时直线2l 与椭圆C 的交点是椭圆C 长轴的端点 不妨设(2,0)A -,(20)B ,,此时12QA k =-,1QB k =-,46
QT k t =- 由于2QA QB
QT k k k +=,故141226t --=?-,解得2
3
t =
②当直线2l 斜率不为零时,可设直线2l 的方程为x ny t =+
11(,)A ny t y +,22(,)B ny t y +,联立方程组22
143
x y x ny t ?+
=???=+?
整理得2
2
2
(34)63120n y nty t +++-=
22222
(6)4(34)(312)034nt n t t n ?=-+->?<+,故1222
122634()31234nt y y n t y y n -?
+=??+*?-??=?+?
而1146QA y k ny t +=
+-,2246QB y k ny t +=+-,46
QT k t =-,又2QA QB QT k k k +=
故
1212448
666
y y ny t ny t t +++=+-+--
整理得2
1212(2128)(6)(64)()0nt n n y y t t n y y --+---+=
将()*代入上式可得,整理得(64)(64)0n t n t ---=,对于任意n 该等式恒成立
故640t -=,解得23
t =
综合①②,可知存在实数2
3
t =
,使得直线,,QA QT QB 的斜率成等差数列 22. 已知函数()(1)ln f x m x =+,2()g x mx x =+,m R ∈. (1)当0m =时,曲线()()()
()1a
x f x a R g x φ=+
-∈在2x =处的切线与直线210x y +-=平行,求函数()y x φ=在2
,e e ????上的最大值(e 为自然对数的底数);
(2)当1m =时,已知0a b <<,证明:
()()4()()f a f b a
a b g a g b a b
->-+--.
【答案】(1)
2
4
1e +;(2)证明见解析. (1)当0m =时,()ln 1a
x x x φ=+
-,因此'21()a x x x
φ=-, 而曲线()y x φ=在2x =处的切线与直线210x y +-=平行, 故'
11
(2)242
a φ=
-=-,解得4a =. 所以4
()ln 1x x x φ=+
-,'24()x x x
φ-=, 故当[),4x e ∈时,'
()0x φ<,即函数()y x φ=在[),4e 上递减,
当(
24,x e ?∈?时,'
()0x φ>,即函数()y x φ=在(
24,e ??上递增,
所以()()(){}
2
max max ,x e e
φφφ??=??,而()4e e φ=
,()
2
241e e
φ=+, 故()
()22
2
(2)0e e e e
φφ--=>,即()
()2
e e φφ>, 所以函数()y x φ=在2,e e ????上的最大值为
24
1e
+. (2)当1m =时,()2ln f x x =,2
()g x x x =+,由于0a b <<,
故要证明
()()4()()f a f b a
a b g a g b a b
->-+--成立.
?证明
22ln ln 2b a a b a a b ->-+成立?证明22
2()
ln ln a b a b a a b -->+成立,
?证明22(1)ln ()1b b a b a a
->+成立.令b
x a
=,因为0a b <<,则1x >,
即只需证明2
2(1)
ln (1)1
x x x x ->>+成立 ?证明2(1)ln 220(1)x x x x +-+>>即可,下面证明该不等式成立.
设2
()(1)ln 22(1)F x x x x x =+-+>,求得'
1
()2ln 2F x x x x x
=++
-, 因为1x >
,所以12x x +
>=, 所以当1x >时,'
()2ln 222ln 0F x x x x x >+-=>, 因此函数()y F x =是(1,)+∞上的增函数,故()(1)0F x F >=, 这就证明了当1x >时,2
(1)ln 220x x x +-+>恒成立,故原命题成立.