下载文档原格式
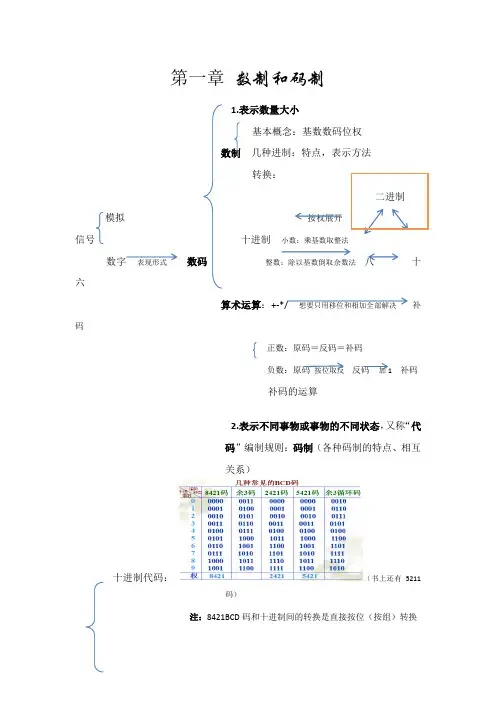
第一章数制和码制1.表示数量大小基本概念：基数数码位权数制几种进制：特点，表示方法转换：二进制模拟按权展开信号十进制小数：乘基数取整法数字表现形式数码整数：除以基数倒取余数法八十六算术运算：+-*/ 想要只用移位和相加全部解决补码正数：原码＝反码＝补码负数：原码按位取反反码加1 补码补码的运算2.表示不同事物或事物的不同状态，又称“代码”编制规则：码制（各种码制的特点、相互关系）十进制代码：（书上还有5211码）注：8421BCD码和十进制间的转换是直接按位（按组）转换如：(36)10=(0011 0110)8421BCD=(110110)8421BCD(101 0001 0111 1001)8421BCD=(5179)10格雷码（循环码）：①相邻性：任意两个相邻码组间仅有一位的状态不同。
②循环性：首尾两个码组也具有相邻性。
ASCII码（美国信息交换标准代码）：采用7位二进制编码，用来表示27（即128）个字符。
注意0~9，a~z,A~Z的ASCII码特点第二章逻辑代数基础一、逻辑代数（开关代数、布尔代数）与（逻辑相乘）Y = A·B = AB1.基本运算或（逻辑相加）Y = A+B非（逻辑求反）Y = （A）‘衍生出：与非：BAY+=或非：BAY+=与或非：CDABY+=异或：BAB ABAY+=⊕=互为反运算同或：ABBABAY+=Θ=2.基本公式（定律）：衍生出常用公式：注意记忆它们的图形符号3.基本定理：（注意结合例题进行练习、理解）代入定理：任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立。
反演定理：对于任意一个逻辑函数式 F ，做如下处理：①运算符“.”与“+”互换,“”与“⊙”互换②常量“0”换成“1”，“1”换成“0”；③原变量换成反变量，反变量换成原变量。
那么得到的新函数式称为原函数式F 的反函数式对偶定理：若两逻辑式相等，则它们对应的对偶式也相等。
数电复习知识点第一章1、了解任意进制数的一般表达式、2-8-10-16进制数之间的相互转换；2、了解码制相关的基本概念和常用二进制编码（8421BCD、格雷码等）；第三章1、掌握与、或、非逻辑运算和常用组合逻辑运算（与非、或非、与或非、异或、同或）及其逻辑符号；2、掌握逻辑问题的描述、逻辑函数及其表达方式、真值表的建立；3、掌握逻辑代数的基本定律、基本公式、基本规则（对偶、反演等）；4、掌握逻辑函数的常用化简法（代数法和卡诺图法）；5、掌握最小项的定义以及逻辑函数的最小项表达式；掌握无关项的表示方法和化简原则；6、掌握逻辑表达式的转换方法（与或式、与非－与非式、与或非式的转换）；第四章1、了解包括MOS在内的半导体元件的开关特性；2、掌握TTL门电路和MOS门电路的逻辑关系的简单分析；3、了解拉电流负载、灌电流负载的概念、噪声容限的概念；4、掌握OD门、OC门及其逻辑符号、使用方法；5、掌握三态门及其逻辑符号、使用方法；6、掌握CMOS传输门及其逻辑符号、使用方法；7、了解正逻辑与负逻辑的定义及其对应关系；8、掌握TTL与CMOS门电路的输入特性（输入端接高阻、接低阻、悬空等）；第五章1、掌握组合逻辑电路的分析与设计方法；2、掌握产生竞争与冒险的原因、检查方法及常用消除方法；3、掌握常用的组合逻辑集成器件（编码器、译码器、数据选择器）；4、掌握用集成译码器实现逻辑函数的方法；5、掌握用2n选一数据选择器实现n或者n＋1个变量的逻辑函数的方法；第六章1、掌握各种触发器（RS、D、JK、T、T’）的功能、特性方程及其常用表达方式（状态转换表、状态转换图、波形图等）；2、了解各种RS触发器的约束条件；3、掌握异步清零端Rd和异步置位端Sd的用法；2、了解不同功能触发器之间的相互转换；第七章1、了解时序逻辑电路的特点和分类；2、掌握时序逻辑电路的描述方法（状态转移表、状态转移图、波形图、驱动方程、状态方程、输出方程）；3、掌握同步时序逻辑电路的分析与设计方法，掌握原始状态转移图的化简；4、了解异步时序逻辑电路的简单分析；5、掌握移位寄存器、计数器的功能、工作原理和实际应用等；6、掌握集成计数器实现任意进制计数器的方法；7、掌握用移位寄存器、计数器以及其他组合逻辑器件构成循环序列发生器的原理；第八章1、掌握门电路和分立元件构成的施密特触发器、单稳态触发器、多谐振荡器的电路组成及工作原理，掌握相关参数的计算方法；2、掌握用555电路构成施密特触发器、单稳态触发器、多谐振荡器的方法以及工作参数的计算或者改变方法；第九章1、了解ROM和RAM的基本概念；2、了解存储器容量的表示方法和扩展方法，了解存储容量与地址线、数据线的关系。
数制和码制的思政元素
数制和码制是计算机科学中重要的基础知识，也与思想政治教育密切相关。
首先，数制和码制涉及到数字的表示和处理方式。
通过学习数制和码制，我们能够深入了解数字在计算机中是如何被处理和运算的。
这不仅可以帮助我们更好地理解计算机的工作原理，也可以启发我们思考数字的本质和价值，从而增强我们的思辨能力。
其次，数制和码制的学习也能够加深我们对计算机技术的认识。
作为一项前沿技术，计算机在推动社会进步、促进经济发展等方面发挥着不可替代的作用。
了解计算机的基础知识，能够帮助我们更好地理解计算机技术对社会的影响和作用，从而更好地为社会服务，实现个人与国家的共同发展。
最后，数制和码制的学习也有助于我们培养自己的创新思维。
通过对数字表示和处理方式的研究，我们可以发现和解决数字处理中的难题，在实践中不断创新。
这种创新思维可以帮助我们在未来的工作和生活中面对各种挑战，获得更多的成功与成就。
总之，数制和码制的学习不仅有助于我们掌握计算机科学的基础知识，也对我们的思想政治教育有很大的启示作用。
这种启示能够推动我们更好地为社会发展贡献力量，实现自身的发展和提高。
微机原理习题册第 1 章数制和码制1.将下列十进制数分别转换为二进制数（4）（1）147 （2）4095 （3）解：147=B 4095=B= =2. 将下列二进制数分别转换为十进制数（3）（1）（2）.001B解：= .001B==3．将二进制数转换成十六进制数（1）B（2）11B（3）101B （4）0B（5）01111111B（6）0B 解：（1）95H（2）34BH（3）FFFDH（4）0815H（5）7FH（6）401H4．已知 a=1011B, b=11001B, c=100110B，按二进制完成下列运算，并用十进制运算检查计算结果：（1）a+b；（2）c-a-b；（3）a·b；（4）c/b；解：a=1011B＝11, b=11001B＝25, c=100110B＝38（1）a+b＝100100B＝36 （2）c-a-b＝10B＝2（3）a·b＝1B＝275 （4）c/b＝1……1101B（＝13）5．设机器字长为 8 位，写出下列各数的原码和补码：（1）+1010101B （2）-1010101B （3）+1111111B （4）-1111111B （5）+1000000B （6）-1000000B 解：（1）+1010101B 原码 01010101B 补码 01010101B（2）-1010101B 原码 B 补码 B（3）+1111111B 原码 01111111B 补码 01111111B（4）-1111111B 原码 B 补码 B（5）+1000000B 原码 01000000B 补码 01000000B（6）-1000000B 原码 B 补码 B6．已知 a=00111000B，b=B，计算下列逻辑运算：（1）aAND b；（2）a OR b；（3）a XOR b；（4）NOT a；解：（1）00000000B（2）1B（3）1B（4）B7．求下列组合 BCD 数的二进制和十六进制表示形式：（）（1）3251；（2）12907；（3）2006 解：（1）0011 0010 0101 0001B，3251H（2）0001 0010 1001 0000 0111 B , 12907H（3）0010 0000 0000 0110B , 2006H8．设下列四组为 8 位二进制补码表示的十六进制数，计算 a+b 和a-b，并判定其结果是否溢出：（1）a=37H，b=57H；（2）a=0B7H，b=0D7H；（3）a=0F7H，b=0D7H；（4）a=37H，b=0C7H。
