
浅论关于三角函数的几种解题技巧
本人在十多年的职中数学教学实践中,面对三角函数内容的相关教学时,积累了一些解题方面的处理技巧以及心得、体会。下面尝试进行探讨一下:
一、关于sin a ± cos sin a cos a(或sin2a)的关系的推广应用:
1、由丁?(sin G 土cos a) 2 = sin2 o + cos? a±2sinacosa = 1 ±2smacosa故知道(sina±cosa), 必可推出sin a cos a(或sin 2a), 例如:
h
例1 已知sin& — cos& 二——,求sin'&-cos‘&。
分析:由于sin' &-COS? & = (sin& - cos&Xsin? & + sin&cos^ + cos2 &)
=(sin 0 - cos ^)[(sin 6 - cos 0)2 +3sin&cos&]
其中,sin0-cos G已知,只要求出sincos0即可,此题是典型的知sin&-cos&,求sin&cos&的题型。
解:?/ (sin&-cos&)2 = l-2sin&cos&
故:l-2sin&cos& = = — => sin^cos^ =—
3 3 3
sin3&一cos3 & = (sin& — cos&)[(sin& — cos^)2 +3sin&cos&]
=^2+3X1 73X1=4^
3 3 3 3 3 9
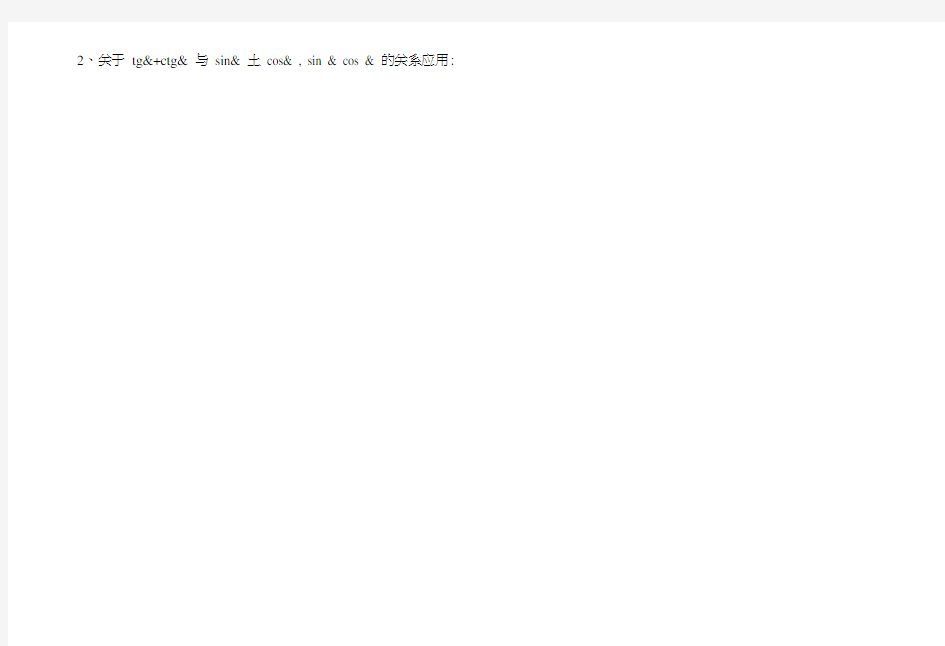
2、关于tg&+ctg& 与sin& 土cos& , sin & cos & 的关系应用:
由于 tg&+ctg"泌 + 致 jiL + COS & 二
cosO sm& sin & cos 0 sm& cos&
故:tg&+ctg&, sin&土cos&, sin&cos&三者中矢II 其一可推出其余式子的值。 例 2 若 sin0+cos0二叫,且 tg0+ctg0二n,则 n 的关系为( )。
A. m 二n
B. m ―— l C ?加=— D. n =—— n n m
分析:观察sin&+cos0与sincos 的关系:
sin&cos&=(sin& + cos&)2-1=也
2 2
而:t20 + ct^O - ------ ---- = n
sin & cos & 故:^-^ = -=>m 2
=- + 1,选 B 。
2 n n
sin 2a = 2sinQcosa => sin 2a =— 2 例 4 己知:tga+ctga 二2,求sin 4 6Z + cos 4 a
分析:由上面例子已知,只要sin 4 6Z + cos 4 a 能化出含sina±cosa 或sinacosa 的式子,则即可根据已知tga^ctga 进行计算。由于 分析: 已知:tga+ctga 二4,则sin2a 的值为 A. - B.-- 2 2 1
tga+ctga 二 --------- sinacosa
4 => si 1 smacosQ = —
4
D. )o
~4
故: 答案选A 。
sincrcoscr =—,此题只要将sin" cr + cos 4 a 化成含sin a cos a 的式子即可: 2
解:sin°a + cos 4a 二sin"a + cos°a+2 sin'acos 2a-2 sir?acos 2a
=(sin a+cos a ) - 2 sin a cos a
= 1~2 (sinacosa)"
1 7 =l-2x(-)
2 2
4
2
二丄
~2
通过以上例了,可以得出以下结论:由于sina 土cosa, sinacosa 及tga+ctga 三者之间可以互化,知其一则必可知其余二。这种性 质适合于隐含此三项式了的三角式的计算。但有一点要注意的;如果通过已知sinacosa,求含sina 土cosa 的式了,必须讨论其象限才能 得出其结果的正、负号。这是由于(sina 土cosa) ?二1 ±2sinacos”,要进行开方运算才能求出sina 士cosa
二、关于“托底”方法的应用:
在三角函数的化简计算或证明题屮,往往需要把式子添加分母,这常用在需把含tga (或ctga)与含sina (或cos6^)的式子的互化 屮,本文把这种添配分母的方法叫做“托底”法。方法如下:
例5已知:tg^=3,求昱g 叱的值。 2sina + cosa ■
分析:由于tga = Sma ,带有分母cosa,因此,可把原式分子、分母各项除以cosa,"造出” tga,即托出底:cosa ; cos a
解:由于 t ga 二3=>QH A7T + —=> COSGH 0 2tga+ctga 二 --------- sinacosd
cosa
故,原式二 cw ‘ =
2 smo | cosa 2fgo + l 2x
3 + 1 cos a cos a
例 6 己知:ctga 二-3,求 sinacosa-cos%二?
用公式:sin 1 2(7 +cos 2 a-\及托底法托出其分母,然后再分子、分母分别除以sina,造出etga : 解:sin 2 cif + cos 2 a- . 2 sintrcoscr-cos 2 a
=1 => sin (7cos a-cos a- ---------- --------- ----
sirr a + cos a cos a cosa 2 ------- ( ------ ) 2
1 +(COSG )
2 l + ctg^a sin er
_-3 + (-3)2_ 6
~ l + (-3)2 "_5
例7 (95年全国成人高考理、工科数学试卷)
iS 0 < x < — ,0 < y < — , K sin x sin y = sin(— - x) sin(— - y)
2 2
3 6
求:(etgx - —)(ctgy - V3)的值 J
分析:此题是典型已知含正弦函数的等式求含正切、余切的式子,故要用“托底法”,由于0 V 兀v|;0vyv 彳,故sinxH0,sinyH0,
分析:
由于eg 二沁 sin er ,故必将式子化成含有沁 sincr
的形式,而此题与例4有所不同,式子本身没有分母,为了使原式先出现分母,利
分子,分母同除以si" Q sin° sin° =clga_c号a
在等式两边同除以sinxsin y ,托出分母sinxsin y 为底,得:
解:由已知等式两边同除以sinxsin y 得:
. 7C 龙 7^ 7C sin( 一 x) sin( --- v) sin — cos- cos — sin x sin — cos y 一 cos 3 6 = ] = 3
3 ________ 6 ' 6 = j sinxsin y sinx sin
1 V3 cos x-sin x cos y - ^siny A
d --------------- ; -------------------- : ---------- = 1
4 sin x sin y => t (4ictgx 一 l)(ctgy 一 Vi) = 1
=> —(ctgx - - )(c/gy - VJ) = 1 4 3
=> (ctgx-¥)(cfgy-V3) = yV3
“托底”适用于通过同角的含正弦及余弦的式子与含正切、余切的式子的互化的计算。由于垢。二沁,ctga = — f 即正切、余切 cos a sin a 与正弦、余弦间是比值关系,故它们间的互化需“托底”,通过保持式子数值不变的情况下添加分母的方法,使它们Z 间可以互相转化,达 到根据已知求值的目的。而添加分母的方法主要有两种:一种利用sin 26r + cos 26r = l,把sin 26Z + cos 2^作为分母,并不改变原式的值,另一 种是通过等式两边同时除以正弦或余弦又或者它们的积,产生分母。
三、关于形如:acosx±bsinx 的式子,在解决三角函数的极值问题时的应用:
可以从公式sin A cos A : ± cos A sin x = sin( A ± x)中得到启示:式子acosx 土bsinx 与上述公式有点相似,如果把a, b 部分变成含sinA, cosA 的式子,则形如acosx±hsinx 的式子都可以变成含sin(A±x)的式子,由于T W sin(A±x) W1,
所以,可考虑用其进行求极值问题的处理,但要注意一点:不能直接把。当成sinA, b 当成cosA,如式子:3cos 兀+ 4sinx 屮,不能设sinA=3,
71 ? sin y
cosA 二4,考虑:TWsinAWl, TWcosAWl,可以如下处理式子:
由于击w 岛)1。
故可设:sin A =. ,贝ij cos A = ±Vl-sin A , 即:cos A 二土 /
J/+方 2 yla 2+b 2
/. GCOS 兀 ±/?sin 兀二 A cos x± cos Asin x) = ^Ja 2 +b 2 sin( A ± x)
无论A±x 取何值,TWsin(A±x)Wl,
- J/ W y/a 2 +b 2 sin(A ± x) W J/ +b ,
即:- J/ +,W dcosx±bsinx W y)a 2 +Z?2
下面观察此式在解决实际极值问题时的应用:
例1 (98年全国成人高考数学考试卷)
求:函数 y = V3 cos 2 x-sinxcosx 的最大值为(AAAA )
D. V3+1
分析:sin J ;cos =丄? 2sin%cosx =丄sin2兀,再想办法把cos?兀变成含cso2x 的式子:
cos2兀=2cos 2兀一1 => cos 2 x 2 2 工曰 rz COS 2兀+1 1 ? “
十疋:y = A /3 ----------------- sin 2x 2 2acosx±bsinx = yja 2 +Z?2 ^a 2 +/?2 sinx
/
B. V3-1 cos2x + l _ 2
——cos 2x + —— sin 2x
2 2 2
=(^- cos 2x- — sin 2x) +
2 2 2
由于这里:"孚q,则7"(¥『+($=i
Aj = lx(T cos2%4sin2x)+T
设:smA=7^F=+=^KIJcosA4
??V3
/? y = sin A cos 2x一cos A sin 2x H
2
sin(/4-2x) + ^-
无论A-2x取何值,都有-lWsin(A-2x)Wl, 故一1 +
2
???『的最大值为1 + —,即答案选A。
例2 (96年全国成人高考理工科数学试卷)
在Z\ABC 中,已知:AB 二2, BC 二1, CA 二馆,分别在边AB 、BC 、CA 上任取点D 、E 、F,使ZSDEF 为正三角形,记ZFEC-Z a ,问:sin a 取 何值时,AEFD 的边长最短?并求此最短边长。
分析:首先,由于BC 2+CA 2 =12+(V3)2
=4 = AB 2 ,可知AABC 为Rt △,其屮AB 为斜边,所对角ZC 为直角,又由于
1 sin A =—= 一,故A = 30。,则 ZB 二
AB 2
90° -ZA=60° ,由于本题要计算ADEF 的最短边长,故必要设正ADEF 的边长为儿且要列出有关/为未知数的方程,对/进行求解。观察 ABDE,已知:ZB=60° , DE=/,再想办法找出另两个量,即可根据正弦定理列出等式,从而产生关于/的方程。在图屮,由于EC" ? cos a ,则 BE=BC-EC=1-/ ? cos a o
而 ZB+ZBDE+Z1=18O°〕
Z a +ZDEF+Z1 二 180° > => ZBDE=Z a
ZB 二60° , ZDEF=60° .
???在ABDE 中,根据正弦定理:
BF DE 1 一/cosa /
— -------- =— ------ a ------- : ------ =— ------ sin Z.BDE sin ZB sin a sin 60°
=/= ----------- - -------- A /3 T ? cos a + sin a 2
在这里,要使/有最小值,必须分母:爭。心认有最大值,观察:耳55書心二后孔
#(1 - /.cosa) = / ? sin =>
V3 V3 2 2 l-cosa = l-sina
.?.晅 cosd+sin —辺(亜 cos”
2 2 7
设: cos a + sin G 二(sin A cos a + cos A sin a)
= *sin(A + a)
的最大值为#
2 _ V21
近—〒
2
而sin(A + a)取最大值为1时, A + a = 2k 兀 H — oc — 2k 兀 H
2 2
故: 即:Z 的最小值为: 则
sin a - sin(2k;r + 彳- A) = cos A
2^7
即:S ma = ^-时,ADEF的边长最短,最短边长为返I
其中最大值为,最小值为一J/+,。在计算三角函数的极值应用题时,只要找出形如GCOSX土bsinx的关系式,即能根据题意,求出相关的极值。
三角函数知识点解题方法总结
一、见“给角求值”问题,运用“新兴”诱导公式
一步到位转换到区间(-90°, 90°)的公式.
1.sin(k n + a ) = (-l)k sin a (k^Z) ;
2. cos (k n + a ) = (-1) k cos a (k^Z);
3. tan (k + a ) = (-1) k tan a (kWZ);
4. cot (k Ji + a ) = (-1) k cot a (kWZ)?
二、见“sina ±cosa ”问题,运用三角“八卦图”
1.sina +cosa >0(或〈0)6a的终边在直线y+x二0的上方(或下方);
2.sin a -cos a >0(或〈0)6 a的终边在直线y-x二0的上方(或下方);
3.|sina |>|cosa |oa的终边在II、III的区域内;
4.|sin a | < | cos a |6 a 的终边在I、IV 区域内.
三、见“知1求5”问题,造RtA,用勾股定理,熟记常用勾股数(3, 4, 5) , (5, 12, 13) , (7, 24, 25),仍然注意“符号看象限”。
四、见“切割”问题,转换成“弦”的问题。
+cos' a .
五、“见齐思弦”二〉“化弦为一”:已知tana,求sina与cos a的齐次式,有些整式情形述可以视其分母为1,转化为sin2
六、见“正弦值或角的平方差”形式,启用“平方差”公式:
1.sin (a + P)sin(a ~6)= sin2 a -sin2 P ;
2. cos ( a + B ) cos ( a - P )= cos2 a -sin2 B ?
七、见“sina ±cos a与sin a cos a ”问题,起用平方法则:
(sina ±cos a )2=1 ±2sin a cos a =1 ±sin2 a ,故
1.若sin a +cos a =t,(且t?W2),则2sin a cos a =t2-l=sin2 a ;
2.若sin a 一cos a =t,(且t'W2),则2sin a cos a =l-t2=sin2 a .
八、见u tan a +tan P与tan a tan B ”问题,启用变形公式:
tan a +tan P =tan ( a + p ) (1-ta.n a tan P ).思考:tan a-tan P =? ? ?
九、见三角函数“对称”问题,启用图象特征代数关系:(AH0)
1.函数y二Asin(wx+(b)和函数y=Acos (wx+ )的图象,关于过最值点且平行于y轴的直线分别成轴对称;
2.函数y二Asin(wx+e)和函数y=Acos(wx+ 4))的图象,关于其中间零点分别成中心对称;
3.同样,利用图象也可以得到函数y二Atan(wx+e)和函数y=Acot (wx+ 4))的对称性质。
十、见“求最值、值域”问题,启用有界性,或者辅助角公式:
1. | sinx | W1, | cosx | W1;
2. (asinx+bcosx)2= (a2+b2) sin2 (x+ 4)) (a2+b2);
3.asinx+bcosx=c有解的充要条件是a'+bLcI
十一、见“高次”,用降幕,见“复角”,用转化.
1.cos2x=l-2sin2x=2cos2x-l.
2.2x=(x+y) + (x-y);2y=(x+y)-(x-y);x~w=(x+y)-(y+w)等角函数公式
两角和公式
sin(A+B)=sinAcosB+cosAsinB
sin(A ?B)=si nAcosB?sinBcosA
cos(A+B)=cosAcosB-sinAsinB cos(A-
B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/( 1 -tanAtanB) tan(A-B)=(tanA-tanB)/( 1 +tanAtanB)
cot(A+B)=(cotAcotB-1 )/(cotB+cotA) cot(A-B)=(cotAcotB+ l)/(cotB-cotA) 倍角公式
tan2A=2tanA/[ 1 -(tanA)A2] cos2a=(cosa)A2-(sina)A2=2(cosa)A2 -1=1 -2(sina)A2
sin2A=2sinA*cosA
半角公式
sin A2(a/2)=(1 -cosa)/2
cos A2(a/2)=(1 +cosa)/2 tan A2(a/2)=(1 -cosa)/(1 +cosa)
和差化积
2sinAcosB=sin(A+B)+sin(A-B)
2cosAsinB=sin(A+B)-sin(A-B))
2cosAcosB=cos(A+B)+cos(A?B)
-2sinAsinB=cos(A+B)-cos(A-B)
sinA+sinB=2sin((A+B)/2)cos((A-B)/2
cosA+cosB=2cos((A+B)/2)sin((A-B)/2)
tanA+tanB=sin(A+B)/cosAcosB
积化和差公式sin(a)sin(b)=-l/2*[cos(a+b)-cos(a-b)J cos(a)cos(b)= 1 /2*[cos(a+b)+cos(a-b)]
sin(a)cos(b)= 1/2 * [sin(a+b)+sin(a-b)] 万能公式sin(a)= (2tan(a/2))/(l +tan A2(a/2))
cos(a)= (1 -tan A2(a/2))/(l +tan A2(a/2))
tan(a)= (2tan(a/2))/(l-tan A2(a/2))
倒数关系:商的关系:平方关系:
tana ?cota= 1
sina *csca= 1
cosa -seca= 1 sina/cosa=tana=seca/csca
cosa/sina=cota=csca/seca sin2a+cos2a= 1 1
+tan2a=sec2a
三角函数经典解题方法与考点题型(教师) 1.最小正周期的确定。 例1 求函数y =s in (2co s|x |)的最小正周期。 【解】 首先,T =2π是函数的周期(事实上,因为co s(-x )=co s x ,所以cos |x |=co s x );其次,当且仅当x =k π+ 2 π 时,y =0(因为|2co s x |≤2<π), 所以若最小正周期为T 0,则T 0=m π, m ∈N +,又s in (2co s0)=s in 2≠s in (2co s π),所以T 0=2π。 过手练习 1.下列函数中,周期为 2π 的是 ( ) A .sin 2x y = B .sin 2y x = C .cos 4 x y = D .cos 4y x = 2.()cos 6f x x πω?? =- ?? ? 的最小正周期为 5 π ,其中0ω>,则ω= 3.(04全国)函数|2 sin |x y =的最小正周期是( ). 4.(1)(04北京)函数x x x f cos sin )(=的最小正周期是 . (2)(04江苏)函数)(1cos 22R x x y ∈+=的最小正周期为( ). 5.(09年广东文)函数1)4 (cos 22 -- =π x y 是 ( ) A .最小正周期为π的奇函数 B. 最小正周期为π的偶函数 C. 最小正周期为 2 π的奇函数 D. 最小正周期为2π 的偶函数 6.(浙江卷2)函数的最小正周期是 . 2.三角最值问题。 例2 已知函数y =s inx +x 2cos 1+,求函数的最大值与最小值。 【解法一】 令s inx =??? ??≤≤=+ππ θθ4304 sin 2cos 1,cos 22 x , 则有y =).4 sin(2sin 2cos 2π θθθ+ =+ 因为 ππ 4304≤≤,所以ππ θπ≤+≤4 2, 所以)4 sin(0π θ+≤≤1, 所以当πθ43=,即x =2k π-2 π (k ∈Z )时,y m in =0, 当4 π θ= ,即x =2k π+ 2 π (k ∈Z )时,y m ax =2. 2 (sin cos )1y x x =++
三角函数专题复习 在三角函数复习过程中,认真研究考纲是必须做的重要工作。三角函数可以当成函数内容中的重要一支,要注意与其它知识的联系。 一、研究考题,探求规律 1. 从表中可以看出:三角函数题在试卷中所处的位置基本上是第一或第二题,本章高考重点考查基础知识,仍将以容易题及中档为主,题目的难度保持稳定,估计这种情况会继续保持下去 2. 特点:由于三角函数中,和差化积与积化和差公式的淡出,考查主体亦发生了变化。偏重化简求值,三角函数的图象和性质。考查运算和图形变换也成为了一个趋势。三角函数试题更加注重立足于课本,注重考查基本知识、基本公式及学生的运算能力和合理变形能力,对三角变换的要求有所降低。三角化简、求值、恒等式证明。图象。最值。 3、对三角函数的考查主要来自于:①课本是试题的基本来源,是高考命题的主要依据,大多数试题的产生是在课本题的基础上组合、加工和发展的结果。②历年高考题成为新高考题的借鉴,有先例可循。 二、典例剖析 例1:函数22()cos 2cos 2x f x x =-的一个单调增区间是 A .2(,)33ππ B .(,)62ππ C .(0,)3π D .(,)66 ππ- 【解析】函数22()cos 2cos 2 x f x x =-=2cos cos 1x x --,从复合函数的角度看,原函数看作2()1g t t t =--,cos t x =,对于2()1g t t t =--,当1[1,]2t ∈-时,()g t 为减函数,当1[,1]2 t ∈时,()g t 为增函数,当2(,)33x ππ∈时,cos t x =减函数,且11(,)22 t ∈-, ∴ 原函数此时是单调增,选A 【温馨提示】求复合函数的单调区间时,需掌握复合函数的性质,以及注意定义域、自变量系数的正负.求复合函数的单调区间一般思路是:①求定义域;②确定复合过程;③根据外层函数f(μ)的单调性,确定φ(x)的单调性;④写出满足φ(x)的单调性的含有x 的式子,并解出x 的范围;⑤得到原函数的单调区间(与定义域求交).求解时切勿盲目判断. 例2、已知tan 2θ=. (Ⅰ)求tan 4πθ??+ ??? 的值; (Ⅱ)求cos2θ的值. 【解析】 (Ⅰ)∵tan 2θ=, tan tan 4tan 41tan tan 4π θπθπθ+??∴+= ???-
求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的几种常用方法 一、定义法 当已知直角三角形的两条边,可直接运用锐角三角函数的定义求锐角三角函数的值. 例1 如图1,在△ABC 中,∠C =90°,AB =13,BC =5,则sin A 的值是( ) (A )513 (B )1213 (C )512 (D )13 5 对应训练: 1.在Rt △ABC 中,∠ C =90°,若BC =1,AB 5,则tan A 的值为 ( ) A . 5 B 25 C .1 2 D .2 二、参数(方程思想)法 锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线 段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题. 例2 在△ABC 中,∠C =90°,如果tan A =5 12,那么sin B 的值是 . 对应训练: 1.在△ABC 中,∠C =90°,sin A=5 3,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 2.已知△ ABC 中, ο 90=∠C ,3cosB=2, AC=5 2 ,则 AB= . 3.已知Rt △ABC 中,,12,4 3 tan ,90==?=∠BC A C 求AC 、AB 和cos B .
4.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?=∠4 3sin AOC 求:AB 及OC 的长. 三、等角代换法 当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等 角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等” 来解决. 例3 在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =5,CD =4,则cos ∠ACD 的值为 . 对应训练 1.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径, 若O ⊙的半径为32,2AC =,则sin B 的值是( )A .2 3
用锐角三角函数概念解题的常见方法 1.锐角三角函数 (1)锐角三角函数的定义 我们规定: sinA=a c ,cosA= b c ,tanA= a b ,cotA= b a . 锐角的正弦、余弦、正切、余切统称为锐角的三角 函数. (2)用计算器由已知角求三角函数值或由已知三 角函数值求角度 对于特殊角的三角函数值我们很容易计算,甚至可 以背诵下来,但是对于一般的锐角又怎样求它的三角函数值呢?用计算器可以帮我们解决大问题. ①已知角求三角函数值; ②已知三角函数值求锐角. 2 直角三角形中,30°的锐角所对的直角边等于斜边的一半. 3.锐角三角函数的性质 (1)0 (2)tan α·cot α=1或tan α=1 cot α ; (3)tan α= sin cos αα,cot α=cos sin α α . (4)sin α=cos (90°-α),tan α=cot (90°-α). 有关锐角三角函数的问题,常用下面几种方法: 一、设参数 例1. 在ABC ?中,?=∠90C ,如果125 tan = A ,那么sin B 的值等于( ) 5 12.12 5. 13 12. 13 5. D C B A 解析:如图1,要求sinB 的值,就是求 AB AC 的值,而已知的12 5 tan =A ,也就是12 5 =AC BC 可设k AC k BC 125==, 则k k k AB 13)12()5(22=+= 13 12 1312sin == ∴k k B ,选B 二、巧代换 例2. 已知3tan =α,求 α αα αcos sin 5cos 2sin +-的值。 解析:已知是正切值,而所求的是有关正弦、余弦的值,我们可以利用关系式 3cos sin tan == α α α,作代换ααcos 3sin =,代入即可达到约分的目的,也可以把所求的分式的分子、分母都除以αcos 。 图1 2018高考数学解题技巧 解答题模板2:三角函数 高考中三角函数解答题是历年高考必考内容之一,成为6道解答题中的第一题,难度一般比较小,三角函数中,以公式多而著称.解题方法也较灵活,但并不是无法可寻,当然有它的规律性,近几年的高考中总能体现出其规律性.而对三角函数的考查解法,归纳起来主要有以下六种方法:能够做好这道题也成了决定高考成败的关键,从近几年高考来看,三角函数解答题有如下几种题型 二、典型例题 弦切互化 例1.已知2tan =θ,求(1) θ θθ θsin cos sin cos -+; 解:(1)2232 121tan 1tan 1cos sin 1cos sin 1sin cos sin cos --=-+=-+=-+ = -+θθθ θθθ θθθθ; 函数的定义域问题 例2、求函数1sin 2+=x y 的定义域。 解:由题意知需01sin 2≥+x ,也即需21sin -≥x ①在一周期?? ????-23,2ππ上符合①的角为??? ???-67,6ππ,由此可 得到函数的定义域为????? ? +-672,62ππππk k ()Z k ∈ 说明:确定三角函数的定义域的依据:(1)正、余弦函数、正切函数的定义域。(2)若函数是分式函数,则分母不能为零。(3)若函数是偶函数,则被开方式不能为负。(4)若函数是形如()() 1,0log ≠>=a a x f y a 的函数,则其定义域由()x f 确定。(5)当函数是有实际问题确定时,其定义域不仅要使解析式有意义同时还要使实际问题有意义。 函数值域及最大值,最小值 (1)求函数的值域 一般函数的值域求法有:观察法,配方法判别式法等,而三角函数是函数的特殊形式,其一般方法也适用,只不过要结合三角函数本身的性质罢了。 例3、求下列函数的值域 (1)x y 2sin 23-= (2)2sin 2cos 2 -+=x y x 分析:利用1cos ≤x 与1sin ≤x 进行求解。 解:(1) 12sin 1≤≤-x ∴[]5,151∈∴≤≤y y (2)()[].0,4,1sin 11sin 1sin 2sin 2sin 22 22 cos -∈∴≤≤---=-+-=-+=y x x x x x x y 锐角三角函数: 知识点一:锐角三角函数的定义: 一、 锐角三角函数定义: 在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA= ∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 【特别提醒:1、sinA 、∠cosA 、tanA 表示的是一个整体,是两条线段的比,没有,这些比值只与 有关,与直角三角形的 无关 2、取值范围 1.已知Rt △ABC 中,,12,43 tan ,90==?=∠BC A C 求AC 、AB 和cos B . 2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?= ∠4 3sin AOC 求:AB 及OC 的长. 3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,?=∠5 3 sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4. 已知A ∠是锐角,17 8 sin =A ,求A cos ,A tan 的值 对应训练: (西城北)3.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为 A . 55 B .255 C .12 D .2 (房山)5.在△ABC 中,∠C =90°,sin A=5 3 ,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 类型二. 利用角度转化求值: 1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点. DE ∶AE =1∶2. 求:sin B 、cos B 、tan B . 浅论关于三角函数的几种解题技巧 本人在十多年的职中数学教学实践中,面对三角函数内容的相关教学时,积累了一些解题方面的处理技巧以及心得、体会。下面尝试进行探讨一下: 一、关于)2sin (cos sin cos sin ααααα或与±的关系的推广应用: 1、由于ααααααααc o s s i n 21c o s s i n 2c o s s i n )c o s (s i n 2 22±=±+=±故知道)c o s (s i n αα±,必可推出)2sin (cos sin ααα或,例如: 例1 已知θθθθ33cos sin ,3 3 cos sin -= -求。 分析:由于)cos cos sin )(sin cos (sin cos sin 2233θθθθθθθθ++-=- ]cos sin 3)cos )[(sin cos (sin 2θθθθθθ+--= 其中,θθcos sin -已知,只要求出θθcos sin 即可,此题是典型的知sin θ-cos θ,求sin θcos θ的题型。 解:∵θθθθcos sin 21)cos (sin 2-=- 故:3 1cos sin 31)33( cos sin 212=?==-θθθθ ]cos sin 3)cos )[(sin cos (sin cos sin 233θθθθθθθθ+--=- 39 4 3133]313)33[(332=?=?+= 2、关于tg θ+ctg θ与sin θ±cos θ,sin θcos θ的关系应用: 由于tg θ+ctg θ=θ θθθθθθθθθcos sin 1cos sin cos sin sin cos cos sin 22=+=+ 故:tg θ+ctg θ,θθcos sin ±,sin θcos θ三者中知其一可推出其余式子的值。 例2 若sin θ+cos θ=m 2,且tg θ+ctg θ=n ,则m 2 n 的关系为( )。 A .m 2=n B .m 2= 12+n C .n m 2 2= D .22m n = 关于三角函数的几种解题技巧 本人在十多年的职中数学教学实践中,面对三角函数内容的相关教学时,积累了一些解题方面的处理技巧以及心得、体会。下面尝试进行探讨一下: 一、关于)2sin (cos sin cos sin ααααα或与±的关系的推广应用: 1、由于ααααααααcos sin 21cos sin 2cos sin )cos (sin 222±=±+=±故知道)cos (sin αα±,必可推出)2sin (cos sin ααα或,例如: 例1 已知θθθθ33cos sin ,3 3cos sin -=-求。 分析:由于)cos cos sin )(sin cos (sin cos sin 2233θθθθθθθθ++-=- ]cos sin 3)cos )[(sin cos (sin 2θθθθθθ+--= 其中,θθcos sin -已知,只要求出θθcos sin 即可,此题是典型的知sin θ-cos θ,求sin θcos θ的题型。 解:∵θθθθcos sin 21)cos (sin 2-=- 故:3 1cos sin 31)33(cos sin 212=?==-θθθθ ]cos sin 3)cos )[(sin cos (sin cos sin 233θθθθθθθθ+--=- 39 43133]313)33[(332=?=?+= 例2 若sin θ+cos θ=m 2,且tg θ+ctg θ=n ,则m 2 n 的关系为( )。 A .m 2=n B .m 2=12+n C .n m 22= D .22m n = 分析:观察sin θ+cos θ与sin θcos θ的关系: sin θcos θ=2 121)cos (sin 22-=-+m θθ 而:n ctg tg ==+θ θθθcos sin 1 故:1212122+=?=-n m n m ,选B 。 例3 已知:tg α+ctg α=4,则sin2α的值为( )。 一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米. 【答案】553 【解析】 【分析】 如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可. 【详解】 解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J. ∵AM⊥CD, ∴∠QMP=∠MPO=∠OQM=90°, ∴四边形OQMP是矩形, ∴QM=OP, ∵OC=OD=10,∠COD=60°, ∴△COD是等边三角形, ∵OP⊥CD, ∠COD=30°, ∴∠COP=1 2 ∴QM=OP=OC?cos30°=3 ∵∠AOC=∠QOP=90°, ∴∠AOQ=∠COP=30°, ∴AQ=1 OA=5(分米), 2 ∴AM=AQ+MQ=5+3 ∵OB∥CD, ∴∠BOD=∠ODC=60° 在Rt△OFK中,KO=OF?cos60°=2(分米),FK=OF?sin60°=23(分米), 在Rt△PKE中,EK=22 -=26(分米), EF FK ∴BE=10?2?26=(8?26)(分米), 在Rt△OFJ中,OJ=OF?cos60°=2(分米),FJ=23(分米), 在Rt△FJE′中,E′J=22 -(2)=26, 63 ∴B′E′=10?(26?2)=12?26, ∴B′E′?BE=4. 故答案为:5+53,4. 【点睛】 本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型. 2.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系; (2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由 (3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长. 【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP62 23 . 【解析】 【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再 锐角三角函数的解题技巧 一、知识点回忆 (一)锐角的三角函数的意义 1、正切 在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比,叫做∠A的正切,记作tanA. 2、正弦和余弦 如图,在Rt△ABC中,∠C=90°,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即 3、三角函数:在直角三角形中,锐角A的正切(tanA)、正弦(sinA)、余弦(cosA),都叫做∠A的三角函数. (二)同角的三角函数之间的关系 (1)平方关系:sin2α+cos2α=1 (2)商数关系: (三)两角的关系 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值,任意锐角的正切值与它的余角的正切值的积等于1.即若A+B=90°,则sinA=cosB,cosA=sinB,tanA·tanB=1. (四)特殊锐角的三角函数值 (五)锐角三角函数值解法 1、用计算器 求整数度数的锐角三角函数值. 在计算器的面板上涉及三角函数的键有和键,当我们计算整数度数的某三角函数值时,可先按这三个键之一,然后再从高位向低位按出表示度数的整数,然后按,则屏幕上就会显示出结果. 例如:计算sin44°. 解: 按键,再依次按键. 则屏幕上显示结果为0.69465837. 求非整数度数的锐角三角函数值. 若度数的单位是用度、分、秒表示的,在用计算器计算三角函数值时,同样先按 和三个键之一,然后再依次按度分秒键,然后按键,则屏幕上就会显示出结果. 2、已知三角函数值,用计算器求角度 已知三角函数值求角度,要用到、键的第二功能“sin-1,cos-1,tan-1”和键.具体操作步骤是:先按键,再按键之一,再依次按三角函数值,最后按键,则屏幕上就会显示出结果. 值得注意的是:型号不同的计算器的用法可能不同。 (六)直角三角形的解法 解直角三角形既是初中几何的重要内容,又是今后学习解斜三角形,三角函数等知识的基础,同时,解直角三角形的知识又广泛应用于测量、工程技术和物理之中,解直角三角形的应用题还有利于培养学生空间想象的能力。因此,通过复习应注意领会以下几个方面的问题: 解直角三角形的重点是锐角三角函数的概念和直角三角形的解法。前者又是复习解直角三角形的难点,更是复习本部分内容的关键。 掌握锐角三角函数和解直角三角形是进行三角运算解决应用问题和进一步研究任意角三角函数的重要基础。因此,解直角三角形既是各地中考的必考内容,更是热点内容。题量一般在4%~10%。分值约在8%~12%题型多以中、低档的填空题和选择题为主。个别省市也有小型综合题和创新题。几乎每份试卷都有一道实际应用题出现。 二、重点难点疑点突破 1、(1)sinA和cosA都是一个整体符号,不能看成sin·A或cos·A. (2)是一个比值,没有单位,只与角的大小有关,而与三角形的大小无关. (3)sinA+sinB≠sin(A+B)sinA·sinB≠sin(AB) (4)sin2A表示(sinA)2,cos2A=(cosA)2 (5)0<sinA<1,0<cosA<1 2、同名三角函数值的变化规律 当角α在0°~90°间变化时,它的正切和正弦三角函数值随着角度的增大而增大; 余弦三角函数值随着角度的增大而减少. 三、解题方法技巧点拨 1、求锐角三角函数的值 例1、(1)在Rt△ABC中,∠C=90°,若,求cosB,tanB的值. 求锐角三角函数值的几种常用方法 一、定义法 当已知直角三角形的两条边,可直接运用锐角三角函数的定义求锐角三角函数的值. 例1 如图1,在△ABC 中,∠C =90°,AB =13,BC =5,则sin A 的值是( ) (A ) 513 (B )1213 (C )512 (D )13 5 对应训练: 1.在Rt △ABC 中,∠ C =90°,若BC =1,AB tan A 的值为( ) A B C .1 2 D .2 二、参数(方程思想)法 锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线 段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题. 例2 在△ABC 中,∠C =90°,如果tan A = 5 12 ,那么sin B 的值是 . 对应训练: 1.在△ABC 中,∠C =90°,sin A= 5 3 ,那么tan A 的值等于( ). A .35 B . 45 C . 34 D . 43 2.已知△ABC 中, 90=∠C ,3cosB=2, AC=52 ,则AB= . 3.已知Rt △ABC 中,,12,4 3tan ,90==?=∠BC A C 求AC 、AB 和cos B . 4.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,?=∠4 3sin AOC 求:AB 及OC 的长. 第8题图 A D E C B F 三、等角代换法 当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等 角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等” 来解决. 例3 在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =5,CD =4,则c o s ∠ACD 的值为 . 对应训练 1.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为 3 2 ,2AC =,则s in B 的值是( )A .23 B .32 C .34 D .4 3 2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =, AB=8,则tan EFC ∠的值为 ( )A.34 B.43 C.35 D.45 3. 如图6,在等腰直角三角形ABC ?中,90C ∠=?,6AC =,D 为AC 上一点,若 1tan 5 DBA ∠ = ,则AD 的长为( ) A .2 C .1 D .4. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧 圆弧上一点,则cos ∠OBC 的值为( )A . 12 B .2 C .35 D .45 5.如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= . 6.(庆阳中考)如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5 A =,则这个菱形的面积= cm 2 . 7. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A AD = 3 3 16求 ∠B 的度数及边BC 、AB 的长. D A B C 龙源期刊网 https://www.doczj.com/doc/d38349527.html, 高中数学三角函数解题方法与技巧分析 作者:王元蕾 来源:《文理导航》2017年第29期 【摘要】在高中学习期间,三角函数是相对独立又颇为重要的一块内容。分析历年来的高考试题可以发现,全国卷中涉及的三角函数的内容一般为选择题(或填空题)和一道大题。选择题的型多变,不易解答。而大题一般出现在第一道大题的位置上,较为简单。另外,数理不分家,三角函数在高中物理的叠加场大题中也发挥着关键作用。总之,加强对于高中数学三角函数内容的学习,十分必要。在本文中,我将介绍自己在高中学习过程中,对三角函数这块内容的理解以及一些解题方法、答题技巧。 【关键词】三角函数;答题技巧;高考 引言 三角函数,顾名思义,与角度和函数有关,数学上对函数的定义为:给定一个数集A,对A施加对应法则f,记作f(A),得到另一数集B,也就是B=f(A),因此,角度也就是函数定义中A了。据专家、老师以及我的分析,在全国卷中,三角函数题属于低档题,而且三 角函数知识属于高中阶段的工具性知识,因此必须熟练掌握。下面我根据个人经验,从三个方面介绍三角函数的答题技巧。 1.解题时要注意灵活运用基础知识 如例2:如右图所示,在三角形ABC中,已知:tan∠B=3/4,sin∠ADC=4/5,AD长度为5米。求:AB的长度。 解析:由sina/cosa=tana、tan∠B=3/4两个条件可以得出,sina=3/4cosa,再由 sina+cosa=1,联立方程组,再观察图一三角形,可以判断正弦值为正数,可以计算出 sin∠B=3/5。又因为知道sin∠ADC=4/5,则sin∠ADB=sin(180°-∠ADC)=sin∠ADC=4/5。由正弦定理得AD/sin∠B=AB/sin∠ADB,代入数值,解得AB的长度为20/3米。 2.解题时要注重题目的隐含条件 我们都知道三角函数隶属于函数,笔者根据高一学函数时总结的经验可以发现,三角函数题(特别是给出图的题,对图中标注的条件观察不仔细而导致题做不出来)有时候会含有隐含条件,例如:奇偶性、极值、锐角三角形等。 如例3:在銳角三角形ABC中,如果tan∠B=2+√3,sin∠C=√3 /2。求∠A的余弦值。 1、平面内,如图17,在□ABCD 中,10AB =,15AD =,4tan 3A =.点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90?得到线段PQ . (1)当10DPQ ∠=?时,求APB ∠的大小; (2)当tan :tan 3:2ABP A ∠=时,求点Q 与点B 间的距离(结果保留根号); (3)若点Q 恰好落在□ABCD 的边所在的直线上,直接写出PB 旋转到PQ 所扫过的面积(结果保留π). 2、如图所示,我国两艘海监船A ,B 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C ,此时,B 船在A 船的正南方向5海里处,A 船测得渔船C 在其南偏东45°方向,B 船测得渔船C 在其南偏东53°方向,已知A 船的航速为30海里/小时,B 船的航速为25海里/小时,问C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈,cos53°≈,tan53°≈,≈1.41) 3、如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5km 到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) B A P C D Q 备用图17 A B C D P Q 4、如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度. 5、一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为米. 6、如图,某小区①号楼与?号楼隔河相望,李明家住在①号楼,他很想知道?号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算?号楼的高度CD. 7、某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31cm,在A处测得甲楼顶部E处的仰角是31°. (1)求甲楼的高度及彩旗的长度;(精确到0.01m) (2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲乙两楼之间的距离.(精确到0.01m) (cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84) 锐角三角函数的题型及解题技巧 锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳 出 锐角三角函数的常见题型,并结合例题介绍一些解题技巧。 、 化简或求值 例1 (1) 已知tan 2cot 1,且 是锐角,求乙tan 2 cot 2 2的值。 (2) 化简 a sin bcos ? acos bsin ?。 分析 (1)由已知可以求出tan 的值,化简?、tan 2 cot 2 2可用 1 tan cot ; (2)先把平方展开,再利用sin 2 cos 2 1化简 解(1)由tan 2cot 1得tan 2 2 tan ,解关于tan 的方程得 tan 2或 tan 1。又是锐角,二 tan 2。二、tan 2 cot 2 2 = 1 2 2 2,「 tan cot 2 = tan cot (2) a sin bcos ? acos bsin 2 -2 ? 2 2 cos b sin cos = a 、已知三角函数值,求角 求C 的度数。 分析 几个非负数的和为0,则这几个数均为0。由此可得cosA 和sin B 的 值,进而求出 代B 的值,然后就可求出 C 的值。 \ tan 2 2tan cot cot 2 = : (tan cot )2 tan cot 由tan 得cot a 2 sin 2 2ab sin cos b 2 cos 2 + a 2 cos 2 2ab cos sin b 2s in 2 2 2 a sin 2 b 2 tan 说明 在化简或求值问题中,经常用到 cot 1 等。 “ 1” 的代换, 即 sin 2 2 cos J 2 例2在厶ABC 中,若cosA — 2 .3 2 sin B 0 A, B 均为锐角, 锐角三角函数的题型及解题技巧 锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。 一、 化简或求值 例1 (1)已知tan 2cot 1αα-=,且α是锐角,的值。 (2)化简()()22 sin cos cos sin a b a b αααα++-。 分析 (1)由已知可以求出tan α1tan cot αα=?;(2)先把平方展开,再利用22sin cos 1αα+=化简。 解 (1)由tan 2cot 1αα-=得2tan 2tan αα-=,解关于tan α的方程得 tan 2α=或tan 1α=-。又α是锐角,∴tan 2α== tan cot αα-。由tan 2α=, 得1cot 2α==tan cot αα-=13222 -=。 (2)()()22sin cos cos sin a b a b αααα++-= 2222sin 2sin cos cos a ab b αααα+??++2222cos 2cos sin sin a ab b αααα-??+=()()222222sin cos sin cos a b αααα+++=22a b +。 说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1αα+=,tan cot 1αα?=等。 二、已知三角函数值,求角 例2 在△ABC 中,若2 cos sin 02A B ?-+= ??(),A B ∠∠均为锐角,求C ∠的度数。 分析 几个非负数的和为0,则这几个数均为0。由此可得cos A 和sin B 的值,进而求出,A B ∠∠的值,然后就可求出C ∠的值。 209 二○一九年一月(下旬) 高 考 ·考试研究· 高中数学三角函数的解题技巧 山东省济宁市实验中学 薛丁方 摘 要:三角函数是高中数学学习中的主要内容,不仅在高中阶段的数学学习中具有重要地位,而且据了解,历年高考数学题中约15%的考察内容与三角函数有关。想要掌握三角函数的解题技巧,首先需要对三角函数概念、性质、公式具备足够的了解,奠定抓实基础,进而在三角函数的解题过程中总结规律,掌握灵活多变的解题方法,做到活学活用,以此提升三角函数的学习质量。本文在三角函数学习的过程中总结了以下几点经验,以供参考与批评。 关键词:高中数学;三角函数;解题技巧 一、掌握基本概念、性质定理,打好基础 三角函数的内容较为复杂,其中涉及到大量的公式与定理,而每一个三角函数公式的使用条件与定理的使用范围受到题目内容的限制,若是在三角函数学习中没有充分的掌握三角函数的概念、公式、性质,理解程度不够,记忆量不足,缺乏知识的灵活运用能力,就会在三角函数解题过程中盲目性解答,出现错用、错套等问题。基于此,笔者认为提升高中生三角函数解题能力,掌握解题技巧的关键在于打好基础。 1.概念与性质的学习是学生三角函数学习中的基础,只有真正吃透三角函数概念,掌握三角函数的性质,才能具有三角函数概念的灵活运用能力,在三角函数的解题过程中灵活应对,周期性与图像性质是我们在高中阶段三角函数学习中的常见性质,在解题中学生应具备三角函数性质的正确判断能力,通过对其性质的判断降低解题难度。如该题目为三角函数周期性类型,学生在该类问题解答中实现利用角度转换的方式,减少解题过程中的计算难度,利用该问题的类型得出解集,利用周期性三角函数在某一特定区间内的奇偶性和单调性,建立图像,利用其特性,迅速找出问题解决的方法。 2.需要重点学习三角函数公式,公式的学习效果以及应用能力的提升,可以让高中生的三角函数解题更加快速、准确。但是,高中阶段的三角函数公式涉及的内容角度,在强行记忆与三角函数有关的公式下,虽然记忆量增加,众多公式也进入的脑袋里,但是,在面对实际问题解答中如何灵活运用,成为了高中生三角函数学习过程中的又一难题。因为用一类型的三角函数公式具有一定的相似度,很多同学会容易记混、错用,因此,我们可以使用口诀记忆的方式,如“一全正,二正弦,三正切,四余弦”、“函数名不变,符号看象限”等,快速记忆,同时需要通过实际的联系,掌握不同公式之间的差异,区分其具体用法,通过总结与分析,掌握不同公式的应该规律。 二、三角函数解题技巧探究 1.利用转化法,灵活多变,解答问题 在充分了解三角函数概念、性质、定理的基础上,需要我们具有清晰的解题思路,掌握科学、简便的解题方法,以求在有限的时间内快速解答出正确的答案。转化法是我们在高中阶段三角函数学习中常用的一种方法,通过转化法在解题中的应用,可以将原本看似复杂的问题转化为简单易懂的形式,在求解,降低了三角函数问题的解答难度。举例说明: 例1已知sinα+cosα=m2,tgα+ctgα=n,求m 2与n 的关系. 此题看似较为复杂,但只要对tgα+ctgα进行适当转换,并找出sinα+cosα与sinαcosα的关系,就可以快 速解出答案.由于tgα+ctgα=1/sinαcosα,根据题目已知条件,可以得出sinαcosα=1/n,又由于sinαcosα=[(sinα+cosα)2-1]/2=m 2-1/2,因此,可以推导出m2与n 的关系式,即m 2=2/n+1. 2.利用托底法简化表达式 上述中的例题属于容易转化的类型,而在面对不易转化的题目类型时,可以采取托底法简化求解,还是结合一道例题进行具体说明. 例2已知tgα=3,求解sinα-3cosα2sinα+cosα的值. 在该题中,只有把求解表达式化简为包含tgα的形式,才能利用已知条件进行求解.根据求解表达式特点,可以将其分子和分母同时除以cosα,将其转化为tgα-3/2tgα+1,代入已知条件后,可以快速求解出, sinα-3cosα/2sinα+cosα=0.3.总结方法规律 首先,在练习的过程中应选择具有典型特征的题型,盲目性的练习不仅不会提升解题能力,还会增加学习负担。其次,针对性练习,每一种三角函数题型都有其自身的一套解题方法,学生可以采取逐个类型练习的方法,从中总结方法与规律,掌握该类型的解题技巧,再次面对此类型题的时候,就能够轻松应对。三角函数的解题方法分为很多种,除了上述提到的转化法、简化法外,还包括排除法、特殊值法、数形结合法等。通过平时练习中的总结经验、积累和归纳,有助于提升解题速度与准确率。 结语:结合上文可知,三角函数的知识内容繁杂,涉及到的公式较多,对于高中生而言具有一定的学习难度。想要掌握三角函数的解题技巧,要一步一步脚印,扎实基础,吃透三角函数的概念,充分了解不同类型公式的使用条件,具有公式的灵活运用能力,能够根据题目的类型及时判断解题方法,通过对条件以及表达式的转化、简化,梳理清晰的解题思路,避免错误理解题目内容、错用公式,总结规律与经验,以此提升高中生的三角函数解题能力,掌握符合自身学习特点的三角函数解题技巧。 参考文献 [1]例析三角函数求值题的解题技巧[J].彭万雷.华夏教师.2016(12) [2]分析高中数学三角函数解题常见误区及正确解题方案[J].宗位勇.数学大世界(下旬).2016(07) 三角函数专项复习 锐角三角函数知识点总结 1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B): 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。 4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。 6、正切的增减性: 当0°<α<90°时,tan α随α的增大而增大, A 90B 90∠-?=∠?=∠+∠得由B A 对 边 C 7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。 依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法) 8、应用举例: (1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。 仰角铅垂线 水平线 视线 视线俯角 (2)坡面的铅直高度h 和水平宽度l 的比叫做 坡度(坡比)。用字母i 表示,即h i l =。坡度一般写成1:m 的形式,如1:5i =等。 把坡面与水平面的夹角记作α(叫做坡角),那么tan h i l α= =。 3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。 4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东45°(东北方向) , 南偏东45°(东南方向), 南偏西45°(西南方向), 北偏西45°(西北方向)。 :i h l =h l α高考数学解题技巧三角函数
初三锐角三角函数知识点与典型例题
三角函数解题技巧和公式(已整理)
(完整版)高中数学三角函数解题技巧和公式(已整理)
人教中考数学锐角三角函数-经典压轴题附详细答案
锐角三角函数的解题技巧
求锐角三角函数值的经典题型+方法归纳(超级经典好用)
高中数学三角函数解题方法与技巧分析
锐角三角函数专项复习经典例题
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧
高中数学三角函数的解题技巧
初三锐角三角函数知识点总结典型例题练习