当前位置：文档之家 › 角动量例题

角动量例题

  • 格式：doc
  • 大小：153.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

刚体角动量 功能例题.ppt

刚体角动量 功能例题.ppt


l 6
3g l l 3g 6l
1 6 1 2
3gl，水平向左． g，竖直向上．
第四章 刚体的转动
9
物理学
第五版
4-3 角动量 角动量守恒定律
思考：如何用刚体定轴转动的动能定理解第二问？
Md
0
1 2
J 2
1 2
J0 2
2
mg
l
cosd
1
J 2
06
2
1 mgl 1 1 ml22
6
29
得 3g
4-3 角动量 角动量守恒定律
v1 2a1h 2h
R1
R1
R1
解得
2h
2(m1R1 m2R2 )g
R1 (M1 2m1)R12 (M 2 2m2 )R22
方法二：Rh机1 械能守h恒 定R2律求RR解12 h
同轴圆柱体、两重物（含绳）、地球组成的系统，机械能守恒。
m1gh
m2 g
mg 1 l 1 J2 1 1 ml22
62
29
得 3g
＝M 0
l
J
(3) vA
rA
l 3
3g 1 l3
3gl，水平向右．
aAn
rA 2
l 3
3g l
g，竖直向下．
vB rB
aBn rB 2
2l 3 2l
3
3g l 3g l
2 3
3gl，水平向左．vC rC
2g，竖直向上． aCn rC 2
物理学
第五版
4-3 角动量 角动量守恒定律
例1：留声机的转盘绕通过盘心垂直盘面的轴在水平面内以
角速率ω 作匀速转动．放上唱片后，唱片将在摩擦力作用下
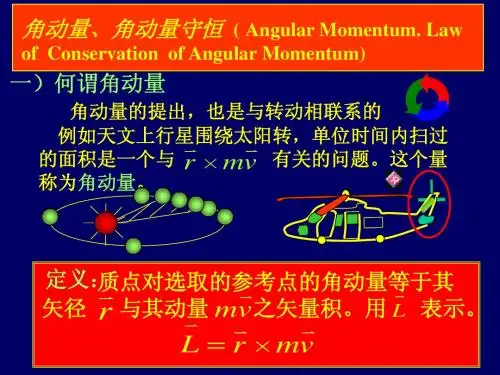
02--6、角动量

02--6、角动量


�
L
∩
h = s sin α = vt sin α
t时间内扫过的面积
s = vt
1Hale Waihona Puke 1 mrvsin α 1 t A = rh = rvt sin α = 2 2 m 2
t时间内扫过的面积
1 r A = rh b O 2 A s 1 = rvt sin α L 2 1 mrvsin α ∴A = 1 L = t t 2m 2 m
2)角动量定理的积分形式 )
∵M =
dL dt
∴M dt = dL(5)
的作用下, 设:在合外力矩M的作用下, 在合外力矩 的作用下 t1 →t2 时间内 称为力矩的角 系统的角动量从 冲量或冲量矩 对(5)式积分: )式积分:
t2
L1 → L2
Mdt = ∫ dL = L2 L (6) 1 ∫
有心力的力矩为零
F
三角动量定理 1)角动量定理的微分形式 ) 对一个质点: 对一个质点:
Z
L M
O X
L = r × P(1)
求导: (1)式对 求导: )式对t求导
r
Y
dL d = (r × P) dt dt dr dP = ×P+r × dt dt
mg
mv
= v ×P+r ×F
= r ×F = M dL ∴M = dt
恒量例4质量为m的小球a以速度沿质量为m的半径为r的地球表面水平切向向右飞出如图地轴oo与平行小球a的轨道与轴oo相交于3r的c点不考虑地球的自转与空气阻力求小球a在c点的为研究对象
角动量,角动量守恒 ( Angular Momentum. Law 角动量,
of Conservation of Angular Momentum)
第六章、角动量定理

第六章、角动量定理


rc

ac

0
i
i

其中 rc 为质心系中质心位矢，它必为零。故
M 0

dL dt
质心系角动 量微分形式
即质点系相对质心的角动量的时间变化率等于外力相
对质心的外力矩总和。
t
0 M0dt L L0
质心系角动 量积分形式
注意：①质心系角动量定理虽与质点或质点系的角动量定理具
O
r
L0
mv
在直角坐标系中
i jk
Lx , Ly , Lz

x
y
z
px py pz
O
R
图6.2、圆锥摆的角动量
其中： p mv
3
二、力矩
作用力F，其作用点的位矢为r，它对O点的力矩被定义为
M rF
方向：由右手定则确定；
大小: M=rFsinθ。
在直角坐标系中，其分量表示
i jk
M x , M y , M z x y z
Fx F y Fz
图6.3、力矩
4
例6.1：试求作用在圆锥摆上的拉力T、重力
mg和合须明确指出是对那点或 那个轴的力矩；
o'
L
力矩
αT
o'点
拉力T 0
重力mg
合力F
mgLsinα× FLcosα×
正方向 量均为m，胶泥的质量为m’, 原来重
h
m' m vv
m
物与盘静止，让胶泥从h高处自由落 下，求胶泥粘到盘上后获得速度。
图v6o .8、题6.5图
解：把盘、重物、胶泥视为质点系，在胶
泥与盘的碰撞过程中，绳的拉力，盘与重物所受的重力对o轴
1.6 动量 动能 角动量

1.6 动量 动能 角动量

2 2x x 2 2 1 mv sin θ + 1 mv = 1 mv + 1 mv = 0 2 1y 2y 1 2 2 2 2
v 2 x = 2v x = 100m / s v 2 y = v1 y = 14.7m / s
设爆炸后第二块飞行t 落地距原点距离为s, 设爆炸后第二块飞行 2秒,落地距原点距离为 , 则:
Mgx 而已落到桌面上的柔绳的重量为: 而已落到桌面上的柔绳的重量为 mg =
所以: 所以 F总 = F + mg = 2 Mgx
L
L
Mgx +
L
= 3mg
3,动量守恒定律 , (1) 质点动量守恒定律 t 由质点动量定理, 由质点动量定理,有: I = ∫t F dt = p2 p1
2 1
若质点所受合外力为零, 则有: 若质点所受合外力为零,即 F = 0则有
dt
dt
根据动量定理,桌面对柔绳的冲力为 根据动量定理,桌面对柔绳的冲力为: dx ρ dx dP dt =- ρ v 2 ′= = F dt dt 柔绳对桌面的冲力F=- =-F′ 柔绳对桌面的冲力 =- 即: M 2 2 2 F = ρv = v ,v = 2 gx ,F = 2 Mgx / L L
s1 = v x t 0 v2 y h = 2g 0 = v y gt
t = 2 s v x = 50m / s
v2
v1
θ
19.6m
s1
设爆炸后第二块速度为v 设爆炸后第二块速度为 2与水平方向夹角为θ,则 由动量守恒得: 由动量守恒得 1 mv cosθ = 1 mv = mv
t ′ = 1s,h = 19.6m 1 2 由题意得: 由题意得 h = v1t ′ gt ' 2
第11章_角动量：转动

第11章_角动量：转动

§11-1 角动量 物体绕定轴旋转
一、角动量
L
对于定点转动而言：
L
r
P
r mv
r
o
刚体的角动量？
r sin
P
mv
m
对于绕固定轴oz转动的
质元 mi 而言:
Li
ri mi
ri2mikvi
对于绕固定轴oz 转动 的整个刚体而言:
z
L
vi ri
mi
L
N
miri2 I
i
角动量的方向沿轴的正向或负向,所以可
上式和牛顿第二定律的微分形式相似，所以上式有时 也叫做角动量定理的微分形式。
牛顿第二运动定律
F ma 或者写成动量形式 F dp dt
类似写出刚体定轴转动定律
I
I I d dt d (I) dt dL dt
d dt
dL dt
二、角动量守恒
dL dt
由上式可知合外力矩为零时，角动量守恒，即：
（2）参考点为质点系或刚体的质心。
§11-5 刚体的角动量和力矩
计算刚体转动沿转轴方向的角动量：
（因为角速度
ur
的方向平行于转轴，所以
沿转轴方向的角动量记为 L ）
物体上任一质点，对O点的角动量为
r Li
rri
pr i
此角动量沿转轴方向的分量为
Li ri pi cos miviri cos r
例11-5 一人站在一个静止的、无摩擦的、可自由旋转的 台面上，手持一个旋转的自行车轮（如图所示）。如果 突然翻转旋转的车轮，即车轮向相反方向旋转，想想看 会发生什么情况？ 解答：将桌子、人、自行车轮看作一个
系统，系统角动量守恒。故自行车轮反 方向旋转后系统仍需保持此角动量。因 此可以断言：此人将按照自行车轮初始 的旋转方向开始转。
角动量——精选推荐

角动量——精选推荐

⾓动量⾓动量第六⼩组：陈⼩松兰婷李强徐继张⽟（组长）outline本章知识框架及总结（张⽟）?本章经典例题讲解与剖析（徐继）?⾓动量的发展与现状（兰婷）⾓动量的知识框架⾓动量⾓动量的算符表⽰（包括分量、⾓动量的平⽅等）⾓动量的对易关系l r p =×v v v $,z x y l l i l = h ⾓动量的本征值⾓动量的矩阵元（矩阵表⽰）⾃旋⾓动量⼆、⾓动量算符１、定义：⾓动量算符分量式为??L rp =×v v v ()()()()()()x z y y x z z y x L yp zp y z i y z i z y z yL zp xp z x i z x i x z x zL xp yp x y i x y i y x y x=?=?=??=?=?=??=?=?=??h h h h h h pv２、⾓动量平⽅算符定义：利⽤直⾓坐标和球坐标变量之间的关系可得222222222()()()x y zL L L L L y z z x x y zy x z y x ==++ =??+?+? v h (,,)(,,)x y z r θ?→2222sin cos sin sin cos /cos /x r r x y z y r z r z r tan y x θ?θ?θθ?==++==== ?(sin cos )?(cos sin )?x y z L i ctg L i ctg L i ?θ?θ?θ?θ?=+?=??=??h h h x y z θ?和３、⾓动量分量算符：222222222?11?(sin )sin sin z L L ?θθθθθ??=?? ???=?+ ??? h h (17) 2222??z z L i L ?=?=h h ?z L z ⼆、⾓动量算符之间的对易关系⼒学量都是坐标和动量的函数，由基本对易关系和恒等式(19)之⼀，可以导出其它⼒学量之间的对易关系。

质点角动量守恒习题课

质点角动量守恒习题课


1 质点的角动量
质量为 m 的质点以速度 v
在空间运动，某时刻相对原点
O 的位矢为 r，质点相对于原
点的角动量 Lr
p
r
mv
大 小 L rmvsin
L 的方向符合右手法则.
L
z
r
xo
L
v
v
m y
r
质点以角速度 作半径
为 r 的圆运动，相对圆心的
角动量
L mr2 J
L
p
o
m r
Mdt
L2
L1
冲量矩
t2
M
dt
t1
质点的角动量定理：对同一参考点 O ，质点所受
的冲量矩等于质点角动量的增量.
3 质点 的角动量守恒定律 M 0, L 恒矢量
质点所受对参考点 O 的合力矩为零时，质点对该 参考点 O 的角动量为一恒矢量.
角动量的定义
质点角动量守恒定律
例1 一小球在光滑平面上作圆运动，小球被穿过中心 的线拉住 。开始时绳半径为r1 ，小球速率为 v1 ；后 来，往下拉绳子，使半径变为 r2 ，小球速率变为 v2 ， 求v2 =？
解：受力分析如图。mg = N 而
T 为小球圆运动的向心力，所以合
外力不等于 T ，但过转轴而无力 矩。合外力矩为 0 ，小球角动量
N
守恒 。 有：
L = mvr = 恒量
即： m v1 r1 =m v2 r2
mg
2
质L 点 的r 角p动 量定理dp
F
,
dL ?
ቤተ መጻሕፍቲ ባይዱ
dL
d
(r
dt
p)
r
dp
dt dr
p
角动量例题

角动量例题

代入数据可, 得
r远 日 5.26 1012 m
7.如图所示，一个长为l 、质量为M 的 匀质杆可绕支点o自由转动.一质量为m 、速 率为v 的子弹以与水平方向成角 600的方向射 入杆内距支点为a 处，使杆的偏转角为 300. 问子弹的初速率为多少？ 解 把子弹和匀质杆作为 0 一个系统, 分析可知在碰 30 撞过程中角动量守恒. 0v 设子弹射入杆后与杆 60 ,则 一同前进的角速度为 1 2 0 2 m v cos 60 a Ml ma 3
6. 哈雷慧星绕太阳运行时的轨道是一个 椭圆，如图所示，它距离太阳最近的距离是 4 -1 10 v 5 . 46 10 m s r近 日 8.75 10 m , 速率 近 日 2 -1 ；它离太阳最远时的速率 v远 日 9.08 10 m s ，这时它离太阳的距离 r远 日 ？ v远 日
8. 如图所示，一根质量为M 、长为2l 的 均匀细棒，可以在竖直平面内绕通过其中心 的光滑水平轴转动，开始时细棒静止于水平 位置. 今有一质量为m 的小球，以速度 u 垂 直向下落到了棒的端点，设小球与棒的碰撞 为完全弹性碰撞. 试求碰撞后小球的回跳速 度 v 及棒绕轴转动的角速度 . m u M o
r近 日
r远 日
v近 日
解 彗星受太阳引力的作用，而引力通过了 太阳，所以对太阳的力矩为零，故彗星在运 行的过程中角动量守恒. 于是有 r近 日 v近 日 r远 日 v远 日 因为 r近日 v近日，r远日 v远日
r近日v近日 所以 r远日 v远日
l
lLeabharlann 解 分析可知,以棒和小球组成的系统的角动 量守恒. 由于碰撞前棒处于静止状态，所以 碰撞前系统的角动量就是小球的角动量 lmu ; 由于碰撞后小球以速度v 回跳，棒获得的角 速度为 ，所以碰撞后系统的角动量为 1 2 lmv Ml 3 由角动量守恒定律得 1 2 lmu lmv Ml 3 由题意知，碰撞是完全弹性碰撞，所以 碰撞前后系统的动能守恒，即
ch05-1 角动量习题课

ch05-1 角动量习题课


守恒
Fx
定轴刚体（不能简化为质点）
o
r v0
l
轴作用力不能忽略，动量不守恒， 但对 o 轴合力矩为零，角动量守恒
m
M
mv 0 l = ml 2ω + 1 Ml 2 ⋅ ω 3
v = ωl
回顾习题 P84 4 -10 F
O
M
m
v r F轴 ≠ 0 m + M系统 p 不守恒; r M 轴 = 0 m + M系统 对O点角动量守恒 m 2 gh ⋅ R = (m + M )vR
-1
m
0
o
30o
r v0
M
r v
例3 . 已知：匀质细棒 m , 长 2l ；在光滑水平面 内以 v 0 平动，与固定支点 O 完全非弹性碰撞。 求：碰后瞬间棒绕 O 的 ω = ?
m
l/2 l/2
B
解：碰撞前后AB棒对O的角动量守恒 O 思考：碰撞前棒对O角动量 L=? 碰撞后棒对O角动量 L′=？ v0
A M r o x2 s
m
B
解：在地面参考系中，建立如图 x 坐标，设绳两端坐标分别为x1，x2， 滑轮半径为 r 有：
l = A A′ + AB + B B ′ = x1 + x 2 + π r
m m AA′ = ⋅ x1 , l m m AB = ⋅ π r l mBB′ m = ⋅ x2 , l
B′
A′
x1 x
s = x1 − x 2
用隔离法列方程：（以逆时针方向为正）
A M r o
CA
m
T1
T2
＋ ＋
B
CB
. CA
动量与角动量经典例题

动量与角动量经典例题

设人蹬墙的时间为△t，因△t 很小，则静摩擦力的冲量远大于人体重力的冲 量，即 I f I G ，由动量定理得： I f N t m y 而在水平方向同样由动量定理可知： N t m x m x mo cos 人蹬墙后获得竖直向上的速度： y y y 0 sin 人蹬墙后再上升的高度
乘积， 即 F ma c ， 其质心加速度：a c
m a
i
i
M
。 定理只给出质心运动情况，
并不涉及质点间的相对运动及它们绕质心的运动。 3．碰撞问题 ⑴弹性碰撞：碰撞时无机械能损失．
m110 m220 m11 m22 1 1 1 1 2 2 2 m110 m220 m112 m22 2 2 2 2 （m m2）10 2m220 由①②可得： 1 1 ， m1 m2
人体重心上升的总高度： H h1 h2 令 tanφ=μ，则
02 (sin cos ) 2
2g
s0
对 0 、s0 一定时，当 即 arctan

2
时 H 最大．
1

时，人体的重心总升高最大．
类型二、动量守恒定律的问题最基本的特征就是和外力为零或某一方向上和 外力为零，当物体系内质点数量比较多时利用质心守恒是解决此类问题的重 要手段之一，解答过程，会比较简单。 例 2．如图 5—4 所示，在光滑的水平地面上静止放有一块质量 m3=2 kg，长 度 L=0. 6 m 的木板，板的左右两端分别放置质量 m1=2 kg，m2=4 kg 的两物 块， 并分别以初速度 1 =0.4 m/s, 2 =0.2 m/s 时相向运动．M1 , m2 和 m3 间 的滑动摩擦因数均为μ=0.22.试求： （1）m2 在木块上的最大位移； （2）m1 在木块上的最大位移； （3）m3 的最大位移． 分析和解：物体 1、2 可能会相碰，可能不会相碰，要予以讨论。讨论后利 用动量守恒（和质心守恒）解答本题，会比较简单。 （1）假设物块 1 、2 在木板上不会相碰，当 2 3 时，2 相对于 3 有最大位 移，则 2 a2t a3t 同
角动量

角动量


在X点需要改变的动能： 2 1 2 1 mgR 2 mgR 2 mv − mv0 = E '− E = − 在X点需要改变的动能： 2( R + h) 2 R + h 2 2
2 gR 3 v = ( 2 R + h)( R + h)
2
mv 0 = ( m − µ )v + µ (u + v0 )
µ=
动量矩守恒
Kepler's Third Law: The ratio of the squares of the revolutionary periods for two planets is equal to the ratio of the cubes of their semimajor axes: 行星绕太阳运行轨道半长轴a的立方 行星绕太阳运行轨道半长轴 的立方 与周期T的平方成正比 与周期 的平方成正比
1 1 2 2
∆v1
m1 r1 r2 ½(r×v) H m2
1
v v v v d(mr ×v ) = −d(m r ×v ) v v v v d(mr ×v + m r ×v ) = 0 o v v v v m r ×v + m r ×v = 常 量 v v L +L =常 量
1 1 1 2 2 2 1 1 1 2 2 2
θ
2
mgr sin θ = ωmvrcosθ = mω Rr cosθ g 2 ω = tanθ R 进动
dL=Mdt
关于点的动量矩定理
Theorem of angular momentum about a point
由 点 力 方 质 动 学 程
v v v d(r ×mv) dr v v d(mv) 动量矩定理: 质点对参考点o的动量 = = 0 v +r × ×m dt dt dt 矩的时间变化率就等于质点所受力对 v v v v d(mv) 于o点的力矩。 d(r ×mv) r× = dt dt v v v d v v v d v M = r × F = (r ×mv) M= L dt dt

大学物理角动量PPT精选文档


解 设盘对地的角速度为
体系初态角动量 [12mR 21m0(12R)2]o
o
末态盘的角动量 1 mR 2
2
R/2
V 人 地 V 人 盘 V 盘地 v
R 2
21
[12m2R1m0(12R)2]o12 mR 2 1m0(R2v)R2
o
2v 21R
o
(2) 欲使盘静止，可令
o
2v 0 21R
R/2
质量为m、长度为L的细直棒，通过质心 C且垂直于棒的轴
I 1 mL2 12
3
上次内容回顾
均质圆盘(m,R)绕中心轴转动时，
I 1 mR2 2
刚体对任一转轴的转动惯量I等于刚体通过质心的 平行轴的转动惯量Ic加上刚体的总质量M乘以两平行 轴间距离d的平方，即
I=Ic+Md2
4
上次内容回顾
LI
M dL dt
l
mg
讨论: (1)当=0时，=3g/2l， =0 ； (2)当=90°时， =0，=(3g/l)1/2。
11
例题5 一质量为m、半径为R的匀质圆盘绕通过盘 心且垂直于盘面的光滑轴正以o的角速度转动。现将 盘置于粗糙的水平桌面上，圆盘与桌面间的摩擦系数 为µ，求圆盘经转几圈将停下来？
I 1 mR 2 2
计算出来摩 擦力矩是关键
o
dr r
M0Rrgm R22rdr
2 3
mgR
12
M0Rrgm R22rdr
2 3
mgR
I 1 mR 2 2
于是得M4g
I 3R
o
dr r
又由2-o2=2，所以停下来前转过的圈数为
N 22o2 136o2R g 13

第五章角动量

1.质点系对参考点的角动量 对参考点
L Li ri pi ri mi vi
i i i
对质点系中的第 i 个质点,有 dL Mi i dt 其中
M i M i外 M i内
上页 下页 返回 结束
M i内 M i外
Lz ri mi vi sin i
2.质点系对轴的角动量定理
质点在垂直于z 轴的平面内运动，第i个 质点
上页 下页 返回 结束
第五章 角动量 关于对称性
dLi d M iz ( ri m i v i sin i ) dt dt
对质点系
Miz Mi外z Mi内z d M i内z M i外z ( ri m i v i sin i ) dt
d ( ri m i v i sin i ) dt
M i内 z M i 外 z 而 M i内 0 M i外z
Mi内z 0
d d ( ri mi v i sin i ) Lz dt dt
——称质点系对z 轴的角动量定理.
上页 下页 返回 结束
对质点系，有
dLi dt
第五章 角动量 关于对称性
M i内 M i外
dLi dt
2.内力的力矩
因质点i与质点 j 间的相互
作用力关系为
Fij F ji
O
rj
d
ri
j
j
i
i
Fij
且二力到参考点O的垂直距离相等，
F ji
故成对出现的内力对O点的力矩矢量和为零.即
上页
下页
返回
结束
第五章 角动量 关于对称性

03 力学：第三章 动量与角动量-课堂练习及部分习题解答


Zhang Shihui
题.设行星的质量为m，它绕太阳运动的角动量为L0，试 推导行星绕太阳运动的掠面速度（即行星的矢径单位时 间内扫过的面积）表达式 。 解：在dt的时间内，矢r 处的速度 v 同向 Δr v 与 夹角为 θ ，即 与 夹角为 θ r r Δ r r h θ Δr 顶点到 r 的距离 h = Δr sin θ 1 在dt的时间内，矢径扫过的面积 ΔS = r Δr sin θ 2 L0 1 1 dS 1 L= ΔtÆ0, dr = vdt 故 = r v sin θ = r × v = 2m 2m 2 dt 2
r
地心O
M = r ×F =0 r1 R + l1 因此，角动量守恒 r1mv1 = r2 mv2⇒ v2 = v1 = v1 r2 R + l2
v
因万有引力F始终沿地心指向卫星， 与矢径方向相同，故
学习指导·第三章 动量和角动量·典型例题第4题
Zhang Shihui
题. 匀质的柔软细绳铅直悬挂着，绳的下端刚好触到水平地 面上。如把绳的上端释放，绳将落到地面上。试证明：在 绳下落过程中，任意时刻作用于地面的压力（大小），等 于已落到地面上的绳重量的三倍。 解：设单位绳长的质量为λ。t时刻已经落到地面 的绳长为x，这部分绳子对地面的压力N0 = (λ x) g 此外，即将接触地面的质元dm对地面的冲量dp 会产生一个额外的冲力F (注：质元长dx，下落 的距离为x) 。设此瞬间质元的速度为v，则
m
解：水平方向M和m组成的系统所受合外 力为零，因此质心在水平方向不受外力作 用，质心水平方向分量保持不变，等于0
Μ
mΔx + M ΔX mx + MX ⇒ Δxc = =0 xc = m+M m+M

角动量(二)


角动量
【解析】
(1) 设发射前飞船沿椭圆轨道运动时远地点的矢径为 r2， 速度为 v2，由相对地心角动量守恒，得 mr1v1 = mr2v2 (1) (2) 1 Mm 1 Mm 2 2 由机械能守恒，有 mv1 − G = mv2 − G 2 r1 2 r2 将 v1 = 2aGM 代入 (1), (2) 式，可得 r1 r1 2 1 r1 1 ( ) − ( ) + ( − 1) = 0 r2 a r2 a
发射后探测器的速度 v = u + v′ 2 将 (1), (7), (8), (9) 式代入 (10) 式，得
m0 2a − 1 2 − 1 a v = v2 + (1 − )u = v2 + (1 − ) ( )v2 m 2 −1 2a 1 − a
角动量
【解析】
1 − 2a + a 1 − 2a + a r1 v2 = = 1− a 1− a r2 1 − 2a + a = 1− a 1 − 2a + a = 1− a 2GM r1 a( ) r2 r2 2GM = r2 2bGM r2 2GM r1
2 2 0
角动量
【例题 10】一艘总质量为 m 的飞船内装质量为 m0 的探 测器，绕地球沿椭圆轨道运动，近地点的矢径为 r1，速 度 v1 =
1 2aGM (M 为地球的质量)。(1) 证明 < a < 1 ; (2) 2 r1
若飞船在近地点向前发射探测器，使之沿抛物线轨道运 动，而飞船则沿圆轨道运动，求 m0/m 的值以及发射时 的相对速度 u；(3) 若在远地点以相同的相对速度 u 向 前发射，求探测器的轨道。
3 v0 , 2
v0 为以地球半径为半径作圆周运动的速度)，求此卫星

刚体的角动量


对上式积分得到角动量定理旳积分形式
t2 t1
M z dt
J2
J1
该式表达：动量旳增量等于力矩对定轴转动刚体
旳时间累积效应
10
三、刚体对转轴旳角动量守恒定律
M zdt dLz dJ
假如 Mz = 0, 则 dLz d( J ) 0 Lz J 恒量
刚体对转轴旳角动量守恒定律 当定轴转动旳 刚体所受外力对转轴旳合力矩为零时,刚体对同一 转轴旳角动量不随时间变化。
满足百分比关系旳最大应力，σE
称百分比极限（ P）。点E 旳应力E是发生弹性形变旳
σP
最大应力，称弹性极限。当
B
EC P
应力 >E时，发生塑性形变。
点C 相应旳应力为 C，若
把外力撤除，固体旳应力与
o o′
ε
应变旳关系沿O C变化，留下一定旳剩余形变OO。
当应力到达点 B 相应旳应力 B时，固体就断裂， B称强度极限。
(1 2
m1R2
m2R2 )1
1 2
m1 R 22
2
1 2
m1R2 m2
1 2
m1R
2
R2
1
1 2
m1 1 2
m2 m1
1
2.31rad
s 1
19
质点直线运动或刚体平动 位移 速度 加速度
匀速直线运动 匀变速直线运动
刚体旳定轴转动 角位移 角速度 角加速度 匀角速定轴转动 匀变角速定轴转动
20
dt
d dt
(J)
试验表白, 此式更具普遍性。
由上式得到
Mz
d dt
( J)
dLz dt
刚体对转轴旳角动量定理 作定轴转动旳刚体
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

智浪教育—普惠英才文库
“角动量守恒”及其应用
在研究“质点或质点系绕某一定点或轴线运动”这类问题时，我们常利用“角动量守恒
定律”来处理此类问题。“角动量守恒定律”是自然界最基本最普遍的定律之一，应用该定
律来处理力学问题在近几年的全国中学生物理竞赛中屡屡出现。从反馈情况来看，能否灵活
应用“角动量守恒”成为解题的“瓶颈”。帮助学生认清该定律的内容及其规律并能够适当
地变式处理此类问题，无疑对参加全国中学物理竞赛有很大的帮助。下面就“角动量守恒”
及其应用作一些简单探讨。
1 角动量守恒定律
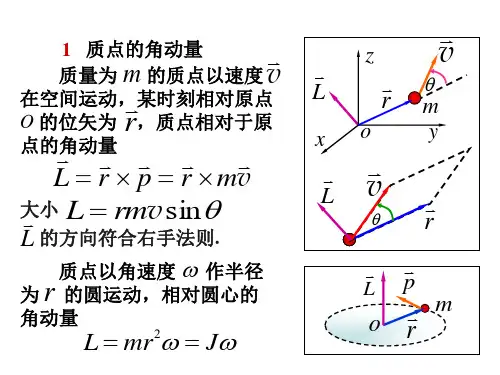
1．1质点对参考点的角动量守恒定律
如图1所示，质点m的动量为P，相对于参考点O的角动量
为L，其值sinprL，其中α是质点的动量与质点相对参考点0
的位置矢量r的夹角。其角动量的变化量L等于外力的冲量矩
tM
（M为外力对参考点O的力矩），即tML。若M=0，得
L
=0，即质点对参考点O的角动量守恒。
1．2质点系对参考点的角动量守恒定律
由n个质点组成的质点系，且处于惯性系中，可以推导出作用于各质点诸力对参考点
的外力矩的冲量tMi，仍等于质点系对该参考点的角动量的变化量，即tMLi。
同样当0iM时，质点系对该参考点的角动量守恒。
如果n个质点组成的质点系，处于非惯性系中，只要把质点系的质心取作参考点，上
述结论仍成立。
1．3角动量守恒的判断
当外力对参考点的力矩为零，即0iM时，质点或质点系对该参考点的角动量守
恒。有四种情况可判断角动量守恒：①质点或质点系不受外力。②所有外力通过参考点。③
每个外力的力矩不为零，但外力矩的矢量和为零。甚至某一方向上的外力矩为零，则在这一
方向上满足角动量守恒。④内力对参考点的力矩远大于外力对参考点的合力矩，即内力矩对
质点系内各质点运动的影响远超过外力矩的
影响，角动量近似守恒。
2 角动量守恒定律的应用
例题1 （第23届物理竞赛复赛第2题）
如图2所示，一根质量可以忽略的细杆，长为
2l，两端和中心处分别固连着质量为m的小球
B、D和C，开始时静止在光滑的水平桌面上。桌面上另有一质量为M的小球A，以一给定
速度v0沿垂直于杆DB的方向与右端小球B作弹性碰撞。求刚碰后小球A、B、C、D的速
度，并详细讨论以后可能发生的运动情况。
本题粗看是一类弹性碰撞类问题，利用动量守恒、能量守恒及杆子牵连速度来求解。但
本题涉及4个物体组成的质点系，未知量多，利用上述关系还不能求解。挖掘题中的守恒规

m m m
M
D B C

A
V0

图2

O
m
P
α

图1
r
智浪教育—普惠英才文库
律成为本题的难点，且守恒规律不易挖掘。
解析 ①小球A、B碰撞瞬间，球A挤压B，其作用力方向垂直于杆，使球B获得沿
0
v

方向的速度
Bv。从而在碰撞瞬间使小球C、D的速度也沿0
v
方向。对质点组B、C、D与A

组成的系统，碰撞前后动量守恒。由于小球C位于由B、C、D三球组成的质点组的质心处，
所以小球C的速度也就是质点组的质心速度。
可得：0AC3MMmvvv （1）
②质点组B、C、D与A是弹性碰撞，碰撞前后质点组的动能相等。碰撞后A、B、C、
D的速度分别为
A
v
、Bv、Cv、Dv，得

22222
0ABCD

11111
+22222MMmmvvmvvv
（2）

③对质点组B、C、D在碰撞瞬间，在B处受到A球的作用力，若取B（与B球重合的
空间固定点）为参考点，则质点组B、C、D在碰撞前后，外力矩等于零，所以质点组角动
量守恒。可得：CD02mlmlvv （3）
④由杆的刚性条件有：DccBvvvv （4）
由（1）、（2）、（3）、（4）式，可得

C0
456M
Mm
vv
（5）

A0
5656MmMm


vv
（6）

B0
1056M
Mm
vv
（7）

D0
256M
Mm
vv
（8）

⑤碰撞后各小球的运动
碰撞后，质点组B、C、D不受外力作用，其质心作匀速运动，即
C0

456M

Mm
vv
，碰

撞后，B、D两小球将绕小球C作匀角速度转动，角速度的大小为
0656B
M
lMm
C
vvv

l

方向为逆时针方向。由（6）式可知，碰后小球A的速度的大小和方向与M、m的大小有关，

由于M、m取值不同而导致运动情形比较复杂，即可以使A0v=；A0v<；A0v>且ACvv；

AC
vv
情景的出现，在此不作详细讨论。

例题2 （第20届物理竞赛复赛第1题）如图3
所示，a为一固定放置的半径为R的均匀带电球
体，O为其球心．己知取无限远处的电势为零时，
球表面处的电势为U=1000 V．在离球心O很远的
O′点附近有一质子b，它以 Ek＝2000 eV 的动能
沿与OO平行的方向射向a．以l表示b与OO
线之间的垂直距离，要使质子b能够与带电球体a的表面相碰，试求l的最大值．把质子换

图3
智浪教育—普惠英才文库
成电子，再求l的最大值．
解析 ①质子在运动过程中受到a球对它的库仑力作用，且库仑力总是通过a球的球心。
类似这样的力我们称之为有心力。如取球心O为参考点，则其作用力对O的力矩始终为零，
即质子在运动过程中对参考点O的角动量守恒。即在有心力作用下角动量守恒。

如图4所示，令m表示质子的质量，0v和v分别表示质子的初速度和到达a球球面处的速
度，e表示元电荷。质子在b处的角动量
为max0lmvLb；到达球a表面时的角

动量为RmvLa
所以得：max0mvlmvR （1）
②质子从b运动到a，能量守恒，由于无穷远处电势能为零，故得：
22
0

11

22
mvmveU
（2）

由式（1）、（2）可得

2
0

max

1/2eUlRmv

代入数据，可得 max22lR
③若把质子换成电子，此时式（2）中e改为e。同理可求得

max
6
2
lR

例题3 如图5所示，滑轮两边悬挂的重物与盘的质量相同，均为M，处于静止。现有距盘
底高为h质量为m的胶泥自由下落，求胶泥粘在盘上时盘获得的初速度。不计滑轮与绳质
量，及轴承摩擦和绳的伸长。
解析 ①对盘、重物、胶泥组成的质点系，在胶泥下落过程中，质点系
对轴心O的外力矩为胶泥的重力矩。当胶泥与盘碰撞时，碰撞内力对O
的内力矩远大于胶泥的重力矩，从而得质点系对O的角动量近似守恒。

②质点系碰撞前对O的角动量rmvL01 （1） （v0为m碰前的
速度，r为滑轮的半径）；
质点系碰撞后瞬间对O的角动量MrvvrMmL2 （2）

③胶泥碰前作自由落体运动，所以ghv20 （3）
由（1）、（2）、（3）式可得ghmMmv22

图4
v
图5
m
M

O
智浪教育—普惠英才文库