
《数列》全章复习与巩固 编稿:张林娟 审稿:孙永钊
【学习目标】
1.系统掌握数列的有关概念和公式;
2.掌握等差数列与等比数列的概念、性质、通项公式与前n 项和公式,并运用这些知识解决问题;
3.了解数列的通项公式n a 与前n 项和公式n S 的关系,能通过前n 项和公式n S 求出数列的通项公式n a ;
4.掌握常见的几种数列求和方法. 【知识网络】
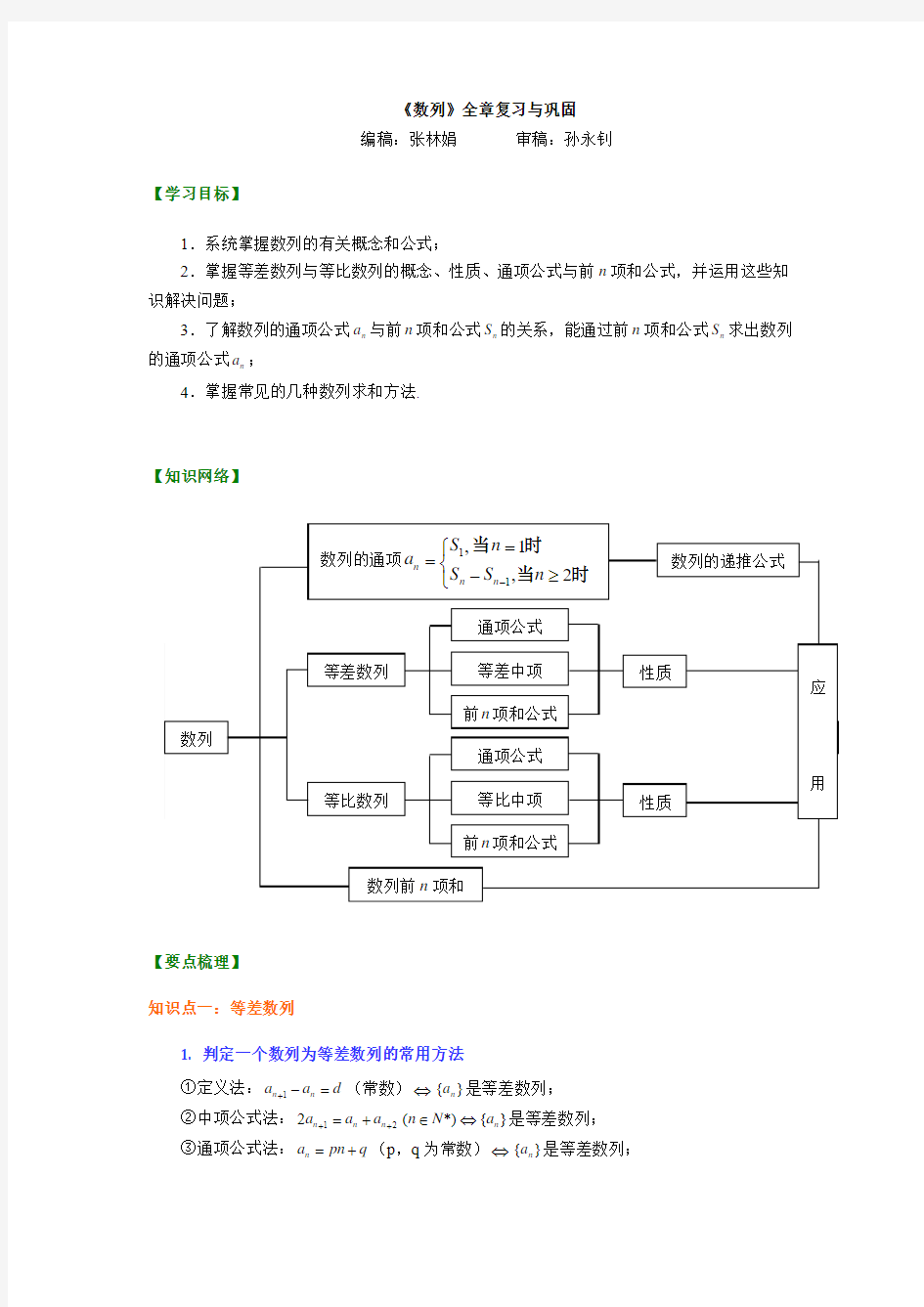
【要点梳理】 知识点一:等差数列
1. 判定一个数列为等差数列的常用方法
①定义法:1n n a a d +-=(常数)?{}n a 是等差数列; ②中项公式法:122(*){}n n n n a a a n N a ++=+∈?是等差数列; ③通项公式法:n a pn q =+(p ,q 为常数)?{}n a 是等差数列;
④前n 项和公式法:2n S An Bn =+(,A B 为常数)?{}n a 是等差数列.
要点诠释:对于探索性较强的问题,则应注意从特例入手,归纳猜想一般特性。 2. 等差数列的通项公式及前n 项和 通项公式:()1=+1n a a n d
要点诠释:
① 该公式可改写为:1= +n a d n a d ?
当d =0时,n a 是关于n 的常函数;当d ≠0时,n a 是关于n 的一次函数;点(n n a )分布在以d 为斜率的直线上,是这条直线上的一列孤立的点.
②通项公式的推广..
:()+n m a a n m d =- 前n 项和公式:()()111+=+=2
2
n n n n n a a S na d
要点诠释:
① 该公式可改写为:21=+22n d d S n a n ?
? ??
?
当d =0时,n S 是关于n 的正比例函数;当d ≠0时,n S 是关于n 的二次函数(无常数项).
② 在应用()
1+=2
n n n a a S 时,注意相关性质的应用。
3. 等差数列有关性质
(1)若*()m n p q m n p q +=+∈N 、、、,则m n p q a a a a +=+; 特别地,若2m n p +=,则2m n p a a a +=; (2)若a b c ,,成等差数列,则+=2a c b ;
(3)公差为d 的等差数列中,连续k 项和232,,k k k k k S S S S S --,… 组成新的等差数列; (4)等差数列{}n a ,前n 项和为n S :
①当n 为奇数时,12
n n S n a +=?;12
n S S a +-=奇偶;
1
1
S n S n +=
-奇偶
; ②当n 为偶数时,122
2n n n a a S n ++??
?=? ? ???;12S S dn -=偶奇;212
n n a S S a +=奇偶. (5)等差数列{}n a ,前n 项和为n S ,则
m n m n
S S S m n m n
+-=
-+(*m n m n ∈≠N 、,且); (6)等差数列{}n a 中,若*m n p q
m n p q m n p q +=+∈≠≠N (、、、,且,),则p q
m n S S S S m n p q
--=--; (7)等差数列{}n a 中,公差d ,依次每k 项和:k S ,2k k S S -,32k k S S -成等差数列,新公差2'd k d =.
4. 等差数列前n 项和n S 的最值问题: 等差数列{}n a 中
① 若1a >0,d <0,n S 有最大值,可由不等式组1
0n n a a +≥??
≤?来确定n ;
② 若1a <0,d >0,n S 有最小值,可由不等式组1
0n n a a +≤??
≥?来确定n ,也可由前n 项和
公式21()22
n d d
S n a n =
+-来确定n . 要点诠释:等差数列的求和中的函数思想是解决最值问题的基本方法. 知识点二 :等比数列
1. 判定一个数列是等比数列的常用方法 (1)定义法:
1
n n
a q a +=(q 是不为0的常数,n ∈N *){}n a ?是等比数列; (2)通项公式法:n n a cq =(c 、q 均是不为0的常数n ∈N*){}n a ?是等比数列;
(3)中项公式法:2
12n n n a a a ++=?(120n n n a a a ++??≠,
*n N ∈){}n a ?是等比数列. 2. 等比数列的通项公式及前n 项和 通项公式:111(*0)n n a a q n a q -=?∈?≠N , 要点诠释:
① 该公式可改写为:1n
n a a q q
=
? 01q q >≠且时,是关于n 的指数型函数;1q = 时,是常数函数;
② 推广:n m n m a a q -=?.
前n 项和公式:111(1)(1)(1)
11n n n na q S a a q
a q q q q =??
=--?=≠?--?
要点诠释:
①在求等比数列前n 项和时,要注意区分1q =和1q ≠
②当1q ≠时,等比数列的两个求和公式,共涉及1a 、n 、q 、n a 、n S 五个量,已知其中任意三个量,通过解方程组,便可求出其余两个量.
3. 等比数列的主要性质:
(1)若*()m n p q m n p q +=+∈N 、、、,则m n p q a a a a ?=?; 特别,若2m n p +=,则2m n p a a a ?=;
(2)等比数列{}n a 中,若*m n p m n p N ∈、、(、、)成等差数列,则m n p a a a 、、成等比数列;
(3)公比为q 的等比数列中,连续k 项和232,,k k k k k S S S S S --,… 组成新的等比数列; (4)等比数列{}n a ,前n 项和为n S ,当n 为偶数时,S S q =偶奇;
(5)等比数列{}n a 中,公比为q ,依次每k 项和:k S ,2k k S S -,32k k S S -…成公比为q k 的等比数列;
(6)若{}n a 为正项等比数列,则{log }a n a (a >0且a ≠1)为等差数列;反之,若{}n a 为等差数列,则{}n
a a (a >0且a ≠1)为等比数列;
(7)等比数列{}n a 前n 项积为n V ,则(1)2
1
(*)n n n
n V a q n -=∈N .
知识点三:常见的数列通项公式求法
1. 已知数列的前几项:
已知数列的前几项,通过观察法,归纳分析出数列的通项公式.
2. 已知等差数列或等比数列:
3. 已知数列的递推关系式:
①形如()1=+ n n a a d d +∈R ,该数列为等差数列....
,利用公式法求数列的通项公式; ②形如()1=0n n a q a q +≠,该数列为等比数列....,利用公式法求数列的通项公式. ③形如()1=+ 01n n a q a d d q q +?∈≠≠R 且,,构造公比为q 的等比数列+
-1n d a q ?
?
????
,利用公式法求解;
④形如()1=+ n n a a f n +,通过累加法...
(迭加法)求数列的通项;
⑤形如()1=g n n a n a +?,通过累乘法...
(迭乘法)求数列的通项. ⑥形如()1,0n n n pa a =p q pa +q +≠,两边取倒数,构造公差为q
p 的等差数列1n a ??????
,利用公式法求通项.
4. 已知n S ,求n a : 利用n a 与n S 的关系,即11,(1),(2)
n n n S n a S S n -=?=?
-≥?,
,可求得数列的通项公式.
5. 已知12n =)a a a f(n ,求n a :
利用作商法,即(1),(1)(),(2).(1)n f n a f n n f n =??
=?≥?
-?
求数列的通项公式.
知识点四:常见的数列求和方法
1. 公式法:
如果一个数列是等差数列或者等比数列,直接用其前n 项和公式求和。 2. 分组求和法:
将通项拆开成等差数列和等比数列相加或相减的形式,然后分别对等差数列和等比数列求和.如:=2+34n n a n .
3. 裂项法:
把数列的通项拆成两项之差,正负相消,剩下首尾若干项的方法.一般通项的分子为非零常数,分母为非常数列的等差数列的两项积的形式.
若1
()()
n a An B An C =++,分子为非零常数,分母为非常数列的等差数列的两项积的形式,
则1111()()()n a An B An C C B An B An C =
=-++-++,如a n = 1(1)n n +11
1
n n =-
+ 4. 错位相减法:
通项为非常数列的等差数列与等比数列的对应项的积的形式:n n n a b c =?, 其中 {}n b 是公差d ≠0等差数列,{}n c 是公比q ≠1等比数列,如()=213n n a n ?.
一般步骤:
112211n n n n n S b c b c b c b c --=++?++,则 1211n n n n n qS b c b c b c -+=+??++
所以有11231(1)()n n n n q S b c c c c d b c +-=+++??-
要点诠释:求和中观察数列的类型,选择合适的变形手段,注意错位相减中变形的要点. 知识点五、通项n a 与前n 项和n S 的关系:
任意数列{}n a 的前n 项和12n n S a a a =++
+;
11
(1)(2)
n n n S n a S S n -=??=?
-≥??
要点诠释:
由前n 项和n S 求数列通项时,要分三步进行: (1)求11a S =,
(2)求出当n ≥2时的n a ,
(3)如果令n ≥2时得出的n a 中的n =1时有11a S =成立,则最后的通项公式可以统一写成一个形式,否则就只能写成分段的形式。
知识点六:数列应用问题
数列应用问题是中学数学教学与研究的一个重要内容,解答数学应用问题的核心是建立数学模型,有关平均增长率、利率(复利)以及等值增减等实际问题,需利用数列知识建立数学模型.
建立数学模型的一般方法步骤.
①认真审题,准确理解题意,达到如下要求: ⑴明确问题属于哪类应用问题; ⑵弄清题目中的主要已知事项; ⑶明确所求的结论是什么.
②抓住数量关系,联想数学知识和数学方法,恰当引入参数变量或适当建立坐标系,将文字语言翻译成数学语言,将数量关系用数学式子表达.
③将实际问题抽象为数学问题,将已知与所求联系起来,据题意列出满足题意的数学关系式(如函数关系、方程、不等式).
要点诠释:数列的建模过程是解决数列应用题的重点,要正确理解题意,恰当设出数列的基本量. 【典型例题】
类型一:等差、等比数列概念及其性质
例1. 已知等差数列{}n a ,25n S =, 2100n S =, 则3n S =( ) A.125 B.175 C.225 D.250
【思路点拨】本题是关于等差数列的求值问题,故用常用的基本量法或者等差数列的性质解决即可。难点在于项数n 不确定,在解题过程中不妨采用合适的方法加以回避。
【答案】C 【解析】
方法一:利用等差数列的性质 ∵{}n a 为等差数列,
∴n S ,2n n S S -,32n n S S -成等差数列,即2322()()n n n n n S S S S S -=+- ∴32(10025)25(100)n S -=+-, 解得3225n S =, ∴选C.
方法二:特殊值法
令1n =,由题意可得1125n S S a ===,2212100n S S a a ==+=, ∴275a =,2150d a a =-=, ∴3313(31)
32252
n S S a d ?-==+=, ∴选C.
方法三:基本量法 1(1)252n n n S na d -=+
=,212(21)
21002
n n n S na d -=+= 两式相减可得1(31)
752n n na d -+=, ∴313(31)
37532252
n n n S na d -=+=?=. ∴选C.
【总结升华】三种解法各有各的特点,注意认真体会每一种解法,灵活应用. 本题还有其他的方法解析,在这里不再一一介绍,同学们有时间可仔细研究。
举一反三:
【变式】已知等比数列{}n b ,48n S =, 260n S =, 则3n S =( ) A.75 B.2880 C.5
4
D.63
【答案】D
例2. 如果一个等差数列的前12项和为354,前12项中偶数项的和与奇数项的和之比为32:27,求公差.
【思路点拨】这是关于等差数列的求值问题,采用基本量法解决即可. 注意奇数项的首项为1a ,公差为2d 22;偶数项首项为2a ,公差为2d .
【答案】5
【解析】设等差数列首项为1a ,公差为d ,则 ()1
1111211123542
65=2=5.6++2322=.
65276+22
a d a d a d d
a d ??+?=????????????,解得,
所以该数列的公差是5. 【总结升华】
1. 恰当地选择设未知数,列方程(组)求解。方程思想在数列中很重要.
2. 等差(比)数列的首项和公差(比)是关键. 举一反三:
【变式1】已知三个数成等比数列,其积为216,若第二个数加上4,则它们构成一个等差数列,求这三个数.
【答案】设这三个数为
a
q
、a 、aq , 由题知216a a aq q
??=,解得6a =, 又∵
6
q
,64+,6q 构成等差数列, ∴6
2(64)6q q
?+=
+,即231030q q -+=, 解得3q =或1
3
q =,
∴这三个数为2,6,18或18,6,2. 【高清课堂:数列综合381084 例1】
【变式2】已知两个等比数列{}n a ,{}n b ,满足1(0)a a a =>,111b a -=,
222b a -=,333b a -=.
(1)若1a =,求数列{}n a 的通项公式; (2)若数列{}n a 唯一,求a 的值.
【答案】(1
)1(2n n a -=
或1(2n n a -= (2)13
a =
例3.等差数列{}n a 中,113a =,311S S =,则它的前_____项和最大,最大项的值是____. 【思路点拨】等差数列的首项1a >0,公差d 必然是负数,这样前n 项和有最大值. 取得
最大值时的项为数列中最后一个正数(或0),它处于正负相间的位置,满足+1
00.n n a a ≥??
≤?,
【答案】7,49
【解析】设公差为d , 由题意得111110
3112
a d a ?+=+
d ,得=2d , ∴{}n a 是首项为正数的递减数列,n S 有最大值. 又311S S =, ∴()45101178113++
++=4+==0a a a a a a S S -,
∴7800.a a ,><
所以7S 为最大值,即7S =7×13+
()76
22
??=49. 【总结升华】等差数列的前n 项和公式是一个二次的函数,当0d <时,函数有最大值. 举一反三:
【变式】若数列{}n a 是等差数列,数列{}n b 满足*12()n n n+n+b =a a a n ??∈N ,{}n b 的前n 项和用n S 表示,若{}n a 中满足512380a a =>,试问n 多大时,n S 取得最大值,证明你的结论.
【答案】∵512380a a =>, ∴()55387a a d =+,解得556
5
a d =>0 ∴176
05
d a d <=-
,, 故{}n a 是首项为正的递减数列.
则有111(1)00n n a a n d a a nd +=+-≥??=+≤?,即76
(1)05
760
5
d n d d nd ?-+-≥????-+≤??
解得:1515≤n ≤161
5
,∴n =16,即16a >0,17a <0
即:121617180a a a a a >>?>>>>>? 于是121417180b b b b b >>?>>>>>??
而15151617··0b a a a =<, 161617
18··0b a a a => ∴1413114151516S S S S S S S >>?>><,, 又15a =-180d a >=
,9
5
d <0, ∴1518151615160a a b b b b <∴<+>,
,即 ∴1614S S >,故n S 中16S 最大.
例4.设n n S T ,分别为等差数列{}n a ,{b n }的前n 项和,满足
71427n n S n T n +=+,求1111
a b . 【思路点拨】用好等差数列中n S 与n a 的一个关系: ()2121n n S n a +=+是解好本题的一个关键.
【答案】111143
a b = 【解析】
方法一:12111111212111111212112121
()
2721142212421273()2
a a a a a a S
b b b b T b b ++?+======+?++
方法二:设()(71),(427)0n n S k n n T k n n k =+=+≠, ∴()()111110117111107101148a S S k k k =-=?+-?+= ()()111110 T T 11411271041027111b k k k =-=?+-?+= ∴
11111484
1113
a k
b k ==. 【总结升华】等差数列的中项在前n 项和式中的应用是解决本例的关键,也应注意到前n 项和与通项公式的联系.
举一反三:
【变式】等差数列{}n a 中,n S =50,123430a a a a +++=,32110n n n n a a a a ---+++=,求项数n .
【解析】123430
(1)a a a a +++=, 32110
(2)n n n n a a a a ---+++=,
由(1)+(2)得:114()40()10n n a a a a +=?+=, 1()10
501022
n n n a a n S n +?=
?=?=. 类型二:n a 与n S 的关系式的综合运用
例5. 已知正项数列{}n a ,其前n 项和n S 满足2
1056n n
n S a a =++,且1315a a a ,,成等比数列,求数列{}n a 的通项n a .
【思路点拨】已知n n S a 与的混合式,一般采用降角标作差的方法,化为n a 的递推关系式
【答案】=53n a n
【解析】∵2
1056n n
n S a a =++, ①
∴21111056a a a =++,解之得1a =2或1a =3.
又2
1111056(2)n n n S a a n ---=++≥, ②
由①-②得22
1110()5()n n n n n a a a a a --=-+-,即11()(5)0n n n n a a a a --+--=
∵()11052n n n n a a a a n --+∴-=≥>,.
当1a =3时,3a =13,15a =73,1315a a a ,,不成等比数列 ∴1a ≠3;
当1a =2时,3a =12,15a =72,有23115=a a a , ∴1a =2,∴=53n a n .
【总结升华】等比数列中通项与求和公式间有很大的联系,它们是
1
1(1)(2)n n
n a n a S S n -=?=?-≥?,尤其注意首项与其他各项的关系.
举一反三:
【变式1】已知数列{n a }的前n 项和公式为32=2n n n n
S -,求数列{n a }的通项公式.
【解析】323==122n
n n n n S -??
???
,则 当n =1时, 1a =1S =1
2;
当n ≥2时, 1=n n n a S S --=-1
331122n
n ??
?????????? ?
???
??
????????=1
1322n ??? ???
, 又n =1时,
12(32)0=1
2
=1a , 满足上式. ∴1
1322
n n a -=?().
【变式2】已知数列{}n a 的前n 项和为n S ,1
(1)(*)3
n n S a n N =-∈.
(1)求12,a a ;
(2)求证:数列{}n a 是等比数列。 【解析】
(1)由111(1)3S a =-,得111
(1)3a a =-,
∴11
2
a =-,
又221(1)3S a =-,即1221
(1)3
a a a +=-,得214a =。
(2)证明:当2n ≥时,1n n n a S S -=-111
(1)(1)33
n n a a -=---,
得
112n n a a -=-,又211
2
a a =-, 所以{}n a 为首项为12-,公比为1
2
-的等比数列。
类型三:特殊数列的求和
例6. 求数列1,22343456,,(0)a a a a a a a a a a ++++++≠,,
的前n 项和n S . 【思路点拨】本题求和后,不宜直接分组,应该把通项化简变形后,再决定如何分组求
和. 本题含参数a ,注意讨论.
【解析】
(1)当1a ≠时,1
22
...n n n n a a a a
--=+++1121(1)1()11n n n n a a a a a a
----==---
3251211
...(1)()()()1n n n S a a a a a a a a
--??∴=
-+-+-++-??- 21242222121(1...)(1...)111(1)(
)111(1)(1)(1)(1)
n n n n n n a a a a a a a a
a a a a a a a a a a --+??=
++++-++++??-??--=-??---??--=
-+ (2)当1a =时,1
(1)2
n S n n =+;
(3)当1a =-,原数列为1,0,1,0,1,0……,
若n 为偶数,令2n k =(*k N ∈),则21010...102n k n
S S k ==++++++==
; 若n 为奇数,令21n k =-(*k N ∈),则21
1010 (1012)
n k n S S +==+++++++=. 【总结升华】分类讨论a 和n 的奇偶是本例化简的关键. 举一反三:
【变式1】求数列2222
1111
{(1)(1)...(1)()}23(1)n n -?--?+的前n 项和。 【答案】
22222222222
213111...23(1)1324(1)(1)1...23(1)12(1)111()21
n n a n n n n n n n n n n ---=??
+??-+=??+=
+=-+
所以可以得到:11(1)212(1)
n n S n n =-
=++。 【变式2】求和:122221*()n n n n n n n S a a b a b a b ab b n N ----=++++++∈
【答案】=0a 或=0b 时,()n n n S b a = 当=a b 时,(1)n n S n a =+; 当a b ≠时,11
n n n a b S a b
++-=-
类型四:求数列的通项公式
例7.写出数列:15-,310,517-,7
26
,… 的一个通项公式.
【思路点拨】观察该数列,各项是由三部分构成:符号、分子和分母. 不妨把它看成三
个数列,分别求其通项.
【答案】通项公式为:221
(1)(1)1
n
n n a n -=-++.
【解析】从各项符号看,负正相间,可用符号(1)n -表示;
数列各项的分子:1,3,5,7,……是个奇数列,可用21n -表示;
数列各项的分母:5,10,17,26,……恰是221+,231+, 241+,251+,…可用2(1)1n ++表示;
所以该数列的通项公式可写为221
(1)(1)1
n n n a n -=-++.
【总结升华】
①求数列的通项公式就是求数列中第n 项与项数n 之间的数学关系式。如果把数列的第1,2,3,…项分别记作(1)f ,(2)f ,(3)f ,…,那么求数列的通项公式就是求以正整数n (项数)为自变量的函数()f n 的表达式;
②通项公式若不要求写多种形式,一般只写出一个常见的公式即可;
③给出数列的构造为分式时,可从各项的符号、分子、分母三方面去分析归纳,还可联想常见数列的通项公式,以此参照进行比较.
举一反三:
【变式1】数列:1-,85,157-,24
9,……的一个通项公式是( )
A.2(1)21
n
n n n
a n +=-+ B.(3)(1)21n n n n a n +=-+
C.2(1)1(1)21
n
n n a n +-=-- D.(2)
(1)21n n n n a n +=-+
【答案】采用验证排除法,令1n =,则A 、B 、C 皆被排除,故选D. 【变式2】给出数表:
1 2 3 4 5 6
7 8 9 10
… … … …
(1)前m 行共有几个数?
(2)第m 行的第一个数和最后一个数各是多少? (3)求第m 行的各数之和; (4)数100是第几行的第几个数? 【答案】 (1)1
(1)2
m m +;
(2)1(1)12m m -+,1
(1)2m m +;
(3)21
(1)2
m m +;
(4)第14行的第9个数。
例8.已知数列{}n a 中,11a =,12
13
n n a a +=+,求n a .
【思路点拨】把1213n n a a +=+整理成12
3(3)3
n n a a +-=-,构造等比数列{3}n a -.
【解析】
法一:设12
()()3n n a A a A ++=+,解得3A =-
即原式化为12
(3)(3)3
n n a a +-=-
设3n n b a =-,则数列{}n b 为等比数列,且1132b a =-=- ∴122
3(2)()33()33
n n n n n b a a -=-=-??=-?
法二:∵12
13n n a a +-= ①
12
1(2)3n n a a n --=≥ ②
由①-②得:112
()3
n n n n a a a a +--=-
设1n n n b a a +=-,则数列{}n b 为等比数列 ∴11222
()()333n n n n n b a a -+=-=?=
∴22
1()33n n n a a +-= ∴233()3
n n a =-?
法三:21213a a =+,2322221()1333a a =+=++,32432222
1()()13333a a =+=+++,……,
112
2
2
1()13
3
3
n n n a a --=+=
=+++, ∴2
33()3
n n a =-?
【总结升华】求数列通项公式,特别是由递推公式给出数列时,除迭加、迭代、迭乘等基本方法外,还应注意根据递推关系式的特点,进行转化,变形为与是等差(等比)有关的数列.
举一反三:
【变式1】 数列{}n a 的首项为3,{}n b 为等差数列且1(*)n n n b a a n N +=-∈.若则
32b =-,1012b =,则8a =( )
A .0
B .3
C . 8
D .11
【答案】B
由已知知128,28,n n n b n a a n +=--=-由叠加法
21328781()()()642024603a a a a a a a a -+-+
+-=-+-+-++++=?==
【变式2】在数列{a n }中,a 1=1,a n+1=1n
n
a na +,求a n . 【答案】11111,1n n n n n n n a na a n na a a a +++=∴==++,∴111
n n
n a a +-= ∴
21
11
1a a -= 32
11
2a a -= ……
1
11(1)(2)n n n n a a --=-≥ 将以上各式叠加,得1
11
12(1)(1)(2)2
n n
n n n a a -=+++-=
-≥ ∴
11(1)(2)2
n n
n n a =+-≥ 又n=1时,1
1
11(11)12
a +-== ∴*2
2
()2
n a n N n n =
∈-+ 类型六:应用题
例9.某商场因管理不善及场内设施陈旧,致使年底结算亏损,决定从今年开始投入资金进行整修,计划第一个月投入80万元,以后每月投入将比上月减少1
5.第一个月
的经营收入约为40万元,预计以后每个月收入会比上个月增加1
4
.
(1) 设n 个月内的总投入为n a 万元,总收入为n b 万元,写出n a ,n b ;
(2) 问经过几个月后商场开始扭亏为盈.
【思路点拨】构建数学模型:各月的月投入构成以80为首项、14
1
=55
为公比的等比数列,总投入n a 是该数列的前n 项和;各月的月收入是以40为首项、15
1+=44
为公比的等比数
列,总收入n b 总是该数列的前n 项和.
【解析】 (1)由题意,得
2
1
4144445808080808040014555515
n
n n n a -??- ?
??????
??
????=+?+?+
+?=?=-?? ? ? ?
?????
??
??????-.
2
1
55540404040444n n b -????
??
=+?+?+
+? ? ? ?
????
??
51544016015414
n
n ??- ?
??????=?=-?? ???????-.
(2)由题意,令a n
.
设54n
t ??= ???,则1512(1)t t ??
-<- ???,即2t 2-7t +5>0.
∵t >1,∴解得t >52,即5542n
??
> ???.
取n =4,则4
551255421282??
??=?< ? ???
??;
取n =5,则5
556255425122??
??=?> ? ???
?? ∴第5月开始扭亏为盈.
【总结升华】解应用题的关键是建立数学模型,只要把模型中的量具体化就可得相应的解析式.
举一反三:
【变式】某地区原有森林木材存量为a ,且每年增长率为25%,因生产建设的需要每年年底要砍伐的木材量为b ,设n a 为n 年后该地区森林木材存量.
(1)写出n a 的表达式.
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量应不少于7
9a ,如果
19
72
b a =
,那么今后该地区会发生水土流失吗?若会,要经过几年?(取lg 20.30=). 【答案】
(1)依题意,第一年森林木材存量为a , 1年后该地区森林木材存量为:15
4
a a
b =-,
2年后该地区森林木材存量为:221555
()(1)444a a b a b =-=-+,
3年后该地区森林木材存量为:32325555
()[()1]4444a a b a b =-=-++,
4年后该地区森林木材存量为:4324355555
()[()()1]44444
a a
b a b =-=-+++,
… …
n 年后该地区森林木材存量为:125555
()[()()...1]4444
n n n n a a b --=-++++
(2)若1972b a =
时,依题意该地区今后会发水土流失,则森林木材存量必须小于7
9
a , 即 55197
()4[()1]44729n n a a a --?<,
解得554n >(),即5lg lg54
n >,
∴lg 51lg 2
7lg 52lg 213lg 2
n ->
==--,
∴8n =.
答:经过8年该地区就开始水土流失.