【真题】17年山西省运城市高三(上)数学期中试卷含答案(文科)
- 格式:doc
- 大小:671.00 KB
- 文档页数:18

2016-2017学年福建省厦门市湖滨中学高三(上)期中数学试卷(文科)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填涂在答题卡上,答在试卷上无效.1.(5分)已知集合A={x|x2﹣x﹣2<0},B={x|﹣1<x<1},则()A.A⊊B B.B⊊A C.A=B D.A∩B=∅2.(5分)若复数z满足=i,其中i为虚数单位,则z=()A.1﹣i B.1+i C.﹣1﹣i D.﹣1+i3.(5分)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1﹣x2,则下列命题中为真命题的是()A.p∧q B.¬p∧q C.p∧¬q D.¬p∧¬q4.(5分)若tanα>0,则()A.sinα>0 B.cosα>0 C.sin2α>0 D.cos2α>05.(5分)设S n为等比数列{a n}的前n项和,已知3S3=a4﹣2,3S2=a3﹣2,则公比q=()A.3 B.4 C.5 D.66.(5分)设变量x,y满足约束条件,则目标函数z=4x+2y的最大值为()A.12 B.10 C.8 D.27.(5分)设函数y=sin2x+cos2x的最小正周期为T,最大值为A,则()A.T=π,B.T=π,A=2 C.T=2π,D.T=2π,A=28.(5分)函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则函数y=f(x)对应的解析式为()A.B.C.D.9.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos2A=0,a=7,c=6,则b=()A.10 B.9 C.8 D.510.(5分)函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是()A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0C.a<0,b<0,c<0,d>0 D.a>0,b>0,c>0,d<011.(5分)已知数列{a n}满足log3a n+1=log3a n+1(n∈N*),且a2+a4+a6=9,则log(a5+a7+a9)的值是()A.﹣5 B.C.5 D.12.(5分)已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是()A.(1,+∞)B.(2,+∞)C.(﹣∞,﹣1)D.(﹣∞,﹣2)二.填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题纸对应题号的横线上.13.(5分)计算sin43°cos13°﹣cos43°sin13°的值为.14.(5分)如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C 点测得∠MCA=60°.已知山高BC=100m,则山高MN=m.15.(5分)设数列{a n}满足a1=1,且a n+1﹣a n=n+1(n∈N*),则数列{}的前10项的和为.16.(5分)当时,4x<log a x,则a的取值范围.三.解答题:本大题共6小题,共70分,请把答案书写在答题纸对应题号的相应区域.17.(10分)设函数f(x)=x3﹣6x+5,x∈R(Ⅰ)求f(x)的单调区间和极值;(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.18.(12分)已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b,求cosB;(Ⅱ)设B=90°,且a=,求△ABC的面积.19.(12分)已知等差数列{a n},满足a3=7,a5+a7=26.(Ⅰ)求数列{a n}的通项a n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.20.(12分)已知函数f(x)=cosx(sinx+cosx)﹣.(1)若0<α<,且sinα=,求f(α)的值;(2)求函数f(x)的最小正周期及单调递增区间.21.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.22.(12分)已知函数f(x)=x﹣1+(a∈R,e为自然对数的底数).(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;(Ⅱ)求函数f(x)的极值;(Ⅲ)当a=1的值时,若直线l:y=kx﹣1与曲线y=f(x)没有公共点,求k的最大值.2016-2017学年福建省厦门市湖滨中学高三(上)期中数学试卷(文科)参考答案与试题解析一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填涂在答题卡上,答在试卷上无效.1.(5分)已知集合A={x|x2﹣x﹣2<0},B={x|﹣1<x<1},则()A.A⊊B B.B⊊A C.A=B D.A∩B=∅【解答】解:由题意可得,A={x|﹣1<x<2},∵B={x|﹣1<x<1},在集合B中的元素都属于集合A,但是在集合A中的元素不一定在集合B中,例如x=∴B⊊A.故选:B.2.(5分)若复数z满足=i,其中i为虚数单位,则z=()A.1﹣i B.1+i C.﹣1﹣i D.﹣1+i【解答】解:=i,则=i(1﹣i)=1+i,可得z=1﹣i.故选:A.3.(5分)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1﹣x2,则下列命题中为真命题的是()A.p∧q B.¬p∧q C.p∧¬q D.¬p∧¬q【解答】解:因为x=﹣1时,2﹣1>3﹣1,所以命题p:∀x∈R,2x<3x为假命题,则¬p为真命题.令f(x)=x3+x2﹣1,因为f(0)=﹣1<0,f(1)=1>0.所以函数f(x)=x3+x2﹣1在(0,1)上存在零点,即命题q:∃x∈R,x3=1﹣x2为真命题.则¬p∧q为真命题.故选:B.4.(5分)若tanα>0,则()A.sinα>0 B.cosα>0 C.sin2α>0 D.cos2α>0【解答】解:∵tanα>0,∴,则sin2α=2sinαcosα>0.故选:C.5.(5分)设S n为等比数列{a n}的前n项和,已知3S3=a4﹣2,3S2=a3﹣2,则公比q=()A.3 B.4 C.5 D.6【解答】解:∵S n为等比数列{a n}的前n项和,3S3=a4﹣2,3S2=a3﹣2,两式相减得3a3=a4﹣a3,a4=4a3,∴公比q=4.故选:B.6.(5分)设变量x,y满足约束条件,则目标函数z=4x+2y的最大值为()A.12 B.10 C.8 D.2【解答】解:本题主要考查目标函数最值的求法,属于容易题,做出可行域,由图可知,当目标函数过直线y=1与x+y=3的交点(2,1)时,z取得最大值10.7.(5分)设函数y=sin2x+cos2x的最小正周期为T,最大值为A,则()A.T=π,B.T=π,A=2 C.T=2π,D.T=2π,A=2【解答】解:由三角函数的公式化简可得:=2()=2(sin2xcos+cos2xsin)=2sin(2x+),∴T==π,A=2故选:B.8.(5分)函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的部分图象如图所示,则函数y=f(x)对应的解析式为()A.B.C.D.【解答】解:由函数的图象可得A=1,=•=﹣,解得ω=2,再把点(,1)代入函数的解析式可得sin(2×+φ)=1,结合,可得φ=,故有,故选:A.9.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos2A=0,a=7,c=6,则b=()A.10 B.9 C.8 D.5【解答】解:∵23cos2A+cos2A=23cos2A+2cos2A﹣1=0,即cos2A=,A为锐角,∴cosA=,又a=7,c=6,根据余弦定理得:a2=b2+c2﹣2bc•cosA,即49=b2+36﹣b,解得:b=5或b=﹣(舍去),则b=5.故选:D.10.(5分)函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是()A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0C.a<0,b<0,c<0,d>0 D.a>0,b>0,c>0,d<0【解答】解:f(0)=d>0,排除D,当x→+∞时,y→+∞,∴a>0,排除C,函数的导数f′(x)=3ax2+2bx+c,则f′(x)=0有两个不同的正实根,则x1+x2=﹣>0且x1x2=>0,(a>0),∴b<0,c>0,方法2:f′(x)=3ax2+2bx+c,由图象知当当x<x1时函数递增,当x1<x<x2时函数递减,则f′(x)对应的图象开口向上,则a>0,且x1+x2=﹣>0且x1x2=>0,(a>0),∴b<0,c>0,故选:A.11.(5分)已知数列{a n}满足log3a n+1=log3a n+1(n∈N*),且a2+a4+a6=9,则log(a5+a7+a9)的值是()A.﹣5 B.C.5 D.【解答】解:∵log3a n+1=log3a n+1∴a n=3a n+1∴数列{a n}是以3为公比的等比数列,∴a2+a4+a6=a2(1+q2+q4)=9∴a5+a7+a9=a5(1+q2+q4)=a2q3(1+q2+q4)=9×33=35故选:A.12.(5分)已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是()A.(1,+∞)B.(2,+∞)C.(﹣∞,﹣1)D.(﹣∞,﹣2)【解答】解:∵f(x)=ax3﹣3x2+1,∴f′(x)=3ax2﹣6x=3x(ax﹣2),f(0)=1;①当a=0时,f(x)=﹣3x2+1有两个零点,不成立;②当a>0时,f(x)=ax3﹣3x2+1在(﹣∞,0)上有零点,故不成立;③当a<0时,f(x)=ax3﹣3x2+1在(0,+∞)上有且只有一个零点;故f(x)=ax3﹣3x2+1在(﹣∞,0)上没有零点;而当x=时,f(x)=ax3﹣3x2+1在(﹣∞,0)上取得最小值;故f()=﹣3•+1>0;故a<﹣2;综上所述,实数a的取值范围是(﹣∞,﹣2);故选:D.二.填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题纸对应题号的横线上.13.(5分)计算sin43°cos13°﹣cos43°sin13°的值为.【解答】解:sin43°cos13°﹣cos43°sin13°=sin(43°﹣13°)=sin30°=,故答案为.14.(5分)如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C 点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.【解答】解:在RT△ABC中,∠CAB=45°,BC=100m,所以AC=100m.在△AMC中,∠MAC=75°,∠MCA=60°,从而∠AMC=45°,由正弦定理得,,因此AM=100m.在RT△MNA中,AM=100m,∠MAN=60°,由得MN=100×=150m.故答案为:150.15.(5分)设数列{a n}满足a1=1,且a n+1﹣a n=n+1(n∈N*),则数列{}的前10项的和为.【解答】解:∵数列{a n}满足a1=1,且a n+1﹣a n=n+1(n∈N*),∴当n≥2时,a n=(a n﹣a n﹣1)+…+(a2﹣a1)+a1=n+…+2+1=.当n=1时,上式也成立,∴a n=.∴=2.∴数列{}的前n项的和S n===.∴数列{}的前10项的和为.故答案为:.16.(5分)当时,4x<log a x,则a的取值范围.【解答】解:当时,函数y=4x的图象如下图所示若不等式4x<log a x恒成立,则y=log a x的图象恒在y=4x的图象的上方(如图中虚线所示)∵y=log a x的图象与y=4x的图象交于(,2)点时,a=故虚线所示的y=log a x的图象对应的底数a应满足<a<1故答案为:(,1)三.解答题:本大题共6小题,共70分,请把答案书写在答题纸对应题号的相应区域.17.(10分)设函数f(x)=x3﹣6x+5,x∈R(Ⅰ)求f(x)的单调区间和极值;(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.【解答】解:(Ⅰ)∴当,∴f(x)的单调递增区间是,单调递减区间是当;当(Ⅱ)由(Ⅰ)的分析可知y=f(x)图象的大致形状及走向,∴当的图象有3个不同交点,即方程f(x)=α有三解.18.(12分)已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b,求cosB;(Ⅱ)设B=90°,且a=,求△ABC的面积.【解答】解:(I)∵sin2B=2sinAsinC,由正弦定理可得:>0,代入可得(bk)2=2ak•ck,∴b2=2ac,∵a=b,∴a=2c,由余弦定理可得:cosB===.(II)由(I)可得:b2=2ac,∵B=90°,且a=,∴a2+c2=b2=2ac,解得a=c=.==1.∴S△ABC19.(12分)已知等差数列{a n},满足a3=7,a5+a7=26.(Ⅰ)求数列{a n}的通项a n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和S n.【解答】解:(Ⅰ)设{a n}的首项为a1,公差为d,∵a5+a7=26∴a6=13,,∴a n=a3+(n﹣3)d=2n+1;(Ⅱ)由(1)可知,∴.20.(12分)已知函数f(x)=cosx(sinx+cosx)﹣.(1)若0<α<,且sinα=,求f(α)的值;(2)求函数f(x)的最小正周期及单调递增区间.【解答】解:(1)∵0<α<,且sinα=∴cosα=,∴f(α)=cosα(sinα+cosα)﹣=×(+)﹣=;(2)∵函数f(x)=cosx(sinx+cosx)﹣=sinxcosx+cos2x﹣=sin2x+﹣=(sin2x+cos2x)=sin(2x+),∴f(x)的最小正周期为T==π;令2kπ﹣≤2x+≤2kπ+,k∈Z,解得kπ﹣≤x≤kπ+,k∈Z;∴f(x)的单调增区间为[kπ﹣,kπ+],k∈Z.21.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.【解答】解:(1)设a1=a,由题意可得,解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.22.(12分)已知函数f(x)=x﹣1+(a∈R,e为自然对数的底数).(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;(Ⅱ)求函数f(x)的极值;(Ⅲ)当a=1的值时,若直线l:y=kx﹣1与曲线y=f(x)没有公共点,求k的最大值.【解答】解:(Ⅰ)由f(x)=x﹣1+,得f′(x)=1﹣,又曲线y=f(x)在点(1,f(1))处的切线平行于x轴,∴f′(1)=0,即1﹣=0,解得a=e.(Ⅱ)f′(x)=1﹣,①当a≤0时,f′(x)>0,f(x)为(﹣∞,+∞)上的增函数,所以f(x)无极值;②当a>0时,令f′(x)=0,得e x=a,x=lna,x∈(﹣∞,lna),f′(x)<0;x∈(lna,+∞),f′(x)>0;∴f(x)在∈(﹣∞,lna)上单调递减,在(lna,+∞)上单调递增,故f(x)在x=lna处取到极小值,且极小值为f(lna)=lna,无极大值.综上,当a≤0时,f(x)无极值;当a>0时,f(x)在x=lna处取到极小值lna,无极大值.(Ⅲ)当a=1时,f (x )=x ﹣1+,令g (x )=f (x )﹣(kx ﹣1)=(1﹣k )x +,则直线l :y=kx ﹣1与曲线y=f (x )没有公共点, 等价于方程g (x )=0在R 上没有实数解. 假设k >1,此时g (0)=1>0,g ()=﹣1+<0,又函数g (x )的图象连续不断,由零点存在定理可知g (x )=0在R 上至少有一解,与“方程g (x )=0在R 上没有实数解”矛盾,故k ≤1. 又k=1时,g (x )=>0,知方程g (x )=0在R 上没有实数解,所以k 的最大值为1.赠送—高中数学知识点【2.1.1】指数与指数幂的运算 (1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n a n 是偶数时,正数a 的正的n n a 表示,负的n 次方根用符号n a -0的n 次方根是0;负数a 没有n 次方根.n a n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()n n a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0) nna a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:(0,,,m nm na a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,mm m nn n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈【2.1.2】指数函数及其性质〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质。
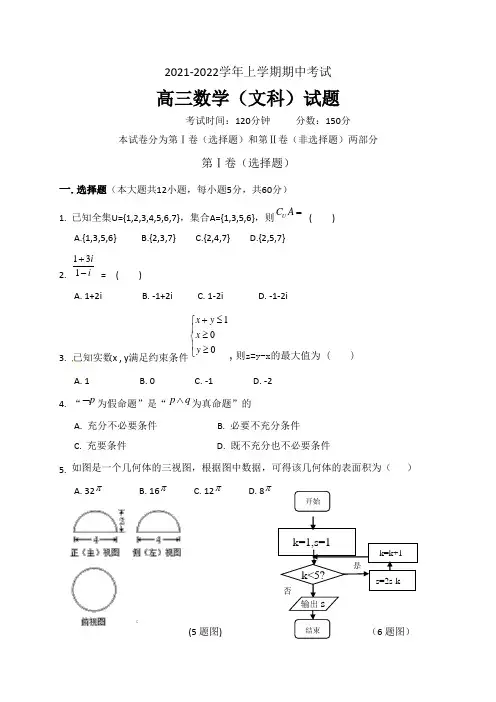
2021-2022学年上学期期中考试高三数学(文科)试题考试时间:120分钟 分数:150分本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题)一.选择题(本大题共12小题,每小题5分,共60分)1. 已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},则U C A =( )A.{1,3,5,6}B.{2,3,7}C.{2,4,7}D.{2,5,7}2. 131ii +- = ( )A. 1+2iB. -1+2iC. 1-2iD. -1-2i3. 已知实数x , y 满足约束条件100x y x y +≤⎧⎪≥⎨⎪≥⎩,则z=y-x 的最大值为 ( )A. 1B. 0C. -1D. -2 4. “p ⌝为假命题”是“p q ∧为真命题”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为( ) A. 32π B. 16π C. 12π D. 8π(5题图) (6题图)是否开始k=1,s=1k<5?输出s结束 k=k+1s=2s-k6. 执行如图所示的程序框图,输出的s 值为 ( ) A. -10 B. -3 C. 4 D. 57. 已知x 与y 之间的几组数据如表:x 0 1 2 3 y267则y 与x 的线性回归方程y b x a ∧∧∧=+必过点 ( )A. (1,2)B. (2,6)C. (315,24) D. (3,7)8. 下列函数中,在定义域内与函数3y x =的单调性与奇偶性都相同的是 ( )A. sin y x =B. 3y x x =-C. 2x y =D.2lg(1)y x x =++9. 对于使()f x N ≥成立的所有常数N 中,我们把N 的最大值叫作()f x 的下确界.若,a b ∈(0, +∞),且2a b +=,则133a b +的下确界为 ( ) A. 163 B. 83 C. 43 D. 2310.如图所示的数阵中,每行、每列的三个数均成等差数列.如果数阵中111213212223313233a a a a a a aa a ⎛⎫ ⎪ ⎪ ⎪⎝⎭所有数的和等于36,那么22a = ( )A. 8B. 4C. 2D. 111.三棱锥P-ABC 的侧棱PA 、PB 、PC 两两垂直,侧面面积分别是6,4,3,则三棱锥的体积是 ( )A. 4B. 6C. 8D.1012.函数()f x 的定义域为R ,f(0)=2,对x R ∀∈,有()()1f x f x '+>,则不等式()1x xe f x e >+ 的解集为 ( ) A. {}|0x x > B. {}|0x x < C. {}|11x x x <->或 D. {}|10x x x <->>或1第Ⅱ卷(非选择题)二.填空题(本大题共4小题,每小题5分,共计20分)13.已知-向量a 与b 的夹角为60°,且a =(-2,-6),10b =,则ab =14.已知数列{}n a 是等比数列,且1344,8a a a ==,则5a 的值为15.抛物线2(0)y ax a =<的焦点坐标为 16.将边长为2的等边∆ABC 沿x 轴正方向滚动,某时刻A 与坐标原点重合(如图),设顶点(,)A x y 的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:①f(x)的值域为[0,2]; ②f(x)是周期函数且周期为6 ; ③()(4)(2015)f f f π<<;④滚动后,当顶点A 第一次落在x 轴上时,f(x)的图象与x 轴所围成的面积为833π+.其中正确命题的序号为三.解答题(本大题共6道题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题12分)在∆ABC 中,内角A,B,C 的对边分别为,,a b c .已知3cos 3cos c b C c B =+(I )求sin sin C A 的值 (II)若1cos ,233B b =-=,求∆ABC 的面积。

2016-2017学年福建省南平市邵武七中高三(上)期中数学试卷(文科)一、选择题1.(5分)已知集合A={x|x<0},B={x|(x+2)(x﹣3)≤0},则A∩B=()A.{x|﹣3≤x<0}B.{x|﹣3<x<﹣2}C.{x|﹣2≤x<0}D.{x|x≤3} 2.(5分)命题“∃x0∈(0,),cosx0>sinx0”的否定是()A.∃x0∈(0,),cosx0≤sinx0B.∀x∈(0,),cosx≤sinxC.∀x∈(0,),cosx>sinx D.∃x0∉(0,),cosx0>sinx03.(5分)将函数y=cos(x﹣)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数图象的一条对称轴是直线()A.x=B.x=C.x=πD.x=4.(5分)函数f(x)=lnx﹣的零点所在的大致区间是()A.(0,1) B.(1,2) C.(2,e) D.(3,4)5.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.6 B.5 C.4 D.5.56.(5分)已知平面向量,为单位向量,|+|=1,则向量,的夹角为()A.B. C.D.7.(5分)已知cosα=﹣,且α∈(,π),则tan(﹣α)=()A.﹣ B.﹣7 C.D.78.(5分)设抛物线y2=2px的焦点在直线2x+3y﹣8=0上,则该抛物线的准线方程为()A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣19.(5分)已知双曲线﹣=1的一个焦点与抛物线x2=12y的焦点相同,则此双曲线的渐近线方程为()A.y=±x B.y=±x C.y=x D.y=x10.(5分)在正项等比数列{a n}中,若3a1,a3,2a2成等差数列,则=()A.3或﹣1 B.9或1 C.3 D.911.(5分)函数f(x)=|lnx|﹣x2的图象大致为()A. B.C.D.12.(5分)函数,则函数的零点个数为()A.3 B.2 C.1 D.0二、填空题:13.(5分)设变量x,y满足约束条件,则z=2x+y+1的最大值为.14.(5分)若关于x的方程x2﹣mx+2=0在区间[1,2]上有解,则实数m的取值范围是.15.(5分)已知钝角△ABC的面积为,AB=1,BC=,则角B=,AC=.三、解答题16.(10分)已知数列{a n}的前n项和s n,满足s n=n(n﹣6),数列{b n}满足(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)记数列{c n}满足,求数列{c n}的前n项和T n.17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,A=2C,且(Ⅰ)求cosC的值;(Ⅱ)若△ABC的面积为,求sinB及边b.18.(12分)已知向量=(cosx,sinx),=(2+sinx,2﹣cosx),函数f(x)=,x∈R.(Ⅰ)求函数f(x)的最大值;(Ⅱ)若x∈(﹣,﹣π)且f(x)=1,求cos(x+)的值.19.(12分)如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=EF.(Ⅰ)求证:DE∥平面ACG;(Ⅱ)求证:CG⊥平面ABE.20.(12分)已知椭圆E:+=1(a>b>0)的焦距为2,离心率为.(Ⅰ)求椭圆E的方程;(Ⅱ)设P是椭圆E上在第一象限内的点,如图,点P关于原点O的对称点为A,关于x轴的对称点为Q,线段PQ与x轴交于点C,点D为线段CQ的中点,直线AD与椭圆E的另一个交点为B,证明:点P在以AB为直径的圆上.21.(12分)已知函数f(x)=,曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).(1)求f(x)的解析式及单调递减区间;(2)是否存在常数k,使得对于定义域内的任意x,f(x)>+2恒成立,若存在,求出k的值;若不存在,请说明理由.[坐标系与参数方程]22.选修4﹣4:坐标系与参数方程曲线C1的参数方程为(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;(2)若射线l:y=kx(x≥0)与曲线C1,C2的交点分别为A,B(A,B异于原点),当斜率k∈(1,]时,求|OA|•|OB|的取值范围.2016-2017学年福建省南平市邵武七中高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题1.(5分)已知集合A={x|x<0},B={x|(x+2)(x﹣3)≤0},则A∩B=()A.{x|﹣3≤x<0}B.{x|﹣3<x<﹣2}C.{x|﹣2≤x<0}D.{x|x≤3}【解答】解:∵集合A={x|x<0},B={x|(x+2)(x﹣3)≤0}={x|﹣2≤x≤3},∴A∩B={x|﹣2≤x<0}.故选:C.2.(5分)命题“∃x0∈(0,),cosx0>sinx0”的否定是()A.∃x0∈(0,),cosx0≤sinx0B.∀x∈(0,),cosx≤sinxC.∀x∈(0,),cosx>sinx D.∃x0∉(0,),cosx0>sinx0【解答】解:命题是特称命题,则命题的否定是全称命题,则命题的否定是∀x∈(0,),cosx≤sinx,故选:B.3.(5分)将函数y=cos(x﹣)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数图象的一条对称轴是直线()A.x=B.x=C.x=πD.x=【解答】解:将函数y=cos(x﹣)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=cos(x﹣)的图象,再向左平移个单位,得到y=cos[(x+)﹣)]即y=cos(x﹣)的图象,令x﹣=kπ可解得x=2kπ+,故函数的对称轴为x=2kπ+,k∈Z,结合选项可得函数图象的一条对称轴是直线x=,故选:D.4.(5分)函数f(x)=lnx﹣的零点所在的大致区间是()A.(0,1) B.(1,2) C.(2,e) D.(3,4)【解答】解:∵y=lnx为(0,+∞)上的增函数,y=在(0,+∞)上为增函数,∴f(x)=lnx﹣在(0,+∞)上为增函数,又f(2)=ln2﹣1<0,,∴函数f(x)=lnx﹣的零点所在的大致区间是(2,e).故选:C.5.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.6 B.5 C.4 D.5.5【解答】解:三视图复原的几何体是长方体,去掉两个三棱锥后的几何体,如图:去掉的三棱锥的高为3,底面是等腰直角三角形,直角边长为1,所求几何体的体积为:2×1×3﹣=5.故选:B.6.(5分)已知平面向量,为单位向量,|+|=1,则向量,的夹角为()A.B. C.D.【解答】解:向量,的夹角为θ,∵平面向量,为单位向量,|+|=1,∴•=||•||cosθ=cos∴|+|2=1+1+2cosθ=1,解得cosθ=﹣,∵0≤θ≤π,∴θ=,故选:D.7.(5分)已知cosα=﹣,且α∈(,π),则tan(﹣α)=()A.﹣ B.﹣7 C.D.7【解答】解:∵cosα=﹣,且α∈(,π),∴sinα==,∴tanα==﹣,则tan(﹣α)==﹣7,故选:B.8.(5分)设抛物线y2=2px的焦点在直线2x+3y﹣8=0上,则该抛物线的准线方程为()A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣1【解答】解:把y=0代入2x+3y﹣8=0得:2x﹣8=0,解得x=4,∴抛物线的焦点坐标为(4,0),∴抛物线的准线方程为x=﹣4.故选:A.9.(5分)已知双曲线﹣=1的一个焦点与抛物线x2=12y的焦点相同,则此双曲线的渐近线方程为()A.y=±x B.y=±x C.y=x D.y=x【解答】解:抛物线x2=12y的焦点为(0,3),由双曲线﹣=1的一个焦点与抛物线x2=12y的焦点相同,可得3=,解得m=4,即有双曲线的方程为﹣=1,可得渐近线方程为y=±x.故选:C.10.(5分)在正项等比数列{a n}中,若3a1,a3,2a2成等差数列,则=()A.3或﹣1 B.9或1 C.3 D.9【解答】解:设正项等比数列{a n}的公比为q>0,∵3a1,a3,2a2成等差数列,∴a3=2a2+3a1,化为,即q2﹣2q﹣3=0,解得q=3.则==q2=9,故选:D.11.(5分)函数f(x)=|lnx|﹣x2的图象大致为()A. B.C.D.【解答】解:f(x)的定义域为{x|x>0},排除A.当x→0+时,f(x)→+∞,排除D.当x>1时,f(x)=lnx﹣,f′(x)=,令f′(x)=0解得x=2,当x>2时,f′(x)<0,∴f(x)在(2,+∞)上是减函数,排除B.故选:C.12.(5分)函数,则函数的零点个数为()A.3 B.2 C.1 D.0【解答】解:由f(x)﹣,得f(x)=,作出函数y=f(x)与y=的图象如图,由图可知,函数的零点个数为3.故选:A.二、填空题:13.(5分)设变量x,y满足约束条件,则z=2x+y+1的最大值为12.【解答】解:作出不等式组,对应的平面区域如图:(阴影部分)由z=2x+y+1得y=﹣2x+z﹣1,平移直线y=﹣2x+z﹣1,由图象可知当直线y=﹣2x+z﹣1经过点A时,直线y=﹣2x+z﹣1的截距最大,此时z最大.由,解得:,即A(6,﹣1),代入目标函数z=2x+y+1得z=2×6﹣1+1=12.即目标函数z=2x+y+1的最大值为12.故答案为:12.14.(5分)若关于x的方程x2﹣mx+2=0在区间[1,2]上有解,则实数m的取值范围是[2,3] .【解答】解:∵方程x2﹣mx+2=0在区间[1,2]上有解∴函数f(x)=x2﹣mx+2在区间[1,2]上与x轴相交①有1个交点时,满足或∴m=3或m=2②有2个交点时,满足,∴2<m≤3.综上所述,得m的取值范围是.15.(5分)已知钝角△ABC的面积为,AB=1,BC=,则角B=,AC=.【解答】解:∵钝角△ABC的面积为,AB=1,BC=,∴=1××sinB,解得:sinB=,∴B=或,∵当B=时,由余弦定理可得AC===1,此时,AB2+AC2=BC2,可得A=,为直角三角形,矛盾,舍去.∴B=,由余弦定理可得AC===,故答案为:;.三、解答题16.(10分)已知数列{a n}的前n项和s n,满足s n=n(n﹣6),数列{b n}满足(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)记数列{c n}满足,求数列{c n}的前n项和T n.【解答】解:(Ⅰ)当n=1时,a1=S1=﹣5,当n≥2时,a n=S n﹣S n﹣1=2n﹣7,又∵当n=1时满足上式,∴a n=2n﹣7;=3b n,b2=3,∵b n+1∴数列{b n}为等比数列,故其通项公式b n=b2•3n﹣2=3n﹣1;(Ⅱ)由(I)可知c n=,当n为偶数是,T n=+=+;当n为奇数时,T n=+=+;综上所述,T n=.17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,A=2C,且(Ⅰ)求cosC的值;(Ⅱ)若△ABC的面积为,求sinB及边b.【解答】解:(I)∵cosA=cos2C=2cos2C﹣1=,∴cosC=±.∵A=2C,∴C是锐角,∴cosC=.(II)∵cosA=,cosC=,∴sinA=,sinC=.∴sinB=sin(A+C)=sinAcosC+cosAsinC=.由正弦定理得.∴a===5,∵S△ABC∴b=5.18.(12分)已知向量=(cosx,sinx),=(2+sinx,2﹣cosx),函数f(x)=,x∈R.(Ⅰ)求函数f(x)的最大值;(Ⅱ)若x∈(﹣,﹣π)且f(x)=1,求cos(x+)的值.【解答】解:(Ⅰ)∵=(cosx,sinx),=(2+sinx,2﹣cosx),∴f(x)==cosx(2+sinx)+sinx(2﹣cosx)=2(sinx+cosx)=4sin(x+),∴函数f(x)的最大值为4;(Ⅱ)∵f(x)=4sin(x+)=1,∴sin(x+)=,∵x∈(﹣,﹣π),∴x+∈(﹣,﹣),∴cos(x+)=﹣,∴cos(x+)=cos[(x+)+]=cos(x+)﹣sin(x+)=﹣×﹣=﹣19.(12分)如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=EF.(Ⅰ)求证:DE∥平面ACG;(Ⅱ)求证:CG⊥平面ABE.【解答】证明:(Ⅰ)∵四边形ABCD为正方形,∴AD∥BC,AD=BC,又BC∥EF,BC=EF,∴AD∥EF,AD=EF,∵G是EF的中点,∴AD∥EG,且AD=EG,∴四边形ADEG为平行四边形,∴DE∥AG,∵AG⊂平面ACG,DE⊄平面ACG,∴DE∥平面ACG.(Ⅱ)∵AB⊥平面BCEF,而CG⊂平面BCEF,∴AB⊥CG,∵BC∥EG,BC=EG,且BC=CE,∴四边形BCEG为菱形,∴BE⊥CG,又AB∩BE=B,∴CG⊥平面ABE.20.(12分)已知椭圆E:+=1(a>b>0)的焦距为2,离心率为.(Ⅰ)求椭圆E的方程;(Ⅱ)设P是椭圆E上在第一象限内的点,如图,点P关于原点O的对称点为A,关于x轴的对称点为Q,线段PQ与x轴交于点C,点D为线段CQ的中点,直线AD与椭圆E的另一个交点为B,证明:点P在以AB为直径的圆上.【解答】解:(I)由题意可得:2c=2,e==,又a2=b2+c2,联立解得a=2,c=,b=1.∴椭圆E的方程为=1.(II)设P(x0,y0),Q(x1,y1),则A(﹣x0,﹣y0),C(x0,0),Q(x0,﹣y0),∴D.k AD==.∴直线AD的方程为:y=(x+x0)﹣y0,联立,化为:x2﹣6x+9﹣16=0.∴x1+(﹣x0)=,即x1=x0+,而y1=(x1+x0)﹣y0,∴而y1=(+2x0)﹣y0=.∴k PB===﹣.∴k PA==,∴.k PB•k PA=﹣1,故PA⊥PB,∴点P在以AB为直径的圆上.21.(12分)已知函数f(x)=,曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).(1)求f(x)的解析式及单调递减区间;(2)是否存在常数k,使得对于定义域内的任意x,f(x)>+2恒成立,若存在,求出k的值;若不存在,请说明理由.【解答】解:(Ⅰ),∵曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直,∴f′(e2)==,解得m=2,∴,∴,令f'(x)<0解得:0<x<1或1<x<e,∴函数f(x)的单调减区间为(0,1)和(1,e).(Ⅱ)∵恒成立,即,①当x∈(0,1)时,lnx<0,则恒成立,令,则g′(x)=,再令,则h′(x)=<0,所以h(x)在(0,1)内递减,所以当x∈(0,1)时,h(x)>h(1)=0,故,所以g(x)在(0,1)内递增,g(x)<g(1)=2∴k≥2.②当x∈(1,+∞)时,lnx>0,则恒成立,由①可知,当x∈(1,+∞)时,h'(x)>0,所以h(x)在(1,+∞)内递增,所以当x∈(1,+∞)时,h(x)>h(1)=0,故,所以g(x)在(1,+∞)内递增,g(x)>g(1)=2⇒k≤2;综合①②可得:k=2.[坐标系与参数方程]22.选修4﹣4:坐标系与参数方程曲线C1的参数方程为(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;(2)若射线l:y=kx(x≥0)与曲线C1,C2的交点分别为A,B(A,B异于原点),当斜率k∈(1,]时,求|OA|•|OB|的取值范围.【解答】解:(1)曲线C1的直角坐标方程为(x﹣1)2+y2=1,即x2+y2﹣2x=0,∴曲线C1的极坐标方程为ρ2﹣2ρcosθ=0,即ρ=2cosθ.∵曲线C2的极坐标方程为ρcos2θ=sinθ,即ρ2cos2θ=ρsinθ,∴曲线C2的直角坐标方程为x2=y.(2)设射线l的倾斜角为α,则射线l的参数方程为(t为参数,).把射线l的参数方程代入曲线C1的普通方程得:t2﹣2tcosα=0,解得t1=0,t2=2cosα.∴|OA|=|t2|=2cosα.把射线l 的参数方程代入曲线C 2的普通方程得:cos 2αt 2=tsinα, 解得t 1=0,t 2=. ∴|OB |=|t 2|=.∴|OA |•|OB |=2cosα•=2tanα=2k .∵k ∈(1,],∴2k ∈(2,2]. ∴|OA |•|OB |的取值范围是(2,2].赠送—高中数学知识点【2.1.1】指数与指数幂的运算 (1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n a n 是偶数时,正数a 的正的n n a 表示,负的n 次方根用符号n a -0的n 次方根是0;负数a 没有n 次方根.n a n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()n n a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0)nna a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:(0,,,m n m na a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质 函数名称指数函数定义函数(0xy a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域 R值域 (0,)+∞过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数函数值的 变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< 变化对 图象的影响 在第一象限内,a 越大图象越高;在第二象限内,a 越大图象越低.〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫xa y =xy(0,1)O1y =xa y =xy (0,1)O 1y =做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质第21页(共21页)。

2020年高考文科数学试卷全国Ⅰ卷(含答案)2020年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 $A=\{x|x^2-3x-4<0\}$,$B=\{-4,1,3,5\}$,则$A$ 为A。
$ \{-4,1\}$B。
$\{1,5\}$C。
$\{3,5\}$D。
$\{1,3\}$2.若 $z=1+2i+i^3$,则 $|z|$ 等于A。
$1$B。
$2$___$D。
$3$3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥。
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A。
$\dfrac{5-\sqrt{5}}{4}$B。
$\dfrac{1}{2}$C。
$\dfrac{5+\sqrt{5}}{4}$D。
$\dfrac{5+\sqrt{10}}{2}$4.设 $O$ 为正方形 $ABCD$ 的中心,在 $O$,$A$,$B$,$C$,$D$ 中任取 $3$ 点,则取到的 $3$ 点共线的概率为A。
$\dfrac{1}{5}$B。
$\dfrac{2}{5}$C。
$\dfrac{4}{5}$D。
$1$5.某校一个课外研究小组为研究某作物种子的发芽率$y$ 和温度 $x$(单位:℃)的关系,在 $20$ 个不同的温度条件下进行种子发芽实验,由实验数据$(x_i,y_i)(i=1,2,\dots,20)$ 得到下面的散点图:在 $10℃$ 至 $40℃$ 之间,下面四个回归方程类型中最适宜作为发芽率 $y$ 和温度 $x$ 的回归方程类型的是A。


长郡中学2025届高三月考试卷(二)数学得分__________.本试卷共8页.时量120分钟.满分150分.一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合{}(){}2,128tAxx B t t ==∈Z ∣∣ ,则A B = ( )A. []1,3−B. {}0,1C. []0,2D. {}0,1,2【答案】D 【解析】【分析】解绝对值不等式与指数不等式可化简集合,A B ,再利用交集的定义求解即可.【详解】{}{}|2=22A x x xx =≤−≤≤∣, 由指数函数的性质可得(){}{}1280,1,2,3tB t t =≤≤∈=Z ∣,所以{}{}{}220,1,2,30,1,2A B xx ∩−≤≤∩∣. 故选:D.2. 已知复数z 满足i 1z −=,则z 的取值范围是( ) A. []0,1 B. [)0,1C. [)0,2D. []0,2【答案】D 【解析】【分析】利用i 1z −=表示以(0,1)为圆心,1为半径的圆,z 表示圆上的点到原点的距离可得答案. 【详解】因为在复平面内,i 1z −=表示到点(0,1)距离为1的所有复数对应的点, 即i 1z −=表示以(0,1)为圆心,1为半径的圆, z 表示圆上的点到原点的距离,所以最短距离为0,最长距离为112+=,则z 的取值范围是[0,2]. 故选:D3. 已知()2:ln (11)1p f x a x x=+−<< −是奇函数,:1q a =−,则p 是q 成立的( ) A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件【答案】A 【解析】【分析】当p 成立,判断q 是否成立,再由q 成立时,判断p 是否成立,即可知p 是q 成立何种条件.【详解】由()f x 奇函数,则()00f =,即()ln 20a +=,解得1a =−, 所以p q ⇒,当1a =−时,()21ln 1ln 11x f x x x +=−=−−,11x −<<, ()()1111ln ln ln 111x x x f x f x x x x −−++∴−===−=− +−−,所以()f x 是奇函数, 所以p q ⇐, 所以p 是q 的充要条件. 故选:A.4. 若锐角α满足sin cos αα−sin 22πα+=( ) A.35B. 35C. 35 或35D. 45−或45【答案】B 【解析】【分析】先利用辅助角公式求出πsin 4α−,再利用角的变换ππsin 2sin 2π24αα+=−+,结合诱导公式和二倍角公式求解即可.【详解】由题意可得πsin cos 4ααα−=−=πsin 4α−.是因为α是锐角,所以πππ,444α −∈−,πcos 4α −所以πππππsin 2sin 2πsin 22sin cos 24444ααααα+=−+=−−=−−−325=−=−. 故选:B.5. 某大学在校学生中,理科生多于文科生,女生多于男生,则下述关于该大学在校学生的结论中,一定成立的是( )A. 理科男生多于文科女生B. 文科女生多于文科男生C. 理科女生多于文科男生D. 理科女生多于理科男生【答案】C 【解析】【分析】将问题转化不等式问题,利用不等式性质求解. 【详解】根据已知条件设理科女生有1x 人,理科男生有2x 人, 文科女生有1y 人,文科男生有2y 人;根据题意可知1212x x y y +>+,2211x y x y +<+,根据异向不等式可减的性质有()()()()12221211x x x y y y x y +−+>+−+, 即有12x y >,所以理科女生多于文科男生,C 正确.其他选项没有足够证据论证. 故选:C.6. 如图,某车间生产一种圆台形零件,其下底面的直径为4cm ,上底面的直径为8cm ,高为4cm ,已知点P 是上底面圆周上不与直径AB 端点重合的一点,且,AP BP O =为上底面圆的圆心,则OP 与平面ABC所成的角的正切值为( )为A. 2B.12C.D.【答案】A 【解析】【分析】作出直线OP 与平面ABC 所成的角,通过解直角三角形来求得直线OP 与平面ABC 所成的角的正切值.【详解】设O ′为下底面圆的圆心,连接,OO CO ′′和CO , 因为AP BP =,所以AB OP ⊥,又因为,,AB OO OP OO O OP OO ′′⊥=⊂′ 、平面OO P ′,所以AB ⊥平面OO P ′, 因为PC 是该圆台的一条母线,所以,,,O O C P ′四点共面,且//O C OP ′, 又AB ⊂平面ABC ,所以平面ABC ⊥平面POC ,又因为平面ABC 平面POC OC =,所以点P 在平面ABC 的射影在直线OC 上, 则OP 与平面ABC 所成的角即为POC OCO ∠=∠′,过点C 作CD OP ⊥于点D ,因为4cm,2cm OP O C ′==, 所以tan tan 2OO POC OCO O C∠=′′∠==′. 故选:A7. 在平面直角坐标系xOy 中,已知直线1:2l y kx =+与圆22:1C x y +=交于,A B 两点,则AOB 的面积的最大值为( )A. 1B.12C.D.【答案】D 【解析】【分析】求得直线过定点以及圆心到直线的距离的取值范围,得出AOB 的面积的表达式利用三角函数单调性即可得出结论.【详解】根据题意可得直线1:2l y kx =+恒过点10,2E,该点在已知园内, 圆22:1C x y +=的圆心为()0,0C ,半径1r =,作CD l ⊥于点D ,如下图所示:易知圆心C 到直线l 的距离为12CD CE ≤=,所以1cos 2CD DCB CB ∠=≤, 又π0,2DCB∠∈,可得ππ,32DCB∠∈; 因此可得2π2,π3ACB DCB∠=∠∈,所以AOB 的面积为112πsin 11sin 223AOB S CA CB ACB =∠≤×××= 故选:D 8. 设函数()()2ln f x xax b x =++,若()0f x ≥,则a 的最小值为( )A. 2−B. 1−C. 2D. 1【答案】B 【解析】【分析】根据对数函数性质判断ln x 在不同区间的符号,在结合二次函数性质得1x =为该二次函数的一个零点,结合恒成立列不等式求参数最值.【详解】函数()f x 定义域为(0,)+∞,而01ln 0x x <<⇒<,1ln 0x x =⇒=,1ln 0x x >⇒>, 要使()0f x ≥,则二次函数2y x ax b =++,在01x <<上0y <,在1x >上0y >, 所以1x =为该二次函数的一个零点,易得1b a =−−, 则2(1)(1)[(1)]y x ax a x x a =+−+=−++,且开口向上, 所以,只需(1)0101a a a −+≤⇒+≥⇒≥−,故a 的最小值为1−.故选:B二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.)9. 已知2n >,且*n ∈N ,下列关于二项分布与超几何分布的说法中,错误的有( ) A. 若1(,)3X B n ,则()22113E X n ++ B. 若1(,)3X B n ,则()4219D X n += C. 若1(,)3X B n ,则()()11P X P X n ===−D. 当样本总数远大于抽取数目时,可以用二项分布近似估计超几何分布 【答案】BC 【解析】【分析】利用二项分布的期望、方差公式及期望、方差的性质计算判断AB ;利用二项分布的概率公式计算判断C ;利用二项分布与超几何分布的关系判断D.【详解】对于A ,由1(,)3X B n ,得()13E X n =,则()22113E X n ++,A 正确; 对于B ,由1(,)3X B n ,得()122339D X n n =×=,则()()82149D X D X n +==,B 错误; 对于C ,由1(,)3X B n ,得11111221(1)C (),(1)C ()3333n n n n n P X P X n −−−==××=−=××,故(1)(1)P X P X n =≠=−,C 错误;对于D ,当样本总数远大于抽取数目时,可以用二项分布近似估计超几何分布,D 正确. 故选:BC10. 已知函数()sin cos (,0)f x x a x x ωωω=+∈>R 的最大值为2,其部分图象如图所示,则( )A. 0a >B. 函数π6f x−为偶函数 C. 满足条件的正实数ω存在且唯一 D. ()f x 是周期函数,且最小正周期为π 【答案】ACD 【解析】【分析】根据题意,求得函数π()2sin(2)3f x x =+,结合三角函数的图象与性质,逐项判定,即可求解.【详解】由函数()sin cos )f x x a x x ωωωϕ=++,且tan a ϕ=,因为函数()f x 的最大值为22=,解得a =,又因为(0)0f a =>,所以a =A 正确; ()πsin 2sin 3f x x x x ωωω ==+因为πππ2sin 1443f ω=+= ,且函数()f x 在π4的附近单调递减,所以ππ5π2π,Z 436k k ω++∈,所以28,Z k k ω=+∈,又因为π24T >,可得π2T >π2>,解得04ω<<,所以2ω=, 此时π()2sin(2)3f x x =+,其最小正周期为πT =,所以C 、D 正确; 设()πππ2sin 22sin 2663F x f x x x=−=−+=,()()2sin[2()]2sin 2F x x x F x −=−=−=−,所以FF (xx )为奇函数,即函数π()6f x −为奇函数,所以B 不正确. 故选:ACD.11. 已知抛物线2:2(0)C y px p =>的焦点为F ,准线交x 轴于点D ,直线l 经过F 且与C 交于,A B 两点,其中点A 在第一象限,线段AF 的中点M 在y 轴上的射影为点N .若MN NF =,则( )A. lB. ABD △是锐角三角形C. 四边形MNDF2 D. 2||BF FA FD ⋅> 【答案】ABD 【解析】【分析】根据题意分析可知MNF 为等边三角形,即可得直线l 的倾斜角和斜率,进而判断A ;可知直线l 的方程,联立方程求点,A B 的坐标,求相应长度,结合长度判断BD ;根据面积关系判断C.【详解】由题意可知:抛物线的焦点为,02p F,准线为2px =−,即,02p D −,设()()112212,,,,0,0A x y B x y y y ><, 则111,,0,2422x y y p M N+,可得, 因为MN NF =,即MN NF MF ==,可知MNF 为等边三角形,即60NMF ∠=°,且MN ∥x 轴,可知直线l 的倾斜角为60°,斜率为tan 60k =°=,故A 正确;则直线:2p l y x =− ,联立方程222p yx y px=− =,解得32p x y ==或6p x y p= =,即32p A,,6p B p,则,M p p N p,可得28,,,2,,33DFp AD p BDp FA p FB p AB p ======,在ABD △中,BD AD AB <<,且2220BD AD AB +−<, 可知ADB ∠为最大角,且为锐角,所以ABD △是锐角三角形,故B 正确;四边形MNDF 的面积为21122MNDF BDF MNF S S S p p p p p =+=×+×=△△,故C 错误; 因为224,3FB FA p FD p ⋅==,所以2||BF FA FD ⋅>,故D 正确; 故选:ABD.【点睛】方法点睛:有关圆锥曲线弦长、面积问题的求解方法(1)涉及弦长的问题中,应熟练地利用根与系数的关系、设而不求计算弦长;涉及垂直关系时也往往利用根与系数的关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解; (2)面积问题常采用12S =× 底×高,其中底往往是弦长,而高用点到直线距离求解即可,选择底很重要,选择容易坐标化的弦长为底.有时根据所研究三角形的位置,灵活选择其面积表达形式,若求多边形的面积问题,常转化为三角形的面积后进行求解;(3)在求解有关直线与圆锥曲线的问题时,应注意数形结合、分类与整合、转化与化归及函数与方程思想的应用.三、填空题(本大题共3小题,每小题5分,共15分.) 12. 在ABC 中,AD 是边BC 上的高,若()()1,3,6,3AB BC==,则AD =______.【解析】【分析】设()6,3BD mBC m m == ,表达出()61,33AD m m =++ ,根据垂直关系得到方程,求出13m =−,进而得到答案.【详解】设()6,3BD mBC m m == ,则()()()1,36,361,33AD AB BD m m m m =+=+=++,由0AD BC = 得6(61)3(33)366990AD BC m m m m =+++=+++=,解得13m =−,故()()12,311,2AD =−−=− ,所以||AD ..13. 已知定义在RR 上的函数()f x 满足()()23e xf x f x =−+,则曲线yy =ff (xx )在点()()0,0f 处的切线方程为_____________. 【答案】3y x =+ 【解析】【分析】利用方程组法求出函数解析式,然后利用导数求切线斜率,由点斜式可得切线方程. 【详解】因为()()23e xf x f x =−+,所以()()23e x f x f x −−=+,联立可解得()=e 2e xx f x −+,所以()03f =,所以()()e2e ,01xx f x f −=′−+=′. 所以曲线()y f x =在点()()0,0f 处的切线方程为3y x −=, 故所求的切线方程为3y x . 故答案为:3y x .14. 小澄玩一个游戏:一开始她在2个盒子,A B 中分别放入3颗糖,然后在游戏的每一轮她投掷一个质地均匀的骰子,如果结果小于3她就将B 中的1颗糖放入A 中,否则将A 中的1颗糖放入B 中,直到无法继续游戏.那么游戏结束时B 中没有糖的概率是__________. 【答案】117【解析】【分析】设最初在A 中有k 颗糖,B 中有6k −颗糖时,游戏结束时B 中没有糖的概率为()0,1,,6k a k = ,归纳找出递推关系,利用方程得出0a ,再由递推关系求3a .【详解】设A 中有k 颗糖,B 中有6k −颗糖,游戏结束时B 中没有糖的概率为()0,1,,6k a k = . 显然0113a a =,()65112112,153333k k k a a a a a k +−=+=+≤≤,可得()112k k k k a a a a +−−=−,则()566510022a a a a a −=−=,()65626765040010002222221a a a a a a a a a a ∴=+=++=+++=− ,同理()256510002221a a a a a =+++=− ,()()760021212133a a ∴−=−+,解得011385255a ==× ()430112115.25517a a ∴=−=×=故答案为:117【点睛】关键点点睛:本题的关键在于建立统一的一个6颗糖果放入2个盒子不同情况的模型,找到统一的递推关系,利用递推关系建立方程求出0a ,即可得出这一统一模型的答案.四、解答题(本大题共5小题,共77分,解签应写出文字说明、证明过程或演算步骤.) 15. 已知数列{}n a 中,11a =,且0,n n a S ≠为数列{}n a 的前nn a =.(1)求数列{}n a 的通项公式;(2)若1(1)n n n n n c a a +−=,求数列{}n c 的前n 项和. 【答案】(1)21na n =− (2)421,42n n n n T n n n − += + − + ,为偶数为奇数 【解析】【分析】(1)1={aa nn }的通项公式; (2) 求出(1)1142121n n c n n − =+ −+,再讨论n 为奇、偶数,利用裂项相消法即可求数列{}n c 的前n 项和. 【小问1详解】 根据题意知1,2n n n a S S n −=−≥0n a +≠=②,1,2n =≥,所以可得1=为首项,1为公差的等差数列,11n n =+−=,所以2n S n =,121,2n n n a n S S n −−==−≥,当1n =时11a =也满足该式,所以21na n =−. 【小问2详解】由(1)结论可知21n a n =−,所以()()1(1)(1)(1)11212142121n n n n n n n n c a a n n n n +−−− ===+ −+−+, 设{}n c 的前n 项和为n T ,则当n 为偶数时,111111111111433557212142142n n T n n n n =−+++−++++=−+=− −+++则当n 为奇数时,1111111111111433557212142142n n T n n n n + =−+++−++−+=−−=− −+++所以421,42n n n n T n n n − += + − + ,为偶数为奇数.16. 如图,在以,,,,,A B C D E F 为顶点的五面体中,四边形ABCD 与四边形CDEF 均为等腰梯形,AB∥,CD EF ∥,224CD CD AB EF ===,AD DE AE ===.(1)证明:平面ABCD ⊥平面CDEF ;(2)若M 为线段CD 1=,求二面角A EM B −−的余弦值.【答案】(1)证明见解析(2【解析】【分析】(1)通过勾股定理及全等得出线线垂直,应用线面垂直判定定理得出OE ⊥平面ABCD ,由OE ⊂平面CDEF 进而得出面面垂直;(2)由面面垂直建立空间直角坐标系,分别求出法向量再应用向量夹角公式计算二面角余弦值.【小问1详解】证明:在平面CDEF 内,过E 做EO 垂直于CD 交CD 于点O ,由CDEF 为等腰梯形,且24CD EF ==,则1,DO =又OE =,所以2OE ,连接AO ,由ADO EDO ≅ ,可知AO CD ⊥且2AO =,所以在三角形OAE 中,222AE OE OA =+,从而OE OA ⊥,又,,,OE CD OA CD O OA CD ⊥∩=⊂平面ABCD ,,所以OE ⊥平面ABCD , 又OE ⊂平面CDEF ,所以平面ABCD ⊥平面CDEF【小问2详解】由(1)知,,,OE OC OA 两两垂直,以O 为坐标原点,建立如图所示的空间直角坐标系,则()()()()0,0,2,2,0,0,0,2,0,0,2,2A E M B ,()()()2,0,2,2,2,0,0,0,2AE EM MB =−=−= ,设平面AEM 的一个法向量为(),,n x y z =, 则00n AE n EM ⋅= ⋅=,即220220x z x y −= −+= , 取1z =,则()1,1,1n = ,设平面BEM 的一个法向量为()111,,m x y z =, 则00m MB m EM ⋅= ⋅=,即11120220z x y = −+= , 取11y =,则()1,1,0m = ,所以cos,m nm nm n⋅==⋅由图可以看出二面角A EM B−−为锐角,故二面角A EM B−−.17. 已知函数2()e2,Rxf x ax a=−∈.(1)求函数()f x的单调区间;(2)若对于任意的0x>,都有()1f x≥恒成立,求a的取值范围.【答案】(1)答案见解析(2)(],1−∞【解析】【分析】(1)对2()e2xf x ax=−求导,可得2()2e2xf x a′=−,再分类讨论a的取值,得出导数的正负即可得出单调区间;(2)对a进行分类讨论,根据导数正负求得()f x的最小值,判断是否满足()1f x≥,即可求解.【小问1详解】对2()e2xf x ax=−求导,可得2()2e2xf x a′=−,令()0f x′=,即22e20x a−=,即2e x a=,当0a≤时,ff′(xx)>0恒成立,()f x在R上单调递增;当0a>时,21e,2ln,ln2x a x a x a===,当1ln2x a<时,()()0,f x f x′<在1,ln2a∞−上单调递减;当1ln2x a>时,ff′(xx)>0,()f x在1ln,2a∞+上单调递增;综上,当0a≤时,()f x单调递增区间为R;当0a>时,()f x的单调递减区间为1,ln2a∞−,单调递增区间为1ln,2a∞+.【小问2详解】因为对于任意的0x>,都有()1f x≥恒成立,的的对2()e 2x f x ax =−求导,可得2()2e 2x f x a ′=−,令()0f x ′=,即22e 20x a −=,即2e x a =,①当0a ≤时,ff ′(xx )>0,则()f x 在(0,+∞)单调递增,()()01f x f >=,符合题意; ②当01a <≤时,2e x a =,则1ln 02x a ≤, 则()0f x ′>,()f x 在(0,+∞)单调递增,()()01f x f >=,符合题意; ③当1a >时,2e x a =,则1ln 02xa >, 当10,ln 2x a∈ 时,()0f x ′<,则()f x 在10,ln 2a单调递减, 当1ln ,2x a ∞ ∈+ 时,()0f x ′>,则()f x 在1ln ,2a ∞ +单调递增, 所以()ln 11ln e 2ln ln 22a f x f a a a a a a ≥=−⋅=−, 令()ln ,1g a a a a a =−>,则()ln 0g a a ′=−<, 所以()g a 在(1,+∞)上单调递减,所以()()11g a g <=,不合题意; 综上所述,(],1a ∞∈−.18. 已知双曲线()2222:10,0x y E a b a b−=>>的左、右焦点分别为12,,F F E 的一条渐近线方程为y =,过1F 且与x 轴垂直的直线与E 交于P ,Q 两点,且2PQF 的周长为16.(1)求E 的方程;(2),A B 为双曲线E 右支上两个不同的点,线段AB 的中垂线过点()0,4C ,求ACB ∠的取值范围.【答案】(1)22:13y E x −=; (2)2π0,3. 【解析】 【分析】(1)将x c =−代入曲线E 得2b y a =±,故得211b PF QF a==,从而结合双曲线定义以及题意得24416b a b a a = +=,解出,a b 即可得解. (2)设:AB y kx m =+,联立双曲线方程求得中点坐标,再结合弦长公式求得ACM ∠的正切值,进而得ACM ∠范围,从而由2ACB ACM ∠=∠即可得解.【小问1详解】将x c =−代入2222:1(0,0)x y E a b a b −=>>,得2b y a=±, 所以211b PF QF a==,所以2222b PF QF a a ==+,所以由题得24416b a b a a= +=,1a b = ⇒ = 所以双曲线E 的方程为22:13y E x −=. 【小问2详解】由题意可知直线AB斜率存在且k ≠,设:AB y kx m =+,AA (xx 1,yy 1),BB (xx 2,yy 2),设AB 的中点为M . 由2233y kx m x y =+ −=消去y 并整理得222(3)230k x kmx m −−−−=,230k −≠, 则22222(2)4(3)(3)12(3)0km k m m k ∆=+−+=+−>,即223m k >−, 12223km x x k+=−,212233m x x k +=−−,12122226()2233km m y y k x x m k m k k +=++=⋅+=−−,于是M 点为2(3km k −,23)3m k −,2223431243M C MC M m y y m k k k km x kmx k −−−+−===−. 由中垂线知1A MC B k k ⋅=−,所以231241m k km k−+=−,解得:23m k =−. 所以由,A B 在双曲线的右支上可得:22221220333033m m x x m k k k m+−<+=−=>⇒⇒=−>−, 且12222003km x x k k k+>⇒>−, 且()()()()()22222222Δ43390333403m k k k k k k =−+>⇒−+−=−−>⇒<或24k >, 综上24k >即2k >,又CM =, 所以tan AM ACM CM ∠===因为24k >,所以213m k =−<−,故2333k 0−−<<(, 所以π0,3ACM∠∈. 所以2π20,3ACB ACM∠=∠∈ . 19. 对于集合,A B ,定义运算符“Δ”:Δ{,A B x x A x B =∈∈∣两式恰有一式成立},A 表示集合A 中元素的个数.(1)设][1,1,0,2A B =−= ,求ΔA B ;(2)对于有限集,,A B C ,证明ΔΔΔA B B C A C +≥,并求出固定,A C 后使该式取等号的B 的数量;(用含,A C 的式子表示)(3)若有限集,,A B C 满足ΔΔΔA B B C A C +=,则称有序三元组(),,A B C 为“联合对”,定义{}*1,2,,,I n n ∈N ,(){},,,,u A B C A B C I ⊆∣. ①设m I ∈,求满足ΔA C m =的“联合对”(),,A B C u ⊆的数量;(用含m 的式子表示) ②根据(2)及(3)①的结果,求u 中“联合对”的数量.【答案】(1)[1,0)(1,2]−∪(2)||2A C ∆(3)①C 2m n m n +⋅②6n【解析】【分析】(1)根据新定义,对区间逐一分析即可得解;(2)利用韦恩图及新定义,求出不等式等号成立的条件,利用集合的性质转化为求子集个数; (3)①分别求出(),A C ,B 取法的种数,再由分步乘法计数原理得解②结合(2)及(3)①的结果,利用二项式定理求解.【小问1详解】对于,,[1),0x x A x B −∈∈∉,故x A B ∈∆;对于,,[0,1]x x A x B ∈∈∈,故x A B ∉∆;对于,,(1,2]x x A x B ∉∈∈,故x A B ∈∆;对于,,[1],2x x A x B ∉−∉∉,故x A B ∉∆,即[10)(12],,A B −∆ .【小问2详解】画出Venn 图,如图,将A B C 划分成7个集合17,,S S ,则14562547||||||||||,||||||||||A B S S S S B C S S S S ∆=+++∆=+++,1267||||||||||A C S S S S ∆=+++,故45||||||2||2||0A B B C A C S S ∆+∆−∆=+≥不等式成立,当且仅当45S S ==∅时取等号, 4S =∅等价于()A C B ∩⊆,5S =∅等价于()B A C ⊆∪,故当且仅当()()A C B A C ∩⊆⊆∪取等号. 设()B A C D =∩∪,其中集合D 与A C 无交集,由于()\()A C A C A C ∆= ,故有()()\ΔD A C A C A C ∅⊆⊆∪∩=,即D 为A C ∆的某一子集,有||2A C ∆种,从而使上式取等的B 有||2A C ∆个.【小问3详解】①设X A C u =∆⊆,有||X m =,故X 有C m n 种取法,对于每一个x ,知X 中每一个元素x 有两种情形:,x A x C ∈∉或,x A x C ∉∈,且/I X 中每一个元素x 有两种情形:,x A x C ∈∉或,x A x C ∉∈,故,x I x ∀∈共有两种选择,也就是这样的(),A C 有||22I n =种,对于每一个(),A C ,由(2)知B 有||22A C m ∆=种取法.故由乘法原理,这样的“联合对(),,A B C 有C 2m n m n +⋅个.②由①知,u 中“联合对”的数量为()00C 22C 212216n n n m n m n m m n m n n nnm m +−===⋅=+=∑∑(二项式定理), 故u 中“联合对”(),,A B C 的数量为6n .【点睛】关键点点睛:集合新定义问题的关键在于理解所给新定义,会抽象的利用集合的知识,分步乘法计数原理,二项式定理推理运算,此类问题难度大.。


()n n ++=11n n ++-+5)9.091≈9.091 6.635> 6.635)0.010=答:在犯错误的概率不超过19.∵EH =AD =BC =BG ,EF ∥BC ,∠ABC =90°. 82BC BE =-BCF 的体积1(83BCF f AE =3234M m a =,所以有,1Dx k =-相似,所以湖南省长沙一中2017届高三上学期月考数学试卷(文科)(五)解析1.【分析】由已知中,集合A={x|x2-2x≤0},解二次不等式求出集合A,再由B={x|x≤a},A⊆B,即可得到实数a的取值范围.【解答】解:∵集合A={x|x2-2x≤0}=[0,2],B={x|x≤a},A⊆B,∴a≥2.2.【分析】利用复数的周期性、共轭复数的定义即可得出.【解答】解:i2017=(i4)504•i=i,复数===+i,则z的共轭复数=-i,3.【分析】先由列举法求出“三人在同一个社团”的概率,再由对立事件概率计算公式求出“三人不在同一个社团”的概率.【解答】解:∵某校有“交通志愿者”和“传统文化宣讲”两个社团,a,b,c三名学生各自随机选择参加其中的一个社团,∴a,b,c三名学生选择社团的结果有:(A,A,A),(A,A,B),(A,B,A),(B,A,A),(A,B,B),(B,A,B),(B,B,A),(B,B,B),共8个等可能性的基本事件,三人在同一个社团的结果有:(A,A,A),(B,B,B),共两个,∴“三人在同一个社团”的概率为p1==,而“三人不在同一个社团”与“三人在同一个社团”是对立事件,∴“三人不在同一个社团”的概率为p=1-=.4.【分析】由条件利用诱导公式、二倍角的正弦公式、同角三角函数的基本关系,求得cos(+2α)的值.【解答】解:∵tanα=2,α∈(0,π),则cos(+2α)=cos(+2α)=-sin2α=-2sinαcosα=-=-═-=-,5.【分析】利用三角形的知识计算CD,∠BCD,利用平面向量的数量积的定义计算数量积.【解答】解:∵AB=BC=3,∠BAC=30°,CD⊥AB,∴∠ABC=120°,∠BCD=30°,∴AC==3,∴CD=ACsin∠CAB=,∴==.6.【分析】模拟执行程序,依次写出每次循环输出的点的坐标,当满足条件,退出循环体,从而得到判定框中应填.【解答】解:模拟执行程序,可得i=1,y=0x=1,y=1,i=2,输出点(1,1),此输出的点恰落在直线y=x上,不满足条件,x=0,y=1,i=3,输出点(0,1)不满足条件,x=-1,y=0,i=4,输出点(-1,0)不满足条件,x=0,y=0,i=5,输出点(0,0),此输出的点恰落在直线y=x上不满足条件,x=1,y=1,i=6,输出点(1,1),此输出的点恰落在直线y=x上由题意,此时,应该满足条件,退出循环,故判断框中可填写的条件是i>5?.7.【分析】由于f(-x)=-f(x)推出函数是奇函数,f(x-2)=f(x+2),得到函数f(x)为周期为4的函数,求出log220的范围,再由已知表达式,和对数恒等式,即可得到答案.【解答】解:由于定义在R上的函数f(x),满足f(-x)=-f(x)所以函数是奇函数,f(x-2)=f(x+2),所以函数f(x)为周期为4的函数,log220∈(4,5),x∈(-1,0)时,f(x)=2x+,则f(log220)=f(log220-4)=-f(4-log220)===-1,8.【分析】根据已知可得该几何体是一个四分之一圆锥,与三棱柱的组合体,分别求出它们的体积,相加可得答案.【解答】解:根据已知可得该几何体是一个四分之一圆锥,与三棱柱的组合体,四分之一圆锥的底面半径为1,高为1,故体积为:=,三棱柱的底面是两直角边分别为1和2的直角三角形,高为1,故体积为:×1×2×1=1,故组合体的体积V=1+,9.【分析】设从下至上各节容积分别为a1,a2,…,a9,则{a n}是等差数列,设公差为d,由题意利用等差数列通项公式列出方程组,由此能求出中间两节的容积.【解答】解:设从下至上各节容积分别为a1,a2,…,a9,则{a n}是等差数列,设公差为d,由题意得,解得a1=1.4,d=-0.1,∴中间两节的容积为:a4+a5=(1.4-0.1×3)+(1.4-0.1×4)=2.1(升).10.【分析】先研究函数的奇偶性知它是奇函数,从而排除两个选项,再由x=-时,f′(0)>0,排除C,即可得解.【解答】解:∵g(x)=2cos(x-)cos(x+)=cos2x,∴将函数g(x)的图象上各点的坐标伸长为原来的2倍(纵坐标不变)后得到h(x)=cosx的图象,∴f(x)=x2+h(x)=x2+cosx,可得:f′(x)=x-sinx,∴可得:f′(-x)=(-x)-sin(-x)=-(x-sinx)=-f′(x),故此函数奇函数,排除B,D.又当x=-时,f′(0)=-+1=1->0,结合选项函数的图象,排除C.11.【分析】过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B.C,且|BC|=|CF2|,可得|BF1|=2a,求出B的坐标,代入双曲线方程,即可求出双曲线的渐近线方程.【解答】解:∵过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B.C,且|BC|=|CF2|,∴|BF1|=2a,设切点为T,B(x,y),则利用三角形的相似可得∴x=,y=∴B(,)代入双曲线方程,整理可得b=(+1)a,∴双曲线的渐近线方程为y=±(+1)x,12.【分析】分情况讨论,当x=2时,f(x)=1,则由f2(x)+bf(x)+c=0得1+b+c=0,求出x1=1;当x>2时,f(x)=lg(x-2),由f2(x)+bf(x)+c=0得[lg(x-2)]2+blg(x-2)-b-1=0,解得lg(x-2)=1,或lg (x-2)=b,从而求出x2和x3;当x<2时,f(x)=lg(2-x),由f2(x)+bf(x)+c=0得[lg(2-x)]2+blg (2-x)-b-1=0),解得lg(2-x)=1,或lg(2-x)=b,从而求出x4和x5,5个不同的实数解x1.x2.x3.x4.x5都求出来后,就能求出f(x1+x2+x3+x4+x5)的值.【解答】解:当x=2时,f(x)=1,则由f2(x)+bf(x)+c=0得1+b+c=0.∴x1=2,c=-b-1.当x>2时,f(x)=lg(x-2),由f2(x)+bf(x)+c=0得[lg(x-2)]2+blg(x-2)-b-1=0,解得lg(x-2)=1,x2=12或lg(x-2)=b,x3=2+10B.当x<2时,f(x)=lg(2-x),由f2(x)+bf(x)+c=0得[lg(2-x)]2+blg(2-x)-b-1=0),解得lg(2-x)=1,x4=-8或lg(2-x)=b,x5=2-10B.∴f(x1+x2+x3+x4+x5)=f(2+12+2+10b-8+2-10b)=f(10)=lg|10-2|=lg8=3lg2.13.【分析】研究知点M(1,2)在圆内,过它的直线与圆交于两点A,B,当∠ACB最小时,直线l与CM 垂直,故先求直线CM的斜率,再根据充要条件求出直线l的斜率,由点斜式写出其方程.【解答】解:验证知点M(1,2)在圆内,当∠ACB最小时,直线l与CM垂直,由圆的方程,圆心C(3,4)∵k CM==1,∴k l=-1∴l:y-2=-(x-1),整理得x+y-3=014.【分析】由③可知,C在散步,A在跳舞,由②④,可知,B在打篮球,D在画画,即可得出结论.【解答】解:由③可知,C在散步,A在跳舞,由②④,可知,B在打篮球,D在画画,15.【分析】先利用余弦定理求得建立等式,利用基本不等式的性质确定AD•DC的最大值,进而根据三角形面积公式求得三角形面积的最大值.【解答】解:在△ACD中,cos∠ADC===-,整理得AD2+CD2=48-AD•DC≥2•AD•DC,∴AD•DC≤16,AD=CD时取等号,∴△ADC的面积S=AD•DC•sin∠ADC=AD•DC≤4,16.【分析】营养学家指出,高中学生良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪.1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费35元;而1kg 食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费28元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?设每天食用xkgA食物,ykgB食物,总成本为z.建立约束条件,利用线性规划的知识进行求解.【解答】解:设每天食用xkgA食物,ykgB食物,总成本为z.则目标函数为z=28x+21y不等式组化简为如图作出可行域(阴影部分)把z=28x+21y 变形为y=-x+,解方程组得M 的坐标为(,)(2)求出数列{b n }的前n 项和为T n ,利用裂项相消法求得数列的前n 项和为H n ,则H 2017可求.31-()n n ++=11n n ++-+5)9.091≈9.091 6.635> 6.635)0.010=答:在犯错误的概率不超过19.【分析】∵EH =AD =BC =BG ,EF ∥BC ,∠ABC =90°.82BC BE=-BCF的体积1(83BCFf AE=320.【分析】(1)过点F的直线交椭圆于A,B两点.|AF|的最大值是M=a+c,|BF|的最小值是m=a-c,结合M•m=a2即可求出离心率;234M m a=,所以有,1Dxk=-相似,所以4⎩23.【分析】(1)由条件利用绝对值三角不等式求得f(x)≥|a|+||,再利用基本不等式证得|a|+||≥2,从而证得结论.(2)f(2)<3,即|2+|+|2-a|<3,再分类讨论求得a的范围,综合可得结论.a>。

2024届高三10月大联考(全国乙卷)文科数学一、单选题(共36 分)1已知集合A={x∈Z∣x2+1<5},B={−1,1,3}则A∪B中元素的个数为()A3B4C5D6【答案】B【分析】化简集合A即可求出A∪B中元素的个数【详解】由题意因为A={x∈Z∣x2+1<5}={x∈Z∣x2<4}={−1,0,1},B={−1,1,3}所以A∪B={−1,0,1,3}有4个元素故选:B2已知命题p:∃x0≥0,√x0>x02则命题p的否定为()A∃x0<0,√x0≤x02B∀x≥0,√x<x2C∀x<0,√x>x2D∀x≥0,√x≤x2【答案】D【分析】利用含有一个量词的命题的否定的定义求解【详解】解:因为命题p:∃x0≥0,√x0>x02是特称命题所以其否定为全称命题即“∀x≥0,√x≤x2”故选:D3若不等式x2−5ax+1<0的解集为(1a,a)则a=()A−12B12C−14D14【答案】A 【分析】根据给定的解集结合一元二次方程根与系数的关系求解即得 【详解】由不等式x 2−5ax +1<0的解集为(1a ,a)得1a ,a 是方程x 2−5ax +1=0的两个根且1a <a 于是a +1a =5a 解得a =±12由a >1a 得−1<a <0或a >1因此a =−12且当a =−12时(−5a)2−4>0所以a =−12 故选:A4若函数f (x )={e x −x,x ≤3lnx −2,x >3则f(f (e 2))=( )A −1B −2 C1 D ln2−2【答案】C 【分析】先计算出f (e 2)=0进而求出f(f (e 2))=f (0)=1 【详解】因为e 2>3所以f (e 2)=lne 2−2=0所以f(f (e 2))=f (0)=e 0−0=1 故选:C5已知p:1<a <53,q:log a 43>2(a >0且a ≠1)则p 是q 的( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件【答案】B 【分析】对于q :利用对数函数单调性解得1<a <2√33再根据包含关系结合充分、必要条件分析判断 【详解】对于q :因为log a 43>2=log a a 2(a >0且a ≠1)当0<a <1时y =log a x 在定义域内单调递减则a 2>43无解; 当a >1时y =log a x 在定义域内单调递增则a 2<43可得1<a <2√33;综上所述:不等式log a 43>2的解集为(1,2√33) 又因为(1,2√33)是(1,53)的真子集所以p 是q 的必要不充分条件 故选:B6函数f (x )=x 2log 42+x2−x 的大致图象是( )A B C D【答案】D 【分析】方法一:根据函数的奇偶性及函数值的符号排除即可判断;方法二:根据函数的奇偶性及某个函数值的符号排除即可判断 【详解】方法一:因为2+x2−x >0即(x +2)⋅(x −2)<0所以−2<x <2 所以函数f (x )=x 2log 42+x2−x 的定义域为(−2,2)关于原点对称又f (−x )=(−x)2log 42−x 2+x =−f (x )所以函数f (x )是奇函数其图象关于原点对称 故排除B,C ;当x ∈(0,2)时2+x2−x >1即log 42+x2−x >0因此f (x )>0故排除A 故选D方法二:由方法一知函数f (x )是奇函数其图象关于原点对称故排除B,C ; 又f (1)=12log 23>0所以排除A 故选:D7白色污染是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓经过长期研究一种全生物可降解塑料(简称PBAT )逐渐被应用于超市购物袋、外卖包装盒等产品研究表明在微生物的作用下PBAT 最终可被完全分解为二氧化碳和水进入大自然当其分解率(分解率=已分解质量总质量×100%)超过60%时就会成为对环境无害的物质为研究总质量为100g 的PBAT 的已分解质量y (单位:g )与时间x (单位:月)之间的关系某研究所人员每隔1个月测量1次PBAT 的已分解质量对通过实验获取的数据做计算处理研究得出已分解质量y 与时间x 的函数关系式为y =100−e 4.6−0.1x 据此研究结果可以推测总质量为100g 的PBAT 被分解为对环境无害的物质的时间至少为( )(参考数据:ln40≈3.7) A8个月 B9个月 C10个月 D11个月【答案】C 【分析】根据题意令y =100−e 4.6−0.1x >60求解即可 【详解】令y =100−e 4.6−0.1x >60得0.1x >4.6−ln40≈0.9解得x >9故至少需要10个月总质量为100g 的PBAT 才会被分解为对环境无害的物质 故选:C8已知α,β∈(0,π2),α>β且cosα(cosα−cosβ)+sinα(sinα−sinβ)=15,sinαcosβ=710则sin (α+β)=( ) A 45 B 35C 25D 310【答案】A 【分析】利用两角和与差的正弦公式和余弦公式化简即可 【详解】因为cosα(cosα−cosβ)+sinα(sinα−sinβ)=15cos 2α−cosαcosβ+sin 2α−sinαsinβ=15即1−cos (α−β)=15所以cos (α−β)=45因为α,β∈(0,π2),α>β所以0<α−β<π2所以sin (α−β)=35即sinαcosβ−cosαsinβ=35又sinαcosβ=710所以cosαsinβ=110所以sin (α+β)=sinαcosβ+cosαsinβ=710+110=45 故选:A9已知O 是△ABC 所在平面内一点若OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0⃗ ,AM ⃗⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ ,AN ⃗⃗⃗⃗⃗⃗ =yAC ⃗⃗⃗⃗⃗ ,MO ⃗⃗⃗⃗⃗⃗ =λON ⃗⃗⃗⃗⃗⃗ ,x,y 均为正数则xy 的最小值为( ) A 12 B 49C1D 43【答案】B 【分析】由题设O 是△ABC 的重心应用向量加法、数乘几何意义可得AO ⃗⃗⃗⃗⃗ =13x AM ⃗⃗⃗⃗⃗⃗ +13y AN ⃗⃗⃗⃗⃗⃗ 根据MO ⃗⃗⃗⃗⃗⃗ =λON ⃗⃗⃗⃗⃗⃗ 得13x +13y =1最后应用基本不等式求xy 最小值注意等号成立条件 【详解】因为OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0⃗ 所以点O 是△ABC 的重心 所以AO ⃗⃗⃗⃗⃗ =23×12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=13(AB ⃗⃗⃗⃗⃗ +AC⃗⃗⃗⃗⃗ ) 因为AM ⃗⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ ,AN ⃗⃗⃗⃗⃗⃗ =yAC ⃗⃗⃗⃗⃗ 所以AB ⃗⃗⃗⃗⃗ =1x AM ⃗⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ =1yAN⃗⃗⃗⃗⃗⃗ 综上AO ⃗⃗⃗⃗⃗ =13x AM ⃗⃗⃗⃗⃗⃗ +13y AN⃗⃗⃗⃗⃗⃗ 因为MO ⃗⃗⃗⃗⃗⃗ =λON⃗⃗⃗⃗⃗⃗ 所以M,O,N 三点共线则13x +13y =1即1x +1y =3 因为x,y 均为正数所以1x +1y ≥2√1xy 则√1xy ≤32所以xy ≥49(当且仅当1x =1y =32即x =y =23时取等号) 所以xy 的最小值为49 故选:B10若函数f (x )=Asin (ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示则下列说法正确的个数为( )①ω=2;②φ=−π6;③f (x )在(π2,5π6)上单调递减;④f (−π2)=√3 A1B2C3D4【答案】C 【分析】由图像经过的特殊点(5π12,2)和(π6,0)逐项判断即可 【详解】由题图得A =2最小正周期T =4×(5π12−π6)=π 又T =2πω=π所以ω=2故①正确;f (x )=2sin (2x +φ)又f (x )的图象过点(5π12,2) 所以2×5π12+φ=2kπ+π2,k ∈Z 所以φ=2kπ−π3,k ∈Z又|φ|<π2所以φ=−π3故②错误; f (x )=2sin (2x −π3)令t =2x −π3当π2<x <5π6时2π3<t <4π3函数y =sint 在(2π3,4π3)上单调递减故③正确;f (−π2)=2sin (−π−π3)=√3故④正确 故选:C11已知函数f (x )是偶函数当x >0时f (x )=|log 2x |−1则不等式x−1f (−x )−2f (x )≥0的解集是( ) A (−12,0)∪(0,12) B (−2,−1]∪[1,2)C (−2,−12)∪(0,12) D (−∞,−2)∪(−12,0)∪(0,12)∪[1,2)【答案】D 【分析】根据已知画出y =f (x )的图象并将不等式化为{f(x)(x −1)≤0f(x)≠0数形结合求不等式解集【详解】根据题意作偶函数y =f (x )的图象如下图示由f(−x)=f(x)不等式可化为x−1−f(x)≥0则{f(x)(x−1)≤0f(x)≠0所以{x−1≥0f(x)<0或{x−1≤0f(x)>0由图知:1≤x<2或0<x<12或−12<x<0或x<−2所以不等式解集为(−∞,−2)∪(−12,0)∪(0,12)∪[1,2)故选:D12已知函数f(x)=a x+a−x+cosx+x2(a>1)则f(√2),f(−e1e),f(π1π)的大小关系为()A f(π1π)<f(−e 1e)<f(√2)B f(√2)<f(π1π)<f(−e1e)C f(π1π)<f(√2)<f(−e1e)D f(−e1e)<f(π1π)<f(√2)【答案】B【分析】根据函数的奇偶性只需要考虑x>0时的情况利用导数求解函数单调性构造函数φ(x)=2x−sinx,g(x)=lnxx即可由导数求解单调性利用函数单调性即可比较大小【详解】易知f(x)=a x+a−x+cosx+x2(a>1)是偶函数f′(x)=(a x−a−x)lna+2x−sinx当x>0时因为a>1所以lna>0,a x−a−x>0令φ(x)=2x−sinx,x>0则φ′(x)=2−cosx>0所以φ(x)单调递增所以φ(x)>φ(0)=0所以f′(x)>0,f(x)在(0,+∞)上单调递增构造函数g(x)=lnxx 则g′(x)=1−lnxx2令g′(x)>0得0<x<e令g′(x)<0得x>e所以g(x)在区间(0,e)上单调递增在区间(e,+∞)上单调递减又ln22=ln44所以g(4)<g(π)<g(e)所以ln22=ln44<lnππ<lnee所以212<π1π<e1e所以f(√2)<f(π1π)<f(e 1e)=f(−e1e)即f(√2)<f(π1π)<f(−e1e)故选:B【点睛】方法点睛:利用导数比较大小的基本步骤:(1)作差或变形;(2)构造新的函数ℎ(x);(3)利用导数研究ℎ(x)的单调性或最值;(4)根据单调性及最值得到所证不等式.二、填空题(共12 分)13已知向量a=(1,−2)b⃗=(2,λ)若a⊥b⃗则实数λ的值为___________【答案】1【分析】根据向量垂直的坐标表示由题中条件列出方程即可求出结果【详解】因为向量a=(1,−2)b⃗=(2,λ)若a⊥b⃗则a⋅b⃗=2−2λ=0解得λ=1故答案为:114请写出一个满足对任意的x1,x2∈(0,+∞);都有f(x1x2)=f(x1)f(x2)的函数__________【答案】f(x)=x−12(答案不唯一)【分析】取幂函数f(x)=x−12验证得到答案【详解】任意定义域为(0,+∞)的幂函数均可例如f(x)=x−12f(x1x2)=(x1x2)−12,f(x1)f(x2)=x1−12⋅x2−12=(x1x2)−12即f(x1x2)=f(x1)f(x2)成立故答案为:f(x)=x−12(答案不唯一)15《海岛算经》是魏晋时期数学家刘徽所著的测量学著作书中有一道测量山上松树高度的题目受此题启发小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度如图把塔底与塔顶分别看作点CDCD 与地面垂直小李先在地面上选取点AB (点A,B 在建筑物的同一侧且点A,B,C,D 位于同一个平面内)测得AB =20√3m 在点A 处测得点C,D 的仰角分别为30∘,67∘在点B 处测得点D 的仰角为33.5∘则塔高CD 为__________m (参考数据:sin37∘≈35)【答案】24 【分析】在△ACD 中求出AD =20√3∠CAD =37∘,∠ACD =120∘利用正弦定理求解即可 【详解】如图延长DC 与BA 的延长线交于点E 则∠DAE =67∘,∠CAE =30∘,∠DBA =33.5∘所以∠ADB =67∘−33.5∘=33.5∘,∠CAE =90∘−30∘=60∘ 所以AD =AB =20√3在△ACD 中∠CAD =67∘−30∘=37∘,∠ACD =180∘−60∘=120∘ 由正弦定理得CD =ADsin37∘sin120∘≈20√3×35√32=24(m )故答案为:2416已知函数f (x )=(x +a )lnx −2x 在定义域上单调递增则实数a 的取值范围为______ 【答案】[1,+∞) 【分析】把原函数在区间上单调递增问题转化为a ≥x −xlnx 在(0,+∞)上恒成立构造函数g (x )=x −xlnx(x>0)利用导数求解函数的最值即可求解【详解】f(x)=(x+a)lnx−2x的定义域为(0,+∞)由f(x)=(x+a)lnx−2x在定义域上单调递增得f′(x)=lnx+ax−1≥0在(0,+∞)上恒成立即a≥x−xlnx在(0,+∞)上恒成立设g(x)=x−xlnx(x>0)所以只需a≥g(x)max又g′(x)=−lnx当0<x<1时g′(x)>0当x>1时g′(x)<0所以g(x)在(0,1)上单调递增在(1,+∞)上单调递减所以g(x)max=g(1)=1所以a≥1所以实数a的取值范围为[1,+∞)故答案为:[1,+∞)【点睛】方法点睛:已知函数在区间上单调递增(递减)求参数范围解决这类问题的一般方法是:利用导数转化为不等式恒成立问题然后参变分离根据分离后的式子结构构造函数利用导数求解函数最值即可解决三、问答题(共12 分)已知向量a=(sinx+cosx,1),b⃗=(2cosx,−1)函数f(x)=a⋅b⃗将函数f(x)的图象向右平移π6个单位长度得到函数g(x)的图象17 求函数f(x)的最小正周期和单调递增区间;18 解方程g(x)=0【答案】17 T=π单调递增区间为[kπ−3π8,kπ+π8],k∈Z18 {x|x=kπ2+π24,k∈Z}【分析】(1)利用向量数量积求出f(x)利用正弦函数的周期性与单调性即可求得f(x)的最小正周期和单调递增区间(2)先求出g(x)表达式根据正弦函数零点取值得到g(x)=0的解集【17题详解】由已知得f(x)=a⋅b⃗=2cosx(sinx+cosx)−1=sin2x +cos2x=√2sin (2x +π4)所以函数f (x )的最小正周期T =2πω=2π2=π由2kπ−π2≤2x +π4≤2kπ+π2,k ∈Z 解得kπ−3π8≤x ≤kπ+π8,k ∈Z所以函数f (x )的单调递增区间为[kπ−3π8,kπ+π8],k ∈Z【18题详解】将函数f (x )的图象向右平移π6个单位长度得到函数g (x )=√2sin [2(x −π6)+π4]=√2sin (2x −π12)的图象令g (x )=√2sin (2x −π12)=0得2x −π12=kπ,k ∈Z 解得x =kπ2+π24,k ∈Z所以方程g (x )=0的解集为{x |x =kπ2+π24,k ∈Z }如图在平行四边形ABCD 中AM ⃗⃗⃗⃗⃗⃗ =13AD ⃗⃗⃗⃗⃗ 令AB ⃗⃗⃗⃗⃗ =a AC⃗⃗⃗⃗⃗ =b ⃗19用a ,b ⃗ 表示AM ⃗⃗⃗⃗⃗⃗ BM ⃗⃗⃗⃗⃗⃗ CM⃗⃗⃗⃗⃗⃗ ; 20若AB =AM =2且AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10求cos⟨a ,b⃗ ⟩ 【答案】19 AM ⃗⃗⃗⃗⃗⃗ =13(b ⃗ −a )BM ⃗⃗⃗⃗⃗⃗ =13b ⃗ −43a CM ⃗⃗⃗⃗⃗⃗ =−13a −23b⃗ 20√3468【分析】(1)利用平面向量的四则运算法则求解即可; (2)利用平面向量数量积的公式和运算律求解即可 【19题详解】因为AB ⃗⃗⃗⃗⃗ =a AC ⃗⃗⃗⃗⃗ =b ⃗ 且ABCD 是平行四边形 所以BC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =b ⃗ −a所以AM ⃗⃗⃗⃗⃗⃗ =13BC ⃗⃗⃗⃗⃗ =13(b ⃗ −a ) 所以BM ⃗⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =13(b ⃗ −a )−a =13b ⃗ −43a所以CM ⃗⃗⃗⃗⃗⃗ =BM ⃗⃗⃗⃗⃗⃗ −BC ⃗⃗⃗⃗⃗ =13b ⃗ −43a −(b ⃗ −a )=−13a −23b ⃗ 【20题详解】方法一:由(1)知AM ⃗⃗⃗⃗⃗⃗ =13(b ⃗ −a ),BM ⃗⃗⃗⃗⃗⃗ =13b ⃗ −43a又AC ⃗⃗⃗⃗⃗ =b ⃗ ,AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10,AB =AM =2所以b ⃗ ⋅(13b ⃗ −43a )=10,|13(b ⃗ −a )|=2,|a |=2即b ⃗ 2−4a ⋅b ⃗ =30,b ⃗ 2+a 2−2a ⋅b ⃗ =36 解得a ⋅b⃗ =1,|b ⃗ |=√34 所以cos⟨a ,b ⃗ ⟩=a ⃗ ⋅b ⃗ |a ⃗ ||b ⃗ |=√3468方法二:因为AM ⃗⃗⃗⃗⃗⃗ =13AD ⃗⃗⃗⃗⃗ ,AM =2所以AD =BC =6因为AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )⋅(BA ⃗⃗⃗⃗⃗ +13BC ⃗⃗⃗⃗⃗ )=−BA ⃗⃗⃗⃗⃗ 2+23BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ +13BC ⃗⃗⃗⃗⃗ 2且AC ⃗⃗⃗⃗⃗ ⋅BM ⃗⃗⃗⃗⃗⃗ =10所以−22+23×6×2×cos∠ABC +13×62=10 解得cos∠ABC =14所以a ⋅b ⃗ =(−BA ⃗⃗⃗⃗⃗ )⋅(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )=−BA ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ 2=−2×6×14+22=1又|a |=2,|b ⃗ |=√(BC ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ )2=√BC ⃗⃗⃗⃗⃗ 2−2BC ⃗⃗⃗⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ 2=√34所以cos⟨a ,b ⃗ ⟩=a ⃗ ⋅b ⃗ |a ⃗ ||b ⃗ |=√3468四、应用题(共 6 分)某公园池塘里浮萍的面积y (单位:m 2)与时间t (单位:月)的关系如下表所示:现有以下三种函数模型可供选择:①y =kt +b ②y =p ⋅a t +q ③y =m ⋅log a t +n 其中k,b,p,q,m,n,a 均为常数a >0且a ≠121 直接选出你认为最符合题意的函数模型并求出y 关于t 的函数解析式;22 若该公园池塘里浮萍的面积蔓延到15m 2,31m 2,211m 2所经过的时间分别为t 1,t 2,t 3写出一种t 1,t 2,t 3满足的等量关系式并说明理由【答案】21 模型②y=2t+122 t1+t2=t3+1理由见解析【分析】(1)根据表格数据选择函数模型然后求解析式;(2)根据指数幂运算公式计算【21题详解】应选择函数模型②y=p⋅a t+q依题意得{p×a1+q=3p×a2+q=5 p×a3+q=9解得{p=1 a=2 q=1所以y关于t的函数解析式为y=2t+1【22题详解】t1+t2=t3+1理由:依题意得2t1+1=152t2+1=312t3+1=211所以2t1=142t2=302t3=210所以2t1⋅2t2=420所以2t1⋅2t2=2t1+t2=420=2×2t3=2t3+1所以t1+t2=t3+1五、问答题(共12 分)在△ABC中内角A,B,C所对的边分别为a,b,c且__________在①√3a =1−cosCsinA;②sinAbc−sinCab=sinA−sinBac两个条件中任选一个填入上面横线处并解决下列问题注:若选择不同的条件分别解答则按第一个解答计分23 求C;24 若△ABC外接圆的半径为2√3,△ABC的面积为√3求△ABC的周长【答案】23 C=π324 4√3+6【分析】(1)选①先利用正弦定理化边为角再利用和差角公式结合角的取值范围即得选②先用正弦定理化边为角再有余弦定理和角的范围即得(2)由正弦定理和外接圆半径求出c再利用余弦定理即可求出答案【23题详解】若选①:由√3a =1−cosCsinA及正弦定理得sinCsinA=√3sinA(1−cosC)∵sinA≠0,∴sinC+√3cosC=√3∴sin(C+π3)=√32又0<C<π,∴π3<C+π3<4π3∴C+π3=2π3,∴C=π3若选②:由sinAbc −sinCab=sinA−sinBac得asinA−csinC=bsinA−bsinB由正弦定理得a2+b2−c2=ab由余弦定理得cosC=a 2+b2−c22ab=ab2ab=12因为C∈(0,π)所以C=π3【24题详解】设△ABC外接圆的半径为R由正弦定理得c=2RsinC=2×2√3×sinπ3=6又S△ABC=12absinC=12ab×√32=√3所以ab=4由c2=a2+b2−2abcosC=(a+b)2−2ab−2ab×12可得36=(a+b)2−12解得a+b=4√3所以△ABC的周长为a+b+c=4√3+6已知函数f(x)=e x−ax2+x−125 当a=1时求曲线y=f(x)在x=1处的切线方程;26 若f(x)=0有两个不等的实根求实数a的取值范围【答案】25 (e−1)x−y=026 (−∞,0)∪{e2+14}【分析】(1)求导得到f(1)=e−1,f′(1)=e−1,进而求出切线方程;(2)f(0)=0故只需当x≠0时f(x)=0有且仅有一个实根参变分离转化为两函数只有1个交点求导得到g(x)=e x+x−1x2(x≠0)的单调性画出其图象数形结合得到参数的取值范围【25题详解】当a=1时f(x)=e x−x2+x−1,f′(x)=e x−2x+1f(1)=e−1,f′(1)=e−1,所以曲线y=f(x)在x=1处的切线方程为y−(e−1)=(e−1)(x−1)即(e−1)x−y=0【26题详解】显然f(0)=0要使方程f(x)=0有两个不等的实根只需当x≠0时f(x)=0有且仅有一个实根当x≠0时由方程f(x)=0得a=e x+x−1 x2令g(x)=e x+x−1x2(x≠0)则直线y=a与g(x)=e x+x−1x2(x≠0)的图象有且仅有一个交点g′(x)=(e x+1)x2−2x(e x+x−1)x4=(x−2)(e x−1)x3又当x<0时g′(x)<0,g(x)单调递减当0<x<2时g′(x)<0,g(x)单调递减当x>2时g′(x)>0,g(x)单调递增所以当x=2时g(x)取得极小值g(2)=e 2+1 4又当x<0时e x<1所以e x+x−1<0即g(x)<0当x>0时e x>1,e x+x−1>0即g(x)>0所以作出g(x)的大致图象如图所示由图象知要使直线y=a与g(x)=e x+x−1x2(x≠0)的图象有且仅有一个交点只需a<0或a=e 2+1 4综上若f(x)=0有两个不等的实根则a的取值范围为(−∞,0)∪{e 2+1 4}六、其它(共6 分)已知函数f(x)=x−alnx−4,a∈R27 讨论函数f(x)的单调性;28 当a=1时令F(x)=(x−2)e x−f(x)若x=x0为F(x)的极大值点证明:0<F(x0)<1【答案】27 答案见解析;28 证明见解析【分析】(1)对参数a分类讨论根据不同情况下导函数函数值的正负即可判断单调性;(2)利用导数判断F(x)的单调性求得x0的范围满足的条件以及F(x0)根据x0的范围夹逼F(x0)的范围即可【27题详解】函数f(x)的定义域为(0,+∞),f′(x)=1−ax =x−ax①当a≤0时f′(x)>0函数f(x)在(0,+∞)上单调递增;②当a>0时由f′(x)>0得x>a由f′(x)<0得0<x<a所以函数f(x)在(a,+∞)上单调递增在(0,a)上单调递减综上当a≤0时函数f(x)在(0,+∞)上单调递增;当a>0时函数f(x)在(a,+∞)上单调递增在(0,a)上单调递减【28题详解】当a=1时F(x)=(x−2)e x−x+lnx+4,F′(x)=(x−1)e x−1+1x =(x−1)(e x−1x)设g(x)=e x−1x 则g′(x)=e x+1x2当x>0时g′(x)>0所以g(x)在(0,+∞)上单调递增又g(12)=√e−2<0,g(1)=e−1>0所以存在x1∈(12,1)使得g(x1)=0且当x∈(0,x1),g(x)<0,x∈(x1,+∞),g(x)>0;又当x∈(0,1),y=x−1<0;x∈(1,+∞),y=x−1>0;故当x∈(0,x1)F′(x)>0;当x∈(x1,1)F′(x)<0;当x∈(1,+∞)F′(x)>0所以F(x)在(0,x1)上单调递增在(x1,1)上单调递减在(1,+∞)上单调递增所以当x=x1时F(x)取得极大值故x0=x1且e x0−1x0=0所以e x0=1x0,lnx0=−x0F(x0)=(x0−2)e x0−x0+lnx0+4=x0−2x0−x0−x0+4=5−2(x0+1x0)又y=x+1x 在(12,1)单调递减所以0<F(x0)<1【点睛】关键点点睛:本题考察含参函数单调性的讨论以及导数中的隐零点问题;处理问题的关键是能够准确分析F(x)的单调性以及求得隐零点的范围以及满足的条件属综合中档题。

人教版数学高三期末测试精选(含答案)学校:___________姓名:___________班级:___________考号:___________一、单选题1.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:2222(1)(21)1236n n n n ++++++=L )A .1624B .1024C .1198D .1560【来源】2020届湖南省高三上学期期末统测数学(文)试题 【答案】B2.在ABC ∆中,若222sin sin sin A B C +<,则ABC ∆的形状是( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .不能确定【来源】海南省文昌中学2018-2019学年高一下学期段考数学试题 【答案】A3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a ﹣b =c cos B ﹣c cos A ,则△ABC 的形状为( ) A .等腰三角形 B .等边三角形C .直角三角形D .等腰三角形或直角三角形【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】D4.已知圆C 1:(x +a )2+(y ﹣2)2=1与圆C 2:(x ﹣b )2+(y ﹣2)2=4相外切,a ,b 为正实数,则ab 的最大值为( )A .B .94C .32D .2【来源】安徽省安庆市五校联盟2018-2019学年高二(上)期中数学(理科)试题 【答案】B5.已知等比数列{}n a 满足122336a a a a +=+=,,则7a =( )【来源】甘肃省兰州市第一中学2016-2017学年高二下学期期末考试数学(文)试题 【答案】A6.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给五个人,使每个人所得成等差数列,最大的三份之和的17是最小的两份之和,则最小的一份的量是 ( ) A .116B .103C .56D .53【来源】湖南省湘南三校联盟2018-2019学年高二10月联考文科数学试卷 【答案】D7.若ABC ∆的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC ∆( ) A .一定是锐角三角形 B .一定是直角三角形C .一定是钝角三角形D .可能是锐角三角形,也可能是钝角三角形【来源】广东省中山市第一中学2019-2020学年高二上学期10月月考数学试题 【答案】C8.若不等式22log (5)0x ax -+>在[4,6]x ∈上恒成立,则a 的取值范围是( )A .(,4)-∞)B .20(,)3-∞ C .(,5)-∞D .29(,)5-∞【来源】重庆市七校(渝北中学、求精中学)2019-2020学年高一上学期期末联考数学试题 【答案】C9.港珠澳大桥通车后,经常往来于珠港澳三地的刘先生采用自驾出行.由于燃油的价格有升也有降,现刘先生有两种加油方案,第一种方案:每次均加30升的燃油;第二种方案,每次加200元的燃油,则下列说法正确的是( ) A .采用第一种方案划算 B .采用第二种方案划算 C .两种方案一样D .无法确定【来源】2020届广东省珠海市高三上学期期末数学(文)试题 【答案】B10.已知正项等比数列{}n a 的前n 项和为n S ,12a =,23434a a a +=,则5S =( )【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题 【答案】A11.在ABC ∆中3AB =,5BC =,7AC =,则边AB 上的高为( )A B C D 【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B12.不等式220ax bx ++>的解集是()1,2-,则a b -=( ) A .3-B .2-C .2D .3【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B13.各项均为正数的数列{}n a ,其前n 项和为n S ,若224n n n a S a -=,则2019S 为( )A .BC .2019D .4038【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】A14.设m ,n 为正数,且2m n +=,则2312m n m n +++++的最小值为( ) A .176B .145 C .114D .83【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B15.已知数列{}n a 的前n 项和为n S ,且314n n S a +=,则使不等式1000成立的n 的最大值为( )A .7B .8C .9D .10【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】C16.ABC ∆中角A ,B ,C 的对边分别是a ,b ,c ,若1a =,b =4B π=,则A =( )A .6π B .56π C .6π或56πD .23π【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】A17.等差数列{}n a 前n 项和为n S ,已知46a =,36S =,则( ) A .410n a n =-B .36n a n =-C .2n S n n =-D .224n S n n =-【来源】2020届安徽省芜湖市高三上学期期末数学(理)试题 【答案】C18.在等差数列{}n a 中,652a a =,则17a a +=( ) A .0B .1C .2-D .3【来源】2020届福建省三明市高三上学期期末质量检测文科数学试题 【答案】A19.若0,0,a b c d >><<则一定有( ) A .a b c d> B .a b c d< C .a b d c> D .a b d c< 【来源】2014年全国普通高等学校招生统一考试理科数学(四川卷带解析) 【答案】D20.已知平面上有四点O ,A ,B ,C ,向量,,OA OB OC u u u r u u u r u u u r 满足:0OA OB OC ++=u u u r u u u r u u u r r1OA OB OB OC OC OA ⋅=⋅=⋅=-u u u v u u u v u u u v u u u v u u u v u u u v,则△ABC 的周长是( )A .B .C .3D .6【来源】福建省晋江市季延中学2017-2018学年高一下学期期末考试数学试题 【答案】A21.在ABC ∆中,60A =︒,1b =,则sin sin sin a b c A B C ++++的值为( )A .1B .2C D .【来源】辽宁省实验中学分校2016-2017学年高一下学期期末数学(文)试题 【答案】B二、填空题22.在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为________. 【来源】2018年全国普通高等学校招生统一考试数学(江苏卷) 【答案】923.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知5a =8b ,A =2B ,则sin B =_____.【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】3524.如图,为测得河对岸塔AB 的高,先在河岸上选一点C,使C 在塔底B 的正东方向上,测得点A 的仰角为60°,再由点C 沿北偏东15°方向走10 m 到位置D,测得∠BDC =45°,则塔AB 的高是_____.【来源】2014届江西省南昌大学附属中学高三第三次月考理科数学试卷(带解析) 【答案】1025.设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为 . 【来源】智能测评与辅导[文]-等比数列 【答案】6426.设x ,y 满足约束条件20260,0x y x y x y +-≥⎧⎪+≤⎨⎪≥≥⎩,则23z x y =-+的最小值是______.【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题 【答案】9-27.已知数列{}n a 是等差数列,且公差0d <,()11a f x =+,20a =,()31a f x =-,其中()242f x x x =-+,则{}n a 的前10项和10S =________.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题 【答案】70-28.若x ,y 满足约束条件22020x x y x y ≤⎧⎪-+≥⎨⎪+-≥⎩,则3z x y =-的最小值为________.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题 【答案】2-29.已知数列{}n a 满足11a =,()13N n n n a a n *+⋅=∈,那么数列{}n a 的前9项和9S =______.【来源】2020届安徽省芜湖市高三上学期期末数学(理)试题 【答案】24130.设a ,b ,c 分别为ABC ∆内角A ,B ,C 的对边.已知2cos cos a B C=,则222a cb ac+-的取值范围为______.【来源】2020届吉林省通化市梅河口市第五中学高三上学期期末数学(理)试题【答案】()()0,2U三、解答题31.如图,在平面四边形ABCD 中,BC =3,CD =5,DA 2=,A 4π=,∠DBA 6π=.(1)求BD 的长: (2)求△BCD 的面积.【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】(1)7;(2 32.近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G ,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产x (千部)手机,需另投入成本()R x 万元,且 210100,040()100007019450,40x x x R x x x x ⎧+<<⎪=⎨+-≥⎪⎩,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.(I )求出2020年的利润()W x (万元)关于年产量x (千部)的函数关系式,(利润=销售额—成本);(II)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?【来源】湖北省四校(襄州一中、枣阳一中、宜城一中、曾都一中)2018-2019学年高一下学期期中联考数学试题【答案】(Ⅰ)210600250,040()10000()9200,40x x x W x x x x ⎧-+-<<⎪=⎨-++≥⎪⎩(Ⅱ)2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元. 33.设集合A={x|x 2<9},B={x|(x-2)(x+4)<0}. (1)求集合A∩B ;(2)若不等式2x 2+ax+b <0的解集为A ∪B ,求a ,b 的值.【来源】2013-2014学年广东阳东广雅、阳春实验中学高二上期末文数学卷(带解析) 【答案】(1){x |3x 2}-<<(2)2,24a b ==- 34.已知数列{}n a 满足11a =,()111n n n a na n ++-=+. (1)求数列{}n a 的通项公式; (2)n S 为数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和,求证:223n S ≤<. 【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题【答案】(1)12n n a +=(2)证明见解析 35.在ABC V 中,a ,b ,c 分别为内角A ,B ,C的对边,且满()(sin sin )sin )b a B A c B C -+=-.(1)求A 的大小;(2)再在①2a =,②4B π=,③=c 这三个条件中,选出两个使ABC V 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求ABC V 的面积. 【来源】2020届山东省滨州市高三上学期期末考试数学试题 【答案】(1)6A π=;(2)见解析36.设函数()22sin cos 3x x f x π⎛⎫=+⎪⎝⎭. (1)若0,2x π⎡⎤∈⎢⎥⎣⎦,求()f x 的单调递增区间;(2)在ABC ∆中,1AB =,2AC =,()2f A =-,且A 为钝角,求sin C 的值. 【来源】2020届浙江省嘉兴市高三上学期期末考试数学试题【答案】(1)5,122ππ⎡⎤⎢⎥⎣⎦(2)1437.在四边形ABCD 中,120BAD ︒∠=,60BCD ︒∠=,1cos 7D =-,2AD DC ==.(1) 求cos DAC ∠及AC 的长; (2) 求BC 的长.【来源】2020届宁夏石嘴山市第三中学高三上学期期末考试数学(文)试题【答案】(1) cos 7DAC ∠=,7AC =;(2) 3 38.在ABC V 中,内角A B C ,,所对的边分别为a b c ,,,已知sin cos 2sin cos A B c bB A b-=.(1)求A ;(2)设5b =,ABC S =V 若D 在边AB 上,且3AD DB =,求CD 的长. 【来源】2020届福建省莆田市(第一联盟体)学年上学期高三联考文科数学试题【答案】(1)3π;(239.在ABC ∆中,45,B AC ︒∠==cos C =. (1)求BC 边长;(2)求AB 边上中线CD 的长.【来源】北京101中学2018-2019学年下学期高一年级期中考试数学试卷【答案】(1)(240.已知函数2()2()f x x mx m R =-++∈,()2x g x =. (1)当2m =时,求2()(log )f x g x >的解集;(2)若对任意的1[1,1]x ∈-,存在2[1,1]x ∈-,使不等式12()()f x g x ≥成立,求实数m 的取值范围.【来源】重庆市七校(渝北中学、求精中学)2019-2020学年高一上学期期末联考数学试题【答案】(1)(0,2)(2)11[,]22-41.已知1x =是函数2()21g x ax ax =-+的零点,()()g x f x x=. (Ⅰ)求实数a 的值;(Ⅱ)若不等式(ln )ln 0f x k x -≥在2,x e e ⎡⎤∈⎣⎦上恒成立,求实数k 的取值范围;(Ⅲ)若方程()3213021xxf k k ⎛⎫⎪-+-= ⎪-⎝⎭有三个不同的实数解,求实数k 的取值范围.【来源】天津市滨海新区2018-2019学年高一上学期期末检测数学试题【答案】(Ⅰ)1;(Ⅱ)(],0-∞;(Ⅲ)103k -<<.42.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,cos sin C c B =. (1)求角C 的大小(2)若c =ABC ∆的面积为,求ABC ∆的周长.【来源】天津市蓟州等部分区2019届高三上学期期末联考数学(文)试题【答案】(Ⅰ)3C π=.(Ⅱ)10+43.已知等差数列{}n a 中,首项11a =,523a a =.(1)求{}n a 的通项公式;(2)若等比数列{}n b 满足13b =,2123b a a a =++,求{}n b 的前n 项和n S . 【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1) 21n a n =-;(2) 1332n n S +-= 44.对于正项数列{}n a ,定义12323nn a a a na G n+++⋅⋅⋅+=为数列{}n a 的“匀称”值.(1)若当数列{}n a 的“匀称”值n G n =,求数列{}n a 的通项公式; (2)若当数列{}n a 的“匀称”值2n G =,设()()128141n n nb n a +=--,求数列{}n b 的前2n 项和2n S 及2n S 的最小值.【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1) 21n n a n -=;(2)21141n S n =-+,4545.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且2sin tan c B b C =.(1)求角C 的值;(2)若c =3a b =,求ABC ∆的面积.【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1)3C π=,(2)ABC S ∆=46.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足1cos cos a cB C b b-=-. (1)求角C 的大小;(2)若2c =,a b +=ABC V 的面积.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题【答案】(1)3C π=;(2)447.已知ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,且sin cos a B A =. (1)求A ;(2)若a =,ABC V 的面积为ABC V 的周长.【来源】2020届福建省三明市高三上学期期末质量检测文科数学试题试卷第11页,总11页 【答案】(1)3A π=(2)7+48.在正项数列{}n a中,11a =,()()2211121n n n n a a a a ++-=-,1n n nb a a =-. (1)求数列{}n a 与{}n b 的通项公式;(2)求数列(){}22n n n a b -的前n 项和nT . 【来源】2020届吉林省通化市梅河口市第五中学高三上学期期末数学(理)试题【答案】(1)22n n a +=,2n n b =,(2)()()13144219n n n T n n +-+=++49.在ABC ∆中,10a b +=,cos C 是方程22320x x --=的一个根,求ABC ∆周长的最小值。

2023年普通高等学校招生全国统一考试(四川)数 学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到8页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己地姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出解析后,用铅笔把答题卡上对应题目地解析标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它解析标号。
不能答在试卷卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出地四个选项中,只有一项是符合题目要求地。
参考公式:如果事件A 、B 互斥,那么 球是表面积公式)()()(B P A P B A P +=+ 24RS π=如果事件A 、B 相互独立,那么 其中R 表示球地半径)()()(B P A P B A P ⋅=⋅ 球地体积公式如果事件A 在一次试验中发生地概率是P,那么334R V π=n 次独立重复试验中恰好发生k 次地概率 其中R 表示球地半径kn k kn n P P C k P --=)1()(一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出地四个选项中,只有一项是符合题目要求地。
1、设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4} ,则C U (A ∩B )=(A ){2,3} (B ) {1,4,5} (C ){4,5} (D ){1,5}2、函数1ln(21),()2y x x =+>-地反函数是(A )11()2x y e x R =- ∈ (B )21()x y e x R =- ∈ (C ) 1(1()2xy e x R =- ) ∈ (D )21()xy e x R =- ∈3、 设平面向量(3,5(2,1)a b = ) ,=- ,则2a b -=(A )(7,3) (B )(7,7) (C )(1,7) (D )(1,3)4、(tanx+cotx)cos 2x=(A )tanx (B )sinx (C )cosx (D )cotx 5、不等式2||2x x -<地解集为(A )(-1,2) (B )(-1,1) (C )(-2,1) (D )(-2,2)6、将直线3y x =绕原点逆时针旋转90°,再向右平移1个单位,所得到地直线为(A )1133y x =-+ (B )113y x =-+ (C )33y x =- (D )31y x =+7、△ABC 地三个内角A 、B 、C 地对边边长分别是a b c 、、 ,若a =,A=2B,则cosB=(A ) (B (C (D学校 班级 姓名 考号/密///////////封/////////////线/////////////内/////////////不/////////////要/////////////答/////////////题///////8、设M 是球O 地半径OP 地中点,分别过M 、O 作垂直于OP 地平面,截球面得到两个圆,则这两个圆地面积比值为(A )14(B )12(C )23(D )349、定义在R 上地函数()f x 满足:()(2)13,(1)2,f x f x f ∙+==则(99)f =(A )13 (B ) 2 (C )132(D )21310、设直线l α⊂平面,过平面α外一点A 且与l 、α都成30°角地直线有且只有(A )1条 (B )2条 (C )3条 (D )4条11、已知双曲线22:1916x y C -=地左右焦点分别为F 1、F 2 ,P 为C 地右支上一点,且||||212PF F F =,则△PF 1F 2 地面积等于(A )24 (B )36 (C )48 (D )9612、若三棱柱地一个侧面是边长为2地正方形,另外两个侧面都是有一个内角为60°地菱形,则该棱柱地体积为(A(B) (C)(D)第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分。
2021年普通⾼等学校招⽣全国统⼀考试(甲卷)⽂科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{}{}1,3,5,7,9,27M N x x ==>,则M N =I ()A.{}7,9 B.{}5,7,9 C.{}3,5,7,9 D.{}1,3,5,7,92. 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间3. 已知2(1)32i z i -=+,则z =()A.312i --B.312i -+ C.32i -+ D.32i --4.下列函数中是增函数的为()A.()f x x=- B.()23xf x æö=ç÷èøC.()2f x x= D.()f x =5. 点()3,0到双曲线221169x y -=的一条渐近线的距离为()A.95B.85C.65D.456.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为()( 1.259»)A.1.5B.1.2C.0.8D.0.67. 在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG -后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A. B. C. D.8.在ABC V 中,已知120B =°,AC =,2AB =,则BC =()A.1B.C.D.39.记n S 为等比数列{}n a 的前n 项和.若24S =,46S =,则6S =()A. 7B. 8C. 9D. 1010.将3个1和2个0随机排成一行,则2个0不相邻的概率为()A. 0.3B. 0.5C. 0.6D. 0.811.若cos 0,,tan 222sin p a a a a æöÎ=ç÷-èø,则tan a =()A.15B.5C.3D.312. 设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f æö-=ç÷èø,则53f æö=ç÷èø()A.53-B.13-C.13D.53二、填空题:本题共4小题,每小题5分,共20分.13.若向量,a b r r满足3,5,1a a b a b =-=×=r r r r r ,则b =r _________.14. 已知一个圆锥的底面半径为6,其体积为30p 则该圆锥的侧面积为________.15. 已知函数()()2cos f x x w j =+的部分图像如图所示,则2f p æö=ç÷èø_______________.16.已知12,F F 为椭圆C :221164x y+=的两个焦点,P ,Q 为C 上关于坐标原点对称的两点,且12PQ F F =,则四边形12PFQF 的面积为________.三、解答题:共70分.解答应写出交字说明、证明过程程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17. 甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:一级品二级品合计甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:22()()()()()n ad bc K a b c d a c b d -=++++()2P K k ³0.0500.0100.001k3.8416.63510.82818.记n S 为数列{}n a 的前n 项和,已知210,3n a a a >=,且数列是等差数列,证明:{}na 是等差数列.19. 已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ^.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ^.20.设函数22()3ln 1f x a x ax x =+-+,其中0a >.(1)讨论()f x 的单调性;(2)若()y f x =的图象与x 轴没有公共点,求a 的取值范围.21.抛物线C 的顶点为坐标原点O .焦点在x 轴上,直线l :1x =交C 于P ,Q 两点,且OP OQ ^.已知点()2,0M ,且M e 与l 相切.(1)求C ,M e 的方程;(2)设123,,A A A 是C 上的三个点,直线12A A ,13A A 均与M e 相切.判断直线23A A 与M e 的位置关系,并说明理由.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为r q =.(1)将C 的极坐标方程化为直角坐标方程;(2)设点A 的直角坐标为()1,0,M 为C 上的动点,点P 满足AP =u u u ru u u r,写出Р的轨迹1C 的参数方程,并判断C 与1C 是否有公共点.[选修4-5:不等式选讲]23.已知函数()2,()2321f x x g x x x =-=+--.(1)画出()y f x =和()y g x =的图像;(2)若()()f x a g x +³,求a 的取值范围.答案及解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{}{}1,3,5,7,9,27M N x x ==>,则M N =I ()A.{}7,9 B.{}5,7,9 C.{}3,5,7,9 D.{}1,3,5,7,9【答案】B 【解析】【分析】求出集合N 后可求M N Ç.【详解】7,2N æö=+¥ç÷èø,故{}5,7,9M N Ç=,故选:B.2. 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间【答案】C 【解析】【分析】根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.【详解】因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为0.020.040.066%+==,故A 正确;该地农户家庭年收入不低于10.5万元的农户比率估计值为0.040.0230.1010%+´==,故B 正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为0.100.140.2020.6464%50%++´==>,故D 正确;该地农户家庭年收入的平均值的估计值为30.0240.0450.1060.1470.2080.2090.10100.10110.04120.02130.02140.027.68´+´+´+´+´+´+´+´+´+´+´+´=(万元),超过6.5万元,故C 错误.综上,给出结论中不正确的是C.故选:C.【点睛】本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于´频率组距组距.3. 已知2(1)32i z i -=+,则z =()A.312i --B.312i -+C.32i -+ D.32i --【答案】B 【解析】【分析】由已知得322iz i+=-,根据复数除法运算法则,即可求解.【详解】2(1)232i z iz i -=-=+,32(32)23312222i i i i z i i i i ++×-+====-+--×.故选:B.4.下列函数中是增函数的为()A.()f x x =-B.()23xf x æö=ç÷èøC.()2f x x= D.()f x =【答案】D 【解析】【分析】根据基本初等函数的性质逐项判断后可得正确的选项.【详解】对于A ,()f x x =-为R 上的减函数,不合题意,舍.对于B ,()23xf x æö=ç÷èø为R 上的减函数,不合题意,舍.对于C ,()2f x x =在(),0-¥为减函数,不合题意,舍.对于D ,()f x =为R 上的增函数,符合题意,故选:D.5. 点()3,0到双曲线221169x y -=的一条渐近线的距离为()A.95B.85C.65 D.45【答案】A 【解析】【分析】首先确定渐近线方程,然后利用点到直线距离公式求得点到一条渐近线的距离即可.【详解】由题意可知,双曲线的渐近线方程为:220169x y -=,即340±=x y ,结合对称性,不妨考虑点()3,0到直线340x y +=的距离:d =故选:A.6. 青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为()( 1.259»)A. 1.5 B. 1.2C. 0.8D. 0.6【答案】C 【解析】【分析】根据,L V 关系,当 4.9L =时,求出lg V ,再用指数表示V ,即可求解.【详解】由5lg L V =+,当 4.9L =时,lg 0.1V =-,则10.11010100.8V --===».故选:C .7.在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG -后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A. B. C. D.【答案】D 【解析】【分析】根据题意及题目所给的正视图还原出几何体的直观图,结合直观图进行判断.【详解】由题意及正视图可得几何体的直观图,如图所示,所以其侧视图为故选:D8. 在ABC V 中,已知120B =°,AC =,2AB =,则BC =()A.1B.C.3【答案】D 【解析】【分析】利用余弦定理得到关于BC 长度的方程,解方程即可求得边长.【详解】设,,AB c AC b BC a ===,结合余弦定理:2222cos b a c ac B =+-可得:21942cos120a a =+-´´o ,即:22150a a +-=,解得:3a =(5a =-舍去),故3BC =.故选:D.【点睛】利用余弦定理及其推论解三角形的类型:(1)已知三角形的三条边求三个角;(2)已知三角形的两边及其夹角求第三边及两角;(3)已知三角形的两边与其中一边的对角,解三角形.9. 记n S 为等比数列{}n a 的前n 项和.若24S =,46S =,则6S =()A.7 B.8 C.9 D.10【答案】A 【解析】【分析】根据题目条件可得2S ,42S S -,64S S -成等比数列,从而求出641S S -=,进一步求出答案.【详解】∵n S 为等比数列{}n a 的前n 项和,∴2S ,42S S -,64S S -成等比数列∴24S =,42642S S -=-=∴641S S -=,∴641167S S =+=+=.故选:A.10. 将3个1和2个0随机排成一行,则2个0不相邻的概率为()A. 0.3B. 0.5C. 0.6D. 0.8【答案】C 【解析】【分析】利用古典概型的概率公式可求概率.【详解】解:将3个1和2个0随机排成一行,可以是:00111,01011,01101,01110,10011,10101,10110,11001,11010,11100,共10种排法,其中2个0不相邻的排列方法为:01011,01101,01110,10101,10110,11010,共6种方法,故2个0不相邻的概率为6=0.610,故选:C.11.若cos 0,,tan 222sin p a a a a æöÎ=ç÷-èø,则tan a =()A.15B.5C.3D.3【答案】A 【解析】【分析】由二倍角公式可得2sin 22sin cos tan 2cos 212sin a a a a a a ==-,再结合已知可求得1sin 4a =,利用同角三角函数的基本关系即可求解.【详解】cos tan 22sin aa a=-Q 2sin 22sin cos cos tan 2cos 212sin 2sin a a a aa a a a\===--,0,2p a æöÎç÷èøQ ,cos 0a \¹,22sin 112sin 2sin a a a \=--,解得1sin 4a =,cos 4a \==,sin tan cos 15a a a \==.故选:A.【点睛】关键点睛:本题考查三角函数的化简问题,解题的关键是利用二倍角公式化简求出sin a .12.设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f æö-=ç÷èø,则53f æö=ç÷èø()A.53-B.13-C.13D.53【答案】C 【解析】【分析】由题意利用函数的奇偶性和函数的递推关系即可求得53f æöç÷èø的值.【详解】由题意可得:522213333f f f f æöæöæöæö=+=-=-ç÷ç÷ç÷ç÷èøèøèøèø,而21111133333f f f f æöæöæöæö=-==--=-ç÷ç÷ç÷ç÷èøèøèøèø,故5133f æö=ç÷èø.故选:C.【点睛】关键点点睛:本题主要考查了函数的奇偶性和函数的递推关系式,灵活利用所给的条件进行转化是解决本题的关键.二、填空题:本题共4小题,每小题5分,共20分.13.若向量,a b r r满足3,5,1a a b a b =-=×=r r r r r ,则b =r _________.【答案】【解析】【分析】根据题目条件,利用a b -r r模的平方可以得出答案【详解】∵5a b -=r r∴222229225a b a b a b b -=+-×=+-=r r r r r r r∴b =r.故答案为:14.已知一个圆锥的底面半径为6,其体积为30p 则该圆锥的侧面积为________.【答案】39p 【解析】【分析】利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.【详解】∵216303V h p p =×=∴52h =∴132l ===∴136392S rl p p p ==´´=侧.故答案为:39p .15.已知函数()()2cos f x x w j =+的部分图像如图所示,则2f p æö=ç÷èø_______________.【答案】【解析】【分析】首先确定函数的解析式,然后求解2f p æöç÷èø的值即可.【详解】由题意可得:31332,,241234T T Tp p p pp w =-=\===,当1312x p =时,()131322,2126x k k k Z p w j j p j p p +=´+=\=-Î,令1k =可得:6pj =-,据此有:()52cos 2,2cos 22cos62266f x x f p p p p p æöæöæö=-=´-==ç÷ç÷ç÷èøèøèø.故答案为:.【点睛】已知f (x )=Acos (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)由ω=2Tp即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0,则令ωx 0+φ=0(或ωx 0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A ,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.16.已知12,F F 为椭圆C :221164x y+=的两个焦点,P ,Q 为C 上关于坐标原点对称的两点,且12PQ F F =,则四边形12PFQF 的面积为________.【答案】8【解析】【分析】根据已知可得12PF PF ^,设12||,||PF m PF n ==,利用勾股定理结合8m n +=,求出mn ,四边形12PFQF 面积等于mn ,即可求解.【详解】因为,P Q 为C 上关于坐标原点对称的两点,且12||||PQ F F =,所以四边形12PFQF 为矩形,设12||,||PF m PF n ==,则228,48m n m n +=+=,所以22264()2482m n m mn n mn =+=++=+,8mn =,即四边形12PFQF 面积等于8.故答案为:8.三、解答题:共70分.解答应写出交字说明、证明过程程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:一级品二级品 合计甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:22()()()()()n ad bc K a b c d a c b d -=++++()2P K k ³0.0500.0100.001k 3.841 6.63510.828【答案】(1)75%;60%;(2)能.【解析】【分析】根据给出公式计算即可【详解】(1)甲机床生产的产品中的一级品的频率为15075%200=,乙机床生产的产品中的一级品的频率为12060%200=.(2)()22400150801205040010 6.63527013020020039K ´-´==>>´´´,故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异.18.记n S 为数列{}n a 的前n 项和,已知210,3n a a a >=,且数列是等差数列,证明:{}na 是等差数列.【答案】证明见解析.【解析】【分析】先根据的公差d ,进一步写出的通项,从而求出{}na 的通项公式,最终得证.【详解】∵数列是等差数列,设公差为d =-==(n =+-=,()n *ÎN ∴12n S a n =,()n *ÎN ∴当2n ³时,()221111112n n n a S S a n a n a n a -=-=--=-当1n =时,11121=a a a ´-,满足112n a a n a =-,∴{}n a 的通项公式为112n a a n a =-,()n *ÎN ∴()()111111221=2n n a a a n a a n a a --=----éùëû∴{}n a 是等差数列.【点睛】在利用1n n n a S S -=-求通项公式时一定要讨论1n =的特殊情况.19. 已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ^.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ^.【答案】(1)13;(2)证明见解析.【解析】【分析】(1)首先求得AC 的长度,然后利用体积公式可得三棱锥的体积;(2)将所给的几何体进行补形,从而把线线垂直的问题转化为证明线面垂直,然后再由线面垂直可得题中的结论.【详解】(1)如图所示,连结AF ,由题意可得:BF ===,由于AB ⊥BB 1,BC ⊥AB ,1BB BC B =I ,故AB ^平面11BCC B ,而BF Ì平面11BCC B ,故AB BF ^,从而有3AF ===,从而AC ===,则222,AB BC AC AB BC +=\^,ABC V 为等腰直角三角形,111221222BCE ABC S s æö==´´´=ç÷èø△△,11111333F EBC BCE V S CF -=´´=´´=△.(2)由(1)的结论可将几何体补形为一个棱长为2的正方体1111ABCM A B C M -,如图所示,取棱,AM BC 的中点,H G ,连结11,,A H HG GB ,正方形11BCC B 中,,G F 为中点,则1BF B G ^,又111111,BF A B A B B G B ^=I ,故BF ^平面11A B GH ,而DE Ì平面11A B GH ,从而BF ^DE .【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.对于空间中垂直关系(线线、线面、面面)的证明经常进行等价转化.20. 设函数22()3ln 1f x a x ax x =+-+,其中0a >.(1)讨论()f x 的单调性;(2)若()y f x =的图象与x 轴没有公共点,求a 的取值范围.【答案】(1)()f x 的减区间为10,a æöç÷èø,增区间为1,+a æö¥ç÷èø;(2)1a e >.【解析】【分析】(1)求出函数的导数,讨论其符号后可得函数的单调性.(2)根据()10f >及(1)的单调性性可得()min 0f x >,从而可求a 的取值范围.【详解】(1)函数的定义域为()0,¥+,又()23(1)()ax ax f x x+-¢=,因为0,0a x >>,故230ax +>,当10x a <<时,()0f x ¢<;当1x a>时,()0f x ¢>;所以()f x 的减区间为10,a æöç÷èø,增区间为1,+a æö¥ç÷èø.(2)因为()2110f a a =++>且()y f x =的图与x 轴没有公共点,所以()y f x =的图象在x 轴的上方,由(1)中函数的单调性可得()min 1133ln 33ln f x f a a a æö==-=+ç÷èø,故33ln 0a +>即1a e>.【点睛】方法点睛:不等式的恒成立问题,往往可转化为函数的最值的符号来讨论,也可以参变分离后转化不含参数的函数的最值问题,转化中注意等价转化.21. 抛物线C 的顶点为坐标原点O .焦点在x 轴上,直线l :1x =交C 于P ,Q 两点,且OP OQ ^.已知点()2,0M ,且M e 与l 相切.(1)求C ,M e 的方程;(2)设123,,A A A 是C 上的三个点,直线12A A ,13A A 均与M e 相切.判断直线23A A 与M e 的位置关系,并说明理由.【答案】(1)抛物线2:C y x =,M e 方程为22(2)1x y -+=;(2)相切,理由见解析【解析】【分析】(1)根据已知抛物线与1x =相交,可得出抛物线开口向右,设出标准方程,再利用对称性设出,P Q 坐标,由OP OQ ^,即可求出p ;由圆M 与直线1x =相切,求出半径,即可得出结论;(2)先考虑12A A 斜率不存在,根据对称性,即可得出结论;若121323,,A A A A A A 斜率存在,由123,,A A A 三点在抛物线上,将直线121223,,A A A A A A 斜率分别用纵坐标表示,再由1212,A A A A 与圆M 相切,得出2323,y y y y +×与1y 的关系,最后求出M 点到直线23A A 的距离,即可得出结论.【详解】(1)依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>-,20,1120,21OP OQ OP OQ y p p ^\×=-=-=\=uu u r uu u r Q ,所以抛物线C 的方程为2y x =,(0,2),M M e 与1x =相切,所以半径为1,所以M e 的方程为22(2)1x y -+=;(2)设111222333(),(,),(,)A x y A x y A x y 若12A A 斜率不存在,则12A A 方程为1x =或3x =,若12A A 方程为1x =,根据对称性不妨设1(1,1)A ,则过1A 与圆M 相切的另一条直线方程为1y =,此时该直线与抛物线只有一个交点,即不存在3A ,不合题意;若12A A 方程为3x =,根据对称性不妨设12(3,A A则过1A 与圆M 相切的直线13A A为(3)3y x -=-,又1313313131,03A A y y k y x x y y -====\=-+,330,(0,0)x A =,此时直线1323,A A A A 关于x 轴对称,所以直线23A A 与圆M 相切;若直线121323,,A A A A A A 斜率均存在,则121323121323111,,A A A A A A k k k y y y y y y ===+++,所以直线12A A 方程为()11121y y x x y y -=-+,整理得1212()0x y y y y y -++=,同理直线13A A 的方程为1313()0x y y y y y -++=,直线23A A 的方程为2323()0x y y y y y -++=,12A A Q 与圆M相切,1=整理得22212121(1)230y y y y y -++-=,13A A 与圆M 相切,同理22213131(1)230y y y y y -++-=所以23,y y 为方程222111(1)230y y y y y -++-=的两根,2112323221123,11y y y y y y y y -+=-×=--,M 到直线23A A的距离为:2123|2|y -+=221==,所以直线23A A 与圆M 相切;综上若直线1213,A A A A 与圆M 相切,则直线23A A 与圆M 相切.【点睛】关键点点睛:(1)过抛物线上的两点直线斜率只需用其纵坐标(或横坐标)表示,将问题转化为只与纵坐标(或横坐标)有关;(2)要充分利用1213,A A A A 的对称性,抽象出2323,y y y y +×与1y 关系,把23,y y 的关系转化为用1y 表示.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为r q =.(1)将C 的极坐标方程化为直角坐标方程;(2)设点A 的直角坐标为()1,0,M 为C 上的动点,点P 满足AP =u u u ru u u r,写出Р的轨迹1C 的参数方程,并判断C 与1C 是否有公共点.【答案】(1)(222x y -+=;(2)P 的轨迹1C 的参数方程为32cos 2sin x y qqì=-+ïí=ïî(q 为参数),C 与1C 没有公共点.【解析】【分析】(1)将曲线C 的极坐标方程化为2cos r q =,将cos ,sin x y r q r q ==代入可得;(2)设(),P x y ,设)Mq q +,根据向量关系即可求得P 的轨迹1C 的参数方程,求出两圆圆心距,和半径之差比较可得.【详解】(1)由曲线C 的极坐标方程r q =可得2cos r q =,将cos ,sin x y r q r q ==代入可得22x y +=,即(222x y -+=,即曲线C 的直角坐标方程为(222x y +=;(2)设(),P x y ,设)Mq qQAP =u u u r u u u r,())()1,22cos x y q q q q \-=+-=+,则122cos 2sin x y q q ì-=+ïí=ïî,即32cos 2sin x y q q ì=+ïí=ïî,故P 的轨迹1C 的参数方程为32cos 2sin x y qqì=+ïí=ïî(q 为参数)Q曲线C 的圆心为),曲线1C 的圆心为()3-,半径为2,则圆心距为3-,32-<-Q ,\两圆内含,故曲线C 与1C 没有公共点.【点睛】关键点睛:本题考查参数方程的求解,解题的关键是设出M 的参数坐标,利用向量关系求解.[选修4-5:不等式选讲]23.已知函数()2,()2321f x x g x x x =-=+--.(1)画出()y f x =和()y g x =的图像;(2)若()()f x a g x +³,求a 的取值范围.【答案】(1)图像见解析;(2)112a ³【解析】【分析】(1)分段去绝对值即可画出图像;(2)根据函数图像数形结和可得需将()y f x =向左平移可满足同角,求得()y f x a =+过1,42A æöç÷èø时a 的值可求.【详解】(1)可得2,2()22,2x x f x x x x -<ì=-=í-³î,画出图像如下:34,231()232142,2214,2x g x x x x x x ì-<-ïïï=+--=+-£<íïï³ïî,画出函数图像如下:(2)()|2|f x a x a +=+-,如图,在同一个坐标系里画出()(),f x g x 图像,()y f x a =+是()y f x =平移了a 个单位得到,则要使()()f x a g x +³,需将()y f x =向左平移,即0a >,当()y f x a =+过1,42A æöç÷èø时,1|2|42a +-=,解得112a =或52-(舍去),则数形结合可得需至少将()y f x =向左平移112个单位,112a \³.【点睛】关键点睛:本题考查绝对值不等式的恒成立问题,解题的关键是根据函数图像数形结合求解.。
2023届高三全国学业质量联合检测2月大联考文科数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}2,1,0,1,2A =--,B 是偶数集,则A B = ()A .{}2B .{}2,2-C .{}0,2D .{}2,0,2-2.已知复数z 满足i i 1zz +=-,则z 在复平面内所对应的点是()A .11,2⎛⎫- ⎪⎝⎭B .13,55⎛⎫-- ⎪⎝⎭C .()1,1--D .33,55⎛⎫ ⎪⎝⎭3.函数()2exx xf x +=的部分图像大致为()A .B .C .D .4.已知点()1,1A ,()2,1B -,向量()2,1a =- ,()1,1b = ,则AB与a b - 的夹角的余弦值为()A .5-B .5-C D 5.已知M 是双曲线C 上的一个动点,且点M 到C 的两个焦点距离的差的绝对值为6,C 的焦点到渐近线的距离为4,则C 的离心率为()A .35B .53C .45D .546.某市2021年1月至2022年6月的平均气温折线图如图,则()A .平均高温不低于30C 的月份有3个B .平均高温的中位数是21CC .平均高温的极差大于平均低温的极差D .月平均高温与低温之差不超过10C 的月份有5个7.若实数x ,y 满足约束条件10,20,0,x y x y y -+≥⎧⎪-≤⎨⎪≥⎩,则22z x y =--的最大值为()A .4B.5C .2D8.已知[]x 表示不超过实数x 的最大整数.执行如图所示的程序框图,则输出的n =()A .3B .4C .5D .69.记数列{}n a 的前n 项和为22n S n n =+.若等比数列{}n b 满足11b a =,24b a =,则数列1n b ⎧⎫⎨⎩⎭的前n 项和n T =()A .332n-B .1332n +-C .1511623n -⎛⎫-⋅ ⎪⎝⎭D .111223n⎛⎫-⋅ ⎪⎝⎭10.已知正三棱柱111ABC A B C -的所有棱长都相等,D ,E ,F 分别是1BB ,11B C ,1AA 的中点,M 是线段BF 上的动点,则下列结论中正确的个数是()①1BF B C ⊥;②1//BF C D ;③11A E B C ⊥;④1//C M 平面1A DE .A .1B .2C .3D .411.已知函数()2tan sin tan 1xf x x x =++,则下列结论正确的是()A .()f x 在区间ππ,33⎛⎫- ⎪⎝⎭上单调递减B .()f x 在区间π0,2⎛⎫ ⎪⎝⎭上有极小值C .设()()2g x f x =-在区间ππ,22⎛⎫- ⎪⎝⎭上的最大值为M ,最小值为m ,则4M m +=D .()f x 在区间ππ,22⎛⎫- ⎪⎝⎭内有且只有一个零点12.已知三棱锥P -ABC 的所有顶点均在半径为2的球的O 球面上,底面ABC 是边长为3的等边三角形.若三棱锥P -ABC 的体积取得最大值时,该三棱锥的内切球的半径为r ,则r =()A .1B .14C .32D .)3114二、填空题13.记函数()()n f x x nx n n *=+-∈N 在1x =处的导数为n a ,则()4216log a a =________.14.写出以原点为圆心且与圆C :22430x y y +-+=相切的一个圆的标准方程为________.15.已知实数a ,b ,m ,n 满足20a b --=,240m n -=,则()()22m a n b -+-的最小值为________.三、双空题16.已知()f x 是定义R 在上的奇函数,当0x >时,()222x xf x -=+,当0x <时,()22x x f x m n -=⋅+⋅,则m n +=________;若方程()()R f x a a =∈有两个不同的实数根,则a 的取值范围是________.四、解答题17.记ABC 的内角A ,B ,C 的对边分别为a ,b ,c 是2a 与πsin6C ⎛⎫+ ⎪⎝⎭的等比中项.(1)求A ﹔(2)若ABC 是锐角三角形,且2c =,求sin a B 的取值范围.18.2020年,教育部启动实施强基计划.强基计划聚焦国家重大战略需求,突出基础学科的支撑引领作用.三年来,强基计划共录取新生1.8万余人.为响应国家号召,某校2022年7月成立了“强基培优”拓展培训班,从高一入校时中考数学成绩前100名的学生中选取了50名对数学学科研究有志向、有兴趣、有天赋的学生进行拓展培训.为了解数学“强基培优”拓展培训的效果,在高二时举办了一次数学竞赛,这100名学生的成绩(满分为150分)情况如下表所示.成绩不低于135分成绩低于135分总计参加过培训401050未参加过培训203050总计6040100(1)能否有99%的把握认为学生的数学竞赛成绩与是否参加“强基培优”拓展培训有关?(2)从成绩不低于135分的这60名学生中,按是否参加过“强基培优”拓展培训采用分层抽样﹐随机抽取了6人,再从这6人中随机抽取2人代表学校参加区里的数学素养大赛,求这2人中至少有一人未参加过培训的概率.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.()20P K k ≥0.100.050.0250.0100.0010k 2.7063.8415.0246.63510.82819.如图①,在平面四边形ABCD 中,2AB AD ==,BC CD ==60BAD ∠= .将BCD △沿着BD 折叠,使得点C 到达点C '的位置,且二面角A BD C '--为直二面角,如图②.已知,,P G F 分别是,,AC AD AB '的中点,E 是棱AB 上的点,且C E '与平面ABD所成角的正切值为3.(1)证明:平面//PGF 平面C DB ';(2)求四棱锥P GFED -的体积.20.已知函数()()ln R f x x ax a =+∈,()f x 的导函数为()f x '.(1)讨论()f x 的极值点的个数;(2)当2a =时,方程()()()0f x f x m m '++=∈R 有两个不相等的实数根,求m 的取值范围.21.已知抛物线E :()220y px p =>的焦点关于其准线的对称点为()3,0P -,椭圆C :()222210x y a b a b+=>>的左,右焦点分别是1F ,2F ,且与E 有一个共同的焦点,线段1PF 的中点是C 的左顶点.过点1F 的直线l 交C 于A ,B 两点,且线段AB 的垂直平分线交x 轴于点M .(1)求C 的方程;(2)证明:114F M AB=.22.在直角坐标系xOy 中,曲线1C 的参数方程为2cos sin xy αα=+⎧⎪⎨=⎪⎩(α为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为()22sin sin 12m m θρθ⎛⎫+-=∈ ⎪⎝⎭R .(1)写出1C 的普通方程;(2)若曲线1C 与2C 有两个交点,M N ,则当m 为何值时,MN 最大?并求出MN 的最大值.23.已知a ,b ,c 都是正实数,且3a b c ++=.证明:(1)3331113a b c ++≥;(2)()2221119a b c a b c ≥⎛⎫++++ ⎪⎝⎭.参考答案:1.D【分析】利用偶数和交集的定义即可求解.【详解】因为在集合{}2,1,0,1,2A =--中,-2,0,2是偶数,所以{}2,0,2A B =- .故选:D.2.B【分析】根据复数的运算求出z ,即可得出z 在复平面内所对应的点.【详解】由i i 1zz +=-,得()()()()i 1i 2i 1i 2i 2i 2z +++===--+13i 55--,所以z 在复平面内所对应的点是13,55⎛⎫-- ⎪⎝⎭.故选:B.3.C【分析】利用特殊值及极限思想即可分析得出.【详解】由1110242f ⎛⎫⎫--< ⎪⎪⎝⎭⎭,故D 错误,当x →+∞时,()0f x →,A ,B 错误.故选:C.4.A【分析】由平面向量的坐标运算求得AB,a b - ,结合平面向量的夹角公式即可求得答案.【详解】由题意,得()1,2AB =- ,()3,0a b -=-,则AB与a b - 的夹角的余弦值为()AB a b ABa b ⋅-==- .故选:A .5.B【分析】不妨设双曲线方程为22221x y a b-=()0,0a b >>,表示出双曲线的渐近线方程,根据双曲线的定义得到3a =,再利用点到直线的距离公式求出b ,从而求出c ,即可得解.【详解】解:不妨设双曲线方程为22221x y a b-=()0,0a b >>,则双曲线的渐近线方程为by x a=±,即0bx ay ±=,由双曲线的定义知,26a =,所以3a =,由双曲线C 的焦点到其渐近线的距离为44b ==,所以5c =,所以C 的离心率53ce a==.故选:B 6.C【分析】根据折线图数据,结合中位数、极差的定义依次判断各个选项即可.【详解】对于A ,平均高温不低于30C 的月份有2021年6,7,8月和2022年6月,共4个,A 错误;对于B ,将各个月份数据按照从小到大顺序排序后,可得中位数为202120.5C 2+= ,B 错误;对于C ,平均高温的极差为36630C -= ,平均低温的极差为()24327C --=,则平均高温的极差大于平均低温的极差,C 正确;对于D ,月平均高温与低温之差不超过10C 的月份有2021年7,8,9,10月和2022年1,2月,共6个,D 错误.故选:C.7.C【分析】目标函数22z x y =--的几何意义是可行域内的点到直线l :220x y --=的距离l 的距离最大的点,求解即可.【详解】由约束条件作出可行域,如图中阴影部分所示.由点到直线的距离公可知,目标函数22z x y =--的几何意义是可行域内的点到直线l :220x y --=数形结合可知,可行域内到直线l 的距离最大的点为()1,0A -,且点A 到直线l 的距离d ==则22z x y =--的最大值为4.故选:C.8.C【分析】列举出每次算法步骤,即可得出输出结果.【详解】执行第一次循环,[]3.141 3.14 5.14b =-+=,[]5.1414a =-=,2n =,5.14 1.14110.2850.0544b a -=-==>;执行第二次循环,[]41 5.148.14b =-+=,[]8.1417a =-=,3n =,8.14 1.14110.1630.0577b a -=-=≈>;执行第三次循环,[]718.1414.14b =-+=,[]14.14113a =-=,4n =,14.14 1.14110.0880.051313b a -=-=≈>;执行第四次循环,[]13114.1426.14b =-+=,[]26.14125a =-=,5n =,26.14 1.14110.04560.052525b a -=-==<,退出循环,输出5n =.故选:C.9.D【分析】由1113b a S ===,24439b a S S ==-=,求出等比数列{}n b 的公比q 及n b ,数列1n b ⎧⎫⎨⎩⎭也是等比数列,利用等比数列求和公式可求出答案.【详解】因为1113b a S ===,24439b a S S ==-=,所以等比数列{}n b 的公比3q =,所以1333n nn b -=⨯=,则113nn b ⎛⎫= ⎪⎝⎭,由11113n n b b +=⋅,可知数列1n b ⎧⎫⎨⎬⎩⎭是以13为首项,13为公比的等比数列,所以111111333122313nnn T ⎛⎫-⋅ ⎪⎛⎫⎝⎭==-⋅ ⎪⎝⎭-.故选:D .10.C【分析】连接1BC ,即可得到111A E B C ⊥,再由正三棱柱的性质得到1A E ⊥平面11BB C C ,即可得到11A E B C ⊥,从而得到1B C ⊥平面1A DE ,再由线面垂直的性质得到11B C A D ⊥,即可说明1BF B C ⊥,即可判断①、②、③,连接1C F ,通过证明平面1//A DE 平面1BFC ,即可说明④.【详解】解:连接1BC ,因为正三棱柱111ABC A B C -的所有棱长都相等,所以111A E B C ⊥,11B C BC ⊥.又D ,E 分别是1BB ,11B C 的中点,所以1//DE BC ,所以1B C DE ⊥.因为11A E CC ⊥,1111B C CC C ⋂=,11B C ,1CC ⊂平面11BB C C ,所以1A E ⊥平面11BB C C .又1B C ⊂平面11BB C C ,所以11A E B C ⊥.又1DE A E E ⋂=,DE ,1A E ⊂平面1A DE ,所以1B C ⊥平面1A DE .又1A D ⊂平面1A DE ,所以11B C A D ⊥.由题意知1//A F BD 且1A F BD =,所以四边形1A FBD 是平行四边形,所以1//BF A D ,所以1BF B C ⊥,故①、③正确;BF 与1C D 是异面直线,故②错误;连接1C F ,因为1//BF A D ,BF ⊂平面1BFC ,1A D ⊄平面1BFC ,所以1A D //平面1BFC 又1//DE BC ,同理可证//DE 平面1BFC ,又1A D DE D ⋂=,1,A D DE ⊂平面1A DE ,所以平面1//A DE 平面1BFC .因为M 是线段BF 上的动点,所以1C M ⊂平面1BFC ,所以1//C M 平面1A DE ,故④正确.故选:C 11.D【分析】由商数关系化简函数,结合导数法可得函数性质及图象,即可逐个判断.【详解】因为()22sin tan cos sin sin tan 1sin 1cos xx x f x x x x x x =+=++⎛⎫+ ⎪⎝⎭πsin sin cos π,2x x x x k k ⎛⎫=+≠+∈ ⎪⎝⎭Z ,所以()()()22cos cos 12cos 1cos 1f x x x x x '=+-=-⋅+.当ππ,22x ⎛⎫∈- ⎪⎝⎭时,令()0f x '=,解得π3x =±,则当x 变化时,()f x ',()f x 的变化情况如下表所示.所以()f x 在区间ππ,22⎛⎫- ⎪⎝⎭上的图象如图所示.对A ,()f x 在区间ππ,33⎛⎫- ⎪⎝⎭上单调递增,A 错;对B ,()f x 在区间π0,2⎛⎫ ⎪⎝⎭上有极大值,无极小值,B 错;对C ,()()2g x f x =-在区间ππ,22⎛⎫- ⎪⎝⎭上的最大值为2M =,最小值为2m =,4M m +=-,C 错;对D ,()f x 在区间ππ,22⎛⎫- ⎪⎝⎭内有且只有一个零点,D 对.故选:D.12.B【分析】设底面ABC 的中心为Q ,根据题意可知,当三棱锥P -ABC 的体积取得最大值时,PQ ⊥底面ABC ,求出体积的最大值,再利用等体积法求出内切球的半径即可.【详解】设底面ABC 的中心为Q ,连接BQ ,OQ ,则233BQ ==OQ ⊥底面ABC ,如图,延长QO 交球面于点P ,连接OB ,此时三棱锥P -ABC 的体积取得最大值,因为球O 的半径为2,所以2OB =,在Rt OQB 中,1OQ ==,所以三棱锥P -ABC 的体积的最大值为()213213V =⨯+=此时PB =所以2133312P ABCS -=+⨯⨯=,所以11434r =⨯⨯,解得r =故选:B.13.72【分析】求导后可得n a ,结合对数运算法则可求得结果.【详解】()1n f x nx n -'=+ ,()12f n '∴=,即2n a n =,()()274216427log log 432log 22a a ∴=⨯==.故答案为:72.14.221x y +=或229x y +=【分析】根据两圆内切与外切的条件求解即可.【详解】圆C :22430x y y +-+=的圆心为()0,2,半径为1.因为两圆圆心距为2,故若两圆外切,则所求圆的半径为211-=,其标准方程为221x y +=;若两圆内切,则所求圆的半径为213+=,其标准方程为229x y +=.故答案为:221x y +=或229x y +=15.12##0.5【分析】根据实数满足的表达式,将表达式转化成直线和抛物线形式,求出解抛物线上到直线距离最近的点,即可求得()()22m a n b -+-的最小值.【详解】由题意知,(),a b 是直线l :20x y --=上的点,(),m n 是抛物线21:4C y x =上的点,()()22m a n b -+-的几何意义是抛物线C 上的点到直线l 上的点的距离的平方.设0x y c -+=与抛物线相切,切点为0,0()P x y 则12y x '=,即0112x =,所以直线与C 切于点()2,1,所以()()22m a n b -+-的最小值为212=.故答案为:1216.5-()()5,44,5--È【分析】由()()f x f x -=-可求出m n +的值;画出()y f x =的图象,由方程()()f x a a R =∈有两个不同的实数根,即()y f x =的图象与y a =的图象由两个交点,结合图象即可得出答案.【详解】令0x <,则0x ->,所以()222x xf x -+-=+.因为()f x 是定义在R 上的奇函数,所以()()f x f x -=-,所以()222422x x x xf x +--=--=-⨯-,所以4m =-,1n =-,则5m n +=-,故()42,020,0,14202x x x x x f x x x ⎧+>⎪⎪⎪==⎨⎪⎛⎫⎪-⋅+< ⎪⎝⎭⎩,当0x >时,()422xx f x =+,令2xt =,则()41y t t t=+>.因为当()0,1x ∈时,2x t =单调递增,且()1,2t ∈,此时4y t t=+单调递减,所以由复合函数的单调性可知()422xx f x =+在区间()0,1上单调递减;因为当()1,x ∈+∞时,2x t =单调递增,且()2,t ∈+∞,此时4y t t=+单调递增,所以由复合函数的单调性可知()422xxf x =+,在区间()1,+∞上单调递增.由奇函数图象的特点作出()y f x =与y a =的图象如下:由图知,若()f x a =有两个不同的实数根,相当于()y f x =与y a =有两个不同的交点,则54a -<<-或45a <<.故答案为:-5;()()5,44,5--È.17.(1)π3(2)2⎛ ⎝【分析】(1是2a 与πsin 6C ⎛⎫+ ⎪⎝⎭的等比中项可得2π2sin 6a C b c ⎛⎫+==+ ⎪⎝⎭,由正弦定理及两角和的正弦公式化简即可求出A ﹔(2)由正弦定理表示出13sin 2tan a B C ⎛==+ ⎝,结合tan y x =的单调性即可得出答案.【详解】(1)是2a 与πsin 6C ⎛⎫+ ⎪⎝⎭的等比中项,所以2π2sin 6a C b c ⎛⎫+==+ ⎪⎝⎭,由正弦定理及两角和的正弦公式,得12sin cos sin sin 22A C C B C ⎛⎫⋅+=+ ⎪ ⎪⎝⎭.因为πA B C ++=,()sin sin cos sin sin sin cos cos sin sin A C A C A C C A C A C C +=++=++,()sin cos 1sin A C A C =+.因为()0,πC ∈,所以sin 0C ≠,cos 1A A -=,即π1sin 62A ⎛⎫-= ⎪⎝⎭.又()0,πA ∈,所以ππ5π,666A ⎛⎫-∈- ⎪⎝⎭,所以ππ66A -=,即π3A =.(2)由正弦定理,得2πsin sin sin 3a b B C ==,所以2π3sin 2sin sin C B a B b CC ⎛⎫- ⎪⎝⎭===3cos 132sin 2tan C C C C+⎛==+⎝.因为ABC 是锐角三角形,所以2ππ032π0,2C C ⎧<-<⎪⎪⎨⎪<<⎪⎩所以ππ62C <<,所以tan C >所以sin a B的取值范围是⎝.18.(1)有99%的把握认为学生的数学竞赛成绩与是否参加“强基培优”拓展培训有关.(2)35【分析】(1)根据表中数据和参考公式代入计算并与6.635比较即可得出结论;(2)由分层抽样可知参加过培训的有4人,未参加过的有2人,列举出6人中随机抽取2人的所有基本事件,再选出符合条件的事件数即可求得结果.【详解】(1))根据列联表代入计算可得:()221004030201050604050503K ⨯⨯-⨯==≈⨯⨯⨯16.667 6.635>,所以有99%的把握认为学生的数学竞赛成绩与是否参加“强基培优”拓展培训有关.(2)由题意可知,所抽取的6名学生中参加过“强基培优”拓展培训的有4人,记为1A ,2A ,3A ,4A ,未参加过“强基培优”拓展培训的有2人,设为甲、乙.从这6人中随机抽取2人的所有基本事件有{}12,A A ,{}13,A A ,{}14,A A ,{}1,A 甲,{}1,A 乙,{}23,A A ,{}24,A A ,{}2,A 甲,{}2,A 乙,{}34,A A ,{}3,A 甲,{}3,A 乙,{}4,A 甲,{}4,A 乙,{},甲乙,共15个,其中至少有一人未参加过培训的基本事件有{}1,A 甲,{}2,A 甲,{}3,A 甲,{}4,A 甲,{},甲乙,{}1,A 乙,{}2,A 乙,{}3,A 乙,{}4,A 乙,共9个.故至少有一人未参加过培训的概率93155P ==.19.(1)证明见解析12【分析】(1)利用三角形中位线性质和线面平行的判定可证得//PG 平面C DB ',//PF 平面C DB ',由面面平行的判定可证得结论;(2)取BD 的中点M ,根据已知的长度关系和面面垂直性质可证得C M '⊥平面ABD ,结合线面角定义可得tan C EM '∠=由此可确定E 点位置,从而求得GFED S 四边形,利用棱锥体积公式可求得结果.【详解】(1),,P G F 分别为,,AC AD AB '的中点,//PG C D '∴,//PF BC ',,PG PF ⊄ 平面C DB ',,C D BC ''⊂平面C DB ',//PG ∴平面C DB ',//PF 平面C DB ',又PG PF P ⋂=,,PG PF ⊂平面PGF ,∴平面//PGF 平面C DB '.(2)取BD 的中点M ,连接,C M EM ',2AB AD == ,60BAD ∠= ,ABD ∴ 为等边三角形,2BD ∴=,又BC C D ''==222BC C D BD ''∴+=,C DB '∴ 为等腰直角三角形,112C M BD '∴==,C M BD '⊥;二面角A BD C '--是直二面角,即平面C DB '⊥平面ABD ,平面C DB '⋂平面ABD BD =,C M '⊂平面C DB ',C M '∴⊥平面ABD ,C EM '∴∠即为C E '与平面ABD 所成角,1tan 3C M C EM EM EM ''∴∠==,解得:2EM =;在EMB △中,由余弦定理得:2222cos60EM BM BE BM BE =+-⋅ ,即2314BE BE =+-,解得:12BE =,E ∴为线段AB 上靠近点B 的四等分点,111442ABD AGF BDE ABD ABD ABD ABD GFED S S S S S S S S ∴=--=--= 四边形211222=⨯⨯⨯111113232P GFED GFED V S C M -'∴=⨯⨯=⨯⨯四棱锥四边形20.(1)答案见解析(2)(),ln 25-∞-【分析】(1)对()f x 求导,分0a ≥和a<0,讨论()f x 的单调性,即可得出对应的极值点的情况;(2)当2a =时,方程()()()0f x f x m m '++=∈R 有两个不相等的实数根,化简为1ln 22m x x x -=+++,即y m =-与1ln 22y x x x =+++的图象有两个交点,令()1ln 22h x x x x=+++,对()h x 求导,得出()h x 的单调性及最值即可得出答案.【详解】(1)函数()f x 的定义域为{}0x x >,()1f x a x'=+.当0a ≥时,()0f x ¢>,()f x 在区间()0,∞+上单调递增,所以()f x 无极值点;当a<0时,令()0f x '=,解得1x a=-,所以当x 变化时,()f x ',()f x 的变化情况如下表所示.x 10,a ⎛⎫- ⎪⎝⎭1a-1,a ∞⎛⎫-+ ⎪⎝⎭()f x '+0-()f x 单调递增极大值单调递减所以()f x 有一个极大值点,无极小值点.综上,当0a ≥时,()f x 无极值点;当a<0时,()f x 有一个极值点.(2)当2a =时,方程()()0f x f x m '++=,即1ln 220x x m x++++=,则1ln 22m x x x-=+++.令()1ln 22h x x x x =+++,0x >,则()()()22121112x x h x x x x +-'=+-=.令()0h x '=,解得12x =或=1x -(舍去).当10,2x ⎛⎫∈ ⎪⎝⎭时,()0h x '<,()h x 在区间10,2⎛⎫ ⎪⎝⎭上单调递减;当1,2x ⎛⎫∈+∞ ⎪⎝⎭时,()0h x '>,()h x 在区间1,2⎛⎫+∞ ⎪⎝⎭上单调递增,所以()()min 15ln 22h x h x h ⎛⎫≥==- ⎪⎝⎭,又x 趋近于0时()h x 趋近正无穷;x 趋近于正无穷时()h x 趋近正无穷,所以5ln 2m ->-,即ln 25m <-,故m 的取值范围是(),ln 25-∞-.21.(1)22143x y +=(2)证明见解析【分析】(1)由题意得332p-=-,从而得出椭圆C 的焦点()11,0F -,()21,0F ,由线段1PF 的中点为()2,0-求得2a =,23b =,可得C 的方程;(2)直线l 的斜率存在,设为k ,分两种情况讨论:当0k =时,直接验证结论;当0k ≠时,设出直线l 的方程,与椭圆方程联立,结合韦达定理求出线段AB 的中点坐标,得到线段AB 的垂直平分线的方程,求得M 坐标及1F M ,利用弦长公式求得AB ,从而证得结论.【详解】(1)抛物线E 的焦点,02p ⎛⎫ ⎪⎝⎭关于其准线2p x =-的对称点为3,02p ⎛⎫-⎪⎝⎭,所以332p-=-,即12p =.因为椭圆C 与抛物线E 有一个共同的焦点,所以()11,0F -,()21,0F ,所以线段1PF 的中点为()2,0-,所以2a =,222213b =-=.故C 的方程为22143x y +=.(2)由题意知,直线l 的斜率存在,设为k .当0k =时,点A ,B 恰为椭圆C 的左、右顶点,y 轴为线段AB 的垂直平分线,()0,0M ,24AB a ==,11F M c ==,则114F M AB=.当0k ≠时,直线l 的方程为()1y k x =+,设()11,A x y ,()22,B x y ,线段AB 的中点为()00,x y ,(),0M M x .联立()221,1,43y k x x y ⎧=+⎪⎨+=⎪⎩,消去y ,得()()2222438430k x k x k +++-=,则2122843k x x k +=-+,()21224343k x x k -=+,所以212024243x x k x k +==-+,则()2002243114343k ky k x k k k ⎛⎫=+=-+= ⎪++⎝⎭.由题意知,线段AB 的垂直平分线的方程为()001y y x x k-=--,令0y =,得200243M kx x ky k =+=-+,则221223314343k k F M k k +=-+=++.又12AB x =-=()2212143k k +=+,所以114F M AB=.综上,114F MAB =.22.(1)()(2221x y -+-=(2)当2m =-时,max 2MN =【分析】(1)消去参数方程中的参数α即可得到普通方程;(2)根据极坐标与直角坐标互化原则可确定1C 为直线,则当直线过圆心时,MN 最大,由此可求得结果.【详解】(1)由2cos sin x y αα=+⎧⎪⎨=+⎪⎩得:()(2221x y -+-=,即1C 的普通方程为:()(2221x y -+-=.(2)由22sin sin 12m θρθ⎛⎫+-= ⎪⎝⎭得:()sin cos sin cos m ρθθρθρθ-=-=,2C ∴的直角坐标方程为:0x y m -+=;当0x y m -+=过圆1C 的圆心(时,MN 取得最大值,即MN 为圆1C 的直径,20m ∴=,解得:2m =,则当2m =时,max 2MN=.23.(1)证明见解析(2)证明见解析【分析】(1)利用三元基本不等式依次证得01abc <≤与3331113a b c ++≥即可,要特别注意等号成立的条件;(2)利用基本不等式依次证得2223a b c ++≥与1113a b c++≥,从而证得()2221119a b c a b c ≥⎛⎫++++ ⎪⎝⎭,要特别注意等号成立的条件.【详解】(1)因为a ,b ,c 都是正实数,且3a b c ++=,所以3a b c =++≥01abc <≤,所以11abc≥,当且仅当a b c ==且3a b c ++=,即1a b c ===时,等号成立,故33311133a b c abc++≥≥,当且仅当333111a b c ==且1a b c ===,即1a b c ===时,等号成立,所以3331113a b c ++≥.(2)因为()()22222222223a b c a b c ab ac bc a b c ++=+++++≤++,3a b c ++=,所以2223a b c ++≥,当且仅当a b c ==且3a b c ++=,即1a b c ===时,等号成立;又()11111113a b c a b c a b c ⎛⎫++=++++ ⎪⎝⎭11113a a b b c c b c ac a b ⎛⎫=++++++++ ⎪⎝⎭113a b c a c b b a a c b c ⎡⎤⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦113⎛≥++ ⎝3=,当且仅当,,a b c a c b b a a c b c ===且3a b c ++=时,即1a b c ===时,等号成立,所以1113a b c++≥;故()2221119a b c a b c ≥⎛⎫++++ ⎪⎝⎭,当且仅当1a b c ===时,等号成立.。
2024年普通高等学校招生全国统一考试 新课标Ⅰ卷数学试卷养成良好的答题习惯,是决定成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
1.已知集合{}355A x x =-<<∣,{3,1,0,2,3}B =--,则A B =( ).A.{1,0}-B.{2,3}C.{3,1,0}--D.{1,0,2}- 2.若1i 1z z =+-,则z =( ). A.1i -- B.1i -+ C.1i - D.1i +3.已知向量(0,1)a =,(2,)b x =,若(4)b b a ⊥-,则x =( ).A.-2B.-1C.1D.24.已知cos()m αβ+=,tan tan 2αβ=,则cos()αβ-=( ).A.3m -B.3m -C.3mD.3m5.( ).A. B. C. D.6.已知函数22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩在R 上单调递增,则a 的取值范围是( ). A.(,0]-∞ B.[1,0]- C.[1,1]- D.[0,)+∞7.当[0,2π]x ∈时,曲线sin y x =与π2sin 36y x ⎛⎫=- ⎪⎝⎭的交点个数为( ). A.3 B.4 C.6 D.88.已知函数()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时,()f x x =,则下列结论中一定正确的是( ).A.(10)100f >B.(20)1000f >C.(10)1000f <D.(20)10000f <9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1X =,样本方差20.01S =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设失去出口后的亩收入Y 服从正态分布()2,N X S ,则( ).(若随机变量Z 服从正态分布()2,N μσ,则()0.8413P Z μμ<+≈)A.(2)0.2P X >>B.()0.5P X Z ><C.()0.5P Y Z >>D.()0.8P Y Z ><10.设函数2()(1)(4)f x x x =--,则( ).A.3x =是()f x 的极小值点B.当01x <<时,()2()f x f x <C.当12x <<时,4(21)0f x -<-<D.当110x -<<时,(2)()f x f x -> 11.造型可以看作图中的曲线C 的一部分,已知C 过坐标原点O ,且C 上的点满足横坐标大于-2,到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4,则( ).A.2a =-B.点0)在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点()00,x y 在C 上时,0042y x ≤+ 12.设双曲线2222:1x y C a b-=(0a >,0b >)的左右焦点分別为1F ,2F ,过2F 作平行于y 轴的直线交C 于A ,B 两点,若113F A =,||10AB =,则C 的离心率为_________.13.若曲线e x y x =+在点(0,1)处的切线也是曲线ln(1)y x a =++的切线,则a =_________.14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两个各自从自己持有的卡片中随机选一张,并比较所选卡片的数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛比赛后,甲的总得分小于2的概率为_________.15.记ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=.(1)求B ;(2)若ABC △的面积为3+,求c .16.已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x y C a b a b +=>>上两点. (1)求C 的率心率;(2)若过P 的直线l 交C 于另一点B ,且ABP △的面积为9,求l 的方程.17.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA PC ==,1BC =,AB =(1)若AD PB ⊥,证明://AD 平面PBC ;(2)若AD DC ⊥,且二面角A CP D --,求AD . 18.已知函数3()ln (1)2x f x ax b x x =++--.(1)若0b =,且()0f x '≥,求a 的最小值;(2)证明:曲线()y f x =是中心对称图形;(3)若()2f x >-,当且仅当12x <<,求b 的取值范围.19.设m 为正整数,数列1a ,2a ,…,42m a +是公差不为0的等差数列,若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列1a ,2a ,…,42m a +是(,)i j ——可分数列.(1)写出所有的(,)i j ,16i j ≤<≤,使数列1a ,2a ,…,6a 是(,)i j ——可分数列;(2)当3m ≥时,证明:数列1a ,2a ,…,42m a +足(2,13)——可分数列;(3)从1,2,…,42m +中一次任取两个数i 和()j i j <,记数列1a ,2a ,…,42m a +足(,)i j ——可分数列的概率为m P ,证明:18m P >.参考答案1.A解析:{1,0}A B =-,选A.2.C解析:3.D解析:4(2,4)b a x -=-,(4)b b a ⊥-,(4)0b b a ∴-=,4(4)0x x ∴+-=,2x ∴=,选D.4.A 解析:cos cos sin sin sin sin 2cos cos m αβαβαβαβ-=⎧⎪⎨=⎪⎩,sin sin 2cos cos m m αβαβ=-⎧∴⎨=-⎩,cos()cos cos sin sin 23m m m αβαβαβ-=+=--=-,选A.5.B解析:设它们底面半径为r ,圆锥母线l,2ππrl ∴=,l ∴==,3r ∴=,1π93V =⋅⋅=,选B.6.B解析:()f x 在R 上↗,00e ln1a a -≥⎧⎨-≤+⎩,10a ∴-≤≤,选B. 7.C解析:6个交点,选C.8.B解析:(1)1f =,(2)2f =,(3)(2)(1)3f f f >+=,(4)(3)(2)5f f f >+>,(5)(4)(3)8f f f >+>,(6)(5)(4)13f f f >+>,(7)(6)(5)21f f f >+>,(8)(7)(6)34f f f >+>,(9)(8)(7)55f f f >+>,(10)(9)(8)89f f f >+>,(11)(10)(9)144f f f >+>,(12)(11)(10)233f f f >+>,(13)(12)(11)377f f f >+>,(14)(13)(12)610f f f >+>,(15)(14)(13)987f f f >+>,(16)1000f >,(20)1000f ∴>,选B.9.BC解析:()2~ 1.8,0.1X N ,()2~ 2.1,0.1Y N ,2 1.820.12μσ=+⨯=+,(2)(2)()10.84130.1587P X P X P X μσμσ>=>+<>+=-=,A 错.(2)( 1.8)0.5P X P X ><>=,B 对.2 2.10.1μσ=-=-,(2)( 2.1)0.5P Y P Y >>>=,C 对.(2)()()0.84130.8P Y P Y P Y μσμσ>=>-=<+=>,D 错,所以选BC.10.ACD解析:A 对,因为()3(1)(3)f x x x '=--;B 错,因为当01x <<时()0f x '>且201x x <<<,所以()2()f x f x <;C 对,因为2(21)4(1)(25)0f x x x -=--<,2(21)44(2)(21)0f x x x -+=-->,2223(2)()(1)(2)(1)(4)(1)(22)2(1)f x f x x x x x x x x --=------=--+=--,11x -<<时,(2)()0f x f x -->,(2)()f x f x ->,D 对.11.ABD解析:A 对,因为O 在曲线上,所以O 到x a =的距离为a -,而2OF =,所以有242a a -⋅=⇒=-,那么曲线的方程为(4x +=.B对,因为代入0)知满足方程;C 错,因为2224(2)()2y x f x x ⎛⎫=--= ⎪+⎝⎭,求导得332()2(2)(2)f x x x '=---+,那么有(2)1f =,1(2)02f '=-<,于是在2x =的左侧必存在一小区间(2,2)ε-上满足()1f x >,因此最大值一定大于1; D 对,因为()22220000004442222y x y x x x ⎛⎫⎛⎫=--≤⇒≤ ⎪ ⎪+++⎝⎭⎝⎭. 12.32解析:由||10AB =知25F A =,即2225b c a a a-==,而121F F F A ⊥,所以1212F F =,即6c =,代回去解得4a =,所以32e =. 13.ln 2解析: 14.12 解析:甲出1一定输,所以最多3分,要得3分,就只有一种组合18-、32-、54-、76-.得2分有三类,分别列举如下:(1)出3和出5的赢,其余输:16-,32-,54-,78-(2)出3和出7的赢,其余输:14-,32-,58-,76-;18-,32-,56-,74-,16-,32-,58-,74-(3)出5和出7的赢,其余输:12-,38-,54-,76-;14-,38-,52-,76-;18-,34-,52-,76-;16-,38-,52-,74-;18-,36-,52-,74-;16-,38-,54-,72-;18-,36-,54-,72-共12种组合满足要求,而所有组合为24,所以甲得分不小于2的概率为1215.(1)π3B = (2)c =解析:(1)已知222a b c +-=,根据余弦定理222cos 2a b c C ab +-=,可得:cos 22C ab ==. 因为(0,π)C ∈,所以π4C =.又因为sin C B =,即πsin4B =,2B =,解得1cos 2B =. 因为(0,π)B ∈,所以π3B =. (2)由(1)知π3B =,π4C =,则ππ5πππ3412A B C =--=--=. 已知ABC △的面积为3+,且1sin 2ABC S ab C =△,则1πsin 324ab =1322ab ⨯=,2(3ab =+. 又由正弦定理sin sin sin a b c A B C ==,可得sin sin sin sin a C b C c A B==. 则π5πsin sin 412c a =,5πsin 12πsin 4c a =,同理πsin 3πsin 4c b =.所以2225ππsin sin 1232(3π1sin 42c c ab ⎝⎭===+解得c =16.(1)12(2)见解析解析:(1)将(0,3)A 、33,2P ⎛⎫ ⎪⎝⎭代入椭圆22220919941a b a b⎧+=⎪⎪⎨⎪+=⎪⎩,则22129a b ⎧=⎨=⎩c =12c e a ∴===.(2)①当L 的斜率不存在时,:3L x =,33,2B ⎛⎫- ⎪⎝⎭,3PB =,A 到PB 距离3d =, 此时1933922ABP S =⨯⨯=≠△不满足条件. ②当L 的斜率存在时,设3:(3)2PB y k x -=-,令()11,P x y 、()22,B x y , 223(3)21129y k x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,消y 可得()()22224324123636270k x k k x k k +--+--= 2122212224124336362743k k x x k k k x x k ⎧-+=⎪⎪+⎨--⎪=⎪+⎩,PB = 17.(1)证明见解析(2)AD =解析:(1)PA ⊥面ABCD ,AD ⊂平面ABCD ,PA AD ∴⊥又AD PB ⊥,PB PA P =,,PB PA ⊂平面P ABAD ∴⊥面PAB ,AB ∴⊂平面PAB ,AD AB ∴⊥ABC △中,222AB BC AC +=,AB BC ∴⊥ A ,B ,C ,D 四点共面,//AD BC ∴又BC ⊂平面PBC ,AD ⊄平面PBC//AD ∴平面PBC .(2)以DA ,DC 为x ,y 轴过D 作与平面ABCD 垂直的线为z 轴建立如图所示空间直角坐标系D xyz -令AD t =,则(,0,0)A t ,(,0,2)P t ,(0,0,0)D,DC =()C设平面ACP 的法向量()1111,,n x y z =不妨设1x =1y t =,10z =,()14,0n t =- 设平面CPD 的法向量为()2222,,n x y z =2200n DP n DC ⎧⋅=⎪⎨⋅=⎪⎩222200tx z +=⎧⎪∴=不妨设2z t =,则22x =-,20y =,2(2,0,)n t =-二面角A CP D --的正弦值7,则余弦值为7 1212122cos ,2n nn n n n t ⋅===t ∴=AD ∴=.18.(1)-2(2)证明见解析(3)23b ≥-解析:(1)0b =时,()ln 2x f x ax x =+-,11()02f x a x x'=++≥-对02x ∀<<恒成立 而11222(2)a a a x x x x ++=+≥+--, 当且仅当1x =时取“=”,故只需202a a +≥⇒≥-,即a 的最小值为-2.(2)方法一:(0,2)x ∈,(2)()f x f x -+332ln (2)(1)ln (1)22x x a x b x ax b x a x x-=+-+-+++-=- ()f x ∴关于(1,)a 中心对称.方法二:将()f x 向左平移一个单位31(1)ln(1)1x f x a x bx x +⇒+=+++-关于(0,)a 中心对称平移回去()f x ⇒关于(1,)a 中心对称.(3)()2f x >-当且仅当12x <<,(1)22f a ∴=-⇒=-3()ln 2(1)22x f x x b x x∴=-+->--对12x ∀<<恒成立 222112(1)2()23(1)3(1)(1)32(2)(2)x f x b x b x x b x x x x x x ⎡⎤-'=+-+-=+-=-+⎢⎥---⎣⎦令2()3(2)g x b x x =+-,∴必有2(1)2303g b b =+≥⇒≥-(必要性) 当23b ≥-时,对(1,2)x ∀∈,32()ln 2(1)()23x f x x x h x x ≥---=- 2222(1)1()2(1)2(1)10(2)(2)x h x x x x x x x ⎡⎤-'=--=-->⎢⎥--⎣⎦对(1,2)x ∀∈恒成立,()(1)2h x h ∴>=-符合条件, 综上:23b ≥-. 19.(1)(1,2),(1,6),(5,6)(2)证明见解析(3)证明见解析解析:(1)以下(,)i j 满足:(1,2),(1,6),(5,6)(2)易知:p a ,q a ,r a ,s a 等差,,,p q r s ⇔等差故只需证明:1,3,4,5,6,7,8,9,10,11,12,14可分分组为(1,4,7,10),(3,6,9,12),(5,8,11,14)即可其余k a ,1542k m ≤≤+,按连续4个为一组即可(3)由第(2)问易发现:1a ,2a ,…,42m a +是(,)i j 可分的1,2,42m ⇔+是(,)i j 可分的.易知:1,2,…,42m +是(41,42)k r ++可分的(0)k r m ≤≤≤因为可分为(1,2,3,4),…,(43,42,41,4)k k k k ---与(4(1)1,4(1),4(1)1,4(1)2)r r r r +-+++++,…,(41,4,41,42)m m m m -++ 此时共211C (1)(1)(2)2m m m m +++=++种 再证:1,2,…,42m +是(42,41)k r ++可分的(0)k r m ≤<≤易知1~4k 与42~42r m ++是可分的只需考虑41k +,43k +,44k +,…,41r -,4r ,42r +记*N p r k =-∈,只需证:1,3,5,…,41p -,4p ,42p +可分1~42p +去掉2与41p +观察:1p =时,1,3,4,6无法做到;2p =时,1,3,4,5,6,7,8,10,可以做到;3p =时,1,3,4,5,6,7,8,9,10,11,12,144p =时,1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,18(1,5,9,13),(3,7,11,15),(4,8,12,16),(6,10,14,18)满足故2p ∀≥,可划分为:(1,1,21,31)p p p +++,(3,3,23,33)p p p +++,(4,4,24,34)p p p +++,(5,5,25,35)p p p +++,…,(,2,3,4)p p p p ,(2,22,32,42)p p p p ++++,共p 组事实上,就是(,,2,3)i p i p i p i +++,1,2,3,,i p =,且把2换成42p +此时(,)k k p +,2p ≥均可行,共211C (1)2m m m m +-=-组 (0,1),(1,2),…,(1,)m m -不可行 综上,可行的(42,41)k r ++与(41,42)k r ++至少11(1)(1)(2)22m m m m -+++组 故()222224212221112C (21)(41)8618m m m m m m m m P m m m m +++++++≥==>++++,得证!。
2021年普通高等学校招生全国统一考试(全国乙卷) 数学(文)一、选择题1.已知全集{1,2,3,4,5}U =,集合{1,2}M =,{3,4}N =,则)(U C M N =( )A.{5}B.{1,2}C.{3,4}D.{1,2,3,4} 2.设43iz i =+,则z =( )A.34i --B.–34i +C.34i -D.34i +3.已知命题:,sin 1p x R x ∃∈<;命题||:,1x q x R e ∈∀≥,则下列命题中为真命题的是( ) A.p q ∧ B.p q ⌝∧ C.p q ∧⌝ D.()p q ⌝∨4.函数()sincos 33x xf x =+的最小正周期和最大值分别是( ) A.3πB.3π和2C.6πD.6π和25.若,x y 满足约束条件2,3,4,y x y x y ≤≤+≥⎧⎪-⎨⎪⎩则3z x y =+的最小值为( )A.18B.10C.6D.46.225coscos 1212ππ-=( ) A.12B.3C.2D.27.在区间1(0,)2随机取1个数,则取到的数小于13的概率为( ) A.34 B.23 C.13 D.168.下列函数中最小值为4的是( )A.224y x x =++ B.4|sin ||sin |y x x =+C.222x xy -=+ D.4n ln l y x x=+9.设函数1(1)xf x x-=+,则下列函数中为奇函数的是( ) A.1()1f x -- B.1()1f x -+ C.1()1f x +- D.1()1f x ++10.在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为A.2π B.3π C.4π D.6π 11.设B 是椭圆C :2215x y +=的上顶点,点P 在C 上,则PB 的最大值为A.52212.设0a ≠,若x a =为函数2()()()f x a x a x b =--的极大值点,则A.a b <B.a b >C.2ab a <D.2ab a > 二、填空题13.已知向量(2,5)a =,(,4)b λ=,若//a b ,则λ= .14.双曲线22145x y -=的右焦点到直线280x y +-=的距离为 .15.记ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,面积为,60B =︒,223a c ac +=,则b = .16.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).17.某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下: 旧设备 9.810.310.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7 新设备 10.1 10.410.110.010.110.310.610.510.410.5旧设备和新设备生产产品的该项指标的样本平均数分别记为x 和y ,样本方差分别记为21s 和22s .(1)求x ,y ,21s ,22s ;(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果2212210s s y x +-≥不认为有显著提高).18.如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ﹔(2)若1PD DC ==,求四棱锥P ABCD -的体积.19.设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a ,成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S ,和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <. 20.已知抛物线C :22(0)y px p =>的焦点F 到准线的距离为2. (1)求C 的方程,(2)已知O 为坐标原点,点P 在C 上,点Q 满足9PQ QF =,求直线OQ 斜率的最大值. 21.已知函数32()1f x x x ax =-++. (1)讨论()f x 的单调性;(2)求曲线()y f x =过坐标原点的切线与曲线()y f x =的公共点的坐标. 22.在直角坐标系xOy 中,C 的圆心为)(2,1C ,半径为1.(1)写出C 的一个参数方程;(2)过点)(4,1F 作C 的两条切线.以坐标原点为极点,x 轴正半轴为极轴建立坐标系,求这两条切线的极坐标方程. 23.已知函数()|||3|f x x a x =-++. (1)当1a =时,求不等式()6f x ≥的解集; (2)若()f x a >-,求a 的取值范围.答案及解析一、选择题1.已知全集{1,2,3,4,5}U =,集合{1,2}M =,{3,4}N =,则)(U C M N =( )A.{5}B.{1,2}C.{3,4}D.{1,2,3,4}2.设43iz i =+,则z =( ) A.34i -- B.–34i + C.34i - D.34i +3.已知命题:,sin 1p x R x ∃∈<;命题||:,1x q x R e ∈∀≥,则下列命题中为真命题的是( ) A.p q ∧B.p q ⌝∧C.p q ∧⌝D.()p q ⌝∨答案: A 解析:根据正弦函数的值域sin [1,1]x ∈-,sin 1x <,故x R ∃∈,p 为真命题,而函数||x y e =为偶函数,且0x ≥时,1x y e =≥,故x R ∀∈,||1x y e =≥恒成立.则q 也为真命题,所以p q∧为真,选A. 4.函数()sin cos 33x xf x =+的最小正周期和最大值分别是( )A.3πB.3π和2C.6πD.6π和2 答案: C 解析:()sin()34x f x π=+max ()f x =,2613T ππ==. 故选C.5.若,x y 满足约束条件2,3,4,y x y x y ≤≤+≥⎧⎪-⎨⎪⎩则3z x y =+的最小值为( )A.18B.10C.6D.4答案: C 解析:根据约束条件可得图像如下,3z x y =+的最小值,即3y x z =-+,y 轴截距最小值.根据图像可知3y x z =-+过点(1,3)B 时满足题意,即min 336z =+=.6.225cos cos 1212ππ-=( ) A.12B.33 C.22 3 答案: D 解析:2222223()sin cos 25cos cos cos cos cos 12121212121262ππππππππ-=-=--==∴选D. 7.在区间1(0,)2随机取1个数,则取到的数小于13的概率为( ) A.34 B.23 C.13 D.16答案: B解析:在区间1(0,)2随机取1个数,可知总长度12d =,取到的数小于13,可知取到的长度范围13d '=,根据几何概型公式123132d p d '===,∴选B.8.下列函数中最小值为4的是( ) A.224y x x =++ B.4|sin ||sin |y x x =+C.222x xy -=+D.4n ln l y x x=+答案: C 解析:对于A ,22224213(1)33y x x x x x =++=+++=++≥.不符合, 对于B ,4|sin ||sin |y x x =+,令|sin |[0,1]t x =∈,∴4y t t=+,根据对勾函数min 145y =+=不符合, 对于C ,242222x x x xy -==++,令20xt =>,∴4224y t t =+≥=⨯=, 当且仅当2t =时取等,符合,对于D ,4n ln l y x x =+,令ln t x R =∈,4y t t=+. 根据对勾函数(,4][4,)y ∈-∞-+∞,不符合.9.设函数1(1)xf x x-=+,则下列函数中为奇函数的是( ) A.1()1f x --B.1()1f x -+C.1()1f x +-D.1()1f x ++答案: B 解析:12()111x f x x x-==-+++, ()f x 向右平移一个单位,向上平移一个单位得到2()g x x=为奇函数. 所以选B.10.在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为A.2πB.3πC.4πD.6π 答案: D 解析:做出图形,11//AD BC ,所以1PBC ∠为异面直线所成角,设棱长为1.1BC,12B P =,12PC =,BP =. 2221111312cos 22BC BP C P PBC BP BC +-+-∠===⋅,即16PBC π∠=,故选D.11.设B 是椭圆C :2215x y +=的上顶点,点P 在C 上,则PB 的最大值为 A.526 5D.2 答案: A 解析:方法一:由22:15x C y +=,(0,1)B 则C 的参数方程:5sin x y θθ⎧=⎪⎨=⎪⎩.22||(sin 1)(5cos )PB θθ=-+24sin 2sin 6θθ=--+212554(sin )442θ=-++≥.∴max 5||2PB =,故选A. 方法二:设00(,)P x y ,则220001([1,1])5x y y +=∈-①,(0,1)B . 因此22200||(1)PB x y =+-②将①式代入②式化简得:22012525||4()444PB y =-++≥,当且仅当014y =-时||PB 的最大值为52,故选A.12.设0a ≠,若x a =为函数2()()()f x a x a x b =--的极大值点,则A.a b <B.a b >C.2ab a <D.2ab a > 答案: D 解析:2()2()()()()(32)f x a x a x b a x a a x a x b a '=--+-=---当0a >时,原函数先增再减后增.原函数在()0f x '=的较小零点时取得极大值. 即23a b a +<,即a b <,∴2a ab <. 当0a <时,原函数先减再增后减.原函数在()0f x '=的较大零点时取得极大值. 即23a b a +>,a b >,2a ab <,故选D. 二、填空题13.已知向量(2,5)a =,(,4)b λ=,若//a b ,则λ= . 答案:85解析:由已知//a b 可得82455λλ⨯=⇒=. 14.双曲线22145x y -=的右焦点到直线280x y +-=的距离为 . 答案:5解析:22145x y -=的右焦点为(3,0),到直线280x y +-=的距离22|38|512d -==+. 15.记ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,面积为3,60B =︒,223a c ac +=,则b = .答案:22解析: 由面积公式1sin 32S ac B ==,且60B =︒,解得4ac =, 又由余弦定理2222cos b a c ac B =+-,223a c ac +=,且0b > 解得22b =.16.以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).答案: ②⑤或③④ 解析:由高度可知,侧视图只能为②或③.侧视图为②,如图(1),平面PAC ⊥平面ABC ,2PA PC ==5BA BC ==2AC =,俯视图为⑤.俯视图为③,如图(2),PA ⊥平面ABC ,1PA =,5AC AB ==,2BC =,俯视图为④.17.某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下: 旧设备 9.810.310.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7 新设备 10.1 10.4 10.110.010.110.310.610.510.410.5旧设备和新设备生产产品的该项指标的样本平均数分别记为x 和y ,样本方差分别记为21s 和22s .(1)求x ,y ,21s ,22s ;(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果2212210s s y x +-≥不认为有显著提高). 答案:见解析 解析:9.810.31010.29.99.81010.110.29.71010x ++++++++==+;10.110.410.11010.110.310.610.510.410.510.310y ++++++++==+.211(0.040.090.040.010.040.010.040.09)10s =+++++++10.360.03610=⨯= 221(0.040.010.040.090.040.090.040.010.04)10s =++++++++10.40.0410=⨯=. (2)10.3100.3y x -=-=22120.0360.04221010s s ++=20.0076=. ∵则0.30.0920.0760.0304=>=,所以可判断新设备生产产品的该项指标的均值较旧设备有显著提高; 没有显著提高.18.如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ﹔(2)若1PD DC ==,求四棱锥P ABCD -的体积.答案: 见解析 解析:19.设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a ,成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S ,和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <. 答案: 见解析 解析:设{}n a 的公比为q ,则1n n a q -=,因为1a ,23a ,39a 成等差数列,所以21923q q +=⨯,解得13q =, 故11()3n n a -=,11313(1)12313n n n S -==--. 又3n n n b =,则1231123133333n n n n nT --=+++++,两边同乘13,则234111231333333n n n n nT +-=+++++,两式相减,得23412111113333333n n n nT +=+++++-,即1111(1)1133(1)332333121n n n n n n n T ++-=-=---, 整理得31323(1)4323423n n n nn n T +=--=-⨯⨯, 323314322()(1)04232323n n n n nn n T S ++-=---=-<⨯⨯,故2n n S T <.20.已知抛物线C :22(0)y px p =>的焦点F 到准线的距离为2. (1)求C 的方程,(2)已知O 为坐标原点,点P 在C 上,点Q 满足9PQ QF =,求直线OQ 斜率的最大值. 答案:见解析 解析:(1)由焦点到准线的距离为p ,则2p =. 抛物线c 的方程:24y x =.(2)设点200(,)4y P y ,(,)Q Q Q x y ,(1,0)F .∵9PQ QF =.∴222000009499(,)9(1,)4104910Q Q Q Q Q Q Q Q Q Q y y x x x y x y y x y y y x y y ⎧+⎪⎧-=-=⎪⎪--=--⇒⇒⎨⎨⎪⎪-=-⎩=⎪⎩则020001193944Q OQ Qy y k y y x y ===≤=++. ∴直线OQ 斜率的最大值为13. 21.已知函数32()1f x x x ax =-++. (1)讨论()f x 的单调性;(2)求曲线()y f x =过坐标原点的切线与曲线()y f x =的公共点的坐标. 答案: 见解析 解析:(1)2()32f x x x a '=-+(i )当4120a ∆=-≤,即13a ≥时,()0f x '≥恒成立,即()f x 在()f x 在x ∈R 上单调递增.(ii )当4120∆=->,即13a <时,()0f x '=解得,113x =,213x +=.∴()f x 在113(,)3a --∞,113()3a -+∞单调递增,在113113(33a a-+单调递减,综上所述:当13a ≥时,()f x 在R 上单调递增;当13a <时,()f x 在113113(,33a a-++单调递减.(2)设可原点切线的切点为32(,1)t t t at -++,切线斜率2()32k f t t t a '==-+.又321t t at k t -++=,可得322132t t at t t a t-++=-+.化简得2(1)(21)0t t t -++=,即1t =.∴切点为(1,1)a +,斜率1k a =+,切线方程为(1)y a x =+,将(1)y a x =+,321y x x ax =-++联立可得321(1)x x ax a x -++=+,化简得2(1)(1)0x x -+=,解得11x =,21x =-.∴过原点的切线与()y f x =公共点坐标为(1,1)a +,(1,1)a ---.22.在直角坐标系xOy 中,C 的圆心为)(2,1C ,半径为1.(1)写出C 的一个参数方程;(2)过点)(4,1F 作C 的两条切线.以坐标原点为极点,x 轴正半轴为极轴建立坐标系,求这两条切线的极坐标方程. 答案: 见解析 解析: (1)C 的参数方程为2cos 1sin x y θθ=+⎧⎨=+⎩(θ为参数)(2)C 的方程为22(2)(1)1x y -+-=①当直线斜率不存在时,直线方程为4x =,此时圆心到直线距离为2r >,舍去;②当直线斜率存在时,设直线方程为1(4)y k x -=-,化简为410kx y k --+=, 此时圆心(2,1)C 到直线的距离为1d r ===,化简得2||k =,两边平方有2241k k =+,所以k =代入直线方程并化简得40x -+=或40x +-=化为极坐标方程为5cos sin 4sin()46πρθθρθ=⇔+=或cos sin 4sin()46πρθθρθ+=⇔+=+23.已知函数()|||3|f x x a x =-++.(1)当1a =时,求不等式()6f x ≥的解集; (2)若()f x a >-,求a 的取值范围. 答案: 见解析 解析:当1a =时,()6|1||3|6f x x x ≥⇔-++≥,当3x ≤-时,不等式136x x ⇔---≥,解得4x ≤-; 当31x -<<时,不等式136x x ⇔-++≥,解得x ∈∅; 当1x ≥时,不等式136x x ⇔-++≥,解得2x ≥. 综上,原不等式的解集为(,4][2,)-∞-+∞. (2)若()f x a >-,即min ()f x a >-,因为()|||3||()(3)||3|f x x a x x a x a =-++≥--+=+(当且仅当()(3)0x a x -+≤时,等号成立),所以min ()|3|f x a =+,所以|3|a a +>-,即3a a +<或3a a +>-,解得3(,)2a ∈-+∞.。
绝密★启用前2017年普通高等学校招生全国统一考试宁夏文科数学试题注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{}{}123234A B ==,,, ,,, 则=A B A. {}123,4,, B. {}123,, C. {}234,, D. {}134,,2.(1+i )(2+i )=A.1-iB. 1+3iC. 3+iD.3+3i 3.函数()fx =πsin (2x+)3的最小正周期为A.4πB.2πC. πD. 2π4.设非零向量a ,b 满足+=-b b a a 则A a ⊥b B. =b a C. a ∥b D. >b a5.若a >1,则双曲线x y a=222-1的离心率的取值范围是A. ∞)B. )C. (1D. 12(,)6.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为 A.90π B.63π C.42π D.36π7.设x、y满足约束条件2+330233030x yx yy-≤⎧⎪-+≥⎨⎪+≥⎩。
则2z x y=+的最小值是A. -15B.-9C. 1 D 98.函数2()ln(28)f x x x=--的单调递增区间是A.(-∞,-2)B. (-∞,-1)C.(1, +∞)D. (4, +∞)9.甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则A.乙可以知道两人的成绩B.丁可能知道两人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩10.执行右面的程序框图,如果输入的a=-1,则输出的S=A.2B.3C.4D.511.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为A.110 B.15 C.310D.2512.过抛物线C:y 2=4x 的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN ⊥l,则M 到直线NF 的距离为A. B. C. D.二、填空题,本题共4小题,每小题5分,共20分. 13.函数()cos sin =2+fx x x 的最大值为 .14.已知函数()f x 是定义在R 上的奇函数,当x ()-,0∈∞时,()322=+f x x x ,则()2=f15.长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 16.△ABC 的内角A,B,C 的对边分别为a,b,c,若2b cosB=a cosC+c cosA,则B=三、解答题:共70分。
第1页(共18页) 2016-2017学年山西省运城市高三(上)期中数学试卷(文科) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)已知集合A={x|﹣1<x<3},B={x|0<x<4},则A∪B=( ) A.(﹣1,4) B.(﹣1,0) C.(0,3) D.(3,4) 2.(5分)已知向量=(2,m),=(m,2),若,则实数m等于( ) A.﹣2 B.2 C.﹣2或2 D.0 3.(5分)已知,且,则tanφ为( )
A. B. C. D. 4.(5分)若a>b>0,c<d<0,则一定有( ) A.ac>bd B.ac<bd C.ad<bc D.ad>bc
5.(5分)函数f(x)=满足f(x)=1的x值为( ) A.1 B.﹣1 C.1或﹣2 D.1或﹣1 6.(5分)把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图象向右平移个单位,这是对应于这个图象的解析式为( )
A. B. C. D. 7.(5分)设函数f(x)是奇函数,且在(0,+∞)内是增函数,又f(﹣3)=0,则f(x)<0的解集是( ) A.{x|﹣3<x<0或x>3} B.{x|x<﹣3或0<x<3} C.{x|x<﹣3或x>3} D.{x|﹣3<x<0或0<x<3} 8.(5分)设向量,满足,,,则=( ) A.2 B. C.4 D. 9.(5分)已知等比数列{an}中,a2a10=6a6,等差数列{bn}中,b4+b6=a6,则数列{bn}的前9项和为( ) 第2页(共18页)
A.9 B.27 C.54 D.72 10.(5分)已知函数f(x)=x2+cosx,f′(x)是函数f(x)的导函数,则f′(x)的图象大致是( )
A. B. C. D. 11.(5分)某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是( ) A.1800元 B.2400元 C.2800元 D.3100元 12.(5分)已知函数f(x)=x2+ex(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( ) A. B.(﹣e,e) C. D.(﹣∞,e)
二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.(5分)若一个幂函数f(x)图象过点,则= .
14.(5分)设数列{an}的前n项和为Sn,已知,则{an}的通项公式为 . 15.(5分)平面向量,,(m∈R),且与的夹角等于与的夹角,则m= . 16.(5分)如图,在△ABC中,∠ABC=90°,,BC=1,P为△ABC内一点,∠BPC=90°,∠APB=120°,则tan∠PBA= . 第3页(共18页)
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(10分)已知函数f(x)=x,x∈R.
(1)求; (2)求函数f(x)的最小正周期与单调减区间. 18.(12分)各项均为正数的数列{an},满足a1=1,a﹣a=2(n∈N*).
(1)求数列{an}的通项公式; (2)求数列{}的前n项和Sn. 19.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,且. (1)求角A的值; (2)若,BC边上中线,求△ABC的面积. 20.(12分)已知函数f(x)=xlnx+ax2﹣1,且f'(1)=﹣1. (1)求f(x)的解析式; (2)若对于任意x∈(0,+∞),都有f(x)﹣mx≤﹣1,求m的最小值. 21.(12分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳得到可利用的化工产品价值为100元. (1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低? (2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至 第4页(共18页)
少需要补贴多少元才能使该单位不亏损? 22.(12分)已知函数f(x)=(a∈R). (1)若a<0,求函数f(x)的极值; (2)当a≤1时,判断函数f(x)在区间[0,2]上零点的个数. 第5页(共18页) 2016-2017学年山西省运城市高三(上)期中数学试卷(文科) 参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)已知集合A={x|﹣1<x<3},B={x|0<x<4},则A∪B=( ) A.(﹣1,4) B.(﹣1,0) C.(0,3) D.(3,4) 【解答】解:∵A=(﹣1,3),B=(0,4), ∴A∪B=(﹣1,4), 故选:A.
2.(5分)已知向量=(2,m),=(m,2),若,则实数m等于( ) A.﹣2 B.2 C.﹣2或2 D.0 【解答】解:向量,,若, 可得m2=4,解得m=±2. 故选:C.
3.(5分)已知,且,则tanφ为( ) A. B. C. D. 【解答】解:∵已知=﹣sinφ,且, ∴sinφ=﹣,cosφ==, 则tanφ==﹣, 故选:C.
4.(5分)若a>b>0,c<d<0,则一定有( ) 第6页(共18页)
A.ac>bd B.ac<bd C.ad<bc D.ad>bc 【解答】解:若a>b>0,c<d<0,则: ac<bc<bd,故ac<bd, 故A错误,B正确; ad与bc的大小无法确定, 故C,D错误; 故选:B.
5.(5分)函数f(x)=满足f(x)=1的x值为( ) A.1 B.﹣1 C.1或﹣2 D.1或﹣1 【解答】解:函数f(x)=满足f(x)=1, 当x≤0时,2﹣x﹣1=1,解得x=﹣1, 当x>0时,=1,解得x=1. 故选:D.
6.(5分)把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图象向右平移个单位,这是对应于这个图象的解析式为( )
A. B. C. D. 【解答】解:函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变, 可以得到函数y=sin2x的图象, 再把图象向右平移个单位,以得到函数y=sin2(x﹣)=sin(2x﹣)的图象. 故选:A.
7.(5分)设函数f(x)是奇函数,且在(0,+∞)内是增函数,又f(﹣3)=0, 第7页(共18页)
则f(x)<0的解集是( ) A.{x|﹣3<x<0或x>3} B.{x|x<﹣3或0<x<3} C.{x|x<﹣3或x>3} D.{x|﹣3<x<0或0<x<3} 【解答】解:∵f(x)是奇函数,f(﹣3)=0, ∴f(﹣3)=﹣f(3)=0,解f(3)=0. ∵函数在(0,+∞)内是增函数, ∴当0<x<3时,f(x)<0. 当x>3时,f(x)>0, ∵函数f(x)是奇函数, ∴当﹣3<x<0时,f(x)>0. 当x<﹣3时,f(x)<0, 则不等式f(x)<0的解是0<x<3或x<﹣3. 故选:B.
8.(5分)设向量,满足,,,则=( ) A.2 B. C.4 D. 【解答】解:由,得,则, 由,得, ∴,得. ∴=4+4+4=12, 则=. 故选:B. 第8页(共18页)
9.(5分)已知等比数列{an}中,a2a10=6a6,等差数列{bn}中,b4+b6=a6,则数列{bn}的前9项和为( ) A.9 B.27 C.54 D.72 【解答】解:∵数列{an}是等比数列, ∴a2•a10=a62, 又a2a10=6a6, ∴a62=6a6, 解得a6=6. ∴b4+b6=a6=6. ∵数列{bn}是等差数列, ∴数列{bn}的前9项和S9====27. 故选:B.
10.(5分)已知函数f(x)=x2+cosx,f′(x)是函数f(x)的导函数,则f′(x)的图象大致是( )
A. B. C. D. 【解答】解:由于f(x)=x2+cosx, ∴f′(x)=x﹣sinx, ∴f′(﹣x)=﹣f′(x),故f′(x)为奇函数,其图象关于原点对称,排除BD, 又当x=时,f′()=﹣sin=﹣1<0,排除C,只有A适合, 故选:A. 第9页(共18页)
11.(5分)某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是( ) A.1800元 B.2400元 C.2800元 D.3100元 【解答】解:设分别生产甲乙两种产品为x桶,y桶,利润为z元
则根据题意可得,z=300x+400y 作出不等式组表示的平面区域,如图所示 作直线L:3x+4y=0,然后把直线向可行域平移, 由可得x=y=4, 此时z最大z=2800
12.(5分)已知函数f(x)=x2+ex(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( ) A. B.(﹣e,e) C. D.(﹣∞,e) 【解答】解:由题意,存在x<0, 使f(x)﹣g(﹣x)=0, 即ex﹣ln(﹣x+a)=0在(﹣∞,0)上有解, 令m(x)=ex﹣ln(﹣x+a), 则m(x)=ex﹣ln(﹣x+a)在其定义域上是增函数, 且x→﹣∞时,m(x)<0,