小学奥数：角度计算.专项练习

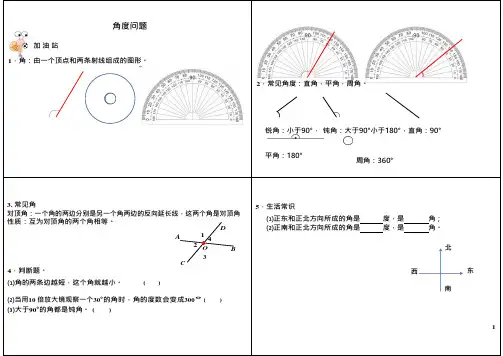
角度问题加油站1．角：由一个顶点和两条射线组成的图形。

2．常见角度：直角，平角，周角。

锐角：小于90°，钝角：大于90°小于180°，直角：90°平角：180°周角：360°3. 常见角对顶角：一个角的两边分别是另一个角两边的反向延长线，这两个角是对顶角性质：互为对顶角的两个角相等。

D 5．生活常识⑴正东和正北方向所成的角是度，是角；⑵正南和正北方向所成的角是度，是角。

4．判断题。

⑴角的两条边越短，这个角就越小。

( )A 1 42 O B 北3C西东南⑵当用10 倍放大镜观察一个30°的角时，角的度数会变成300°( )⑶大于90°的角都是钝角。

( )【铺垫】试用实例说明三角形内角和等于180°7. 常用结论加油站6．常用性质：三角形内角和＝180°内角＋外角＝180°31 231 2内角和＝内角和＝内角和＝n边形内角和（n－2）×180°【例1】(★★)如图所示，∠1＝120°，∠2＝100°，那么∠3＝度31 4 5 2【大海招牌菜】天太冷了，怎么能快速取暖呢？【例3】(★★★)如图所示，∠1＝30°，∠2＝60°，∠3比∠4大10°，∠4＝度。

【例2】(★★)试求下图中∠A的度数。

DCE 140°BA1 45 6 32题） 【例4】(★★)试求正六边形一个内角多少度？【例5】(★★)如图：一个正六边形和一个正方形的一条边重合在一起，那么∠1等于多少度？1【例6】(★★★★★)80°【金牌挑战】(★★★★★)（希望杯四年级一试试 如图，已知∠1＝2∠2，试求∠1和∠2 。

1260°70° 如图，∠1=∠2，∠3=∠4，∠5=130度，那么∠A = ( )度。

1 53 24本讲总结①常见角：周平直锐钝、对顶角②常用结论：n 边形内角和：（n －2）×180° ③正多边形：边相等，角相等 ④内角＋外角＝180°重点例题：例1，例3，例4，例6。

小学数学四年级上册角度换算专项练习题一、单项选择题1. 一个圆的周长等于长度为12 cm的一段线，这段线的长度是（）。

A. 12°B. 12 cmC. 12 mD. 12 mm2. 一个时钟的时针每小时转过（）。

A. 30°B. 60°C. 90°D. 180°3. 张三将一张纸对折两次，然后展开后，纸上有几个角（）？A. 1B. 2C. 3D. 44. 小明正在观察太阳从早上升起到午饭时间过去的时间，太阳大约转过了几个角（）？A. 1B. 2C. 3D. 4二、填空题1. 一周有（）天。

2. 直角的角度是（）°。

3. 一个全圆的角度是（）°。

4. 两个互为补角的角度和是（）。

5. 两个互为对顶角的角度和是（）。

三、解答题1. 小明观察了一个季节的一天里太阳升起和落下的时间，并画出了太阳位置的示意图。

根据图中的太阳位置，你能估计一天中太阳转过的角度吗？请说明估计过程和答案。

2. 阅读下面的信息，回答问题。

一个环由一段圆的弯曲的线段和一段直线连接构成。

在环的直线部分上，量角器测得的角度为120°。

求环上弯曲的线段相对于圆心的角度是多少？请说明求解步骤和答案。

四、应用题1. 根据实际长度估算下面各物品所对应的夹角，并填充到对应的表格中。

物品 | 实际长度（cm） | 夹角（°）---|---|---长方形 | 10 |圆 | 6 |正方形 | 8 |三角形 | 5 |2. 小明正在进行一项科学实验，他用手指估算他和试管之间的夹角。

他伸直手指，将试管放在手指前方，然后通过观察试管和相邻的物体比较，估算出试管和他中指之间的夹角大约是多少度？五、综合题用尺测量小花家中养的鹅的起居室的长度是3米，小花发现其长度约等于鹅笼左侧竖杆到笼顶的长度。

同时，她还观察到鹅笼左侧竖杆与笼底水平杆之间的夹角是100°。

请你帮小花算一算，鹅笼右侧竖杆与笼底水平杆之间的夹角是多少度？参考答案一、单项选择题1. B2. D3. D4. C二、填空题1. 72. 903. 3604. 905. 180三、解答题1. 太阳从早上升起到午饭时间过去的时间大约为半个圆的角度。

人教版小学三年级上册数学专项练习：角
度练习题
本文档为人教版小学三年级上册数学专项练，重点针对角度的练题。

下面是一些角度练题的例子，供学生们练和巩固对角度的理解。

1. 请你用直尺和量角器画出下列角度：
a) 45度
b) 90度
c) 120度
d) 180度
2. 用图中已知的角度，回答下列问题：
a) 图中的角度A是多少度？
b) 图中的角度B是多少度？
c) 图中的角度C是多少度？
3. 用图所示的角度关系，判断下列说法是否正确：
a) 若角度D和角度E互为补角，则它们的和是180度。

b) 若角度F是直角，则角度G是锐角。

c) 若角度H是钝角，则角度I是锐角。

4. 下面的角度是锐角、直角、钝角还是平角？
a) 30度
b) 60度
c) 90度
d) 135度
5. 按照大小关系，从小到大或从大到小，排列下列角度：
a) 25度、90度、120度、45度
b) 80度、110度、60度、130度
这些练习题可以帮助学生们巩固对角度的认识和运用，在解答
过程中培养他们思维能力和逻辑思维能力。

提醒学生们在解答过程
中注意使用直尺、量角器等工具，合理排列计算步骤，并仔细审题。

愿这些练习题对学生们的学习有所帮助。

小学奥数练习卷（知识点：长度和角度）注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）一．选择题（共2小题）1．在如图的三角形ABC中，EB=ED，FC=FD，∠EDF=72°，则∠AED+∠AFD=（）A．200°B．216°C．224°D．240°2．如果一个三角形的两个内角和等于第三个内角，那么这个三角形一定是（）A．等腰三角形B．锐角三角形C．直角三角形D．钝角三角形第Ⅱ卷（非选择题）二．填空题（共43小题）3．如图，把一个边长是5cm的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向移动其中的4个长方形，则所得图形的周长是cm．4．如图所示，∠1+∠5=∠2+∠4=∠3，那么∠3=度．5．直线上有A、B、C三个点，AB长26厘米，BC长18厘米，那么线段AC的长是厘米．6．点P是面积为168的四边形ABCD内一点，满足PA=9，PB=PD=12，PC=5，四边形ABCD的周长为．7．如图，在正五边形ABCDE中，∠CAD=．8．如图所示，∠l=∠2，∠3=∠4，如果∠A=68°，那么∠E=9．如图，已知ABCDEFGHI为正九边形，那么∠DIG=度．10．已知α是锐角，β是钝角，4位同学在计算0.25（α+β）时，得到的结果依次是15.2°、45.3°、78.6°、112°，其中可能正确的是．11．一个正方形和一个长方形的周长相等，长方形长是7分米，宽是5分米，正方形的面积是平方分米．12．如图，长方形周长20，面积24．另一个长方形，面积为20，周长为24．它的长为是．13．如图所示，一根吸管竖直插在水杯中，此时，吸管的斜置部分与水平线的夹角是30度，那么竖直部分与斜置部分之间的夹角（小于180度的角）是度．14．如图中，AB=5厘米，∠ABC=85°，∠BCA=45°，∠DBC=20°，AD=厘米．15．图中，AB=AD，∠DBC=21°，∠ACB=39°，则∠ABC=度．16．如图，O，P，M是线段AB上的三个点，AO=AB，BP=AB，M是AB的中点，且OM=2，那么PM 长为．17．如图，长方形ABCD的长AB为20厘米，宽BC为16厘米，长方形内放着两个重叠的正方形DEFG和BHIJ，已知三个阴影长方形的周长相等，那么长方形INFM的面积为平方厘米．18．如图，∠A=80°，∠ABO=30°，∠OCD=50°，∠D=度．19．如图，一个大三角形ABC被三条线段分成了七部分，其中四部分是三角形，另外三部分是四边形，三个四边形的周长之和为25厘米，四个三角形的周长之和为20厘米，三角形ABC的周长为19厘米，那么AD+BE+CF=厘米．20．如图所示，BD，CE分别是∠ABC的角平分线，如果∠BAC=62°，那么，∠BFC=°．21．如图，∠E=30°则∠A+∠B+∠C+∠D+∠E+∠F=．22．如图所示，已知∠ABC=90度，∠1+∠2=∠3，那么∠3=度．23．一张正方形的纸片，如图进行两次对折，折成一个小正方形，从右下角的顶点，沿斜虚线剪去一个角（如图三）剪下的实际是四个小三角形，再把余下的部分展开，展开后的这个图形的内角和是度．24．角可以用它的两边上的两个大写字母和顶点的字母表示，如图1的∠AOB 符号（“∠”表示角）也可以用∠O表示（顶点处只有一个角时）．如图2的三角形ABC中，∠BAO=∠CAO，∠CBO=∠ABO，∠ACO=∠BCO，∠AOC=110°则∠CBO=．25．如图，∠1=∠2=∠3=∠4=∠5=∠6=30°，则图中所有锐角度数的和是．26．已知一个等腰三角形的最大角是最小角的4倍，那么最大角与最小角的差是度．27．如图，在△ABC中，已知AB=AC，AE⊥BC，CD=CA，AD=DB，则角DAE=度．28．如图，所有的角度都已标注在图中，∠α=．29．如图，把左边4颗钉子围起来用去的绳子比把右边6颗钉子围起来用去的绳子短4厘米，把左边4颗钉子围起来用去绳子厘米．30．如图，∠1=∠2=60 度，那么，∠AOD 的大小是度．31．用180°与五边形的每一个内角作差，所得到的值叫做这个内角的角亏．如图所示五边形所有内角角亏之和为度．32．如图，∠B=30°，∠D=20°，∠A=60°，则∠BCD（图中有圆弧部分的那个角）的度数为°．33．如图，在长方形ABCD中，BC边的中点为E．小明从A走到B再到E，走了22米．小白从D到A再到B最后到E，走了32米．那么这个长方形的周长是米．34．如图，在三角形ABC中，点D在BC边上，且∠ABC=∠ACB，∠ADC=∠DAC，∠DAB=21°，则∠ABC的度数是．35．如图，在一个正六边形的内部有一个正五边形，那么∠1的度数是．36．如图有8条边，要求它的周长，至少要测量条边的长度．37．A、B、C、D四个点从左向右依次排在一条直线上，以这四个点为端点，可以组成六条线段，已知这六条线段的长度分别是12、18、30、32、44、62 （单位：厘米），那么线段BC的长度是厘米．38．有A、B、C、D四个点从左向右依次排在一条直线上．以这四个点为端点，可以组成6条线段．已知这6条线段的长度分别是14、21、34、35、48、69 （单位：毫米），那么线段BC的长度是毫米．39．如图．有一只蚂蚁从A点出发，按顺时针方向沿着图中实线爬行，最后又回到了A点．如果不计算在B，C，D处原地转向时转过的角度，则这只蚂蚁在行进过程中共转过的角度为．40．如图，∠A+∠B+∠C+∠D+∠E+∠F=．41．如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=度．42．等腰直角三角形中两个锐角的和是度．43．等腰三角形的一个内角是50度，另外两个内角可能是度和度，也可能是度和度．44．一根长30厘米的铁丝，可以围成种不同的长方形（边长是整厘米数）．45．直线上依次分布着A、B、C、D、E共5个点，已知AB=19cm，CE=97cm，AC=BD．那么DE=cm．三．解答题（共5小题）46．如图，已知AD=100，BD=65，AC=75．求BC．47．阅读材料：我们知道“两点之间线段最短”，如图1所示，AB两点之间，线段AB最短，由此结论可知：在三角形中，任意两边之和大于第三边，任意两边之差小于第三边．根据以上结论：（1）若三角形三边分別为2，3．x，那么，边长x不可能为．A、2B、3C、4D、6（2）若三角形三边分別为5，7，x，则x的范围是＜x＜；（3）如图2，线段AB、CD交于点o，比较AC+BD与AB+CD的大小关系并简要说明理由；（4）如图3，四边形处ABCD的对角线AC与BD相交于点E，比校2（AC+BD）和AB+BC+CD+DA的大小关系并简单说明理由．．．．．．．48．三角形的内角和是不变的，即在任意三角形ABC中，∠A+∠B+∠C=180°．利用三角形内角和是180度这一性质，可以推出一个非常重要的结论：三角形的一个外角等于和它不相邻的两个内角的和，如图所示：∠A+∠B=∠ACD．根据以上内容，解答下面的题目：（1）已知在三角形ABC 中，∠C=80°，∠A﹣∠B=20°，那么∠B的度数是．A.60° B.30° C.20° D.40°（2）如图2，P是三角形ABC内一点，比较∠BPC与∠A的大小并简单说明理由．（3）如图3，∠1=27.5°，∠2=95°，3=38.5°，那么∠4=．49．如图是一个三角形纸片折叠后的平面图形，折痕为DE，已知：∠B=74°，∠A=70°，∠CEB=20°，那么∠ADC等于多少度？50．三角形的内角和是不变的，即在任意三角形ABC中，∠A+∠B+∠C=180°，剩用三角形内角和是180度这一性质，可以推出一个非常重要的结论：三角形的一个外角等于和它不相邻的两个内角的和，如图1所示：∠A+∠B=∠ACD 根据内容，解答下面的题目：（1）已知在三角形ABC中，∠C=80°，∠A﹣∠B=20°，那么∠B的度数是．A.60° B.30° C.20° D.40°（2）如图2，P是三角形ABC内一点，比较∠BPC与∠A的大小并简单说明理由．（3）如图3，∠1=27.5，∠2=95°，∠3=38.5°，那么∠4=．（4）如图4，在三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在三角形ABC内，如果∠1=20°，那么∠2=．参考答案与试题解析一．选择题（共2小题）1．在如图的三角形ABC中，EB=ED，FC=FD，∠EDF=72°，则∠AED+∠AFD=（）A．200°B．216°C．224°D．240°【分析】由题意，∠B=∠EDB，∠C=∠FDC，再利用内角和，即可得出结论．【解答】解：由题意，∠B=∠EDB，∠C=∠FDC，∴∠AED+∠AFD=360°﹣（∠A+∠EDF）=360°﹣（∠A+∠EDF）=360°﹣（180°﹣∠B﹣∠C+∠EDF）=180°+∠B+∠C﹣∠EDF=180°+∠EDB+∠FDC﹣∠EDF=180°+180°﹣∠EDF﹣∠EDF=360°﹣2×72°=216°，故选：B．【点评】本题考查角度的计算，考查等腰三角形的性质，正确转化是关键．2．如果一个三角形的两个内角和等于第三个内角，那么这个三角形一定是（）A．等腰三角形B．锐角三角形C．直角三角形D．钝角三角形【分析】因为三角形的内角和为180度，如果一个三角形的两个内角和等于第三个内角，则第三个内角度数的2倍为180度，即可求出第三个内角的度数，据此判断出该三角形为何种三角形即可．【解答】解：180÷2=90（度），答：这个三角形一定是直角三角形．故选：C．【点评】此题主要考查利用三角形内角和为180度，根据已知条件求出一个角的度数，判断何种三角形．二．填空题（共43小题）3．如图，把一个边长是5cm的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向移动其中的4个长方形，则所得图形的周长是40cm．【分析】本题考察图形边长的平移．【解答】解：画出移动后的图，所得图形的周长是5×2+（5+1×2+2×2+3×2+4×2+5）=10+30=40cm．【点评】本题主要抓住平移后的图形每条边边长为多少即可求解．4．如图所示，∠1+∠5=∠2+∠4=∠3，那么∠3=60度．【分析】最下面一根直线上方的整个180度可以看成是由（1+1+1）倍的∠3组成的，所以∠3=180÷3=60度．【解答】解：因为∠1+∠5=∠2+∠4=∠3，所以平角相当于∠3的3倍，∠3=180÷3=60（度）故答案为：60．【点评】本题关键是根据等量代换把∠1+∠5、∠2+∠4都换成∠3，然后再根据和倍公式解答即可．5．直线上有A、B、C三个点，AB长26厘米，BC长18厘米，那么线段AC的长是8或44厘米．【分析】根据上图两种情况解答即可．【解答】解：①C在线段AB上，AC的长是：26﹣18=8（厘米）②C在线段AB的延长线上，AC的长是：26+18=44（厘米）故答案为：8或44．【点评】本题考查了两点间距离的计算，灵活利用数形结合的思想和分情况讨论的思想是解答的关键．6．点P是面积为168的四边形ABCD内一点，满足PA=9，PB=PD=12，PC=5，四边形ABCD的周长为56．【分析】由题意，由于12×（9+5）=168，所以可得P为对角线AC与BD的交点，且AC与BD垂直时，结论成立，利用勾股定理可得结论．【解答】解：由题意，由于12×（9+5）=168，所以可得P为对角线AC与BD 的交点，且AC与BD垂直时，结论成立，所以由勾股定理可得AD=AB==15，BC=CD==13，所以四边形ABCD的周长为15×2+13×2=56，故答案为56．【点评】本题给出四边形满足的条件，求四边形的周长，考查勾股定理的运用，确定P的位置是解题的关键．7．如图，在正五边形ABCDE中，∠CAD=36°．【分析】首先可根据五边形内角和公式求出每个内角的度数，然后求出∠BAC和∠EAD，即可求出∠CAD．【解答】解：根据正多边形内角和公式可得，正五边形ABCDE的内角和=180°×（5﹣2）=540°，则∠BAE=∠BAE=∠B=∠E==108°，则∠BAC=∠EAD==36°，所以∠CAD=108°﹣36°×2=36°．故答案为：36°．【点评】本题考查多边形内角和公式，属于简单试题．8．如图所示，∠l=∠2，∠3=∠4，如果∠A=68°，那么∠E=34°【分析】首先根据外角等于不相邻的两个内角和可列出等式关系．同时找到∠A 与∠4和∠2之间的关系即可求解．【解答】解：依题意可知：外角∠3+∠4=∠1+∠2+∠A．，∠l=∠2，∠3=∠4；2∠4=2∠2+∠A∠4=∠2+34°∠A+∠1+∠2+∠ACB=180°．∠E+∠4+∠1+∠ACB=180°∴∠A=∠E+34°．∠E=34°．故答案为：34°【点评】本题考查对长度和角度的理解和运用，关键是找到已知角和所求的角之间的关系．问题解决．9．如图，已知ABCDEFGHI为正九边形，那么∠DIG=60°度．【分析】可以利用九边形的内角和，以及三角形的内角和，作辅助线，连接正九边形的中心，则OI=OD=OG，从而可以求得∠DIG的度数．【解答】解：根据分析，如图，O为正九边形中心，则OI=OD=OG，∠DIG=∠DIO+∠OIG==∠DOG=×（360°÷9×3）=60°故答案是：60°．【点评】本题考查了长度和角度，突破点是：利用九边形的内角和，以及三角形的内角和，作辅助线，连接正九边形的中心，则OI=OD=OG，从而可以求得∠DIG的度数10．已知α是锐角，β是钝角，4位同学在计算0.25（α+β）时，得到的结果依次是15.2°、45.3°、78.6°、112°，其中可能正确的是45.3°．【分析】可以根据锐角和钝角的取值范围，求得0.25（α+β）的取值范围，可以排除掉不可能的取值．【解答】解：根据分析，0＜α＜90°，90＜β＜180°，故：90°＜（α+β）＜90°+180°=270°，0.25×90°=22.5°＜0.25（α+β）＜0.25×270°=67.5°∴15.2°、45.3°、78.6°、112°中只有22.5°＜45.3°＜67.5°是可能正确的结果．故答案是：45.3°．【点评】本题考查长度和角度，突破点是：根据锐角和钝角的取值范围，求得0.25（α+β）的取值范围．11．一个正方形和一个长方形的周长相等，长方形长是7分米，宽是5分米，正方形的面积是36平方分米．【分析】根据长方形的周长公式C=（a+b）×2，求出长方形的周长，即正方形的周长，再根据正方形的周长公式C=4a，知道a=C÷4，即可求出正方形的边长；再根据正方形的面积公式S=a2，解答即可．【解答】解：长方形的周长：（7+5）×2=12×2=24（分米）正方形边长是：24÷4=6（分米）面积是：6×6=36（平方分米）答：正方形的面积是36平方分米．故答案为：36．【点评】此题主要考查了长方形、正方形周长和面积公式的灵活应用．12．如图，长方形周长20，面积24．另一个长方形，面积为20，周长为24．它的长为是10．【分析】周长为24，则长+宽=24÷2=12；面积为20，则长×宽=20=1×20=2×10=4×5，从中找到，长加宽的和是12的两个数，因为10+2=12，所以它的长为10；据此解答即可．【解答】解：周长为24，则长+宽=24÷2=12；面积为20，则长×宽=20=1×20=2×10=4×5，因为10+2=12，所以它的长为10；答：它的长为是10．故答案为：10．【点评】本题考查了长方形周长和面积公式的灵活应用．13．如图所示，一根吸管竖直插在水杯中，此时，吸管的斜置部分与水平线的夹角是30度，那么竖直部分与斜置部分之间的夹角（小于180度的角）是120度．【分析】吸管的斜置部分与水平线的夹角是30度，水平线与竖直线之间的夹角是90度，所以竖直部分与斜置部分之间的夹角（小于180度的角）是30+90=120度；据此解答即可．【解答】解：根据分析可得，30+90=120（度）答：竖直部分与斜置部分之间的夹角（小于180度的角）是120度．故答案为：120．【点评】本题关键是明确水平线与竖直线之间的夹角是90度．14．如图中，AB=5厘米，∠ABC=85°，∠BCA=45°，∠DBC=20°，AD=5厘米．【分析】首先根据题意可知∠ABC=85°，∠BCA=45°．那么根据三角形内角和为180度可知∠A=50°．继续推理即可．【解答】解：依题意可知：∠ABC=85°，∠BCA=45°．那么∠A=50°．∠ABD=∠ABC﹣∠DBC=85°﹣20°=65°∠ADB=180°﹣∠A﹣∠ABD=180°﹣50°﹣65°=65°；∠ADB=∠ABD，∴AB=AD=5故答案为：5【点评】悲痛考查对长度问题的理解和运用，关键问题是找到角度之间的等量关系，问题解决．15．图中，AB=AD，∠DBC=21°，∠ACB=39°，则∠ABC=81度．【分析】如果想求出∠ABC的度数，那么需要求出∠ABD度数，根据AB=AD可知底角相等．再根据外角即可求解．【解答】解：依题意可知：∠DBC=21°，∠ACB=39°根据外角等于不相邻的内角和可知∠ADB=∠C+∠DBC=21°+39°=60°．∵AB=AD．∴∠ADB=∠ABD=60°．∠ABC=∠ABD+∠DBC=60°+21°=81°．故答案为：81【点评】本题考查对长度和角度的立即和运用，关键是找到角之间的等量关系．问题解决．16．如图，O，P，M是线段AB上的三个点，AO=AB，BP=AB，M是AB的中点，且OM=2，那么PM 长为．【分析】如果想求出PM那么必须找到和OM的关系，在这些线段中都和AB进行的比较，可以转换为OM，PM和AB的关系即可求解．【解答】解：依题意可知：PM=AM﹣AP=AB﹣（AB﹣BP）=AB﹣AB=AB．OM=MB﹣OB=AB﹣（AB﹣AO）=AB﹣AB=AB=2∴AB=PM=故答案为：【点评】本题的关键是找到如果想求出PM需要转换成求线段AB，再用OM求出AB，都转换成和AB的关系那么问题解决．17．如图，长方形ABCD的长AB为20厘米，宽BC为16厘米，长方形内放着两个重叠的正方形DEFG和BHIJ，已知三个阴影长方形的周长相等，那么长方形INFM的面积为32平方厘米．【分析】首先根据平移法求出阴影部分的边长和是72，再根据周长相等求出所求的长方形的长和宽的和．再根据两个正方形边长相等关系转换求出所求长方形的长和宽的差．转换为和差问题求两个数．即可求解．【解答】解：阴影部分的总周长为：（20+16）×2=72，四边形IMFN的周长是72÷3=24，所以MF+FN=12 ①，因为正方形的边长相等：MF+MG=FN+EN，则MF﹣FN=EN﹣GM，所以EN﹣GM=EN+BJ﹣（GM+BH）=AB﹣BC=4，则MF﹣FN=4 ②，根据①②式可得：（12+4）÷2=8，（12﹣4）÷2=4，长方形IMFN的面积为4×8=32．故答案为：32．【点评】本题考查平移法求阴影部分的边长．同时求出长宽的和．和差问题的关键就是找到数量和与数量差．在等量关系转换时需要仔细认真．和差问题是以后学习中的重点内容．18．如图，∠A=80°，∠ABO=30°，∠OCD=50°，∠D=60度．【分析】∠A+∠ABO+∠AOB=∠D+∠DCO+∠DOC=180°【解答】解：∠AOB=180°﹣∠A﹣∠ABO=180°﹣80°﹣30°=70°∠COD=∠AOB=70°∠D=180°﹣∠COD﹣∠OCD=180°﹣70°﹣50°=60°．故填60．【点评】此题主要考查三角形内角和是180度这个知识．19．如图，一个大三角形ABC被三条线段分成了七部分，其中四部分是三角形，另外三部分是四边形，三个四边形的周长之和为25厘米，四个三角形的周长之和为20厘米，三角形ABC的周长为19厘米，那么AD+BE+CF=13厘米．【分析】如果我们将三个四边形的周长之和与四个三角形的周长之和相加，那么中间的线段都被加了两次，而AB，BC，CA都只出现一次，由此即可求出AD+BE+CF．【解答】解：如果我们将三个四边形的周长之和与四个三角形的周长之和相加，那么中间的线段都被加了两次，比如图中的GH，它既是四边形GFBH的一条边，又是△GHI的一条边，而AB，BC，CA都只出现一次，比如AF+BF=AB，所以我们要求的线段的和为（25+20﹣19）÷2=13厘米．故答案为13．【点评】本题考查线段的和，考查学生分析解决问题的能力，解题的关键是将三个四边形的周长之和与四个三角形的周长之和相加，那么中间的线段都被加了两次，而AB，BC，CA都只出现一次．20．如图所示，BD，CE分别是∠ABC的角平分线，如果∠BAC=62°，那么，∠BFC= 121°．【分析】根据三角形的内角和，得知：∠A+∠ABC+∠ACB=180°⇒∠A+2∠FBC+2∠FCB=180°⇒∠FBC+∠FCB=（180°﹣∠A）==59°．【解答】解：根据分析，根据三角形的内角和，得知：∠A+∠ABC+∠ACB=180°⇒∠A+2∠FBC+2∠FCB=180°⇒∠FBC+∠FCB=（180°﹣∠A）==59°又∵∠BFC=180°﹣∠FBC﹣∠FCB=180°﹣59°=121°．故答案是：121°．【点评】本题考查了长度和角度，突破点是：根据三角形的内角和以及角平分线的性质，可以求得∠BFC．21．如图，∠E=30°则∠A+∠B+∠C+∠D+∠E+∠F=420°．【分析】利用三角形的外角和以及内角和，∠B+∠C+∠D=360﹣∠BHD，∠A+∠F=180﹣∠AGF，不难求得∠A+∠B+∠C+∠D+∠E+∠F．【解答】解：根据分析，如图，∠B+∠C+∠D=360﹣∠BHD∠A+∠F=180﹣∠AGF．【点评】本题考查了长度和角度，突破点是：利用三角形的外角和以及内角和，∠B+∠C+∠D=360﹣∠BHD，∠A+∠F=180﹣∠AGF，不难求得∠A+∠B+∠C+∠D+∠E+∠F．22．如图所示，已知∠ABC=90度，∠1+∠2=∠3，那么∠3=45度．【分析】观察图形可得，∠1+∠2+∠3=90度，又因为∠1+∠2=∠3，所以∠3+∠3=90度，然后用90除以2即可解决问题．【解答】解：∠1+∠2+∠3=90度，把∠1+∠2=∠3代入上式可得，∠3+∠3=90度，所以，∠3=90÷2=45度，故答案为：45．【点评】本题考查了线与角的综合，关键是得出∠ABC相当于∠3的2倍．23．一张正方形的纸片，如图进行两次对折，折成一个小正方形，从右下角的顶点，沿斜虚线剪去一个角（如图三）剪下的实际是四个小三角形，再把余下的部分展开，展开后的这个图形的内角和是1080度．【分析】可得展开后的这个图形是八边形，根据多边形的内角和定理求解即可．【解答】解：展开后的这个图形是八边形，180°×（8﹣2）=180°×6=1080°答：展开后的这个图形的内角和是1080度．故答案为：1080．【点评】考查了多边形的内角和，多边形内角和定理：n边形的内角的和等于：（n﹣2）×180°（n大于等于3）．24．角可以用它的两边上的两个大写字母和顶点的字母表示，如图1的∠AOB 符号（“∠”表示角）也可以用∠O表示（顶点处只有一个角时）．如图2的三角形ABC中，∠BAO=∠CAO，∠CBO=∠ABO，∠ACO=∠BCO，∠AOC=110°则∠CBO=20°．【分析】由题意知，如图，在三角形AOC中，∠AOC=110°，由三角形的内角和为180°，可知∠CAO+∠ACO=180°﹣110°=70°，由∠BAO=∠CAO，∠ACO=∠BCO，则有∠BAO+∠BCO=∠CAO+∠ACO=70°，可得∠BAC+∠BCA=70°+70°=140°，因此∠ABC=180°﹣140°=40°，又∠CBO=∠ABO，所以∠CBO=40°÷2=20°．由此即可解决．【解答】解：在三角形AOC中，∠CAO+∠ACO=180°﹣∠AOC=180°﹣110°=70°，因为∠BAO=∠CAO，∠ACO=∠BCO，所以∠BAO+∠BCO=∠CAO+∠ACO=70°，所以∠BAC+∠BCA=70°+70°=140°，在三角形ABC中，∠ABC=180°﹣（∠BAC+∠BCA）=180°﹣140°=40°，所以∠CBO=∠ABO=40°÷2=20°．答：∠CBO的度数是20°．故答案为：20°．【点评】解决此题的关键是理解并灵活运用三角形的内角和定理．25．如图，∠1=∠2=∠3=∠4=∠5=∠6=30°，则图中所有锐角度数的和是480°．【分析】观察图形可知，图中由一个角组成的锐角有6个，∠1=∠2=∠3=∠4=∠5=∠6=30°；两个角组成的锐角有5个：∠1+∠2；∠2+∠3；∠3+∠4；∠4+∠5；∠5+∠6，它们的度数都是30°+30°=60°；三个角组成的角已经不是锐角而是直角；因此图中锐角共11个，6个30°的，5个60°的，由此把它们都加起来，即可解决问题．【解答】解：由分析可知，图中所有锐角度数的和是：30°×6+60°×5=180°+300°=480°．答：图中所有锐角度数的和是480°．故答案为：480°．【点评】解答此题的关键是，正确找出图形中的所有的锐角．26．已知一个等腰三角形的最大角是最小角的4倍，那么最大角与最小角的差是90或60度．【分析】分两种情形讨论，列出方程即可解决问题．【解答】解：有两种情形①如图1中，设顶角为4x，两个底角为x，则6x=180，∴x=30°，∴最大角与最小角的差是=120°﹣30°=90°②如图2中，设顶角为x，两个底角为4x，则9x=180，∴x=20°，∴最大角与最小角的差是=80°﹣20°=60°故答案为90或60．【点评】本题考查三角形的面积、等腰三角形的性质、一元一次方程等知识，解题的关键是学会用分类讨论的思想思考问题．27．如图，在△ABC中，已知AB=AC，AE⊥BC，CD=CA，AD=DB，则角DAE=18度．【分析】主要根据等腰三角形两个低角相等、外角定理、直角三角形两个锐角和为90度求解．【解答】解：因为AB=AC，所以∠B=∠C；因为AD=DB，所以∠B=∠BAD，即：∠B=∠BAD=∠C，设：∠B=∠BAD=∠C=α，因为∠ADE是△ABD的外角，则：∠ADE=∠B+∠BAD=2α；设：∠DAE=β，在△ADC中，由于CD=CA，所以∠ADE=∠DAC，即：2α=β+∠CAE，则：∠CAE=2α﹣β…①式；在RT△CAE中，∠CAE+∠C=90°，即：2α﹣β+α=90°，在RT△ADE中，∠ADE+∠DAE=90°，即：2α+β=90°…②式；解由①、②式组成的方程组得：β=18°；故：填18．【点评】通过设未知数，相同的角用一个字母表示，这样题目就会简单易解．28．如图，所有的角度都已标注在图中，∠α=45°．【分析】首先根据邻补角的定义可求出四边形的三个内角，再根据四边形内角和为360度即可求解．【解答】解：依题意可知：根据邻补角的定义可得∠β=180°﹣30°=150°，∠γ=180°﹣110°=70°，∠δ=180°﹣85°=95°；根据四边形内角为360°可得∠α=360°﹣150°﹣70°﹣95°=45°．故答案为：45°【点评】本题考查对长度和角度的理解和运用，关键是找到邻补角和内角和，问题解决．29．如图，把左边4颗钉子围起来用去的绳子比把右边6颗钉子围起来用去的绳子短4厘米，把左边4颗钉子围起来用去绳子8厘米．【分析】首先分析两图相差的是2个边长．绳子短4厘米，那么每一条边长就是4÷2=2（厘米）．继续计算即可求解．【解答】解：依题意可知：两图相比相差2条边长，短4厘米，那么每一条边长就是4÷2=2（厘米）．左边的周长为4×2=8（厘米）；故答案为：8【点评】本题考查对长度和角度的理解和运用，关键问题是找到边长的长度．问题解决．30．如图，∠1=∠2=60 度，那么，∠AOD 的大小是120度．【分析】观察图形可得：∠1+∠2+∠COD=180 度，又因为∠COD+∠AOD=180度，所以，根据等量代换可得：∠1+∠2+∠COD=∠COD+∠AOD，从而得到：∠AOD=∠1+∠2，然后解答即可．【解答】解：根据题意可得，∠1+∠2+∠COD=180 度，又因为∠COD+∠AOD=180度，所以，1+∠2+∠COD=∠COD+∠AOD，所以∠AOD=∠1+∠2=60+60=120度；答：∠AOD 的大小是120度．故答案为：120．【点评】本题考查了线与角的综合应用，关键是利用代换思想得出∠AOD=∠1+∠2．31．用180°与五边形的每一个内角作差，所得到的值叫做这个内角的角亏．如图所示五边形所有内角角亏之和为360度．【分析】用180°与五边形的每一个内角作差，所得到的值叫做这个内角的角亏，所以用180°分别减去五边形的每个内角即是所有内角角亏，再相加即可．【解答】解：（180°﹣∠A）+（180°﹣∠B）+（180°﹣∠C）+（180°﹣∠D）+（180°﹣∠E）=180°×5﹣（∠A+∠B+∠C+∠D+∠E）=900°﹣（5﹣2）×180°=900°﹣540°=360°故答案为：360°．【点评】本题主要考查了多边形的内角和．（n﹣2）×180°，熟记多边形的内角和公式是解题的关键．32．如图，∠B=30°，∠D=20°，∠A=60°，则∠BCD（图中有圆弧部分的那个角）的度数为250°．【分析】延长BC交AD于点E，根据三角形的一个外角等于与它不相邻的两个内角的和先求出∠CED的度数，再次利用三角形的一个外角等于与它不相邻的两个内角的和即可求出∠BCD的度数．【解答】解：如图所示，延长BC交AD于点E，因为∠A=60°，∠B=30°，所以∠CED=∠A+∠B=60°+30°=90°，=∠CED+∠D=90°+20°=110°，因为∠BCD小∠BCD=360°﹣110°=250°；大故答案为：250°．【点评】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，作出辅助线是解题的关键．33．如图，在长方形ABCD中，BC边的中点为E．小明从A走到B再到E，走了22米．小白从D到A再到B最后到E，走了32米．那么这个长方形的周长是54米．【分析】小明从A走到B再到E，走了22米，即AB+BE=22米①；同理，小白从D到A再到B最后到E，走了32米，即AD+AB+BE=32米②；然后①+②可得长方形的周长．【解答】解：根据题意可得，AB+BE=22米…①AD+AB+BE=32米…②①+②可得：AB+BE+AD+AB+BE=22+32又因为AB=CD，BC边的中点为E，可得，BE=EC，所以，AB+BE+EC+AD+CD=22+32=54米即，长方形的周长是54米．答：这个长方形的周长是54米．故答案为：54．【点评】解答本题关键是明确两人行走的路线的特点，然后根据长方形对边相等以及中点的性质解答即可．34．如图，在三角形ABC中，点D在BC边上，且∠ABC=∠ACB，∠ADC=∠DAC，∠DAB=21°，则∠ABC的度数是46°．【分析】因为三角形的内角和是180°，所以∠DAC+∠ADC+∠C=180°，而∠DAC=∠ADC=∠B+21，∠B=∠C，所以3×∠B+21°=180°，然后求出∠B的度数．【解答】解：因为∠DAC+∠ADC+∠C=180°，而∠DAC=∠ADC=∠B+21°，∠B=∠C，所以3×∠B+21°=180°，因为∠B=46°．故答案为46°．【点评】本题考查三角形的外角关系和内角和定理，熟记三角形的外角关系和内角和定理是解决此题的关键．35．如图，在一个正六边形的内部有一个正五边形，那么∠1的度数是12°．【分析】利用多边形的内角和为（n﹣2）•180°求出正六边形的内角和，再结合等边三角形的底角的求法进行解答即可．【解答】解：根据多边形的内角和定理可得：正五边形的每个内角的度数=（5﹣2）×180°÷5=108°正六边形的每个内角的度数=（6﹣2）×180°÷6=120°∠2=120°﹣108°=12°因为AM、MH是正五边形的边，所以AM=MH，即∠3=（180°﹣108°）÷2=36°，因为AB、BC是正六边形的边，所以AB=BC，即∠4=（180°﹣120°）÷2=30°，∠1=120°﹣12°﹣36°﹣30°=42°故答案为：42°．【点评】本题需仔细分析题意，利用多边形的内角和公式即可解决问题．36．如图有8条边，要求它的周长，至少要测量3条边的长度．【分析】如图：把右面的三条竖线段分别向左平移，则得出要求的该图形的周长，即长方形的周长加上2个c的长度的和，据此可知：只要知道a、b、c的长度即可．【解答】解：如图：如图有8条边，要求它的周长，至少要测量出a、b、c，3条边的长度就能算出图形的周长；故答案为：3．【点评】此题应结合图进行认真分析，找出边与边之间的关系，进而得出结论．37．A、B、C、D四个点从左向右依次排在一条直线上，以这四个点为端点，可以组成六条线段，已知这六条线段的长度分别是12、18、30、32、44、62 （单位：厘米），那么线段BC的长度是12厘米．【分析】如图所示，根据题意，AD=62cm，AB+BC+CD=62=12+18+32；又因为30=12+18，44=12+32，所以BC=12cm．【解答】解：根据题干分析可得：AD=62cm，AB+BC+CD=62=12+18+32；又因为30=12+18，44=12+32，所以BC=12cm．答：线段BC的长度是12厘米．故答案为：12．【点评】考查了长度比较，注意本题给出的图形中线段BC是直线上最短的一条线段．38．有A、B、C、D四个点从左向右依次排在一条直线上．以这四个点为端点，可以组成6条线段．已知这6条线段的长度分别是14、21、34、35、48、69 （单位：毫米），那么线段BC的长度是14毫米．【分析】观察图形可知线段BC是直线上最短的一条线段，在所给6条线段的长度中找到最小的即为所求．【解答】解：观察图形可知，线段BC的长度最小，故线段BC的长度是14毫米．故答案为：14．【点评】考查了长度比较，注意本题给出的图形中线段BC是直线上最短的一条线段．39．如图．有一只蚂蚁从A点出发，按顺时针方向沿着图中实线爬行，最后又回到了A点．如果不计算在B，C，D处原地转向时转过的角度，则这只蚂蚁在行进过程中共转过的角度为1800°．。

五年级角度数练习题为了帮助五年级学生更好地掌握角度数的概念和计算方法，以下是一些角度数练习题。

通过解答这些问题，你将能够提高自己对角度的理解和应用能力。

Question 1: 请用常用角度单位度度量以下角度，并判断它们是锐角、直角还是钝角。

a) 30度b) 90度c) 150度d) 180度e) 270度f) 360度Question 2: 判断以下各组角度是否互补、补角或同位角，并说明理由。

a) 30度和150度b) 45度和135度c) 90度和100度d) 120度和60度e) 80度和100度Question 3: 计算以下角度的相对补角。

a) 20度b) 45度c) 80度d) 120度Question 4: 在下图中，每个角的度数是多少？(插入一个包含多个角的图示，角的位置可以根据需要进行布局，但是需要有足够的角度变化，以便学生进行计算。

)Question 5: 利用你所学的知识，判断下列说法是否正确，如果不正确，请纠正并给出正确的说法。

a) 锐角的度数一定小于90度。

b) 直角的度数一定等于90度。

c) 钝角的度数一定大于90度。

d) 互补角之和等于90度。

e) 补角之和等于180度。

Question 6: 如果一个角是其补角的4倍，求这个角的度数。

Question 7: 某个角的两个相对补角分别是60度和80度，求这个角的度数。

Question 8: 如果两个角互为补角，其中一个角的度数是75度，求另一个角的度数。

Question 9: 两个角是同位角，其中一个角的度数是60度，求另一个角度的度数。

Question 10: 如果两个角互为同位角，其中一个角的度数是110度，求另一个角的度数。

通过解答以上练习题，你可以加深对角度数的理解和运用。

希望这些题目对你五年级的学习有所帮助。

继续努力，掌握好角度的概念和计算方法，提升数学能力！。

角度的计算知识点1：角的分类1.锐角：小于 90°的角2.直角：等于 90°的角3.钝角：大于 90°小于 180°的角4.平角：等于 180°的角5.周角：等于 360°的角知识点2:角度的计算1.对顶角相等2.三角形内角和为180°3.多边形内角和：（边数﹣2）×180°知识点3:特殊角度1.一个锐角为30°的直角三角形，斜边的长度是较短直角边的2倍；2.一个角为45°的直角三角形为等腰直角三角形；3.正三角形（等边三角形）的三个内角均为 60°【例题精讲】例题1.（1）三角形的内角和是多少度？（2）四边形的内角和是多少度？（3）五边形的内角和是多少度？【答案】（1）180°；（2）360°；（3）540°。

【解析】根据画图的方法，分析出来三角形，四边形，五边形的内角和，（1）如下图三角形中，内角和=平角=180 °（2）我们可以发现，任意四边形都可以被分成两个三角形，利用三角形的内角和180°，那么两个三角形的内角和就是2×180° = 360°。

（3）如上图得知：任意五边形都可以被分成三个三角形，利用三角形的内角和180°，那么三个三角形的内角和就是3×180°= 540°。

从而得到内角和与边数的关系式，内角和公式：（边数－2）×180°＝540°【铺垫或引入】利用三角形纸片证明三角形内角和为180°，利用三角形内角和进而推导出四边形内角和、五边形内角和，得出结论：多边形内角和＝（边数－2）×180°【拓展或总结】拓展：八边形内角和多少度？已知一多边形内角和1800°，是几边形？ 【小结】多边形内角和：（边数﹣2）×180°练习1. 一个六边形的内角和是多少度？【答案】720°。

人教版四年级数学上册角度换算专项练习
题
以下是一系列针对四年级学生的角度换算专项练题。

通过这些练题，学生可以巩固和提高他们在角度换算方面的能力。

题目一
将以下角度用度数表示：
1. 30分钟的角
2. 90秒的角
3. 45°的角
4. 1小时的角
题目二
将以下角度用度分秒表示：
1. 180°的角
2. 270°的角
3. 90°的角
4. 120°的角
题目三
将以下角度转换为弧度：
1. 60°的角
2. 90°的角
3. 45°的角
4. 120°的角
题目四
将以下角度转换为百分度：
1. 1.5弧度的角
2. 0.8弧度的角
3. 0.25弧度的角
4. 2.3弧度的角
题目五
通过计算，求解下列问题：
1. 两条直线的夹角分别为60°和30°，这两条直线之间共有多少弧度？
2. 一个角是45°，另一个角是90°，这两个角之间共有多少弧度？
3. 一个角是120°，另一个角是60°，这两个角之间共有多少百分度？
以上是本次的角度换算专项练题。

希望这些练题能够帮助学生巩固和提高他们在角度换算方面的能力。

请学生们认真完成每道题目，并与老师一起讨论解答方法和结果。

祝愿学生们取得优秀的成绩！。