
使用蒙特卡罗光子模拟法对发光二极管的分析
Song Jae Lee
蒙特卡洛光子模拟法基于对芯片内光子的统计追踪,已经作为一种成熟的LED分析法在大多数情况下被使用。同时,这种分析法还包含有对经常用于提高光输出功率的表面结构的实际建模。这种方法凭借其独特的灵活性适用于模拟各种结构和尺寸芯片的诸多重要参数,如光子输出耦合效率,光子的精确运行数据,光子输出分布格局。据推测,这种方法可以很容易的被用来拓展LED灯和LED组件的发展。?2001 美国光学学会
卷期号:230.3670, 230.0230
1.介绍
因为一些发光二极管(LED)的发光效率已经大大超过未过滤的白炽灯,广泛认为LED技术将在发光领域取代白炽灯1。LED技术因此可以总的视为成熟。然而,LED的设计却仍然主要仰赖直觉,而且很可能没有被充分优化;光输出功率还有很大的提高空间。在LED中,在有源区产生的光子一般随机定向,并且,芯片耦合输出的大小很容易受到光子发射方向的影响。因而,从某种意义上说,LED的分析和设计相比于光子运行模式由腔体模式所精确确定的激光二极管(LD)的分析和设计,可能不是一个简单的任务。
通常,LED使用逃逸锥面模型进行分析2,3。然而,这种模型仅限于定性分析。此外,这种方法有诸多的限制条件,尤其是当芯片的几何结构较复杂时。例如,使用非共振腔LED时,粗糙的表面或变形的芯片几何形状,都不易用逃逸锥法分析4-6。本文我们将探讨可以克服逃逸锥面模型的种种限制并可以适用于几乎所有几何形状芯片的蒙特卡洛光子模拟法方法。事实上,蒙特卡洛光子模拟法经过广泛的验证,在过去的几十年中,它被广泛的用于解决各种问题,例如在放射性材料中的中子传递问题和半导体材料中的电子传递问题7。蒙特卡洛光子模拟法独特的通用性使得修改LED的分析和设计变的更为简单。基本上,蒙特卡洛光子模拟法是基于芯片中光子的统计规律,并且模拟结果通常具有相当的可行性。此外,蒙特卡洛光子模拟法还可以脚容易的合并复杂的光子传播模型。在我们的分析中包含有光子在一种特殊表面纹理上的反射模型,这种表面纹理常常用于高亮LED以提高光耦合输出和光提取效率。我们相信具有独特通用性的蒙特卡洛光子模型法将使LED灯和LED器件的设计变的更为简单。
2.LED 结构分析的原理
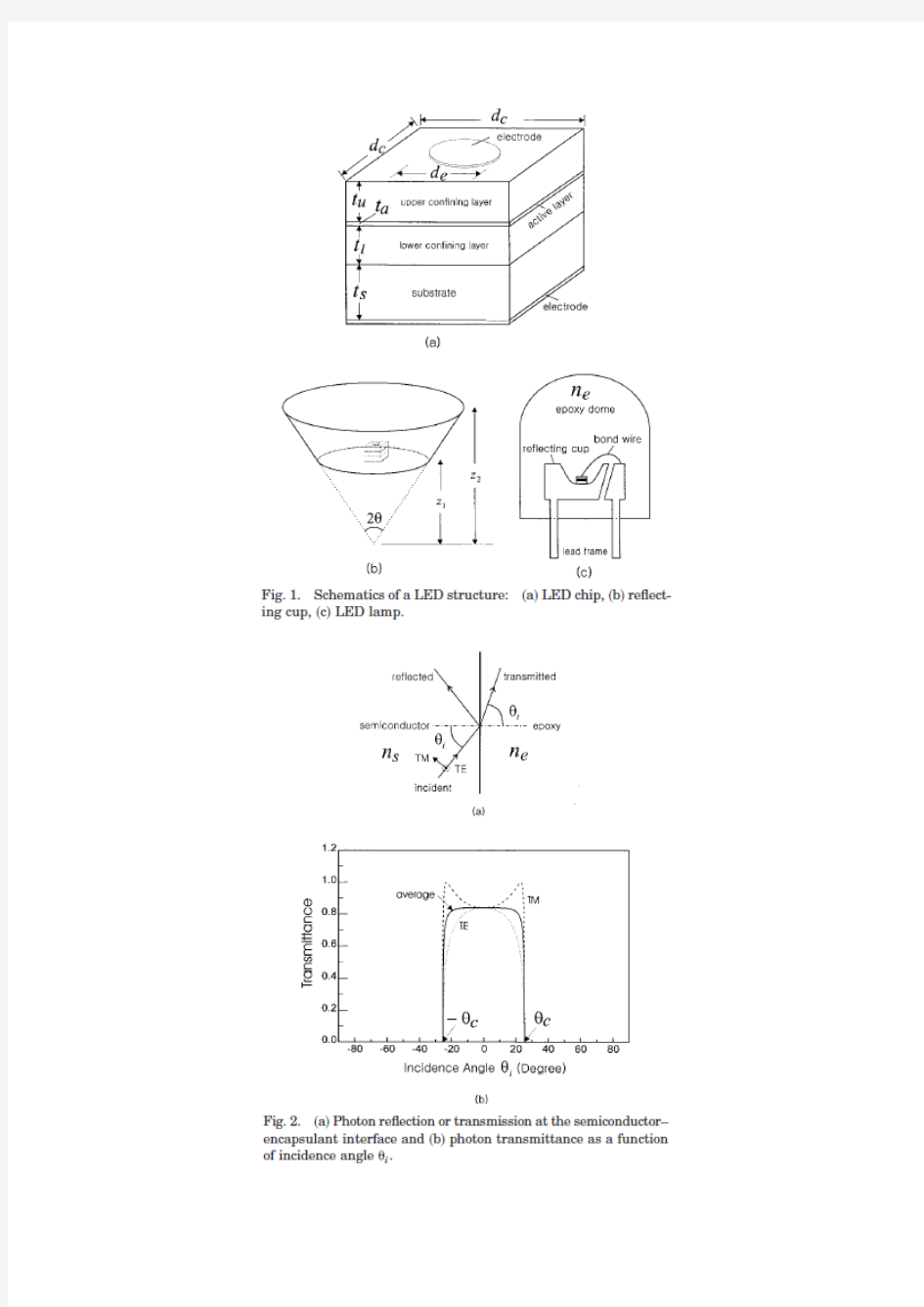
典型的LED 灯和LED 器件的概略结构如图1所示。光子在有源区激发后,除非在内部被吸收,否则会入射到芯片外壁,如图2(a)所示。光子反射系数ГTE 和ГTM (分别为横向电场和横向磁场极化方向)由下式给出:
其中,n s 和n e 分别为芯片半导体材料和密封环氧树脂的折射率,θi 和θt 分别为光子入射角和折射角。角θi 和θt 相互之间符合斯涅耳定律:
实际上,大多数LED 中,n s 通常要大于n e 。因此,如果入射角θi 大于临界角θc ,
此时,ГTE 和ГTM 的幅值相一致,意味着出现所谓的全内反射。ГTE 光子和ГTM 光子的透过率分别为ГTE 和ГTM ,由下式给出:
其中R TE =|ГTE |2和R TM =|ГTM |2分别为偏振光TE 和TM 的光反射系数。在LED 中,偏振光的光子在到达壁垒时一般是随机的。因为任意的光子极化方向可以表达为TE 极化方向和TM 极化方向的线性组合,任意极化方向的光子的反射率R 可以由下式得:
其中,δTM 是TM 的极化因子,由极化向量在入射面上的投影得到。图2(b )说明典型情况下光子透射率为变量,而光子反射角θi 为函数。请注意,由于布儒斯特角现象,TM 极化的透射率总是大于TE 极化。
较大幅度的光子传输窗口在入射角到θ
c 之间,θ
c
将会导致逃逸锥
的出现。如图3(a)。如果不同半导体材料层之间的折射率差异较小,LED芯片可以被认为大致具有相同的折射率n
s
。这样,六个逃逸锥(芯
片的每个面有一个)具有相同的立体角Ω
c
,又下式表示:
在芯片为具有扁平表面的长方或立方形时,光子一旦从溢出锥发射出来就会不断的发生全内反射,被困在椎体内,如图3(b)。被困住的那
部分光子,η
trap
,可以由下式大致得出:
在AlGaAs和InGaAlP系统中,η
trap 大约为70%,n
e
≈1.5,n
s
≈3.5;在InGaN
系统中η
trap 大约为40%。有这样大的一部分被困光子最终被吸收掉,
外部量子效率将受到严重限制。使得被困光子发射出逃逸锥的方法之一是使芯片表面粗糙化,如图3(c)4,8。光子经过粗糙表面的入射后其将会表现出随机轨迹,其中的一些就有可能离开芯片,无论其飞行方向是怎样的。
的环氧密封材在LED灯中,LED芯片处于被圆顶形的折射率为n
e
可以由下式料包裹住的状态。在这种情况下,光子的输出耦合效率η
c
大约表示:
是光子离开芯片进入环氧树脂的概率,函数:
其中,η
trap
是正入射光子在环氧树脂—空气界面的透射率。正入射情况非常的合理,尤其是当环氧树脂密封圆顶的尺寸远大于芯片和加上反射罩时。而事实上,大多数的LED灯正是这样的。
但,即使逃脱锥的概念提供了关于光子的耦合输出过程的一般想法,这种概念在大量分析结构时仍有显著的限制。最令人感到麻烦的效果是光子被欧姆损耗电极所屏蔽,这种屏蔽取决于光子的运行方向。并且,即使在一个逃逸锥内,这种屏蔽也会使光子的耦合输出概率呈现显著变化。此外,这种屏蔽对逃逸锥的影响程度极易受到光子在有源区的产生位置的影响。因此,用逃逸锥概念来判断光子耦合输出功率并不是一个轻松的工作,并且经常会出现重大错误。
3.蒙特卡洛光子模型
在LED中,芯片表面的光学反馈效果是基本上可以忽略的,因此,大多数自发发射激发的光子是不连续的。我们完全可以在大多数情况下将不连续的光子看作粒子,而不是波。自发发射的不连续光子将会在随机方向上自由运行直到有发生将其运行阻断的事件。这些事件中最重要的也许是散射,吸收和有源区的再发射(光子循环),其他半导体层内的吸收,菲涅尔反射或不同折射率介质材质接触面的传递。在这项研究中我们将只考虑内部光子吸收和菲涅尔反射或在分界面上的传递。在半导体晶体质量相对较好的情况下,由晶体缺陷造成的
光子散射可以基本忽略。同样的,在有源区的光子循环效应也可以忽略,尤其是当有源区的体积相对于芯片的整体较小时,正如大多数的高亮LED 。蒙特卡洛光子模型所做出的最重要的推断是在有源区的一点激发的某个光子的平均行为和在同一点激发的大量独立光子所展现出的行为是一致的。这种情况下他们的方向仍是随机的。这样,在蒙特卡洛光子模型中必不可少的一步是建立一个可以跟踪单个光子的过程。基本上,光子的跟踪过程是由预测光子在每次自由运行过程的结尾的行为来实现的,并且每次使用具有同样概率分布函数的随机数作为特定的运行阻断事件。下面的描述是蒙特卡洛光子模型中的重要一步。
首先我们介绍一个概念:光子状态P 。它有两个值:
P =1 (光子存在)
P =0 (光子被吸收)
光子刚从有源区发出时其状态P =1,并将持续为1直到光子被吸收。当光子被吸收后,P =0。并且光子追踪也到此结束。除此之外,我们可以使用一种强度概念,例如,指定光子刚发出时为单位强度I =1。然而,在这种情况下,光子追踪应该持续到光子彻底衰减为I =0或耦合出芯片,这会使模拟的时间出现显著增长。另外一个单个光子强度分配的问题是单个光子不能被部分吸收导致单个光子出现分数。这样,虽然两种方法在对最终的结果预测上没有发现明显的不同,但光子状态概念比光子强度概念更为优越。
除了光子状态函数P 外,有必要指出初试极化向量e 0,位置矢量r 0和速度向量υ0,由下式表示:
其中,,,是直角坐标系里的单位向量;e ox ,e oy 和e oz 是极化向量沿坐标轴的投影;x 0,y 0,z 0是有源区内光子发生的坐标;c 是光速;n 是光子运行所在的介质的折射率;θ0和Φ0是球坐标下的方向角。角θ0
和Φ0应该使在同一位置r 0所发出的大量光子在所有的方向上具有一致的指向。
当光子到达各层之间的分界面时,其自由行程被打断。除非他被吸收掉,否则将会进入下一层,即在(n-1)层从新的界面位置r n+1发出,可以由下式表示:
其中,r n ,υn ,τn 分别表示第n 次发出时的初始位置、初始速度和持续
时间。然而,现实中总会有光子在运行过程中被吸收的概率。很显然这种吸收概率与运行传递损失A n 有关:
其中l n 是第n 次运行的路径长度,αn 是光子运行所在层介质的光子吸收
系数。在蒙特卡洛光子模型中,光子总是以单个光子的形式被跟踪,飞行传递损失A n 可以解释为光子在第n 层运行过程中的存活概率。基于这种解释,光子是否被吸收或存活可以由随机数p 来确定,其分布与光子的状态相一致:
P =1
p n (光子存在) (19) P =1
p
n (光子被吸收) (20) 在式(19)中没有被吸收的光子将在新的位置r n+1发生反射或透射。新的运行速度υn+1由另一个符合以下条件的随机数f 所确定:
υ
n+1=υref f R (光子反射) (21) υ
n+1=υtr f
R (光子透射) (22) 其中,R ,υref ,υtr 分别为界面位置r n+1的光子反射系数,菲涅尔反射速度和透射速度。同样的,无论光子是反射或透射,新的极化向量 e n+1也被相应确定。
光子有时会进入电极下的欧姆区。光子在欧姆区中的吸收是一个复杂的过程,通常欧姆区的深度和它的吸收系数都和极大地取决于材料的结构。然而,欧姆区通常都是较浅的,因此,在本文中我们设定
,同时,参数光子在欧姆区中的吸收总的归结为一个总吸收概率A
ohm
极大地取决于材料的结构。在这种设定下,光子进入欧姆区后的A
ohm
状态P可以由符合以下条件的随机数
确定:
ohm
P=1
(光子存在)(23)
P=1
(光子被吸收)(24)
图4为在有源区指定位置产生的光子的跟踪流程图。在有源区指
定点发出的光子的精确运行过程一般是关于光子初始运行方向角Φ
0的函数。因此,我们可以通过求得在某一点生成的覆盖所有方向和θ
的足够大量光子的平均特性来估计在这一点随机生成的光子所具有的特性。例如,我们可以通过测定在某一点r
产生的大量覆盖所有方
向的光子中耦合输出光子的比例来得到这点的光子耦合输出效率。
4.材质表面模型
正如上文所述,芯片表面织构化可以让光子轨迹随机化,是一种提高光子耦合输出的重要方法,并被广泛应用于高亮LED。因此,建立一个表面织构化的可行性模型将非常重要。理论上,如果可以得到织构化表面的详细显微结构,就可以使用同一个蒙特卡洛过程得到光子的精确运行轨迹。然而,精确的显微结构特征,包括特定空间维度的细节,都取决于许多不同的限制因素。如,材料的结构系统和复杂的织构化过程。在本文中,我们设想一种相当灵活的织构化表面模型,以适应现实情况。在提高光子耦合输出的过程中,织构化表面的最终作用是使光子在织构化表面轨迹随机化,这样,无论光子的初始发射方向是怎样的,都会有一定概率到达逃逸锥。在这种情况下,无需考虑光子与与织构化表面的相互作用。因此,从LED分析的角度来说,可以只集中考虑与织构化表面发生作用而具有随机方向的光子。
在我们的织构化表面模型中,我们首先假设光子入射点中心的微分区域足够宽,可以容纳入射光子,而正常情况下,微分表面的方向是随机的。在这种情况下,只要一般的d S方向给定,我们就可以找到光子的反射或投射方向,就像在非织构化表面芯片腔中使用菲涅尔反射理论一样容易。因此,微分表面正常情况下的随机方向可以直接与光子的随机轨迹相关联。另一个假设是微分表面d S的一般方向符合随
机分布函数N(θ
n )。这里,θ
i
是参考方向与d S的垂直方向所成的角,称
作局部正交方向角。参考方向的一个合理的选择是参考方向垂直于非
织构化参考平面。图五所示是光子在非织构化参考平面以入射角θi 入射到微分表面d S 。我们必须确定局部正交方向角θn 以追踪光子入射到d S 的情况。在现实中,θn 有两度的自由度,可以被分解为角θni 和θnt ,换言之,角被分别投影到入射面和另一个同时垂直于入射面和光子入射方向的面。我们注意到入射面由参考面和光子入射方向的法线决定。在这里,我们介绍角θni 的概率分布函数N i 和θnt 的概率分布函数N t ,由下式给出:
其中,k i 和k t 为待定常数,n st 为织构指数,与表面随机纹理有关。随着n st 的增加,表面将变得更为平坦,而概率分布函数N i (θni )和N t (θnt )将会在垂直参考平面方向上出现急剧高峰。例如,n st =∞的极端情况就相当于非织构化参考面。在模拟中,我们可以根据织构化表面的显微细节来调整织构指数n st 从而只需简单的增加或减少n st 就可以更好的适应给定的情况。
我们注意到,入射到d S 的光子和入射到d S 的、横截面的光子成比例。在入射面上d S 的横截面的尺度将随函数C i (θi ,θni )简化:
其中(θni -θi )是入射面上的入射角。显然,光量子在以角θi 入射时被一在入射平面上以角θni 倾斜的微分平面d S 挡住的概率P i 由下式给出
同样的,垂直面上d S 的横截面尺度可以由函数C t (θi ,θni )简化:
光量子在以角θ
i 入射时被一在垂直面上以角θ
nt
倾斜的微分平面d S挡住
的概率P
t
由下式给出:
角θ
ni 和θ
nt
由两个随机数
ni
和
nt
确定,其关系为:
随着d S上正交角θ
ni 和θ
nt
的获得,追踪入射到d S上的光子轨迹所必须的
反射速度υref和透射速度υtr都可以求得。
5.模拟结果
图6为一个LED 芯片使用蒙特卡洛模拟后的结果。其中最重要的参数为水平形变角αh 和垂直形变角αv 。αh =900和αv =00的情况和传统的矩形芯片相一致。当αh 不是900时,芯片的水平平面将变形为菱形。在这种情况下,大多数的平行于水平面运行的电子会到达逃逸锥,如图6(b)所示。同样的,当选择适当的垂直平面变形角αv 时,大多数垂直方向运行的电子也会较易的找到逃逸锥。显然,如果水平面和垂直面都相应的变形,则大多数在有源区发出的光子无论其运行方向,都会避过大多数的矩形芯片内的反射,使光子耦合输出效率大幅提高。5图6(a)所示的结构同时使用了用于高亮LED 的底部电极。此时,射入开放欧姆区的光子一般会被安装芯片的镀银金属引线框所反射回,并有一定的概率耦合出芯片,从而提高光子的耦合输出效率。10
无论在AlGaAs 系统还是InGaAlP 系统中,折射率n 和吸收系数α可以被假设:上下两层n =3.4,α=8cm -1;活跃层n =3.6,α=200cm -1;吸收基n =3.6,α=8000cm -1;环氧封装层n e =1.5。很少被人注意到的是,由于材料的不同,光子在欧姆区中的吸收会有很大的不同。在本文中我们假设AlGaAs 和InGaAlP 系统中的欧姆电极A ohm =0.5。需要注意的是,欧姆吸收在宽能隙半导体如GaN 中要明显小于AlGaAs 或InGaAlP 中,所以,A ohm 应该相应的调整。9除非专门指定,否则典型的矩形芯片设计的限制条件如下:最上层厚度t u =60μm ,活性层厚度t a =0.5μm ,最下层厚度t l =120μm ,吸收基厚度t s =0μm ,芯片尺寸d c =250μm ,顶电极直径d e =100μm ,光栅底部电极开放部分γbe =0.5,织构化表面指数n st =20。在菱形芯片中,为了可以公正的比较两种结构,我们将芯片尺寸调整为d c ,使芯片表面区域和矩形芯片相同。
图7表示在传统的矩形芯片中,光子耦合输出效率 ηc (x ,y) 是光子在活性区激发位置的函数。光子在活性区中央激发时有很大的可能性会被顶部损耗电极遮挡,导致 ηc (x ,y)降低。由于ηc (x ,y)取决于光子激发位置,光子耦合效率ηcavg 可以通过先把 ηc (x ,y)和电流密度J (x ,y)加权,在平均到整个活性区空间来求的。然而,活性区电流密度J 取决于诸多参数,如电极的设计和芯片各半导体层的厚度及电阻率,这些参数都难以获得。在本文中,平均电子耦合输出效率ηcavg 近似等于有源区某些典型点光子耦合输出效率的简单平均,如图8所示。图中,阴影椭圆是顶电极在有源区平面上的投影,实心小圆点标示出用以求得光子耦合输出效率 ηc (x ,y) 平均值的点。
图9说明,在直角坐标系中,光子耦合输出效率是限制层厚度t u 的函数。随着t u 的增加,明显的,侧面逃逸锥中的电子将和顶损耗电极发生更少的相互作用。这样一来,众所周知,平均光子耦合输出效率ηcavg 将会有显著增加。3,10但是,如果限制层厚度有太多增加,芯片内光子传输损耗将相应增加。这样,光子耦合输出效率将会饱和。
图10显示,无论是矩形芯片还是异形芯片,光子耦合输出效率是表面织构化指数n st 的函数。正如上文所说,在织构化表面模型中,随
着n st 的减小,表面随机增加。我们注意到,正如预想中的,尽管在异型芯片中光子耦合输出效率和表面织构化指数几乎没有关联,但在矩形芯片中,随着n st 的减少,光子耦合输出效率有明显增加。这个事实说明,织构化表面使光子轨道随机化的概率完全被形变腔所产生的光子轨迹的宏观变化所压倒。此外,在形变腔中,光子轨迹事实上是可以控制的,而不是随机化,这样,光子在耦合运行期间就可以到达逃逸锥。结果是,传统矩形芯片的耦合输出效率提高了约100%。最近,惠普的Krames et al .6发明了一种非共振截断倒金字塔结构,和图5所示的几何结构模型非常相似。他们的外量子效应达到了令人映像深刻的55%,使传统的矩形芯片外量子效应提高了近100%。10这也说明了,我们的模拟结果大致正确。在下文中,除非另外说明,否则表面织构化指数n st =20。当n st =20时,传统的矩形芯片(αh =900,αv =00)的耦合输出可以达到25%,与实验数据相接近。5,10
图11说明,光子耦合输出效率是水平面倾斜角αh 的函数。随着αh 减小,水平面捕获的光子也相应减小,导致光子耦合输出效率增加。同样的,如图12所示,光子耦合输出效率也会随着垂直面倾斜角αv 的增加而增加。然而,当αv 为负角度时,耦合效率下降。αv 为负时,光子从倾斜的侧壁上反射回时大多数会向下运动,其中一些会被底部欧姆电极吸收,导致光子耦合输出效率下降。倾斜的侧壁也会影响很少一部分从顶部输出的光子,正如图13所示。正如预测的,当αv 为正时,顶部输出有少量增加。然而,在αv 为负角度时,相当一部分光子从侧壁反射回后射入底部电极,随后,被反射回顶层。结果,极少的顶输出将不会减少太多。输出光子的空间分布会受到形变腔的显著影响。
图14所示为侧壁的耦合输出光子在水平平面的空间分布。从水平面的分布情况来看,我们可以设想一个直径为r c 的圆柱面围绕着芯片。在这种情况下从侧壁耦合输出的光子大多数都将射到这个面上。光子在圆柱面上的入射点投影到水平面上,且入射光子的强度是方位角Ф的函数。这里角Ф是参考方向和芯片中心与投影的之间连线的夹角。注意,在菱形芯片中,光子分布趋势在水平面的次对角线方向上有一个峰值,并且和矩形芯片会有明显不同。在表面织构化指数n st =20时,输出光子的方向也将会随机化,导致强度模式出现一个敏感的角关
系。
在LED 灯中,大多数的耦合输出光子将会从金属反射罩向上反射。这样,水平面的强度分布将会提供设计金属反射罩和环氧树脂密封镜片的重要信息。一个简单的反射罩如图1(c)所示,看起来像一个被切去顶端的锥形。可以由下式表达:
其中,θ是圆锥顶角的一半,z 1和z 2分别为锥顶到锥底和上边缘的距离。图15所示为一个LED 灯在远场垂直平面上的强度分布,其中,金属反射罩安装在一个无限大的球形环氧树脂镜片的中央。
6.结论
最后,蒙特卡洛光子模型已经被更多的用在LED 的量化研究和设计上。无论传统矩形芯片还是菱形芯片,模拟结果都直观有效。其中一些与实验结果有相当的吻合度。5,6,10蒙特卡洛光子模型建立在总体可行的设想上,所以,当诸如折射率和各层的吸收系数等数据合理时,取得的结果也高度精确。
另外,我们加入了一种织构化表明的实践模型,这种织构化常在晶圆切割流程中用于芯片处理。模拟结果显示,在常用的矩形芯片中,光子耦合输出效率将随表面粗糙程度或随意程度而明显增加。然而,当腔的形变度足够的时候,表面织构化的效果就微不足道了,即便这样,和矩形结构加织构化表面相比,耦合输出效率有了100%的大幅提高。这个结果表明形变腔外壁产生的光子宏观轨迹的改变在提高光子耦合输出效率上对由织构化表面改变光子围观轨迹所产生的影响具有压倒性优势。蒙特卡洛光子模型以其独特的通用性适用于多种芯片结构,并提供了诸如光子耦合输出效率,光子运行的详细统计数据和光子输出分布等重要参数。根据光子强度分布的例子推断,我们可以很容易的将蒙特卡洛模型用于LED 灯,包括反射罩,环氧树脂密封镜片和LED 封装。
作者在此感谢Korean Ministry 在信息和通讯方面提供的基础研究程序。
参考文献:
1. T. Mukai, M. Yamada, and S. Nakamura, “InGaN-based uvy blueygreenyamberyred LEDs,”in Light-Emitting Diodes: Research, Manufacturing, and Applications III, I. T. Ferguson, E. Schubert, and H. Yao, eds., Proc. SPIE 3621, 2–14 ~1999!.
2. G. B. Stringfellow and M. G. Craford, High Brightness Light Emitting Diodes ~Academic, New York, 1997!.
3. S. J. Lee, “Design rules for high-brightness light-emitting diodes grown on GaAs substrate,”Jpn. J. Appl. Phys. 37, 509–
516 ~1998!.
4. R. Windish, P. Heremans, B. Dutta, M. Kuijk, S. Schoberth, P. Kiesel, G. H. Do¨hler, and G. Borghs, “High-efficiency nonresonant cavity light-emitting diodes,”Electron. Lett. 34,
1153–1154 ~1998!.
5. S. J. Lee and S. W. Song, “Efficiency improvement in lightemitting diodes based on geometrically deformed chips,”in
Light-Emitting Diodes: Research, Manufacturing, and Applications III, I. T. Ferguson, E. Schubert, and H. Yao, eds., Proc.
SPIE 3621, 237–248 ~1999!.
6. M. R. Krames, M. Ochiai-Holcomb, G. E. Hoffler, C. Carter- Coman, E. I. Chen, I.-H. Tan, P. Grillot, N. F. Gardner, H. C. Chui, J.-W. Huang, S. A. Stockman, F. A. Kishi, M. G. Craford,
T. S. Tan, C. P. Kocot, M. Hueschen, J. Rosselt, B. Loh, G.
Sasser, and D. Collins, “High-power truncated-pyramid
~Al x Ga-12x!0.5In0.5PyGaP light-emitting diodes exhibiting
.50% external quantum efficiency,”Appl. Phys. Lett. 75,
2365–2367 ~1999!.
7. C. Jacoboni and P. Lugli, The Monte Carlo Method for Semiconductor Device Simulation ~Spring-Verlag, New York, 1989!.
8. I. Schnitzer and E. Yablonovitch, “30% external quantum efficiency form surface textured, thin-film light-emitting diodes,”
Appl. Phys. Lett. 63, 2174–2176 ~1993!.
9. H. Morkoc, S. Strite, G. B. Gao, M. E. Lin, B. Sverdlov, and M. Burns, “Large-band-bandgap SiC, III–V nitride, and II–VI ZnSe-based semiconductor device technoloies,”J. Appl. Phys.
76, 1363–1398 ~1994!.
10. F. A. Kishi, F. M. Steranka, D. C. DeFevere, D. A. Vanderwater, K. G. Park, C. P. Kuo, T. D. Osentowski, M. J.
Peanasky, J. G. Yu, R. M. Fletcher, D. A. Steigerwald, M. G. Craford, and V. M. Robins, “Very high-efficiency semiconductor wafer-bonded transparent-substrate ~Al x Ga12x!0.5In0.5Py
GaP light-emitting diodes,”Appl. Phys. Lett. 64, 2839–2841
~1994!.
11. K. H. Huang, J. G. Yu, C. P. Kuo, R. M. Fletcher, T. D. Osentowski,
L. J. Stinson, M. G. Craford, and A. S. Liao, “Twofold efficiency improvement in high performance AlGaInP lightemitting diodes in the 555–620 nm spectral region using a
thick GaP window layer,”Appl. Phys. Lett. 61, 1045–1047 ~1992!
当科学家们使用计算机来试图预测复杂的趋势和事件时, 他们通常应用一类需要长串的随机数的复杂计算。设计这种用来预测复杂趋势和事件的数字模型越来越依赖于一种称为蒙特卡罗模似的统计手段, 而这种模拟进一步又要取决于可靠的无穷尽的随机数目来源。 蒙特卡罗模拟因摩纳哥著名的赌场而得名。它能够帮助人们从数学上表述物理、化学、工程、经济学以及环境动力学中一些非常复杂的相互作用。数学家们称这种表述为“模式”, 而当一种模式足够精确时, 他能产生与实际操作中对同一条件相同的反应。但蒙特卡罗模拟有一个危险的缺陷: 如果必须输入一个模式中的随机数并不像设想的那样是随机数, 而却构成一些微妙的非随机模式, 那么整个的模拟(及其预测结果)都可能是错的。 最近, 由美国佐治亚大学的费伦博格博士作出的一分报告证明了最普遍用以产生随机数串 的计算机程序中有5个在用于一个简单的模拟磁性晶体中原子行为的数学模型时出现错误。科学家们发现, 出现这些错误的根源在于这5个程序产生的数串其实并不随机, 它们实际上隐藏了一些相互关系和样式, 这一点只是在这种微小的非随机性歪曲了晶体模型的已知特 性时才表露出来。贝尔实验室的里德博士告诫人们记住伟大的诺伊曼的忠告:“任何人如果相信计算机能够产生出真正的随机的数序组都是疯子。” 蒙特卡罗方法(MC) 蒙特卡罗(Monte Carlo)方法: 蒙特卡罗(Monte Carlo)方法,又称随机抽样或统计试验方法,属于计算数学的一个分支,它是在本世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。传统的经验方法由于不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡罗方法由于能够真实地模拟实际物理过程,故解决问题与实际非常符合,可以得到很圆满的结果。这也是我们采用该方法的原因。 蒙特卡罗方法的基本原理及思想如下: 当所要求解的问题是某种事件出现的概率,或者是某个随机变量的期望值时,它们可以通过某种“试验”的方法,得到这种事件出现的频率,或者这个随机变数的平均值,并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征,利用数学方法来加以模拟,即进行一种数字模拟实验。它是以一个概率模型为基础,按照这个模型所描绘的过程,通过模拟实验的结果,作为问题的近似解。可以把蒙特卡罗解题归结为三个主要步骤:构造或描述概率过程;实现从已知概率分布抽样;建立各种估计量。 蒙特卡罗解题三个主要步骤: 构造或描述概率过程: 对于本身就具有随机性质的问题,如粒子输运问题,主要是正确描述和模拟这个概率过程,对于本来不是随机性质的确定性问题,比如计算定积分,就必须事先构造一个人为的概率过程,它的某些参量正好是所要求问题的解。即要将不具有随机性质的问题转化为随机性质的问题。 实现从已知概率分布抽样: 构造了概率模型以后,由于各种概率模型都可以看作是由各种各样的概率分布构成的,因此产生已知概率分布的随机变量(或随机向量),就成为实现蒙特卡罗方法模拟实验的基本手段,这也是蒙特卡罗方法被称为随机抽样的原因。最简单、最基本、最重要的一个概率分布是(0,1)上的均匀分布(或称矩形分布)。随机数就是具有这种均匀分布的随机变量。随机数序列就是具有这种分布的总体的一个简单子样,也就是一个具有这种分布的相互独立的随机变数序列。产生随机数的问题,就是从这个分布的抽样问题。在计算机上,可以用物理方法产生随机数,但价格昂贵,不能重复,使用不便。另一种方法是用数学递推公式产生。这样
系列一 蒙特卡洛随机模拟 实验目的:学会用计算机随机模拟方法来解决随机性问题 蒙特卡洛模拟法简介 蒙特卡洛(Monte Carlo)方法是一种应用随机数来进行计算机摸你的方法。此方法对研究对象进行随机抽样,通过对样本值的观察统计,求得所研究系统的某些参数。作为随机模拟方法,起源可追溯到18世纪下半叶蒲峰实验。 蒙特卡洛模拟法的应用领域 蒙特卡洛模拟法的应用领域主要有: 1.直接应用蒙特卡洛模拟:应用大规模的随机数列来模拟复杂系统,得到某些参数或重要指标。 2.蒙特卡洛积分:利用随机数列计算积分,维数越高,积分效率越高。 蒙特卡洛模拟法求解步骤 应用此方法求解工程技术问题可以分为两类:确定性问题和随机性问题。解题步骤如下: 1.根据提出的问题构造一个简单、适用的概率模型或随机模型,使问题的解对应于该模型中随机变量的某些特征(如概率、均值和方差等),所构造的模型在主要特征参量方面要与实际问题或系统相一致 2 .根据模型中各个随机变量的分布,在计算机上产生随机数,实现一次模拟过程所需的足够数量的随机数。通常先产生均匀分布的随机数,然后生成服从某一分布的随机数,方可进行随机模拟试验。 3. 根据概率模型的特点和随机变量的分布特性,设计和选取合适的抽样方法,并对每个随机变量进行抽样(包括直接抽样、分层抽样、相关抽样、重要抽样等)。 4.按照所建立的模型进行仿真试验、计算,求出问题的随机解。 5. 统计分析模拟试验结果,给出问题的概率解以及解的精度估计。 在可靠性分析和设计中,用蒙特卡洛模拟法可以确定复杂随机变量的概率分布和数字特征,可以通过随机模拟估算系统和零件的可靠度,也可以模拟随机过程、寻求系统最优参数等。 一. 预备知识: 随机数的产生 提示:均匀分布(0, 1)U 的随机数可由C 语言或Matlab 自动产生,在此基础上可产生其他分布的随机数. 1.逆变换法: 设随机变量U 服从(0,1)上的均匀分布,则)(1U F X -=的分布函数为)(x F . 步骤:(1) 产生)1,0(U 的随机数U ;(2) 计算)(1 U F X -=, 则X 服从)(x F 分布. 问题:练习用此方法产生常见分布随机数.例如“指数分布,均匀分布),(b a U ”.还有其它哪种常见分布的随机数可用此方法方便产生?
通信原理 课程设计报告 题目:基于蒙特卡罗法2FSK系统抗噪声性能仿真院系: 专业: 班级: 姓名: 指导教师: 2010年12月27日-2010年12月31日
编写MA TLAB的M文件,用该文件的采用相干解调法的2FSK系统的抗噪性能进行1000个符号的蒙特卡罗法仿真,画出误码率与信噪比之间的关系曲线,其中信噪比的取值为r=0dB、2dB、4dB、6dB…10dB,同时画出误码率与信噪比的理论曲线,其中信噪比的取值为r=0dB、0.1dB、0.2dB…10dB。 分步实施: 1)熟悉2FSK系统调制解调,熟悉蒙特卡洛法;熟悉误码率计算; 2)编写主要程序; 3)画出系统仿真误码率曲线的系统理论误码率曲线。
1、蒙特卡罗思想概述 蒙特卡罗方法也称为随机模拟方法,有时也称为随机抽样技术或统计实验方法。它的基本思想是:为了求解数学、物理、工程技术以及生产管理等方面的问题,首先建立一个概率模型或随机过程,使它的参数等于问题的解;然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征,最后给出所求解的近似值。而解得精确度可用估计值的标准误差来表示。 蒙特卡罗方法可以解决各种类型的问题,但总的来说,视其是否涉及随机过程的性态和结果,该方法处理的问题可以分为两类:第一类是确定性的数学问题,首先建立一个与所求解有关的概率模型,使所求的解就是我们所建立模型的概率分布或数学期望;然后对其进行随机抽样观察,即产生随机变量;最后用其算术平均值作为所求解的近似估计值。第二类是随机性问题,被考察的元素更多的受到随机性的影响,一般情况下采用直接模拟方法,即根据实际物理情况的概率法则,用电子计算机进行抽样试验。 在应用蒙特卡罗方法解决实际问题的过程中,大体有如下几个内容: (1)对求解的问题建立简单而又便于实现的概率统计模型,使所求的解恰好是所建立模型的概率分布或数学期望。 (2)根据概率统计模型的特点和计算实践的需要,尽量改进模型,以便减小方差和费用,提高计算效率。 (3)建立对随机变量的抽样方法,其中包括建立产生伪随机数的方法和建立对所遇到的分布产生随机变量的随机抽样方法。 (4)给出获得所求解的统计估计值及其方差或标准误差的方法。 2、2FSK 系统调制解调原理 频移键控是利用载波的频率变化来传递数字信息。在2FSK 中,载波的频率随二进制基带信号在f1和f2两个频率间变化。用f1和f2分别表示二进制“1”和“0”。因此,2FSK 信号的时域表达式为 )cos()()cos()()(212n n s n n n s n FSK t nT t g a t nT t g a t e θωφω+?? ? ???-++??????-=∑∑∞-∞→∞ -∞ →
蒙特卡洛方法 1、蒙特卡洛方法的由来 蒙特卡罗分析法(Monte Carlo method),又称为统计模拟法,是一种采用随机抽样(Random Sampling)统计来估算结果的计算方法。由于计算结果的精确度很大程度上取决于抽取样本的数量,一般需要大量的样本数据,因此在没有计算机的时代并没有受到重视。 第二次世界大战时期,美国曼哈顿原子弹计划的主要科学家之一,匈牙利美藉数学家约翰·冯·诺伊曼(现代电子计算机创始人之一)在研究物质裂变时中子扩散的实验中采用了随机抽样统计的手法,因为当时随机数的想法来自掷色子及轮盘等赌博用具,因此他采用摩洛哥著名赌城蒙特卡罗来命名这种计算方法,为这种算法增加了一层神秘色彩。 蒙特卡罗方法提出的初衷是用于物理数值模拟问题, 后来随着计算机的快速发展, 这一方法很快在函数值极小化、计算几何、组合计数等方面得到应用, 于是它作为一种独立的方法被提出来, 并发展成为一门新兴的计算科学, 属于计算数学的一个分支。如今MC方法已是求解科学、工程和科学技术领域大量应用问题的常用数值方法。 2、蒙特卡洛方法的核心—随机数 蒙特卡洛方法的基本理论就是通过对大量的随机数样本进行统计分析,从而得到我们所需要的变量。因此蒙特卡洛方法的核心就是随机数,只有样本中的随机数具有随机性,所得到的变量值才具有可信性和科学性。
在连续型随机变量的分布中, 最基本的分布是[0, 1]区间上的均匀分布, 也称单位均匀分布。由该分布抽取的简单子样ξ1,ξ2ξ3……称为随机数序列, 其中每一个体称为随机数, 有时称为标准随机数或真随机数, 独立性和均匀性是其必备的两个特点。真随机数是数学上的抽象, 真随机数序列是不可预计的, 因而也不可能重复产生两个相同的真随机数序列。真随机数只能用某些随机物理过程来产生, 如放射性衰变、电子设备的热噪音、宇宙射线的触发时间等。 实际使用的随机数通常都是采用某些数学公式产生的,称为伪随机数。真随机数只是一种数学的理想化概念,实际中我们所接触到的和使用的都是伪随机数。要把伪随机数当成真随机数来使用, 必须要通过随机数的一系列的统计检验。 无论伪随机数用什么方法产生,它的局限性都在于这些随机数总是一个有限长的循环集合, 而且序列偏差的上确界达到最大值。所以若能产生低偏差的确定性序列是很有用的,产生的序列应该具有这样的性质, 即任意长的子序列都能均匀地填充函数空间。 人们已经产生了若干种满足这个要求的序列,如Halton序列、Faure序列、Sobol序列和Niederreiter序列等。称这些序列为拟随机数序列。伪随机序列是为了模拟随机性, 而拟随机序列更致力于均匀性。 3、蒙特卡洛方法的原理 当问题可以抽象为某个确定的数学问题时,应当首先建立一个恰当的概率模型,即确定某个随机事件A或随机变量X,使得待求的解等
蒙特卡罗仿真原理 蒙特卡罗(MonteCarlo)方法,又称随机抽样或统计模拟方法,泛指所有基于统计采样进行数值计算的方法。在第二次世界大战期间,美国参与“曼哈顿计划’’的几位科学家Stanislaw Ulam,John Von Neumann 和N.Metropolis等首先将这种方法用于解决原子弹研制中的一个关键问题。后来N.Metropolis用驰名世界的赌城---摩纳哥的MonteCarlo一来命名这种方法,为它蒙上了一层神秘色彩。随着现代计算机技术的飞速发展,蒙特卡罗方法已经在统计物理、经济学、社会学甚至气象学等方面的科学研究中发挥了极其重要的作用,将蒙特卡罗方法用于仿真即为蒙特卡罗仿真。蒙特卡罗方法适用于两类问题,第一类是本身就具有随机性的问题,第二类是能够转化为概率模型进行求解的确定性问题。 ※蒙特卡罗方法求解问题的一般步骤 用蒙特卡罗方法求解问题一般包括构造或描述概率过程、从已知概率分布抽样和建立估计量三个步骤。 构造或描述概率过程实际上就是建立随机试验模型,构造概率过程是对确定性问题而言的,描述概率过程是对随机性问题而言的,不同的问题所需要建立的随机试验模型各不相同。 所谓的从已知概率分布抽样指的是随机试验过程,随机模型中必要包含某些已知概率分布的随机变量或随机过程作为输入,进行随机试验的过程就是对这些随机变量的样本或随机过程的样本函数作为输入产生相应输出的过程,因此通常被称为对已知概率分布的抽样。如何产生已知分布的随机变量或随机过程是蒙特卡罗方法中的一个关键问题。 最后一个步骤是获得估计量,蒙特卡罗方法所得到的问题的解总是对真实解的一个估计,本身也是一个随机变量,这个随机变量是由随机试验模型输出通过统计处理得到的。
蒙特卡洛习题 1.利用蒙特卡洛计算数值积分 () ()() 1280ln 1tan x x x xe dx +++? clear all ;clc;close all ; n=1000; count=0; x=0:0.01:1; y=log((1+x).^2+(tan(x).^8)+x.*exp(x)); plot(x,y,'linewidth',2) hold on for i=1:n x1=rand; y1=rand*y(end); plot(x1,y1,'g*') pause(0.01) if y1 2.分别用理论计算和计算机模拟计算,求连续掷两颗骰子,点数之和大于6且第一次掷出的点数大于第二次掷出点数的概率。 clear all;clc;close all; count=0; n=100000; for i=1:n x=floor(rand*6+1); y=ceil(rand*6); if x+y>6&&x>y count=count+1; end end P=count/n 3. clear all;clc;close all; count=0; n=2000; ezplot('x^2/9+y^2/36=1'); hold on ezplot('x^2/36+y^2=1'); hold on ezplot('(x-2)^2+(y+1)^2=9') for i=1:n x=rand*12-6; y=rand*12-6; plot(x,y,'gh','linewidth',2) pause(0.01) if x^2/9+y^2/36<1&&x^2/36+y^2<1&&(x-2)^2+(y+1)^2<9 蒙特卡罗也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。蒙特卡罗方法的名字来源于摩纳哥的一个城市蒙地卡罗,该城市以赌博业闻名,而蒙特·罗方法正是以概率为基础的方法。与它对应的是确定性算法。 蒙特卡罗方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。 基本思想 当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。有一个例子可以使你比较直观地了解蒙特卡罗方法:假设我们要计算一个不规则图形的面积,那么图形的不规则程度和分析性计算(比如,积分)的复杂程度是成正比的。蒙特卡罗方法是怎么计算的呢?假想你有一袋豆子,把豆子均匀地朝这个图形上撒,然后数这个图形之中有多少颗豆子,这个豆子的数目就是图形的面积。当你的豆子越小,撒的越多的时候,结果就越精确。在这里我们要假定豆子都在一个平面上,相互之间没有重叠。 工作过程 在解决实际问题的时候应用蒙特卡罗方法主要有两部分工作: 用蒙特卡罗方法模拟某一过程时,需要产生各种概率分布的随机变量。 用统计方法把模型的数字特征估计出来,从而得到实际问题的数值解。 计算步骤 使用蒙特卡罗方法进行分子模拟计算是按照以下步骤进行的: ① 使用随机数发生器产生一个随机的分子构型。 ②对此分子构型的其中粒子坐标做无规则的改变,产生一个新的分子构型。 ③计算新的分子构型的能量。 ④比较新的分子构型于改变前的分子构型的能量变化,判断是否接受该构型。 若新的分子构型能量低于原分子构型的能量,则接受新的构型,使用这个构型重复再做下一次迭代。 若新的分子构型能量高于原分子构型的能量,则计算玻尔兹曼常数,同时产生一个随机数。 蒙特卡罗方法的解题过程可以归结为三个主要步骤:构造或描述概率过程;实现从已知概率分布抽样;建立各种估计量。 蒙特卡罗方法解题过程的三个主要步骤: (1)构造或描述概率过程 对于本身就具有随机性质的问题,如粒子输运问题,主要是正确描述和模拟这个概率过程,对于本来不是随机性质的确定性问题,比如计算定积分,就必须事先构造一个人为的概率过程,它的某些参量正好是所要求问题的解。即要将不具有随机性质的问题转化为随机性质的问题。 (2)实现从已知概率分布抽样 构造了概率模型以后,由于各种概率模型都可以看作是由各种各样的概率分布构成的,因此产生已知概率分布的随机变量(或随机向量),就成为实现蒙特卡罗方法模拟实验的基本手段,这也是蒙特卡罗方法被称为随机抽样的原因。最简单、最基本、最重要的一个概率分布是(0,1)上的均匀分布(或称矩形分布)。随机数就是具有这种均匀分布的随机变量。随机数序列就是具有这种分布的总体的一个简单子样,也就是一个具有这种分布的相互独立的随机变数序列。产生随机数的问题,就是从这个分布的抽样问题。在计算机上,可以用物理方法产生随机数,但价格昂贵,不能重复,使用不便。另一种方法是用数学递推公式产生。这样产生的序列,与真正的随机数序列不同,所以称为伪随机数,或伪随机数序列。不过,经过多种统计检验表明,它与真正的随机数,或随机数序列具有相近的性质,因此可把它作为真正的随机数来使用。由已知分布随机抽样有各种方法,与从(0,1)上均匀分布抽样不同,这些方法都是借助于随机序列来实现的,也就是说,都是以产生随机数为前提的。由此可见,随机数是我们实现蒙特卡罗模拟的基本工具。 (3)建立各种估计量 一般说来,构造了概率模型并能从中抽样后,即实现模拟实验后,我们就要确定一个随机变量,作为所要求的问题的解,我们称它为无偏估计。建立各种估计量,相当于对模拟实验的结果进行考察和登记,从中得到问题的解。 蒙特卡洛法模拟蒲丰(Buffon)投针实验-使用Matlab 2010年03月31日星期三8:47 蒲丰投针实验是一个著名的概率实验,其原理请参见此页: https://www.doczj.com/doc/dc616789.html,/reese/buffon/buffon.html 现在我们利用Matlab来做模拟,顺便说一下,这种随机模拟方法便是传说中的“蒙特- 期权定价中的蒙特卡洛模拟方法 期权作为最基础的金融衍生产品之一,为其定价一直是金融工程的重要研究领域,主要使用的定价方法有偏微分方程法、鞅方法和数值方法。而数值方法又包括了二叉树方法、有限差分法和蒙特卡洛模拟方法。 蒙特卡洛方法的理论基础是概率论与数理统计,其实质是通过模拟标的资产价格路径预测期权的平均回报并得到期权价格估计值。蒙特卡洛方法的最大优势是误差收敛率不依赖于问题的维数,从而非常适宜为高维期权定价。 §1. 预备知识 ◆两个重要的定理:柯尔莫哥洛夫(Kolmogorov)强大数定律和莱维一林德贝格(Levy-Lindeberg)中心极限定理。 大数定律是概率论中用以说明大量随机现象平均结果稳定性的一系列极限定律。在蒙特卡洛方法中用到的是随机变量序列同分布的Kolmogorov 强大数定律: 设12,,ξξL 为独立同分布的随机变量序列,若 [],1,2,k E k ξμ=<∞=L 则有1 1(lim )1n k n k p n ξμ→∞===∑ 显然,若12,,,n ξξξL 是由同一总体中得到的抽样,那么由 此大数定律可知样本均值1 1n k k n ξ=∑当 n 很大时以概率1收敛于 总体均值μ。 中心极限定理是研究随机变量之和的极限分布在何种情形下是正态的,并由此应用正态分布的良好性质解决实际问题。 设12,,ξξL 为独立同分布的随机变量序列,若 2 [],[],1,2,k k E D k ξμξσ=<∞=<∞=L (0,1)n k d n N ξ μ -??→∑ 其等价形式为2 1 1lim ()exp(),2n x k k n t n P x dt x ξμσ =→∞ -∞ -≤= --∞<<∞∑?。 ◆Black-Scholes 期权定价模型 模型的假设条件: 1、标的证券的价格遵循几何布朗运动 dS dt dW S μσ=+ 其中,标的资产的价格S 是时间t 的函数,μ为标的资产 的瞬时期望收益率,σ为标的资产的波动率,dW 是维纳过程。 2、证券允许卖空、证券交易连续和证券高度可分。 3、不考虑交易费用或税收等交易成本。 4、在衍生证券的存续期内不支付红利。 5、市场上不存在无风险的套利机会。 6、无风险利率r 为一个固定的常数。 下面,通过构造标的资产与期权的资产组合并根据无套利定价原理建立期权定价模型。首先,为了得到期权的微分形式,先介绍随机微积分中的最重要的伊藤公式。 蒙特卡罗方法及应用 实验讲义 东华理工大学核工系 2016.8 实验一 蒙特卡罗方法基本思想 一、实验目的 1、了解蒙特卡罗方法方法的基本思想; 2、掌握蒙特卡罗方法计算面积、体积的方法; 3、掌握由已知分布的随机抽样方法。 二、实验原理 Monte Carlo 方法,又称统计模拟方法或计算机随机模拟方法,是一种基于“随机数”进行数值模拟的方法,一种采用统计抽样理论近似求解物理或数学问题的方法。 如待求量可以表述成某些特征量的期望值、某些事件出现的概率或两者的函数形式,那么可采用蒙特卡罗方法求解。在求解某些特征量的期望值或某些事件出现的概率时,必须构建合符实际的数学模型。例如采用蒙特卡罗方法计算某函数所围面积时,构建的数学模型是构造一已知面积的可均匀抽样区域,在该区域投点,由伯努利定理大数定理可知,进入待求区域投点的频率依概率1收敛于该事件出现的概率(面积之比)。 由已知分布的随机抽样方法指的是由已知分布的总体中抽取简单子样。具体方法很多,详见教材第三章。 三、实验内容 1、安装所需计算工具(MATLAB 、fortran 、C++等); 2、学习使用rand(m,n)、unifrnd(a,b,m,n)函数 3、求解下列问题: 3.0、蒲丰氏投针求圆周率。 3.1、给定曲线y =2 – x 2 和曲线y 3 = x 2,曲线的交点为:P 1( – 1,1 )、P 2( 1,1 )。曲线围成平面有限区域,用蒙特卡罗方法计算区域面积; 3.2 、计算1z z ?≥??≤??所围体积 其中{(,,)|11,11,02}x y z x y z Ω=-≤≤-≤≤≤≤。 4、对以下已知分布进行随机抽样: 运用蒙特卡罗模拟进行风险分析 蒙特卡罗模拟由著名的摩纳哥赌城而得名,他是一种非常强有力的方法学。对专业人员来说,这种模拟为方便的解决困难而复杂的实际问题开启了一扇大门。估计蒙特卡罗模拟最著名的早期使用是诺贝尔奖物理学家Enrico Fermi(有时也说是原子弹之父)在1930年的应用,那时他用一种随机方法来计算刚发现的中子的性质。蒙特卡罗模拟是曼哈顿计划所用到的模拟的核心部分,在20世纪50年代蒙特卡罗模拟就用在Los Alamos国家实验室发展氢弹的早期工作中,并流行于物理学和运筹学研究领域。兰德公司和美国空军是这个时期主要的两个负责资助和传播蒙特卡罗方法的组织,今天蒙特卡罗模拟也被广泛应用于不同的领域,包括工程,物理学,研发,商业和金融。 简而言之,蒙特卡罗模拟创造了一种假设的未来,它是通过产生数以千计甚至成千上万的样本结果并分析他们的共性实现的。在实践中,蒙特卡罗模拟法用于风险分析,风险鉴定,敏感度分析和预测。模拟的一个替代方法是极其复杂的随机闭合数学模型。对一个公司的分析,使用研究生层次的高等数学和统计学显然不合逻辑和实际。一个出色的分析家会使用所有他或她可得的工具以最简单和最实际的方式去得到相同的结果。任何情况下,建模正确时,蒙特卡罗模拟可以提供与更完美的数学方法相似的答案。此外,有许多实际生活应用中不存在闭合模型并且唯一的途径就是应用模拟法。那么,到底什么是蒙特卡罗模拟以及它是怎么工作的? 什么是蒙特卡罗模拟? 今天,高速计算机使许多过去看来棘手的复杂计算成为可能。对科学家,工程师,统计学家,管理者,商业分析家和其他人来说,计算机使创建一个模拟现实的模型成为可能,这有助于做出预测,其中一种方法应用于模拟真实系统,它通过调查数以百计甚至数以千计的可能情况来解释随机性和未来不确定性。结果通过编译后用于决策。这就是蒙特卡罗模拟的全部内容。 形式最简单的蒙特卡罗模拟是一个随机数字生成器,它对预测,估计和风险分析都很有用。一个模拟计算模型的许多情况,这通过反复地从预先定义的特定变量概率分布中采集数据并将之应用于模型来实现。因为所有的情况都产生相应的结果,每种情况都可以蕴含一种预测。预测的是你定义为重要模型结果的事项(通常含有公式或函数)。 将蒙特卡罗模拟法想象为从一个大篮子里可放回的反复拿出高尔夫球。拦在的大小和形 蒙特卡罗随机模拟投点法在数字积分中的 应用 数学与应用数学0901班:张瑞宸 指导老师:任明慧 摘要:本文首先介绍了蒙特卡罗方法的产生和发展,然后分析了蒙特卡罗方法计算数值积分的理论原理,最后给出了蒙特卡罗方法计算数值积分的MATLAB编程实现,全文主要是讨论了蒙特卡罗方法在定积分计算的应用。而蒙特卡罗的优点:可以计算被积函数非常复杂的定积分、重积分,并且维数没有限制,这是别的数值积分方法还未达到的。蒙特卡罗的缺点:收敛速度慢,误差一般较大,且是概率的误差,不是真正的误差。 关键词:蒙特卡罗方法,均值估计法,数值积分,Matlab编程 Abstract:This paper first introduces the emergence and development of the Monte Carlo method, and then analyze the theoretical principles of Monte Carlo numerical integration method, Full-text mainly discussed the application of the Monte Carlo method in the definite integral. The advantages of Monte Carlo: can be calculated the integrable functions very complex definite integral, Multiple integrals, and dimension no limit, other numerical integration methods have not yet reached. Monte Carlo Disadvantages: slow convergence speed, error generally higher, and the probability of error, not a real error. Keywords: Monte Carlo method,Mean estimation method,numerical integral,Matlab programming 0 引言 历史上有记载的蒙特卡罗试验始于十八世纪末期(约1777年),当时布丰(Buffon)为了计算圆周率,设计了一个“投针试验”,后文会给出。虽然方法已经存在了200多年,此方法命名为蒙特卡罗则是在二十世纪四十年,美国原子弹计划的一个子项目需要使用蒙特卡罗方法模拟中子对某种特殊材料的穿透作用。出于保密缘故,每个项目都要一个代号,传闻命名代号时,项目负责人之一von Neumann灵犀一点选择摩洛哥著名赌城蒙特卡罗(Monte Carlo)作为该项目名称,自此这种方法也就被命名为Monte Carlo方法广为流传。 蒙特卡罗方法,又名随机模拟法或统计实验法它是以概率统计理论为基础,依据大数定律(样本均值替代总体均值)利用电子计算机数字模拟技术,解 蒙特卡洛模拟法 蒙特卡洛(Monte Carlo)模拟是一种通过设定随机过程,反复生成时间序列,计算参数估计量和统计量,进而研究其分布特征的方法。具体的,当系统中各个单元的可靠性特征量已知,但系统的可靠性过于复杂,难以建立可靠性预计的精确数学模型或模型太复杂而不便应用时,可用随机模拟法近似计算出系统可靠性的预计值;随着模拟次数的增多,其预计精度也逐渐增高。由于涉及到时间序列的反复生成,蒙特卡洛模拟法是以高容量和高速度的计算机为前提条件的,因此只是在近些年才得到广泛推广。 这个术语是二战时期美国物理学家Metropolis执行曼哈顿计划的过程中提出来的。 蒙特卡洛模拟方法的原理是当问题或对象本身具有概率特征时,可以用计算机模拟的方法产生抽样结果,根据抽样计算统计量或者参数的值;随着模拟次数的增多,可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。 蒙特卡洛模拟法的应用领域 蒙特卡洛模拟法的应用领域主要有: 1.直接应用蒙特卡洛模拟:应用大规模的随机数列来模拟复杂系统,得到某些参数或重要指标。 2.蒙特卡洛积分:利用随机数列计算积分,维数越高,积分效率越高。 3.MCMC:这是直接应用蒙特卡洛模拟方法的推广,该方法中随机数的产生是采用的马尔科夫链形式。 (也叫随机模拟法)当系统中各个单元的可靠性特征量已知,但系统的可靠性过于复杂,难以建立可靠性预计的精确数学模型或模型太复杂而不便应用则可用随机模拟法近似计算出系统可靠性的预计值。随着模拟次数的增多,其预计精度也逐渐增高。由于需要大量反复的计算,一般均用计算机来完成。 应用此方法求解工程技术问题可以分为两类:确定性问题和随机性问题。解题步骤如下: 1.根据提出的问题构造一个简单、适用的概率模型或随机模型,使问题的解对应于该模型中随机变量的某些特征(如概率、均值和方差等),所构造的模型在主要特征参量方面要与实际问题或系统相一致 2 .根据模型中各个随机变量的分布,在计算机上产生随机数,实现一次模拟过程所需的足够数量的随机数。通常先产生均匀分布的随机数,然后生成服从某一分布的随机数,方可进行随机模拟试验。 例在我方某前沿防守地域,敌人以一个炮排(含两门火炮)为单位对我方进行干扰和破坏.为躲避我方打击,敌方对其阵地进行了伪装并经常变换射击地点. 经过长期观察发现,我方指挥所对敌方目标的指示有50%是准确的,而我方火力单位,在指示正确时,有1/3的射击效果能毁伤敌人一门火炮,有1/6的射击效果能全部毁伤敌人火炮. 现在希望能用某种方式把我方将要对敌人实施的20次打击结果显现出来,确定有效射击的比率及毁伤敌方火炮的平均值。 使用蒙特卡洛方法模拟50次打击结果: function [out1 out2 out3 out4]=Msc(N) % N开炮次数 % out1射中概率 % out2平均每次击中次数 % out3击中敌人一门火炮的射击总数 % out4击中敌人2门火炮的射击总数 k1=0; k2=0; k3=0; for i=1:N x0=randperm(2)-1; y0=x0(1); if y0==1 fprintf('第%d次:指示正确||',i); x1=randperm(6); y1=x1(1); if y1==1|y1==2|y1==3 fprintf('第%d次:击中0炮||',i); k1=k1+1; elseif y1==4|y1==5 fprintf('第%d次:击中1炮||',i); k2=k2+1; else fprintf('第%d次:击中2炮||',i); k3=k3+1; end else fprintf('第%d次:指示错误,击中0炮||',i); k1+1; end fprintf('\n'); end out1=(k2+k3)/N; out2=(0*k1+k2+2*k3)/20; out3=k2/N; out4=k3/N; 运行: 1.[out1 out2 out3 out4]=Msc(50) 结果: 1.第1次:指示正确||第1次:击中2炮|| 2.第2次:指示错误,击中0炮|| 3.第3次:指示错误,击中0炮|| 4.第4次:指示正确||第4次:击中0炮|| 5.第5次:指示错误,击中0炮|| 6.第6次:指示正确||第6次:击中1炮|| 7.第7次:指示正确||第7次:击中0炮|| 8.第8次:指示错误,击中0炮|| 9.第9次:指示正确||第9次:击中2炮|| 10.第10次:指示正确||第10次:击中1炮|| 11.第11次:指示正确||第11次:击中1炮|| 12.第12次:指示正确||第12次:击中2炮|| 13.第13次:指示错误,击中0炮|| 14.第14次:指示正确||第14次:击中1炮|| 15.第15次:指示错误,击中0炮|| 16.第16次:指示错误,击中0炮|| 17.第17次:指示正确||第17次:击中0炮|| 18.第18次:指示错误,击中0炮|| 蒙特卡洛方法及其应用 1风险评估及蒙特卡洛方法概述 1.1蒙特卡洛方法。 蒙特卡洛方法,又称随机模拟方法或统计模拟方法,是在20世纪40年代随着电子计算机的发明而提出的。它是以统计抽样理论为基础,利用随机数,经过对随机变量已有数据的统计进行抽样实验或随机模拟,以求得统计量的某个数字特征并将其作为待解决问题的数值解。 蒙特卡洛模拟方法的基本原理是:假定随机变量X1、X2、X3……X n、Y,其中X1、X2、X3……X n 的概率分布已知,且X1、X2、X3……X n、Y有函数关系:Y=F(X1、X2、X3……X n),希望求得随机变量Y的近似分布情况及数字特征。通过抽取符合其概率分布的随机数列X1、X2、X3……X n带入其函数关系式计算获得Y的值。当模拟的次数足够多的时候,我们就可以得到与实际情况相近的函数Y的概率分布和数字特征。 蒙特卡洛法的特点是预测结果给出了预测值的最大值,最小值和最可能值,给出了预测值的区间范围及分布规律。 1.2风险评估概述。 风险表现为损损益的不确定性,说明风险产生的结果可能带来损失、获利或是无损失也无获利,属于广义风险。正是因为未来的不确定性使得每一个项目都存在风险。对于一个公司而言,各种投资项目通常会具有不同程度的风险,这些风险对于一个公司的影响不可小视,小到一个项目投资资本的按时回收,大到公司的总风险、公司正常运营。因此,对于风险的测量以及控制是非常重要的一个环节。 风险评估就是量化测评某一事件或事物带来的影响的可能程度。根据“经济人”假设,收益最大化是投资者的主要追求目标,面对不可避免的风险时,降低风险,防止或减少损失,以实现预期最佳是投资的目标。 当评价风险大小时,常有两种评价方式:定性分析与定量分析法。定性分析一般是根据风险度或风险大小等指标对风险因素进行优先级排序,为进一步分析或处理风险提供参考。这种方法适用于对比不同项目的风险程度,但这种方法最大的缺陷是在于,在多个项目中风险最小者也有可能亏损。而定量分析法则是将一些风险指标量化得到一系列的量化指标。通过这些简单易懂的指标,才能使公司的经营者、投资者对于项目分风险有正确的评估与判断, 产业与科技论坛2012年第11卷第17期 2012.(11).17 Industrial &Science Tribune 蒙特卡罗仿真的原理及应用 □戚苇苇 【内容摘要】蒙特卡罗法又称随机抽样技巧法或统计试验法,在目前结构可靠度计算中,它被认为是一种相对精确法,具有在计 算机上实现蒙特卡罗计算时程序结构清晰简单,便于编制和调试的特点。【关键词】通信技术;蒙特卡罗法;仿真;误码率 【作者单位】戚苇苇,江苏省扬州技师学院 一、通信仿真概述 (一)通信的基本概念以及分类。通信是通过某种媒体进行的信息传递。古代,人们通过驿站、飞鸽传书、烽火报警 等方式进行信息传递。今天, 随着科学水平的飞速发展,相继出现了无线电,固话,手机,互联网甚至可视电话等各种通 信方式。对于点到点之间的通信, 按消息传送的方向与时间的关系,通信方式可分为:单工通信、半双工通信、全双工通 信。数字通信中,按照数字信号码元排列方法不同,通信方式可分为:串行传输和并行传输。 (二)通信系统的组成。 1.信息源。信源是发出信息的源,其作用是把各种可能消息转换成原始电信号。信源可分为模拟信源和数字信源。模拟信源(如电话机、电视摄像机)输出连续幅度的模拟信号;数字信源(如电传机、计算机等各种数字终端设备)输出 离散的数字信号。 2.变换器。因语声、图像等原始的消息不能以电磁波来传送,所以需要通过变换器将原始的非电消息变换成电信号,并再对这种电信号进一步转换,使其变换成适合某种具体信道传输的电信号。这种电信号同样载有原有的信息。例如电话机的送话器,就是将语声变换成幅度连续变化的电话信号,再进一步转换后送到信道上去。 3.信道。信道是指传输信号的通道,可以是有线的,也可以是无线的,有线和无线均有多种传输媒质。信道既给信号以通路,也对信号产生各种干扰和噪声。传输媒质的固有特性和干扰直接关系到通信的质量。 4.反变换器。反变换器的基本功能是完成变换器的反继续提升水头,管涌便不断向上游发展直至达到临界坡降,此时管涌通道便不能趋于稳定,不断有砂粒起动运移一直到与上游连通,连通的管涌水流强力冲刷堤基并最终导致堤基整体破坏和溃堤。 产生上述现象的原因是:孔口处出现沙沸使地基砂体液化,继续增加水头,砂粒便会从沙沸处向外涌出形成砂环,由于堤基砂层的水平破坏坡降比垂直破坏坡降要小得多,因此地基便会有砂粒从沙沸处涌出形成管涌通道,在未达到临界坡降前管涌通道最终趋于稳定,这是由于砂粒向沙沸处输送,积聚在孔口附近具有了一定的反滤作用,从而加大了局部水头损失,还有管涌通道中的砂粒被水流带出堆积在沙沸处形成砂环,从而抬升了水位降低了有效作用水头。由于地基砂粒的离散性具有随机性,因此这种稳定需要很长时间,条件的微小改变就有可能打破这种稳定,因此时间是影响管涌破坏发生与否非常重要的因素。 (三)管涌破坏位置分析。管涌产生的位置都是发生在强弱透水层接触面的浅层,对深层地基的渗流并无影响,其主要原因是:一是堤基砂层顶面的渗径最短因此此处水平水力坡降最大;二是堤基砂层的水平破坏坡降比垂直破坏坡降要小得多。 三、结语 堤基管涌发展的原因主要是在水平渗透力作用下的水平向浅层破坏。因此,垂直防渗是在发生管涌后地基渗透破 坏治理的优选方法。堤基管涌通道能否趋于稳定与管涌口是否涌砂有很大关系。所以,反滤压盖阻止堤基管涌通道内的砂粒持续涌出应当作为抗洪抢险时的首选。管涌通道趋于稳定的主要原因是:管涌通道的发展使管涌通道前端堤基砂层的水平渗透比降逐渐降低,和管涌口垂直破坏坡降不断增大,直至等于砂层的局部破坏比降。【参考文献】1.刘忠玉,乐金朝,苗天德.无黏性土中管涌的毛管模型及其应用[ J ].岩石力学与工程学报,20042.毛昶熙,段祥宝,蔡金傍,茹建辉.堤基渗流管涌发展的理论分析[J ].水利学报,20043.李广信,周晓杰.堤基管涌发生发展过程的试验模拟[J ].水利水电科技进展,20054.姚秋玲,丁留谦.单层和双层堤基管涌砂槽模型试验研究[J ].水利水电技术,2007 5.陈建生,李兴文,赵维炳.堤防管涌产生集中渗漏通道机理与探测方法研究[J ].水利学报,20006.朱伟,山村和也.日本阿武隈川的洪水灾害及其综合治理[J ].河海大学学报,2000 7.郭书亮.堤基管涌模型试验及形成机理研究[D ].河北工程大学, 2012· 67· 二、蒙特卡洛模拟原理及步骤 (一)蒙特卡洛模拟原理:经济生活中存在大量的不确定与风险问题,很多确定性问题实际上是不确定与风险型问题的特例与简化,财务管理、管理会计中同样也存在大量的不确定与风险型问题,由于该问题比较复杂,一般教材对此问题涉及较少,但利用蒙特卡洛模拟可以揭示不确定与风险型问题的统计规律,还原一个真实的经济与管理客观面貌。 与常用确定性的数值计算方法不同,蒙特卡洛模拟是用来解决工程和经济中的非确定性问题,通过成千上万次的模拟,涵盖相应的可能概率分布空间,从而获得一定概率下的不同数据和频度分布,通过对大量样本值的统计分析,得到满足一定精度的结果,因此蒙特卡洛模拟是进行不确定与风险型问题的有力武器。 1、由于蒙特卡洛模拟是以实验为基础的,因此可以成为财务人员进行风险分析的“实验库”,获得大量有关财务风险等方面的信息,弥补确定型分析手段的不足,避免对不确定与风险决策问题的误导; 2、财务管理、管理会计中存在大量的不确定与风险型问题,目前大多数教材很少涉及这类问题,通过蒙特卡洛模拟,可以对其进行有效分析,解决常用决策方法所无法解决的难题,更加全面深入地分析不确定与风险型问题。 (二)蒙特卡洛模拟步骤以概率型量本利分析为例,蒙特卡洛模拟的分析步骤如下: 1、分析评价参数的特征,如企业经营中的销售数量、销售价格、产品生产的变动成本以及固定成本等,并根据历史资料或专家意见,确定随机变量的某些统计参数; 2、按照一定的参数分布规律,在计算机上产生随机数,如利用EXCEL提供的RAND函数,模拟量本利分析的概率分布,并利用VLOOKUP寻找对应概率分布下的销售数量、销售价格、产品生产的变动成本以及固定成本等参数; 3、建立管理会计的数学模型,对于概率型量本利分析有如下关系式,产品利润=产品销售数量×(产品单位销售价格-单位变动成本)-固定成本,这里需要说明的是以上分析参数不是确定型的,是依据某些概率分布存在的; 4、通过足够数量的计算机仿真,如文章利用RAND、VLOOKUP等函数进行30000次的模拟,得到30000组不同概率分布的各参数的排列与组合,由于模拟的数量比较大,所取得的实验数据具有一定的规律性; 5、根据计算机仿真的参数样本值,利用函数MAX、MIN、A VERAGE等,求出概率型量本利分析评价需要的指标值,通过对大量的评价指标值的样本分析,得到量本利分析中的利润点可能的概率分布,从而掌握企业经营与财务中的风险,为财务决策提供重要的参考。三、概率型量本利分析与比较 (一)期望值分析方法假设某企业为生产与销售单一产品的企业,经过全面分析与研究,预计未来年度的单位销售价格、销售数量、单位变动成本和固定成本的估计值及相应的概率如表1,其中销售数量单位为件,其余反映价值的指标单位为元,试计算该企业的生产利润。表1概率型量本利分析参数 项目概率数值 单位销售价格0.3 40 0.4 43 0.3 45 单位变动成本0.4 16 0.2 18 0.4 20 固定成本0.6 28000 0.4 30000蒙特卡罗也称统计模拟方法
蒙特卡罗方法的解题过程可以归结为三个主要步骤
(定价策略)期权定价中的蒙特卡洛模拟方法
蒙特卡罗方法及应用实验讲义2016资料
运用蒙特卡罗模拟进行风险分析
蒙特卡罗随机模拟投点法
蒙特卡洛模拟法
蒙特卡洛方法模拟小例子
蒙特卡洛方法及其在风险评估中的应用
蒙特卡罗仿真的原理及应用
蒙特卡洛模拟原理及步骤