当前位置：文档之家› 二次函数图像中三角形面积最值问题(一)

二次函数图像中三角形面积最值问题(一)

二次函数和三角形面积的综合

二次函数与三角形面积的综合寻找类 1、重点：中考压轴题的重点在于寻找分析问题，解决问题的思路和方法。能应对这部分题的关键需要熟练几部分知识点：（1）二次函数与一次函数，反比例函数的解析式（2）勾股定理（3）四边形（4）相似三角形和三角形全等（5）锐角三角函数（6）轴对称和中心对称（7）求交点的方法（8）知识的综合运用 2、难点：寻找联系是这部分内容的一个关键所在，也是一个难点。尤其是遇到二次函数与三角形面积的综合题的解题思路。运用面积求坐标等等的合理运用，以及运用的重要因素在哪里？ 3、易错点：面积中涉及求面积的方法，坐标漏找或错找，坐标与线段长度之间的联系，坐标在不在二次函数的图像上。这些都是在考试中容易失分的地方。 4、切入点：例如：根据已有条件求坐标，首先要想到平面直角坐标系与锐角三角函数的联系，尤其是正切的运用。这样直观的可以求出坐标（前提必须建立直角三角形），如果不是直角三角形可以想法构建直角三角形，这是求坐标的最好方法，此方法不通的情况下可以运用勾股定理进行求解，很少运用相似求。掌握了求解方法再做题的时候就知道如何下手了。而次部分求面积的时候要先找到点的坐标的具体位置以及如何通过面积求坐标。 5.求面积常用的方法 a.直接法b。简单的组合c。面积不变同底等高或等底等高的转换 d.相似 e.三角函数f。找面积的最大最小值利用二次函数的性质（1）直接法若题已经给出或能由已知条件推出个边的长度并且通过坐标能找到对应的

的高，那么三角形的面积能直接用公式算出来。此题中的三角形的面积就能直接求出。（2）通过简单的重新组合就能求出面积。第6题（2009年贵州安顺市）27、（本题满分12分）如图，已知抛物线与x交于A(－1，0)、E(3，0)两点，与y轴交于点B(0，3)。

求二次函数中三角形面积最大值压轴题专题汇编

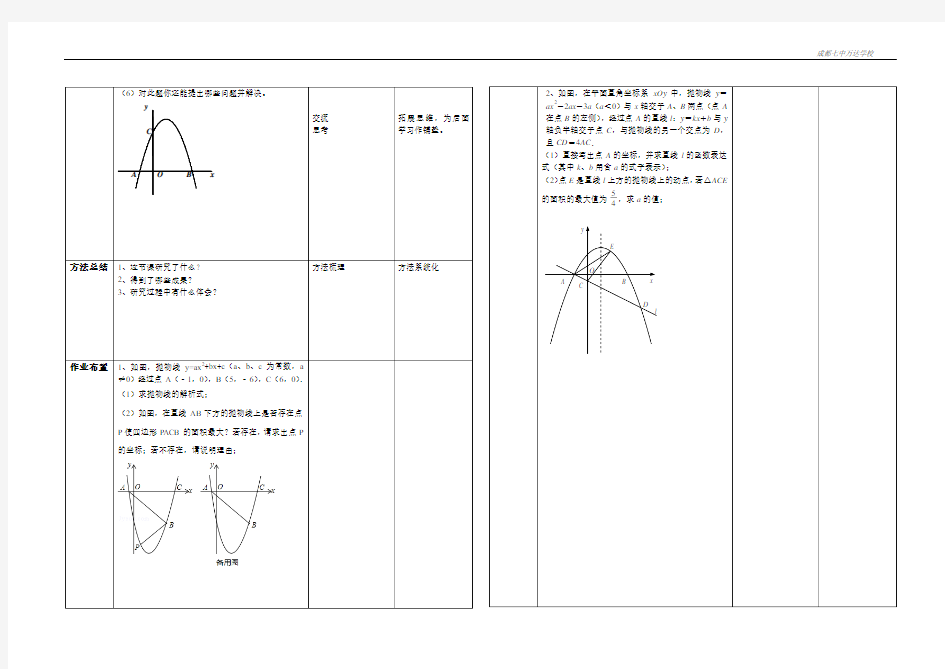
M N B C x A O y 求二次函数中三角形面积最大值压轴题专题汇编 28．（甘肃白银）如图，已知二次函数24y ax bx =++的图象与x 轴交于点()2,0B -，点()8,0C ，与y 轴交于点A ．（1）求二次函数24y ax bx =++的表达式；（2）连接,AC AB ，若点N 在线段BC 上运动（不与点,B C 重合），过点N 作 //NM AC ，交AB 于点M ，当AMN ?面积最大时，求N 点的坐标；（3）连接OM ，在（2）的结论下，求OM 与A C 的数量关系．解：（1）将点B ，点C 的坐标分别代入24y ax bx =++，得：4240 64840a b a b -+=??++=? ， 1分解得：1 4 a =-，32 b =． ∴该二次函数的表达式为 213 442 y x x =-++． 3分（2）设点N 的坐标为（n ，0）（-2＜n ＜8），则2BN n =+，8CN n =-． ∵B （-2，0）, C （8，0）, ∴BC =10. 令0x =，解得：4y =， ∴点A （0，4），OA =4，

∵MN ∥AC ， ∴ 810 AM NC n AB BC -== ． 4分 ∵OA =4，BC =10， ∴1 14102022 ABC S BC OA =?=??=V ． 5分 11 22222 810ABN AMN ABN S BN OA n+n+S AM CN n , S AB CB = ?=?-===（）4=（）又V V V Q ∴2811 (8)(2)(3)51055 AMN ABN n S S n n n -= =-+=--+V V ． 6分 ∴当n =3时，即N （3，0）时，△AMN 的面积最大． 7 分（3）当N （3，0）时，N 为BC 边中点. ∴M 为AB 边中点，∴12 OM AB.= 8分 ∵AB = AC ∴12AB AC,= 9分 ∴1 4 OM AC =． 10分 24（海南）.抛物线23y ax bx =++经过点()1,0A 和点()5,0B 。（1）求该抛物线所对应的函数解析式；（2）该抛物线与直线3 35 y x = + 相交于C D 、两点，点P 是抛物线上的动点且位于x 轴下方。直线//PM y 轴，分别与x 轴和直线CD 交与点M N 、。 ①连结PC PD 、，如图12-1，在点P 运动过程中，PCD ?的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由； ②连结PB ，过点C 作CQ PM ⊥，垂足为点Q ，如图12-2。是否存在点P ，使得CNQ ?与PBM ?相似？若存在，求出满足条件的点P 的坐标；若不存在，说明理由。

二次函数与等腰三角形

以二次函数与等腰三角形问题为背景的解答题【学习目标】这类问题主要是以一点（或以一条线段）为依托，动点和函数思想相结合以几何图形为背景，以动点为元素,构造动态型几何问题。解此类题目，应从相关图形的性质和数量关系分类讨论来解决。此类问题较多地关注学生对图形性质的理解,用动态的观点去看待一般函数和图形结合的问题,具有较强的综合性. 【教学过程】解题思路：等腰三角形的存在性的解题方法：①几何法三步：先分类；再画图；后计算．② 代数法三步：先罗列三边；再分类列方程；后解方程、检验．再以二次函数与等腰三角形问题为背景的解答题中，这两种方法往往结合使用. 一、考点突破 12 例1、如图，已知抛物线y=﹣x2+bx+4 与x 轴相交于A、B两点，与y 轴相交于点C，若 4 已知 A 点的坐标为（﹣2，0）．（1）求抛物线的解析式； 2）连接AC、BC，求线段BC 所在直线的解析式； P，使△ACP为等腰三角形？若存在，求出符合条件的（3）在抛物线的对称轴上是否存在点P 点坐标；若不存在，请说明理

【例2】如图，在平面直角坐标系中，直线y=﹣2x+10与x 轴，y 轴相交于A，B 两点，点C 的坐标是（8，4），连接AC，BC．（1）求过O，A，C三点的抛物线的解析式，并判断△ABC的形状；（2）动点P从点O出发，沿OB以每秒 2 个单位长度的速度向点 B 运动；同时，动点Q 从点 B 出发，沿BC以每秒 1 个单位长度的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t 秒，当t 为何值时，PA=QA？（3）在抛物线的对称轴上，是否存在点M ，使以A，B，M 为顶点的三角形是等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．

二次函数中三角形面积问题

二次函数中三角形面积问题【典型例题】:如图，二次函数y=-x2+2x+3与y轴,x轴交于点A ,B，点C是直线AB上方抛物线上的一个动点（不与点A ，B重合），求△ABC面积的最大值．【方法一】竖割法：过点C作CD⊥x轴，垂足为D，交AB于点E， S△ABC＝S△ACE ＋S△BCE ＝1/2CE·(xc--xA)+1/2CE·(xB-xC)=1/2OB·CE 解：令x=0, y=3 点C的坐标为（0，3）；令y=0, 则-x2+2x+3=0 ，解得：x1=-1 x2=3 点B的坐标为（3，0），设AB所在直线的解析式为y=kx+b. 求出直线AB所在直线的解析式为y=-x+3. 设点E的坐标为（m,-m+3) ,则点C的坐标为（m, -m2+2m+3) CE=y C-y E= -m2+2m+3-(-m+3)= -m2+3m S△ABC＝S△ACE ＋S△BCE ＝1/2CE·(xc--xA)+1/2CE·(xB-xC) =1/2OB·CE =1/2×3( -m2+3m) =--3m2/2+9m/2 S△ABC最大值＝4ac-b2/4a=27/8 【方法二】割补法：连接OC，S△ABC＝S△OAC ＋S△OBC－S△OAB 解：S△ABC＝S△OAC＋S△OBC－S△OAB ＝1/2×OA·X C+1/2×OB·Y C-1/2×OA×OB ＝1/2×3×m+1/2×3×(-m2+2m+3)-1/2×3×3 ＝-3m2/2+9m/2 S△ABC最大值＝4ac-b2/4a=27/8 【方法三】平移法:平移直线AB，当直线AB与抛物线只有一个交点时，此时三角形ABC的面积最大。解：设和y=-x+3平行的动直线的解析式为y=-x+b,用y=-x+b和y=-x2+2x+3联立方程组得：-x+b=-x2+2x+3，整理得：x2－3x+b-3=0 当Δ＝0时，b=21/4,此时的点C的坐标为（3/2,9/2)。 SΔABC=(21/4-3)×3×1/2=27/8 【举一反三】 1.如图，已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E 点的坐标．

二次函数中三角形面积最大值综合题

精心整理 2017中考数学全国试题汇编------二次函数中三角形面积最大值综合题 28．（2017甘肃白银）如图，已知二次函数24y ax bx =++的图象与x 轴交于点()2,0B -，点()8,0C ，与y 轴交于点A ．（1）求二次函数24y ax bx =++的表达式；（2）AB 于点M （3∴ 810 AM NC n AB BC -== ．4分 ∵OA =4，BC =10， ∴11 4102022ABC S BC OA =?=??=V ．5分 ∴2811(8)(2)(3)51055 AMN ABN n S S n n n -==-+=--+V V ．6分 ∴当n =3时，即N （3，0）时，△AMN 的面积最大．7分（3）当N （3，0）时，N 为BC 边中点.

∴M 为AB 边中点，∴12 OM AB.=8分 ∵2241625AB OB OA =+=+=， 22641645AC OC OA =+=+=， ∴12AB AC,=9分 ∴1 4 OM AC =．10分 24（2017海南）.抛物线23y ax bx =++经过点()和点()。（1）求该抛物线所对应的函数解析式；（2）该抛物线与直线3 35 y x = +相交于C D 、两点，点P 是抛物线上的动点且位于x 轴下方。直线//PM y 轴，分别与x 轴和直线CD 交与点M N 、。 ①连结PC PD 、，如图12-1，在点P 运动过程中，PCD ?的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由； ②连结PB ，过点C 作CQ PM ⊥，垂足为点Q ，如图12-2。是否存在点P ，使得CNQ ?与PBM ?相似？若存在，求出满足条件的点P 的坐标；若不存在，说明理由。【分析】（1）由A 、B 两点的坐标，利用待定系数法可求得抛物线解析式；（2）①可设出P 点坐标，则可表示出M 、N 的坐标，联立直线与抛物线解析式可求得C 、D 的坐标，过C 、D 作PN 的垂线，可用t 表示出△PCD 的面积，利用二次函数的性质可求得其最大值； ②当△CNQ 与△PBM 相似时有 = 或 = 两种情况，利用P 点坐标，可分别表示出线段的长，可得到关于P 点坐标的方程，可求得P 点坐标．【解答】解：（1）∵抛物线y=ax 2+bx +3经过点A （1，0）和点B （5，0）， ∴，解得， ∴该抛物线对应的函数解析式为y=x 2﹣x +3；（2）①∵点P 是抛物线上的动点且位于x 轴下方， ∴可设P （t ，t 2﹣ t +3）（1＜t ＜5）， ∵直线PM ∥y 轴，分别与x 轴和直线C D 交于点M 、N ，

《周长固定三角形面积的最大值》

《周长固定三角形面积的最大值》——数学建模一例谈到，周长固定围成面积的问题，许多人会想到正方形和二次函数。好吧，就从矩形开始吧！问题是这样的，说有一根长度固定为L 的绳子，现在要围成一个矩形，问：什么样的矩形面积才是最大的？首先，我们要建立数学模型！那么什么是矩形呢？它有些什么性质呢？初等几何说：有一个角位直角（90°或者π/2）的平行四边形，叫做矩形。那么什么是平行四边形呢？它有些什么性质呢？几何又说：两组对边分别平行的四边形，叫做平行四边形。其中，平行四边形有一条重要的性质：平行四边形的对边相等。好了，现在我们对矩形也有一个印象了。简单来说是一个，四条互相垂直的线段组成的东西。而且我们知道它的面积公式：s=a*b，由平行四边形的性质：平行四边形的对边相等。可知它的周长公式：L=2*(a + b)。有了这些，就可以建模分析了：首先，我们分析L=2*(a + b)，经过简单的变形处理（+、-、*、/）有：b=L/2-a 要注意条件，a是不为0的，即（a>0）。现在，把b=L/2-a 代入s=a*b 就有：s=a*( L/2-a)= -a^2+ (L/2) *a （a>0）；这是关于a的一个二次函数，并且A=-1<0，函数s 有最大值。微积分的解法：因为：s= -a^2+ (L/2) *a （a>0），所以s`=-2a+L/2 （a>0）令 s`=0有：2a= L/2 所以a= L/4。所以Smax = L/4(L/2- L/4)= L^2/16 max：最大值 b=a= L/4 (此时，矩形为正方形) 也可以用不等式：因为 (a - b)^2≥0，又因(a - b)^2=(a + b)^2-4ab，所以有：(a + b)^2-4ab≥0 即a*b≤(a + b)^2/4 当a=b，去―=‖，s有最大值因为： a + b= L/2，s=a*b 所以：s≤（L/2）^2/4= L^2/16 。现在，来谈一谈周长固定三角形面积的问题，说有一根长度固定为L的绳子，现在要围成一个三角形，问：什么样的三角形面积才是最大的？好像，一般三角形的性质并不多，一个三边关系定理：三角形两边之和大于第三边。和一个内角和定理：三角形三个内角的和等于180°。还有个推论：三角形两边之差小于第三边。不妨设绳子L，围成的三角形一边为x，则另外两边之和为L-x 。根据三边关系定理有：x2c。可以，以2c=x 的中点建立坐标系，则：a^2= (L-x/2)^2 ，b^2= (L-x/2)^2-(x/2)^2=L(L-2x)/ 。三角形与椭圆所以椭圆方程为：X^2/(L-x/2)^2 +Y^2/ L(L+2x)/4=1 函数图像的直观反映，三角形的面积为：s=(1/2)*( 2c)*Y ，因为，x=2c是固定的，所以s取决于Y，当Y取max时，即Y=b 时，s有最大值。即：S=s(x)max （且此时，该三角形为等要三角形）=c*[(L^2-2Lx)/4]^1/2 =(1/4)*x(L^2-2Lx)^1/2 (0

二次函数与三角形综合题型

22．如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（，）和B（4，m），点P 是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．（1）求抛物线的解析式；（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；（3）求△PAC为直角三角形时点P的坐标． 20．如图，抛物线y=x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）若点M是抛物线在x轴下方上的动点，过点M作MN∥y轴交直线BC于点N，求线段MN的最大值；（3）在（2）的条件下，当MN取得最大值时，在抛物线的对称轴l上是否存在点P，使△PBN是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由． 23．已知抛物线C1的顶点为P（1，0），且过点（0，）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．（1）求抛物线C1的解析式的一般形式；（2）当m=2时，求h的值；

（3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF ﹣tan∠ECP=． 22．解：（1）∵B（4，m）在直线y=x+2上， ∴m=4+2=6， ∴B（4，6）， ∵A（，）、B（4，6）在抛物线y=ax2+bx+6上， ∴，解得， ∴抛物线的解析式为y=2x2﹣8x+6．（2）设动点P的坐标为（n，n+2），则C点的坐标为（n，2n2﹣8n+6）， ∴PC=（n+2）﹣（2n2﹣8n+6）， =﹣2n2+9n﹣4， =﹣2（n﹣）2+， ∵PC＞0， ∴当n=时，线段PC最大且为．

二次函数与三角形

二次函数与三角形抛物线与三角形的结合是抛物线与平面几何结合生成综合性问题的一种重要形式，这类问题以抛物线为背景，探讨是否存在一些点，使其能构成某些特殊图形，有以下常见的形式：（1）抛物线上的点能否构成特殊的线段；（2）抛物线上的点能否构成特殊的角；（3）抛物线上的点能否构成特殊三角形；（4）抛物线上的点能否构成全等三角形、相似三角形；这类问题把抛物线性质和平面图形性质有机结合，需综合运用待定系数法、数形结合、分类讨论等思想方法。 1、如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．（1）求抛物线的解析式；（2）在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的坐标；（3）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t 为何值时，以P、B、C为顶点的三角形是直角三角形？直接写出所有符合条件的t值．

2、如图，在平面直角坐标系中，点O是原点，矩形OABC的顶点A在x轴的正半轴上，顶点C在y的正半轴上，点B的坐标是（5，3），抛物线y=x2+bx+c经过A、C两点，与x轴的另一个交点是点D，连接 BD．（1）求抛物线的解析式；（2）点M是抛物线对称轴上的一点，以M、B、D为顶点的三角形的面积是6，求点M的坐标；（3）点P从点D出发，以每秒1个单位长度的速度沿D→B匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度沿B→A→D匀速运动，当点P到达点B时，P、Q同时停止运动，设运动的时间为t秒，当t为何值时，以D、P、Q为顶点的三角形是等腰三角形？请直接写出所有符合条件的值． 3、已知函数2 3 2 2 y kx x =-+（k是常数）

专题三角形中的最值与取值范围问题

专题三角形中的最值与取值范围问题三角形中的边与角的最值与取值范围问题，是复习过程中的难点，在高考中考查形式灵活，常常在知识的交汇点处命题，与函数、几何、不等式等知识结合在一起。我们知道三角形只要满足三个条件，那么这个三角形就基本唯一确定了，而少于三个条件时，有些边角周长面积就可以变化，从而就有了求这些量的取值范围问题。这类问题的实质是将几何问题转化为代数问题，求解主要是充分运用三角形的内角和定理，正余弦定理，面积公式，基本不等式，三角恒等变形，三角函数的图像和性质来进行解题，非常综合，是解三角形中的难点问题。下面对这类问题的解法做下探讨。类型一：已知一角+对边例题1：在?ABC 中，A=60°，（1）ABC ?面积的最大值；（2）b c +的取值范围；（3）2b c +的最大值；（4）BC 边上高的最大值。类型二：已知一角+边的等量关系例题2：在?ABC 中，A=60°，1b c +=，求（1）ABC S ?的最大值；（2）a 的取值范围；（3）周长的取值范围。类型三：已知一角+面积例题3：在?ABC 中，A=60°，ABC S ?= （1）b c +的最小值；（2）a 的最小值。（3）周长的最小值。（4） 112b c +的最小值。类型四：已知角的等量关系例题4：在?ABC 中，A=2B ，则c b 的取值范围为

变式：在锐角?ABC 中，A=2B ，则c b 的取值范围为类型五：已知两边，求面积的最值例题5：在?ABC 中，已知1,2AB BC ==，求（1）ABC S ?的最大值；（2）角C 的取值范围。类型六：已知一边+另两边的等量关系例题6：在?ABC 中，已知6,10BC AB AC =+ =，求ABC S ?的最大值。变式：在?ABC 中，已知6,BC AC ==，求ABC S ?的最大值。类型七：三边的等量关系例题7：在?ABC 中，角A ，B ，C 所对的边分别为a,b,c,若2222a b c +=，求cos C 的最小值。

(完整版)二次函数与三角形面积最大值专题(4)

二次函数与三角形最大面积 1、在坐标系中求三角形的面积有3种方法：（1）割法：（和、差）的相互转化三角形的面积一般都是通过分割成几个三角形然后计算几个三角形的面积和，然后利用坐标来表示三角形的面积，这样三角形的面积即为一个二次函数，下面求解二次函数的最值即可。公式法：? 2 1 铅垂高*水平宽（2）补法：用大图形的面积–其他图形的面积（大三角形的面积–小三角形的积） 1、直线AB经过x轴上的一点A（2,0），且与抛物线y=ax2相交于B，C两点，已知点B坐标为（1，1）（1）求直线和抛物线的解析式；（2）如果D为抛物线上的一点，使得△AOD与△OBC的面积相等，求点D坐标． 2、如图：如图，直线x y 2 1 - =与抛物线6 4 1 2+ - =x y交于A、B两点，（1）求A、B两点的坐标。（2）点Q 在X轴上方的抛物线上，当Q点的坐标为多少时，△ABQ的面积最大？最大面积有为多少？ 3、、在平面直角坐标系中，已知抛物线经过A(-4,0)、B(0，-4)、C(2,0)三点，（1）求抛物线的解析式，（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m, △AMB的面积为S,求S关于m的函数关系式，并求出S的最大值。（3）若点P为抛物线上的动点，点Q是直线y= - x上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标 A B C M O x y X A B Y

4、（广安）如图，已知抛物线y=x2+bx+c经过点（1，-5）和（-2，4）（1）求这条抛物线的解析式；（2）设此抛物线与直线y=x相交于点A，B（点B在点A的侧），平行于y轴的直线x=m（0＜m＜5+1）与抛物线交于点M，与直线y=x交于点N，交x轴于点P，求线段MN的长（用含m的代数式表示）；（3）在条件（2）的情况下，连接OM、BM，是否存在m的值，使△BOM的面积S最大？若存在，请求出m的值；若不存在，请说明理由 5、已知：抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C．其中点A在x轴的负半轴上，点C在y轴的负半轴上，线段OA、OC的长（OA＜OC）是方程x2-5x+4=0的两个根，且抛物线的对称轴是直线x=1．（1）求A、B、C三点的坐标；（2）求此抛物线的解析式；（3）若点D是线段AB上的一个动点（与点A、B不重合），过点D作DE∥BC交AC于点E，连接CD，设BD的长为m，△CDE的面积为S，求S与m的函数关系式，并写出自变量m的取值范围．S是否存在最大值？若存在，求出最大值并求此时D点坐标；若不存在，请说明理由．

(完整版)二次函数与三角形的存在性问题的解法

二次函数与三角形的存在性问题一、预备知识 1、坐标系中或抛物线上有两个点为P （x1，y ），Q （x2，y ） (1)线段对称轴是直线2x 2 1x x += (2)AB 两点之间距离公式：221221)()(y y x x PQ -+-= 中点公式：已知两点 ()()2211y ,x Q ,y ,x P ，则线段PQ 的中点M 为??? ??++222121y y ,x x 。 2、两直线的解析式为11b x k y +=与 22b x k y += 如果这两天两直线互相垂直，则有121-=?k k 3、平面内两直线之间的位置关系：两直线分别为：L1：y=k1x+b1 L2：y=k2x+b2 （1）当k1=k2，b1≠b2 ，L1∥L2 （2）当k1≠k2，，L1与L2相交（3）K1×k2= -1时， L1与L2垂直二、三角形的存在性问题探究：三角形的存在性问题主要涉及到的是等腰三角形，等边三角形，直角三角形（一）三角形的性质和判定： 1、等腰三角形性质：两腰相等，两底角相等，三线合一（中线、高线、角平分线）。判定：两腰相等，两底角相等，三线合一（中线、高线、角平分线）的三角形是等腰三角形。 2、直角三角形性质：满足勾股定理的三边关系，斜边上的中线等于斜边的一半。判定：有一个角是直角的三角形是直角三角形。 3、等腰直角三角形性质：具有等腰三角形和等边三角形的所以性质，两底角相等且等于45°。判定：具有等腰三角形和等边三角形的所以性质的三角形是等腰直角三角形 4、等边三角形性质：三边相等，三个角相等且等于60°，三线合一，具有等腰三角形的一切性质。判定：三边相等，抛物线或坐标轴或对称轴上三个角相等，有一个角是60°的等腰三角形是等边三角形。

一道三角形面积最小值的计算

来路、思路、出路 ——一道求三角形面积最小值问题（于都三中蔡家禄）题目：如图，已知点P （2，3），过点P 的直线l 交y 轴的正半轴于点A ，交x 轴的正半轴于点B.求△ABO 的面积s 的最小值. 来路：由三角形面积公式可知，12 s OA OB =?，观察图象，A 、P 、B 三点共线，当OB 增大时，OA 减小.反之，当OB 减小时，OA 增大.若设点A 的坐标为（0，b ），则由A （0，b ）、P （2，3）两点坐标用待定系数法可求得直线l 的解析式为32b y x b ?= +.进而可求出点B 的坐标为（23 b b ?，0），因此212233b b s b b b =??=??.从中可看出s 是b 的函数.但遗憾的是此函数模型并非初中学生所熟悉的，因此解题至此陷入困境. 思路：当解决问题受阻时，不防退一步，从特殊情形出发（赋值法）. 设4b =，则2 41643 s ==?；设5b =，则2 512.553 s ==?；设6b =，则2 61263 s ==?；设7b =，则2 712.2573 s ==?…… 此时，我们便可猜想：当6b =时，s 最小为12. 我们再反过来思考：若s =16，则2 163 b b =?，去分母后解得14b =，212b =.结合图象思考，就是当△ABO 的面积为16时，对应的直线l 有两种位置，即过点（0，4）或过点（0，12）；若s =12，则2 123 b b =?，去分母后解得126b b ==.结合图象思考，就是当△ABO 的面

积为12时，对应的直线l 只有一种位置情况，即过点（0，6）.结合图象分析△ABO 的面积变化情况可知，s 只有最小值，没有最大值.当s 为最小值时，直线l 对应的位置是唯一的，而非最小值时，直线l 对应的位置有两个.因此，s 的最小值应为12. 出路：由以上探究可知，s 与b 是相互关联的，即2 3 b s b =?.又直线l 与两数轴的正半轴有交点A 、B ，在2 3 b s b =?中，显然30b ?>，因此可化为230b sb s ?+=.对于此方程，我们可以作以下理解：（1）s 表示△ABO 的面积，b 表示直线l 与y 轴交点的纵坐标，即决定直线l 与y 轴交点的位置；（2）s 可以看作是关于b 的一元二次方程的系数，它保证该方程有实数解；（3）求s 的最小值. 基于以上思考与认识，于是我们找到以下解题出路: 解：设点A 的坐标为（0，b ），则经过点P （2，3）和点A （0，b ）的直线l 的解析式为32b y x b ?= +.当0y =时，得23b x b =?，即B （23 b b ?，0）. 所以△ABO 的面积2 12233 b b s b b b =??=??. 因为直线l 与两数轴的正半轴有交点A 、B ，所以30b ?>，因此，去分母并整理可得230b sb s ?+=.又因为关于b 的一元二次方程有实数解，所以2()4130s s ?=????≥，解得12s ≥(0s ≤舍去)，因此，所求△ABC 的面积s 的最小值为12.

二次函数及三角形周长,面积最值问题

二次函数与三角形周长，面积最值问题知识点：1、二次函数线段，周长问题 2、二次函数线段和最小值线段差最大值问题 3、二次函数面积最大值问题【新授课】考点1：线段、周长问题例1.(2018·)在平面直角坐标系中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=x与抛物线交于A、B两点，直线l为y=﹣1．（1）求抛物线的解析式；（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．拓展：在l上是否存在一点P，使PB-PA取得最大值？若存在，求出点P的坐标。

练习 1、如图，已知二次函数24 =-+的图象与坐标轴交于点A（-1，0）和点B（0，-5）． y ax x c （1）求该二次函数的解析式；

（2）已知该函数图象的对称轴上存在一点P，使得△ABP的周长最小．请求出点P的坐标． 2、如图，抛物线y=ax2-5ax+4（a＜0）经过△ABC的三个顶点，已知BC ∥x轴，点A在x轴上，点C在y轴上，且AC=BC．（1）求抛物线的解析式．（2）在抛物线的对称轴上是否存在点M，使|MA-MB|最大？若存在，求出点M的坐标；若不存在，请说明理由．

例2. (2018?莱芜)如图，抛物线y=ax2+bx+c经过A（﹣1，0），B（4，0），C （0，3）三点，D为直线BC上方抛物线上一动点，DE⊥BC于E．（1）求抛物线的函数表达式；（2）如图1，求线段DE长度的最大值；练习 1x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（一1，1、如图，抛物线y= 2

中考数学复习二次函数与三角形的面积问题

二次函数与三角形的面积问题 1.运用2 铅垂高水平宽?= s ； 2.运用y ； 3.将不规则的图形分割成规则图形，从而便于求出图形的总面积。类型一：三角形的某一条边在坐标轴上或者与坐标轴平行例1.已知：抛物线的顶点为D （1，-4），并经过点E （4，5），求: （1）抛物线解析式；（2）抛物线与x 轴的交点A 、B ，与y 轴交点C ；（3）求下列图形的面积△ABD 、△ABC 、△ABE 、△OCD 、△OCE 。解题思路：求出函数解析式________________；写出下列点的坐标：A______；B_______；C_______；求出下列线段的长：AO________；BO________；AB________；OC_________。求出下列图形的面积△ABD 、△ABC 、△ABE 、△OCD 、△OCE 。一般地，这类题目的做题步骤：1.求出二次函数的解析式；2.求出相关点的坐标；3.求出相关线段的长；4.选择合适方法求出图形的面积。训练1.如图所示，已知抛物线()02 ≠++=a c bx ax y 与x 轴相交于两点A ()0,1x ， B ()0,2x ()21x x <，与y 轴负半轴相交于点C ，若抛物线顶点P 的横坐标是1，A 、 B 两点间的距离为4，且△ABC 的面积为6。（1）求点A 和B 的坐标；（2）求此抛物线的解析式；（3）求四边形ACPB 的面积。类型二：三角形三边均不与坐标轴轴平行，做三角形的铅垂高。（歪歪三角形拦腰来一刀）关于2 铅垂高水平宽?= ?S 的知识点：如图1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法：ah S ABC 2 1 =?，即三角形面积等于水平宽与铅垂高乘积的一半. 想一想：在直角坐标系中，水平宽如何求？铅垂高如何求？例2．如图2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结P A ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ?；(3)是否存在一点P ，使S △P AB = 8 9S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由. 解题思路：求出直线AB 的解析式是为了求出D ．点的纵坐标．．．．．D y ； x A B O C y P B C 铅垂高水平宽 h a 图1 图-2 x C O y A B D 1 1

解析几何-三角形面积相关最值问题

? 难度：★★ ? 特点：已知高（作为一个限制弦的条件），求弦长的最大值 ? 来源：07陕西高考已知椭圆C :2222b y a x +=1(a ＞b ＞0)的离心率为36,短轴一个端点到右焦点的距离为3.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线l 与椭圆C 交于A 、B 两点，坐标原点O 到直线l 的距离为2 3，求△AOB 面积的最大值. 解：（Ⅰ）设椭圆的半焦距为c ，依题意c a a ?=???=? 1b ∴=，∴所求椭圆方程为2213x y +=. （Ⅱ）设11()A x y ，，22()B x y ，.（1）当AB x ⊥ 轴时，AB =.（2）当AB 与x 轴不垂直时，设直线AB 的方程为y kx m =+. =，得223(1)4 m k =+.把y kx m =+代入椭圆方程，整理得222(31)6330k x kmx m +++-=， 122631 km x x k -∴+=+，21223(1)31m x x k -=+.2 2221(1)()AB k x x ∴=+-22222223612(1)(1)(31)31k m m k k k ??-=+-??++?? 222222222 12(1)(31)3(1)(91)(31)(31)k k m k k k k ++-++==++2422212121233(0)34196123696k k k k k k =+=+≠+=++?+++≤. 当且仅当2219k k =，即k =时等号成立.当0k = 时，AB =综上所述max 2AB =. ∴当AB 最大时，AOB △ 面积取最大值max 12S AB =?=. ? 难度：★★ ? 特点：椭圆已知，直线过定点（由椭圆定），求三角形面积的最大值 ? 来源：已知椭圆的中心在坐标原点O ，焦点在x 轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，两准线间的距离为4. (Ⅰ)求椭圆的方程；(Ⅱ)直线l 过点P(0,2)且与椭圆相交于A 、B 两点，当ΔAOB 面积取得最大值时，求直线l 的方程.

二次函数与直角三角形

二次函数与直角三角形 1．（10分）（2006河南22题）二次函数2 18 y x = 的图象如图所示，过y 轴上一点()02M ，的直线与抛物线交于A ，B 两点，过点A ，B 分别作y 轴的垂线，垂足分别为C ，D ．（1）当点A 的横坐标为2-时，求点B 的坐标；（2）在（1）的情况下，分别过点A ，B 作AE x ⊥轴于E ，BF x ⊥轴于F ，在EF 上是否存在点P ，使APB ∠为直角．若存在，求点P 的坐标；若不存在，请说明理由；（3）当点A 在抛物线上运动时（点A 与点O 不重合），求AC BD 的值．解：（1）根据题意，设点B 的坐标为2 18 x x ?? ?? ? ，，其中0x >．点A 的横坐标为2-，122A ? ?∴- ??? ，． ······································································ 2分 AC y ⊥轴，BD y ⊥轴，()02M ，， AC BD ∴∥，32MC = ，2 128 MD x =-． Rt Rt BDM ACM ∴△∽△． BD MD AC MC ∴=．即2 1282 2 x x -=．解得12x =-（舍去），28x =． ()88B ∴，． ··················································································································· 5分（2）存在． ··················································································································· 6分连结AP ，BP ．由（1），1 2 AE = ，8BF =，10EF =．设EP a =，则10PF a =-． AE x ⊥轴，BF x ⊥轴，90APB =∠， y D B M A C O x

文档之家