求向量组的极大无关组_图文
- 格式:ppt
- 大小:243.00 KB
- 文档页数:20




![4[1].3向量组的秩和极大线性无关组](https://uimg.taocdn.com/6e3036264b35eefdc8d333e1.webp)

向量组的极大无关组向量组的极大无关组,是线性代数中一个重要的概念。
在研究向量组的性质和线性相关性时,极大无关组起着至关重要的作用。
我们来了解一下什么是向量组。
向量组是由一组向量所组成的集合,而向量是一种具有大小和方向的量。
在线性代数中,我们常常将向量表示为列向量,用一列数字表示。
接下来,我们来看一下什么是线性相关和线性无关。
在一个向量组中,如果存在一组不全为零的系数,使得这些向量的线性组合等于零向量,那么这个向量组就是线性相关的。
反之,如果不存在这样的系数,那么这个向量组就是线性无关的。
在一个向量组中,可能存在很多个向量,但是其中只有一部分是起着决定性作用的。
这些起着决定性作用的向量就是极大无关组。
换句话说,极大无关组是一个线性无关的向量组,并且再增加任何一个向量都会导致线性相关。
那么如何找到一个向量组的极大无关组呢?我们可以通过高斯消元法来进行求解。
首先,将向量组表示成增广矩阵的形式,然后进行初等行变换,将矩阵化简为行阶梯形矩阵。
接着,我们可以根据化简后的矩阵,找到主元列对应的向量,这些向量就是极大无关组。
举个例子来说明。
假设有一个向量组V,包含向量v1、v2、v3和v4。
我们可以将这个向量组表示为增广矩阵:```[v1 v2 v3 v4]```经过高斯消元法的操作,得到化简后的行阶梯形矩阵:```[1 0 0 2][0 1 0 3][0 0 1 4][0 0 0 0]```从化简后的矩阵中可以看出,v1、v2和v3对应的列是主元列,因此它们就是向量组V的极大无关组。
极大无关组在线性代数中具有重要的应用价值。
首先,它可以帮助我们判断一个向量组是否线性相关。
如果一个向量组的极大无关组为空集,那么它就是线性相关的;反之,如果极大无关组不为空集,那么它就是线性无关的。
极大无关组还可以帮助我们求解线性方程组。
对于一个线性方程组,我们可以将其系数矩阵化简为行阶梯形矩阵,然后找到主元列对应的未知数,这些未知数就是方程组的极大无关组。

向量组的极大无关组在线性代数中常常会遇到向量组的问题,其中一个重要的问题是如何确定一个向量组的基。
而要解决这个问题,就需要考虑向量组中向量的线性相关性。
如果一个向量可以表示成其他向量的线性组合,那么这个向量就不是基向量,也就无法作为向量组的一部分。
而向量组中极大线性无关的向量组成的集合,就被称作向量组的极大无关组。
先定义一下向量组的线性相关性:设 $\alpha_1, \alpha_2, ...,\alpha_n$ 为向量组,则如果存在不全为零的数 $k_1, k_2, ..., k_n$,使得 $k_1\alpha_1 + k_2\alpha_2 + ... + k_n\alpha_n = \boldsymbol{0}$,那么这个向量组就是线性相关的。
反之,如果这样的向量组不存在,那么就称这个向量组是线性无关的。
接下来,我们来定义一下“极大无关组”这个概念。
假设 $\alpha_1,\alpha_2, ..., \alpha_n$ 是一个向量组,那么它的一个子集 $\beta_1,\beta_2, ..., \beta_k$ 是极大无关组,当且仅当:- $\beta_1, \beta_2, ..., \beta_k$ 中的向量是线性无关的;- $k < n$;- 如果将 $\beta_1, \beta_2, ..., \beta_k$ 中的任何一个向量去掉,剩下的向量就是线性相关的。
举个例子,假设有一个向量组 $\boldsymbol{v_1}, \boldsymbol{v_2}, \boldsymbol{v_3}, \boldsymbol{v_4}, \boldsymbol{v_5}$,其中$\boldsymbol{v_1}, \boldsymbol{v_2}$ 和 $\boldsymbol{v_3},\boldsymbol{v_4}$ 是线性相关的。
那么,$\boldsymbol{v_1},\boldsymbol{v_2}, \boldsymbol{v_5}$ 和 $\boldsymbol{v_3},\boldsymbol{v_4}, \boldsymbol{v_5}$ 都是向量组的极大无关组。

关于用初等变换求向量组的极大无关组的方法
向量组的极大无关组是一种常见的线性代数问题,在现实应用中,经常用初等变换来求解。
这里我们就介绍一下用初等变换求向量组的极大无关组的方法。
假设我们要计算极大无关组,求解过程采用分治思想,即向量组中元素成组,每组采用初等变换求解极大无关组。
首先介绍初等变换的基本步骤。
要将向量组T中的一个n元组A=(a1,a2,a3,…,an)变换为(b1,b2,b3,…,bn),只需执行以下操作:
(1)将a1乘以某正数个数,再加上某向量(若该向量为零向量则不需要加上)使其变换为b1。
(2)将a2乘以某正数个数,再加上某向量(若该向量为零向量则不需要加上)使其变换为b2。
(3)将a3乘以某正数个数,再加上某向量(若该向量为零向量则不需要加上)使其变换为b3。
以此类推,直到将an乘以某正数个数,加上某向量(若该向量为零向量则不需要加上)使其变换为bn。
其次,介绍如何使用初等变换求解向量组的极大无关组。
如果要对向量组T中的n元组求解极大无关组,采用“每组采用初等变换求解极大无关组”进行分治处理:
(1)将n元组拆分为m个m元组,分别求解m个m元组的极大无关组。
(2)将分别求解出来的m个极大无关组合并在一起,即构成最终的极大无关组。
(3)由m个m元组的极大无关组构及的n元组的极大无关组(即新的n元组)也不能线性表示原n元组,所以应当重复执行以上步骤,直到所得到的n元组可以线性表示原n元组停止步骤,此时的n元组就是该向量组的极大无关组。
最后,经过上述步骤,就可以用初等变换解决向量组的极大无关组问题,将大问题拆解成小问题,再分别求解小问题,从而得到大问题的答案,大大提高了求解的效率。

向量组的极大线性无关组怎么求
具体方法:
矩阵初等行变换化成行阶梯矩阵
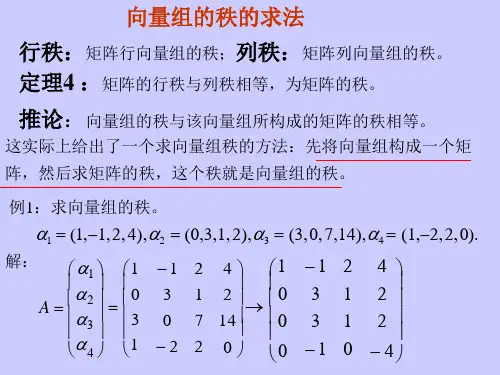
然后从同一层台阶只取一个对应的列向量,总共取矩阵的秩个
重新组成一个矩阵
然后重新画一画阶梯,看看阶梯数是否依旧等于秩的值
是的话,这些个向量组就是一个极大无关线性组,否则就不是啦~
(当然有些新矩阵可以重新再行变换一下,就又是秩等于原矩阵的秩了,所以也是的)
所以直接取行阶梯矩阵每行第一个非0所在列所组成的新矩阵,阶梯数一定等于新矩阵的秩,就一定是原矩阵的一个极大线性无关组。
这样取得的首非零元所在列组成的必然是极大线性无关组,但题目要求我们找出所有的极大线性无关组,所以除了这一线性无关组,我们应继续寻找,就是从所有列中任取矩阵的秩个列,组成一个组,但是这样组成的组可能不是线性无关组,因此每一组都需要进行一下验证(验证他是不是秩等于总秩)。
同时这样的任取过程应该是有顺序可言的,在下文的注解中有详细的介绍。
举个例子⑧
(注:这里说明一下列举的顺序。
1.首先是找到所有含第一列的极大线性无关组。
而本例也是只列举了包含①的极大线性无关组。
2.其次,如要列出所有,则需要先去掉第一列,再按此方法化成阶梯
型,再寻找,就能找出所有含②的极大无关组,同理在此基础上去掉第二列...以此类推,就能找出所有极大线性无关组)。
行向量组的极大无关组原理行向量组的极大无关组原理是线性代数中的一个重要定理,用于确定行向量组中的极大无关向量组并进行相关的运算和推导。
极大无关组是指在一个向量组中,任何一个向量都不可由其他向量线性表示出来的向量组合集合。
在具体操作中,我们可以通过以下步骤来确定行向量组的极大无关组:1. 将行向量组写成矩阵形式,假设该行向量组中有n个向量,每个向量有m个分量,那么可以得到一个n ×m 的矩阵A。
\[ A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1m} \\ a_{21} &a_{22} & \dots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nm} \end{bmatrix} \]2. 对A进行初等变换,使得A的行阶梯形矩阵形式为\[ \begin{bmatrix} 1 & a_{12}' & \dots & a_{1m}' \\ 0 & 1 & \dots &a_{2m}' \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1\end{bmatrix} \]其中,'表示通过初等变换得到的新的分量。
3. 根据行阶梯形矩阵的性质,从上到下找到第一个主元(非零首个元素)所在的行,将该行作为极大无关组的首个向量。
4. 从上一个确定的向量的下一行开始,找到下一个主元所在的行,将该行作为极大无关组的下一个向量。
5. 重复以上步骤,直到不能再找到主元为止。