中心极限定理

中心极限定理举例
中心极限定理(Central Limit Theorem)是统计学中非常重要的一个定理，用于研究各种概率分布的数据值。

它表明，当一个总体抽样数足够大时，抽样分布的均值服从一定分布，该分布称为标准正态分布。

举例来说，假设我们从一个总体中抽取20个样本，每次抽样的均值都会有所不同，但是如果我们重复的抽20个样本，抽样的均值就会收敛到一个概率分布上。

中心极限定理告诉我们，当抽样样本增加时，这个概率分布就会越来越接近标准正态分布。

比如，我们要研究一群鸟的体重数据。

假设这群鸟的体重服从某个随机分布，那么我们可以用中心极限定理来求出抽样均值的概率分布。

当样本增加到一定规模时，抽取的体重均值就会收敛到标准正太分布，我们就可以用这种分布来进行数据分析，研究鸟群的体重变化情况。

中心极限定理是一个强大的定理，为我们理解概率分布提供了很大的帮助。

它不仅可以用于研究采样观测值，也可以用于大样本分析，如基于网络等新技术的信息采集。

它对统计学和概率分析有着重大意义，使我们能够更好地掌握现实世界中各种随机现象。

简述中心极限定理内容
中心极限定理是概率统计学中的重要定理之一。

该定理关注的是当一个样本数量足够大时，其样本均值的分布会越来越接近于正态分布，即使该样本的总体分布不是正态分布。

中心极限定理是一个十分有用的工具，它在我们进行数据分析、做出决策以及制定政策时都有着广泛的应用。

特别是在实际应用中，我们通常只能接触到一小部分数据，所以从这一小部分数据来推断总体的特征是非常重要的。

中心极限定理则提供了一种借助样本均值来推断总体均值的方法。

举个例子，假设我们想要知道某城市的人口平均身高是多少。

但要测量每个人的身高是不现实的，我们只能随机从人群中抽样一小部分，在这个样本中计算出平均身高。

如果我们多次重复这个过程，得到的平均身高会有所变化。

中心极限定理告诉我们，当我们的样本数量足够大时，所有得到的样本均值的分布会聚集在一个值附近并逐渐趋向于正态分布。

因此，我们可以使用这个正态分布的均值来估计总体均值，并根据误差的大小来评估这个估计值的可靠性。

中心极限定理的严格表述为：在一定条件下，这个样本均值的分布将会趋向于正态分布，该分布的均值等于总体的均值，方差等于总体方差除以样本容量。

具体说来，要求样本是随机抽取、样本容量足够大，且总体的方差不能过大。

总之，中心极限定理提供了一种使用样本均值来估计总体均值的方法，并在统计分析和数据模型建立中发挥着巨大的作用。

对于我们的日常生活和工作，了解并掌握中心极限定理可以帮助我们更好地理解数据，做出更准确的判断。

中心极限定理是概率论中一个非常重要的定理，它告诉我们在一定条件下，当样本容量足够大时，样本均值的分布将近似于正态分布。

这个定理对于统计推断和假设检验有着重要的意义，因此被广泛应用于各个领域。

1. 中心极限定理的概念中心极限定理是指在一定条件下，当样本容量足够大时，样本均值的分布将近似于正态分布。

无论总体的分布是什么样子，只要样本容量足够大，样本均值的分布都会接近正态分布。

这个定理对于统计学来说非常重要，因为它告诉我们在很多情况下，我们可以使用正态分布来近似描述样本均值的分布。

2. 为什么中心极限定理成立中心极限定理之所以成立，是因为当样本容量足够大时，样本均值的分布受到多个随机因素的影响，而这些随机因素的总和近似呈现出正态分布的特征。

这也是为什么无论总体的分布是什么样子，只要样本容量足够大，样本均值的分布都会近似于正态分布的原因。

3. 中心极限定理的应用中心极限定理在统计学中有着广泛的应用。

在假设检验中，我们经常需要根据样本均值对总体均值做出推断。

而根据中心极限定理，我们可以知道当样本容量足够大时，样本均值的分布近似于正态分布，这样我们就可以使用正态分布的性质来进行推断和计算。

4. n趋近无穷的意义在中心极限定理中，n代表样本容量，当n趋近无穷时，样本均值的分布就会趋近于正态分布。

这也说明了中心极限定理的一个重要特点，即样本容量越大，样本均值的分布越接近正态分布。

当我们需要进行统计推断时，可以通过增大样本容量来让样本均值的分布更接近于正态分布，从而使得推断结果更加可靠。

5. 标准正态分布的意义标准正态分布是统计学中一个非常重要的分布，它的概率密度函数是一个钟形曲线，均值为0，标准差为1。

在实际的统计推断和假设检验中，很多情况下都需要使用标准正态分布来进行计算和推断。

而根据中心极限定理，当样本容量足够大时，样本均值的分布近似于正态分布，因此我们可以使用标准正态分布的性质来进行推断和计算，这对于统计学的应用具有重要的意义。

中心极限定理
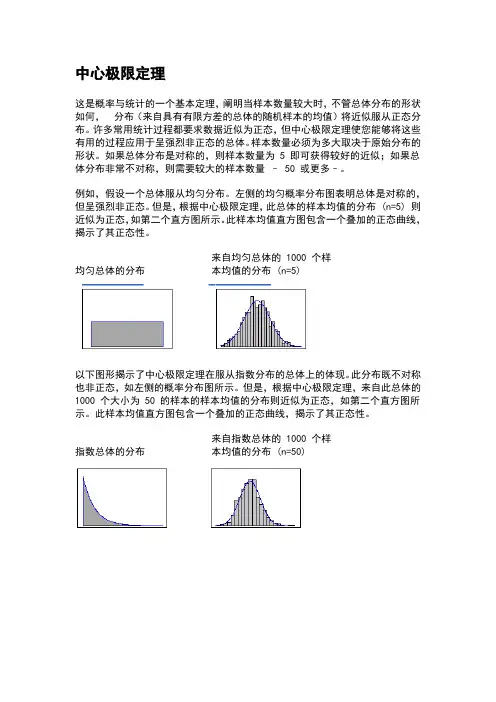
这是概率与统计的一个基本定理，阐明当样本数量较大时，不管总体分布的形状如何，分布（来自具有有限方差的总体的随机样本的均值）将近似服从正态分布。

许多常用统计过程都要求数据近似为正态，但中心极限定理使您能够将这些有用的过程应用于呈强烈非正态的总体。

样本数量必须为多大取决于原始分布的形状。

如果总体分布是对称的，则样本数量为 5 即可获得较好的近似；如果总体分布非常不对称，则需要较大的样本数量– 50 或更多–。

例如，假设一个总体服从均匀分布。

左侧的均匀概率分布图表明总体是对称的，但呈强烈非正态。

但是，根据中心极限定理，此总体的样本均值的分布 (n=5) 则近似为正态，如第二个直方图所示。

此样本均值直方图包含一个叠加的正态曲线，揭示了其正态性。

均匀总体的分布来自均匀总体的 1000 个样本均值的分布 (n=5)
以下图形揭示了中心极限定理在服从指数分布的总体上的体现。

此分布既不对称也非正态，如左侧的概率分布图所示。

但是，根据中心极限定理，来自此总体的1000 个大小为 50 的样本的样本均值的分布则近似为正态，如第二个直方图所示。

此样本均值直方图包含一个叠加的正态曲线，揭示了其正态性。

指数总体的分布来自指数总体的 1000 个样本均值的分布 (n=50)。

中心极限定理的概念和意义1. 什么是中心极限定理？中心极限定理，听起来像个高深的数学名词，其实它就像一道神奇的魔法，能够把许多复杂的事情简单化。

简单来说，中心极限定理告诉我们，当我们对一个大样本进行多次独立抽样时，不管原始数据的分布是什么样的，样本均值的分布都会逐渐趋向于正态分布，尤其是在样本量很大的时候。

就像你把各种水果放进果汁机，搅拌后，不管你放了苹果、香蕉还是橙子，最后出来的果汁看起来都是一样的好喝。

这就说明了，无论你起初的配方是什么，经过“搅拌”之后，结果会趋于一致。

再简单一点说，假如你在学校里收集了班上每个人的数学考试成绩，结果发现有些人考得很好，有些人却很糟糕，但当你把这所有的成绩加起来，算出平均分，你会发现这个平均值往往是一个相对稳定的数字，不管班上有多少人，成绩好坏参差不齐。

这种稳定性就是中心极限定理的魔力所在。

2. 中心极限定理的意义2.1 统计学的基石要说这个定理的重要性，那可真是“举足轻重”。

它是统计学中的一块基石，几乎所有的统计推断都离不开它。

比如，想知道一所学校学生的身高平均值，你不可能把每一个学生都量一遍，但你可以随机抽取一些学生，算出他们的平均身高。

根据中心极限定理，即使你只量了少数几个人，结果也能反映出全校的平均身高。

这种“以小见大”的智慧，简直就是统计界的“金钥匙”。

2.2 应用广泛再说说它的应用，中心极限定理简直是无处不在！比如在保险公司，他们要计算风险，得出保费，都会用到这个定理。

商家在做市场调查时，抽样调查也是通过它来推算出顾客的消费习惯。

这就好比打猎，猎人并不需要每一只动物的详细资料，只要找出一小部分的样本，就能知道整个森林里动物的情况，做到心中有数，真是一举两得。

3. 生活中的例子3.1 不怕风雨生活中，我们其实每天都在体验中心极限定理的作用。

比如你买彩票，很多人总是抱怨运气不佳，觉得自己永远不可能中大奖。

但是如果你从统计的角度来看，每次购买彩票的结果就是一个个小样本，虽然单个结果可能天差地别，但如果你连续购买彩票几次，最终的平均中奖概率会变得更加可预测。

中心极限定理例题引言中心极限定理是概率论中的一个重要定理，它描述了在一定条件下，大量独立同分布随机变量的和的分布会趋近于高斯分布，即正态分布。

这个定理在统计学中有着广泛的应用。

本文将通过几个例题来说明中心极限定理的应用和推导过程。

例题1假设有一个质量为1 kg的物体，在连续3次抛掷中，每次都以同样的力量抛出，求这3次抛掷的总共落地位置与平均落地位置之间的差距。

解：设第一次、第二次和第三次抛掷的落地位置分别为X1, X2和X3，平均落地位置为X。

由题意可知，X1, X2和X3是独立同分布的随机变量，且服从均值为0，方差为1的标准正态分布。

根据中心极限定理，当独立随机变量的数量足够大时，他们的和呈现出正态分布的特点。

因此，3次抛掷的总共落地位置可以表示为：Sum = X1 + X2 + X3根据中心极限定理，我们可以得到：Sum ～ N(0, 3)所以，总共落地位置与平均落地位置之间的差距可以表示为：Difference = Sum - 3 * X根据正态分布的性质，我们知道均值为0的正态分布减去均值为μ的正态分布的期望值为0，即：E[Difference] = E[Sum - 3 * X] = E[Sum] - E[3 * X] = 0 - 0 = 0所以，总共落地位置与平均落地位置之间的差距的期望值为0。

这意味着平均而言，总共落地位置与平均落地位置没有偏移。

例题2某超市每天出售的可乐数量服从均值为1000，标准差为10的正态分布。

今天超市售出的可乐数量为2000瓶，求今天超市售出的可乐数量与平均值之间的差距。

解：设今天超市售出的可乐数量为X，平均值为X。

由题意可知，X服从均值为1000，标准差为10的正态分布。

根据中心极限定理，当独立随机变量的数量足够大时，他们的和呈现出正态分布的特点。

我们知道，每天超市售出的可乐数量与平均值之间的差距可以表示为：Difference = X - X根据正态分布的性质，我们知道均值为μ的正态分布减去均值为μ的正态分布的期望值为0，即：E[Difference] = E[X - X] = 0所以，今天超市售出的可乐数量与平均值之间的差距的期望值为0。

中心极限定理内容
中心极限定理是概率论和统计学中的一个重要定理，它指出，对于一个具有相同分布和有限均值和方差的独立随机变量样本，它们的平均值的分布在样本量足够大时趋近于正态分布。

中心极限定理的含义在于，当样本量增大时，样本均值的变异性逐渐减小，而均值的分布逐渐趋近于一个确定的正态分布。

这一定理充分展示了正态分布作为统计学中常用分布的优越性。

中心极限定理具有广泛的应用，例如在样本比例推断和回归分析中，可以使用中心极限定理来计算样本均值的置信区间和标准误差。

因此，中心极限定理是概率论和统计学中最重要的定理之一，是许多统计学方法的基础。

浅谈中心极限定理及其应用中心极限定理（CentralLimitTheorem，简称CLT）是统计学中最基本的定理，可以提供数学理论支持和方便的引用，以解决许多实际问题。

这个定理的完整表述是：当抽取的样本量足够大的时候，样本平均数的分布曲线接近于正态分布，即属于类正态分布，其平均值接近于总体平均数，其标准差接近于总体标准差的平方根。

中心极限定理的应用方面，可以涉及到许多方面：一、测定总体参数。

中心极限定理可以用来估计总体参数，包括总体均值、总体方差和总体分布等。

二、假设检验。

中心极限定理可以用于检验统计模型的参数，即样本和总体的分布形式是否一致，研究者可以利用其来进行假设检验，从而评估统计模型的正确性。

三、置信区间估计。

中心极限定理也可以利用来估计总体参数所处的置信区间，在样本量足够大的情况下，置信区间会变得紧密，从而使得置信度得到提高。

四、回归分析。

在回归分析中，中心极限定理可用于评估模型的参数置信区间，也可用于评估线性回归模型的拟合程度，从而推出结论。

具体来讲，中心极限定理的应用非常灵活，并且无处不在，几乎所有的统计分析和统计模型都可以借助它求解。

在实际数据处理中，中心极限定理是统计学中最基本定理，将它运用在模型构建中，将有助于增强模型的可靠性和准确性。

总之，中心极限定理可以用来估计总体参数，也可以用于假设检验，能够确定模型的参数，估计总体参数所处的置信区间范围，及对回归分析进行验证。

它是统计学基础理论，在数据处理中起着重要作用，为研究者提供了便利。

中心极限定理实际上是一个概率模型，它可以分析我们观察到的大量数据，帮助我们做出更准确的决策。

而且，它也是数据挖掘和机器学习的基础理论，对于统计数据处理和模型建立有着重要意义。

概率论中的中心极限定理分析概率论中的中心极限定理是一项重要的数学定理，它描述了独立随机变量和的极限分布的性质。

中心极限定理为我们理解概率和统计学提供了重要的工具，本文将对中心极限定理进行分析和解释。

1. 中心极限定理的概念中心极限定理是指当我们从一个总体中进行多次抽样，并计算这些样本的均值或总和时，这些样本的分布将逐渐收敛于正态分布。

其中最著名的是拉普拉斯-高斯中心极限定理和切比雪夫中心极限定理。

2. 拉普拉斯-高斯中心极限定理拉普拉斯-高斯中心极限定理是中心极限定理的最常见形式，它适用于独立同分布的随机变量。

定理表明，当抽样数量足够大时，这些独立同分布的随机变量的和将近似服从正态分布。

以一个掷硬币的例子来说明这个定理。

当我们将硬币掷1000次，每次记录正面朝上的次数。

根据概率分布，正面朝上的次数应该是一个接近500的数值。

然而，如果我们多次重复这个实验，并将每次正面朝上的次数求和，这些和将近似服从正态分布。

3. 切比雪夫中心极限定理切比雪夫中心极限定理比拉普拉斯-高斯中心极限定理更为一般化，它适用于独立但不一定同分布的随机变量。

定理表明，对于任意的随机变量，当样本数量足够大时，这些随机变量的和将近似服从正态分布。

切比雪夫中心极限定理的一个重要应用是在推断统计学中确定估计量的抽样分布。

通过样本数量的增加，可以提高估计量的准确性，并且使其更接近于真实参数值。

4. 应用和意义中心极限定理在实际中有广泛的应用，尤其在统计分析、假设检验和置信区间等领域中。

通过应用该定理，我们可以使用正态分布作为近似来进行各种分析。

此外，中心极限定理还为概率和统计学的理论提供了基础，并在概率论和统计学的发展中起到了重要的推动作用。

它不仅使我们对随机过程有了更深入的理解，还为建立更精确的模型提供了指导。

总结：中心极限定理是一项重要的数学定理，它描述了独立随机变量和的极限分布的性质。

拉普拉斯-高斯中心极限定理和切比雪夫中心极限定理是其中最重要的两个形式。