水的粘度计算表

水的粘度计算表-水的动力粘度计算公式水的粘度计算表水的动力粘度计算公式在物理学和工程学领域，水的粘度是一个重要的参数。

了解水的粘度以及如何计算它对于许多应用至关重要，例如流体流动的研究、管道设计、热交换器的优化等。

接下来，让我们深入探讨水的粘度计算表以及水的动力粘度计算公式。

首先，我们需要明白什么是粘度。

简单来说，粘度就是流体内部抵抗流动的一种性质。

想象一下，你把蜂蜜和水分别倒在一个平面上，蜂蜜流动得很慢，而水流动得相对较快。

这就是因为蜂蜜的粘度比水大，它内部的分子之间有着更强的相互作用力，阻碍了流动。

水的粘度会受到温度的显著影响。

一般来说，温度越高，水的粘度越低；温度越低，水的粘度越高。

这是因为在较高温度下，水分子的热运动更加剧烈，它们之间的相互作用相对较弱，所以更容易流动。

接下来，我们看一下水的动力粘度计算公式。

在国际单位制中，水的动力粘度通常用μ表示，单位是帕斯卡秒（Pa·s）。

常见的计算公式是通过实验数据拟合得到的经验公式。

其中一个被广泛使用的公式是：μ ＝ A × 10^（B ／（T C)）在这个公式中，μ是水的动力粘度，T 是温度（单位为开尔文，K），A、B 和 C 是通过实验确定的常数。

不同的研究和实验可能会得出略有不同的常数数值，但大致的形式是相似的。

为了方便计算和使用，通常会将这个公式制作成水的粘度计算表。

水的粘度计算表一般会列出不同温度下对应的水的动力粘度值。

这样，在实际应用中，我们只需要查找表格中对应的温度，就可以快速得到水的粘度值，而无需每次都进行复杂的公式计算。

比如说，在 20℃时，通过查阅计算表或者使用上述公式计算，我们可以得到水的动力粘度约为 1002×10^（－3) Pa·s。

在工程和科学研究中，准确地知道水的粘度对于设计和优化各种系统非常重要。

例如，在设计管道输送系统时，如果对水的粘度估计不准确，可能会导致管道内的压力损失计算错误，从而影响整个系统的性能和效率。

水的黏度表0～40℃水的物理性质F3 Viscosity decreases with pressure at temperatures below 33°CViscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of these voids reduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior can be explained by the increased pressure up to about 150 MPa causing deformation, so reducing the strength of the hydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume. It is thus a direct consequence of the between hydrogen bonding effects and the van der Waals dispersion forces in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures and densities, the between hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining are stronger due to the closer proximity of the contributing oxygen atoms . Viscosity, then, increases with pressure. The dashed line opposite indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where at low temperatures both the translational and rotational motion of water anomalously increase as the pressure increases.。

水的粘度计算公式水的粘度是一个在物理学和工程学中经常会涉及到的概念。

对于水的粘度计算，这可不是一个简单的事儿。

先来说说什么是粘度。

想象一下，你在搅拌一碗蜂蜜和一碗水，明显感觉搅拌蜂蜜更费劲，这就是因为蜂蜜的粘度比水大。

粘度简单理解，就是液体流动时内部的阻力大小。

水的粘度会受到温度的影响。

温度越高，水的粘度越低；温度越低，水的粘度就越高。

那怎么计算水的粘度呢？这就得用到一个公式啦。

水的粘度计算公式通常是：μ = A×10^(B / (T - C)) 。

这里的μ就是水的粘度，T 表示的是温度（单位是开尔文），A、B、C 是特定的常数。

这个公式看起来挺复杂，实际用起来也得小心。

比如说，在实际计算的时候，温度的单位一定要搞对，不然算出来的结果可就差之千里啦。

我记得有一次，在实验室里，我们小组正在做一个关于水的粘度和温度关系的实验。

当时，大家都特别认真，各种仪器设备摆了一桌。

我们小心地控制着水温，然后用粘度计测量水的粘度。

可没想到，一开始就出了岔子，有个小伙伴把温度的单位给弄错了，结果算出来的粘度值那叫一个离谱。

大家面面相觑，然后哄堂大笑。

不过笑归笑，我们赶紧重新测量，认真核对每一个数据和单位，最终得到了准确的结果。

通过这次实验，我更深刻地体会到了准确运用水的粘度计算公式的重要性。

一点点的小错误，都可能导致完全不同的结果。

在实际的工程应用中，比如在设计管道输送水的系统时，就得准确计算水的粘度，不然可能会出现水流不畅、压力过大等问题。

又比如在汽车发动机的冷却系统里，水的粘度也会影响冷却效果。

总之，水的粘度计算公式虽然复杂，但只要我们认真对待，搞清楚每个参数的含义和单位，就能准确地计算出水在不同温度下的粘度，为各种实际应用提供可靠的数据支持。

希望通过这篇文章，能让您对水的粘度计算公式有更清楚的了解，以后在遇到相关问题的时候，能够轻松应对！。

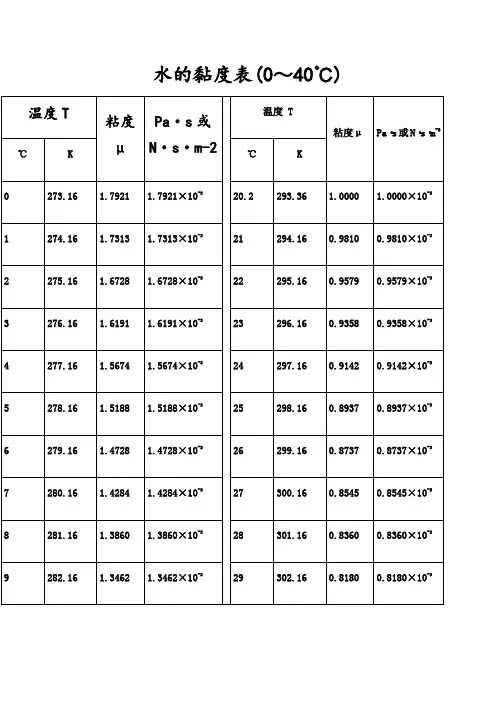
水的黏度表(0～40℃)水的物理性质F3??? Viscosity decreases with pressure(at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of these voids reduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior [534] can be explained by the increased pressure (up to about 150 MPa) causing deformation, so reducing the strength of the hydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume.It is thus a direct consequence of the balance between hydrogen bonding effects and the van der Waals dispersion forces [558] in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures (and densities), the balance between hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining hydrogen bonds are stronger due to the closer proximity of the contributing oxygen atoms [655]. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.。

液体粘度公式(一)液体粘度公式1. 粘度的定义•粘度是指液体流动阻力的大小。

它描述了液体内部分子间相互作用力的强度。

2. 粘度的测量单位•粘度的国际单位是帕斯卡·秒（Pa·s），也可以用更小的单位（毫帕秒或千帕秒）表示。

3. 斯托克斯公式•斯托克斯公式用于计算小球在液体中的阻力，从而间接计算液体的粘度。

•公式: [stokes_equation](•例子: 当小球半径为 mm，在水中下落速度为10 cm/s时，根据斯托克斯公式可以计算出水的粘度为Pa·s。

4. 流动粘度与剪切应力的关系•流动粘度是指液体在受到剪切应力时表现出来的粘滞性。

•流动粘度与剪切应力的关系可以用牛顿黏度定律表达。

•公式: [newton_viscosity](•例子: 当应用大小为1 N/m^2（Pa）的剪切应力，液体的流动粘度为Pa·s，根据牛顿黏度定律可以计算出液体的剪切速率为2s^-1。

5. 流体的力学模型：牛顿流体和非牛顿流体•牛顿流体在任何剪切速率下都遵守牛顿黏度定律，其流动粘度保持不变。

•非牛顿流体的流动粘度随剪切速率的变化而变化。

•非牛顿流体的模型可以用功率律模型、卡塞格伦模型等公式描述。

6. 功率律模型•功率律模型可用来描述某些非牛顿流体的流动粘度与剪切速率的关系。

•公式: [power_law](•例子: 取α = ，K = Pa·sn，当剪切速率为1 s^-1时，根据功率律模型可以计算出流体的流动粘度为Pa·s。

7. 卡塞格伦模型•卡塞格伦模型可以用来描述另一类非牛顿流体的流动粘度与剪切速率的关系。

•公式: [casson_model](•例子: 取η_0 = Pa·s^(1/2)，τ_y = Pa，当剪切速率为2 s^-1时，根据卡塞格伦模型可以计算出流体的流动粘度为Pa·s。

结论•液体粘度公式是描述液体流动阻力的数学表达式，涉及到粘度的定义、测量单位、斯托克斯公式、牛顿黏度定律以及功率律模型和卡塞格伦模型等公式。

水的粘度计算表 Revised as of 23 November 2020水的黏度表(0～40℃)水的物理性质F3 Viscosity decreases with pressure(at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of thesevoids reduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior [] can be explained by the increased pressure (up to about 150 MPa) causing deformation, so reducing the strength of the hydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume. It is thus a direct consequence of the between hydrogen bonding effects and the van der Waals dispersion forces [] in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures (and densities), the between hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining are stronger due to the closer proximity of the contributing oxygen atoms []. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.。

粘度kgms换算粘度是指液体流动阻力的大小，通常用单位面积上受力单位时间内的位移来表示。

常见的粘度单位有Pa·s、mPa·s和kg/ms等。

其中，kg/ms是一种较少使用的粘度单位，下面将详细介绍如何进行kg/ms 与其他常见粘度单位之间的换算。

一、kg/ms与Pa·s的换算1.定义：Pa·s是帕斯卡秒的缩写，是国际标准单位制中表示动态黏度的基本单位。

2.公式：1 Pa·s = 1 kg/m*s3.计算方法：将kg/ms乘以1000即可得到对应的Pa·s值。

例如：将5 kg/ms转换为Pa·s，则有：5 kg/ms * 1000 = 5000 Pa·s二、kg/ms与mPa·s的换算1.定义：mPa·s是毫帕秒的缩写，也称为cP（厘泊）或mPas（毫帕秒），是一种常见的低黏度液体测量单位。

2.公式：1 mPa·s = 0.001 kg/m*s3.计算方法：将kg/ms除以0.001即可得到对应的mPa·s值。

例如：将10 kg/ms转换为mPa·s，则有：10 kg/ms ÷ 0.001 = 10000 mPa·s三、kg/ms与cSt的换算1.定义：cSt是厘斯特克（centistoke）的缩写，是一种用于测量液体黏度的单位。

2.公式：1 cSt = 0.001 kg/m*s3.计算方法：将kg/ms除以0.001即可得到对应的cSt值。

例如：将8 kg/ms转换为cSt，则有：8 kg/ms ÷ 0.001 = 8000 cSt四、kg/ms与SSU的换算1.定义：SSU是Saybolt秒单位的缩写，是一种用于测量石油产品黏度的单位。

2.公式：1 SSU = 0.000145 kg/m*s3.计算方法：将kg/ms除以0.000145即可得到对应的SSU值。

水的动力粘度计算公式水的粘度约为2.98×10-3pa·s。

水是地球上最常见的物质之一。

地球表面有71%被水覆盖。

它是包括无机化合、人类在内所有生命生存的重要资源，也是生物体最重要的组成部分。

纯水导电性十分微弱，属于极弱的电解质。

日常生活中的水由于溶解了其他电解质而有较多的阴阳离子，才有较为明显的导电性。

动力粘度，也被称为动态粘度、绝对粘度或简单粘度，定义为应力与应变速率之比，其数值上等于面积为1㎡相距1m的两平板，以1m/s的速度作相对运动时，因之间存在的流体互相作用所产生的内摩擦力。

单位为n·s/㎡（牛顿秒每米方），即pa·s（帕秒），其量纲为m/（l·t）。

表征液体粘性的内摩擦系数，用μ表示。

常见液体的粘度随温度升高而减小，常见气体的粘度随温度升高而增大。

度量流体粘性大小的物理量。

又称粘性系数、动力粘度，比例系数，粘性阻尼系数，记为μ。

牛顿粘性定律指出，在纯剪切流动中相邻两流体层之间的剪应力（或粘性摩擦应力）为式中dv/dy为垂直流动方向的法向速度梯度。

粘度数值上等于单位速度梯度下流体所受的剪应力。

速度梯度也表示流体运动中的角变形率，故粘度也表示剪应力与角变形率之间比值关系。

按国际单位制，粘度的单位为帕·秒。

有时也用泊或厘泊(1泊=10^(-1)帕·秒，1厘泊= 10^(-2)泊）。

粘度是流体的一种属性，不同流体的粘度数值不同。

同种流体的粘度显著地与温度有关，而与压强几乎无关。

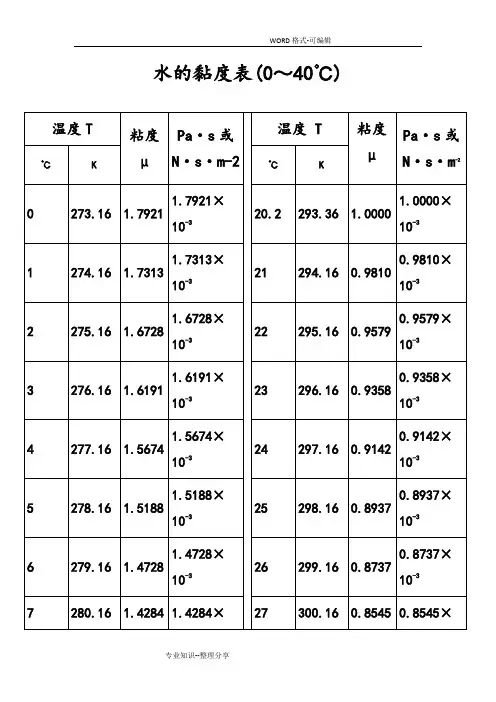
水的黏度表(0～40℃)水的物理性质F3 Viscosity decreases with pressure (at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of these voids reduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior [534] can be explained by the increased pressure (up to about 150 MPa) causing deformation, so reducing the strength of the hydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume. It is thus a direct consequence of the balance between hydrogen bonding effects and the van der Waals dispersion forces [558] in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures (and densities), the balance between hydrogen bonding effects and the van der Waals dispersionforces is tipped in favor of the dispersion forces and the remaining hydrogen bonds are stronger due to the closer proximity of the contributing oxygen atoms [655]. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.。

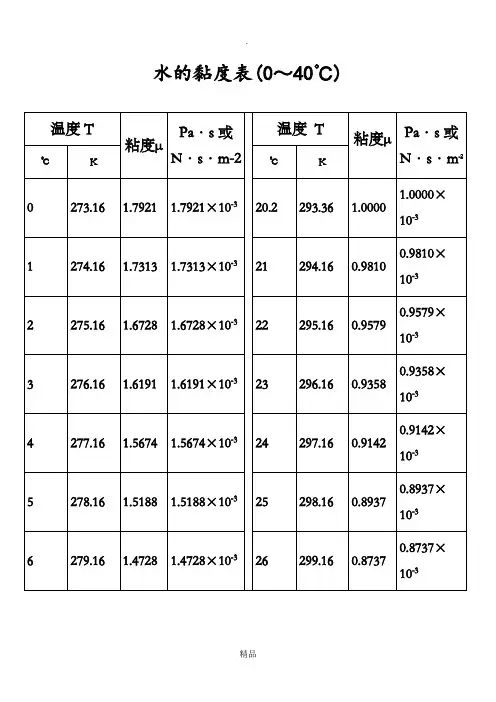
水的黏度表(0～40℃)水的物理性质F3 Viscosity decreases with pressure(at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of these voids reduces, sonormally increasing pressure increases the viscosity.37021040.9450.51892.4340.31933.73 5.692640.48 6.80Water's pressure-viscosity behavior [534] can be explained by the increased pressure (up to about 150 MPa) causing deformation, so reducing the strength of thehydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume. It is thus a direct consequence of thebalance between hydrogen bonding effects and the van der Waals dispersion forces [558] in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures (and densities), the balance between hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining hydrogen bonds are stronger due to the closer proximity of the contributing oxygen atoms [655]. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima..The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.如有侵权请联系告知删除，感谢你们的配合！精品。