下载文档原格式
数据结构——KMP算法算法介绍 KMP算法是⼀种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此⼈们称它为克努特—莫⾥斯—普拉特操作（简称KMP算法）。
KMP算法的核⼼是利⽤匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的⽬的。
具体实现就是通过⼀个next()函数实现，函数本⾝包含了模式串的局部匹配信息。
KMP算法的时间复杂度O(m+n)。
next数组 我们记主串为字符串S，模式串为字符串P。
我们⽤next[j]表⽰以字符Pj结尾的⼦串的长度相等的前缀字符串与后缀字符串长度的最⼤值。
特别地，当没有满⾜条件的⼦串时，next[j] = 0。
为了⽅便起见，我们将字符串从下标1开始匹配。
如此，next数组所表⽰的长度就与下标数值相等了。
算法思路 我们从左到右依次枚举S的每⼀个字符Si，对于当前待匹配字符Si，我们假设当前P字符串中已匹配到Pj。
那么我们只需判断Si和Pj+1，若两者相同，则继续匹配。
若两者不相同，那么我们使j=next[j]，即可最⼤限度的减少匹配次数。
因为S字符串的从某位置开始到前i-1的部分与P字符串的前j个字符已匹配(即完全相同)，如图中两蓝⾊直线所夹的S、P的两段，⽽P1到Pnext[j]部分是长度最⼤的与以Pj结尾的后缀完全相同的前缀（图中绿⾊线段），⽽该以Pj结尾的后缀则必定与S中⼀段以Si-1结尾的⼦串完全相同，因⽽保证了上述操作的正确性。
接下去只需重复上述操作即可。
⽽对于next数组的预处理，也同上述操作类似，我们只需要以字符串P来匹配字符串P即可。
模板呈现 模板题链接： 代码如下：#include <iostream>#include <algorithm>#include <cstdio>using namespace std;const int M = 1e5+10;int n,m;int ne[M];char s[M],p[M];int main(){cin>>n>>p+1;cin>>m>>s+1;for(int i=2,j=0;i<=n;i++){while(j && p[i]!=p[j+1])j=ne[j];if(p[i]==p[j+1])j++;ne[i]=j;}for(int i=1,j=0;i<=m;i++){while(j && s[i]!=p[j+1])j=ne[j];if(s[i]==p[j+1])j++;if(j==n){printf("%d ",i-n+1-1);j=ne[j]; //可有可⽆，好习惯要加上。
KMP算法的详细解释什么是kmp算法呢？这是⼀个处理字符串的算法，⽤来判断给出的模式串p是否存在于⽂本串t中（p的长度⼩于t）。
在本⽂中，字符串储存在字符数组中，并且第⼀个字符放在下标为1的元素中。
那么如何理解kmp算法呢？⾸先要从最朴素的匹配算法说起。
我们判断p是否存在于t中，最原始的⽅法就是从头到尾⼀直遍历。
定义变量i为⽂本串t中的下标，定义变量j为模式串p中的下标，然后i表⽰看⽂本串的前i个字符，j表⽰判断这前i个字符组成的⼦串中，长度为j的前后缀是否相等。
如果t[i] = p[j]，则i与j同时后移⼀位，⽐较下⼀位是否相同，如果t[i] != p[j]，则表⽰串t在i位置处“失配”，需要重新进⾏匹配，i保持不动，并且j 必须返回到模式串p的开头，也就是相当于回退到1，然后再次进⾏循环。
如果t的长度为m，p的长度为n时，这样做的时间复杂度为O(m*n)kmp就是在这种最原始匹配算法的基础之上的改进算法。
Kmp的改进之处在哪⾥呢？上⾯这种复杂度最⼤的朴素⽅法中，有⼀个步骤，当“失配”时，我们的i不移动，但是j需要回到串p的开头，这样每⼀次失配，我们都需要再从模式串的开头重新开始匹配，相当于将j直接回退到1，然后再从1开始去试满⾜的最⼤的相同前后缀长度，多了好多次循环，聪明的科学家们想到的办法是：假设现在有这样⼀种情况：在遍历到⽂本串t的的前i-1个字符组成的⼦串之后，我们已经确定了该⼦串中的长度为j-1的前后缀是相同的，那么现在在考虑下⼀个字符（第a个）时发⽣失配，也就是第a个字符不等于第b个，我们不想让b直接回退到1，⽽是回退到1和b之间的某个值，以减⼩复杂度。
我们先放下这个问题，思考另外⼀个问题：如果要求⼀个字符串中相同的前缀和后缀的最长长度，怎么求呢？和上⾯的kmp其实特别像，还是分治的思想：假设我们现在已经看到了字符串的前i-1个元素，并且在这i-1个元素的⼦串中，长度为j-1的后缀和前缀是⼀样的，表⽰匹配到了j-1的长度，那么我们就可以考虑第字符串中第i个元素是否和第j个元素相同了，如果相同就继续匹配下去，如果不同，j仍要回退，但是不能把j直接回退到1然后递增地去判断，这样复杂度太⼤。
算法导论————KMP【例题传送门：】KMP模版：⼦串是否出现【题意】有两个字符串SA和SB，SA是母串，SB是⼦串，问⼦串SB是否在母串SA中出现过。
如果出现过输出第⼀次出现的起始位置和结束位置，否则输出"NO"【输⼊⽂件】第⼀⾏SA（1<= 长度<=1000000）第⼆⾏SB（1<= 长度<=1000）【输出⽂件】如果SB在SA中出现过输出第⼀次出现的起始位置和结束位置，否则输出"NO"【样例1输⼊】aaaaabaaaab【样例1输出】4 6【样例2输⼊】aaaaabaaaax【样例2输出】NO算法分析： KMP其实就是⼀种偷懒的⽅式，通过访问前⾯已经遍历过的位置来⾸先给定⼀个可继承的值，然后暴⼒（汗......） ⾸先定义⼀个p数组，p[i]=j时，代表SA字符串[1...j]与SA字符串[i-j+1...i]所形成的⼦串完全相同 那么我们怎么得出这个p数组呢？ 就是暴⼒+偷懒（其实前⾯已经讲了，尴尬） 当我们访问到i这个点时，我们先访问⼀下i-1，因为我们访问到i的时候已经把1~i-1的p数组求出来了，那么请看下⾯的图： 我们设j=p[i-1]，i-1-j+1=i-j，那么我们可以知道SA[1...j]=SA[i-j...i-1]，也就是上图的红⾊区间，那假如SA[j+1]=SA[i]的话，我们就可以直接p[i]=j+1对吧 但是现实是残酷的（AC没有那么容易~），那么当SA[j+1]!=SA[i]的时候怎么办呢？那么我们就找p[j]如图： 我们再设⼀个变量k=p[j]，因为p[j]的定义，所以我们可以得到SA[1...k]=SA[j-k+1...j]，也就是前两个棕⾊区间，这时因为两个红⾊区间相同，所以我们可以得到SA[1...k]=SA[i-j...i-j+k-1]，也就是第⼀个和第三个棕⾊区间相等，接着⼜可以得到SA[j-k+1...j]=SA[i-k(i-1-k+1)...i-1]，也就是第⼆个和第四个的棕⾊区间相等，然后我们得到四个棕⾊区间相等我们就可以判断SA[k+1]和SA[i]是否相等来求p[i]，如果相等，p[i]=k+1，否则继续找p[k]。
KMP算法详解范文KMP算法（Knuth-Morris-Pratt算法）是一种经典的字符串匹配算法，用于在文本中查找一个模式串（pattern）的出现位置。
相对于朴素的字符串匹配算法，KMP算法具有更高的效率，特别是在处理大量数据时。
KMP算法的核心思想是利用已经匹配过的信息来避免不必要的回溯。
朴素的字符串匹配算法是一种从文本的每一位字符开始与模式串进行比较的方法，当匹配失败时，会进行回溯，然后再继续从下一位字符开始匹配。
这样的回溯操作会导致算法的效率降低。
KMP算法通过构造一个部分匹配表（partial match table）来实现。
部分匹配表是一个数组，用于记录模式串中每个位置的最长匹配前缀的长度。
具体来说，部分匹配表中的每个元素记录的是对应位置前缀的最长相等前后缀的长度。
例如，假设模式串为"ABCDABD"，部分匹配表的内容如下：位置0123456模式串ABCDABD部分匹配值0000120部分匹配表的构造过程是通过逐个字符的比较来完成的。
具体的步骤如下：1.第一个位置的部分匹配值设为0；2.从第二个位置开始，如果模式串中当前位置的字符与前面位置的字符相等，则部分匹配值为前一个位置的部分匹配值加1；3.如果模式串中当前位置的字符与前面位置的字符不相等，则需要找到前一个位置的最长匹配前后缀，并将当前位置的部分匹配值更新为最长匹配前后缀的长度。
这是通过比较当前位置字符与前一个位置的最长匹配前后缀的下一个字符来实现的，直到找到最长匹配前后缀或者无法再找到为止。
利用部分匹配表，KMP算法可以在匹配过程中避免进行不必要的回溯。
具体的匹配过程如下：1.设置文本串的索引i和模式串的索引j，两者都从0开始；2.对比文本串的第i位和模式串的第j位进行字符比较；3.如果匹配成功，将i和j都加1；4.如果不匹配，则利用部分匹配表来确定模式串的下一个比较位置。
具体来说，如果j大于0，则将j更新为部分匹配表中j-1位置的部分匹配值，然后再与i进行比较；如果j等于0，则将i加15.重复步骤2到步骤4，直到模式串匹配成功或者遍历完文本串。
KMP算法详解KMP 算法详解KMP 算法是⼀个⼗分⾼效的字符串查找算法，⽬的是在⼀个字符串 s 中，查询 s 是否包含⼦字符串 p，若包含，则返回 p 在 s 中起点的下标。
KMP 算法全称为 Knuth-Morris-Pratt 算法，由 Knuth 和 Pratt 在1974年构思，同年 Morris 也独⽴地设计出该算法，最终由三⼈于1977年联合发表。
举⼀个简单的例⼦，在字符串 s = ababcabababca 中查找⼦字符串 p = abababca，如果暴⼒查找，我们会遍历 s 中的每⼀个字符，若 s[i] = p[0]，则向后查询p.length() 位是否都相等。
这种朴素的暴⼒的算法复杂度为O(m×n)，其中m和n分别是 p 和 s 的长度。
KMP 算法可以⽅便地简化这⼀查询的时间复杂度，达到O(m+n)。
1. PMT 序列PMT 序列是 KMP 算法的核⼼，即 Partial Match Table（部分匹配表）。
举个例⼦：char a b a b a b c aindex01234567PMT00123401PMT 的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
PMT[0] = 0: 字符串 a 既没有前缀，也没有后缀；PMT[1] = 0: 字符串 ab 前缀集合为 {a}，后缀集合为 {b}，没有交集；PMT[2] = 1: 字符串 aba 前缀集合为 {a, ab}，后缀集合为 {ba, a}，交集为 {a}，交集元素的最长长度为1；PMT[3] = 2: 字符串 abab 前缀集合为 {a, ab, aba}，后缀集合为 {bab, ab, b}，交集为 {ab}，交集元素的最长长度为2；…… 以此类推。
2. 算法主体现在我们已经知道了 PMT 序列的含义，那么假设在 PMT 序列已经给定的情况下，如何加速字符串匹配算法？tar 存储 s 的下标，从 0 开始，若 tar > s.length() - 1，代表匹配失败；pos 存储 p 的下标，从 0 开始，若 s[tar] != p[pos]，则 pos ⾛到下⼀个可能匹配的位置。
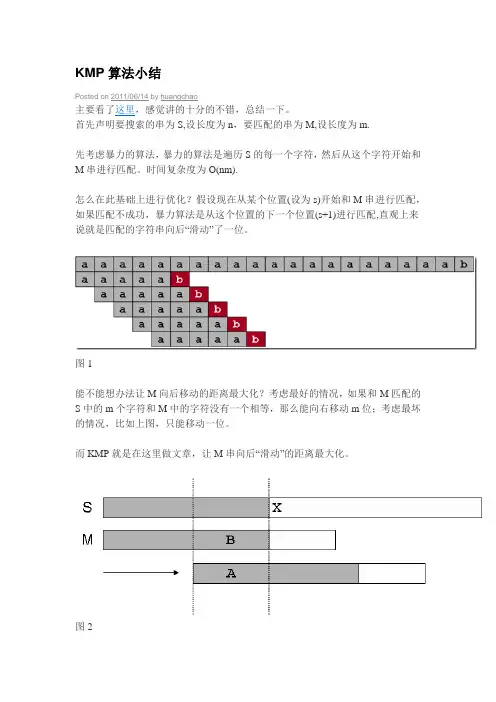
KMP算法小结Posted on 2011/06/14 by huangchao主要看了这里，感觉讲的十分的不错，总结一下。
首先声明要搜索的串为S,设长度为n，要匹配的串为M,设长度为m.先考虑暴力的算法，暴力的算法是遍历S的每一个字符，然后从这个字符开始和M串进行匹配。
时间复杂度为O(nm).怎么在此基础上进行优化？假设现在从某个位置(设为s)开始和M串进行匹配，如果匹配不成功，暴力算法是从这个位置的下一个位置(s+1)进行匹配,直观上来说就是匹配的字符串向后“滑动”了一位。
图1能不能想办法让M向后移动的距离最大化？考虑最好的情况，如果和M匹配的S中的m个字符和M中的字符没有一个相等，那么能向右移动m位；考虑最坏的情况，比如上图，只能移动一位。
而KMP就是在这里做文章，让M串向后“滑动”的距离最大化。
图2考虑上面的图，M中灰色部分已经和S的灰色部分匹配上了，而灰色部分后一个字符不匹配，则现在M要向后滑动，假设一直向后滑动，直到如图位置又和S再一次匹配上了，那么从这里我们可以得到如下的结论：▪A段字符串是M的一个前缀。
▪B段字符串是M的一个后缀。
▪A段字符串和B段字符串相等。
这样，如果暂时不考虑S，只看M的话，假设已经匹配的M的字串(即图中M 中灰色部分)为subM，则subM有个【相等】的【前缀】和【后缀】。
而且M在遇到不匹配的时候可以直接滑动到使subM的前缀和subM的后缀重合的地方。
而M向后滑动的时候，第一次subM的前缀和后缀重合意味着此时这个相等的subM的前缀和后缀的长度是最大的。
我们的任务就是要寻找subM的最长的前缀和后缀相等的串。
知道了这一点，离KMP的真谛也就不远了。
现在结合这上面的图模拟一下KMP 算法的整个流程：▪将S串和M串从第一个字符开始匹配；▪如果匹配成功，则subM即灰色部分增加；▪如果不成功，则M向后滑动使滑动后的subM的前缀和滑动前的subM的后缀重合，再进行匹配，如果还不成功，则再次滑动M，直到匹配成功或者M 滑动到X处。
KMP算法（字符串匹配）遇到字符串匹配问题,⼀般我就只能想到O(nm)的朴素算法...今天有这样⼀种算法,使得复杂度变为O(n),这就是KMP(烤馍⽚)算法粘⼀个模板题先:给出两个字符串s1和s2，其中s2为s1的⼦串，求出s2在s1中所有出现的位置。
然后本题还要求输出所有s2中字符的前缀数组,现在留下⼀个疑点,前缀数组(这是啥?),先往后看⾸先确定⼀点,就是在进⾏字符串匹配时,会是拿⼀个字符串与另⼀个字符串的⼀部分进⾏⽐较,那么我们有以下称呼(拿本题进⾏举例):s2叫做模式串,s1叫做母串我们先分析朴素算法的原理与弊端:朴素算法是将每⼀个母串字符拿出⽐较,⼀旦不符合就会放弃前⾯匹配的所有信息,重头再来,然⽽KMP不然,KMP就是⼀种"失败为成功之母"的算法,每次在匹配失败时利⽤前⾯信息进⾏更⾼效的匹配,具体的思想需要⽤到这个"前缀数组"那么这是啥呢?先考虑⼀个问题:如何利⽤失败信息,如果匹配失败,我们会放弃当前匹配,然⽽这起码证明前⾯的匹配都是成功的,也就是说,只要我找到模式串前⾯的能与⾃⼰(当前匹配失败之前的⼀个位置)匹配上的⼦串,那么⼀定也能与前⾯匹配,进⾏再次查找,⽽不⽤进⾏朴素算法暴⼒枚举,前缀数组就是保存这样的指针的数组,预处理⼤概是这样的:inline void init(){p[1]=0;int j=0;for(int i=1;i<m;i++){while(j>0&&b[j+1]!=b[i+1]) j=p[j];if(b[j+1]==b[i+1]) j++;p[i+1]=j;}}总体代码是这样的:#include<cstdio>#include<cstring>#include<string>using namespace std;char a[1000005];char b[1000005];int p[1000005];int n,m;inline void init(){p[1]=0;int j=0;for(int i=1;i<m;i++){while(j>0&&b[j+1]!=b[i+1]) j=p[j];if(b[j+1]==b[i+1]) j++;p[i+1]=j;}}inline void find(){int j=0;for(int i=0;i<n;i++){while(j>0&&a[i+1]!=b[j+1]) j=p[j];if(b[j+1]==a[i+1]) j++;if(j==m){printf("%d\n",i-m+2);j=p[j];}}}int main(){scanf("%s%s",a+1,b+1);n=strlen(a+1);m=strlen(b+1);init();find();for(int i=1;i<=m;i++)printf("%d ",p[i]);return 0;}为什么KMP主体与预处理这么像呢?因为预处理本⾝就是我\ \ \ \ 匹配\ \ \ \ \ 我⾃⼰最后就是输出前缀数组了Processing math: 100%。
KMP算法思想80页在讲KMP算法的开始先举了个例子，让我们对KMP的基本思想有了最初的认识。
目的在于指出“由此，在整个匹配的过程中，i指针没有回溯，”。
我们继续往下看：现在讨论一般情况。
假设主串：s: ‘s(1) s(2) s(3) ……s(n)’ ; 模式串：p: ‘p(1) p(2) p(3)…..p(m)’把课本上的这一段看完后，继续现在我们假设主串第i个字符与模式串的第j(j<=m)个字符‘失配’后，主串第i个字符与模式串的第k(k<j)个字符继续比较此时，s(i)≠p(j), 有主串： S(1)…… s(i-j+1)…… s(i-1) s(i) ………….|| (相配) || ≠(失配)匹配串： P(1) ……. p(j-1) p(j)由此，我们得到关系式‘p(1) p(2) p(3)…..p(j-1)’ = ’ s(i-j+1)……s(i-1)’由于s(i)≠p(j)，接下来s(i)将与p(k)继续比较，则模式串中的前(k-1)个字符的子串必须满足下列关系式，并且不可能存在 k’>k 满足下列关系式：(k<j),‘p(1) p(2) p(3)…..p(k-1)’ = ’ s(i-k+1)s(i-k+2)……s(i-1)’即：主串： S(1)……s(i-k +1) s(i-k +2) ……s(i-1) s(i) ………….|| (相配) || || ?(有待比较)匹配串：P(1) p(2) …… p(k-1) p(k)现在我们把前面总结的关系综合一下有：S(1)…s(i-j +1)… s(i-k +1) s(i-k +2) …… s(i-1) s(i) ……|| (相配) || || || ≠(失配)P(1) ……p(j-k+1) p(j-k+2) ….... p(j-1) p(j)|| (相配) || || ?(有待比较)P(1) p(2) ……. p(k-1) p(k)由上，我们得到关系：‘p(1) p(2) p(3)…..p(k-1)’ = ’ s(j-k+1)s(j-k+2)……s(j-1)’接下来看“反之，若模式串中存在满足式(4-4)。
希望对大家有所帮助，多谢您的浏览！1 KMP 算法思想朴素匹配模式最差的情况需 O(|T||P|)的代价，每次模式不比配时，都要返回到模式头比较。
即右移模式到模式的第一位。
其实，每次右移到哪一位与目标串无关，仅依赖于模式本身。
需要在朴素匹配模式进行改进 KMP 算法：预先处理模式本身，分析其字符分布情况。
并为模式中的每一个字符计算失配时 应该右移到哪一位。
（特征向量）2 字符串的特征向量字符串模式的使用方法： 在 P 与目标 T 的匹配过程中，当 Pi != Tj 时，意味着此前的匹配历史中满足：P(0…i-1) = T(j-I … j-1)(1)P(0…i-2) = P(1…i-1)(2) 此为假设条件： 字符串模式自身的特征P(1…i-1) = T(j-I+1 … j-1)(3) 由(1)式得出P(0…i-2) = T(j-I+1 … j-1)(4) 将(2)式代入(3)得到此时利用模式自身的特征，在 P 与 T 比较时，可以直接使用之前已有的结果{即(4)式} 。
之后的操作直接比较 Pi-1 与 Tj字符模式的相关定义： k 值：在 P[i]之前的字符串 P(0 … i-1)中，总可以找到P(0 … k-1) = P(i-k … i-1)(5) 即前缀子串(首串) = 后缀子串(尾串)对于模式位置 i 上的字符 P[i]而言，一旦与目标 Tj 失配时，模式 P 的下标从位置 i 移动 到 k，P[k]直接与 Tj 比较，跳过 P(0 … k-1)。
特征数 next[i]: 把对应于模式中每个字符 P[i]的 k 值为特征数。
即 P(0 … i-1)中最大相 同前缀子串和后缀子串。
特征向量 next[ ]: 所有的特征数组成的。
表示了模式 P 的字符分布特征。
特征向量 next 的计算方法：next[i]-1 max { k: 0<k<I && P(0 … k-1) = P(i-k … i-1)} 0对于 i=0 如果 k 存在 否则计算 next[i]时，充分利用了位置 i 之前的各个字符的 next 值，若用 ni 表示 next[i], ni 可以递归定义：(后面详细解释) (1) n0 = -1;对于 i>0 的 ni，假定已知前一位置的特征数 n[i-1] =k. (2)若 i>0 且 P[i] = P[k]，则 n[i]=k+1. 此时的 i 和 k 还未自增 1 (3)当 P[i] != P[k]且 k!=0 时，则令 k = next[k] ,内循环执行直到 P[i] = P[k] 或 k=0.// k = next[k-1]?? (4)当 P[i] != P[k]且 k=0 时，则 n[i]=0 函数实现：授课：XXX希望对大家有所帮助，多谢您的浏览！int *findNext (String P) {int i=0;int k=-1;int m=P.length(); //m 为字符串 P 的长度assert(m>0);//若 m 退出int * next=new int[m];//动态存储区开辟整数数组assert (next != 0); //若开辟存储区域失败，退出next[0] =-1;while(i<m){ //计算 i=1 …m-1 的 next 值while(k>0&&P[i]!=P[k]) //求最大首尾子串k=next[k];i++;k++;if(i==m)break;if(P[i]==P[k])next[i] = next[k]; P[i]和 P[k]相等，优化else next[i]=k; //不需要优化，就是位置 i 的首尾子串长度}return next;}授课：XXX举例解释: 已知条件：希望对大家有所帮助，多谢您的浏览！next[7]=3 即 i=7 时，k=3P0P1P2P3P4P5P6P7P8next[2]=2 即 i=2 时，k=2P0P1P2P3 P4P5P6P7P8解释内循环（1）：while(k>0&&P[i]!=P[k]) //求最大首尾子串 k=next[k];当在求 next[8] 的大循环时，k=3>=0 &&P[7]!=P[3],则进入内循环，将已知的两个条件合 并得：P0P1P2P3P4P5P6P7P8由 next[i]定义得： next[7]=3 即 P[0]~P[2] = P[4]~P[6] ; 橙线 next[2]=2 即 P[0]~P[1] = P[1]~P[2]= P[4]~P[5] ; 蓝线P[0]~P[1] = P[5]~P[6] ; 黑线 //对应程序中的 k=next[k]; 此时判断 P[2] ?= P[7] 若等于的话，跳出内循环，由黑线得到绿线，以下结果：P[0]~P[2] = P[5]~P[7] ; 绿线 关键步骤：橙线包含蓝线，才能够进一步推导出黑线。
改进的模式匹配算法的理论分析设T = t0 t1 … t s-1 t s t s+1 t s+2 … t s+j-1 t s+j t s+j+1 … t n-1P = p0 p1 p2 … p j-1 p m-1．若在匹配过程中出现了如下情况：t s t s+1t s+2… t s+j-1= p0p1p2… p j-1，(1)但t s+j ≠ p j．也就是说，在匹配过程出现了：T t0 t1 … t s-1t s t s+1t s+2… t s+j-1t s+j t s+j+1… t s+m-1 … t n-1‖ ‖ ‖ … ‖ ⨯P p0p1p2 … p j-1p j p j-1… p m-1则本次匹配失败．由朴素的模式匹配算法，我们需要下一趟匹配，即需要验证下式是否成立：t s+1t s+2… t s+j-1 t s+j … t s+m?= p0p1 … p j-2p j-1… p m-1(2)如果（2）式成立，则匹配成功，返回s+1；否则需要再下一趟的匹配：t s+2t s+3… t s+j-1t s+j… t s+m+1?= p0p1… p j-3p j-2 …p m-1 (2')以此类推．下面给出两个互逆的条件p0p1… p j-2 = p1p2 …p j-1 (3)p0p1… p j-2 ≠p1p2 …p j-1 (3')显然，这两个条件能且只能满足一个．下面并分情况讨论：【1】如果(3) 式成立，则由(1) (2) (3) 式，可以断定p0 p1 …p j-2 = t s+1 t s+2 … t s+j-1成立，即在（3）式条件下，对(2) 式的验证只需要从p j-和t s+j 开始逐个往后比较，而不必从p0 和t s+2 开始．1【2】如果(3') 式成立，则由(1) (2) (3') 式，可以断定p0 p1 …p j-2 ≠t s+1 t s+2 … t s+j-1成立，即在(3')式条件下，(2)式一定不能成立，应该直接进行下下次验证，即对(2') 进行验证．对于(2')，也引进两个互逆的条件p0p1… p j-3 = p2p3 …p j-1 (4)p0p1… p j-3 ≠p2p3 …p j-1 (4')这两个条件也是只能满足一个，分情况讨论：【2.1】如果(4) 式成立，则由(1) (2') (4)，可以断定p0 p1 …p j-3 = t s+2 t s+3 … t s+j-1成立，即：对(2') 式的判断从p j-2和t s+j开始逐个往后比较，而不必从p0和t s+2开始．【2.2】如果(4')式成立，则由(1) (2') (4')，可断定p0 p1 …p j-3 ≠t s+2 t s+2… t s+j-1成立，即(2')一定不成立，应该开始再下一次的判断，即：t s+3 t s+4 … t s+j-1 t s+j … t s+m+2 ?= p0 p1 … p j-4 p j-3 …p m-1没必要再往下做了，下面把刚才的两次匹配过程总结一下，找出规律来：【1】如果(3) 式成立，则对(2)式的验证可以从p j-1和t s+j开始继续往后进行，而不必从p0和t s+1开始．【2】如果(3') 成立，则需要进行下下次匹配【见(2')式】：【3】如果(3') 和(4) 式成立，则对(2') 式的验证可以从p j-2和t s+j开始继续往后进行，而不必从p0和t s+1开始．【4】如果(3') 和(4') 式成立，则需要进行下下下次匹配：t s+3 t s+4 … t s+j-1 t s+j … t s+m+2 ?= p0 p1 … p j-4 p j-3 …p m-1由刚才总结的第【3】种情况，我们可以设想存在一个k，使得p0p1… p j-2 ≠p1p2 …p j-1 (3')p0p1… p j-3 ≠p2p3 …p j-1 (4')… … … …p0p1… p k ≠p j-k-1p j-k …p j-1 (5')p0p1… p k-1 = p j-k p j-k+1 …p j-1 (6)显然，如果这样的k 存在，则0 <= k < j-1（当k == 0 时，(6)式的左右都为空串）．再由刚才总结的第【2】和【4】种情况可知：如果(3') (4') …(5') 都成立，哪些判断不用做了呢？这需要发现(2)、(2') 的变化规律．刚才，由(3') 式，则(2) 式不用再判断了；由(4') 式，则(2') 式不用再判断了．换句话说，根据(5') 式，●当k = j – 2时【(3')式成立】，(2)式不用判断了；●当k = j – 3时【(4')式成立】，(2')式不用判断了；●… …由此可以推出：当k时，下面的(7) 式不用判断了t s+j-k-1t s+j-k… t s+j-1t s+j… t s+j-k+m-2 ?= p0p1… p k p k+1… p m-1 (7)也就是说，当k 时，也就是(5') 成立时，(7) 式子不用判断了．此时需继续判断如下的(8) 式是否成立t s+j-k t s+j-k+1… t s+j-1t s+j… t s+j-k+m-1?= p0p1… p k-1p k… p m-1 (8)由(6) 式和(8) 式，再考虑到(1) 式并改写(1) 式t s t s+1… t s+j-k t s+j-k+1… t s+j-1= p0p1… p j-k p j-k+1 …p j-1(1)可以断定：p0 p1 …p k-1 = t s+j-k t s+j-k+1 … t s+j-1，因此，下次比较从p k和t s+j开始即可．综上：若在上述的失配情况下，且存在最大的正整数k，换句话说，当k = j-2, j-3, …, k 时，(5') 式都是成立的．但是，当k-1 时，(5') 不再成立，而(6) 式成立，则下一次的比较从p k和t s+j开始即可．那么，这样的k 是否存在？如何确定呢？下面把刚才的问题再次重述一下，从而明确我们要做的具体任务：若t s t s+1 t s+2 … t s+j-1 = p0 p1 p2 … p j-1，但t s+j p j，则本次匹配失败．则我们用一个next向量来确定k，也就是说，当模式P 中第j 个字符p j与目标T 中第s+j 个字符t s+j失配时，应当用模式P 中字符p k （next[j] = k）与目标T 中的t s+j继续进行比较．那么k 怎么求呢？下面介绍确定k 的方法．显然，k的取值是由(5') 和(6) 式确定．进一步发现，k的取值只与模式P有关，和目标T无关，因此把next向量称为模式的特征向量（描述了模式的一个特征，和主串无关）．由上述分析可知，next[j] 的值可以按如s下的公式来计算：next[j]={−1,j=0;k,0<k<j−1,且使得p0p1…p k−1=p j−k p j−k+1…p j−1的最大整数k 0,其他情况.示例：若P = "abaabcac"，则设在进行某一趟匹配比较时在模式P 的第j 位失配：●如果j > 0，那么在下一趟比较时模式串P的起始比较字符是p k，即p next(j)，而目标串T 的指针不回溯，仍指向刚才失配的字符；●如果j = 0，则目标串T 的指针进一，模式串P 指针回到字符p0，继续进行下一趟匹配比较．上述两种情况就是KMP算法的核心内容。
假设next[ ] 已知，则KMP算法的C++代码如下：int AString::fastFind(const AString& pat, int next[ ],int k) const {// 从k 开始寻找pat 在this 串中匹配的位置。
若找到，函数// 返回pat 在this 串中开始位置，否则函数返回-1。
数组// next[ ] 存放pat 的next[j] 值。
int posP = 0,posT = k;// 两个串的扫描指针int lengthP = pat.curLength;// 模式串长度int lengthT = curLength;// 目标串长度while (posP < lengthP && posT < lengthT)if (posP == -1 || pat.ch[posP] == ch[posT]){ posP++; posT++; }// 对应字符匹配else posP = next[posP];// 求pat下趟比较位置if (posP < lengthP) return -1;// 匹配失败else return posT-lengthP;// 匹配成功}此算法的时间复杂度取决于while循环．由于是无回溯的算法，执行循环时，目标串字符比较有进无退，要么执行posT和posP进1，要么查找next[ ] 数组进行模式位置的右移，然后继续向后比较．字符的比较次数最多为O(n)，不超过目标的长度．举例：利用next特征向量进行匹配处理刚才的KMP算法是在next[ ] 已知的情况下进行的。
那么next[ ]是如何计算的呢？由刚才的计算next[ ] 的推导公式发现，我们还无法让计算机来实现，这是因为从公式中（如下）next[j]={−1,j=0;k,0<k<j−1,且使得p0p1…p k−1=p j−k p j−k+1…p j−1的最大整数k 0,其他情况.红色部分只给出了k应满足的条件，还没有给出具体算法，所以我们也无法用计算机语言写出来。
那么，我们怎么把这段话用算法写出来呢？下面：首先分析并推导，然后给出算法和代码。
计算next特征向量的理论推导设模式P = p0 p1 p2 …p m-1，由m个字符组成，而next特征向量为next = n0 n1 n2 … n m-1，表示了模式的字符分布特征．由next[j] 的定义，计算next[j] 就是要在串P j = p0 p1 p2 …p j-1中找出最长且相等的前缀子串P k 和后缀子串P-k ，其中：P k = p0 p1 p2 …p k-1，P-k = p j-k p j-k+1 p j-k+2…p j-1用递推的思想：假设next[j] = k 是已知的，则P k = P-k，即：p0 p1 …p k-1= p j-k p j-k+1 …p j-1，(9)则，计算next[j+1]需先验证p0 p1 …p k-1p k?= p j-k p j-k+1 …p j-1p j，(10)由(9)式可知，若验证(10)式，只需验证p k?= p j(11)下面分情况讨论：【1】若(11)式成立，即p k = p j，则(11)式成立，即：next[j+1] = k + 1 = next[j] + 1 (12)【那么，为什么next[j+1] 不能是k+2，或更大呢？】假设next[j+1] = k + 2，则p0 p1 …p k-1 p k p k+1 = p j-k-1 p j-k p j-k+1 …p j-1 p j，这说明p0 p1 …p k-1 p k = p j-k-1 p j-k p j-k+1 …p j-1，从而说明next[j] = k + 1，和已知矛盾，故当next[j] = k时，next[j+1] <= k+1．【证毕】【2】若(11)式不成立，即p k≠ p j，由(9)式可知：p0 p1 … p j-k-1p j-k p j-k+1 … p j-1p j‖ ‖ ‖ ⨯p0 p1 … p k-1p k此问题转换成了在p0 p1 … p k-1中寻找下一次要与p j进行比较的字符p h，即：是否存在最大的正整数h，使得p0 p1 … p h ≠p k-h-1 p k-h … p k-1，(13)p0 p1 …p h-1= p k-h p k-h+1 …p k-1，(14)成立？若h 存在，则需要比较p h ?= p j．还分两种情况：【2.1】找到h (h ≥ 0)，由next[k]的定义可知：next[k] = h，从而(14)式成立，联立(9)式并改写(9)式，p0 p1 … p k-h p k-h+1 …p k-1= p j-k p j-k+1 … p j-h p j-h+1 … p j-1(9)可得，p0 p1 …p h-1= p j-h p j-h+1 …p j-1(15)因此，下一步只需比较p h ?= p j．类似地，若p h = p j，则next[j+1] = h+1 = next[k]+1= next[next[j]]+1；否则，还需要在p0p1 …p h-1中寻找更小的next[h]，直到next[t] = -1为止．【2.2】找不到h，（即h = -1），则next[j+1] = 0 = h + 1 = next[0] + 1．next特征向量的算法和C++代码next特征向量从0, 1, 2, …, m-1逐项递推计算：[1] 当j == 0时，n0 = -1．设j≥ 0 时n j = k;[2] 当(k == -1) || (p j ==p k)，则n j+1 = k+1 = n j + 1．[3] 当p j≠p k且k ≠ -1，令k = n k，并让[3] 循环直到条件不满足．[4] 当k == -1，则n j+1 = 0 = k + 1 = n0 + 1．例如：C++代码：void AString::getNext(int next[ ])const { int j = 0, k = -1, lengthP = curLength;next[0] = -1;while (j < lengthP)// 计算next[j]if ( k == -1 || ch[j] == ch[k]) {j++; k++;next[j] = k;}elsek = next[k];}完整的例子#include <iostream>#include <cstring>#include <cassert>using namespace std;const int defaultSize = 128; // 字符串的最大长度class AString { // 字符串类private:char *ch;// 存放串的数组首地址int curLength;// 串的实际长度int maxSize;// 存放串数组的最大长度public:AString(int sz = defaultSize);// 构造函数AString(const char *init );// 构造函数AString(const AString& ob);// 复制构造函数~AString( ) { delete [ ]ch; }// 析构函数int Length( ) const { return curLength; }// 求长度AString operator( ) (int pos, int len);// 求子串bool operator == (AString& ob) const // 判串相等{ return strcmp (ch, ob.ch) == 0; } // 若相等, 返回true bool operator != (AString& ob) const // 判串不等{ return strcmp (ch, ob.ch) != 0; } // 若不等, 返回true bool operator ! ( ) const { return curLength == 0; }AString& operator = (const AString& ob); // 串赋值AString& operator += (const AString& ob); // 串连接char operator [ ] (int i);// 取第i 个字符int Find (const AString& pat, int k = 0) const; // 串匹配int fastFind(const AString& pat, int next[ ], int k = 0) const;void getNext(int next[ ])const;};AString::AString(int sz) { // 构造函数：创建一个空串maxSize = sz;assert(ch = new char[maxSize+1]); // 创建串数组curLength = 0;ch[0] = '\0'; // 串的结束符为'\0'}AString::AString(const char *init) {// 构造函数: 从已有字符数组init 复制int len = strlen(init);maxSize = (len > defaultSize) ? len : defaultSize;assert(ch = new char[maxSize + 1];) // 创建串数组curLength = len;// 复制串长度strcpy(ch, init);// 复制串值}AString :: AString(const AString& ob) {// 复制构造函数：从已有串ob 复制maxSize = ob.maxSize; // 复制串最大长度assert(ch = new char[maxSize + 1]); // 创建串数组curLength = ob.curLength; // 复制串长度strcpy(ch, ob.ch); // 复制串值}AString AString::operator ( ) (int pos, int len) {// 从串中第pos 个位置起连续提取len 个字符形成子串返回if (pos < 0 || len <= 0 || pos+len-1 >= curLength){ AString t1; return t1; } // pos 或len不合法，返回空串int n = defaultSize > len ? defaultSize : len;AString temp(n + 1);temp.curLength = len; // 子串长度for (int i = 0, j = pos; i < len; i++, j++) temp.ch[i] = ch[j];temp.ch[len] = '\0'; // 子串结束return temp;}AString& AString::operator = (const AString &ob) {// 串赋值if (&ob != this) {// 若两个串不是自己给自己赋值delete [ ]ch;maxSize = ob.maxSize;assert(ch = new char[maxSize + 1]); // 重新分配curLength = ob.curLength; strcpy(ch, ob.ch);}return *this;}char AString::operator [ ] (int i) {// 提取当前串*this 的第i 个字符if (i < 0 && i >= curLength){ cout << "字符串下标超界!\n"; exit(1); }return ch[i];}AString& AString::operator+= (const AString &ob) {// 串链接int n = curLength + ob.curLength;// 串长度累加if (n > maxSize) {maxSize = n; curLength = n;char *temp = ch;// 暂存原串数组assert(ch = new char[n+1]);strcpy(ch, temp);delete [ ]temp;}strcat(ch, ob.ch);// 连接ob 串数组return *this;}int AString::Find(const AString& pat, int k) const {// 在当前串中从第k 个字符开始寻找模式pat 在当// 前串中匹配的位置。
