下载文档原格式
5经典图论问题5.1 一笔画问题一笔画算法即是从起点a开始选择关联边（第一这条边不是往回倒，第二这条边在前面延伸路上没有出现过）向前延伸，如果到达终点b，得到a—b迹，判断路上的的边数是否为图的总边数，是就终止，否则选择迹上某个关联边没有用完的顶点v，用同样方式再搜索v—v的闭迹，添加到a—b迹上，即得到a—v---v—b迹，如果这个迹的边数还没有达到总边数，则再选择迹上某个关联边没有用完的顶点。
逐步扩展即可。
二、弗罗莱（Fleury ）算法任取v 0∈V(G)，令P 0=v 0；设P i =v 0e 1v 1e 2…e i v i 已经行遍，按下面方法从中选取e i+1： （a ）e i+1与v i 相关联；（b ）除非无别的边可供行遍，否则e i+1不应该为G i =G-{e 1,e 2, …, e i }中的桥（所谓桥是一条删除后使连通图不再连通的边）；（c ）当（b ）不能再进行时，算法停止。
5.2 中国邮递员问题（CPP ）规划模型：设ij x 为经过边j i v v 的次数，则得如下模型。
∑∈=Ev v ij ijji x z ϖmin∑∑E∈E∈∈=j i i k v v i v v ki ij V v x x ,E ∈∈≤j i ij v v N x ,1..t s5.3旅行推销员问题（TSP，货郎担问题）（NPC问题）定义：包含图G的所有定点的路（圈）称为哈密顿路（圈），含有哈密顿圈得图称为哈密顿图。
分析：从一个哈密顿圈出发，算法一：（哈密顿圈的充要条件：一包含所有顶点的连通子图，二每个顶点度数为2）象求最小生成树一样，从最小权边加边，顶点度数大于3以及形成小回路的边去掉。
算法二：算法三：示例：设旅行推销员的矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛01086100111281101565150规划模型：先将一般加权连通图转化成一个等价的加权完全图，设当从i v 到j v 时，1=ij x ，否则，0=ij x ，则得如下模型。
离散数学路和圈第4讲定义4.1(1) G 中顶点与边的交错序列P=v i e j v i e j … e j v i 称为从v i 到v i 的途径。
(2) 其中v i ，v i 为e j 的端点,r=1,2,…,s 。
v i ,v i 分别是P 的始点和终点.(3) P 中边的条数s 称为P 的长度。
设G 为无向标定图，0112s s 0s 0s r-1r r 注：默认s 1定义4.1进一步，①若v i =v i ，则称途径P 为闭的。
②若P 中所有边各异，则称P 为迹。
若还有v i =v i ，则称P 为闭迹。
③若P 中所有顶点各异(必然有所有边也各异），则称P 为路。
0s 0s定义 4.1④若除了v i =v i 外顶点都各异，且所有边也各异,则称P 为圈;将长度为奇数的圈称为奇圈;将长度为偶数的圈称为偶圈。
s 0可类似定义有向图的上述概念，但要保持方向的一致性。
1在定义圈的时候，我们加上了边也各异的条件是为了排除下面的情形：v 0e 1v 1e 1v 02注意环是长为1的圈，两条平行边构成长为2的圈。
3（1）只用边的序列表示途径。
定义4.1中的P 可以表示成e j e j … e j 。
（2）在无平行边的图中也可以只用顶点序列表示途径。
定义中的P 可以表示成v i v i … v i 。
还可以用更简单的表示法表示途径。
412s12s在n 阶图G 中，若顶点v i 和v j (v i ≠v j )存在途径，则v i 和v j 之间存在长度小于或等于（n-1）的途径。
定理4.1推论：在n 阶图G 中，若从顶点v i 到v j (v i ≠ v j )存在途径，则v i 到v j一定存在长度小于或等于n-1的路。
定理4.2在一个n阶图G中，若存在v i到自身的闭途径，则一定存在v i到自身长度小于或等于n的闭途径。
推论：在一个n阶图G中，若存在v i到自身的闭迹，则一定存在长度小于或等于n的圈。
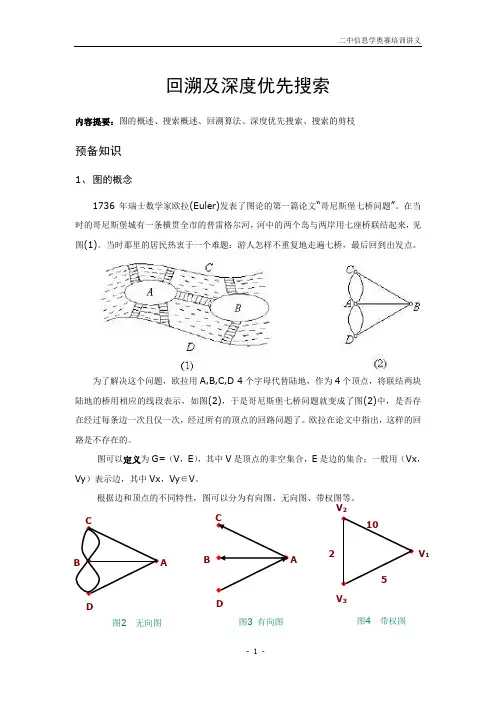
回溯及深度优先搜索内容提要：图的概述、搜索概述、回溯算法、深度优先搜索、搜索的剪枝预备知识1、图的概念1736年瑞士数学家欧拉(Euler)发表了图论的第一篇论文“哥尼斯堡七桥问题”。
在当时的哥尼斯堡城有一条横贯全市的普雷格尔河，河中的两个岛与两岸用七座桥联结起来，见图(1)。
当时那里的居民热衷于一个难题：游人怎样不重复地走遍七桥，最后回到出发点。
为了解决这个问题，欧拉用A,B,C,D 4个字母代替陆地，作为4个顶点，将联结两块陆地的桥用相应的线段表示，如图(2)，于是哥尼斯堡七桥问题就变成了图(2)中，是否存在经过每条边一次且仅一次，经过所有的顶点的回路问题了。
欧拉在论文中指出，这样的回路是不存在的。
图可以定义为G=（V，E），其中V是顶点的非空集合，E是边的集合；一般用（Vx，Vy）表示边，其中Vx，Vy∈V。
根据边和顶点的不同特性，图可以分为有向图、无向图、带权图等。
DA图2 无向图BDA图3 有向图V1V32图4 带权图V2图的遍历：即从某个顶点出发，依次访问每个顶点一次。
【例题】两只蚂蚁比赛问题。
两只蚂蚁甲、乙分别处在图G中的顶点a,b处，并设图中各边长度相等。
甲提出同乙比赛：从它们所在顶点出发，走过图中所有边最后到达顶点c处。
如果它们速度相同，问谁最先到达目的地？2、树的概念树形结构是结点之间有分支，并具有层次关系的结构，它非常类似于自然界中的树。
树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示。
以上表示很像一棵倒画的树。
其中“树根”是张源，树的“分支点”是张明、张亮和张平，该家族的其余成员均是"树叶"，而树枝(即图中的线段)则描述了家族成员之间的关系。
显然，以张源为根的树是一个大家庭。
它可以分成张明、张亮和张丽为根的三个小家庭；每个小家庭又都是一个树形结构。
树可以用树形图、嵌套集合、凹入表等方式表示。
其中树形图表示是树结构的主要表示方法：结点用圆圈表示，结点的名字写在圆圈旁边（有时亦可写在圆圈内）。
《数学史概论》导言一、为什么要开设数学史选修课？数学史研究数学概念、数学方法和数学思想的起源与发展，及其与社会、经济和一般文化的联系。
对于深刻认识作为科学的数学本身，及全面了解整个人类文明的发展都具有重要的意义。
庞加莱（法，1854－1912年）：如果我们想要预见数学的将来，适当的途径是研究这门科学的历史和现状。
萨顿（美，1884－1956年）：学习数学史倒不一定产生更出色的数学家，但它产生更温雅的数学家，学习数学史能丰富他们的思想，抚慰他们的心灵，并且培植他们高雅的质量。
萨顿号称“科学史之父”是当之无愧的。
二、数学史要学习什么？数学史的分期：一是数学的起源与早期发展（公元前6世纪）；二是初等数学时期（公元前6－公元16世纪）；三是近代数学时期（17－18世纪）；四是现代数学时期（1820年至今）。
文明背景（古代埃及、古代巴比伦、古印度、中国简史、古希腊简史），帝国兴衰（罗马帝国、阿拉伯帝国、神圣罗马帝国、波旁王朝、哈布斯堡王朝、普鲁士王国、奥匈帝国），宗教特色（印度教、犹太教、基督教、天主教、伊斯兰教、佛教），革命文化运动（欧洲翻译运动、文艺复兴运动、哥白尼革命、英国产业革命、法国启蒙运动、法国大革命、欧洲1848年革命）。
处于数学中心区发展的主要成就，介绍100多位著名数学家的工作及重要著作，各个历史时期中国数学的状况，传统的几何、代数、三角的基础上发展起来的近代数学的主要成就：解析几何与微积分学，及近现代数学分支，如射影几何、非欧几何、微分几何、复变函数论、微分方程、动力系统、变分法、实变函数论、泛函分析、数论、布尔代数、逻辑代数、数理逻辑、抽象代数、集合论、图论、拓扑学、概率论等。
促进数学发展的相关学科，如力学、物理学、天文学的发展。
三、教学工作安排第一讲：数学的起源与早期发展；第二讲：古代希腊数学；第三讲：中世纪的东西方数学I；第四讲：中世纪的东西方数学II；第五讲：文艺复兴时期的数学；第六讲：牛顿时代：解析几何与微积分的创立；第七讲：分析时代：18世纪的数学；第八讲：19世纪的代数；第九讲：19世纪的几何；第十讲：19世纪的分析；第十一讲：20世纪数学概观I；第十二讲：20世纪数学概观II；第十三讲：20世纪数学概观III；选讲：数学论文写作初步。
《集合论与图论》课程教学大纲一、课程基本信息课程编号：CS31111课程名称：集合论与图论英文名称：SET THEORY AND GRAPH THEORY课程学时：64；讲课学时： 48；实验学时：上机学时：习题学时：16;课程学分：4.0开课单位：计算机科学与技术学院授课对象：计算机大类专业（包括计算机科学与技术、物联网工程、生物信息学、信息安全）、软件工程大类专业开课学期： 1春先修课程：工科数学分析、线性代数二、课程目标《集合论与图论》是计算机大类/软件工程大类专业的一门专业基础课程。
本课程为后继的专业基础课及专业课提供必要的数学工具，为描述离散模型提供数学语言。
该课程的设置主要是为了培养学生的抽象思维和逻辑推理能力，提高学生分析问题和解决问题的能力，提高学生的数学修养及计算机科学素质。
要想用计算机解决问题就要为它建立数学模型，即描述研究对象及对象与对象之间的联系，并通过事物之间的联系找出事物的运动规律。
集合论与图论为此提供了强有力的描述工具与推理理论。
本课程的目标是通过理论学习，为计算机科学与技术专业的后继课及将来的科学研究提供必要的相关数学知识，提供建立离散系统的数学模型的数学描述工具；使学生正确地理解概念，正确地使用概念进行推理，养成一个好的思维习惯，理解理论与实践的关系；引导学生观察生活、社会和大自然，分析事物间的联系，建立系统的模型，提出和解决其中的复杂工程问题。
课程具体目标如下：课程目标1：掌握集合论与图论的基本概念、基本原理、基本方法等基本知识，培养形式化、模型化的抽象思维能力，使学生能够利用集合论与图论的概念、理论与方法识别、表达计算相关的复杂工程问题，逐步学会为计算类复杂工程问题建立数学模型；课程目标2：掌握直接证明法、反证法、数学归纳法、构造法等常用的证明方法，培养机械化、自动化的逻辑推理能力，使学生能够利用集合论与图论的概念、理论与方法并通过文献研究分析复杂工程问题，并能获得有效的结论，理解并逐步设计求解这些问题的算法基本思想；课程目标3：掌握资料查阅方法，学会对课堂所学理论知识进行扩展，培养自学能力。
第七章 图论与网络优化模型
图论与网络优化是数学建模的一个重要方面，经济管理、工业工程、通讯与网络技术等诸多领域中的问题都可以化为图论和网络模型进行研究。本章在介绍有关图的一些基本概念的基础上，主要介绍图与网络中的最短路、最小生成树、最大匹配等数学模型及其解法，最后，给出几个应用实例。
第一节 图的概念和最小生成树 一、图与网络优化的例子 上述三个实例有两个共同的特点：一是它们的目的都是从若干可能的安排或方案中寻求某种意义下的最优方案或安排，数学称这种问题为优化问题；二是它们都易于用图形的形式直观地描述和表达，数学上把这种与图相关的结构称为网络，与图和网络有关的优化问题称为网络优化。 二、图的概念 图的理论研究已经有了200多年的历史。早期的研究与数学游戏有关，哥尼斯堡七桥问题就是其中之一。 18世纪德国哥尼斯堡有一条河，河中有两个岛，两岸与两岛间共架有七座桥。那时候，哥尼斯堡市民生活很富足，市民们喜欢四处散步，于是便产生这样的问题：是否可以设计一种方案，使得人们从自己家里出发，经过每座桥恰好一次，最后回到家里。即一个人能否不重复地走遍七座桥而回到原地。这便是著名的“哥尼斯堡七桥问题”。
图7-1-1（a） 热衷于这个有趣问题的人们试图解决它，但一段时间内竟然没有人能给出答案。后来，问题传到了著名数学家欧拉那里，居然也激起了他的兴趣。他从人们寻求路线屡遭失败的教训中敏锐地领悟到，也许这样的方案根本就不存在。欧拉经过悉心的研究，1736年，年方29岁的欧拉终于解决了这个问题，并向圣彼得堡科学院递交了一份题为《哥尼斯堡的七座桥》的论文。论文不仅仅是解决了这一难题，而且引发了一门新的数学分支——图论的诞生。 欧拉解决七桥问题时采用了图的方法。既然岛与陆地无非是桥梁连接的，那么就不妨把A、B、C、D 4处抽象成4个点。并把7座桥抽象成7条边，便得到了七桥问题的模拟图。这样当然并未改变问题的实质，于是无重复地走过7座桥的问题就等价于一笔画出上述图形的问题，每条边必须且只能经过一次，即“一笔画”问题。
图7-1-1（b）
欧拉解决七桥问题时先考虑一般化的情况：如果任意给定一个河与任意多座桥，可否判断每座桥能否恰好走过一次呢？一般化的问题就要有一个一般解法，才有实际的意义。对此欧拉给出一般结论：
欧拉结论：连接奇数个桥的陆地仅有两个时，可实现要求。则从两者任一陆地出发，可以实现恰好经过每座桥一次，又回到家中。 可见，图论中所研究的图是由实际问题抽象出来的逻辑关系，这种图的画法具有一定的随意性，在保持相对位置和相互关系不变的前提下，点的位置不一定要按实际要求画，线的长度也不一定表示实际长度，而且画成直线或曲线都可以。通俗地说，这种图是一种关系示意图。 图：是由顶点集和边集组成的集合对,GVE，其中
12(){,,,}VGvvv为节点集合， 12(){,,,}mEGeee为边集合，图的节点可以表示城市、车站、计算机、人等，图的边可以是铁路、公路、输电线路、网线等，也可以是一种关系。 例1 图7-1-2（a）(b)表示6家企业间的业务往来关系，其中点a,b,c,d,e,f分别表示6家企业，两点的连线表示两家企业之间的业务联系。 子图：对于图,GVE，若有11,,VVEE则称1G是G的子图； 生成子图：如果，11,VVEE，则称1G是G的生成子图； 有向图：对于图,GVE，12{,,,},,mkijjiEeeeevvvv，反之，无向图； 赋权图：若图,GVE中的每条边,ijvv都赋予一个数ij，称为赋权图，记为,,GVEW; 链：图,GVE中节点和边交替出现的序列称为链，记为0112kkveveev。 圈：两个端点重合的链称为圈。 路：有向图,GVA中的节点和边交替出现的序列称为路，0112kkveveev称为从0v到kv的路；两个端点重合的路称为回路。 连通图：若图,GVE中任意两点iv到jv间至少有一条链，则称,GVE为连通图。 树: 连通且不含圈的无向图称为树。树有以下显而易见的性质： （1）树是连通图，但无圈； （2）树中任意两个顶点间必有且仅有一条链； （3）在树的两个不相邻的顶点间添上一条边，就得到一个圈； （4）在树中去掉任何一条边，图就不连通； （5）含有p个顶点的树有1p个边。 生成树：任意一个连通图或者是树，去掉一些边后可形成一棵树，这样的树称为连通图的生成树。生成树一般不唯一。 例2 图7-1-4（b）是7-1-4（a）的一个生成树。 三、最小生成树 在赋权图,,GVEW的所有生成树中，权数最小的生成树称为最小生成树，最小生成树的背景是线路最短、费用最小等问题。 例3 图7-1-5（a）表示5个村庄的线路图，每边旁的数字表示村庄之间道路的长度，现要求沿道路架设有线广播线，不仅使各村都能听到有线广播，而且使广播总长度最短。
显然，这个问题不光是要找出连接5个村庄的生成树，而且要找到一个广播总长最短的生成树，即最小生成树。 最小生成树用Kruskal（克鲁斯卡尔）算法（避圈法）计算，其步骤如下： （1）把图,,GVEW中的所有边按其权数大小排列，将权数最小的边取进生成树T中。 （2）从剩下的边中按（1）的方法取下一条边，若该边与前面所取的边形成回路，则舍去该边，否则，就将这条边放进T中。 （3）重复这一过程，直到边数比节点数目少1. 例4 求 图7-1-6所示的赋权图的最小生成树。
解：最小生成树示意图： 注：最小生成树不唯一，但不同的最小生成树的边权之和是唯一的。 练习：（最小生成树应用练习）：要在11个城市间建立通讯联络网，顶点----表示城市，权---城市间建立通讯线路所花费代价。问题：希望找到一个最小生成树，使它的每条边上的权值之和（即建立通讯网所需花费的总代价）最小----最小代价生成树（最小生成树）。 第二节 最短路
在生产实践、运输管理和工程建设的很多活动中，诸如物资的运输线路、各种工艺路线的安排、管道线网的铺设等等问题，都与寻找一个图的最短路密切相关，最短路问题是网络分析中的一个基本问题，它不仅可以直接应用于解决实际中的许多问题，而且经常被作为一个基本工具用于其它的优化问题。 一、两点之间的最短路 设给定赋权图,,GVEW，12(){,,,}kVGvvv，{,},ijEvv ,ijijvv，求从一个节点iv到另个节点jv的最短距离。
我们的目的就是在图,,GVEW中找到一条节点iv
到另一个节点jv的路径，并使其长度之和最短。
Dijkstra在1959年提出了一种算法，是目前公认的求最短路径的较好的算法之一。 Dijkstra算法的基本思路是动态规划的最优化原理：若1231,,,,,kkvvvvv是1v到kv的最短的路径。 112231,,,,minkkkdvvvvvvvv
则1231,,,,kvvvv是1v到1kv之间距离最短的路径。 11122321,,,,minkkkdvvvvvvvv
事实上，如果这个结论不成立，便可以找到从1v到1kv的更短路径，将原来的路径换掉以后就可以得到更短的路径，从而产生矛盾。 Dijkstra算法其实是一种标号法，适用于所有权数大于零的情形。它的基本思想是从起点1v出发，逐步向外探寻最短路，每一步都在寻找1v到这一个点的最小距离。执行过程中，给每一个顶点jv标号，使用临时标号和永久性标号，反复修改临时标号，并且把某一个具有临时标号的点改变为永久标号的点，从而使G中具有永久标号的顶点数多一个。这样至多经过1k步，就可以求出从1v到kv的最短的路径。 Dijkstra算法的具体步骤为： （1）给始点1v标上永久标号1()0pv，给其余各点标上临时标号()jtv，2,3,4,,jn，其中，jv与1v直接相连，1(),jjtvvv；若jv与1v不直接相连，则()jtv。这里()jtv表
示从jv一步到1v的距离。令 123,,,,cnSvSvvv
（complementary set）
（2）寻找1v到cs距离最短的点1jv，赋予永久标号 1()()mincjjjvSpvtv，
令 11,jSvv，\cSVS 修改cS中各临时标号，对cjvS 11()min(),(),jjjjjtvtvpvvv 新的()jtv是cjvS一步直接到1v，或者经过1jv两步到达1v的最短距离。 （3）重复（2），直到kv进入S停止，找到最短路径和距离。
例5 图7-2-1所示是某地区交通运输路线的示意图。用Dijkstra算法分别求从0v到3v，0v到4v，0v到7v的最短路。
解：利用Dijkstra算法进行计算。第一次临时标号的值如表7-2-1的第一行所示。0,Sv 1237,,,,cSvvvv
在这些临时标号中，1()tv最小，给1v赋予
永久标号1()1pv。令 01237,,,,,,cSvvSvvv
重新计算cS种各节点的临时标号
