回归方程数据处理
- 格式:doc
- 大小:184.00 KB
- 文档页数:16

根据stata回归结果写回归方程在实证研究中,回归方程是其中最为常见的模型之一,它用于解释因变量与自变量之间的关系。
而Stata是实证研究中十分常用的数据处理工具,它可以进行数据处理、回归分析等操作,为我们进行回归模型的建立提供了方便。
那么,在得到回归结果后,我们该如何根据Stata回归结果来写回归方程呢?第一步,看回归方程的中标准误(Std. Err),根据其值判断是否太大或太小。
若标准误过大,则会影响模型的可靠性,需要进行修正;若过小,则可能会忽略实际上有显著差异的指标,因此需要重新设定变量。
常规情况下,标准误的取值应该在0.8~1.2之间。
第二步,查看回归方程的截距项(Constant)和变量项(Coefficient),确认它们的符号是否正确,根据回归方程的设计,指标是否应该呈现负相关或正相关等。
确认符号的正确性,有助于保证回归方程的可靠性和精度。
第三步,通过回归方程中的t值(t-Value)和p值(P>|t|),来判断变量项(Coefficient)的显著性。
t值的值越大,表明显著性越高,p值的取值应该小于0.05,才能够认为是显著的。
若进行了多项回归模型,则应当注意变量之间的共线性。
第四步,根据上述内容,可以得到回归方程的基本设计。
例如:y = β0 + β1*x1 + β2*x2 + β3*x3 + ε,其中y表示因变量,x1、x2、x3表示自变量,β0为截距项,β1、β2、β3为变量项。
ε表示误差项,在回归方程中应当对其进行控制。
需要注意的是,回归方程的设计必须考虑现实情况和实证研究的实际需要。
第五步,对于回归方程的特殊情况,还需要根据具体情况进行调整。
例如,如果需要调整数据的标准化或者对某个变量进行对数化等处理,需要经过严格的推导和计算,保证结果的正确性和可靠性。
以上便是根据Stata回归结果写回归方程的常见步骤。
在实际研究中,还需要根据数据的特点和实际需求进行具体调整。

高中数学:线性回归方程线性回归是利用数理统计中的回归分析来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法,是变量间的相关关系中最重要的一部分,主要考查概率与统计知识,考察学生的阅读能力、数据处理能力及运算能力,题目难度中等,应用广泛.一线性回归方程公式二规律总结(3)回归分析是处理变量相关关系的一种数学方法.主要用来解决:①确定特定量之间是否有相关关系,如果有就找出它们之间贴近的数学表达式;②根据一组观察值,预测变量的取值及判断变量取值的变化趋势;③求线性回归方程.线性回归方程的求法1四线性回归方程的应用例2例3例4例5例6推导2个样本点的线性回归方程例7 设有两个点A(x1,y1),B(x2,y2),用最小二乘法推导其线性回归方程并进行分析。
解:由最小二乘法,设,则样本点到该直线的“距离之和”为从而可知:当时,b有最小值。
将代入“距离和”计算式中,视其为关于b的二次函数,再用配方法,可知:此时直线方程为:设AB中点为M,则上述线性回归方程为可以看出,由两个样本点推导的线性回归方程即为过这两点的直线方程。
这和我们的认识是一致的:对两个样本点,最好的拟合直线就是过这两点的直线。
上面我们是用最小二乘法对有两个样本点的线性回归直线方程进行了直接推导,主要是分别对关于a和b的二次函数进行研究,由配方法求其最值及所需条件。
实际上,由线性回归系数计算公式:可得到线性回归方程为设AB中点为M,则上述线性回归方程为。
求回归直线方程例8 在硝酸钠的溶解试验中,测得在不同温度下,溶解于100份水中的硝酸钠份数的数据如下0 4 10 15 21 29 36 51 6866.7 71.0 76.3 80.6 85.7 92.9 99.4 113.6 125.1 描出散点图并求其回归直线方程.解:建立坐标系,绘出散点图如下:由散点图可以看出:两组数据呈线性相关性。
设回归直线方程为:由回归系数计算公式:可求得:b=0.87,a=67.52,从而回归直线方程为:y=0.87x+67.52。

实验数据处理的3种方法实验数据处理是全世界科学家最普遍的研究方法之一,也是非常重要的研究工具。
它可以帮助科学家们从实验中提取有用的信息,并产生科学研究成果。
实验数据处理可以分为几种方法,比如回归分析、相关分析和分类分析,这三种方法都可以帮助科学家深入理解实验数据,从而给出有用的结论。
本文将讨论这三种常用的实验数据处理方法,并分析其各自的特点和优势。
二、回归分析回归分析是最常用的实验数据处理方法之一,它可以帮助科学家从实验数据中了解不同因素的关系,从而得出有用的结论。
它还可以帮助研究者分析观测值是否符合某种理论模型,以及任何变异是否具有统计学意义。
在回归分析的过程中,数据会用回归方程拟合,从而准确预测研究结果。
三、相关分析相关分析是一种类似回归分析的实验数据处理方法,它旨在找出两个变量之间的相关性,并通过计算两个变量之间的相关系数,来检测变量之间的相关关系。
相关分析可以帮助科学家们从实验数据中发现不同变量之间的关系,这能够帮助研究者进行更有效的实验。
四、分类分析分类分析是另一种非常有用的实验数据处理方法,它旨在将一组观测值划分为不同的类别,从而找出不同变量之间的关系。
它可以将实验结果根据统计学原则进行排序,并可以确定组成类别的变量。
在分类分析的过程中,还可以进行数据预测,以改善实验结果的准确性。
五、结论本文讨论了实验数据处理的三种常用方法,即回归分析、相关分析和分类分析。
它们都可以帮助科学家们更有效地发现实验数据之间的关系,从而进行有价值的研究。
因此,实验数据处理方法的重要性不言而喻,它能够帮助研究者从实验中发现有价值的信息,从而得出有价值的研究结果。

回归方程计算
回归方程又称为拟合方程,是对一组数据进行拟合得到的模型。
在数据分析中,回归方程可以用于预测和估算某种情况下的变量值。
一般来说,回归方程可以分为线性回归方程和非线性回归方程两种类型。
在线性回归方程中,目标是寻找一条直线,将所有的数据点尽可能的拟合,可以表述为:
y=a+bX
其中,y表示因变量或响应变量,x表示自变量或预测变量,a和b表示回归方程的系数。
a被称为截距,表示当自变量为0时,因变量的值。
b表示斜率,表示当自变量增加1单位,因变量的变化情况。
非线性回归方程表示为:
y=f(x,a,b,c,...)
其中f表示非线性方程的形式,a、b、c等表示方程中的其他参数。
在非线性回归中,需要确定方程中各个参数的值,通常采用最小二乘法来求解,将实际的数据值与预测值之间的误差平方和最小化。
总之,回归方程是可以用于拟合一组数据的模型,通过它可以预测和估算某种情况下的变量值。
线性回归方程和非线性回归方程是数据分析中常见的两种类型,求解时通常采用最小二乘法等方法。

线性回归方程公式线性回归是一种常见的统计学方法,用于建立一个预测目标变量与一个或多个自变量之间的线性关系模型。
它是一种广泛应用的回归方法,适用于各种领域,如经济学、金融学、社会学、生物学和工程学等。
线性回归模型可以表示为以下形式:Y = b0 + b1*X1 + b2*X2+ ... + bp*Xp,其中Y是目标变量,X1、X2、...、Xp是自变量,b0、b1、b2、...、bp是回归系数。
这个方程描述了目标变量Y与自变量X之间的线性关系,通过调整回归系数的值可以拟合数据并预测未知数据的值。
线性回归模型的目标是找到最佳拟合直线,使得预测值与实际观测值之间的误差最小化。
常用的误差衡量指标是残差平方和(RSS),也可以使用其他指标如平均绝对误差(MAE)和均方根误差(RMSE)。
线性回归模型的建立过程包括两个主要步骤:参数估计和模型评估。
参数估计是通过最小化误差来确定回归系数的值。
最常用的方法是最小二乘法,通过最小化残差平方和来估计回归系数。
模型评估是用来评估模型的拟合优度和预测能力,常用的指标包括决定系数(R^2)、调整决定系数(Adjusted R^2)和F统计量。
线性回归模型的假设包括线性关系、误差项的独立性、误差项的方差恒定以及误差项服从正态分布。
如果这些假设不成立,可能会导致模型的拟合效果不佳或不可靠的预测结果。
对于线性回归模型的建立,首先需要收集相关的数据,然后进行数据的处理和变量选择。
数据处理包括缺失值处理、异常值处理和变量转换等。
变量选择是通过统计方法或经验判断来选择对目标变量有影响的自变量。
常见的变量选择方法包括逐步回归、岭回归和lasso回归等。
在建立模型之后,需要对模型进行评估和验证。
评估模型的拟合优度是通过决定系数和F统计量来实现的,较高的决定系数和较小的F统计量表明模型的拟合效果较好。
验证模型的预测能力可以使用交叉验证等方法。
线性回归模型还有一些扩展形式,如多项式回归、加权回归和广义线性回归等。


利用回归方程进行预测的步骤利用回归方程进行预测涉及以下步骤:
1. 数据收集,首先需要收集相关的数据,包括自变量(预测因子)和因变量(要预测的变量)的观测数值。
这些数据可以通过实验、调查或者其他方式收集而来。
2. 拟合回归模型,接下来,需要选择合适的回归模型来拟合数据。
常见的回归模型包括线性回归、多项式回归、岭回归等。
通过拟合回归模型,我们可以得到回归方程,该方程描述了自变量和因变量之间的关系。
3. 检验模型,在使用回归方程进行预测之前,需要对拟合的回归模型进行检验,以确保模型的准确性和可靠性。
常见的检验方法包括检查残差的分布、观察预测值与实际值的差异等。
4. 进行预测,一旦通过检验确认了回归模型的可靠性,就可以利用回归方程进行预测。
预测的过程就是将新的自变量值代入回归方程中,从而得到相应的因变量的预测值。
5. 评估预测结果,最后,需要对预测结果进行评估,以了解预测的准确性和可信度。
通常可以使用一些指标如均方误差(MSE)、决定系数(R-squared)等来评估预测结果的好坏。
总的来说,利用回归方程进行预测的步骤包括数据收集、拟合回归模型、模型检验、预测和结果评估。
这些步骤有助于确保预测的准确性和可靠性。

经验回归方程回归分析是由于其简单易操作的特点,在日常学习及工作中,常常被广泛使用。
这种分析方法能够研究两个或多个自变量之间的关系,回归分析依赖于统计学上处理数据的方法,最常见的回归分析应用是线性回归,用于描述一类事物间关系,并建立它们之间线性模型。
线性回归分析可以用来研究某一变量和某些条件变量联系方面的数据,例如研究薪资水平是否随着经验增加而增加。
线性回归的目的是找到变量之间相互依赖的关系,这个关系可以是正相关或者负相关。
线性回归通过拟合数据,可以得到自变量对因变量的线性关系,并对结果进行检验和分析。
经验回归方程是根据已知数据计算出来的,它是独立变量和预测变量之间的统计关系,概括的说就是“任意的独立变量的变化,将会如何改变预测变量的值”。
经验回归方程是从一组已知的数据中建立的,他们形成了函数的表达式,这个表达式就叫做经验回归方程式。
经验回归方程式包括:y=a+bx,其中a,b为未知数量,x作为独立变量,y是因变量,a是函数值在x=0时刻的值,b是独立变量x轴步距。
一般经验回归方程求解也是求a,b的值,使结果尽可能接近实际情况。
经验回归方程主要用来寻找自变量和因变量之间的关系,研究自变量和因变量之间的变化。
一般来说,两个变量之间成线性关系,因此其实经验回归方程的解决方案的基本原理也是线性回归,即通过最小二乘法拟合直线,使得数据点到直线的最小距离最小,并求得最小距离的参数n。
一般过程:首先,根据实际情况,建立模型。
模型形式为y= ax+b(1),其中a,b为未知数量,x为自变量,y为因变量,需要通过求解未知数a,b 来确定最终结果。
假如已有m个x与y的观测点,把上述公式代入拟合出M 个方程,接下来便可利用最小二乘法。

回归方程公式详细步骤例题嘿,朋友们!今天咱就来讲讲回归方程公式那些事儿。
你可别小瞧它,这玩意儿在好多地方都大有用处呢!咱先说说回归方程公式是啥。
简单来说,它就是能帮我们找到两个变量之间关系的一个工具。
就好像是在一堆杂乱的数据中找到那根能把它们串起来的线。
那怎么用这个公式呢?来,咱一步一步看。
首先得有一堆数据吧,就像做菜得有食材一样。
然后呢,要计算一些关键的数值,比如均值啦,方差啦。
这就好比是给食材进行预处理。
比如说,有这么一组数据,是关于同学们的身高和体重的。
咱要通过这些数据找出身高和体重之间的关系。
这可不是随便猜猜就能行的哦!计算那些数值的时候可得细心点儿,一个小错误可能就会让结果差之千里。
这就跟走路一样,一步走歪了,后面可能就跑偏啦!等算出这些关键数值后,就可以把它们代入回归方程公式里啦。
这时候就像是把各种调料放进锅里,要开始炒出美味的菜肴啦!哎呀,你想想,通过这么一番操作,就能得出一个能描述身高和体重关系的式子,多神奇呀!以后再看到一个同学的身高,咱就能大概猜到他的体重啦,是不是很有意思?再举个例子,比如研究汽车速度和油耗的关系。
咱通过收集大量的数据,然后用回归方程公式一捣鼓,嘿,就能知道速度怎么变化会影响油耗啦!这对司机朋友们多有用啊,可以根据这个来调整开车的方式,省油省钱呢!总之,回归方程公式就像是一把钥匙,能打开数据背后隐藏的秘密。
它能让我们更清楚地了解事物之间的联系,帮助我们做出更准确的判断和决策。
所以啊,朋友们,可别小看了这小小的回归方程公式。
它虽然看起来有点复杂,但只要咱认真去学,去理解,就一定能掌握它。
到时候,咱就能在数据的海洋里畅游啦,哈哈!怎么样,是不是对回归方程公式有了更清楚的认识啦?赶紧去试试吧!。
回归方程是用于描述两个变量之间关系的一种数学模型,而横截面数据则是一种用于描述不同个体之间特征差异的数据。
当将回归方程应用于横截面数据时,我们可以分析不同个体在特定特征下的表现,并探究这些特征与所观察结果之间的关系。
假设我们有一个横截面数据集,其中包含不同个体在不同条件下的观察结果。
例如,我们可能有一个数据集,其中包含不同学生的考试成绩和他们的年龄、性别、家庭背景等特征。
我们想要探究这些特征与考试成绩之间的关系,并使用回归方程来拟合这些关系。
通过使用回归方程,我们可以建立一个数学模型来描述这些特征与考试成绩之间的关系。
这个模型通常包含一个或多个自变量(特征),以及一个因变量(结果)。
通过拟合这个模型,我们可以预测在没有观察到特定特征的情况下,结果的值。
具体来说,如果我们将年龄作为自变量,考试成绩作为因变量,并使用线性回归方程进行拟合,那么回归方程可能会呈现出如下形式:
考试成绩= a + b*年龄+ e
其中a是截距,b是斜率,e是误差项。
这个方程表示了考试成绩与年龄之间的线性关系。
通过拟合这个方程,我们可以得到b的值,即年龄每增加一个单位,考试成绩增加或减少的量。
然而,需要注意的是,横截面数据可能受到许多其他因素的影响,而这些因素可能对结果产生重要影响。
因此,回归方程的结果只能作为一个估计值,而不是绝对的预测。
此外,回归方程也可能会受到多重共线性的影响,这可能会影响模型的解释能力。
总之,将回归方程应用于横截面数据可以帮助我们探究不同个体在特定特征下的表现,并了解这些特征与结果之间的关系。
然而,回归方程的结果需要谨慎解释,并可能需要结合其他信息进行评估。
回归方程公式回归方程是一种特殊的统计关系,它允许你使用数学表达式来预测变量之间的关系。
使用一个或多个自变量(例如年龄,收入,教育,种族等)来预测另一个变量,例如财富或健康状况。
归方程使用变量之间的数据来确定回归系数以及预测结果。
回归方程的公式是什么?回归方程的公式通常形式为:Y=a+bX,其中a是回归系数,b是X变量的系数,X是被预测变量,Y是预测结果。
例如,假设您正在预测财富与年龄之间的关系,则回归方程可能是Y = a + bX,其中Y 表示财富,X表示年龄,a和b表示回归系数。
求解回归方程的方法回归方程的求解分为两个主要步骤。
先,使用X变量的数据集(例如,年龄)拟合一个数学拟合曲线,称为回归曲线。
外,需要使用回归曲线对Y变量(例如,财富)求和平方差,以得出回归系数a和b。
回归曲线可以分为线性回归曲线和非线性回归曲线。
性回归曲线是具有确定性系数的线性关系,它可以明确地预测变量之间的关系。
线性回归曲线是具有不确定性系数的非线性关系,它不能明确地预测变量之间的关系。
为了求解回归方程,需要使用数据拟合技术,例如最小二乘法,线性回归和非线性回归。
小二乘法可以用来拟合线性模型,同时确定模型中每个变量的权重。
性回归可以用来拟合线性模型,而非线性回归可以用来拟合非线性模型。
由于每种拟合技术的方法不同,因此可能需要使用不同的算法来求解每种类型的回归方程。
例如,使用最小二乘法拟合线性回归模型时,可以使用最小二乘法的梯度下降算法来求解回归方程;而使用非线性回归模型时,可以使用多项式回归,神经网络或其他类似的算法来求解该方程。
回归方程的应用回归方程是统计学中常用的工具,它可以用来研究变量之间的关系,特别是当变量之间存在某种可能的统计关系时,回归方程可以帮助我们对变量之间的关系进行更详细的分析。
例如,可以使用回归方程来研究收入与教育程度之间的关系,或研究冠状动脉病变(CVD)和高血压之间的关系等。
此外,回归方程可能还可以用于模拟和预测变量之间的关系,例如通过模拟股票价格的变化,预测经济增长,或者预测政治事件对市场的影响等。
stata估计回归方程Stata是一种广泛使用的统计软件,可用于估计回归方程。
回归分析是一种数据分析技术,可用于确定两个或多个变量之间的关系。
回归模型旨在解释响应变量(也称为因变量)和自变量(也称为解释变量)之间的关系。
在Stata中,可以使用命令reg命令来估计简单线性回归模型和多元线性回归模型。
在本文中,我们将讨论如何使用Stata估计回归方程。
一、简单线性回归方程简单线性回归方程是一种使用单个自变量解释响应变量的回归模型。
下面是一个示例,其中Y是响应变量,X是解释变量。
Y = β0 + β1X + ε其中,Y:响应变量X: 解释变量β0和β1:回归系数ε:误差项在Stata中,可以使用以下代码估计简单线性回归方程:reg y x这将生成以下输出:------------------------------------------------------------------------------y | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+----------------------------------------------------------------x | .4534248 .0153275 29.580.000 .4223481 .4845014_cons | 3.117376 .3083924 10.10 0.000 2.493708 3.741044------------------------------------------------------------------------------在这个输出中,.453424是解释变量X的回归系数,表明在解释变量每增加1个单位的情况下,响应变量Y预计增加0.453424个单位。
_cons给出截距,表示在解释变量为零时的响应变量。
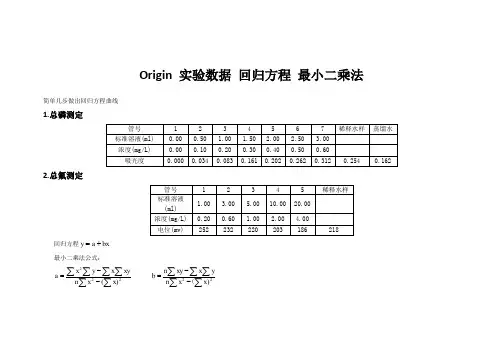
回归方程数据处理 实验
姓名: 沟超辉 学号:101001106 一、实验目的 回归分析是数理统计中的一个重要分支,在工农业生产和科学研究中有着广泛的应用。通过本次实验要求掌握一元线性回归和一元非线性回归。
二、实验原理 回归分析是处理变量之间相关关系的一种数理统计方法。即用数学的方法,对大量的观测数据进行处理,从而得出比较符合事物内部规律的数学表达式。利用最小二乘估计,得到一元线性回归的回归方程为 ^ y =b0+bx 式中b0,b为回归方程的回归系数,y代表抗剪强度。 求出∑xi,∑yi,∑xi2,∑y i 2,∑xiyi,∑xi∑yi 于是x=1/n∑xi, y=1/n∑yi
lxx =∑xi2 – (∑xi)2 /n
lxy =∑xiyi –(∑xi∑yi)/n
b= lxy / lxx
b0=y-bx
三、实验内容及程序结果(一) (1)材料的抗剪强度与材料承受的正应力有关。对某种材料试验的数据如下 正应力x/pa 26.8 25.4 23.6 27.7
抗剪强度y/pa 26.5 27.3 27.1 23.6 23.9 24.7 28.1 26.9 27.4 22.6 25.6 25.9 26.3 22.5 21.7 21.4 25.8 24.9
假设正应力是精确的,求抗剪强度与正应力的线性回归方程
当正应力为24.5pa时,抗剪强度的估计值? 程序及运行结果: for i=0
X=[26.8 25.4 23.6 27.7 23.9 24.7 28.1 26.9 27.4 22.6 25.6]; Y=[26.5 27.3 27.1 23.6 25.9 26.3 22.5 21.7 21.4 25.8 24.9]; N=length(X); lxx=sum(X.*X)-sum(X).^2./N; lxy=sum(X.*Y)-sum(X).*sum(Y)/N; b=lxy./lxx; b0=mean(Y)-b.*mean(X); x=(21:0.01:31); y=b.*x+b0; plot(X,Y,'b*',x,y,'r-') end 实验结果: lxx= 43.0467 lxy= -29.5333 b= -0.6861 b0=42.5818 材料的抗剪强度与材料承受的正应力关系为: y=42.5818-0.6861x 实验内容及程序结果(二) (2)下表给出在不同质量下弹簧长度的观测值(设质量的观测值无误差): 质量/g 5 10 15 20 25 30 长度/cm 7.25 8.12 8.95 9.90 10.9 11.8
做散点图,观察质量与长度之间是否呈线性关系;求弹簧的刚性系
数和自由状态下的长度。 程序及运行结果: for i=0 X=[5 10 15 20 25 30]; Y=[7.25 8.12 8.95 9.90 10.9 11.8]; N=length(X); lxy=sum(X.*Y)-sum(X).*sum(Y)./N; lxx=sum(X.*X)-((sum(X)).^2)./N; b=lxy./lxx; b0=mean(Y)-b.*mean(X); x=(5:0.01:30); y=b.*x+b0; plot(X,Y,'b*',x,y,'r-') end 以刚性系数k=b=0.1831,自由长度x0=b0=6.2827 四、实验小结 一元回归是处理两个变量之间的关系,即两个变量x和y之间若存在一定的关系,则可通过实验的方法,分析所得数据,找出两者之间关系的经验公式。假如两个变量之间的关系是线性的就称为一元线性回归,这就是工程上和科研中场遇到的直线拟合问题。 Java实现k-means
1. 数据来源描述 本数据集中一共包含600组数据,每一组数据都有60个分量,也就是数据是60维的。数据一共可以分成6个聚类,分别是: 1-100 Normal (正常) 101-200 Cyclic (循环) 201-300 Increasing trend (增加趋势) 301-400 Decreasing trend (减少趋势) 401-500 Upward shift (上升变化) 501-600 Downward shift (下降变化)
2. 数据预处理 由于本数据集的数据维数较多,所以本实验采用了结构体来存储60维的数据,并使用指针来进行对数据的操作,以提高速度。在数据预处理过程中,首先将数据从data文件中读出,后依次存入结构体数组dataset[600]中。 3. k-means聚类算法 k-means 算法接受参数 k ;然后将事先输入的n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。 K-means算法是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一。K-means算法的基本思想是:以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。 (1)算法思路: 首先从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然 后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到标准测度函数开始收敛为止。一般都采用均方差作为标准测度函数. k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。 该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。 (2)算法步骤: step.1---初始化距离K个聚类的质心(随机产生) step.2---计算所有数据样本与每个质心的欧氏距离,将数据样本加入与其欧氏距离最短的那个质心的簇中(记录其数据样本的编号) step.3---计算现在每个簇的质心,进行更新,判断新质心是否与原质心相等,若相等,则迭代结束,若不相等,回到step2继续迭代。 4. 数据挖掘实现的源代码 //111060850.cpp KMeans聚类算法 //
#include "stdafx.h" #include #include #include #include #include #include using namespace std; const int N=36000; //数据个数 const int D=60; //数据维度 struct DataSet{ //用来存储数据的结构体 double arg[D]; }; const int K=6; //集合个数 int *CenterIndex; //质心索引集合 //struct DataSet *Center; //质心集合 //struct DataSet *CenterCopy[]; DataSet Center[K]; //保存现在的质心 DataSet CenterCopy[K]; //保存上一次迭代中的质心 //double *DataSet; int Cluster[6][N/D]; //保存每个簇包含的数据的索引值 int *Top; ifstream fin; char ch; string fDataSet[N/D][D]; /*算法描述: kmeans聚类算法采用的是给定类的个数K,将N个元素(对象)分配到K个类中去 使得类内对象之间的相似性最大,而类之间的相似性最小 */ //数据存储在结构体中
//函数声明部分 void InitData(struct DataSet* dataset); //对数据集进行初始化,从文件中将其读取出后转化为double型依次存入结构体中 void InitCenter(struct DataSet* dataset); //初始化质心 void CreateRandomArray(int n,int k,int *centerIndex); //随机产生一组索引值,用于初始化质心 void CopyCenter(struct DataSet* dataset); //复制保存上一次迭代的质心 void UpdateCluster(struct DataSet* dataset); //更新簇 void UpdateCenter(struct DataSet* dataset); //更新质心 int GetIndex(struct DataSet* dataset,struct DataSet* centerIndex); //本程序的核心,计算每一数据元素属于哪一个聚类,并返回其索引值 void AddtoCluster(int index,int value); //根据索引值将数据元素的索引加入到簇之中 void print(struct DataSet* dataset);